Adaptive Decentralized Cooperative Localization for Firefighters Based on UWB and Autonomous Navigation
Abstract
1. Introduction
- (1)
- The DCL for firefighter localization was proposed. This method differed from the CCL structure, and it is also distinct from the other distributed structures proposed by other researchers. In our proposed DCL structure, we derived explicit expressions for the inter-member collaboration instead of using approximations, which led to higher localization accuracy.
- (2)
- To address the issue of the reduced localization accuracy caused by NLOS errors in UWB systems, we proposed using an adaptive extended Kalman filter algorithm to estimate measurement noise. In contrast to fixed noise parameter settings, which reduce the adverse effects of NLOS errors, the adaptive filter showed greater adaptability to the time-varying noise caused by environmental changes.
2. System Model
2.1. Inertial Navigation System Model
2.2. Non-Line-of-Sight Identification of Ultra-Wideband
2.3. Decentralized Cooperative Localization Model
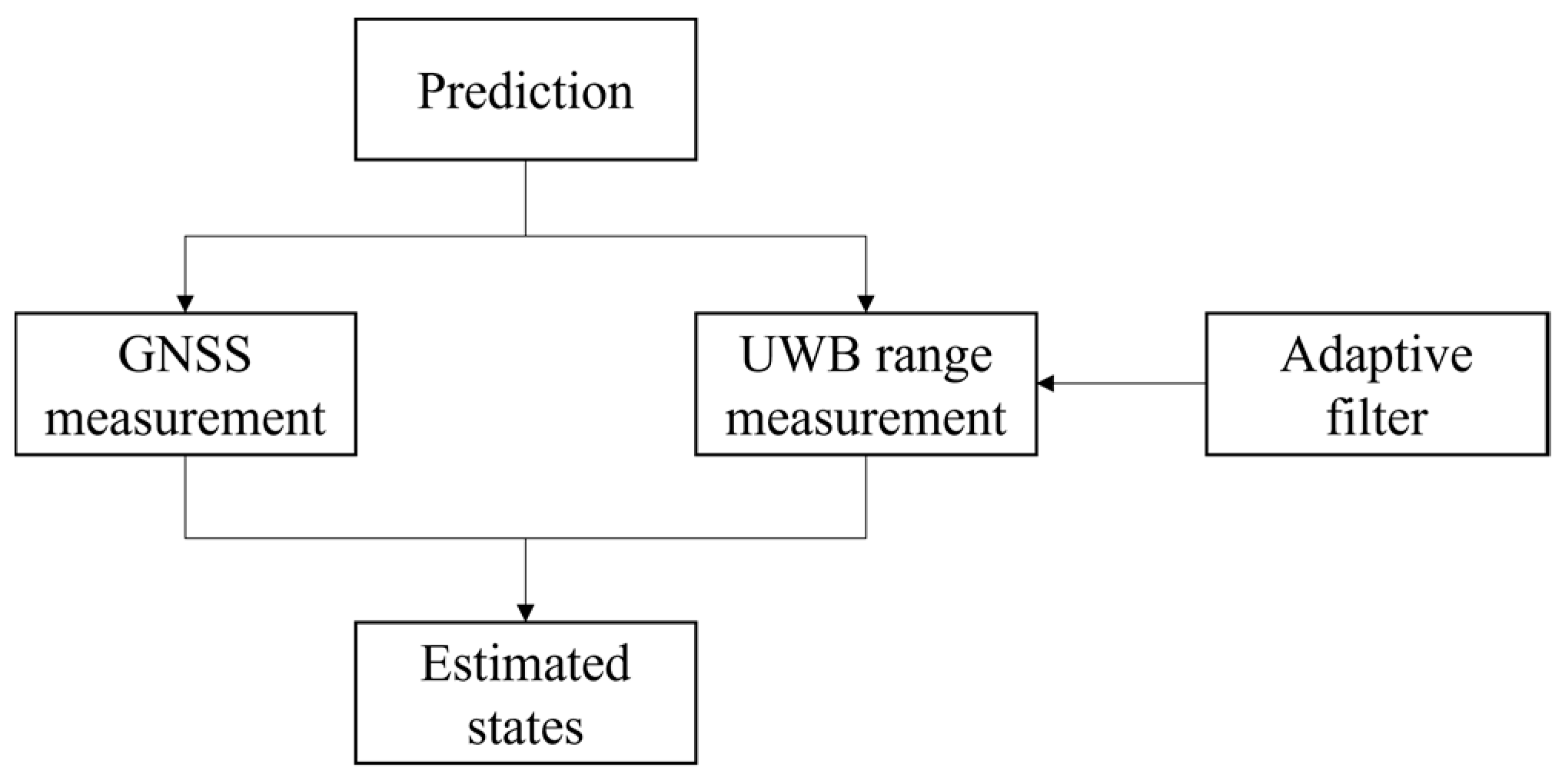
2.4. Adaptive Extended Kalman Filter Algorithm
3. Experiments and Analysis
3.1. Experimental Setup
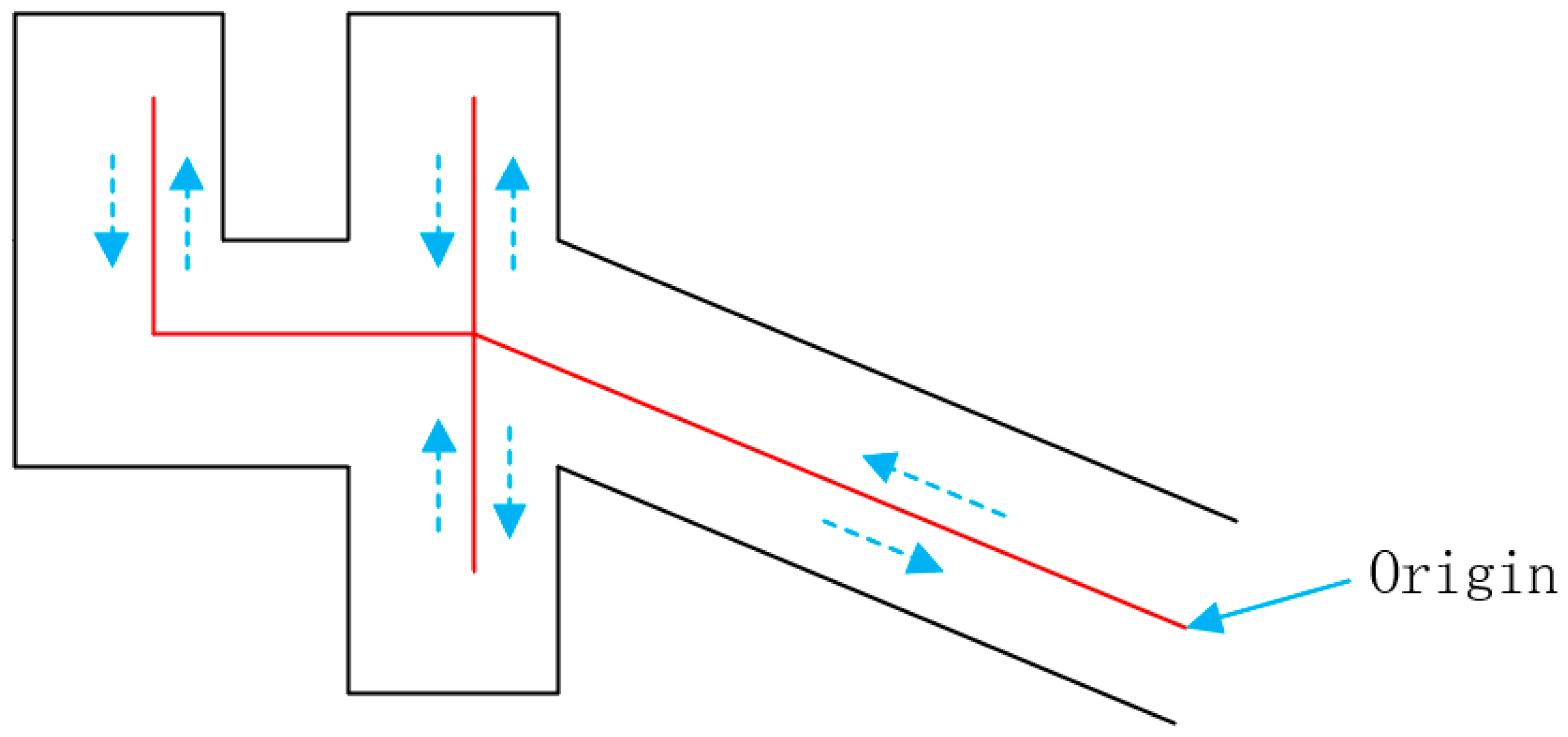
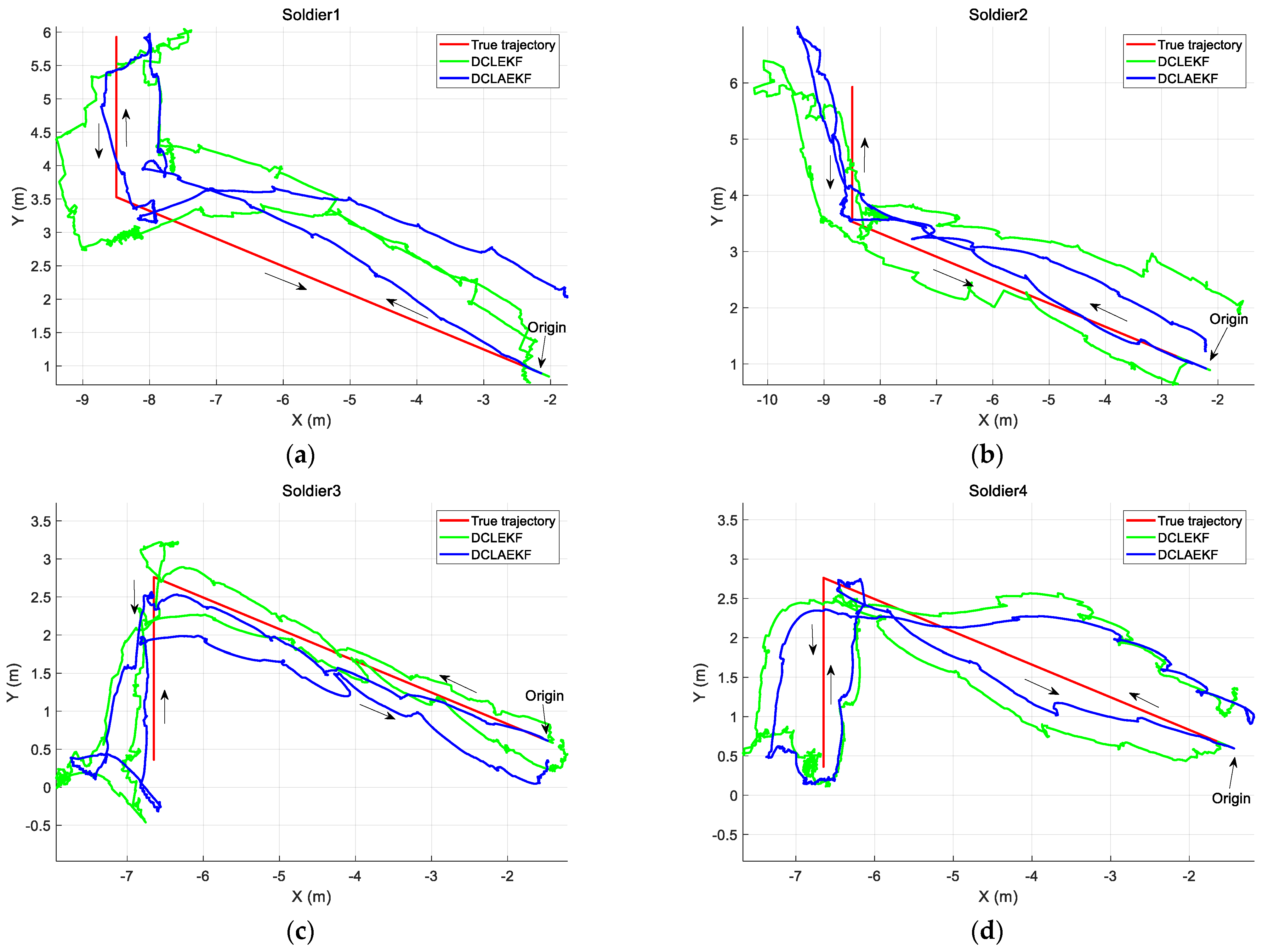
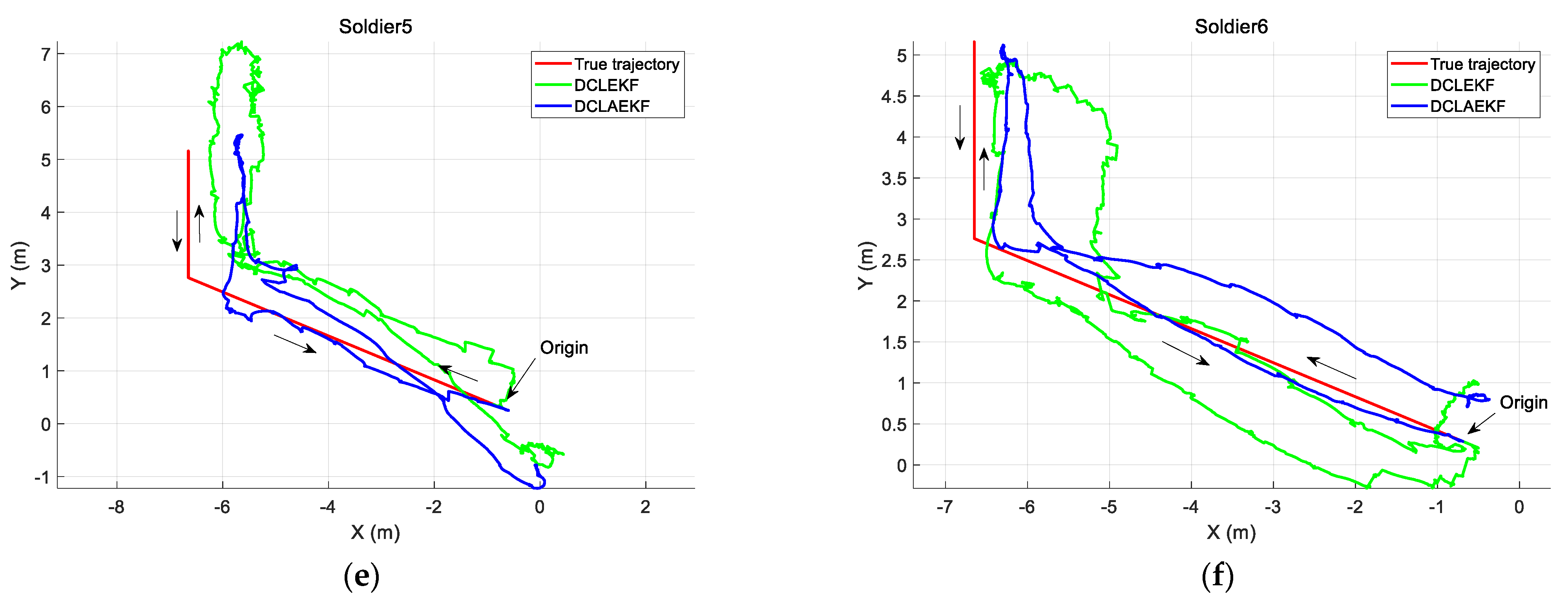
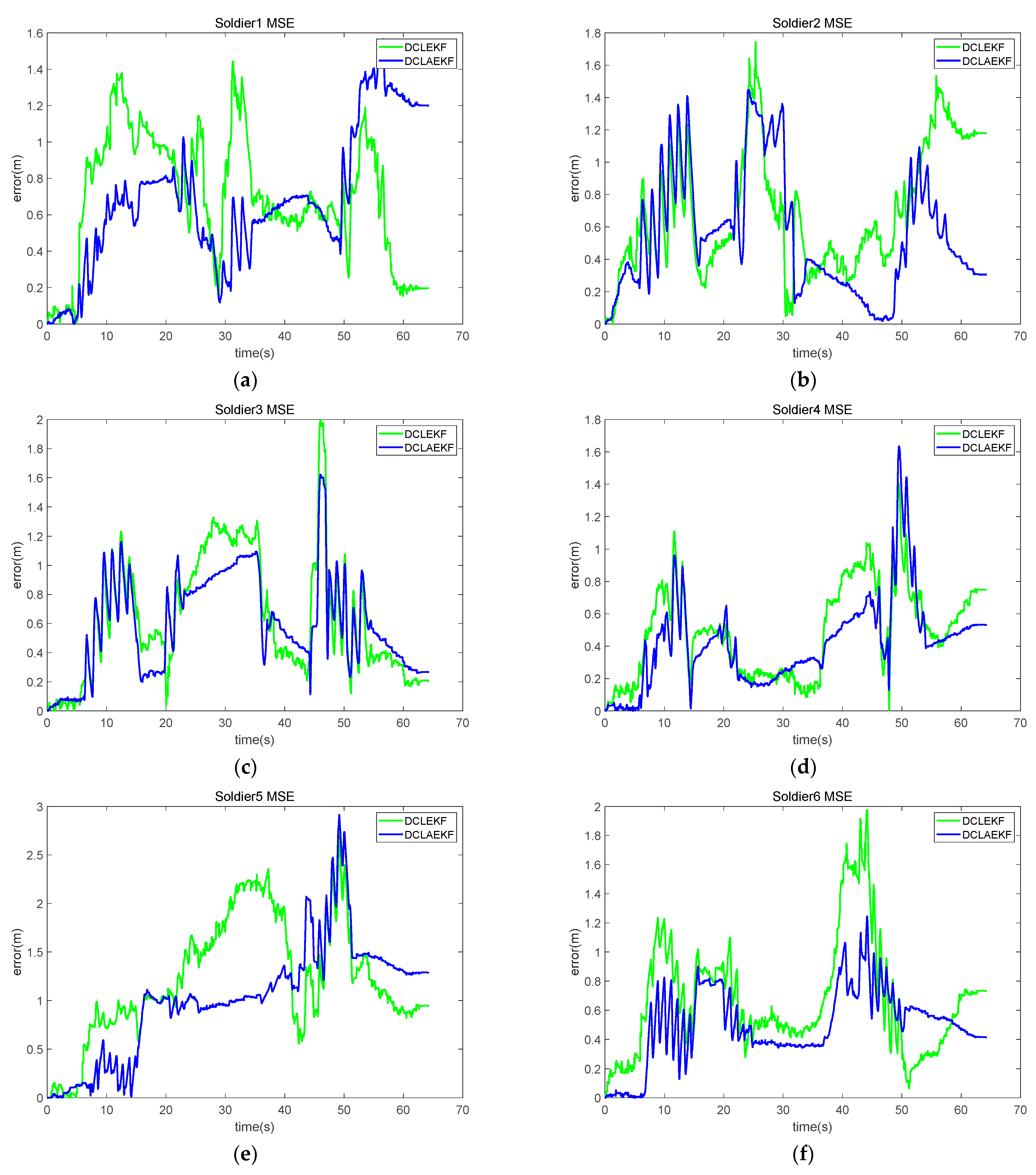
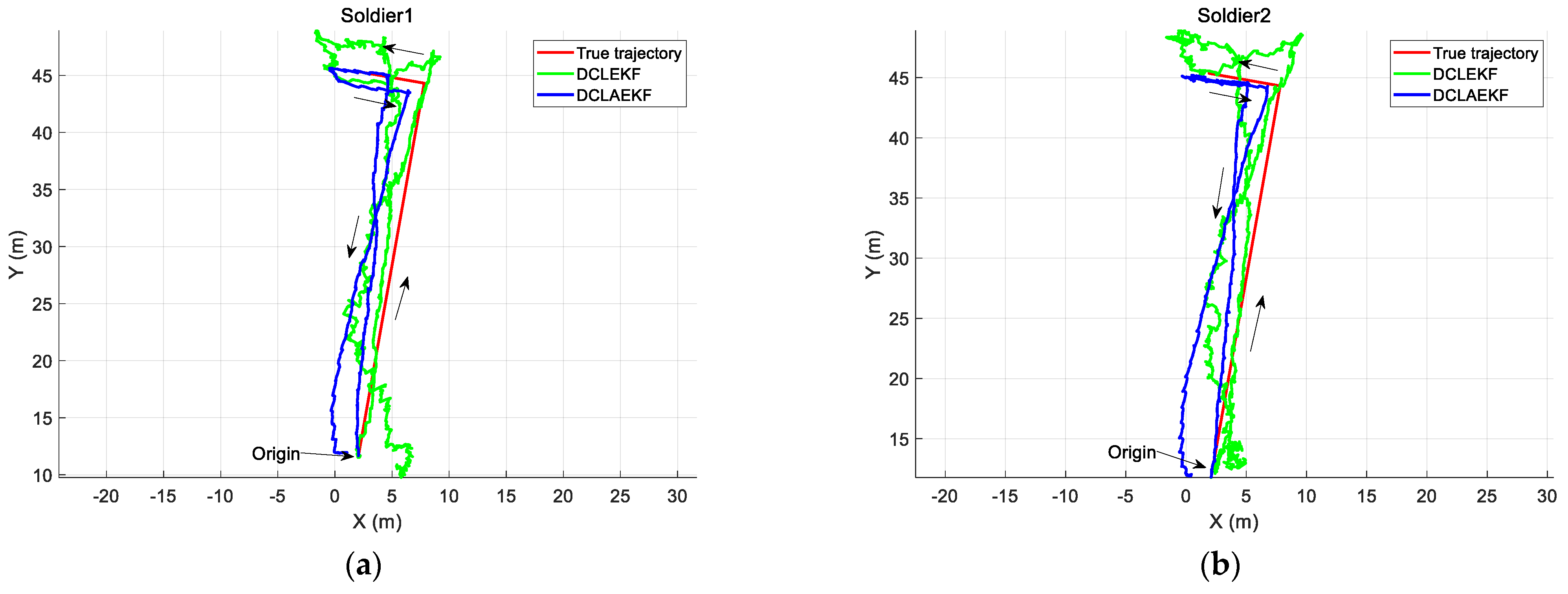
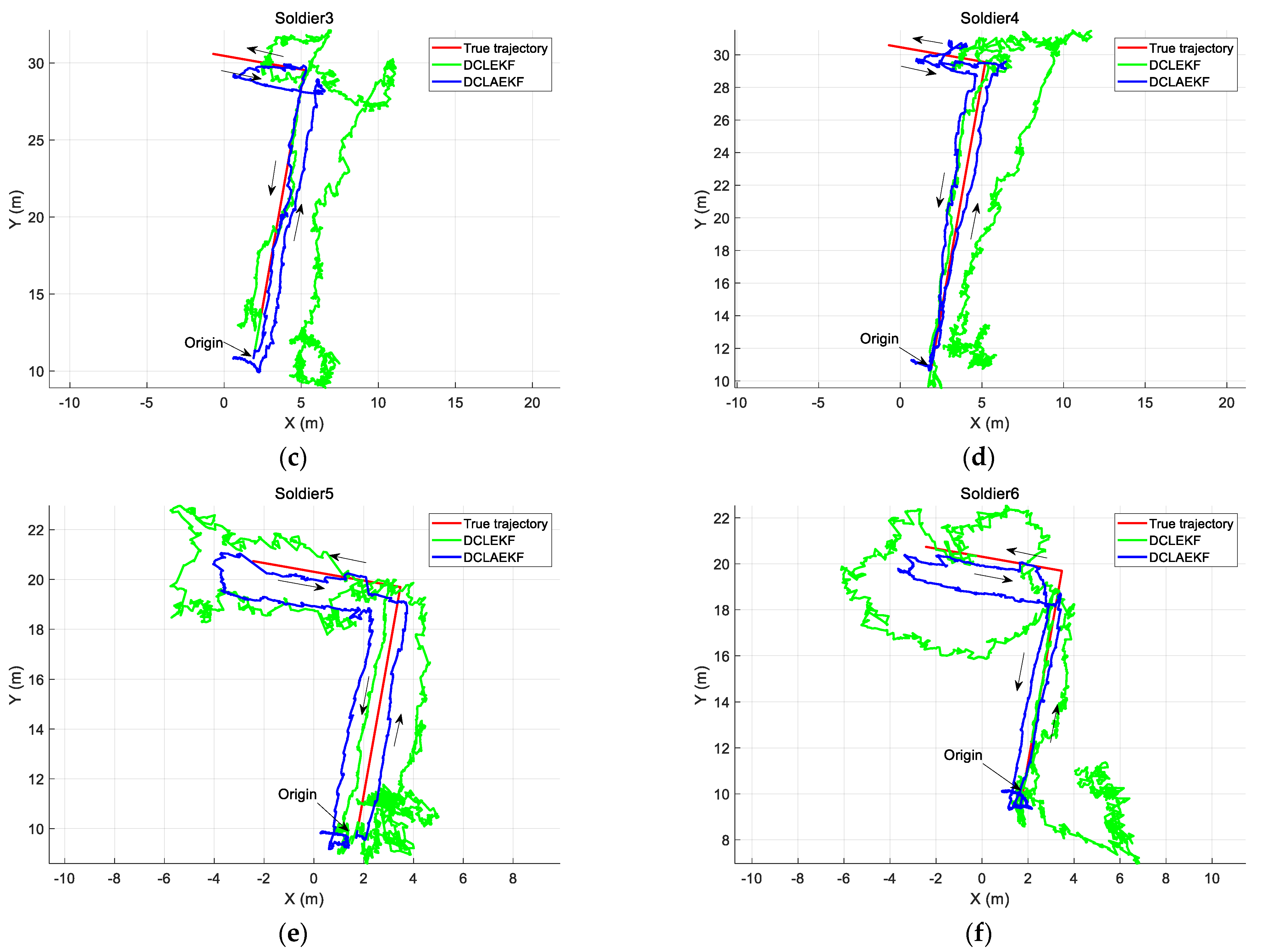
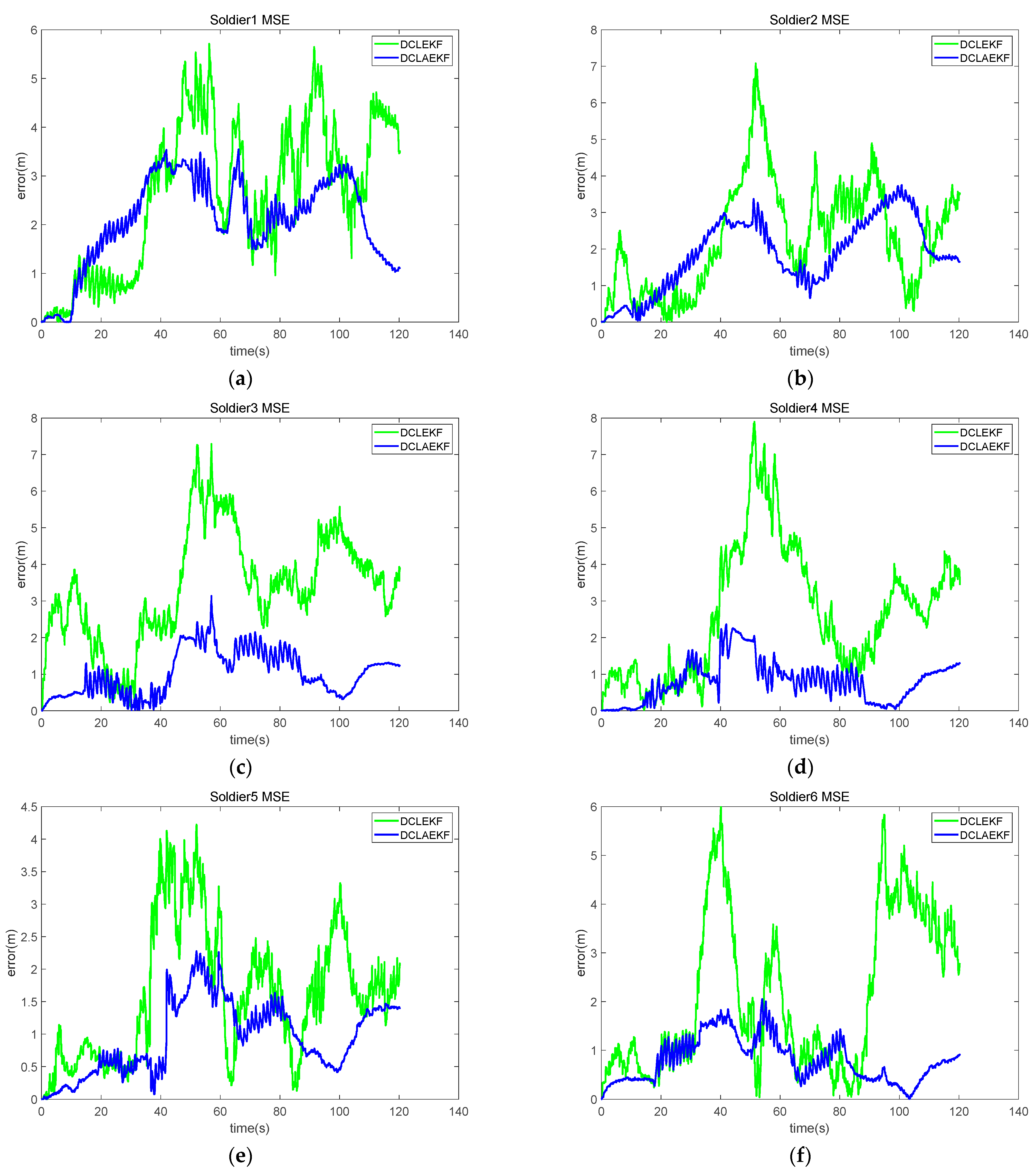
3.2. Building Environment Experiment
3.3. Forest Environment Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CL | Cooperative localization |
| UAV | Unmanned Aerial Vehicles |
| DCL | Decentralized cooperative localization |
| NLOS | Non-line-of-sight |
| UWB | Ultra-wideband |
| DCLEKF | Decentralized cooperative localization extended Kalman filter |
| GNSS | Global navigation satellite system |
| IMU | Inertial measurement unit |
| INS | Inertial navigation system |
| CCL | Centralized cooperative localization |
| DCLAEKF | Adaptive extended Kalman filter decentralized cooperative localization |
| ESKF | Error-state Kalman filter |
| LOS | Line-of-sight |
| MSE | Mean square error |
References
- Liu, Y.; Yan, R.; Lian, B.; Zhao, H. Hybrid IMU/UWB Cooperative Localization Algorithm in Single-Anchor Networks. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Li, L.; Xu, S.; Nie, H.; Mao, Y.; Yu, S. Collaborative Target Search Algorithm for UAV Based on Chaotic Disturbance Pigeon-Inspired Optimization. Appl. Sci. 2021, 11, 7358. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Zhang, J.; Guo, Y.; Razzaqi, A.A. A Novel Adaptive Filtering for Cooperative Localization Under Compass Failure and Non-Gaussian Noise. IEEE Trans. Veh. Technol. 2022, 71, 3737–3749. [Google Scholar] [CrossRef]
- Tian, Q.; Wang, K.I.-K.; Salcic, Z. An INS and UWB Fusion Approach With Adaptive Ranging Error Mitigation for Pedestrian Tracking. IEEE Sens. J. 2020, 20, 4372–4381. [Google Scholar] [CrossRef]
- Zhu, J.; Kia, S.S. Decentralized Cooperative Localization With LoS and NLoS UWB Inter-Agent Ranging. IEEE Sens. J. 2022, 22, 5447–5456. [Google Scholar] [CrossRef]
- Wang, J.; Xu, X.; Liu, J. Pedestrian Inertial Navigation Based on Full-Phase Constraints of Lower Limb Kinematics. IEEE Trans. Instrum. Meas. 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Shi, L.-F.; Feng, B.-L.; Dai, Y.-F.; Liu, G.-X.; Shi, Y. Pedestrian Indoor Localization Method Based on Integrated Particle Filter. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Wang, Q.; Cheng, M.; Noureldin, A.; Guo, Z. Research on the Improved Method for Dual Foot-Mounted Inertial/Magnetometer Pedestrian Positioning Based on Adaptive Inequality Constraints Kalman Filter Algorithm. Measurement 2019, 135, 189–198. [Google Scholar] [CrossRef]
- Li, Z.; Xu, X.; Ji, M.; Wang, J.; Wang, J. Pedestrian Positioning Based on Dual Inertial Sensors and Foot Geometric Constraints. IEEE Trans. Ind. Electron. 2022, 69, 6401–6409. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, K.; Sun, Z.; Cai, M.; Cheng, M. Research on the Heading Calibration for Foot-Mounted Inertial Pedestrian-Positioning System Based on Accelerometer Attitude. Electronics 2019, 8, 1405. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Yang, Z.; Shao, K.; Chen, W. Motion Model-Assisted GNSS/MEMS-IMU Integrated Navigation System for Land Vehicle. Gps Solut. 2022, 26, 131. [Google Scholar] [CrossRef]
- Wahlstrom, J.; Skog, I. Fifteen Years of Progress at Zero Velocity: A Review. IEEE Sens. J. 2021, 21, 1139–1151. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Sun, J. A Hybrid Framework for Mitigating Heading Drift for a Wearable Pedestrian Navigation System through Adaptive Fusion of Inertial and Magnetic Measurements. Appl. Sci. 2021, 11, 1902. [Google Scholar] [CrossRef]
- Tao, X.; Zhu, F.; Hu, X.; Liu, W.; Zhang, X. An Enhanced Foot-Mounted PDR Method with Adaptive ZUPT and Multi-Sensors Fusion for Seamless Pedestrian Navigation. Gps Solut. 2021, 26, 13. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, J.; Li, Y.; Niu, X. Magnetic Field-Enhanced Learning-Based Inertial Odometry for Indoor Pedestrian. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, H.; Xiong, H.; Men, A.; Zhao, F.; Xia, M.; Ou, C. Pedestrian Dead Reckoning Based on Walking Pattern Recognition and Online Magnetic Fingerprint Trajectory Calibration. IEEE Internet Things J. 2021, 8, 2011–2026. [Google Scholar] [CrossRef]
- Li, W.; Chen, R.; Yu, Y.; Wu, Y.; Zhou, H. Pedestrian Dead Reckoning with Novel Heading Estimation under Magnetic Interference and Multiple Smartphone Postures. Measurement 2021, 182, 109610. [Google Scholar] [CrossRef]
- Wang, J.; Xu, X.; Yu, Z.; Li, Z.; Liu, S. A Novel Suppression Method of Height Drift for Pedestrian Navigation With a Circular Hypotheses on Terrain Slope. IEEE Sens. J. 2022, 22, 12054–12063. [Google Scholar] [CrossRef]
- Chiang, K.-W.; Chang, H.-W.; Li, Y.-H.; Tsai, G.-J.; Tseng, C.-L.; Tien, Y.-C.; Hsu, P.-C. Assessment for INS/GNSS/Odometer/Barometer Integration in Loosely-Coupled and Tightly-Coupled Scheme in a GNSS-Degraded Environment. IEEE Sens. J. 2020, 20, 3057–3069. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, J.; Sha, X.; Yu, J.; Duan, H.; Shi, G.; Li, W.J. Estimation of Pedestrian Altitude Inside a Multi-Story Building Using an Integrated Micro-IMU and Barometer Device. IEEE Access 2019, 7, 84680–84689. [Google Scholar] [CrossRef]
- Ji, M.; Xu, X.; Guo, Y. An Adaptive Heading Correction Algorithm for Suppressing Magnetic Interference in Inertial Navigation System. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Basso, M.; Galanti, M.; Innocenti, G.; Miceli, D. Triggered INS/GNSS Data Fusion Algorithms for Enhanced Pedestrian Navigation System. IEEE Sens. J. 2020, 20, 7447–7459. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, Y.; Chen, C.; Jia, J.; Sun, H.; Wang, T.; Hyyppä, J. Smartphone PDR/GNSS Integration via Factor Graph Optimization for Pedestrian Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Zhao, M.; Zhang, T.; Wang, D. A Novel UWB Positioning Method Based on a Maximum-Correntropy Unscented Kalman Filter. Appl. Sci. 2022, 12, 12735. [Google Scholar] [CrossRef]
- Li, D.; Wang, X.; Chen, D.; Zhang, Q.; Yang, Y. A Precise Ultra-Wideband Ranging Method Using Pre-Corrected Strategy and Particle Swarm Optimization Algorithm. Measurement 2022, 194, 110966. [Google Scholar] [CrossRef]
- Yao, L.; Yao, L.; Wu, Y.-W. Analysis and Improvement of Indoor Positioning Accuracy for UWB Sensors. Sensors 2021, 21, 5731. [Google Scholar] [CrossRef]
- Xu, Y.; Shmaliy, Y.S.; Ahn, C.K.; Shen, T.; Zhuang, Y. Tightly Coupled Integration of INS and UWB Using Fixed-Lag Extended UFIR Smoothing for Quadrotor Localization. IEEE Internet Things J. 2021, 8, 1716–1727. [Google Scholar] [CrossRef]
- Wen, K.; Yu, K.; Li, Y.; Zhang, S.; Zhang, W. A New Quaternion Kalman Filter Based Foot-Mounted IMU and UWB Tightly-Coupled Method for Indoor Pedestrian Navigation. IEEE Trans. Veh. Technol. 2020, 69, 4340–4352. [Google Scholar] [CrossRef]
- Kia, S.S.; Rounds, S.; Martinez, S. Cooperative Localization for Mobile Agents: A Recursive Decentralized Algorithm Based on Kalman-Filter Decoupling. IEEE Control Syst. 2016, 36, 86–101. [Google Scholar]
- Jao, C.-S.; Abdallah, A.A.; Chen, C.; Seo, M.-W.; Kia, S.S.; Kassas, Z.M.; Shkel, A.M. PINDOC: Pedestrian Indoor Navigation System Integrating Deterministic, Opportunistic, and Cooperative Functionalities. IEEE Sens. J. 2022, 22, 14424–14435. [Google Scholar] [CrossRef]
- Zhu, P.; Ren, W. Fully Distributed Joint Localization and Target Tracking With Mobile Robot Networks. IEEE Trans. Control Syst. Technol. 2021, 29, 1519–1532. [Google Scholar] [CrossRef]
- Zhu, J.; Kia, S.S. Cooperative Localization Under Limited Connectivity. IEEE Trans. Robot. 2019, 35, 1523–1530. [Google Scholar] [CrossRef]
- Luft, L.; Schubert, T.; Roumeliotis, S.I.; Burgard, W. Recursive Decentralized Localization for Multi-Robot Systems with Asynchronous Pairwise Communication. Int. J. Robot. Res. 2018, 37, 1152–1167. [Google Scholar] [CrossRef]
- Zhao, L.; Dai, H.-Y.; Lang, L.; Zhang, M. An Adaptive Filtering Method for Cooperative Localization in Leader–Follower AUVs. Sensors 2022, 22, 5016. [Google Scholar] [CrossRef] [PubMed]
- Dai, J.; Hao, X.; Liu, S.; Ren, Z. Research on UAV Robust Adaptive Positioning Algorithm Based on IMU/GNSS/VO in Complex Scenes. Sensors 2022, 22, 2832. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Sun, C.; Zhang, B.; Wang, P. Adaptive Error-State Kalman Filter for Attitude Determination on a Moving Platform. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Li, S.; Li, Z.; Li, J.; Fernando, T.; Iu, H.H.-C.; Wang, Q.; Liu, X. Application of Event-Triggered Cubature Kalman Filter for Remote Nonlinear State Estimation in Wireless Sensor Network. IEEE Trans. Ind. Electron. 2021, 68, 5133–5145. [Google Scholar] [CrossRef]
- Yang, X.; Wang, J.; Song, D.; Feng, B.; Ye, H. A Novel NLOS Error Compensation Method Based IMU for UWB Indoor Positioning System. IEEE Sens. J. 2021, 21, 11203–11212. [Google Scholar] [CrossRef]
- Zhang, Y.; Tan, X.; Zhao, C. UWB/INS Integrated Pedestrian Positioning for Robust Indoor Environments. IEEE Sens. J. 2020, 20, 14401–14409. [Google Scholar] [CrossRef]
- Gururaj, K.; Rajendra, A.K.; Song, Y.; Law, C.L.; Cai, G. Real-Time Identification of NLOS Range Measurements for Enhanced UWB Localization. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017. [Google Scholar]
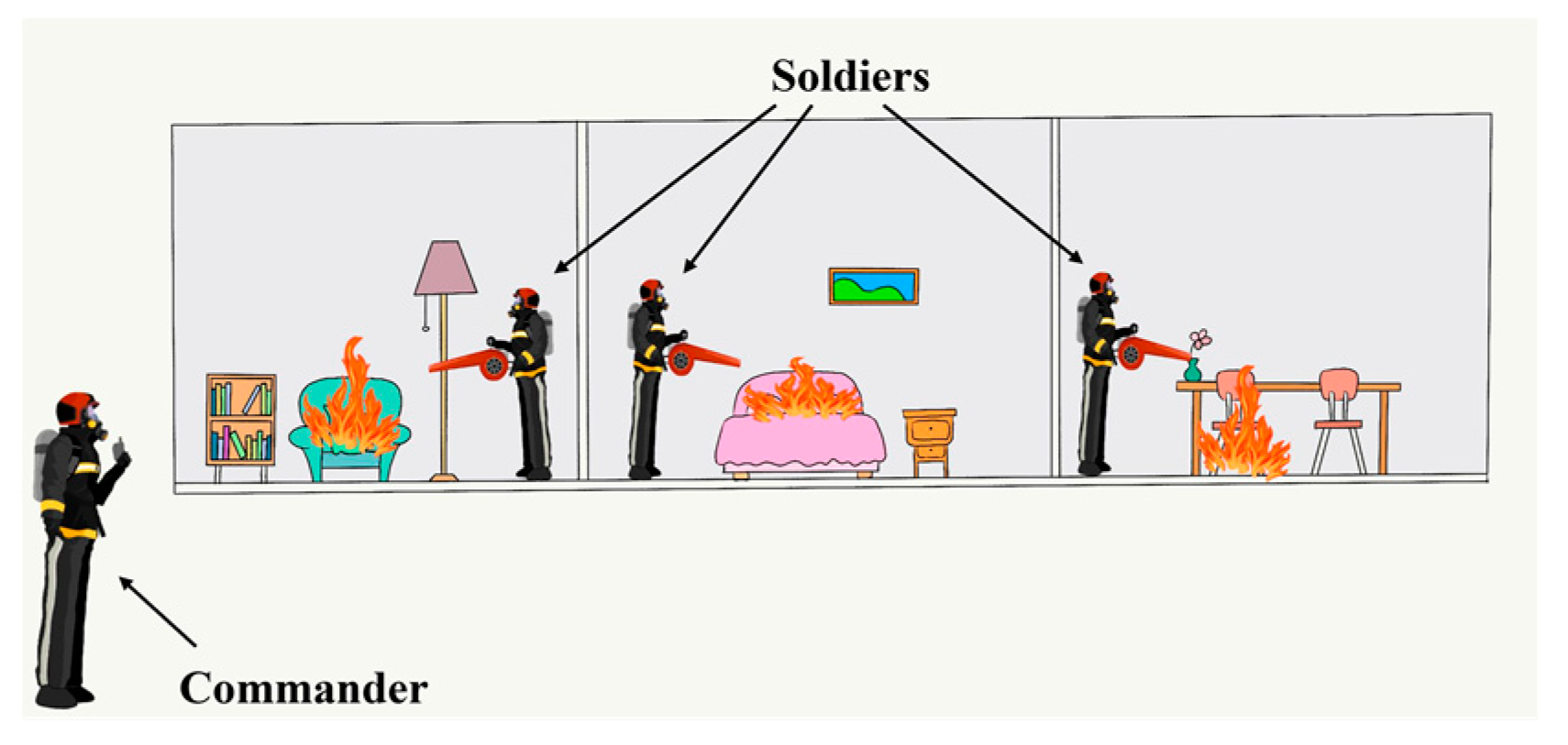




| Sensors | Sampling Frequency (Hz) | Experimenters | Experimental Sites |
|---|---|---|---|
| ICM-42688-P | 100 | Six soldiers and one commander | Building environment site |
| IST8310 | 100 | ||
| SPL06-001 | 100 | Forest environment site | |
| SKG122S | 1 | ||
| DW1000 | 40 |
| Soldiers | DCLEKF | DCLAEKF |
|---|---|---|
| Soldier 1 | 0.69 m | 0.68 m |
| Soldier 2 | 0.70 m | 0.54 m |
| Soldier 3 | 0.63 m | 0.59 m |
| Soldier 4 | 0.49 m | 0.42 m |
| Soldier 5 | 1.21 m | 1.01 m |
| Soldier 6 | 0.67 m | 0.50 m |
| Soldiers | DCLEKF | DCLAEKF |
|---|---|---|
| Soldier 1 | 2.62 m | 2.09 m |
| Soldier 2 | 2.33 m | 1.87 m |
| Soldier 3 | 3.38 m | 1.03 m |
| Soldier 4 | 2.65 m | 0.81 m |
| Soldier 5 | 1.60 m | 0.94 m |
| Soldier 6 | 2.10 m | 0.80 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chong, Y.; Xu, X.; Guo, N.; Shu, L.; Zhang, Q. Adaptive Decentralized Cooperative Localization for Firefighters Based on UWB and Autonomous Navigation. Appl. Sci. 2023, 13, 5177. https://doi.org/10.3390/app13085177
Chong Y, Xu X, Guo N, Shu L, Zhang Q. Adaptive Decentralized Cooperative Localization for Firefighters Based on UWB and Autonomous Navigation. Applied Sciences. 2023; 13(8):5177. https://doi.org/10.3390/app13085177
Chicago/Turabian StyleChong, Yang, Xiangbo Xu, Ningyan Guo, Longkai Shu, and Qingyuan Zhang. 2023. "Adaptive Decentralized Cooperative Localization for Firefighters Based on UWB and Autonomous Navigation" Applied Sciences 13, no. 8: 5177. https://doi.org/10.3390/app13085177
APA StyleChong, Y., Xu, X., Guo, N., Shu, L., & Zhang, Q. (2023). Adaptive Decentralized Cooperative Localization for Firefighters Based on UWB and Autonomous Navigation. Applied Sciences, 13(8), 5177. https://doi.org/10.3390/app13085177






