A Numerical Comparison between Preisach, J-A and D-D-D Hysteresis Models in Computational Electromagnetics
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Hysteresis Models
2.2.1. CPM Model
2.2.2. J-A Model
2.2.3. D-D-D Model
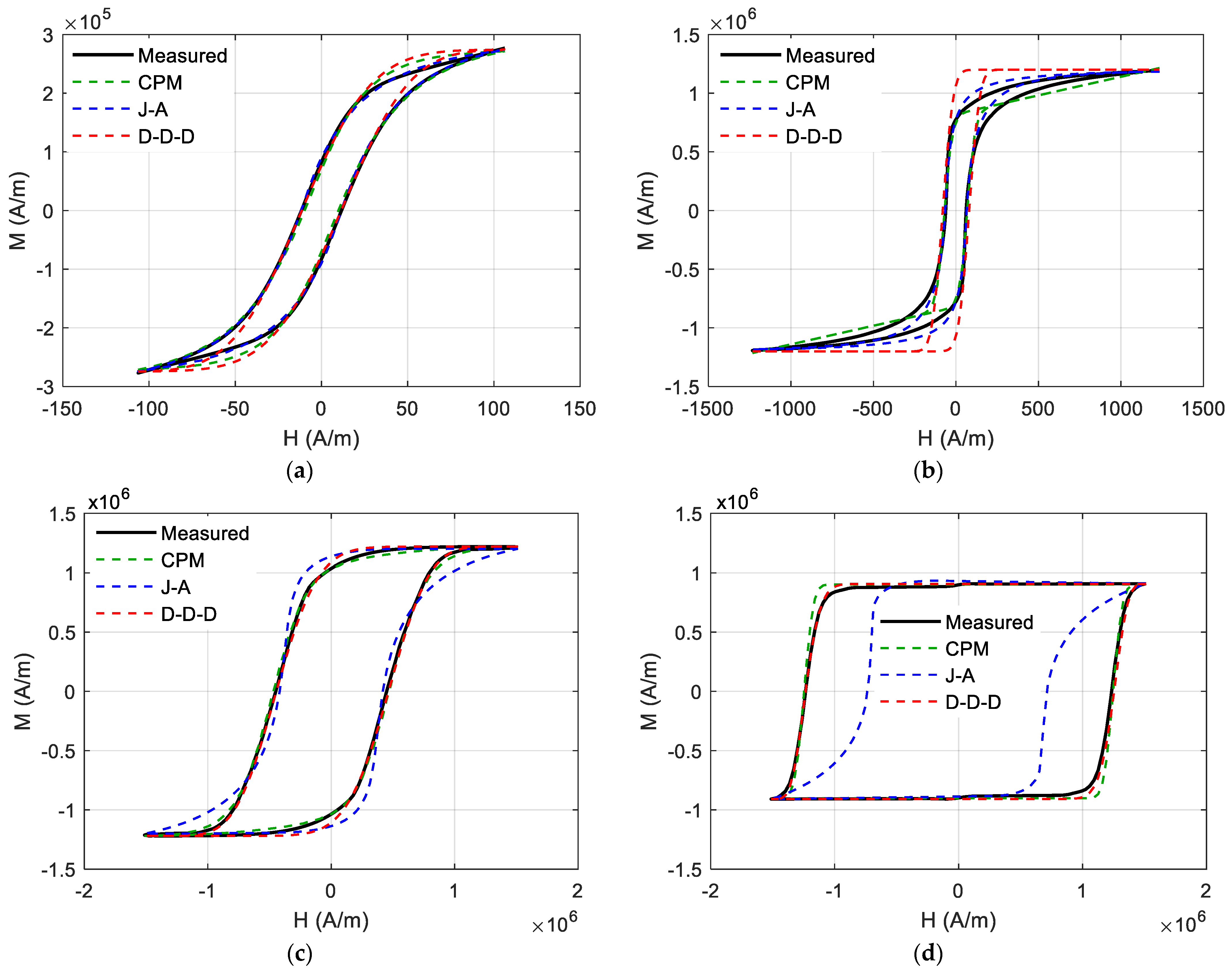
3. Results
3.1. Accuracy
3.2. Computational Time
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bozorth, R.M. Ferromagnetism; IEEE Press: New York, NY, USA, 1993; ISBN 0780310322. [Google Scholar]
- Noori, M.; Altabey, W.A. Hysteresis in engineering systems. Appl. Sci. 2022, 12, 9428. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and Their Applications; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Chua, L.O.; Stromsmoe, K.A. Lumped-circuit models for nonlinear inductors exhibiting hysteresis loops. IEEE Trans. Circuit Theory 1970, 17, 564–574. [Google Scholar] [CrossRef]
- Hodgdon, M.L. Applications of a theory of ferromagnetic hysteresis. IEEE Trans. Magn. 1988, 24, 218–221. [Google Scholar] [CrossRef]
- Stoner, E.C.; Wohlfarth, E.P. A mechanism of magnetic hysteresis in heterogeneous alloys. Philos. Trans. R. Soc. A Math. Phys. Sci. 1948, 240, 599–642. [Google Scholar] [CrossRef]
- Jiles, D.; Atherton, D. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Preisach, F. Uber die magnetische nachwirkung. Z. Physic. 1935, 94, 277–302. [Google Scholar]
- Bobbio, S.; Miano, G.; Serpico, C.; Visone, C. Models of magnetic hysteresis based on play and stop hysterons. IEEE Trans. Magn. 1997, 11, 4417–4426. [Google Scholar] [CrossRef]
- Riganti-Fulginei, F.; Salvini, A. Neural network approach for modelling hysteretic magnetic materials under distorted excitations. IEEE Trans. Magn. 2012, 48, 307–310. [Google Scholar] [CrossRef]
- El Bidweihy, H. Rotational magnetization lag-angle plots using the anisotropic Stoner-Wohlfarth model. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Li, Y.; Wang, H.; Zhu, L. Modeling dynamic magnetostriction of amorphous core materials based on Jiles-Atherton theory for finite element simulations. J. Magn. Magn. Mater. 2021, 529, 167854. [Google Scholar] [CrossRef]
- Hoffmann, K.; Bastos, J.P.A.; Leite, J.V.; Sadowski, N. A vector Jiles-Atherton model for improving the FEM convergence. IEEE Trans. Magn. 2017, 53, 7300304. [Google Scholar] [CrossRef]
- Della Torre, E. Magnetic Hysteresis; IEEE Press: Piscataway, NJ, USA, 1999. [Google Scholar]
- Cardelli, E. A general hysteresis operator for the modeling of vector fields. IEEE Trans. Magn. 2011, 47, 2056–2067. [Google Scholar] [CrossRef]
- Hussain, S.; Lowther, D.A. An efficient implementation of the classical Preisach model. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Scoretti, R.; Riganti-Fulginei, F.; Salvini, A.; Quandam, S. Algorithms to reduce the computational cost of vector Preisach model in view of Finite Element analysis. J. Magn. Magn. Mater. 2021, 546, 168876. [Google Scholar] [CrossRef]
- D’Aquino, V.; Serpico, C.; Visone, C.; Adly, A.A. A new vector model of magnetic hysteresis based on a novel class of play hysterons. IEEE Trans. Magn. 2003, 39, 2537–2539. [Google Scholar] [CrossRef]
- Leite, J.V.; Sadowski, N.; Da Silva, P.A.; Batistela, N.J.; Kuo-Peng, P.; Bastos, J.P.A. Modeling magnetic vector hysteresis with play hysterons. IEEE Trans. Magn. 2007, 43, 1401–1404. [Google Scholar] [CrossRef]
- Lin, D.; Zhou, P.; Rahaman, M.A. A practical anisotropic vector hysteresis model based on play hysteron. IEEE Trans. Magn. 2017, 53, 1–6. [Google Scholar] [CrossRef]
- Matsuo, T.; Takahashi, Y.; Fujiwara, K. Anisotropic vector play model and its application in magnetization analysis. IEEE Trans. Magn. 2023. [Google Scholar] [CrossRef]
- Wang, Y.; Rui, X.U.; Zhou, M. Prandtl-Ishlinskii modeling for giant magnetostrictive actuator based on internal time-delay recurrent neural network. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar]
- Wang, Z.; Zhang, Y.; Ren, Z.; Koh, C.-S.; Mohammed, O.A. Modeling of anisotropic magnetostriction under DC bias based on an optimized BP neural network. IEEE Trans. Magn. 2020, 56, 1–4. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J.; Li, Y.; Zhu, L. A hybrid Jiles-Atherton and Preisach model of dynamic magnetic hysteresis based on backpropagation neural networks. J. Magn. Magn. Mater. 2021, 554, 168655. [Google Scholar] [CrossRef]
- Quondam Antonio, S.; Bonaiuto, V.; Sargeni, F.; Salvini, A. Neural network modeling of arbitrary hysteresis processes: Application to GO ferromagnetic steel. Magnetochemistry 2022, 8, 18. [Google Scholar] [CrossRef]
- Philips, D.A.; Dupre, L.R.; Melkebeek, J.A. Comparison of Jiles and Preisach hysteresis models in magnetodynamics. IEEE Trans. Magn. 1995, 31, 3551–3553. [Google Scholar] [CrossRef]
- Benabou, A.; Clenet, S.; Piriou, F. Comparison of Preisach and Jiles-Atherton models to take into account hysteresis phenomenon for finite element analysis. J. Magn. Magn. Mater. 2003, 261, 139–160. [Google Scholar] [CrossRef]
- D’Aloia, A.G.; Di Francesco, A.; De Santis, V. A novel computational method to identify/analyze hysteresis loops of hard magnetic materials. Magnetochemistry 2021, 7, 10. [Google Scholar] [CrossRef]
- Szewczyk, R.; Nowicki, M. Sensitivity of Jiles-Atherton model parameters identified during the optimization process. In Proc. AIP Conf. 2018, 1996, 020046. [Google Scholar] [CrossRef]
- Bottauscio, O.; Chiampi, M.; Ragusa, C.; Rege, L.; Repetto, M. Description of TEAM problem 32: A Test-Case for Validation of Magnetic Field Analysis with Vector Hysteresis. Istituto Elettrotecnico Nazionale Galileo Ferraris, Turin, Italy, Tech. Rep. 2004. Available online: http://www.compumag.org/jsite/images/stories/TEAM/problem32.pdf (accessed on 1 February 2021).
- Szabó, Z.; Tugyi, I.; Kádár, G.; Füzi, J. Identification procedures for scalar Preisach model. Phys. B Condes. Matter 2004, 343, 142–147. [Google Scholar] [CrossRef]
- Szabó, Z.; Füzi, J. Implementation and identification of Preisach type hysteresis models with Everett function in closed form. J. Magn. Magn. Mater. 2016, 406, 251–258. [Google Scholar] [CrossRef]
- Szabó, Z. Preisach Type Hysteresis Models Implemented in Matlab. 2003–2021. Available online: https://sourceforge.net/projects/hysteresis (accessed on 15 December 2022).
- Szewczyk, R. Computational problems connected with Jiles-Atherton model of magnetic hysteresis. Adv. Intell. Syst. Comput. 2014, 267, 275. [Google Scholar]
- Lewis, L.H.; Gao, J.; Jiles, D.C.; Welch, D.O. Modeling of permanent magnets: Interpretation of parameters obtained from the Jiles-Atherton hysteresis model. J. Appl. Phys. 1996, 79, 6470–6472. [Google Scholar] [CrossRef]
- Brachtendorf, H.G.; Laur, R. A hysteresis model for hard magnetic core materials. IEEE Trans. Magn. 1997, 33, 723–727. [Google Scholar] [CrossRef]
| Material | Model | Parameter Number 1 | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| MnZn ferrite | CPM | 0.049 | −8.73 | 17.495 | 0.95∙10−3 | - |
| J-A | 3.178∙105 | 1.099∙10−7 | 12.649 | 12.448 | 0.844 | |
| D-D-D | 2.74∙105 | 5.5 | 0.116 | - | - | |
| Fe-Si loop 11 | CPM | 0.044 | 69.12 | 23.212 | 4∙10−4 | - |
| J-A | 1.23∙106 | 1∙10−4 | 47 | 66 | 0.99 | |
| D-D-D | 1.194∙106 | 300 | 0.07 | - | - | |
| NdFeB at 80 °C | CPM | 6.6∙10−3 | 4.56∙105 | 1.49∙105 | 0.5∙10−3 | - |
| J-A | 1.18∙106 | 0.46 | 1.25∙105 | 5.24∙105 | 0.05 | |
| D-D-D | 1.13∙106 | 12.5 | 0.3 | - | - | |
| NdFeB at 27 °C | CPM | 0.016 | 1.24∙106 | 5.44∙104 | 0.2∙10−4 | - |
| J-A | 0.954∙106 | 1.1 | 1.45∙105 | 1∙106 | 1∙10−6 | |
| D-D-D | 0.909∙106 | 20 | 1.02 | - | - | |
| Material | Model | e (%) | r2 | CT (s) |
|---|---|---|---|---|
| MnZn ferrite | CPM | 4.05629 | 0.99785 | 0.09182 |
| J-A | 1.51375 | 0.99948 | 0.15134 | |
| D-D-D | 4.53686 | 0.99718 | 0.00685 | |
| Fe-Si loop 11 | CPM | 15.24575 | 0.91456 | 0.08678 |
| J-A | 5.0458 3 | 0.99212 | 0.22523 | |
| D-D-D | 4.91653 | 0.97532 | 0.00976 | |
| NdFeB at 80 °C | CPM | 0.19651 | 0.99927 | 0.07080 |
| J-A | 9.62853 | 0.93845 | 0.26254 | |
| D-D-D | 2.03716 | 0.99921 | 0.00766 | |
| NdFeB at 27 °C | CPM | 2.18167 | 0.99584 | 0.07430 |
| J-A | 31.31527 | 0.79565 | 0.35150 | |
| D-D-D | 2.16800 | 0.99872 | 0.00660 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Santis, V.; Di Francesco, A.; D’Aloia, A.G. A Numerical Comparison between Preisach, J-A and D-D-D Hysteresis Models in Computational Electromagnetics. Appl. Sci. 2023, 13, 5181. https://doi.org/10.3390/app13085181
De Santis V, Di Francesco A, D’Aloia AG. A Numerical Comparison between Preisach, J-A and D-D-D Hysteresis Models in Computational Electromagnetics. Applied Sciences. 2023; 13(8):5181. https://doi.org/10.3390/app13085181
Chicago/Turabian StyleDe Santis, Valerio, Antonio Di Francesco, and Alessandro G. D’Aloia. 2023. "A Numerical Comparison between Preisach, J-A and D-D-D Hysteresis Models in Computational Electromagnetics" Applied Sciences 13, no. 8: 5181. https://doi.org/10.3390/app13085181
APA StyleDe Santis, V., Di Francesco, A., & D’Aloia, A. G. (2023). A Numerical Comparison between Preisach, J-A and D-D-D Hysteresis Models in Computational Electromagnetics. Applied Sciences, 13(8), 5181. https://doi.org/10.3390/app13085181








