Abstract
The anterior cruciate ligament (ACL) is critical for controlling the motion of the knee joint, but it is prone to injury during sports activities and physical work. If left untreated, ACL injuries can lead to various pathologies such as meniscal damage and osteoarthritis. While previous studies have used deep learning to diagnose ACL tears, there has been a lack of standardization in human unit classification, leading to mismatches between their findings and actual clinical diagnoses. To address this, we perform a triple classification task based on various tear classes using an ordinal loss on the KneeMRI dataset. We utilize a channel correction module to address image distribution issues across multiple patients, along with a spatial attention module, and test its effectiveness with various backbone networks. Our results show that the modules are effective on various backbone networks, achieving an accuracy of 83.3% on ResNet-18, a 6.65% improvement compared to the baseline. Additionally, we carry out an ablation experiment to verify the effectiveness of the three modules and present our findings with figures and tables. Overall, our study demonstrates the potential of deep learning in diagnosing ACL tear and provides insights into improving the accuracy and standardization of such diagnoses.
1. Introduction
The knee is a hinge joint held together by four ligaments. The ligaments are a structure in the knee that hold the bones together and help control joint motion. As shown in Figure 1, there is a ligament (collateral ligament) on each side of the knee and two ligaments deep within the knee. The anterior cruciate ligament (ACL) and posterior cruciate ligament (PCL) are the two ligaments in the knee that cross each other. The two ligaments attach to the end of the thigh bone on one side and the top of the tibia on the other.
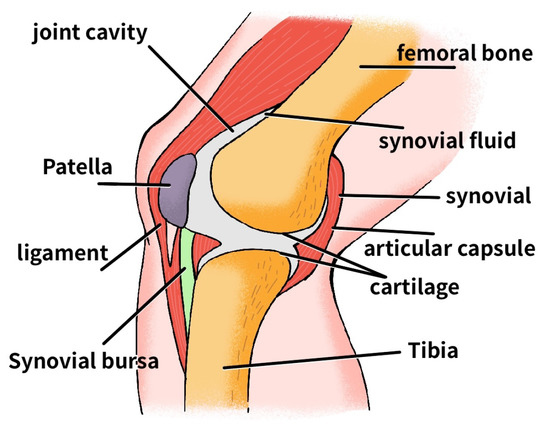
Figure 1.
Knee joint structure.
The anterior gliding of the tibia over the femur is controlled by the ACL, which essentially prevents too much forward motion [1]. A certain degree of anterior motion is necessary for the knee joint, but too much activity may damage other knee structures.
ACL injuries are prevalent in sports activities [2,3], and their incidence of has been on the rise in the US [4]. The cost of diagnosis and treatment of ACL injuries surpasses USD 7 billion annually, directly or indirectly [5]. If left untreated, ACL injuries can cause knee instability, meniscal damage [6], and osteoarthritis [7], significantly impacting an individual’s health and daily life. Raising awareness about ACL injuries and encouraging athletes to take necessary precautions is vital. Timely and accurate diagnosis in combination with effective treatment are essential for preventing further damage and improving outcomes for patients.
X-ray, ultrasound, and computed tomography (CT) can usually diagnose ACL injuries, and magnetic resonance imaging (MRI) is often used in the medical field [8]. MRI has become the imaging technique of choice for evaluating the ACL because it is more accurate and sensitive for that ligament [9]. Tears in the ACL are generally rated in three grades. Grade 0 means that the ACL is intact, grade 1 is a partial tear, and grade 2 is a complete tear [10].
In recent years, with the continuous development of deep learning techniques, computers have assisted in medical diagnosis as an emerging field. Examples include the classification, detection, or segmentation of medical images. The use of computer-assisted diagnosis of the ACL has gone through two phases, including the use of traditional machine learning-assisted diagnosis and the use of neural network-assisted diagnosis.
Štajduhar et al. [11] created the KneeMRI dataset and used machine learning to diagnose the severity of ACL tears. They used two feature extraction techniques, histogram of oriented gradients (HOG) and gist, and trained support vector machine (SVM) and random forest (RF) models using these features. They tested multiple hyperparameters and found that an SVM with HOG features had the best performance, achieving an 89.4% area under curve (AUC) for damage detection and a 94.3% AUC for complete tear detection.
In the field of deep learning, Kapoor et al. [12] compared various machine learning and deep learning algorithms on region of interest (ROI) data and found that SVMs and convolutional neural networks (CNN) achieved the best results. Namiri et al. [13] used both two-dimensional (2D) and three-dimensional (3D) CNNs to classify ACL tears, with overall accuracy rates of 89% and 92%, respectively. Jeon et al. [14] enhanced the interpretability and reduced the model size of a lightweight network by incorporating attention and squeeze modules, resulting in an average AUC of 98.3% on the Chiba knee dataset and 98.0% on the Stanford knee dataset. Belton et al. [15] utilized spatial attention [16] integrated onto ResNet-18 to optimize knee injury detection, achieving a high AUC of 97.7% for ACL tear detection. Awan et al. [17] designed a custom CNN model to classify ACL tears, achieving excellent performance with accuracy, precision, sensitivity, specificity, and F1-score metrics all above 98%. Chang et al. [18] conducted a study on the influence of input field of view and dimensionality on ACL tear detection. They found that using a five-slice dynamic patch-based sampling algorithm resulted in high performance, with an AUC, sensitivity, and specificity of 97.1%, 96.7%, and 100%, respectively. Minamoto et al. [19] compared the accuracy of CNN classification with classification by an experienced physician, and it was concluded that a CNN network can help to identify ACL tears from a single MRI slice with good sensitivity and specificity while being superior to physician classification. All of these studies have contributed to the development of intelligent ACL tear diagnosis.
However, there are areas for improvement in the studies mentioned above. First, some of the studies [13,17,19] were trained and evaluated using slices, which is inconsistent with the actual clinical application in medicine. The exact circumstance should be categorized as a person using all their slices. The second is that most of the studies [12,14,18] define ACL tear classification as a binary classification, which cannot differentiate tear conditions according to the three given classes and requires manual judgment in clinical diagnosis. A complex training problem caused by the small sample size and data imbalance arises in the triple classification study of ACL tears in a human unit. The human-based ACL triple classification problem, which is crucial for clinical medical aid diagnosis, is effectively improved in this paper by utilizing channel correction and ordinal loss.
This study effectively models MRI images of the ACL based on the KneeMRI dataset with a deep learning algorithm. This study also improves the evaluation metrics of sensitivity, specificity, and accuracy for diagnosing ACL tears at baseline based on triple classification training for ACL MRI images on a small data set, which is different from most binary classification tasks. In addition, this work can provide reference information for the selection of clinical treatment plans and surgery, which is promoted in clinical aid diagnosis. The main contributions of this paper are as follows:
- (i)
- In this paper, a channel correction module is used for the correlative MRI dataset. The negative effects of different ACL MRI image distributions for various patients are attenuated.
- (ii)
- An ordinal loss function is introduced into this task because ACL tear grades are as sequential as knee injury grades, and the ordinal loss function serves as a solution to the training difficulties caused by label imbalances in a small sample dataset.
- (iii)
- The effectiveness of the designed network structure is tested in different backbone networks, and the generalizability of the framework is demonstrated, as it can be added to many backbone networks.
- (iv)
- The ablation experiments on ResNet-18 show that the channel correction module, spatial attention module, and ordinal loss function used in this paper are practical and improve the accuracy by 6.6% over the baseline.
2. Related Work
2.1. Medical Image Classification
With the increasing development of machine learning, good results have been achieved on traditional image analysis tasks with the help of computers. Therefore, more people are focusing on applications in various fields, such as face recognition, vehicle detection, and other tasks. Medical image analysis has been of great help in medical research, clinical disease diagnosis, and treatment. Computer-aided methods, called Computer-Aided Detection/Diagnosis (CAD), have become a trend in this field. Among them, medical image classification generally belongs to the field of Computer-Aided Diagnosis and is one of its most popular applications.
CAD based on medical images can be traced back to the 1960s. To identify cardiac lesions, Becker et al. [20] input X-ray images into a computer to calculate the cardiothoracic ratio. Medical image-based CAD was developed as a direct result of this. Lee et al. [21] proposed classifying ultrasound liver images by selecting fractal feature vectors based on the M-band wavelet transform. Paredes et al. [22] obtained small square windows, i.e., local representations, from images and combined this approach with k-nearest neighbor techniques to achieve state-of-the-art results. Caicedo et al. [23] used bag-of-features combined with SVM to select appropriate kernel functions for processing. Moreover, they conducted extensive experiments on the use of different strategies and analyzed the impact of each configuration on the classification results.
Medical imaging has evolved more rapidly with the introduction of convolutional neural networks. The lung nodule classification problem was addressed in [24]. A multiscale CNN extracts discriminative features from alternately stacked layers while capturing nodule heterogeneity. Payan et al. [25] used sparse autoencoders and 3DCNNs to diagnose Alzheimer’s disease, and the results demonstrated that 3DCNNs produced state-of-the-art results. Gong et al. [26] extended the interpretability of deep networks and implemented complex spatial variations by deformable Gabor convolution (DGConv). This approach improved the representativeness and robustness of complex objects, resulting in a Deformable Gabor Feature Network (DGFN). Wei et al. [27] considered histopathology image classification as part of course learning and proposed a simple course learning method based on this, which resulted in a 4.5% improvement in the AUC compared with vanilla training.
2.2. Attention Mechanism
Attention mechanisms are designed to mimic the ability of humans to find salient regions in a scene, and such mechanisms can be used to highlight a specific part of the feature map by weighting the feature map. Attention mechanisms are usually classified into channel attention mechanisms, spatial attention mechanisms, temporal attention mechanisms, branching attention mechanisms, channel spatial attention mechanisms, and spatio-temporal attention mechanisms [28]. Spatial attention mechanisms, channel attention mechanisms, and hybrid domain attention mechanisms are more commonly used in image analysis.
The spatial attention mechanism starts from finding regions on the image spatial domain that are helpful for the task. For instance, according to [29], it was suggested that Spatial Transformer Networks (STN) should be able to learn how to adaptively spatially transform various data to obtain spatial transformation invariance.
On the other hand, the channel attention mechanism calculates the weight of each channel in the network to form the attention on the channel domain. Hu et al. [30] weighted the original features by dimensionality using a three-step operation of the squeeze, excitation, and attention on SeNet.
Woo et al. [31] designed the Convolutional Block Attention Module (CBAM) by combining the spatial and channel attention mechanisms. A simple and efficient forward CNN attention module is designed by combining two different dimensions, spatial and channel, to generate an attention map.
In medical image analysis, Schlempe et al. [32] proposed a novel Attention Gate (AG) model for medical imaging, which can automatically learn to focus on target structures of different shapes and sizes. An interactive attention mechanism was developed by Dai et al. [33] to implicitly instruct the network to focus on pathological tissue in multimodal data. Tao et al. [16] introduced an inter-slice contextual attention mechanism and an intra-slice spatial attention mechanism in lesion detection to improve model performance using fewer slices.
2.3. Loss Function
The loss function is used to evaluate the difference between the output and true label, which is the objective optimization function of the model. The smaller the loss, i.e., the closer the output is to the accurate label, the better the model works.
The standard loss functions in image classification are the 0–1 loss function, the binary cross-entropy loss function, and the multiclassification cross-entropy loss function. The 0–1 loss function is a discontinuous segmentation function, which is challenging to solve due to its minimization problem. Since Rubinstein et al. [34] proposed an adaptive algorithm using cross-entropy to estimate the probability of rare events in complex random networks, cross-entropy loss has also been applied to classification tasks [35]. In the time since then, many improvements have been made to cross-entropy. Liu et al. [36] proposed that large-margin softmax (L-Softmax) loss encourages the learning of intra-class compactness and inter-class separation features. Circle loss was proposed by Sun et al. [37] to re-weight those similarity scores that were not optimized to improve pair-based similarity.
Lin et al. [38] proposed focal loss for unbalanced samples to solve the complicated training problem by assigning relatively large weights to the losses of complex samples in the unbalanced dataset. Based on this, Li et al. [39] proposed GFocal loss to turn the labels into continuous values between 0 and 1, using the expanded form of focal loss on continuous labels to process them.
In medical imaging, Mazumdar et al. [40] proposed a new composite loss function for medical image segmentation by combining the Dice, focus, and Hausdorff distance loss functions. This function handles extreme class imbalances and directly optimizes Dice score and HD, thus significantly improving segmentation accuracy. According to the sequential nature of the knee injury classes, Chen et al. [41] developed a novel ordinal loss for the detection of knee osteoarthritis. This loss imposes a greater penalty for misclassification with a greater distance between the actual knee injury class and the predicted knee injury class. Liu et al. [42] addressed the drawback that the ordinal loss cannot be varied by proposing an adaptive ordinal weight adjustment strategy on this basis.
3. Method
3.1. Framework
As shown in Figure 2, the network framework consists of four parts: a backbone network, a channel correction module, a spatial attention module, and an ordinal loss function. A backbone network is used to extract features from the doctor-labeled slices, turning the data of size into a feature map of size , where denotes the number of images of the ith patient annotated and denote the dimensionality and size of the feature map. The feature maps are channel-corrected and then weighted by a spatial attention mechanism. The weighted feature maps are fed into the pooling and fully connected layers to obtain the vectors. In order to combine the information of multiple slices of the same person, the top feature at each position is taken as the representative feature for all slices, i.e., a vector of size is obtained by taking the maximum value, according to the conclusion of Su et al. [43]. Finally, the ordinal loss is used to train the fully connected layer’s classification results.

Figure 2.
The proposed framework in this paper, where Fc represents the fully connected layer, Avgpool represents the average pooling layer, and Max represents taking the maximum value in the first dimension of the feature map.
3.2. Channel Correction Module
The classes of the test set in the few-shot classification task are not seen in training compared to the general classification task. The importance of the quality of the image features learned in training is also illustrated in some works. Luo et al. [44] argued that the feature distribution of the test set will significantly affect the results when they are different from the training set. For example, animal images are often identified with plants as the background, and the discrimination is made according to some parts of the animal’s body that are unrelated to the background. Then, the model will ignore the information about plants so that when it comes to classifying the plants, the results will be better.
That also applies to the ACL tear classification, as shown in Figure 3. The MRI images of the ACL for each individual in the ACL tear classification task are significantly different. The images of different patients are very different, even if only the region labeled by the physician is used for classification, and this variability affects the model’s effectiveness. The testing and training sets do not contain the same patients, and the image distribution differs. A function is then introduced for channel correction, inspired by Luo’s approach to the few-shot classification task, to eliminate or reduce the effect of different patient image distributions. The function is shown below, where k is a hyperparameter:
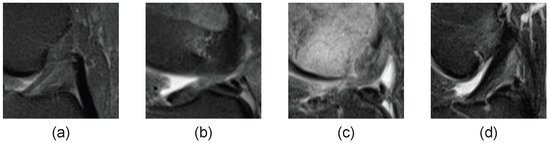
Figure 3.
MRI images of different patients. (a–d) are MRI images of the cruciate ligament in four distinct patients, each displaying a unique distribution pattern.
The mean magnitude of the channel (MMC) represents the average value on each channel, and this function suppresses channels with high MMC and boosts channels with low MMC. This function is applied to each channel of the feature map to reduce the adverse effects caused by the different distributions of the patient’s ACL images.
3.3. Spatial Attention
A spatial attention mechanism weights the feature maps following channel correction. Tao et al. [16] proposed this mechanism for spatial attention and incorporated it into VGG16 to detect deep lesions. Belton et al. [15] integrated it onto ResNet-18 and used it to optimize knee injury detection and validate localization capabilities. We used it on a triple classification task for the ACL tear and integrated it into different networks.
Figure 4 shows the structure of the module. The feature maps are input into a 1 × 1 convolution layer, and the output is the same shape as the input, after which the feature maps on different channels are obtained by spatial softmax. The feature map undergoes maxed normalization to obtain the attention weight map, and the weighted feature map is obtained by multiplying the attention map with the original feature map.
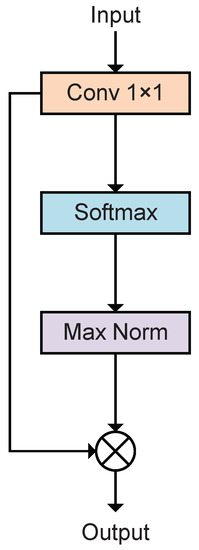
Figure 4.
Structure of spatial attention mechanism.
The equations are shown as follows:
where denotes the convolution layer and and denote the feature maps before and after being weighted. Equations (2)–(5) correspond to the functions performed by the convolution layer, softmax activation function, maximum normalization function, and dot product function, respectively, as shown in Figure 4.
3.4. Ordinal Loss
Chen et al. [41] suggested that there is a relationship between different severity grades in knee osteoarthritis. A higher loss should be obtained if the predicted and actual grades are farther apart in order. For example, knee osteoarthritis has five grades, and the weight loss for misclassifying grade 2 as grade 1 and grade 0 should be different. Therefore, on the basis of the focal loss, an ordinal loss is proposed to detect osteoarthritis.
ACL tears are divided into three grades: grade 0 being no tear, grade 1 being partial tears, and grade 2 being complete tears. The ordinal loss also applies to this case since the different tear grades are correlated in order. A 3 × 3 matrix of ordinal loss weights is assumed. represents the ordinal weight of the predicted class i for the true class j. The ordinal weight ought to be greater the further apart the predicted class is from the actual class. The loss is similar to the cross-entropy loss, as follows:
where and is the predicted probability value. The weights are re-weighted to simplify the computation and to make the form closer to cross-entropy loss. The new weight matrix is , where the loss is equivalent to .
As shown in Figure 5, suppose ; then, . The actual grade j is grade 1 and the predicted grade i is grade 1; then, .
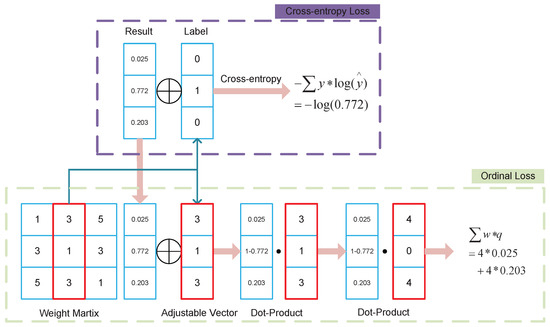
Figure 5.
Process of ordinal loss.
Ordinal loss is used in ACL classification to optimize the hard-to-train problem in the classification task, which is caused by the small number of samples and sample imbalance.
4. Experiment
4.1. Data and Task
The dataset is derived from the KneeMRI dataset and contains multiple ACL MRI data from 917 patients, of which 690 are healthy, 172 are partial tears, and 55 are complete tears. The region of interest (ROI) in the images the doctor labels is selected as the data, classified in human units. The dataset is randomly divided into five folds for experiments. Each fold divides the training set, validation set, and test set in the ratio of 7:1:2, where the class ratio is kept consistent. The test sets of all folds are disjointed, and the union is the entire data set.
The task of this experiment is to perform a triple classification task for the KneeMRI dataset. It is challenging to train with each patient as a sample because of the dataset’s small sample size and imbalanced data, which can be effectively improved by the method in this paper.
4.2. Implementation Details and Metrics
4.2.1. Training
The optimizer is set as the Adam optimizer, the learning rate is , and the loss function used in the baseline is the cross-entropy loss function. Each fold is trained for 50 epochs on the 5-fold dataset, the best model on the validation set is taken for testing, and each evaluation index is finally the average of the 5-fold results.
4.2.2. Evaluation Metrics
Accuracy, precision, recall, specificity, and F1-score are commonly used as evaluation metrics in classification tasks.
True Positive (TP) denotes an optimistic prediction and a positive label. False Positive (FP) indicates both a negative label and an optimistic prediction. False Negative (FN) indicates both a positive label and a pessimistic prediction. Moreover, True Negative (TN) shows a pessimistic prediction and a negative label. Accuracy indicates the number of correctly predicted samples as a percentage of the total, which is calculated as:
Precision indicates the percentage of positive samples that are genuinely predicted to be positive by the model and is calculated as:
Recall indicates the percentage of samples that are actually positive that are predicted to be positive and is calculated as:
Specificity indicates the percentage of samples that are predicted to be negative out of those that are actually negative and is calculated as:
The F1-score, which is the weighted summed average of precision and recall, is calculated as follows:
The above metrics are all for the binary classification task. For the multiclassification task, precision, recall, specificity, and F1 are calculated separately for each category and then averaged to obtain macro-precision, macro-recall, macro-specificity, and macro-F1.
4.3. Results
4.3.1. Different Backbone
We tested the modules on different backbone networks. As shown in Table 1, the experimental results show that the results increase in different backbone networks by adding the modules. Figure 6 depicts increases in accuracy of 6.65% for ResNet-18, 3.60% for DenseNet121, 2.84% for VGG16, 3.59% for InceptionNet, 6.54% for MobileNet, and 2.61% for EfficientNet. Among them, the optimal result of 83.3% was reached on ResNet-18, and the increase in recall, specificity, and F1 was 2.90%, 3.11%, and 1.75%, respectively.

Table 1.
Experimental results on different backbone networks.
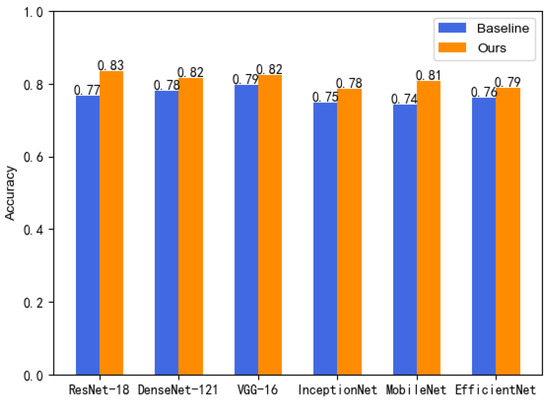
Figure 6.
Growth in accuracy.
The experimental results are also analyzed using the macro-ROC curves and macro-AUC. As shown in Figure 7, the ROC curves on the six popular backbone networks showed improvements in the results, and the AUC values of our method were all larger than those of the baseline.
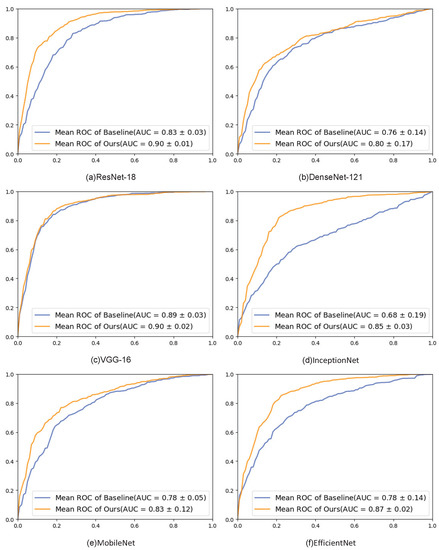
Figure 7.
ROC graphs of different backbone networks. Each subfigure shows the results of the ROC curve on a particular network.
The In conclusion, the method proposed in this paper has been effectively validated in several popular deep networks, and the results are substantially improved. The experimental results demonstrate the effectiveness of our proposed method, which can be better targeted to the specificity of the ACL tear classification task. Additionally, its direct integration into any network demonstrates the method’s generalizability and has improved the performance of numerous networks.
4.3.2. Ablation Experiments
On ResNet-18, ablation experiments are conducted to see if each module works effectively, and the overall results are shown in Table 2. Table 2 demonstrates that each module was successful and contributed to a final increase in accuracy of 6.65% for ResNet-18. A detailed analysis of each module is presented below.

Table 2.
Ablation experiment on ResNet-18 network.
Channel Correction
The channel correction module makes the MMC gap of feature maps on each channel smaller by applying a simple function to each channel. The simple function is applied to each channel, which suppresses the high MMC and boosts the low MMC. It smooths out the overall distribution of the channels without altering them, as shown in Figure 8.
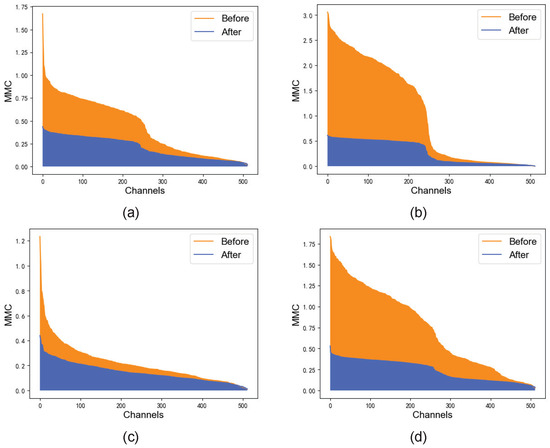
Figure 8.
MMC before and after channel correction. (a–d) show randomly selected MRI images.
Spacial Attention
Tao and Belton verified the effectiveness of the spatial attention module. As shown in Figure 9, the visualization results show that the key regions can be displayed better after the spatial attention module.
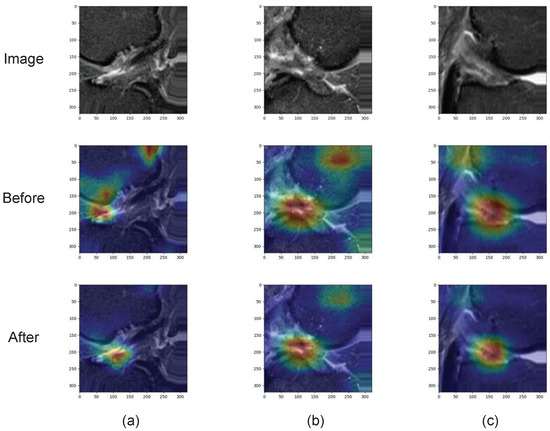
Figure 9.
Heat maps of attention before and after attention mechanism. (a–c) show randomly selected MRI images.
Ordinal Loss
The ordinal loss effectively improves the training results for the unbalanced data set. As shown in Table 3, other metrics such as precision, recall, specificity, and F1-score are improved after using ordinal loss.

Table 3.
Evaluation metrics before and after replacing the loss function.
5. Discussion
In this paper, based on the triple classification problem of an ACL tear, the channel correction module is used to address the complex training problem caused by the different MRI image distributions of different patients. Furthermore, the ordinal loss function is used to address the class imbalance problem with the grade classification of ACL tears. A generic framework is proposed in conjunction with the spatial attention mechanism. The best result of 83.3% accuracy is achieved using ResNet-18 as the backbone network, which is a 6.65% improvement compared to the baseline. The improvement over the baseline is also observed on other backbone networks.
In Table 2, various combination schemes of the three modules are also validated, proving the effectiveness of all modules. The proposed framework is tested in several well-known backbone networks in addition to ResNet-18. The proposed framework improves accuracy on these backbone networks, as shown in Table 1.
Deep learning studies of MRI image classification tasks based on ACL tears are common. Štajduhar et al. [11] created the KneeMRI dataset. Kapoor et al. [12] determined that SVM and CNN yield superior results in analyzing ROI data. Su et al. [43] proposed the idea of integrating all sliced information of individuals. The research conducted by them and others has been highly beneficial for further studies. However, only a few analyses have classified all three tear grades in the human unit. For example, Awan et al. [17] achieved a good AUC and accuracy for ACL tear classification, but their method only used single slices as the unit of analysis. This limitation is not ideal for clinical applications. Chang’s [18] experiments demonstrated the importance of cropped slices and 3D inputs for achieving high algorithmic performance in ACL tear classification. However, their study only classified ACL tears into normal and complete tear categories, requiring manual judgment for partially torn samples, which limits its the potential for intelligent ACL tear diagnosis. A human unit is more consistent with clinical applications in practical terms, and performing the triple classification task can accelerate the diagnosis. Therefore, we propose a network framework for such a problem.
The study in this paper still has the following limitations, and some directions for improvement are shown below:
- (1)
- In this paper, a simple function is used to work on the channel correction, but the function’s parameter is set according to human experience. Therefore, using the algorithm to obtain the hyperparameters and design a function more suitable for this task can be considered.
- (2)
- Ordinal loss function is used as the loss function for classification, and the initial weight matrix is set according to human experience. A more reasonable heuristic method can be considered to obtain suitable initial weights for the data.
- (3)
- The method proposed in this paper is applied to a triple classification task for ACL tears. In addition, the modules are applicable to many datasets. Channel correction, for instance, can be used in datasets with different image distributions, the ordinal loss can be used in datasets with orderliness between them, and so on, which merits further discussion.
6. Conclusions
In this paper, we propose a network framework to address the training problem caused by the small sample size and unbalanced samples of the ACL tear triple classification task. Our framework consists of a backbone network and three modules, and its effectiveness is verified on various popular deep learning networks. The best result of 83.3% accuracy is achieved using ResNet-18 as the backbone network, which is a 6.65% improvement compared to the baseline. The improvement over the baseline is also observed on other backbone networks. This method can also be extended to diagnostic tasks for other MRI images. The results in other works were not trained using the human unit, and the data folds were divided differently. Therefore, the results in this paper are not compared to those in other works.
Author Contributions
Conceptualization, W.L. and K.M.; methodology, W.L. and K.M.; software, W.L.; validation, W.L.; formal analysis, W.L.; investigation, W.L.; resources, K.M.; data curation, W.L.; writing—original draft preparation, W.L.; writing—review and editing, K.M.; visualization, W.L.; supervision, K.M.; project administration, K.M.; funding acquisition, K.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data we use were obtained from http://www.riteh.uniri.hr/~istajduh/projects/kneeMRI/, accessed on 21 October 2022.
Acknowledgments
The authors wish to thank the anonymous reviewers for their valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brantigan, O.C.; Voshell, A.F. The Mechanics of the Ligaments and Menisci of the Knee Joint. J. Bone Jt. Surg. Am. 1941, 23, 44–66. [Google Scholar]
- Agel, J.; Arendt, E.; Bershadsky, B. Anterior Cruciate Ligament Injury in National Collegiate Athletic Association Basketball and Soccer: A 13-Year Review. Am. J. Sports Med. 2005, 33, 524–530. [Google Scholar] [CrossRef] [PubMed]
- Pujol, N.; Blanchi, M.; Chambat, P. The Incidence of Anterior Cruciate Ligament Injuries Among Competitive Alpine Skiers: A 25-year Investigation. Am. J. Sports Med. 2007, 35, 1070–1074. [Google Scholar] [CrossRef]
- Herzog, M.; Marshall, S.; Lund, J.; Pate, V.; Mack, C.; Spang, J. Trends in Incidence of ACL Reconstruction and Concomitant Procedures Among Commercially Insured Individuals in the United States, 2002–2014. Sports Health Multidiscip. Approach 2018, 10, 523–531. [Google Scholar] [CrossRef]
- Kaeding, C.; Léger-St-Jean, B.; Magnussen, R. Epidemiology and Diagnosis of Anterior Cruciate Ligament Injuries. Clin. Sports Med. 2016, 36, 1–8. [Google Scholar] [CrossRef]
- Gupta, R.; Singhal, A.; Rai, A.; Shail, S.; Masih, G. Strong association of meniscus tears with complete Anterior Cruciate Ligament (ACL) injuries relative to partial ACL injuries. J. Clin. Orthop. Trauma 2021, 23, 101671. [Google Scholar] [CrossRef]
- Simon, D.; Mascarenhas, R.; Saltzman, B.; Rollins, M.; Bach, B.; Macdonald, P. The Relationship between Anterior Cruciate Ligament Injury and Osteoarthritis of the Knee. Adv. Orthop. 2015, 2015, 928301. [Google Scholar] [CrossRef] [PubMed]
- Schwenke, M.; Singh, M.; Chow, B. Anterior Cruciate Ligament and Meniscal Tears: A Multi-modality Review. Appl. Radiol. 2020, 49, 42–49. [Google Scholar] [CrossRef]
- Roberts, C.; Towers, J.; Spangehl, M.; Carrino, J.; Morrison, W. Advanced MR Imaging of the Cruciate Ligaments. Radiol. Clin. N. Am. 2007, 45, 1003–1016. [Google Scholar] [CrossRef]
- Moon, S.; Hong, S.; Choi, J.Y.; Jun, W.; Choi, J.A.; Park, E.A.; Kang, H.; Kwon, J. Grading Anterior Cruciate Ligament Graft Injury after Ligament Reconstruction Surgery: Diagnostic Efficacy of Oblique Coronal MR Imaging of the Knee. Korean J. Radiol. Off. J. Korean Radiol. Soc. 2008, 9, 155–161. [Google Scholar] [CrossRef]
- Štajduhar, I.; Mamula, M.; Miletić, D.; Ünal, G. Semi-automated detection of anterior cruciate ligament injury from MRI. Comput. Methods Programs Biomed. 2017, 140, 151–164. [Google Scholar] [CrossRef]
- Kapoor, V.; Tyagi, N.; Manocha, B.; Arora, A.; Roy, S.; Nagrath, P. Detection of Anterior Cruciate Ligament Tear Using Deep Learning and Machine Learning Techniques. In Data Analytics and Management; Khanna, A., Gupta, D., Pólkowski, Z., Bhattacharyya, S., Castillo, O., Eds.; Springer Nature: Singapore, 2021; pp. 9–22. [Google Scholar]
- Namiri, N.; Flament, I.; Astuto, B.; Shah, R.; Tibrewala, R.; Caliva, F.; Link, T.; Pedoia, V.; Majumdar, S. Deep Learning for Hierarchical Severity Staging of Anterior Cruciate Ligament Injuries from MRI. Radiology 2020, 2, e190207. [Google Scholar] [CrossRef] [PubMed]
- Jeon, Y.; Watanabe, A.; Hagiwara, S.; Yoshino, K.; Yoshioka, H.; Quek, S.; Feng, M. Interpretable and Lightweight 3-D Deep Learning Model For Automated ACL Diagnosis. IEEE J. Biomed. Health Inform. 2021, 25, 2388–2397. [Google Scholar] [CrossRef]
- Belton, N.; Welaratne, I.; Dahlan, A.; Hearne, R.; Hagos, M.T.; Lawlor, A.; Curran, K. Optimising Knee Injury Detection with Spatial Attention and Validating Localisation Ability. In MIUA 2021: Medical Image Understanding and Analysis; Springer: Cham, Switzerland, 2021; pp. 71–86. [Google Scholar] [CrossRef]
- Tao, Q.; Ge, Z.; Cai, J.; Yin, J.; See, S. Improving Deep Lesion Detection Using 3D Contextual and Spatial Attention. In MICCAI 2019: Medical Image Computing and Computer Assisted Intervention; Springer: Cham, Switzerland, 2019; pp. 185–193. [Google Scholar] [CrossRef]
- Awan, M.; Rahim, M.; Salim, N.; Rehman, A.; Nobanee, H.; Shabir, H. Improved Deep Convolutional Neural Network to Classify Osteoarthritis from Anterior Cruciate Ligament Tear Using Magnetic Resonance Imaging. J. Pers. Med. 2021, 11, 1163. [Google Scholar] [CrossRef] [PubMed]
- Chang, P.; Wong, T.; Rasiej, M. Deep Learning for Detection of Complete Anterior Cruciate Ligament Tear. J. Digit. Imaging 2019, 32, 980–986. [Google Scholar] [CrossRef]
- Minamoto, Y.; Akagi, R.; Maki, S.; Shiko, Y.; Tozawa, R.; Kimura, S.; Yamaguchi, S.; Kawasaki, Y.; Ohtori, S.; Sasho, T. Automated detection of anterior cruciate ligament tears using a deep convolutional neural network. BMC Musculoskelet. Disord. 2022, 23, 577. [Google Scholar] [CrossRef]
- Becker, H.C.; Nettleton, W.J.; Meyers, P.H.; Sweeney, J.W.; Nice, C.M. Digital Computer Determination of a Medical Diagnostic Index Directly from Chest X-Ray Images. IEEE Trans. Biomed. Eng. 1964, BME-11, 67–72. [Google Scholar] [CrossRef]
- Lee, W.L.; Chen, Y.C.; Hsieh, K.S. Ultrasonic liver tissue classification by fractal feature vector based on M-band wavelet transform. IEEE Trans. Med. Imaging 2003, 22, 382–392. [Google Scholar] [CrossRef]
- Paredes, R.; Keysers, D.; Lehmann, T.; Wein, B.; Ney, H.; Vidal, E. Classification of Medical Images Using Local Representations. In Bildverarbeitung für die Medizin 2002; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Caicedo, J.; Cruz-Roa, A.; González, F. Histopathology Image Classification Using Bag of Features and Kernel Functions. In AIME 2009: Artificial Intelligence in Medicine; Springer: Berlin/Heidelberg, Germany, 2009; pp. 126–135. [Google Scholar] [CrossRef]
- Shen, W.; Zhou, M.; Yang, F.; Yang, C.; Tian, J. Multi-scale Convolutional Neural Networks for Lung Nodule Classification. In IPMI 2015: Information Processing in Medical Imaging; Springer: Cham, Switzerland, 2015; Volume 24, pp. 588–599. [Google Scholar] [CrossRef]
- Payan, A.; Montana, G. Predicting Alzheimer’s disease: A neuroimaging study with 3D convolutional neural networks. In Proceedings of the ICPRAM 2015—4th International Conference on Pattern Recognition Applications and Methods, Lisbon, Portugal, 10–12 January 2015; Volume 2. [Google Scholar]
- Gong, X.; Xia, X.; Zhu, W.; Zhang, B.; Doermann, D.S.; Zhuo, L. Deformable Gabor Feature Networks for Biomedical Image Classification. arXiv 2020, arXiv:2012.04109. Available online: http://xxx.lanl.gov/abs/2012.04109 (accessed on 10 March 2023).
- Wei, J.; Suriawinata, A.; Ren, B.; Liu, X.; Lisovsky, M.; Vaickus, L.; Brown, C.; Baker, M.; Nasir-Moin, M.; Tomita, N.; et al. Learn like a Pathologist: Curriculum Learning by Annotator Agreement for Histopathology Image Classification. In Proceedings of the 2021 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2021; pp. 2472–2482. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.; Cheng, M.M.; Hu, S.M. Attention Mechanisms in Computer Vision: A Survey. Comput. Vis. Media 2021, 8, 331–368. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A.; Kavukcuoglu, K. Spatial Transformer Networks. In Proceedings of the NIPS, Montreal, QB, Canada, 7–12 December 2015. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. arXiv 2017, arXiv:1709.01507. Available online: http://xxx.lanl.gov/abs/1709.01507 (accessed on 10 March 2023).
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Schlemper, J.; Oktay, O.; Schaap, M.; Heinrich, M.; Kainz, B.; Glocker, B.; Rueckert, D. Attention Gated Networks: Learning to Leverage Salient Regions in Medical Images. Med. Image Anal. 2019, 53, 197–207. [Google Scholar] [CrossRef]
- Dai, Y.; Gao, Y.; Liu, F.; Fu, J. Mutual Attention-based Hybrid Dimensional Network for Multimodal Imaging Computer-aided Diagnosis. arXiv 2022, arXiv:2201.09421. [Google Scholar]
- Rubinstein, R.Y. The Cross-Entropy Method for Combinatorial and Continuous Optimization. Methodol. Comput. Appl. Probab. 1999, 1, 127–190. [Google Scholar] [CrossRef]
- Mannor, S.; Peleg, D.; Rubinstein, R. The Cross Entropy Method for Classification. In ICML ’05: Proceedings of the 22nd International Conference on Machine Learning; Association for Computing Machinery: New York, NY, USA, 2005; pp. 561–568. [Google Scholar] [CrossRef]
- Liu, W.; Wen, Y.; Yu, Z.; Yang, M. Large-Margin Softmax Loss for Convolutional Neural Networks. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 507–516. [Google Scholar]
- Sun, Y.; Cheng, C.; Zhang, Y.; Zhang, C.; Zheng, L.; Wang, Z.; Wei, Y. Circle Loss: A Unified Perspective of Pair Similarity Optimization. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 6397–6406. [Google Scholar] [CrossRef]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal Loss for Dense Object Detection. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2999–3007. [Google Scholar] [CrossRef]
- Li, X.; Wang, W.; Wu, L.; Chen, S.; Hu, X.; Li, J.; Tang, J.; Yang, J. Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection. In Proceedings of the NeurIPS, Virtual, 6–12 December 2020. [Google Scholar]
- Mazumdar, I.; Mukherjee, J. Fully Automatic MRI Brain Tumor Segmentation Using Efficient Spatial Attention Convolutional Networks with Composite Loss. Neurocomputing 2022, 500, 243–254. [Google Scholar] [CrossRef]
- Chen, P.; Gao, L.; Shi, X.; Allen, K.; Yang, L. Fully Automatic Knee Osteoarthritis Severity Grading Using Deep Neural Networks with a Novel Ordinal Loss. Comput. Med. Imaging Graph. 2019, 75, 84–92. [Google Scholar] [CrossRef]
- Liu, W.; Ge, T.; Luo, L.; Hong, P.; Xu, X.; Chen, Y.; Zhuang, Z. A Novel Focal Ordinal Loss for Assessment of Knee Osteoarthritis Severity. Neural Process. Lett. 2022, 54, 5199–5224. [Google Scholar] [CrossRef]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-view Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar] [CrossRef]
- Luo, X.; Xu, J.; Xu, Z. Channel Importance Matters in Few-Shot Image Classification. Int. Conf. Mach. Learn. 2022, 162, 14542–14559. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).