Efficient False Positive Control Algorithms in Big Data Mining
Abstract
1. Introduction
- (1)
- A distributed PFWER false positive control algorithm is proposed. Based on the proof that the threshold calculation task is decomposable, the PFWER false-positive control threshold calculation problem on large data is extended to a distributed solvable problem through task decomposition and the merging of local results. Theoretical analysis and experimental findings indicate that the algorithm outperforms similar algorithms in terms of execution efficiency.
- (2)
- An FP tree with an index structure and a pruning strategy is proposed. The pruning strategy can reduce the number of condition trees constructed, and the index structure can reduce the computation of redundant patterns in FP tree construction. The experimental findings show that the two strategies can significantly reduce the number of traversals of the dataset and the pattern computation overhead, which greatly improves computational efficiency.
2. Related Concepts and Techniques
2.1. Concepts Related to False Positives
2.1.1. Hypothesis Testing
2.1.2. Multiple Hypothesis Testing
2.1.3. False Positive
2.1.4. Calculation of p-Value
- (1)
- Fisher’s exact test
- (2)
- Barnard’s exact test
2.2. False Positive Control-Related Methods
- Direct adjustment method: The direct adjustment method is the direct control of false positives using the implementation algorithm of FWER or FDR. A common direct adjustment method for FWER is the Bonferroni correction [27,28], which calculates the hypothesized p-value and considers it significant if the p-value is not greater than . A common direct adjustment method for FDR is the BH procedure [19], where the p-values are sorted in ascending order , if , holds, it is considered that is statistically significant.
- Permutation-based approach: The permutation-based approach [29] is to randomly disrupt the class labels and then recombine them with the transactions and recalculate the p-values [30,31]. Since the individual hypothesis tests are dependent on each other, the random disturbance is used to break the association between the transactions and the class labels. The distribution of the recalculated p-values is, therefore, an approximation of the null distribution, which allows a more precise determination of the truncation threshold (corrected significance threshold) of the p-values.
- 3.
- Maintenance assessment method: The hold-evaluation method [32] divides the dataset into two parts, the exploration dataset and the evaluation dataset. First, the hypotheses to be tested need to be identified from the exploration dataset first, and then the hypotheses with p-values no greater than are passed to the evaluation dataset for validation. To control the FWER at the level, the Bonferroni correction [27,28] can be used to adjust the p-values of the hypotheses to be tested on the evaluation dataset. To control the FDR at the level, the method proposed by Benjamini and Hochberg can be used in a similar way.
2.3. Pattern Mining-Related Techniques
2.4. Distributed Computing Frameworks
- Hadoop framework: Hadoop [21] is a distributed infrastructure framework developed by the Apache Foundation, which is mainly used to solve the problem of massive data storage and massive data analysis and can be applied to logistics warehouses, the retail industry, recommendation systems, the insurance and finance industry, and the artificial intelligence industry. Hadoop is suitable for processing large-scale data, and it can handle more than one million data [39,40]. Hadoop uses HDFS for dis tributed file management, which automatically saves multiple copies of the data and can recover the data from backups of other nodes in case of power failure or program bugs, thus increasing the system’s tolerance for errors.
- 2.
- Spark Framework: Spark is an in-memory-based big data processing engine [41]. Spark makes up for the shortcomings of the Hadoop 1.x framework, which is not suitable for iterative computing, has very slow performance, and has high coupling. Spark itself can support multiple programming languages, so big data developers can choose the most suitable language for program development according to the program usage scenarios and their own coding habits. Spark can be installed and used on laptops as well as on large server clusters. It can not only provide learning convenience for beginners but also process large-scale data in actual production applications [42]. Spark supports SQL and stream processing as well as machine learning tasks.
3. PFWER-Based Distributed False Positive Control Algorithm
3.1. Problem Definition
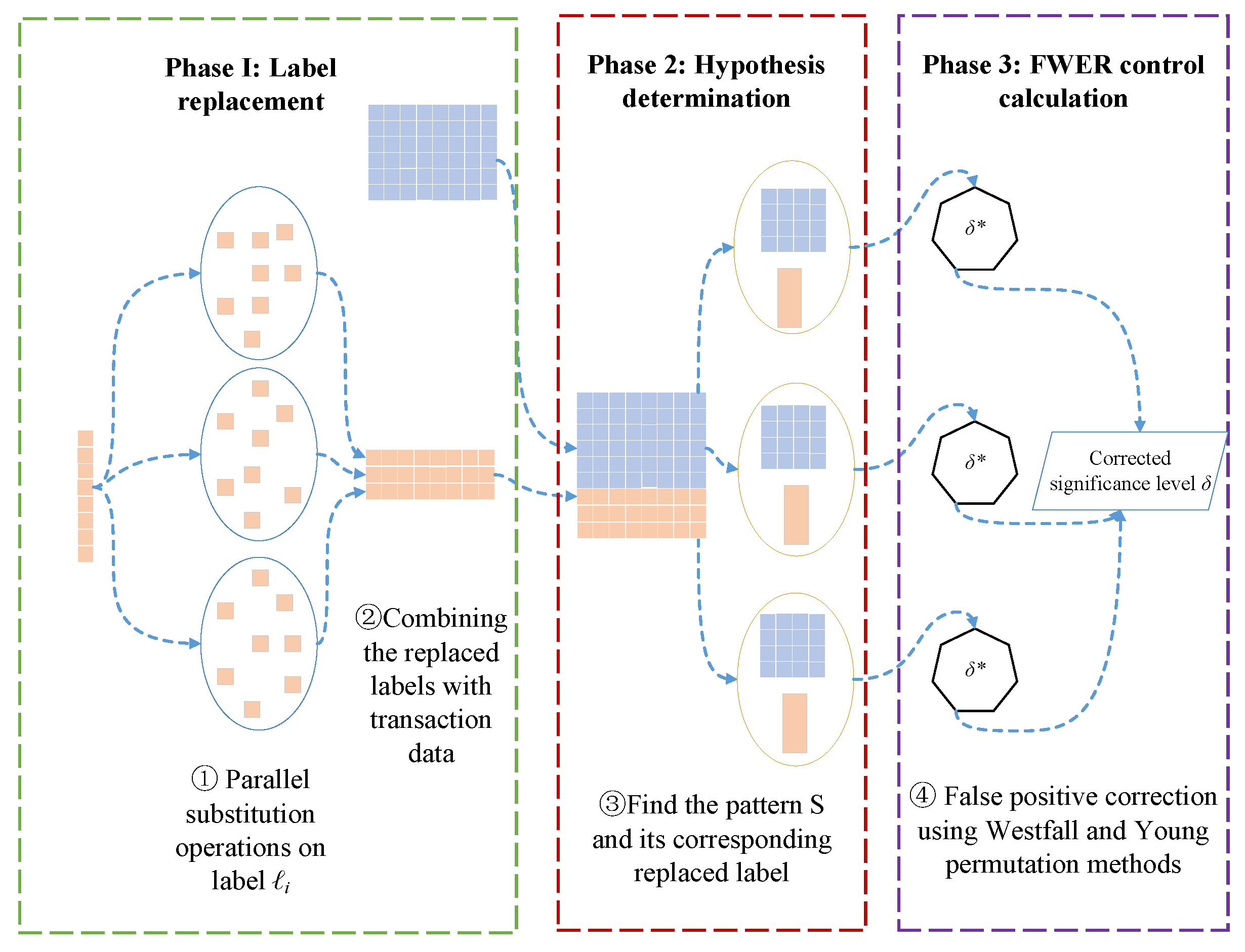
3.2. Overall Framework of the Algorithm
- Label permutation operation. According to the replacement method proposed by Westfall and Young [30,43], it is known that to calculate the truncated p-value (corrected significance level ) more accurately, it is necessary to perform a replacement operation on the label (generally performing times replacement) to achieve the purpose of breaking the association between pattern S and label .
- Finding the hypothesis to be tested in multiple hypothesis testing. Since the null hypothesis is composed of two key elements, pattern S and label , the main task of the second stage of the algorithm is to find all patterns S and their corresponding labels in the transactional dataset D.
- False-positive correction calculation. After finding the hypotheses to be tested and permuting the labels, the p-value of each hypothesis was calculated according to Fisher’s exact test. The false-positive correction was then performed according to the Westfall and Young [30,43] replacement method, and finally, the FWER was controlled at the level.
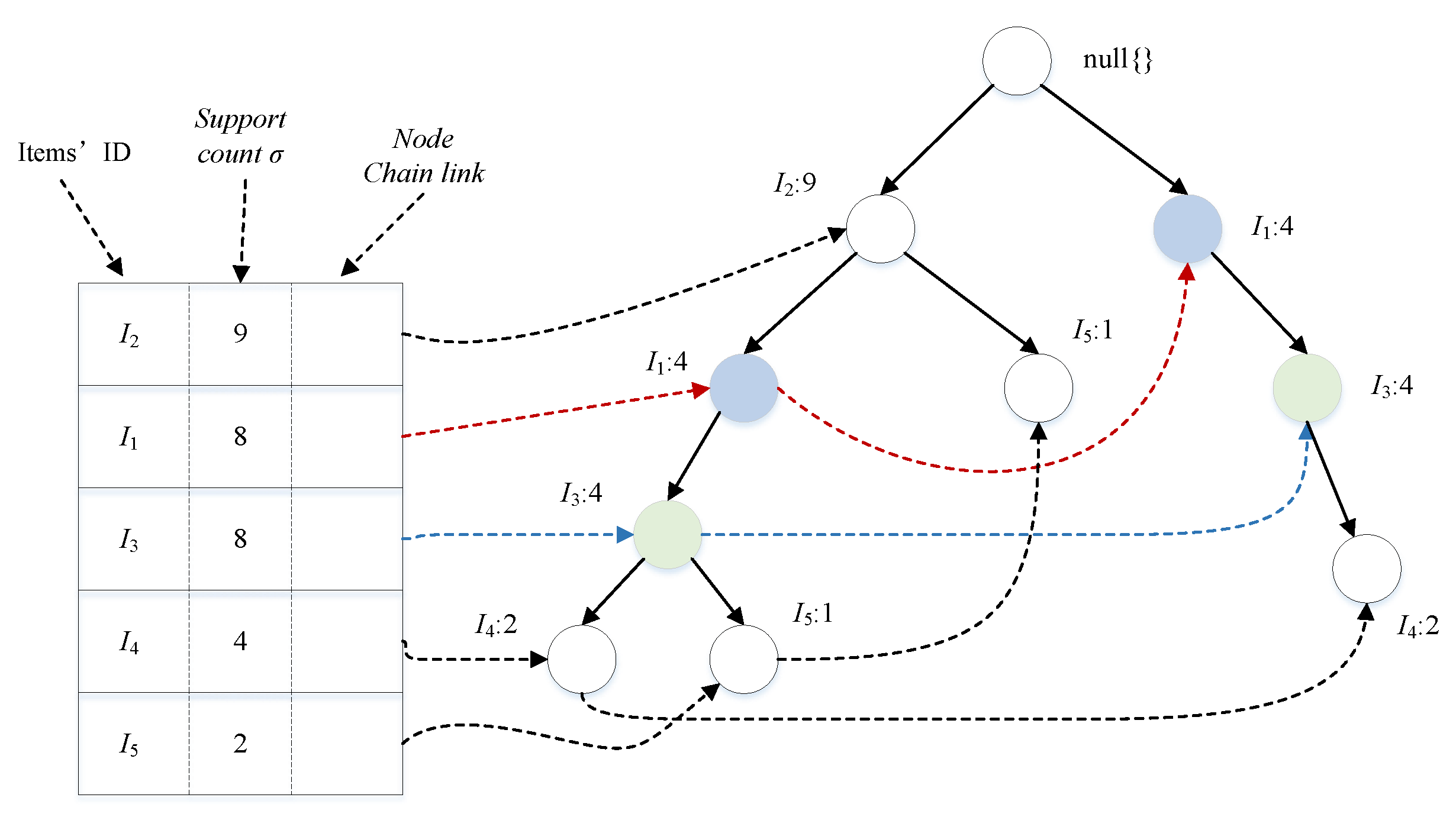
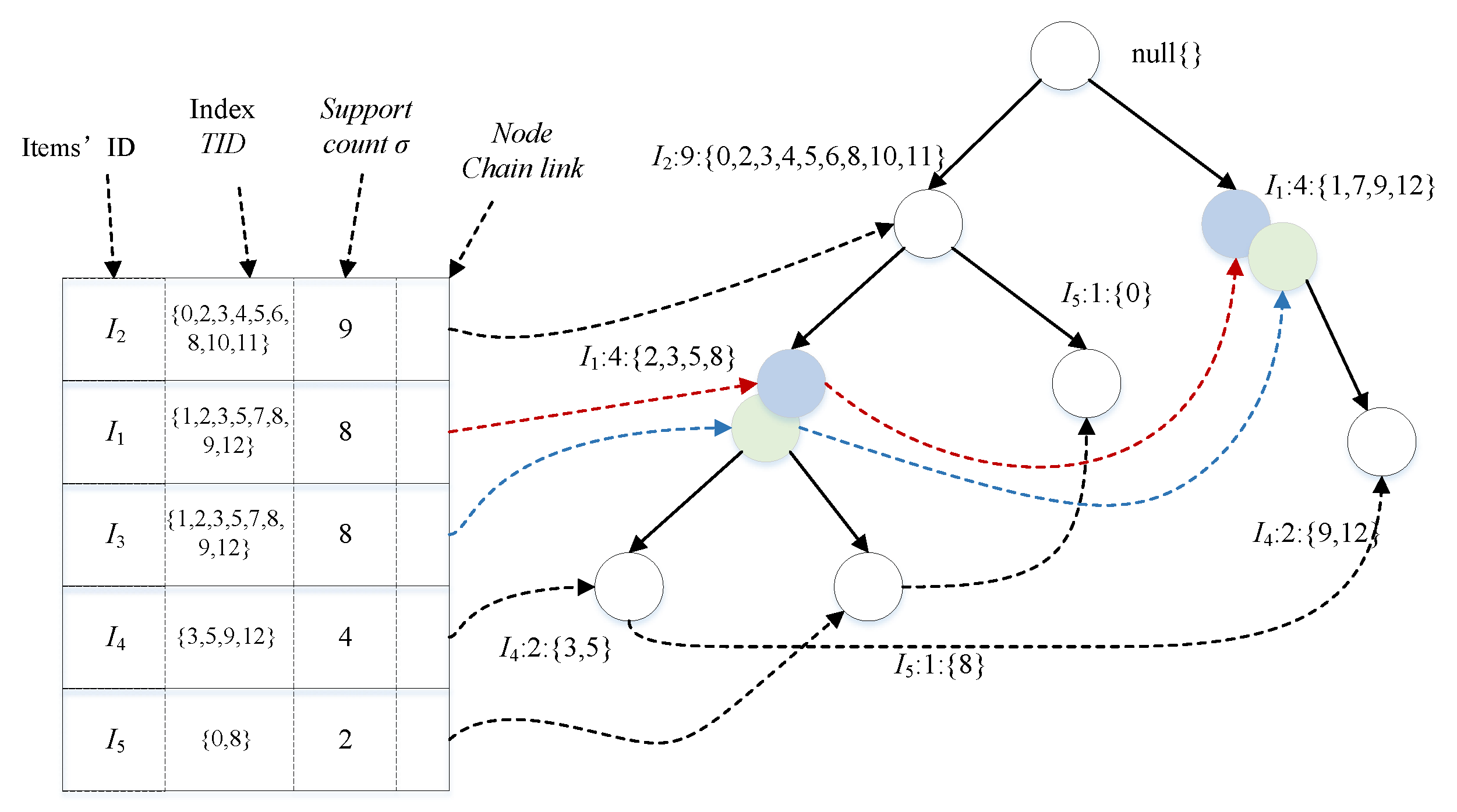
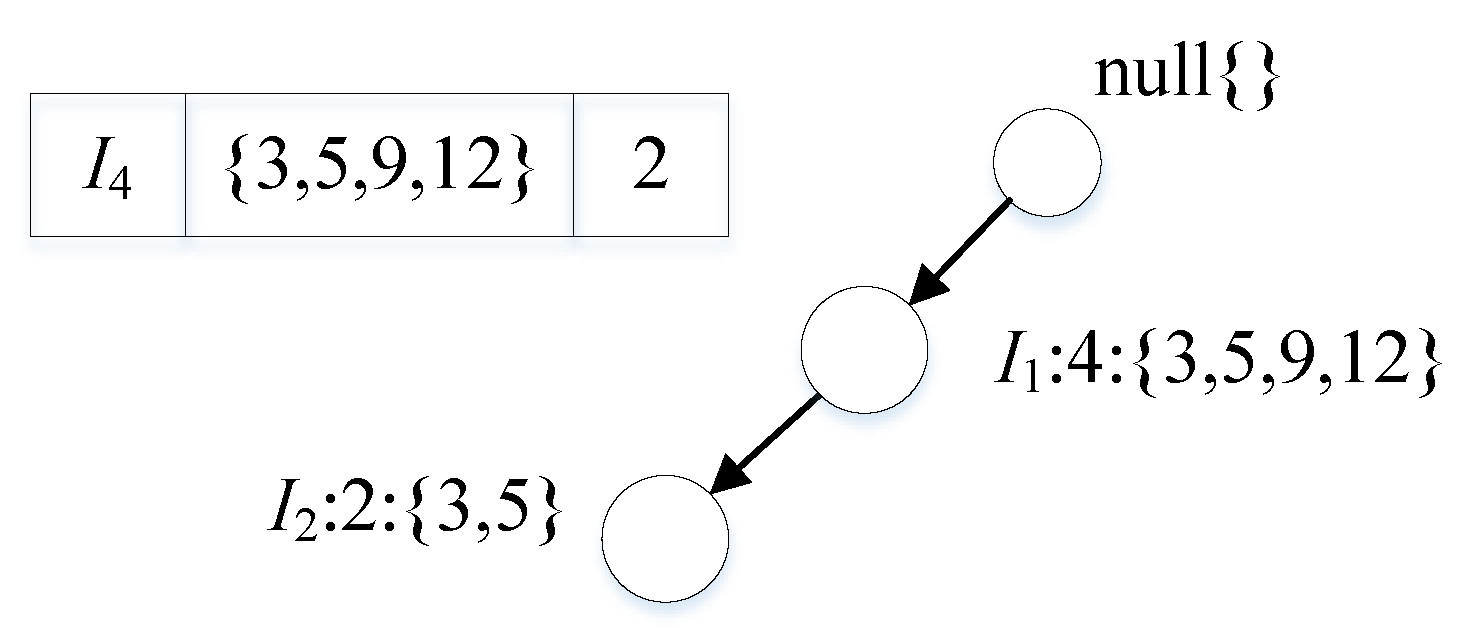
3.3. Index-Tree Algorithm
3.3.1. Pattern Mining
3.3.2. Pruning Operation
3.3.3. Index Optimization
| Algorithm 1 Index Tree |
| Require: Ensure: 1: 2: 3: 4: 5: if then 6: for do 7: 8: end for 9: else 10: for each do 11: 12: 13: 14: 15: if then 16: 17: end if 18: end for 19: end if |
| Algorithm 2 IPFP Tree |
| Require:
Ensure: 1: for do 2: if then 3: for , do 4: if then 5: if and then 6: 7: 8: end if 9: end if 10: end for 11: end if 12: 13: end for |
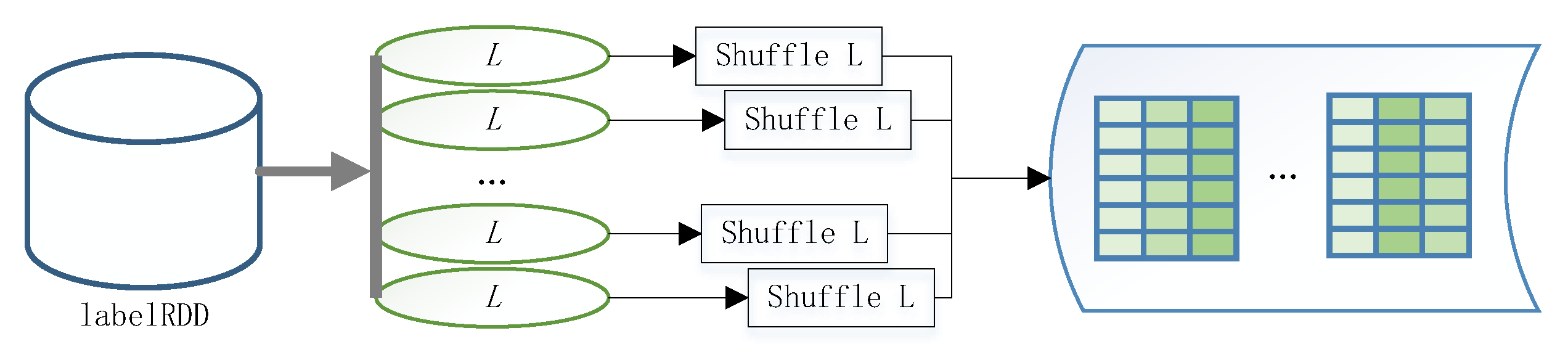
3.4. Distributed PFWER Control Algorithm
3.4.1. Label Replacement
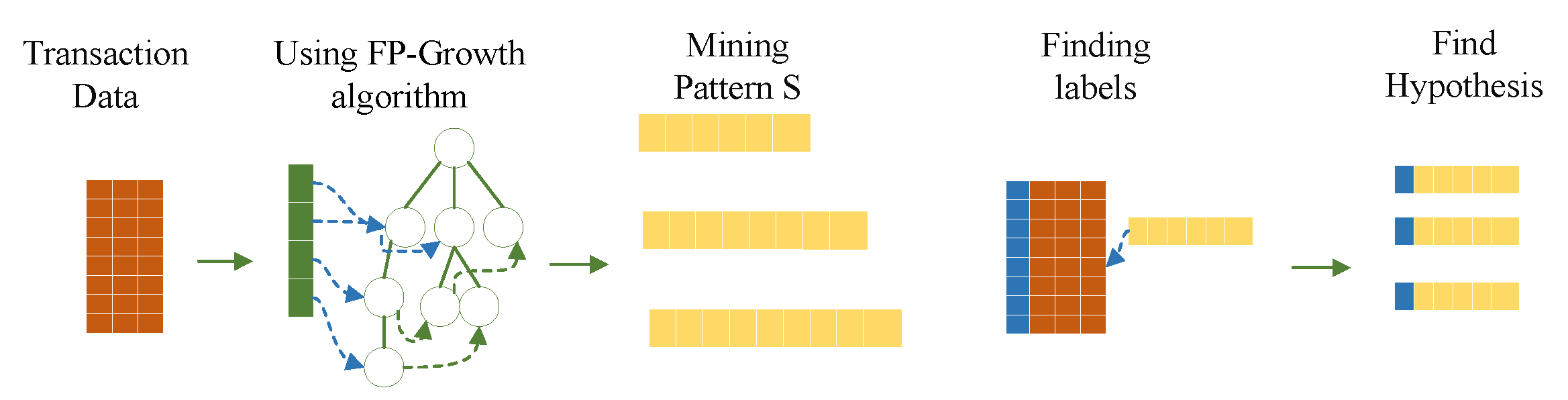
3.4.2. Hypothesis Determination
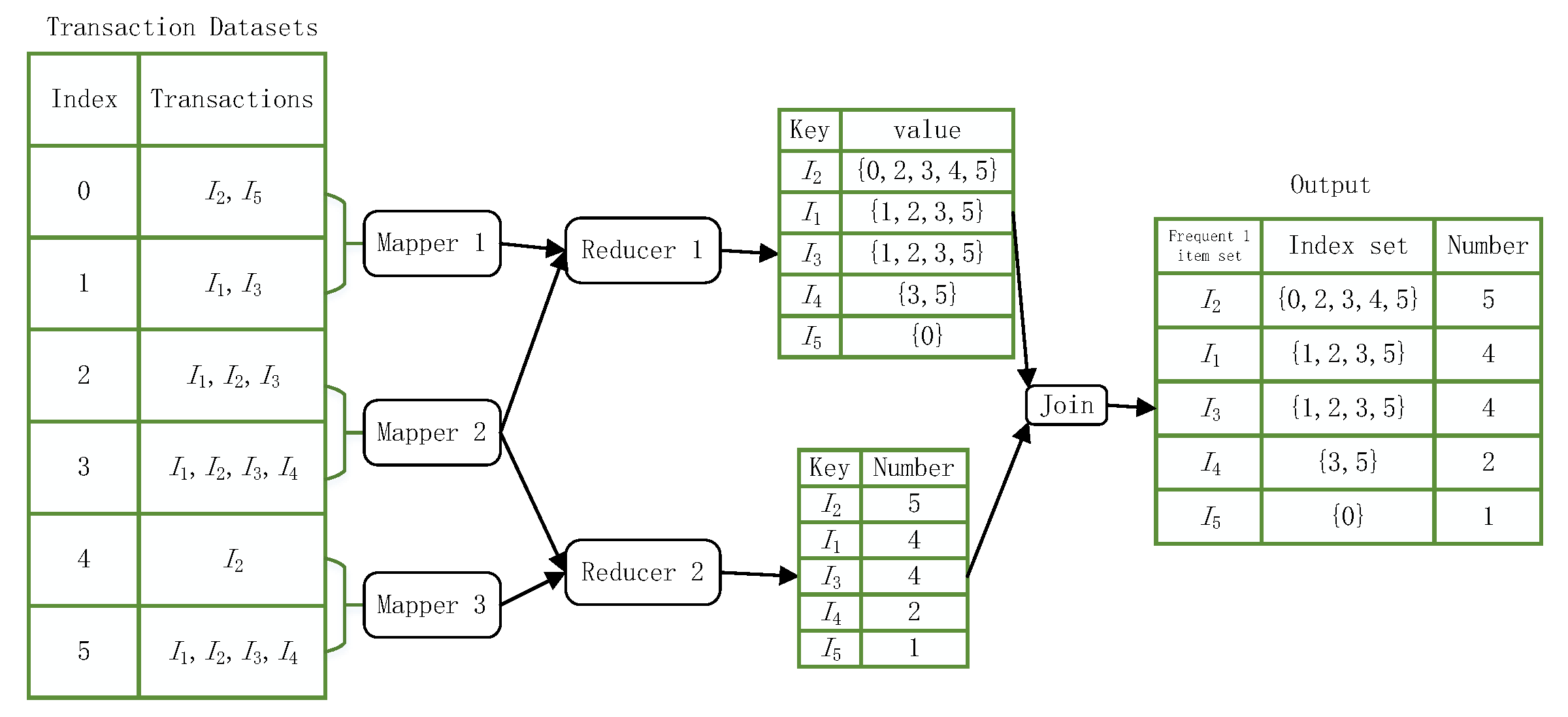
- First, the items in the dataset should be split using the flatMap operator to construct <key = item,value = index> key-value pairs in parallel and the map operator to construct <key = item,value = 1> key-value pairs.
- Secondly, the key-value pairs of <key = item,value = 1> are computed cumulatively using the reduceByKey algorithm. The computed key is the item name, and the value is the number of items in the dataset.
- Next, the key-value pair <key=item,value = index> is computed using the groupByKey operator to obtain a new key-value pair <key = item,value = index>, where the value is the index set containing the key values.
- Finally, use the join operator to combine <key = item,value = index> and <key = item,value = count> into a new key-value pair <key = item,value = count + index> and output it in descending order of the count of the values in each key-value pair to get the item header table for subsequent calculations.
3.4.3. False Positive Control
| Algorithm 3 DS-FWER(D) |
| Require:
D Ensure: 1: 2: 3: , 4: , 5: , 6: 7: , 8: 9: 10: 11: Return quantile of |
| Algorithm 4 WY Algorithm |
| Require: Ensure: 1: 2: for do 3: Compute 4: 5: end for 6: 7: while do 8: 9: 10: end while 11: for do 12: Compute 13: if then 14: 15: end if 16: end for |
3.5. Proof of Correctness
4. Experiments and Performance Analysis
4.1. Experimental Environment Configuration
4.2. Experimental Dataset
4.3. Distributed PFWER False Positive Control Experiment
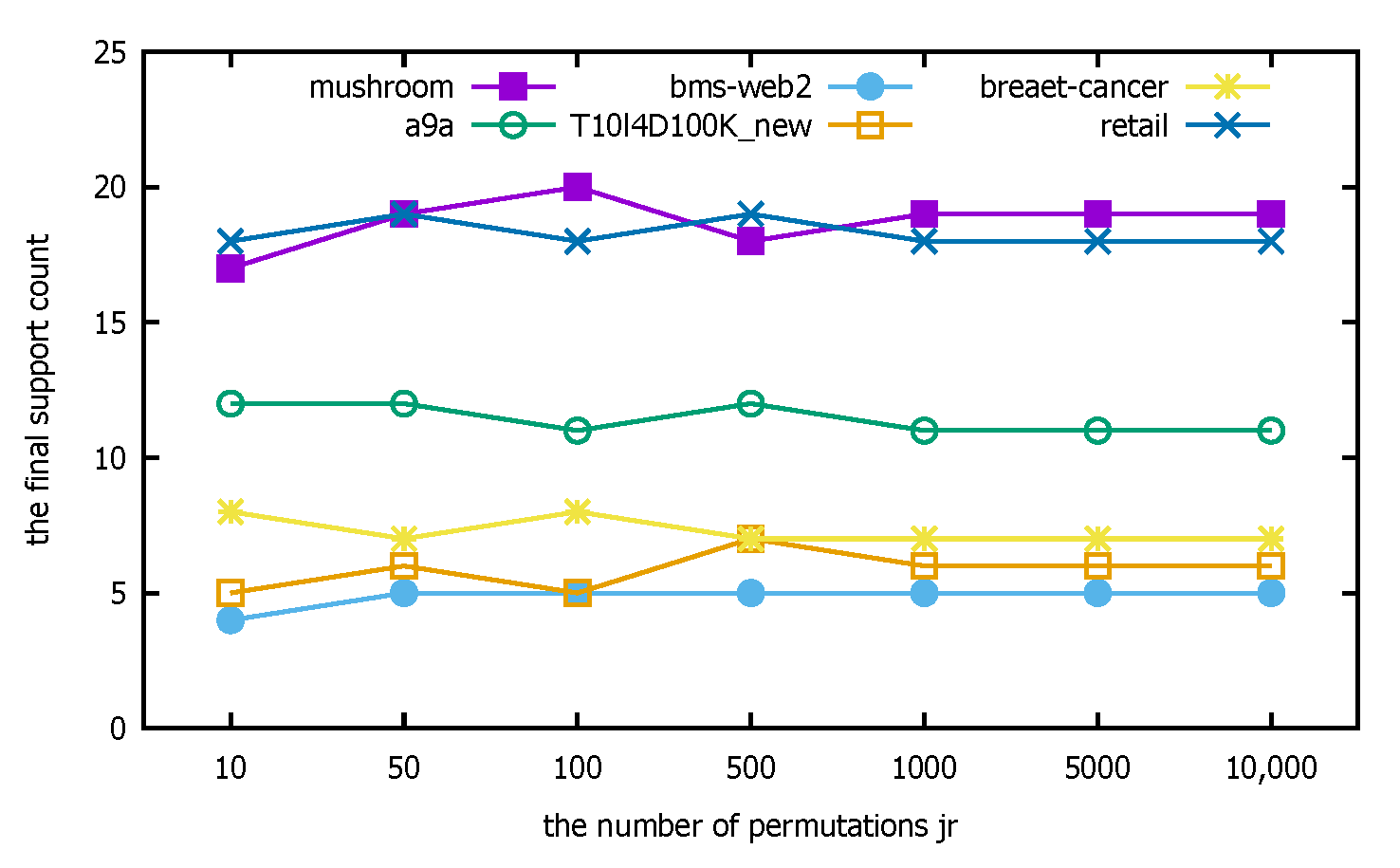
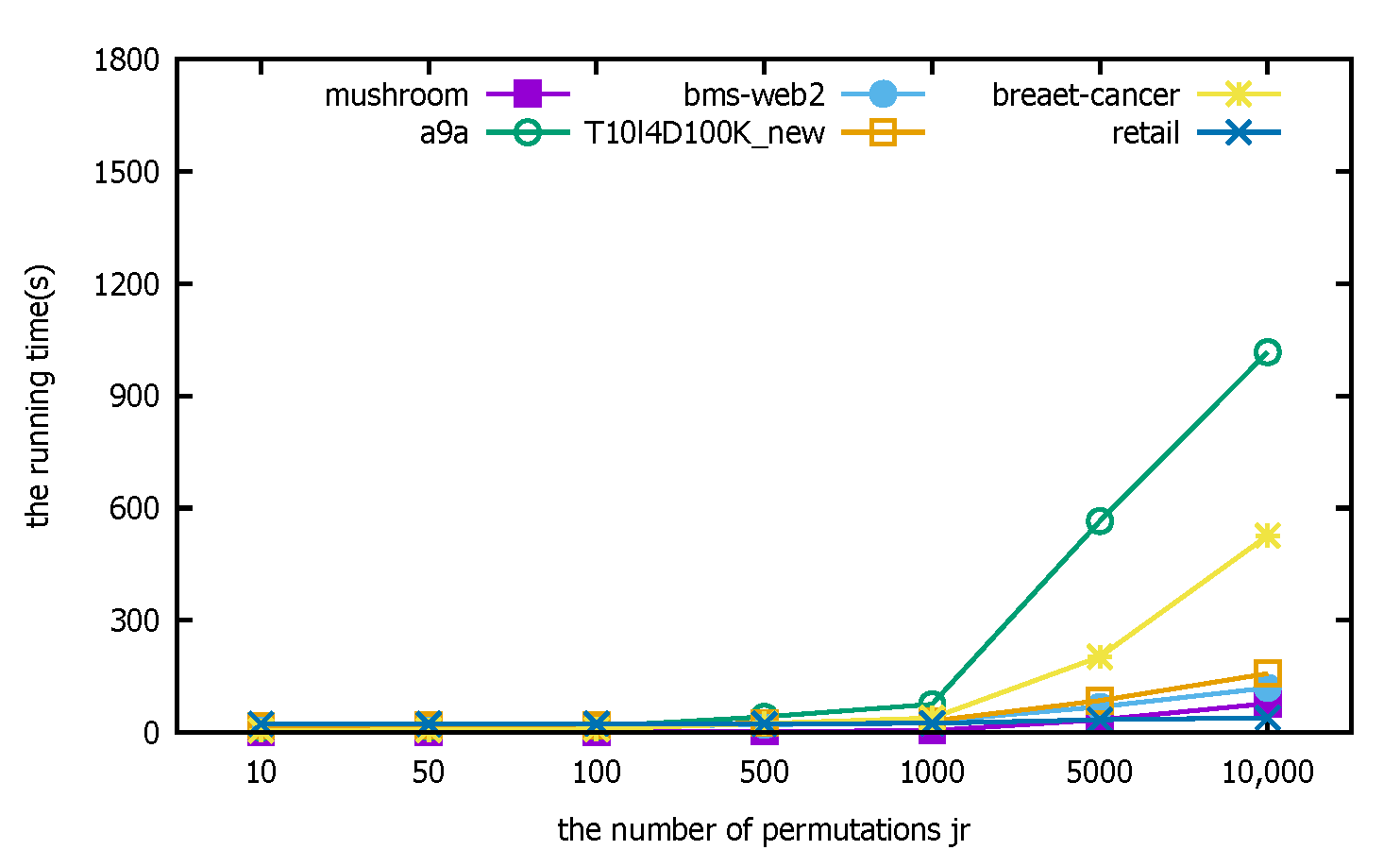
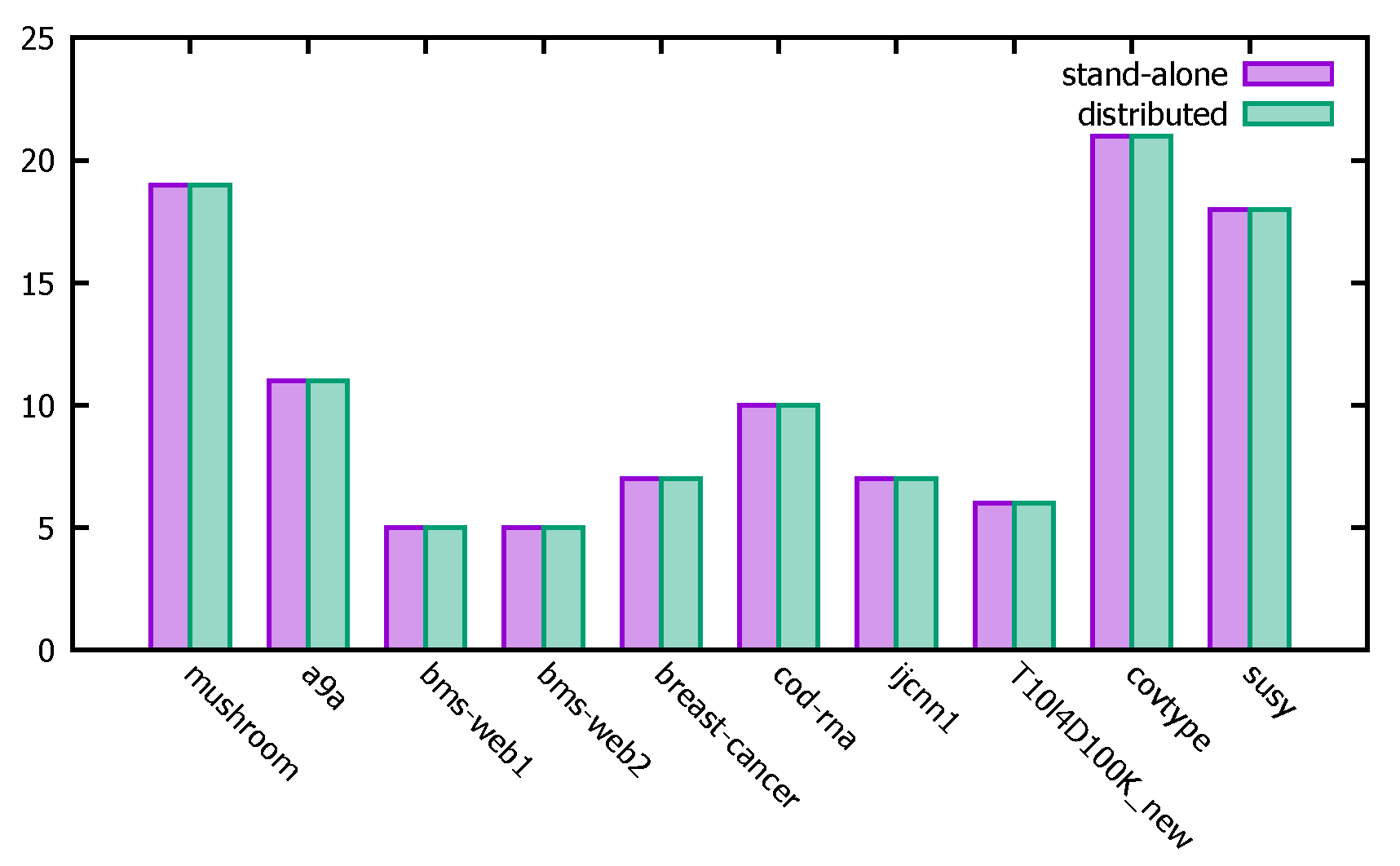
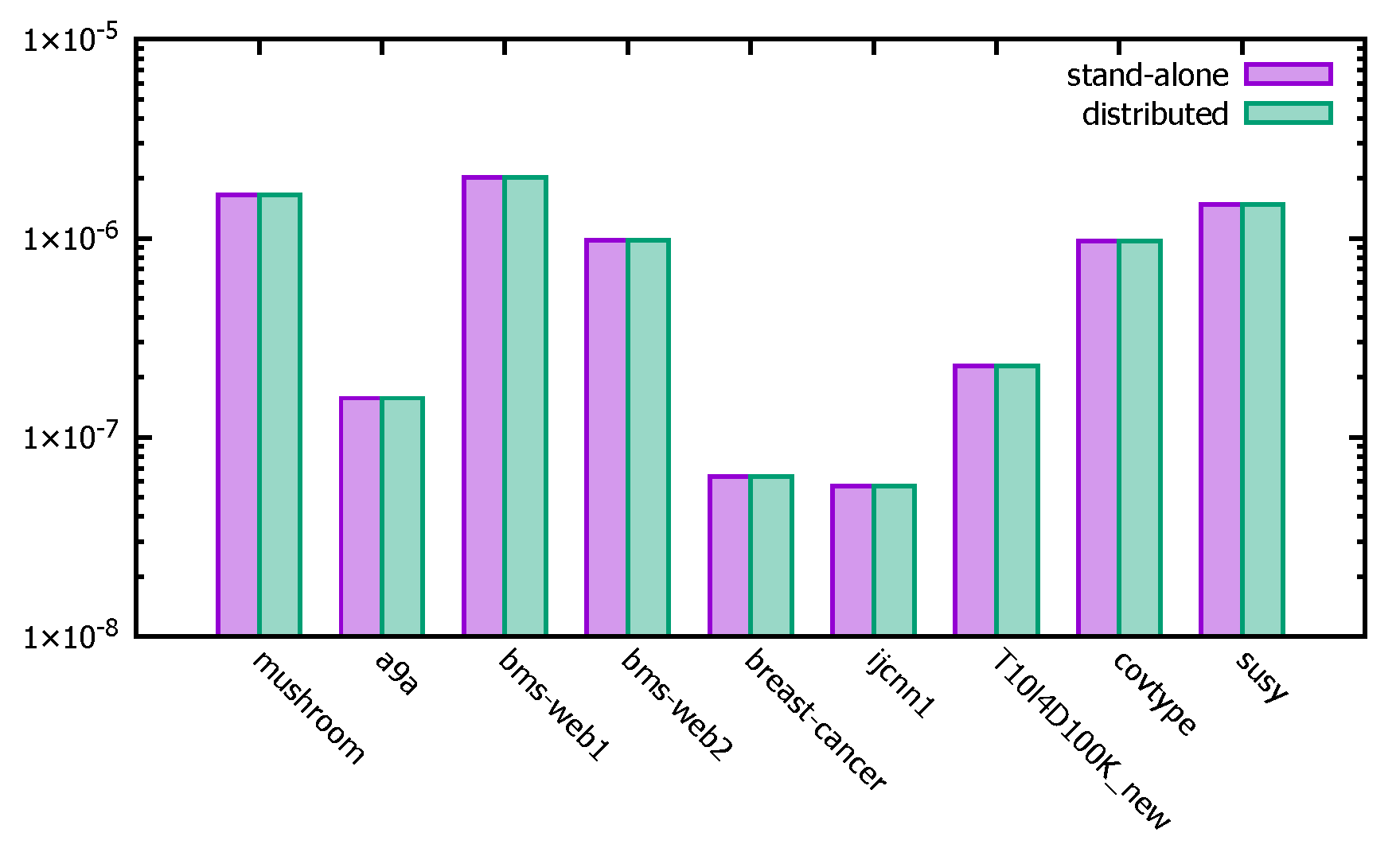
4.3.1. Determination of The Number of Permutations
- Experimental description: This section focuses on determining the parameter used in the distributed PFWER false positive control, i.e., the number of label replacements, jr. Label replacement is an important element to ensure the accuracy of the distributed PFWER false positive control results, and its purpose is to make sure there is no relationship between labels and patterns. The null hypothesis proposed in this paper is satisfied by the absence of an association between the mode and label and by avoiding the influence of inter-mode dependencies on the computational results. The experiment is to test the effect of the PFWER false positive control algorithm on the false positive control effect by setting different numbers of substitutions in the label substitution stage. In this paper, the FP-Growth algorithm will be used to perform the pattern mining operation for all comparison experiments.
- Experimental analysis: The distributed PFWER false positive control uses a permutation-based approach for the control calculation. The known cost in setting the permutation value, jr, is that the larger the jr, the more accurate the final corrected significance threshold is estimated, but the cost is that the running time increases with the increase in jr. The following figure represents the computation for different datasets with different jr.
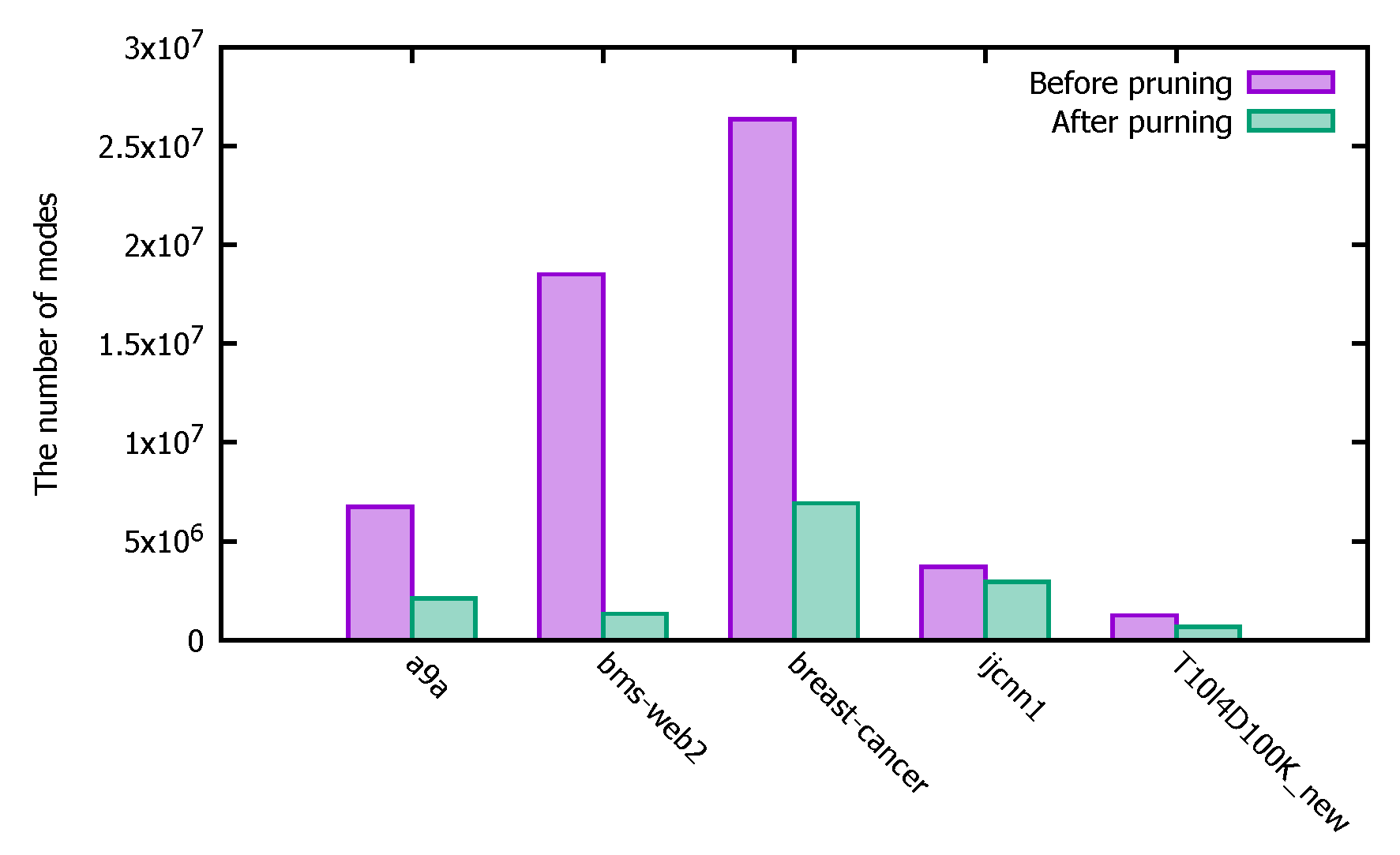
4.3.2. Pruning Efficiency Analysis
- (1)
- Experimental description
- (2)
- Experimental analysis
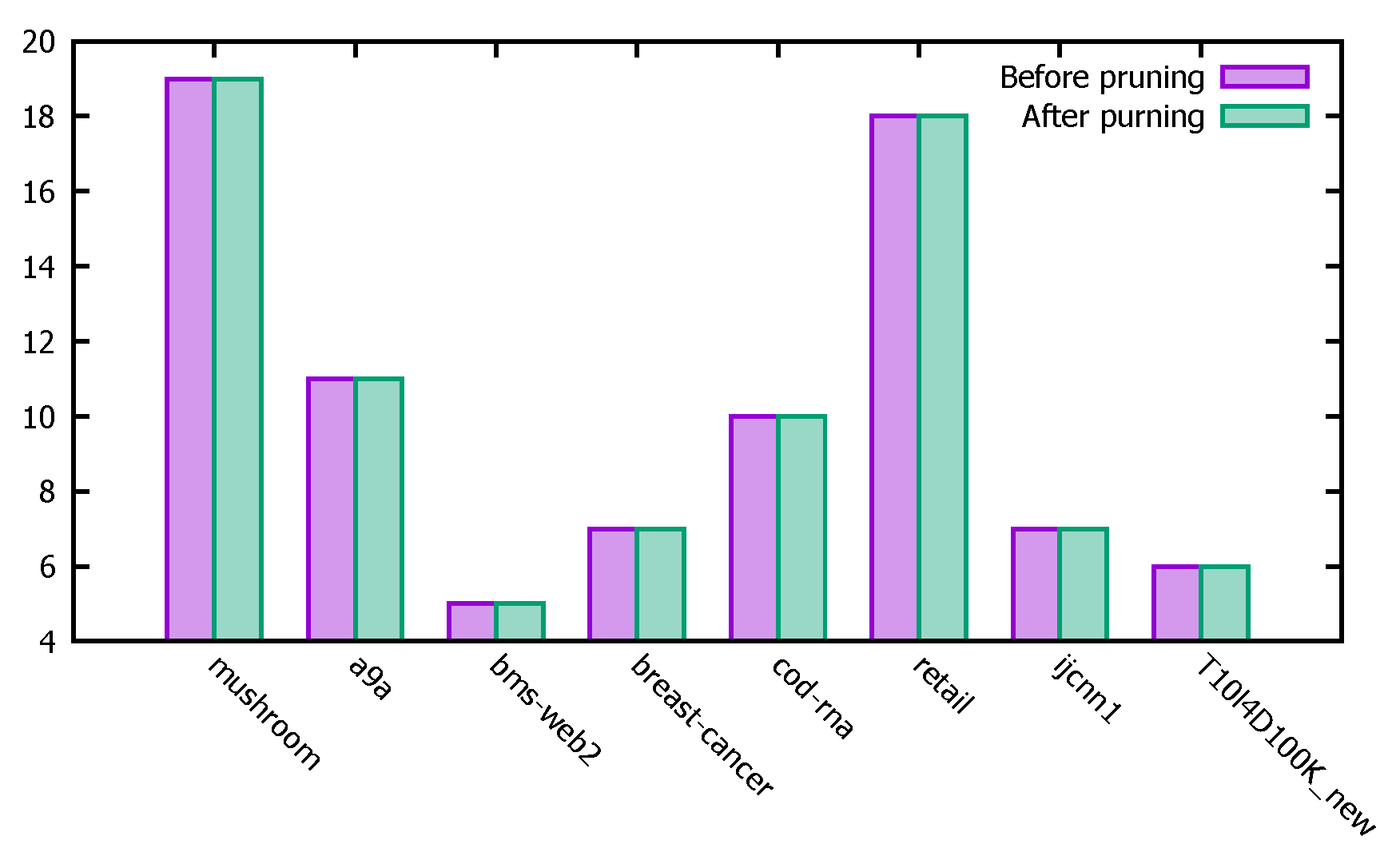
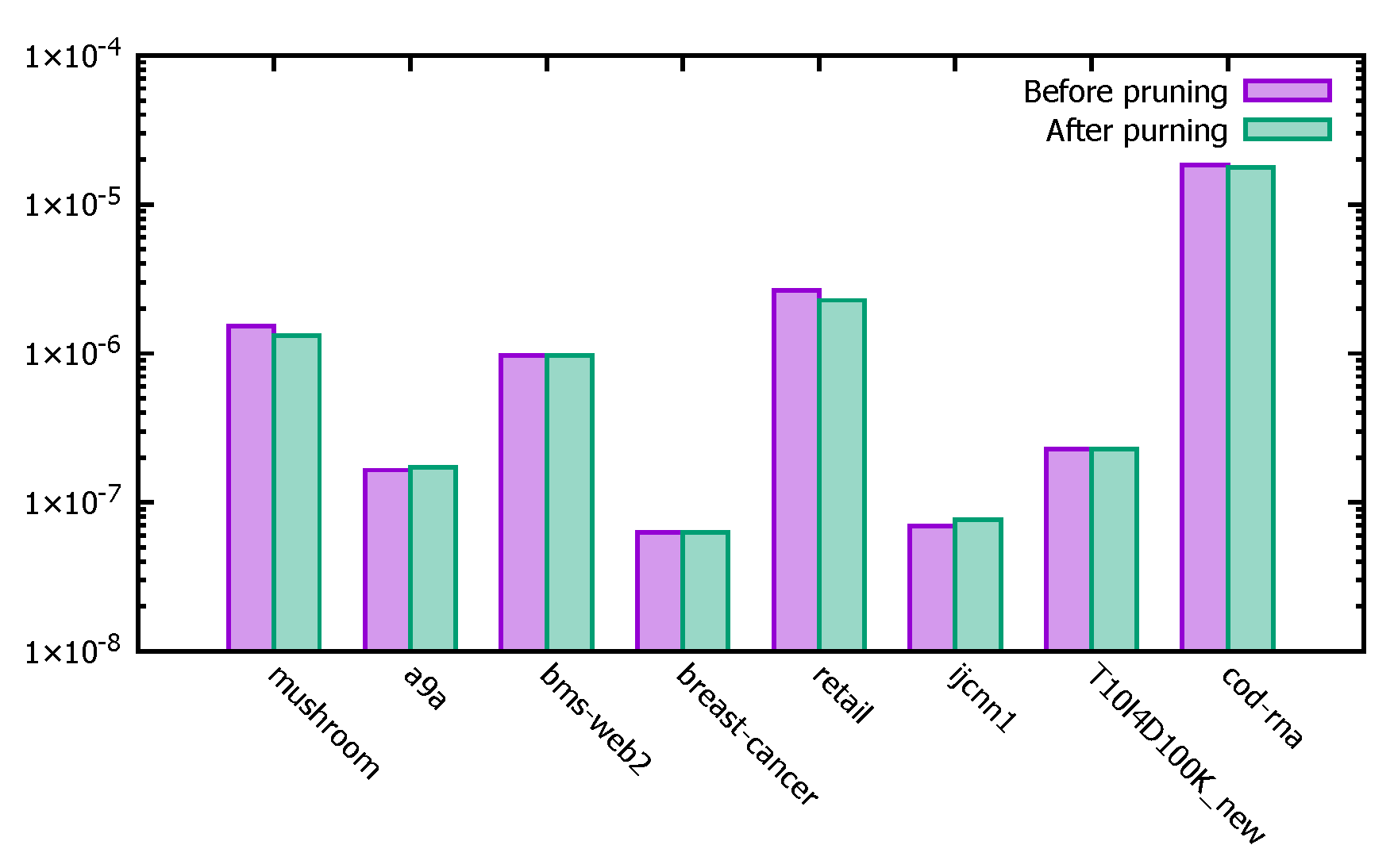
4.3.3. Accuracy Test
- (1)
- Experiment Description
- (2)
- Experimental Analysis
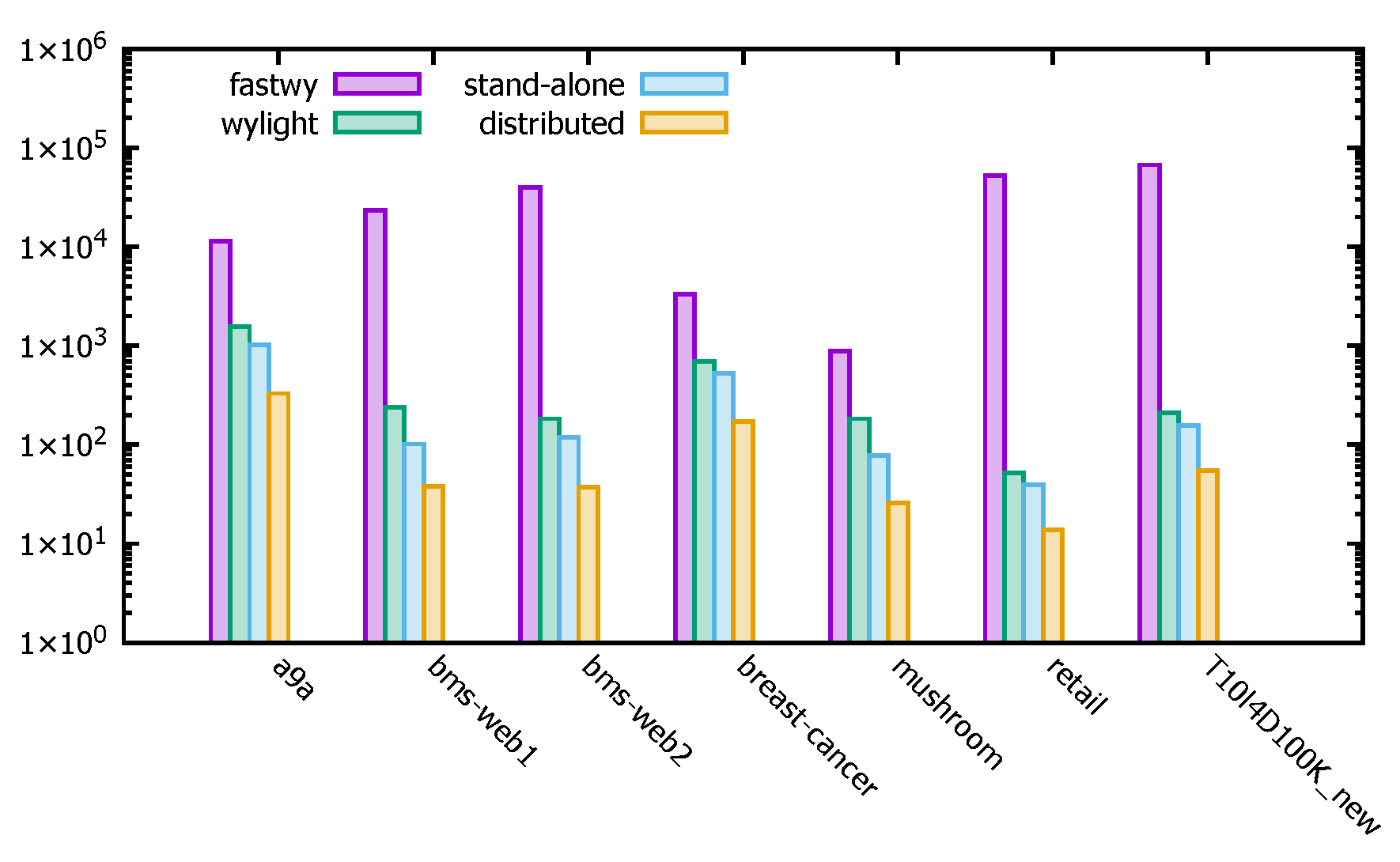
4.3.4. Operational Efficiency Test
- (1)
- Experimental Description
- (2)
- Experimental Analysis
4.4. Summary
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Erdogmus, H. Bayesian Hypothesis Testing Illustrated: An Introduction for Software Engineering Researchers. ACM Comput. Surv. 2023, 55, 119:1–119:28. [Google Scholar] [CrossRef]
- Munoz, A.; Martos, G.; Gonzalez, J. Level Sets Semimetrics for Probability Measures with Applications in Hypothesis Testing. Methodol. Comput. Appl. Probab. 2023, 25, 21. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, C.; Shelby, L.; Huan, T.C. Customers’ self-image congruity and brand preference: A moderated mediation model of self-brand connection and self-motivation. J. Prod. Brand Manag. 2022, 31, 798–807. [Google Scholar] [CrossRef]
- Jensen, R.I.T.; Iosifidis, A. Qualifying and raising anti-money laundering alarms with deep learning. Expert Syst. Appl. 2023, 214, 119037. [Google Scholar] [CrossRef]
- Llinares-López, F.; Sugiyama, M.; Papaxanthos, L.; Borgwardt, K.M. Fast and Memory-Efficient Significant Pattern Mining via Permutation Testing. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; Cao, L., Zhang, C., Joachims, T., Webb, G.I., Margineantu, D.D., Williams, G., Eds.; ACM: New York, NY, USA, 2015; pp. 725–734. [Google Scholar] [CrossRef]
- Dey, M.; Bhandari, S.K. FWER goes to zero for correlated normal. Stat. Probab. Lett. 2023, 193, 109700. [Google Scholar] [CrossRef]
- Samarskiĭ, A. Claverie JM: The significance of digital gene expression profiles. Genome Res. 1997, 7, 986–995. [Google Scholar]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Simes, R.J. An improved Bonferroni procedure for multiple tests of significance. Biometrika 1986, 73, 751–754. [Google Scholar] [CrossRef]
- Hochberg, Y. A sharper Bonferroni procedure for multiple tests of significance. Biometrika 1988, 75, 800–802. [Google Scholar] [CrossRef]
- Pellegrina, L.; Vandin, F. Efficient Mining of the Most Significant Patterns with Permutation Testing. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD 2018), London, UK, 19–23 August 2018; Guo, Y., Farooq, F., Eds.; ACM: New York, NY, USA, 2018; pp. 2070–2079. [Google Scholar] [CrossRef]
- Hang, D.; Zeleznik, O.A.; Lu, J.; Joshi, A.D.; Wu, K.; Hu, Z.; Shen, H.; Clish, C.B.; Liang, L.; Eliassen, A.H.; et al. Plasma metabolomic profiles for colorectal cancer precursors in women. Eur. J. Epidemiol. 2022, 37, 413–422. [Google Scholar] [CrossRef]
- Terada, A.; Tsuda, K.; Sese, J. Fast Westfall-Young permutation procedure for combinatorial regulation discovery. In Proceedings of the IEEE International Conference on Bioinformatics & Biomedicine, Belfast, UK, 2–5 November 2014. [Google Scholar]
- Harvey, C.R.; Liu, Y. False (and Missed) Discoveries in Financial Economics. J. Financ. 2020, 75, 2503–2553. [Google Scholar] [CrossRef]
- Kelter, R. Power analysis and type I and type II error rates of Bayesian nonparametric two-sample tests for location-shifts based on the Bayes factor under Cauchy priors. Comput. Stat. Data Anal. 2022, 165, 107326. [Google Scholar] [CrossRef]
- Andrade, C. Multiple Testing and Protection Against a Type 1 (False Positive) Error Using the Bonferroni and Hochberg Corrections. Indian J. Psychol. Med. 2019, 41, 99–100. [Google Scholar] [CrossRef] [PubMed]
- Blostein, S.D.; Huang, T.S. Detecting small, moving objects in image sequences using sequential hypothesis testing. IEEE Trans. Signal Process. 1991, 39, 1611–1629. [Google Scholar] [CrossRef]
- Babu, P.; Stoica, P. Multiple Hypothesis Testing-Based Cepstrum Thresholding for Nonparametric Spectral Estimation. IEEE Signal Process. Lett. 2022, 29, 2367–2371. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodological 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. On the Adaptive Control of the False Discovery Rate in Multiple Testing With Independent Statistics. J. Educ. Behav. Stat. 2000, 25, 60–83. [Google Scholar] [CrossRef]
- Yekutieli, K.D. Adaptive linear step-up procedures that control the false discovery rate. Biometrika 2006, 93, 491–507. [Google Scholar]
- D’Alberto, R.; Raggi, M. From collection to integration: Non-parametric Statistical Matching between primary and secondary farm data. Stat. J. IAOS 2021, 37, 579–589. [Google Scholar] [CrossRef]
- Pawlak, M.; Lv, J. Nonparametric Testing for Hammerstein Systems. IEEE Trans. Autom. Control. 2022, 67, 4568–4584. [Google Scholar] [CrossRef]
- Carlson, J.M.; Heckerman, D.; Shani, G. Estimating False Discovery Rates for Contingency Tables. Technical Report MSR-TR-2009-53, 2009, 1–24. Available online: https://www.microsoft.com/en-us/research/publication/estimating-false-discovery-rates-for-contingency-tables/ (accessed on 13 February 2023).
- Bestgen, Y. Using Fisher’s Exact Test to Evaluate Association Measures for N-grams. arXiv 2021, arXiv:2104.14209. [Google Scholar]
- Pellegrina, L.; Riondato, M.; Vandin, F. SPuManTE: Significant Pattern Mining with Unconditional Testing. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar]
- Terada, A.; Sese, J. Bonferroni correction hides significant motif combinations. In Proceedings of the 13th IEEE International Conference on BioInformatics and BioEngineering (BIBE 2013), Chania, Greece, 10–13 November 2013; pp. 1–4. [Google Scholar] [CrossRef]
- Sultanov, A.; Protsyk, M.; Kuzyshyn, M.; Omelkina, D.; Shevchuk, V.; Farenyuk, O. A statistics-based performance testing methodology: A case study for the I/O bound tasks. In Proceedings of the 17th IEEE International Conference on Computer Sciences and Information Technologies (CSIT 2022), Lviv, Ukraine, 10–12 November 2022; pp. 486–489. [Google Scholar] [CrossRef]
- Paschali, M.; Zhao, Q.; Adeli, E.; Pohl, K.M. Bridging the Gap Between Deep Learning and Hypothesis-Driven Analysis via Permutation Testing; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Young, S.S.; Young, S.S.; Young, S.S. Resampling-Based Multiple Testing: Examples and Methods for p-value Adjustment; John Wiley & Sons: Hoboken, NJ, USA, 1993. [Google Scholar]
- Schwender, H.; Sandrine, D.; Mark, J.; van der Laan, J. Multiple Testing Procedures with Applications to Genomics. Stat. Pap. 2009, 50, 681–682. [Google Scholar] [CrossRef]
- Webb, G.I. Discovering Significant Patterns. Mach. Learn. 2007, 68, 1–33. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, H.; Wong, L. Controlling False Positives in Association Rule Mining. In Proceedings of the VLDB Endowment, Seattle, WA, USA, 29 August–3 September 2011. [Google Scholar]
- Yan, D.; Qu, W.; Guo, G.; Wang, X. PrefixFPM: A Parallel Framework for General-Purpose Frequent Pattern Mining. In Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), Dallas, TX, USA, 20–24 April 2020. [Google Scholar]
- Messner, W. Hypothesis Testing and Machine Learning: Interpreting Variable Effects in Deep Artificial Neural Networks using Cohen’s f2. arXiv 2023, arXiv:2302.01407. [Google Scholar]
- Yu, J.; Wen, Y.; Yang, L.; Zhao, Z.; Guo, Y.; Guo, X. Monitoring on triboelectric nanogenerator and deep learning method. Nano Energy 2022, 92, 106698. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011; pp. 248–253. [Google Scholar]
- Han, J.; Jian, P.; Yin, Y.; Mao, R. Mining Frequent Patterns without Candidate Generation: A Frequent-Pattern Tree Approach. Data Min. Knowl. Discov. 2004, 8, 53–87. [Google Scholar] [CrossRef]
- White, T. Hadoop—The Definitive Guide: Storage and Analysis at Internet Scale, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2011. [Google Scholar]
- Ji, K.; Kwon, Y. New Spam Filtering Method with Hadoop Tuning-Based MapReduce Naïve Bayes. Comput. Syst. Sci. Eng. 2023, 45, 201–214. [Google Scholar] [CrossRef]
- Zaharia, M.; Chowdhury, M.; Das, T.; Dave, A.; Stoica, I. Resilient distributed datasets: A fault-tolerant abstraction for in-memory cluster computing. In Proceedings of the 9th USENIX conference on Networked Systems Design and Implementation, San Jose, CA, USA, 25–27 April 2012. [Google Scholar]
- Chambers, B.; Zaharia, M. Spark: The Definitive Guide: Big Data Processing Made Simple; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Dalleiger, S.; Vreeken, J. Discovering Significant Patterns under Sequential False Discovery Control. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 14–18 August 2022; Zhang, A., Rangwala, H., Eds.; ACM: New York, NY, USA, 2022; pp. 263–272. [Google Scholar] [CrossRef]

| Do Not Reject | Reject | Total | |
|---|---|---|---|
| Original hypothesis is true | U | V | |
| Original hypothesis is false | T | S | n- |
| Total | n-R | R | n |
| Total | |||
|---|---|---|---|
| a | b | a + b | |
| c | d | c + d | |
| Total | a + c | b + d | n |
| Variables | Do Not Reject | Reject | Column Total |
|---|---|---|---|
| Row total | n |
| Index TID | Labels | Transaction |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | |
| 2 | 1 | |
| 3 | 0 | |
| 4 | 0 | |
| 5 | 1 | |
| 6 | 1 | |
| 7 | 1 | |
| 8 | 0 | |
| 9 | 0 | |
| 10 | 1 | |
| 11 | 1 | |
| 12 | 0 |
| Item Set | TID-Set |
|---|---|
| Encoding Software and Hardware Environment | |
|---|---|
| CPU | Intel(R) Core(TM) i7-10750H CPU @ 2.60 GHz 2.59 GHz |
| Memory | 16.00 GB |
| Hard disk | 500 GB |
| Operating System | Windows 10 |
| System type | 64-bit OS, x64-based processor |
| Development tools | IEDA |
| Development environment | JDK1.8, Hadoop2.7.7, Spark2.4.4 |
| Test Software and Hardware Environment | |
|---|---|
| CPU | Intel(R) Xeon(R) CPU E5-2420 0 @ 1.90 GHz |
| Memory | 24.00 GB |
| Hard disk | 2TB |
| Operating system | Red Hat Enterprise Linux Server release 6.3 |
| System type | X86_64 |
| Experimental environment | JDK1.8,Hadoop2.7.7,Spark2.4.4 |
| Dataset | |D| | Number of Items | Average Length of Transactions | |
|---|---|---|---|---|
| Mushroom(L) | 8124 | 118 | 22 | 2.08 |
| Breast Cancer(L) | 7325 | 1129 | 6.7 | 11.11 |
| A9a(L) | 32,561 | 247 | 13.9 | 4.17 |
| Bms-Web1(U) | 58,136 | 60,978 | 2.51 | 33.33 |
| Bms-Web2(U) | 77,158 | 330,285 | 4.59 | 25 |
| Retail(U) | 88,162 | 16,470 | 10.3 | 2.13 |
| Ijcnn1(L) | 91,701 | 44 | 13 | 10 |
| T10I4D100K_new(U) | 100,000 | 870 | 10.1 | 12.5 |
| Codrna(L) | 271,617 | 16 | 8 | 3.03 |
| Covtype(L) | 581,012 | 64 | 11.9 | 2.04 |
| Susy(U) | 5,000,000 | 190 | 43 | 2.08 |
| Dataset | Mushroom | A9a | Bms-Web2 | Breast Cancer | Cod-Rna | Retail | Ijcnn1 |
|---|---|---|---|---|---|---|---|
| Before pruning (s) | 656.3 | 1706.9 | 226.0 | 833.9 | 1066.3 | 53.4 | 8837.0 |
| After pruning (s) | 77.5 | 1016.5 | 119.25 | 526.3 | 844.2 | 39.5 | 7157.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Zhao, Y.; Xu, T.; Wahab, F.; Sun, Y.; Chen, C. Efficient False Positive Control Algorithms in Big Data Mining. Appl. Sci. 2023, 13, 5006. https://doi.org/10.3390/app13085006
Liu X, Zhao Y, Xu T, Wahab F, Sun Y, Chen C. Efficient False Positive Control Algorithms in Big Data Mining. Applied Sciences. 2023; 13(8):5006. https://doi.org/10.3390/app13085006
Chicago/Turabian StyleLiu, Xuze, Yuhai Zhao, Tongze Xu, Fazal Wahab, Yiming Sun, and Chen Chen. 2023. "Efficient False Positive Control Algorithms in Big Data Mining" Applied Sciences 13, no. 8: 5006. https://doi.org/10.3390/app13085006
APA StyleLiu, X., Zhao, Y., Xu, T., Wahab, F., Sun, Y., & Chen, C. (2023). Efficient False Positive Control Algorithms in Big Data Mining. Applied Sciences, 13(8), 5006. https://doi.org/10.3390/app13085006






