Abstract
An arbitrary amount of entanglement shared among nodes of a quantum network might be nondistillable if the nodes lack the information on the entangled Bell pairs they share. Making such a system distillable, which is called the superactivation of bound entanglement (BE), was shown to be possible through systematic quantum teleportation between the nodes, requiring the implementation of controlled-gates scaling with the number of nodes. In this work, we show in two scenarios that the superactivation of BE is possible if nodes implement the proposed local quantum Zeno strategies based on only single qubit rotations and simple threshold measurements. In the first scenario we consider, we obtain a two-qubit distillable entanglement system as in the original superactivation proposal. In the second scenario, we show that superactivation can be achieved among the entire network of eight qubits in five nodes. In addition to obtaining all-particle distillable entanglement, the overall entanglement of the system in terms of the sum of bipartite cuts is increased. We also design a general algorithm with variable greediness for optimizing the QZD evolution tasks. Implementing our algorithm for the second scenario, we show that a significant improvement can be obtained by driving the initial BE system into a maximally entangled state. We believe our work contributes to quantum technologies from both practical and fundamental perspectives bridging nonlocality, bound entanglement and the quantum Zeno dynamics among a quantum network.
1. Introduction
Bound entanglement (BE) is one of the most interesting features of quantum mechanics [1]. Although a BE state is inseparable from the prior entanglement required to form it, no entanglement can be distilled from it [2,3,4]. Therefore, inseparable quantum systems that cannot be written in product form can be categorized as either free (FE) or bound entangled depending on whether finite entanglement can be distilled or not, yielding negative or positive partial transpose, respectively. BE can exist in two-qutrit systems as the smallest dimension, and in qubit systems, the minimum number of qubits to observe BE is four [2].
For qubits interacting directly or indirectly through ancillary qubits, strategies were designed to liberate BE [5,6,7]. Limited to local operations and classical communications (LOCC), though, one way to benefit from BE systems is to find particular tasks impossible to realize with separable systems yet not requiring free entanglement, such as powering up quantum heat engines [8], distilling private keys for QKD [9], converting pure states shared between distant parties [10], and quantum metrology [11]. The other way is to activate [12] or superactivate [13] BE. In [12], Horodecki et al. considered two spatially separated parties sharing a bipartite mixed FE system and many copies of a bipartite BE system, and all the particles are qutrits. In an iterative fashion, each party applies a two-qutrit operation on the particle of the FE state and the particle of one of the BE states. Then they measure the latter particle on a z-basis and communicate the results. If the results match, the entanglement of the FE state is increased in each iteration. Otherwise, it is not decreased. In the next iteration, a new BE state is used.
As will be detailed below, Shor et al. considered two four-qubit BE states shared among five nodes of a quantum network [13]. By teleporting the unknown state of particles, nodes can obtain a two-qubit distillable FE state, which is called the superactivation of BE.
In this work, we seek the possibility of superactivating bound entanglement via quantum Zeno dynamics (QZD). Beyond a practical point of view, by removing the controlled gates, our work contributes to the fundamentals of quantum entanglement and measurements. What is more, following the distillation of two-qubit entanglement as in the original superactivation work [13], our first major contribution is to show how all the qubits in the quantum network among five nodes can be made free entangled by implementing a simple QZD procedure. Our second major contribution is the design of a general algorithm for optimizing the QZD evolution.
This paper is organized as follows. First, we introduce the superactivation of BE by Shor et al. [13] and review the basics of QZD. In Section 2, we present our QZD procedure and how to confirm the superactivation, and we present our optimization algorithm. In Section 3, we present two scenarios for the superactivation of BE and apply the algorithm to the second scenario. We discuss various aspects of our scenarios, including the drawbacks and future works.
1.1. Superactivation of Bound Entanglement
The four two-qubit maximally entangled Bell states are given as [1]
For simplicity, we consider the following assignment , , , and . In their work on the family of bound entangled states that can be activated, Dür and Cirac presented a four-party state that Alice (A) and Bob (B) are given one of the four Bell states, but they do not know which one [4]. Charlie (C) and Dave (D) are also given the same state, and they do not know which one either. This state can be written as
Because neither pair knows which state they possess, they have a maximally mixed state that they cannot use to realize any quantum task such as teleportation. If Alice and Bob can bring their qubits together, due to the orthogonality of Bell states, they can perform a Bell measurement to find out which Bell state they are given. Receiving the measurement result over a classical channel, Charlie and Dave learn which Bell state they have. Therefore, their state is now a maximally entangled Bell state. However, in accordance with the notion of quantum networks, if parties remain spatially separated, no entanglement can be distilled from [4]. Because this state is entangled but nondistillable, it is a BE state.
Considering two such BE states shared among five parties, Shor et al. showed that bound entanglement can be superactivated [13]. As illustrated in Figure 1a, the first state is shared among Alice and Charlie and Bob and Dave, while the second state is shared among Alice and Bob and Charlie and Emma (E). Therefore, parties Alice, Bob, and Charlie each have a system of two qubits, while parties Dave and Emma each have a system of one qubit. Denoting the first system as and the second system as , the joint system is
which we rewrite for a more intuitive representation considering the qubits held by each party as
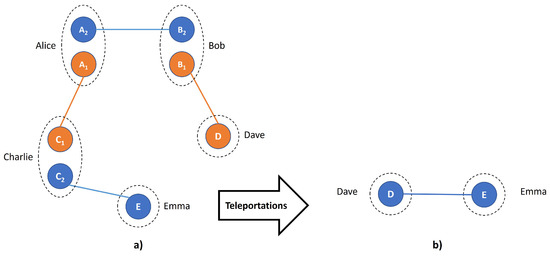
Figure 1.
Superactivation of bound entanglement (BE) introduced by Shor et al. [13]. (a) Alice and Charlie are given a Bell state of qubits and , but they do not know which Bell state it is. The same state is given to Bob and Dave (qubits and D), and they do not know which state is given, too. In the same way, pairs Alice and Bob, and Charlie and Emma, are each given an unknown but the same Bell states of qubits – and –E. Both four-qubit systems are BE. (b) Following a systematic teleportation procedure, qubits D and E are left in a Bell state.
Because four-qubit bound entangled states are separable, no entanglement can be distilled from this eight-qubit system , i.e., is also bound entanglement. However, it was shown in [13] that it can be superactivated by the following simple teleportation procedure.
- (i)
- Alice teleports to Charlie by using the pair.
- (ii)
- Bob teleports to Dave by using the pair.
- (iii)
- Charlie performs a Bell measurement on the two qubits he now possesses, and communicates the result to Dave and Eve.
Because the and states are unknown, each teleportation process adds a factor of a Pauli operator to the teleported qubit. However, these factors cancel each other, leaving a known EPR pair between Dave and Emma, as shown in Figure 1b. In summary, a two-qubit maximally entangled Bell state can be distilled from an eight-qubit bound entangled state distributed to a quantum network of five nodes through a teleportation mechanism. This process is recognized as the superactivation of bound entanglement, and it was experimentally demonstrated by Jia et al. in a continuous-variable optical system [14]. Four-qubit bound entangled Smolin state, and its entanglement unlocking were also experimentally demonstrated [15].
1.2. Quantum Zeno Dynamics
Let be the Hamiltonian acting on a quantum system prepared initially in the state. Then the probability of finding the system in the same state at time t is [16]
If the system is subjected to n projective measurements with sufficiently short intervals , the probability of finding it in the initial state increases with decreasing , and approaches unity for [17]. This shows that carefully designed frequent measurements can slow down the evolution of a quantum system, which is known as the quantum Zeno effect (QZE).
QZE is promising for protecting a quantum system by slowing down its interactions with its environment [18,19,20,21,22]. Frequent measurements can also speed up the interaction of a quantum system and its environment, which is known as the anti-Zeno effect [17]. The anti-Zeno effect has been recently attracting attention to improve our understanding of the decay of quantum systems [23,24,25,26] and has been finding interesting applications, such as enabling advantages in quantum heat engines [27]. QZE is also studied in nonlinear systems [28,29] and is considered to be playing an important role in understanding quantum tunneling [30] and the transition from the quantum to the classical world [31].
As will be detailed in Section 2, let us consider an iteration step consisting of a set of quantum operations implementing and projective measurements implementing . Through a sufficient number of iterations, the system can be driven to a target state that is known as the quantum Zeno dynamics (QZD), and it has been finding interesting applications in quantum information. A key study in the field by Wang et al. showed that entanglement could be created between two initially separated qubits requiring no two-qubit controlled-gates but only single-qubit gates and simple threshold measurements [32]. Ozaydin et al. recently showed that BE activation of Horodecki et al. [12] can be realized via QZD without requiring difficult to implement three-level controlled gates [33]. Bayrakci and Ozaydin have designed a QZD-based entanglement swapping protocol and extended it to realize quantum repeaters for long-distance quantum communications [34].
2. Materials and Methods
2.1. Rotate–Measure Operation for QZD
We consider an iterative two-qubit local QZD procedure. First, the same procedure is considered for the two-qubit systems , , and , for the spatially separated parties Alice, Bob, and Charlie, respectively, for simplicity. Later, an optimization algorithm will be proposed and tested. Each iteration consists of single-qubit rotations and simple threshold measurements. Each party applies the following single-qubit rotation operator on his/her qubits separately.
Then, the following two-qubit threshold measurement is performed
Here, and I is the identity operator for a single-qubit. Note that this is a simple measurement that does not require Bell measurement, the implementation of two-qubit controlled gates, or synchronization [32]. Following the threshold measurement, the system is either collapsed to subspace with probability or projected to the subspace with probability . With a careful design of parameters, can be made very small throughout the iterative process. This can be considered the inhibition of the subspace, and through single-qubit rotations, the system can be driven to a target state through the evolution in the subspace.
Three separated parties, Alice, Bob, and Charlie, each apply the rotate-measure operation in each iteration, and qubits D and E are untouched. The state of the eight-qubit system evolves through the rotate-measure procedure as where
and
Note that the overall rotation operators and threshold measurements with identity operators on the system of eight qubits can be written in a more compact way as and , respectively, though from the perspective of a quantum network with spatially separated nodes possessing two-qubit systems, we find it more intuitive to write in the form of Equations (8) and (9).
Similar to the QZD procedure in [32,33,34], as the QZD iterations start, the initially separated two-qubit systems become entangled. Because the initially separated qubits held by parties (nodes of the quantum network) Alice, Bob, and Charlie are entangled to qubits in other nodes, as shown in Figure 1a, implementing the local QZD on their initially separable qubits and entangling them, all the eight qubits in the network are entangled without performing teleportation or Bell measurements.
In the first scenario for distilling a two-qubit entangled state shared by Dave and Emma, after a sufficient number of iterations, Alice, Bob, and Charlie measure their qubits on a z-basis, and communicate the results with Dave and Emma.
2.2. Logarithmic Negativity of Bipartitions as KPI
To quantify the bipartite entanglement, we use the standard logarithmic negativity measure as the key performance indicator (KPI), which is an entanglement monotone and normalized to yield 0 for separable (or PPT) states, and 1 for maximally entangled Bell states. The negativity of a bipartite state is calculated via the absolute sum of its negative eigenvalues of its partial transpose with respect to subsystem A, or equivalently as [35,36]
where is the trace norm of operator X [37]. Logarithmic negativity is calculated based on negativity as [38]
In our second scenario, which is the major contribution of the present work, we show that by implementing the QZD with a sufficient number of iterations, all the eight qubits in five nodes of the network are entangled without requiring quantum state teleportation, Bell measurements, or even the z-basis measurements as in the final step of the first scenario.
Witnessing all-particle genuine entanglement requires inseparability (or non-zero entanglement) among all bipartite cuts. Inseparability in all bipartite cuts is also stated in [13] as a necessary condition for entanglement distillation between E and D. For the eight-qubit system, we take the following seven bipartite cuts with . Due to the existence of PPT in systems beyond two-qutrits or four-qubits, inseparability does not imply distillable entanglement or a non-zero entanglement measure value. However, a non-zero entanglement value such as implies inseparability.
Bipartite cuts assume that qubits in each cut are in one site so that global operations such as Bell measurements are applicable in each cut. Hence, considering the cut, for example, the result of a Bell measurement on and E qubits can be communicated to Alice and Bob so that entanglement between and qubits can be made distillable, yielding . Therefore, while the logarithmic negativity of bipartite cuts of are , after rewriting the state, the logarithmic negativity of bipartite cuts of , as illustrated in Figure 2, yield . Because the entanglement between and , also between and D, illustrated with orange lines in Figure 2d, is unknown to the parties, the bipartite system of and is separable, yielding . Therefore, due to this separability, considering the five nodes spatially separated, no entanglement can be distilled from , implying bound entanglement.
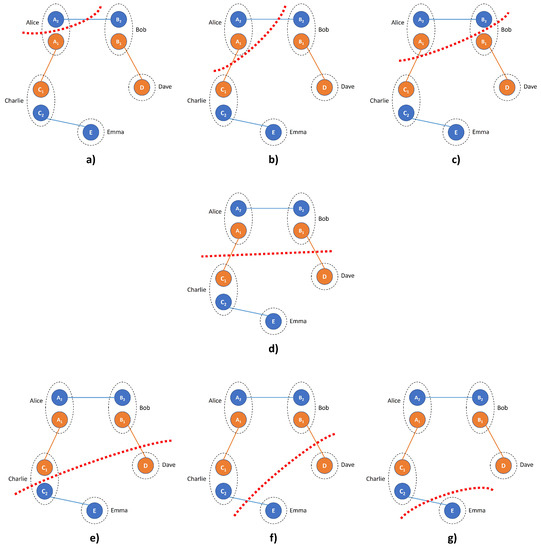
Figure 2.
Bipartite cuts with of the eight-qubit system are presented from (a–g). Cuts are denoted with dashed red lines. The cut shown in (d) is separable. Please see text for details.
After presenting the results of Scenario 1 in Figure 3 and Figure 4, our aim will be to show that it is possible to make all the bipartite cuts of the eight qubits in five nodes inseparable through a simple QZD procedure, illustrated with the transition of a network’s state from Figure 5a,b. Note that the blue lines connecting qubits in Figure 5b do not imply a cyclic entanglement but rather show that all the qubits in the system are entangled.
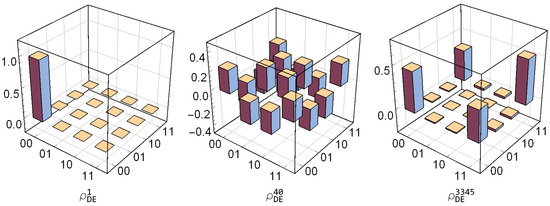
Figure 3.
Bar plots of density matrices , , and for visualizing how distillable entanglement is obtained between D and E throughout QZD.
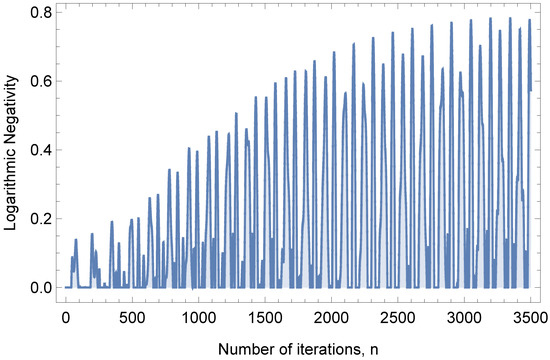
Figure 4.
Logarithmic negativity of after the implementation of quantum Zeno dynamics with n iterations. The numerical simulation yields for , showing the superactivation of bound entanglement of the initial state following the scenario in Figure 1 but without requiring quantum state teleportations or Bell measurements.
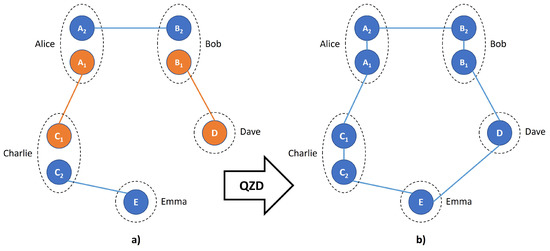
Figure 5.
Superactivation of BE in (a) by entangling all the qubits via QZD results in a genuine eight-qubit FE state in (b).
2.3. Proposed Algorithm for Optimizing the QZD Evolution
In the raw QZD evolution, the same threshold operators are considered for all the qubits in all the iterations, potentially screening the achievable performance of our contribution. To overcome this problem, we propose an algorithm with a variable greediness level for optimizing the evolution throughout QZD. Unlike the raw evolution with a single threshold operator corresponding to a fixed inhibited subspace, our algorithm starts with applying all the available threshold operators in parallel for t iterations. In other words, the QZD evolution takes place in all the possible 64 uninhibited subspaces in parallel universes for t iterations. Next, the best result based on the chosen KPI is evaluated, and the corresponding system is set as the new starting point for the next evolution block of t iterations. Repeating this step k times, the overall iterations are completed.
Without loss of generalization, the algorithm is illustrated in Figure 6 for the present problem as an example where QZD is performed on six qubits, implying 64 available threshold operators in each iteration running from and , to . Here, note that the operator is applied in each rotate–measure step, and in the presentation, we omit the identity operators for the untouched two qubits, D and E, for simplicity.
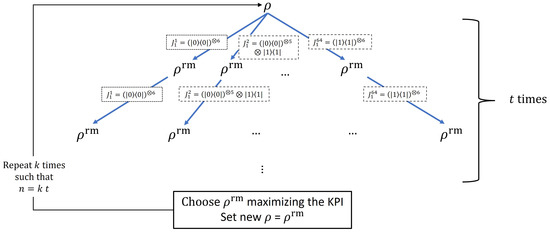
Figure 6.
Algorithm for optimizing the QZD evolution. For t iterations, the evolution takes place in all the possible uninhibited subspaces with the threshold operators as the basic evolution block. Then the best is chosen and set as the new starting point for the next block of t operations. Repeating the block of t operations for k times, the overall operations are completed. Parameter t determines the level of the greediness of the algorithm. Please see the text for details.
Parameter t determines the level of greediness where corresponds to the greediest case such that the KPI evaluation is performed and the best system is set as the new starting point in every single iteration. Similar to Dijkstra’s algorithm, considering that acting upon a small gain in each iteration might miss a greater gain in the longer run, we will consider scenarios as well.
The raw QZD algorithm can be considered the special case of the optimized algorithm where only the rightmost branch in Figure 6 is performed in every iteration with and . Recording throughout the simulation which threshold operator yields the best throughput in each block of t iterations provides the guideline for experimentalists to choose the optimal subspace to inhibit the evolution.
The current optimization’s drawback is the increased computational complexity. In addition to finding the best throughput system after each block of t iterations by maximization over the KPI, not a single but b times rotate–measure operations are performed in each iteration, b being the branching factor, which is in the present problem.
Note that if all the possible threshold measurement operators are applied after each measurement, i.e., all the possible b branches follow each branch in Figure 6, better results can be expected with the drawback of further increasing the computational complexity of the simulation by performing the rotate–measure operation times.
For simplicity, we assumed a fix t throughout the evolution. However, similar to the iterative deepening search strategy, t can be varied on the go, such as setting greater t in the beginning and then smaller t for fine tuning.
3. Results
3.1. Scenario 1
In our first scenario, we show how to superactivate bound entanglement by obtaining distillable two-qubit entanglement between qubits D and E, as in the original superactivation work [13] via implementing a simple QZD procedure, which does not require teleportation or Bell measurements. Through numerical solutions, we find that choosing with and for parties Alice, Bob, and Charlie in all the iterations suffice to achieve the superactivation. As we will discuss in the next section, we do not claim that this choice of parameters is the best, and choosing different values in each iteration and for each party found by intelligent techniques potentially increases the performance of QZD and decreases the number of iterations significantly, which we consider for future work. In this work, we aim to present a proof of concept that due to the power of QZD, even with an arbitrary choice of parameters, bound entanglement can be superactivated by only single-qubit operations and simple threshold measurements.
With and , we implement QZD by repeating the step and denote the obtained state as after the nth iteration. In each iteration, each of the first six qubits are measured on a z-basis, and the results are communicated to Dave and Emma, potentially leaving the system of spatially separated and never interacted qubits D and E entangled, which is detected by calculating the logarithmic negativity using Equation (11). Although becomes non-zero after around 70 iterations, showing the superactivation of bound entanglement, we continue the iteration to obtain a more entangled state .
Tracing out the first six qubits from the initial state in Equation (4), i.e., before starting the QZD procedure, is left in the maximally mixed state, and if the first six qubits are measured on a z-basis and are all found in the state, for example, is left in the state. If a single iteration of QZD is performed with the same z-measurement results, is found in the following state
and in the following state if two iterations are performed
with . However, after 40 iterations, is achieved with state
providing the proof of concept for the superactivation of BE via QZD. If QZD is executed for 76 iterations, is achieved with state
We find that after 3345 iterations, can be achieved where
3.2. Scenario 2
Our second scenario is to superactivate bound entanglement by entangling all the qubits in the nodes of the given quantum network, as illustrated in Figure 5, via QZD. Note that the blue lines connecting qubits do not imply a cyclic entanglement, they only show that every qubit is entangled. The obtained free entangled state of the eight-qubit system is not a GHZ or W state, but it can be considered a generic graph state. Unlike the first scenario and the original superactivation [13], where a two-qubit entangled state is obtained, the eight-qubit bound entangled state, we show that an eight-qubit genuine multiparticle entanglement can be obtained. Moreover, because no qubit is measured on a z-basis, our second scenario is free from the probabilistic results, which enables the superactivation to have a significantly smaller number of iterations.
Distillable entanglement in the eight-qubit system requires inseparability among all bipartite cuts. In the initial state , the cut is separable, i.e., . Then the question turns to find a QZD procedure achieving .
Not surprisingly, it is straightforward to show that implementing the proposed QZD procedure, can be easily obtained. We plot the results of our numerical simulations up to 700 iterations in Figure 7, and the maximum m is achieved in 611 iterations with . The logarithmic negativity of all bipartite cuts of is found as .
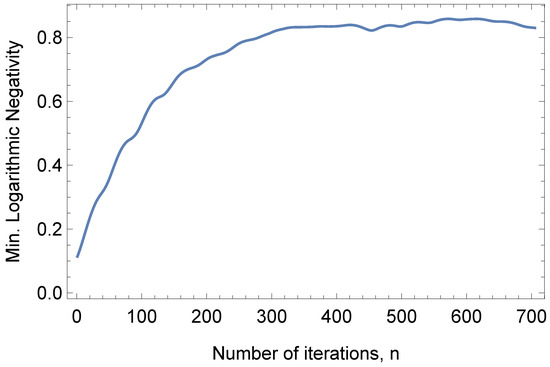
Figure 7.
Minimum logarithmic negativity of all bipartite cuts of the eight-qubit system after n iterations of QZD procedure, i.e., . Obtaining implies no separable bipartite cut, therefore, superactivation of bound entanglement among all the qubits of the network.
While , achieving a greater value would show that QZD increases the amount of total entanglement in the network. Therefore, we plot in Figure 8 the sum of logarithmic negativity values of bipartite cuts of the system throughout the QZD procedure and find that . By implementing QZD, this result shows that as an EPR pair was obtained out of two separable qubits in [32] and entanglement swapping was achieved by entangling initially separable qubits in [33], the procedure proposed herein both superactivates bound entanglement and also increases the total entanglement in terms of the sum of entanglement of bipartite cuts.
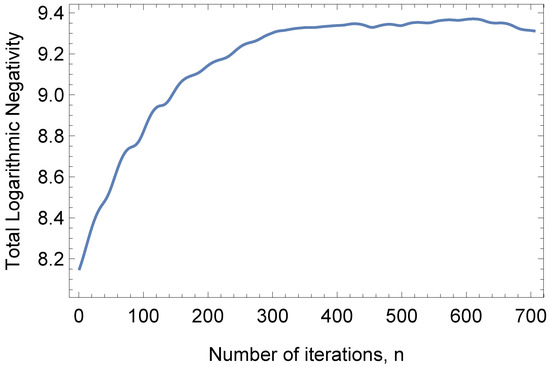
Figure 8.
Sum of logarithmic negativity of bipartite cuts of the eight-qubit system throughout QZD, i.e., . Because this sum is initially equal to 8, yet the entanglement is nondistillable, achieving a greater value shows that in addition to superactivating bound entanglement, our QZD procedure increases the amount of entanglement of the quantum network.
In order to confirm that no bipartite cut of is separable in that writing, we also rewrite it in the same order of qubits, i.e., as in and denote it . Then we find for with . We further detail our analysis on by investigating the inseparability of its subsystems. We first trace out the first and the last four qubits of , respectively, and calculate the logarithmic negativity of bipartite cuts of the remaining subsystem. Due to the symmetry of the system, for both subsystems, we find
where .
In both scenarios above and, in general, in QZD, the idea of the threshold measurements is that throughout the iterative process, the probability that the system collapses to the inhibited subspace is very small and the probability that the system continues its evolution in the uninhibited subspace upon successful projection to it is close to unity. However, in reality, an arbitrary depending on the initial state and chosen threshold operators is observed in the first iteration, which then approaches unity throughout the QZD. Here, an important factor is the fraction of the dimension of the inhibited subspace to the entire space, which is and in the cases of a two-qubit system as in [32], and a two-qutrit system as in [33], respectively. In the latter, the successful projection probability starts with in the first iteration, jumps to in the second iteration and stays very close to unity throughout the evolution.
In the present work, where QZD is applied to six qubits, the dimension of the inhibited subspace is of the entire space. Therefore, a higher success probability can be expected in the first iteration in general, which is found to be and greater than throughout the QZD in both scenarios studied herein.
3.3. Testing the Optimized QZD Evolution Algorithm
We test the performance of our optimized algorithm on Scenario 2 with three different greediness levels, , , and , corresponding to the greediest case. In accordance with the results of the raw scenario, we run the optimized simulation for parallel iteration sets. As shown in Figure 9, while each of the three choices of t provides a significant improvement over the raw QZD evolution, in this particular problem, the greediest choice with performs the best. Because the sum of logarithmic negativity of all linear bipartite cuts of an eight-qubit system can yield maximum , we find that our proposed algorithm with can even yield a maximally entangled state in only around 300 iterations.
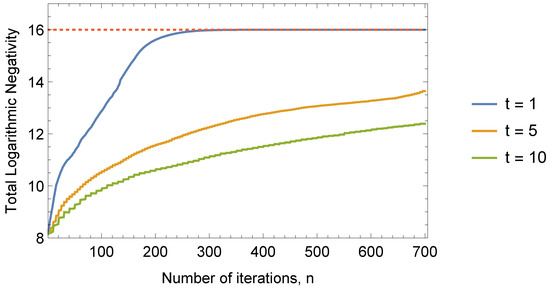
Figure 9.
Sum of logarithmic negativity of all bipartite cuts of the eight-qubit system throughout QZD with three choices for greediness, , , and , as explained in the flowchart of the algorithm in Figure 6. The greediest choice performs the best, driving the system to a maximally entangled state with in only around 300 iterations.
4. Discussions
Although the result in Scenario 1 is not the major contribution of our work and we considered it only to show that the original superactivation of bound entanglement by Shor et al. in [13] can be realized by leaving two-qubit distillable entanglement via QZD, is worth discussing its drawbacks in detail. Following n iterations, the first three pairs of qubits, each possessed by Alice, Bob, and Charlie, are measured on a z-basis. Because QZD is inhibiting the subspace for each pair, and the evolution of the system takes place in the uninhibited subspace; the z-measurements have 63 possible outcomes with probabilities oscillating around throughout the evolution. The result we presented achieving is for the outcome . Superactivation is actually observed in several outcomes with almost all , though achieving smaller logarithmic negativity.
However, for the proof of concept in Scenario 1, we considered a simple QZD procedure with the same threshold measurement operator and single-qubit rotation angle for all the parties and all the iterations. In [32], for creating entanglement between initially separable two qubits via QZD, Wang et al. were able to find an intelligent evolution strategy after 100 iterations; they implement a single-qubit quantum operation followed by another 50 iterations, which improves the overall procedure.
As also discussed by Ozaydin et al. in [33], due to the size of the parameter search space, a brute force approach for finding an optimal set of measurement operators and rotations for each iteration is not feasible, requiring artificial intelligence (AI) techniques. Finding an optimal parameter set, the final distillable two-qubit entanglement could be made even closer to a maximally entangled Bell state. More importantly, if it could be obtained regardless of the outcome of z-basis measurements, then after implementing QZD, the first six qubits can be simply traced out, also eliminating the final classical communications for the outcomes. Therefore, we point out developing a quantum AI-based search strategy for improving the proposed QZD procedure.
Scenario 2 is free from z-measurements, and in addition to superactivation bound entanglement, it increases the total amount of entanglement among the eight-qubit quantum network in terms of bipartite cuts. Further, a significantly smaller number of iterations is sufficient to obtain these results. Nevertheless, it would benefit from such an intelligent evolution, too. More importantly, in this work, we have not considered a particular class of quantum network such as GHZ [1], W [39], or a generic unweighted [40] and even weighted [41] graph state for one-way quantum computation. Therefore, quantum AI strategies could help generate multipartite entangled systems in particular classes via QZD.
As the second major contribution of this work, we designed a universal optimization algorithm with variable greediness that can be applied to QZD evolution in both qubit systems, such as in [32,34], and higher dimension systems, such as in [33], with an arbitrary number of particles. We implemented the algorithm for the present setting and showed that while the raw (un-optimized) evolution can increase the entanglement from to in 700 iterations, the optimization algorithm can increase it up to 16, the maximum value in only around 300 iterations.
This algorithm aimed to increase the entanglement of the system. However, it would be an interesting problem to modify it to drive the system into a particular state.
In Scenario 1, while is of –type, is of –type entanglement. We observed such flip-flops throughout the numerical simulation. As a matter of fact, as can be seen in Figure 4, a successive process of entanglement death and revival between D and E is obtained after a number of iterations. The resulting state after n iterations with logarithmic negativity achieving each local maximum in Figure 4 is one of the Bell state types in Equation (1). Hence, the flip-flop is potentially (but not necessarily) observed in each revival leading to a new local maximum of the logarithmic negativity. We interpret this process as follows. After each entanglement death, QZD leads to the revival entanglement of one of the four types, which is then reinforced in the following iterations until it reaches the local maximum. In other words, we observe a meandering process of entanglement formation towards one of the four Bell states.
Unlike Scenario 1, where the entanglement of the system of only two-qubits is considered in one of the four orthogonal Bell-type states, in Scenario 2, the entanglement of the eight-qubit system is considered, which is more sophisticated, making it more difficult to observe and interpret the entanglement dynamics such as the oscillations in the type of entanglement. Hence, it would be interesting to study the meandering type of entanglement formation in genuine multiparticle entanglement (GME) settings.
Regarding the generation of W-type multipartite entangled states via QZD, we would like to raise two interesting questions for future works. Fusion and expansion are the two widely recognized strategies for generating large-scale W or W-type states. In the fusion strategy, one qubit from each small W state, say of sizes n and m, are sent to a fusion mechanism with a non-zero probability, the two W states are fused, and the result is a W state of size [42,43,44,45,46,47]. In addition to the qubit loss-free mechanism for W states [48], a special fusion mechanism was designed for fusing W-type states for perfect teleportation and superdense coding [49]. Deterministic expansion strategy expands an n-qubit W state with n ancillary qubits to a -qubit W state [50,51,52] by applying two two-qubit controlled operations for each pair of qubits, the first being a qubit of the W state and the second being the ancillary qubit. Therefore, its drawback is that it requires controlled two-qubit operations. What is more, this strategy only works for W states and a strategy for the W-type states for teleportation and superdense coding is missing. Considering the quantum circuit complexity reduction by eliminating the controlled operations in generating two-qubit entanglement from separable qubits [32], as well as the new entanglement swapping protocol and quantum repeater design [34], both the probabilistic fusion and the deterministic expansion strategy can greatly benefit from designing new QZD procedures with intelligent evolution.
Due to experimental difficulties and desired success probability, especially considering the scalability of the quantum task, regardless of the physical qubits and technology used to realize it, implementing single-qubit gates is preferred over multi-qubit gates [1]. Hence, a trade-off appears between the traditional circuit model requiring a few two-qubit controlled gates and QZD requiring only single-qubit gates and simple threshold measurements, but many of them.
The implementation of the single-qubit rotation operator is straightforward. In [32], Wang et al. presented the implementation of two-qubit threshold measurements, which can be directly adapted to the procedure presented in this work. Further, the analysis they performed shows the robustness of the overall QZD procedure in similar settings to the one herein.
5. Conclusions
Through a systematic quantum state teleportation sequence, Shor et al. showed that bound entanglement (BE) distributed among eight qubits of a quantum network of five nodes can be superactivated by obtaining a distillable quantum system of two qubits [13]. In this work, we showed that the superactivation of BE can be realized without implementing quantum teleportations, each requiring the realization of two-qubit controlled gates. Our proposal is based on quantum Zeno dynamics (QZD), which requires the realization of only single-qubit gates and simple threshold measurements. In our first application scenario, we showed that the original scenario of Shor et al. [13] can be realized by obtaining a distillable entangled system of two qubits. The first major contribution of this work is that in our second scenario, we showed that superactivation can be obtained among all the nodes in the quantum network. In particular, we showed that the eight-qubit BE state can be transformed into an eight-qubit FE state by implementing local QZD procedures at each node. As the second major contribution, we designed an algorithm with variable greediness for optimizing the QZD evolution in a given task. Implementing our algorithm for the second scenario, we showed that a significant improvement could be obtained by driving the initially BE system into a maximally entangled state. We also raised several open questions for future research.
Author Contributions
Conceptualization, F.O., V.B., A.A.A. and C.B.; methodology, F.O., V.B., A.A.A. and C.B.; software, F.O. and V.B.; validation, F.O., V.B., A.A.A. and C.B.; formal analysis, F.O., V.B., A.A.A. and C.B.; investigation, F.O., V.B., A.A.A. and C.B.; resources, F.O. and V.B.; data curation, F.O. and V.B.; writing—original draft preparation, F.O., V.B., A.A.A. and C.B.; visualization, F.O. and V.B.; supervision, F.O. and A.A.A.; funding acquisition, F.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Personal Research Fund of Tokyo International University.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All the data in this study can be generated through the presented methods.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial intelligence |
| BE | Bound entanglement or bound entangled |
| FE | Free entanglement |
| GME | Genuine multiparticle entanglement |
| KPI | Key performance indicator |
| LOCC | Local operations and classical communications |
| QKD | Quantum key distribution |
| QZD | Quantum Zeno dynamics |
| QZE | Quantum Zeno effect |
References
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Horodecki, P. Separability criterion and inseparable mixed states with positive partial transposition. Phys. Lett. A 1997, 232, 333–339. [Google Scholar] [CrossRef]
- Horodecki, M.; Horodecki, P.; Horodecki, R. Mixed-state entanglement and distillation: Is there a “bound” entanglement in nature? Phys. Rev. Lett. 1998, 80, 5239. [Google Scholar] [CrossRef]
- Dür, W.; Cirac, J. Activating bound entanglement in multiparticle systems. Phys. Rev. A 2000, 62, 022302. [Google Scholar] [CrossRef]
- Derkacz, Ł.; Jakóbczyk, L. Delayed birth of distillable entanglement in the evolution of bound entangled states. Phys. Rev. A 2010, 82, 022312. [Google Scholar] [CrossRef]
- Sharma, K.K.; Pandey, S. Dzyaloshinskii–Moriya interaction as an agent to free the bound entangled states. Quantum Inf. Process. 2016, 15, 1539–1551. [Google Scholar] [CrossRef]
- Sharma, K.K.; Sinha, S.; Chandra, K. Efficacy of Moriya interaction to free the bound entangled state. Quantum Inf. Process. 2022, 21, 21. [Google Scholar] [CrossRef]
- Tuncer, A.; Izadyari, M.; Dağ, C.B.; Ozaydin, F.; Müstecaplıoğlu, Ö.E. Work and heat value of bound entanglement. Quantum Inf. Process. 2019, 18, 373. [Google Scholar] [CrossRef]
- Horodecki, K.; Horodecki, M.; Horodecki, P.; Oppenheim, J. Secure key from bound entanglement. Phys. Rev. Lett. 2005, 94, 160502. [Google Scholar] [CrossRef]
- Ishizaka, S. Bound entanglement provides convertibility of pure entangled states. Phys. Rev. Lett. 2004, 93, 190501. [Google Scholar] [CrossRef]
- Czekaj, Ł.; Przysiężna, A.; Horodecki, M.; Horodecki, P. Quantum metrology: Heisenberg limit with bound entanglement. Phys. Rev. A 2015, 92, 062303. [Google Scholar] [CrossRef]
- Horodecki, P.; Horodecki, M.; Horodecki, R. Bound entanglement can be activated. Phys. Rev. Lett. 1999, 82, 1056. [Google Scholar] [CrossRef]
- Shor, P.W.; Smolin, J.A.; Thapliyal, A.V. Superactivation of bound entanglement. Phys. Rev. Lett. 2003, 90, 107901. [Google Scholar] [CrossRef]
- Jia, X.; Zhang, J.; Wang, Y.; Zhao, Y.; Xie, C.; Peng, K. Superactivation of multipartite unlockable bound entanglement. Phys. Rev. Lett. 2012, 108, 190501. [Google Scholar] [CrossRef] [PubMed]
- Amselem, E.; Bourennane, M. Experimental four-qubit bound entanglement. Nat. Phys. 2009, 5, 748–752. [Google Scholar] [CrossRef]
- Misra, B.; Sudarshan, E.G. The Zeno’s paradox in quantum theory. J. Math. Phys. 1977, 18, 756–763. [Google Scholar] [CrossRef]
- Kofman, A.G.; Kurizki, G. Acceleration of quantum decay processes by frequent observations. Nature 2000, 405, 546–550. [Google Scholar] [CrossRef]
- Bernu, J.; Deléglise, S.; Sayrin, C.; Kuhr, S.; Dotsenko, I.; Brune, M.; Raimond, J.M.; Haroche, S. Freezing coherent field growth in a cavity by the quantum Zeno effect. Phys. Rev. Lett. 2008, 101, 180402. [Google Scholar] [CrossRef]
- Raimond, J.M.; Facchi, P.; Peaudecerf, B.; Pascazio, S.; Sayrin, C.; Dotsenko, I.; Gleyzes, S.; Brune, M.; Haroche, S. Quantum Zeno dynamics of a field in a cavity. Phys. Rev. A 2012, 86, 032120. [Google Scholar] [CrossRef]
- Signoles, A.; Facon, A.; Grosso, D.; Dotsenko, I.; Haroche, S.; Raimond, J.M.; Brune, M.; Gleyzes, S. Confined quantum Zeno dynamics of a watched atomic arrow. Nat. Phys. 2014, 10, 715–719. [Google Scholar] [CrossRef]
- Shringarpure, S.; Franson, J. Inhibiting phase drift in multi-atom clocks using the quantum Zeno effect. arXiv 2022, arXiv:2208.06301. [Google Scholar] [CrossRef]
- Gramegna, G.; Burgarth, D.; Facchi, P.; Pascazio, S. Continuous and Pulsed Quantum Control. Proceedings 2019, 12, 15. [Google Scholar] [CrossRef]
- Chaudhry, A.Z. A general framework for the Quantum Zeno and anti-Zeno effects. Sci. Rep. 2016, 6, 29497. [Google Scholar] [CrossRef] [PubMed]
- Majeed, M.; Chaudhry, A.Z. The quantum Zeno and anti-Zeno effects with driving fields in the weak and strong coupling regimes. Sci. Rep. 2021, 11, 1836. [Google Scholar] [CrossRef] [PubMed]
- Chaudhry, A.Z.; Gong, J. Zeno and anti-Zeno effects on dephasing. Phys. Rev. A 2014, 90, 012101. [Google Scholar] [CrossRef]
- Mohamed, A.B.A.; Hassan, S.S.; Alharbey, R.A. Quantum Interference Effects on Information Phase Space and Entropy Squeezing. Entropy 2019, 21, 147. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, V.; Kofman, A.G.; Kurizki, G. Anti-Zeno quantum advantage in fast-driven heat machines. Commun. Phys. 2020, 3, 8. [Google Scholar] [CrossRef]
- Bayındır, C.; Ozaydin, F. Freezing optical rogue waves by Zeno dynamics. Opt. Commun. 2018, 413, 141–146. [Google Scholar] [CrossRef]
- Bayındır, C. Zeno dynamics of quantum chirps. Phys. Lett. A 2021, 389, 127096. [Google Scholar] [CrossRef]
- Miret-Artés, S.; Dumont, R.S.; Rivlin, T.; Pollak, E. The influence of the symmetry of identical particles on flight times. Entropy 2021, 23, 1675. [Google Scholar] [CrossRef]
- Kauffman, S.; Patra, S. A testable theory for the emergence of the classical world. Entropy 2022, 24, 844. [Google Scholar] [CrossRef]
- Wang, X.B.; You, J.Q.; Nori, F. Quantum entanglement via two-qubit quantum Zeno dynamics. Phys. Rev. A 2008, 77, 062339. [Google Scholar] [CrossRef]
- Ozaydin, F.; Bayındır, C.; Altintas, A.A.; Yesilyurt, C. Nonlocal activation of bound entanglement via local quantum Zeno dynamics. Phys. Rev. A 2022, 105, 022439. [Google Scholar] [CrossRef]
- Bayrakci, V.; Ozaydin, F. Quantum Zeno repeaters. Sci. Rep. 2022, 12, 15302. [Google Scholar] [CrossRef] [PubMed]
- Eisert, J.; Plenio, M.B. A comparison of entanglement measures. J. Mod. Opt. 1999, 46, 145–154. [Google Scholar] [CrossRef]
- Vidal, G.; Werner, R.F. Computable measure of entanglement. Phys. Rev. A 2002, 65, 032314. [Google Scholar] [CrossRef]
- Bhatia, R. Matrix Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 169. [Google Scholar]
- Plenio, M.B. Logarithmic negativity: A full entanglement monotone that is not convex. Phys. Rev. Lett. 2005, 95, 090503. [Google Scholar] [CrossRef]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Raussendorf, R.; Briegel, H.J. A one-way quantum computer. Phys. Rev. Lett. 2001, 86, 5188. [Google Scholar] [CrossRef]
- Tame, M.; Özdemir, Ş.; Koashi, M.; Imoto, N.; Kim, M. Compact Toffoli gate using weighted graph states. Phys. Rev. A 2009, 79, 020302. [Google Scholar] [CrossRef]
- Ozdemir, S.K.; Matsunaga, E.; Tashima, T.; Yamamoto, T.; Koashi, M.; Imoto, N. An Optical Fusion Gate for W-States. New J. Phys. 2011, 13, 103003. [Google Scholar] [CrossRef]
- Bugu, S.; Yesilyurt, C.; Ozaydin, F. Enhancing the W-State Quantum-Network-Fusion Process with a Single Fredkin Gate. Phys. Rev. A 2013, 87, 032331. [Google Scholar] [CrossRef]
- Yesilyurt, C.; Bugu, S.; Ozaydin, F. An Optical Gate for Simultaneous Fusion of Four Photonic W or Bell States. Quantum Inf. Process. 2013, 12, 2965. [Google Scholar] [CrossRef]
- Ozaydin, F.; Bugu, S.; Yesilyurt, C.; Altintas, A.A.; Tame, M.; Ozdemir, S.K. Fusing Multiple W States Simultaneously with a Fredkin Gate. Phys. Rev. A 2014, 89, 042311. [Google Scholar] [CrossRef]
- Zang, X.P.; Yang, M.; Ozaydin, F.; Song, W.; Cao, Z.L. Generating Multi-Atom Entangled W States via Light-Matter Interface Based Fusion Mechanism. Sci. Rep. 2015, 5, 16245. [Google Scholar] [CrossRef] [PubMed]
- Bugu, S.; Ozaydin, F.; Ferrus, T.; Kodera, T. Preparing Multipartite Entangled Spin Qubits via Pauli Spin Blockade. Sci. Rep. 2020, 10, 3481. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Kong, F.Z.; Yang, M.; Yang, Q.; Cao, Z.L. Qubit-Loss-Free Fusion of W States. Phys. Rev. A 2016, 94, 062315. [Google Scholar] [CrossRef]
- Li, K.; Kong, F.Z.; Yang, M.; Ozaydin, F.; Yang, Q.; Cao, Z.L. Generating Multi-Photon W-like States for Perfect Quantum Teleportation and Superdense Coding. Quantum Inf. Process. 2016, 15, 3137. [Google Scholar] [CrossRef]
- Yesilyurt, C.; Bugu, S.; Ozaydin, F.; Altintas, A.A.; Tame, M.; Yang, L.; Ozdemir, S.K. Deterministic Local Doubling of W states. J. Opt. Soc. Am. B 2016, 33, 2313. [Google Scholar] [CrossRef]
- Zang, X.P.; Yang, M.; Ozaydin, F.; Song, W.; Cao, Z.L. Deterministic Generation of Large Scale Atomic W States. Opt. Express 2015, 24, 12293. [Google Scholar] [CrossRef]
- Ozaydin, F.; Yesilyurt, C.; Bugu, S.; Koashi, M. Deterministic preparation of W states via spin-photon interactions. Phys. Rev. A 2021, 103, 052421. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).