Abstract
Similarly efficient feature groups occur in prediction procedures such as Olive phenology forecasting. This study proposes a procedure that can be used to extract the most representative feature grouping from Market Basket Analysis-derived methodologies and other techniques. The computed association patterns in this process are visualized through graph analytic tools, comparing centrality metrics and spacial distribution approaches. Finally, highlighted feature formations are located and analyzed within the efficiency distribution of all proposed feature combinations for validation purposes.
1. Introduction
In pursuit of enhancing the effectiveness, robustness, and feasibility of predictive models, the analysis of relevant features has become a necessary task in machine learning and data mining projects. The benefits of feature selection are several [1]: ameliorating the prediction performance of the predictors, producing speedier and more cost-effective predictors, and presenting a better interpretability context of the generated data [2], or avoidance of curse of dimensionality [3,4].
Selection techniques can be divided according to the contribution of their application. Some cover the dimensionality of the original data set with Feature Extraction techniques like Principal Component Analysis [5], t-Distributed Stochastic Neighbor Embedding [6], or aggregation models [7]. Others focus on creating a feature ranking [8] to select the most influential features, through methods such as Feature Importance from Tree-Based Models [9], Recursive Feature Elimination (RFE) [10], Mutual Information [11], Correlation-Based Feature Ranking [12], between others. Another feature selection approach focuses on creating new variables from simple combinations such as polynomial features [13].
The feature selection process can also be classified as a filter [14], wrapper [15], or embedded [16] method according to the implementation of variable elimination procedure within the data mining process [1]. Filter method, popular for high feature quantities, is independent of the model, while the embedded method selects features during model building and wrapper techniques use a predictive model to select the features.
The selection of a specific technique depends strongly on the predictive objective and the nature of the data. Recent studies have shown that in certain cases, there may be combinations of features that are similarly efficient and that techniques such as RFE are not efficient [17]. In the case of highly correlated features, the inefficacity of standard RFE might be similar [18], but the combination of distinct strategies can improve the efficiency of standard techniques, as in [2], where a hybrid RFE strategy provide better results than single RFE methods.
Another important part of the data mining is the interpretability of the resultant feature selection. Comprehensible and useful information can be extracted from feature combinations, and the relationships between feature entities can be explored through distinct connection criteria, such as association rule mining [19], also known as Market Basket Analysis techniques [20]. These practices are popular to identify changing trends of market data [21,22], but also to reduce the dimensionality of input parameters [23].
In what follows, a wrapper-kind methodology is presented in order to extract a representative feature group from feature association trends. For validation purposes, the proposed strategy is applied to a data set already mentioned in [17], as detailed in Section 2. Secondly, the definition of two distinct association metrics introduces the principal comparison of this research in Section 2.2.1. Subsequently, selected graph analysis techniques are described in order to distinguish visually the effect of those association rules. Straightaway, a section is dedicated to scrutinizing the validation procedures. Finally, all numerical and visual results are displayed in comparative tables and figures. The main contribution is the highlighted subgroup of combination with a common feature core, and a final two feature collections derived from both distinct association metrics.
2. Materials and Methods
This section presents a multi-stage procedure for analyzing association relations among similarly efficient feature groups. The procedure is applied to a well-documented data set detailed in recent studies [17], which includes various climatic and geographic feature combinations that demonstrate accurate prediction of olive phenological status. This approach is presented due to its potential to enhance the post-processing phase in prediction modeling schemes that employ decision tree-based patterns.
The first part, Section 2.1 contains a summary of the original data sources, as well as the machine learning procedures and evaluation metrics employed to construct the data set under study. The second part, Section 2.2, describes the two main stages of the proposed strategy. The first stage, Section 2.2.1, involves the definition of association metrics between features, while the second stage, Section 2.2.2, details the implemented graph network centrality and distribution techniques.
2.1. Data Set
This section describes the followed procedure to obtain the data set explored in this study, which is partially summarized in Section 2.2. The main objective of these combinations is to predict the phenological status of the olive. The original olive phenology data collection that motivated this study, which has already been explored in recent studies [17,24], is the result of three years of monitoring (2008–2010) performed in Tuscan olive groves (Italy). Frantoio cultivar olive trees, selected due to their closeness to regional agrometeorological stations, were observed during the distinct phases of the olive development course: from January to March with bi-weekly periodicity and every week in April. The biological status of each phenology phase was represented with the popular numeric BBCH scale (Biologische Bundesanstalt, Bundessortenamt, und CHemische Industrie [24,25]). The explored phenology observations were synchronized with climatic and geographic history derived from the ERA5, ECMWF atmospheric reanalysis open access service, as detailed in the study [17].
The input features considered to predict the olive phenology are listed in Table 1, grouped in two sets: Original and Created features. The first ones are raw data extracted from indicated data sources within the Table 1, while created features accumulate the indicated quantities from the first day of January, until the day of observation, denoted by Day of the Year (DOY). In order to create the efficiency feature combinations detailed in Table 2 the extra-tree regressor method [26] was selected based on its remarkable efficiency outcomes published in [17]. This method, characterized by its extremely randomized trees, was combined with 5-fold-cross validation splitting techniques to compute the results available in Table 2. Originally, all possible feature combinations were analyzed, but due to improvement objectives, this study collects only the most capable feature consolidations. Indeed, the combinations with an inferior RMSE of 0.65 were eliminated, to ensure better performance results than the ones obtained using standard feature elimination methods such as RFE and Hierarchical clustering [17]. In addition, the DOY is a mandatory feature in all combinations, as it determines the forecasting day and the limit of created features Table 1. Thus, it has been eliminated to focus on the relations between the optional features. The error outcomes of Table 2 demonstrate the similar efficiency of those combinations. Unfortunately, this extensive registry does not provide an insightful and definitive feature proposition despite the high accuracy results. This is why this study aims to propose a methodology to extract a representative feature grouping from Table 2.



Table 1.
Description of features used as predictors for the phenological phases of olive trees.
Table 1.
Description of features used as predictors for the phenological phases of olive trees.
| Abbreviated | Original Features | Predictor | Data | Resolution |
|---|---|---|---|---|
| Feature Name | Type | Source | (km) | |
| DOY | Day of year | Time | ||
| mean temp | Average air temperature at 2 m height (daily average) | Meteo | ERA 5 | ∼28 |
| min temp | Minimal air temperature at 2 m height (daily minimum) | Meteo | ERA 5 | ∼28 |
| max temp | Maximal air temperature at 2 m height (daily maximum) | Meteo | ERA 5 | ∼28 |
| dewp temp | Dewpoint temperature at 2 m height (daily average) | Meteo | ERA 5 | ∼28 |
| total precip | Total precipitation (daily sums) | Meteo | ERA 5 | ∼28 |
| surface pressure | Surface pressure (daily average) | Meteo | ERA 5 | ∼28 |
| sea level | Mean sea-level pressure (daily average) | Meteo | ERA 5 | ∼28 |
| wind u | Horizontal speed of air moving towards the east, | |||
| at a height of 10 m above the surface of Earth. | Meteo | ERA 5 | ∼28 | |
| wind w | Horizontal speed of air moving towards the north. | Meteo | ERA 5 | ∼28 |
| EVI | Enhanced vegetation index (EVI) generated from the | 006 MOD09GA | ||
| Near-IR, red, and blue bands of each scene. | MODIS | EVI | 1 km | |
| NDVI | Normalized difference vegetation index generated | 006 MOD09GA | ||
| from the near-IR and red bands of each scene. | MODIS | NDVI | 1 km | |
| RED | Red surface reflectance (sur refl b01) | MODIS | 006 MOD09GQ | 0.25 km |
| NIR | NIR surface reflectance (sur refl b02) | MODIS | 006 MOD09GQ | 0.25 km |
| sur refl b03 | Blue surface reflectance, 16-day frequency | MODIS | 006 MOD13Q1 | 0.25 km |
| sur refl b07 | MIR surface reflectance, 16-day frequency | MODIS | 006 MOD13Q1 | 0.25 km |
| view zenith | View zenith angle, 16-day frequency | MODIS | 006 MOD13Q1 | 0.25 km |
| solar zenith | Solar zenith angle, 16-day frequency | MODIS | 006 MOD13Q1 | 0.25 km |
| rel azim | Relative azimuth angle, 16-day frequency | MODIS | 006 MOD13Q1 | 0.25 km |
| lat | Latitude | Spatial | ||
| lon | Longitude | Spatial | ||
| slope | Landform classes created by combining the ALOS CHILI | |||
| and ALOS mTPI data sets. | Spatial | ALOS Landform | ||
| Created features | ||||
| GDD | Growing degree day from GEE temperature measurements; t is base temperature used. | |||
| precip cum | Precipitation accumulated from the first of January until DOY. | |||
| EVIcum | EVI accumulated from the first of January until DOY. | |||
| NDVIcum | NDVI accumulated from 1 January until DOY. | |||
| REDcum | RED accumulated from 1 January until DOY. | |||
| NIRcum | NIR accumulated from 1 January until DOY. | |||

Table 2.
Quantitative and characteristic description in an efficiency descending order of F Feature lists belonging to the space of all analyzed combinations .
Table 2.
Quantitative and characteristic description in an efficiency descending order of F Feature lists belonging to the space of all analyzed combinations .
| RMSE | Feature List |
|---|---|
| Mean | |
| 0.5857 | slope, sea level, NDVI, lat, cum precip, surface pressure |
| 0.5865 | EVI, slope, sea level, lat, cum precip, surface pressure, mean temp |
| 0.5877 | EVI, slope, sea level, lat, cum precip, surface pressure |
| 0.5879 | slope, sea level, lat, cum precip, surface pressure |
| 0.5885 | slope, sea level, lat, cum precip, mean temp, GDD |
| 0.5887 | EVI, slope, sea level, lat, cum precip, mean temp, GDD |
| 0.5897 | EVI, slope, min temp, sea level, lat, cum precip, surface pressure |
| 0.5904 | EVI, slope, sea level, lat, surface pressure, mean temp |
| 0.5905 | slope, sea level, lat, cum precip, surface pressure, mean temp |
| 0.5905 | EVI, slope, sea level, NDVI, lat, cum precip, mean temp, GDD |
| 0.5908 | EVI, slope, min temp, sea level, lat, cum precip, surface pressure, GDD |
| 0.5911 | slope, min temp, sea level, NDVI, lat, cum precip, surface pressure, GDD |
| 0.5911 | slope, sea level, NDVI, lat, cum precip, surface pressure, GDD |
| 0.5915 | EVI, slope, min temp, sea level, lat, cum precip, mean temp, GDD |
| 0.5916 | EVI, slope, min temp, sea level, lat, cum precip, GDD |
| 0.5916 | slope, sea level, NDVI, lat, cum precip, surface pressure, mean temp, GDD |
| 0.5917 | slope, min temp, sea level, lat, cum precip, GDD |
| 0.5919 | EVI, slope, sea level, NDVI, lat, cum precip, surface pressure, mean temp, GDD |
| 0.5924 | EVI, slope, min temp, sea level, NDVI, lat, cum precip, surface pressure, GDD |
| 0.5924 | EVI, slope, sea level, NDVI, lat, cum precip, surface pressure |
| 0.5926 | slope, min temp, sea level, NDVI, lat, cum precip, surface pressure, mean temp, GDD |
| 0.5927 | EVI, slope, min temp, sea level, lat, mean temp, GDD |
| 0.5927 | slope, sea level, NDVI, lat, cum precip, surface pressure, mean temp |
| 0.5931 | EVI, slope, min temp, sea level, NDVI, lat, cum precip, GDD |
| 0.5931 | EVI, slope, sea level, NDVI, lat, cum precip, surface pressure, mean temp |
2.2. Methodology
This part collects the technicalities of the wrapper feature selection technique to extract a subgroup of robust characteristics, retrieving the significance of features with regard to their repetitive presence in different combinations. For this purpose, the following graphs depict the relationships of the characteristics, where the nodes represent the characteristics, and the edges symbolize the interdependence between them. The weights of these edges are established through two association metrics. The networks that emerged from those associations are analyzed with several weighted centrality metrics. The resulting graph configurations—spatial distribution and feature sizing—are interpreted according to the computed association and centrality metrics, enhancing a meaningful feature set.
2.2.1. Association Metrics
This part clarifies the distinction of the proposed association metrics: a Market Basket Analysis’ derived support metric and a simpler metric already employed in study [17].
- Metric 1 (M1): The weight assigned to each edge , symbolizing the connection between two features x, y, is directly proportional to the Root Mean Square Error (RMSE) mean values presented in the ranked quantities in Table 2. Computation of this weight involves the aggregation of the average RMSE, which is accomplished by summing the corresponding values across all combinations in which the two features overlap x, y, as detailed by Equation (1). The outcome of employing this association metric M1 is the generation of an undirected weighted graph.
- Metric 2 (M2): In Market basket analysis, the associations between products are unveiled by analyzing combinations of products that frequently appear in transactions. Among the most commonly used metrics, the support, confidence and lift metrics are often used to justify strategic decisions in a marketing campaign, or product rearrangement in stores [23]:
- -
- Support: this metric quantifies the proportion of combinations in the data set containing a specific item. It represents the ratio of collections containing the itemset to the total number of combinations in the data set.
- -
- Confidence: it measures the proportion of collections that contain the antecedent x that also contains the consequent y. It is calculated as the ratio of the number of collections that contain both the antecedent x and the consequent y to the number of combinations that contain the antecedent x.
- -
- Lift: it calculates the ratio of the analyzed support to the expected support under the assumption of independence between the antecedent and the consequent. It indicates how likely the consequent is to occur when the antecedent is present compared to when the antecedent is absent. It is calculated as the confidence ratio of to support the consequent y.
In this study, the edges characterizing the relation between features are computed by applying the lift criteria to the list partially detailed in the publication [17], as indicated by Equation (5). In addition, a minimal support quantity of 0.00001 is required to compute the frequent item sets. This task has been completed using the functionalities apriori and association rules of library Frequent Patterns [27]. Each edge connects the antecedent x and consequent y items weighted by the support quantity, creating an undirected weighted graph through this orientation.
2.2.2. Graph Network Analysis
Centrality metrics and distribution criteria created from networks as a result of the association metrics defined in Section 2.2.1, have been analyzed by the open-source platform Gephi 0.9.2. [28], an open-source software application. As it is a network where almost all nodes are connected, measures such as eccentricity and betweenness have been discarded as they provide uniform values and are not contributable. In addition, in order to extract valuable information from the weights defined according to distinct association metrics, weighted measures such as degree and PageRank centralities, and the modularity are presented. Those metrics are defined as follows:
- Degree Centrality: The degree of a node is the number of edges that are adjacent to the node, multiplied by corresponding weights define in Section 2.2.1.
- PageRank Centrality: An iterative algorithm that measures the importance of each node within the network. The page rank values are the values in the eigenvector with the highest corresponding eigenvalue of a normalized adjacency matrix derived from the graph [29].
- Modularity: A high modularity score indicates sophisticated internal structure. This structure, often called a community structure, describes how the the network is compartmentalized into sub-networks. These sub-networks (or communities) have been shown to have significant real-world meaning [30].
In order to perform variable visual comparison, the following distribution layouts are implemented:
- Fruchterman Reingold: The Fruchterman-Reingold Algorithm is a force-directed layout algorithm. The idea of a force-directed layout algorithm is to consider a force between any two nodes. In this algorithm, the nodes are represented by steel rings and the edges are springs between them. The attractive force is analogous to the spring force and the repulsive force is analogous to the electrical force. The basic idea is to minimize the energy of the system by moving the nodes and changing the forces between them [31].
- Force Atlas 2: The main property of this force-directed layout consists of its implementation of distinct methods such as the Barnes Hut simulation, degree-dependent repulsive force, and local and global adaptive temperatures [32].
2.3. Validation Procedure
The validation procedure encompasses two main phases. The initial phase entails utilizing both association metrics in order to identify the most fundamental combination of features from the arrays delineated in Table 2. In order to measure the capacity of this selection, a visual comparison is performed of the normalized efficiency distribution of both groups: the original complete data set collected in Table 2 against the reduced set sharing the fundamental or core feature group. Subsequently, in order to extract more concrete results, two specific feature arrangements listed in Table 2 are highlighted according to both association metrics. These feature collections are contrasted with the efficiency distribution of the reduced data set.
The second phase compares the final feature groupings to other groupings derived from standard feature selection methods. More exactly, univariate feature selection procedures, characterized by the preference based on univariate statistical tests such as Pearson correlation coefficient [33] and Mutual Info Regression [11], or Sequential Feature Selector, based on cross-validation score to select or discard iteratively the features. Principal Component Analysis and other popular feature preprocessing methods have been eluded, as the strategy in consideration focus on feature elimination strategies.
3. Results
Exploration of the complete data collection distribution is partially detailed in Table 2, to gain insights into its characteristics. The distribution is visualized in Figure 1, while a statistical summary is provided in Table 3. The complete data set comprises an extensive collection of 157,135 feature combinations, a substantial quantity that has sparked interest in applying association rules to our specific case study. This large data set size further fuels our curiosity and motivates us to investigate the application of association rules in this context. The RMSE mean of all these quantities is 0.63, while the whole interval is defined by the minimum and maximum RMSE values of 0.55 and 0.66, respectively. Following the interpretation of Table 3, the mean of feature quantities of 6.54, the percentile of 25–100% of six and seven features, respectively, indicates that the majority of feature combinations contains between six and seven features.
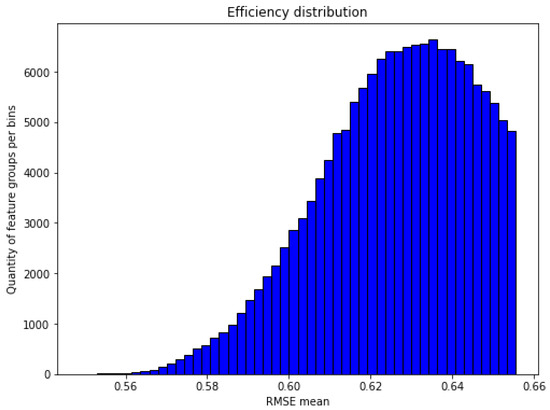
Figure 1.
Complete data distribution.

Table 3.
Statistics of complete data collection.
It is also important to analyze the dependence and independence relationships between variables. Therefore, correlation relations between all features (including the target BBCH and the mandatory input parameter DOY) are depicted in Figure A1, where two main highly correlated feature groupings appear: BBCH, DOY, mean temp, max temp, min temp, and dewp temp, most of them temperature-derived features. On the other hand, accumulative quantities (precip cum, GDD, NDVIcum, EVIcum, REDcum and NIRcum) are highly related between them, as well as to BBCH and DOY (both of them have an increasing trend), and slightly less correlated to temperature-derived features. Low correlation quantities are equally important, as a result of the independence between features.
3.1. Association Metrics
The following section computes the two feature-weighted associations from metrics defined in Section 2.2.1.
3.1.1. M1 Based Feature Association
The weights assigned to both nodes and edges according to Equation (1) are collected in the following Table 4. The interpretation of the Table is straight, as all features are ranked in a unique way. The most prominent attributes, ranked in descending order, include cum precip, latitude, max temp, sea level, slope and min temp.

Table 4.
Efficiency metric-based weight accumulation for features.
3.1.2. M2 Based Feature Association
The following section describes the experimental setup of Market Basket Analysis (MBA) techniques in frequent item set mining [22]. The relationships between features are examined, with a particular focus on identifying frequent patterns according to M2, defined in Section 2.2.1.
The most important metric of this analysis is support, which indicates how frequent a combination is. Therefore, when analyzing Table 5 which corresponds to the association metrics obtained by selecting the entire set of all the combinations described in the previous section, it is observable that the best-positioned combination of cum precipitation and length has a very small support of 0.1. Despite the individual presence of cum precipitation being 0.47, the goal of this study is to extract the most robust or significant feature combinations as a whole, not individually. Therefore, the supports of the antecedents as well as the consequents do not acquire much importance in this analysis. Moreover, the interpretation of the lift and leverage metrics indicates a high independence between the variables in question. On the contrary, the correlations detailed in Figure A1, demonstrate the high dependence between accumulated features and temperature-derived features. lat and sea level seem to be totally independent between them due to their null correlation, but lat is slightly correlated to precip cum, with a correlation of 0.33, and it appears related as an antecedent or consequent with numerous features.

Table 5.
RMSE threshold 0.6549, 100%.
However, the total number of analyzed combinations is very large, with around 150,000 possible combinations (see the previous section). Consequently, the number of combinations must be analyzed by selecting the best combinations of 75%, 50%, 25%, 10%, and 1% of the entire data set. The association metrics corresponding to these selections and the RMSE limit are described in Table 6, Table 7, Table 8, Table 9 and Table 10, respectively. Indeed, Table 6, Table 7 and Table 8 depict results corresponding to the 75%, 50%, and 25% percentages of the data set, where the support maximum values depict values below 0.17 despite the data set reduction. In the best case, visible in Table 8, the support has risen to 0.16 with the combination of slope and latitude (lat) being the most frequent combination. However, Table 9 and Table 10 (corresponding to 10% and 1% of the data set) visualize an increase in the support metric, with respective maximum values of 0.23 and 0.33, and both cases highlight the same most representative feature combination: maximum temperature and accumulated precipitation. The following most representative combination is that of latitude and slope in Table 9, while in Table 10, it is the couple of latitude and sea level. In both cases, these are geographic characteristics. However, in the case of Table 10, there is additional information, since combinations of more than two characteristics begin to stand out, i.e., the combination of cum precipitation and max temp and latitude. Moreover, the confidence corresponding to such combinations is very high and significant. The quantities that characterize the possible independence of the characteristics in question, i.e. lift and leverage, are still of concern.

Table 6.
RMSE threshold 0.64053, 75%.

Table 7.
RMSE threshold 0.62765, 50%.

Table 8.
RMSE threshold 0.61336, 25%.

Table 9.
RMSE threshold 0.59993, 10%.

Table 10.
RMSE threshold 0.5778, 1%.
Furthermore, a reduced portion, specifically 0.5, of the data set has been selected. As the descending order based on support is maintained, further reduction of the data set has been discarded.
The feature combinations highlighted in Table 10 reflect that the core of the feature combination is the combination of the following features: cum precip, max temp, lat and sea level (the same grouping leading the Table 4). Indeed, this combination is present in the 0.34% of the data set listed in Table 2, and following the metrics resulted in Table 10, the final selected feature combination would be cum precip, max temp, lat, sea level, dew point, and REDcum.
3.2. Network Visualization
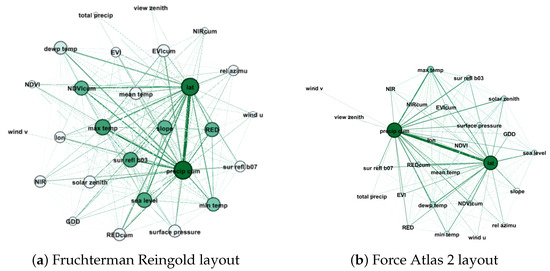
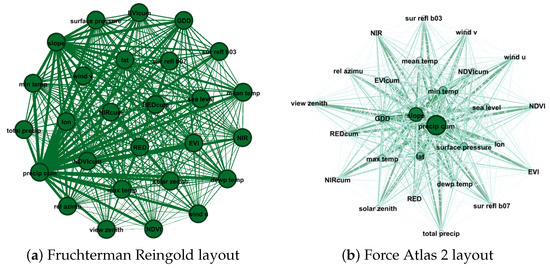
Subsequently, Figure 2 and Figure 3 visualize the networks derived from the association metrics M1 and M2, respectively, outlined in the preceding section. This task has been facilitated by Gephi 0.9.2. https://gephi.org/, (accessed on 2 October 2023), an open-source software renowned for its adeptness in network visualization. Figure 2a,b and Figure 3a,b depict two distinguishable layouts characterized by Fruchtherman Reingold and Atlas Force strategies, respectively and configured according to parameters collected in Table A1 and Table A2. Fruchtherman distribution prioritizes maintaining the equidistance between the nodes, while Force Atlas 2 requires adapting the configuration parameters to find a balance to avoid overlapping. In parallel, coloration and shaping of nodes follow computed centrality metrics detailed in Table A3 and Table A4. More exactly, toning and sizing are proportional to the Degree statistics in Figure 2a and Figure 3a, while in Figure 2b and Figure 3b depend on Weighted Degree and pageranks centrality results. The construction of the network derived from M1 metric considers the total original data set, without any reduction, and therefore, the average degree of all nodes is the same (see Table A3), whereas the network associated with the M2 metric implies the reduction to the 0.1 of the data set as specified in Section 3.1.2, resulting in distinct average degree values (see Table A4). These measure differences directly affect the node sizes and coloring variation of Figure 2a and Figure 3a, where the first one contains equal shapes and colors for all nodes. Regarding the evolution from Fruchterman to Force Atlas 2 layout, a noticeable change is observed in Figure 2, since the most relevant nodes according to the centrality metrics of Table A3 are relocated in the center of the network. The gravity center contains the couple precip cum, slope while features as lat, surface pressure compose the outer circumference of the center. In this way, the core of the features is visually highlighted. On the contrary, in Figure 3, layout adjustment’s effect seems to be insignificant. Indeed, in both cases, the spatial distribution locates the most relevant features precip cum, with a lat that is close but not in the middle of the center. With the configuration change from Figure 3a to Figure 3b, the group of secondary nodes NDVIcum, slope, RED, …is reduced, and loses relevance in centrality metrics (node sizing and coloring). In addition, those that maintain a degree of importance (max temp, dewp temp, …) move a little to the peripheries. In conclusion, the associated weights according to the metrics M1 and M2 highlight, in a notorious way, a binary feature combination in both cases; create a group of secondary ones; and despite having distinct centrality distribution of core features, in both cases, the configuration transition totally scatters to the extremities of the networks those characteristics without much weight or importance.
3.3. Validation
In order to validate the usefulness of these methods, the following procedure contains two phases. First, the Feature Core is analyzed as a result of merging the rankings of Table 4 and Table 10. Indeed, as an intersection of the feature ordering and groupings concluded from the methods M1 and M2, the cornerstone feature combination of the most performant models is as follows:
- Feature Core: accumulated precipitation, maximal air temperature, latitude and sea level pressure.
This feature grouping is present in the 0.3% percentage of the data set, a total amount of 529 feature combinations listed in Table 2. A visual performance comparison between this reduction against the total data set is illustrated in Figure 4. More concretely, Figure 4a contains the normalized efficiency distribution of all feature sets of Table 2, while Figure 4b depicts the normalized efficiency distribution of the limited combinations characterized by their common Feature Core. The normalization of the results facilitates analyzing the impact of the data set reduction, resulting in a change in the distribution trend in Figure 4a,b, transferring the main concentration from higher RMSE values to lower ones. The conclusion is that this reduction strategy provides a more competent collection.
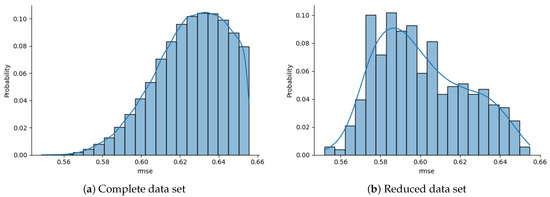
Figure 4.
Normalized efficiency distribution comparison between all feature combinations from Table 2 versus reduced selection. The main characteristic of the limited ensemble is that all feature combinations contain the following core: accumulated precipitation, maximal air temperature, latitude and sea level.
This reduction can be limited to concrete feature groupings considering the analysis performed in Section 3. Two specific feature combinations G1 and G2 arise from both association metrics, M1 and M2, respectively. Both feature combinations keep the same Feature Core, and two additional distinct features as detailed as follows:
- G1: Feature Core, slope, minimal air temperature
- G2: Feature Core, dewpoint temperature, accumulated RED.
Figure 5 illustrates the competency of feature groups G1–G2 in comparison to the efficiency distribution of the reduced data set according to the Feature Core criteria. The RMSE of 0.555 for the G2 collection is slightly better than the RMSE of 0.579 for G1. Therefore, from an efficiency point of view, the feature set G2 is better. On the other hand, the physical meaning of accumulated RED is harder to explain rather than slope or minimal air temperature features. Consequently, for the sake of interpretability, the feature collection G1 may be more interesting from a biological point of view.
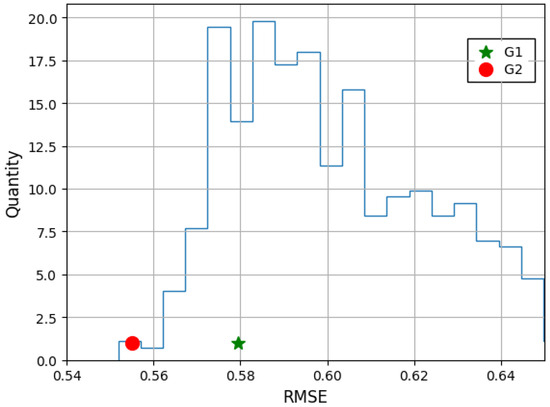
Figure 5.
RMSE position of G1 and G2 feature combinations in comparison to the normalized efficiency distribution of the Feature Core-based reduced data set.
- G3: GDD, NIRcum, EVIcum, REDcum, NDVIcum, precip cum
- G4: GDD, NIRcum, EVIcum, solar zenith, NDVIcum, mean temperature
- G5: sea level pressure, GDD, slope, wind u, blue surface reflectance, dewpoint temperature
In addition, in order to compare the capacity of this feature processing, the following standard methodologies have been applied to the original data set: Pearson Correlation Coefficient, Mutual Info Regression, Sequential Feature Selector. The best scored features according to the first two techniques are listed in Table A5 and Table A6 and grouped, respectively, in feature groups G3 and G4. The Sequential Feature Selector outputs in a Boolean manner, and the selected features are grouped in G5.
Figure 6 contains the accuracy comparison between all considered feature priorization techniques. The RMSE mean in almost all cases is similar, being slightly lower in the G3 and G5 groupings, and slightly better in the G4 grouping. However, if we look at the variability of the data, the results with the least variability, and therefore the most consistent, correspond to the G2 cluster. In the case of the G1 grouping, it also shows a lower variability than G4, the difference being negligible.
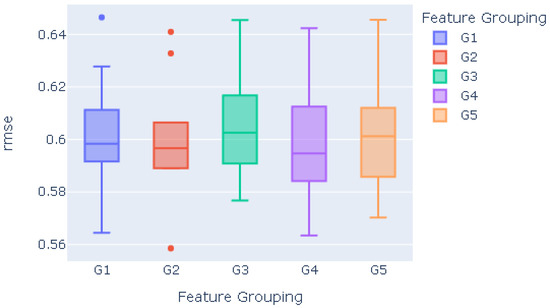
Figure 6.
Accuracy comparison for distinct feature selection methodologies.
As a conclusion, the feature extraction methodology proposed by this study provides efficiency outcomes similar to existent standard approaches. In this particular context, both M1 and M2 association metrics provide more competent results than R Regression and a Sequential Feature Selector, but a lower efficacy than Mutual Info Regression. On the contrary, the main contribution or novelty of these methods is the balance between the efficiency and robustness of the predictions, especially in the case of the MBA. The distribution of the errors visible in Figure 6 highlights the reliability and consistency of the MBA-based strategy’s predictions (a statistical description is available in Table A7).
4. Discussion
As we can see, the forecast is very accurate; we obtained a mean relative error of 0.85%. Note that we would have used the RMSE or the MAPE to validate our results if we had to predict multiple values. Since we only wanted to predict a specific DOY, we had to employ the relative error instead as a way to test the accuracy of our forecast.
5. Conclusions
The modeling of predictive processes based on machine learning or deep learning requires a section for properly selecting features. These methodologies can be categorized into three distinct selection types, namely filter, wrapper, and embedded techniques. In this study, our focus converges on a wrapper approach, based on results retrieved from a recent publication [17]. On several occasions, the application of exhaustive search mechanisms can provide an immense number of feature combinations that are equally efficient at predicting a particular phenomenon, such as the phenological state in this case. The main goal of this investigation has been to analyze two distinct methods to extract useful information from the particular case presented in [17], gaining practical knowledge in a format of a reduced and representative group of characteristics.
One of the methods consists of using metrics derived from market basket analysis, which is popularly used to explore the associations between purchased objects, or the properties of groupings in a more generalized case. In the present study, it has been observed that the utilization of this approach, in conjunction with another more basic technique, has facilitated the extraction of a central characteristic set. The value of limiting the original data set to groups containing this central collection lies in the improved efficiency of the resulting group. Furthermore, rather than combining the implementation of both methods, the independent application terminates in two distinct sets of specific features. Both feature combinations represent high accuracy levels, thus validating the strategy for selecting a representative and efficient subset of features.
In conclusion, the proposed methodologies are useful for selecting a group of robust characteristics for the phenological prediction of olive trees. In order to extend this strategy to other predictions, it is important to remember that this wrapper-kind feature selection process is intrinsically linked to a specific prediction model. This implies that the transference of this tactic to other modeling procedures requires a preliminary assessment to determine a prediction model appropriate to the data and the context.
Nonetheless, it is significant that efficiency of the combination of features obtained in this procedure is similar to that offered by standard processing techniques. A noteworthy limitation of this evidence is that the running time of the whole process (creating all possible combinations and then analyzing them using MBA techniques) may be unnecessarily costly. Therefore, its implementation would be recommended for non-urgent contexts, in situations that value robustness and stability of the results apart from the accuracy.
Author Contributions
Conceptualization and methodology, software and formal analysis, I.A.; validation and investigation, I.A.; writing—original-draft preparation, I.A.; review and editing, I.G.O. and M.Q.; supervision, I.G.O. and M.Q.; project administration and funding acquisition, I.G.O. and M.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This material is based upon work funded by the H2020 DEMETER project, grant agreement ID 857202, funded under H2020-EU.2.1.1.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GDD | Growing degree days. |
| MBA | Market Basket Analysis. |
| BBCH | Biologische Bundesanstalt, Bundessortenamt, und CHemische Industrie. |
| DOY | Day Of Year. |
| EVI | Enhanced vegetation index. |
| NDVI | Normalized difference vegetation index. |
| GEE | Google Earth Engine. |
| RMSE | Root-mean-square deviation. |
| M1 | Metric 1, 1-RMSE weight proportional metric. |
| M2 | Metric 2, MBA-derived metric |
| G1 | Group 1, feature grouping derived from M1. |
| G2 | Group 2, feature grouping derived from M2. |
| G3 | Group 3, feature grouping derived from Pearson correlation coefficient. |
| G4 | Group 4, feature grouping derived from Mutual Info Regression. |
| G5 | Group 5, feature grouping derived from Sequential Feature Selector. |
Appendix A. Correlation Matrix
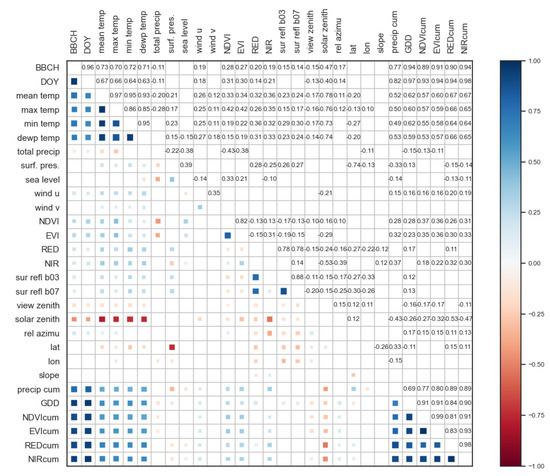
Figure A1.
Correlation matrix association of the complete feature set.
Appendix B. Gephi Configuration and Metrics
Appendix B.1. Layout Configuration Parameters

Table A1.
Configuration of Fruchterman Reingold Layout parameters.
Table A1.
Configuration of Fruchterman Reingold Layout parameters.
| Fruchterman Reingold | M1 | M2 |
|---|---|---|
| area | 10 × 10 | 10 × 10 |
| Gravity | 10 | 10 |
| Speed | 1 | 1 |

Table A2.
Configuration of Force Atlas Layout parameters.
Table A2.
Configuration of Force Atlas Layout parameters.
| Force Atlas Parameters | M1 | M2 |
|---|---|---|
| Inertia | ||
| Repulsion strength | 2 × 10+5 | 200 |
| Attraction strength | 10 | 1 |
| Maximum displacement | 10 | 10 |
| Auto stabilize function | True | True |
| Autostab Strength | 80 | 800 |
| Autostab sensibility | ||
| Gravity | 1 | 1 |
| Attraction Distrib. | True | True |
| Adjust by Sizes | True | False |
| Speed | 1 | 1 |
Appendix B.2. Centrality Metrics

Table A3.
Centrality statistics of M1-based feature distributions.
Table A3.
Centrality statistics of M1-based feature distributions.
| Label | Degree | Weighted Degree | Modularity Class | Pageranks |
|---|---|---|---|---|
| precip cum | 26 | 353,741 | 0 | 0.08 |
| max temp | 26 | 152,735 | 0 | 0.04 |
| lat | 26 | 174367 | 0 | 0.04 |
| EVIcum | 26 | 148,232 | 0 | 0.04 |
| sur refl b03 | 26 | 123,661 | 0 | 0.03 |
| NIRcum | 26 | 116,685 | 0 | 0.03 |
| dewp temp | 26 | 144,798 | 0 | 0.04 |
| sea level | 26 | 149,325 | 0 | 0.04 |
| slope | 26 | 268,762 | 0 | 0.06 |
| min temp | 26 | 169,226 | 0 | 0.04 |
| sur refl b07 | 26 | 118,982 | 0 | 0.03 |
| REDcum | 26 | 129,930 | 0 | 0.03 |
| RED | 26 | 134,682 | 0 | 0.03 |
| NIR | 26 | 123,034 | 0 | 0.03 |
| mean temp | 26 | 146,211 | 0 | 0.04 |
| NDVIcum | 26 | 145,919 | 0 | 0.04 |
| solar zenith | 26 | 126,423 | 0 | 0.03 |
| rel azimu | 26 | 127,205 | 0 | 0.03 |
| surface pressure | 26 | 159,210 | 0 | 0.04 |
| lon | 26 | 141,790 | 0 | 0.04 |
| GDD | 26 | 167,743 | 0 | 0.04 |
| EVI | 26 | 108,710 | 0 | 0.03 |
| NDVI | 26 | 113,647 | 0 | 0.03 |
| wind v | 26 | 129,516 | 0 | 0.03 |
| total precip | 26 | 115,039 | 0 | 0.03 |
| wind u | 26 | 118,379 | 0 | 0.03 |
| view zenith | 26 | 103,406 | 0 | 0.03 |

Table A4.
Centrality statistics of M2-based feature distributions.
Table A4.
Centrality statistics of M2-based feature distributions.
| Label | Degree | Weighted Degree | Modularity Class | Pageranks |
|---|---|---|---|---|
| precip cum | 26 | 8604 | 0 | 0.16 |
| lat | 25 | 8354 | 1 | 0.15 |
| max temp | 22 | 2694 | 0 | 0.05 |
| sur refl b03 | 21 | 1968 | 0 | 0.04 |
| sea level | 21 | 1904 | 1 | 0.04 |
| slope | 20 | 1542 | 1 | 0.03 |
| RED | 20 | 1444 | 1 | 0.03 |
| NDVIcum | 20 | 1890 | 1 | 0.04 |
| min temp | 19 | 1716 | 1 | 0.03 |
| dewp temp | 18 | 2220 | 1 | 0.04 |
| surface pressure | 17 | 1822 | 2 | 0.04 |
| EVIcum | 17 | 1972 | 0 | 0.04 |
| solar zenith | 17 | 2046 | 2 | 0.04 |
| REDcum | 17 | 1992 | 1 | 0.04 |
| mean temp | 17 | 2032 | 2 | 0.04 |
| NIR | 16 | 840 | 0 | 0.02 |
| lon | 15 | 1276 | 0 | 0.03 |
| sur refl b07 | 15 | 1152 | 1 | 0.02 |
| rel azimu | 14 | 1046 | 1 | 0.02 |
| EVI | 13 | 910 | 1 | 0.02 |
| GDD | 11 | 1030 | 1 | 0.02 |
| NDVI | 9 | 602 | 0 | 0.02 |
| NIRcum | 8 | 402 | 0 | 0.01 |
| wind u | 7 | 338 | 1 | 0.01 |
| total precip | 4 | 126 | 1 | 0.01 |
| view zenith | 2 | 8 | 0 | 0.01 |
| wind v | 1 | 2 | 0 | 0.01 |
Appendix C. Validation Section Extra Info

Table A5.
Descending order of the Pearson correlation coefficients between BBCH and all input candidates.
Table A5.
Descending order of the Pearson correlation coefficients between BBCH and all input candidates.
| Features | Scores |
|---|---|
| GDD | 6806.02 |
| NIRcum | 6383.33 |
| EVIcum | 3927.72 |
| REDcum | 3605.50 |
| NDVIcum | 3264.47 |
| precip cum | 1216.78 |
| mean temp | 962.07 |
| min temp | 887.57 |
| dewp temp | 829.22 |
| max temp | 799.95 |
| solar zenith | 226.54 |
| NDVI | 69.70 |
| EVI | 65.79 |
| RED | 34.90 |
| NIR | 31.40 |
| wind u | 30.94 |
| rel azimu | 25.39 |
| view zenith | 18.10 |
| sur refl b03 | 17.83 |
| sur refl b07 | 16.64 |
| total precip | 9.45 |
| sea level | 4.72 |
| lon | 3.75 |
| lat | 1.90 |
| surf. pres. | 1.07 |
| wind v | 0.28 |
| slope | 0.06 |

Table A6.
Descending order of the mutual information between BBCH and all input candidates.
Table A6.
Descending order of the mutual information between BBCH and all input candidates.
| Features | Scores |
|---|---|
| GDD | 1.72 |
| NIRcum | 1.29 |
| EVIcum | 1.27 |
| solar zenith | 1.23 |
| NDVIcum | 1.22 |
| mean temp | 1.11 |
| sea level | 1.04 |
| REDcum | 1.01 |
| dewp temp | 1.00 |
| min temp | 0.93 |
| max temp | 0.93 |
| precip cum | 0.73 |
| total precip | 0.45 |
| wind u | 0.36 |
| surf. pres. | 0.33 |
| wind v | 0.33 |
| rel azimu | 0.28 |
| view zenith | 0.24 |
| NIR | 0.24 |
| NDVI | 0.17 |
| EVI | 0.15 |
| sur refl b07 | 0.11 |
| RED | 0.09 |
| sur refl b03 | 0.08 |
| slope | 0.00 |
| lon | 0.00 |
| lat | 0.00 |

Table A7.
Statistical description of the distinct feature grouping comparison.
Table A7.
Statistical description of the distinct feature grouping comparison.
| Feature | RMSE | ||||||
|---|---|---|---|---|---|---|---|
| Grouping | Mean | std | Min | 25% | 50% | 75% | Max |
| G1 | 0.602 | 0.023 | 0.564 | 0.592 | 0.598 | 0.609 | 0.646 |
| G2 | 0.600 | 0.023 | 0.559 | 0.590 | 0.597 | 0.605 | 0.641 |
| G3 | 0.604 | 0.019 | 0.577 | 0.591 | 0.603 | 0.615 | 0.645 |
| G4 | 0.600 | 0.024 | 0.563 | 0.584 | 0.595 | 0.610 | 0.642 |
| G5 | 0.603 | 0.021 | 0.570 | 0.589 | 0.601 | 0.611 | 0.646 |
References
- Chandrashekar, G.; Sahin, F. A survey on feature selection methods. Comput. Electr. Eng. 2014, 40, 16–28. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Keogh, E.; Mueen, A. Curse of Dimensionality. In Encyclopedia of Machine Learning and Data Mining; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2017; pp. 314–315. [Google Scholar]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Hasan, B.M.S.; Abdulazeez, A.M. A review of principal component analysis algorithm for dimensionality reduction. J. Soft Comput. Data Min. 2021, 2, 20–30. [Google Scholar]
- Zhou, H.; Wang, F.; Tao, P. t-Distributed stochastic neighbor embedding method with the least information loss for macromolecular simulations. J. Chem. Theory Comput. 2018, 14, 5499–5510. [Google Scholar] [CrossRef]
- Salman, R.; Alzaatreh, A.; Sulieman, H. The stability of different aggregation techniques in ensemble feature selection. J. Big Data 2022, 9, 1–23. [Google Scholar] [CrossRef]
- Duch, W.; Wieczorek, T.; Biesiada, J.; Blachnik, M. Comparison of feature ranking methods based on information entropy. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks (IEEE Cat. No. 04CH37541), Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 1415–1419. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, X.W.; Jeong, J.C. Enhanced recursive feature elimination. In Proceedings of the IEEE Sixth International Conference on Machine Learning and Applications (ICMLA 2007), Cincinnati, OH, USA, 13–15 December 2007; pp. 429–435. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2011, 69, 066138. [Google Scholar] [CrossRef]
- Doshi, M. Correlation based feature selection (CFS) technique to predict student Perfromance. Int. J. Comput. Netw. Commun. 2014, 6, 197. [Google Scholar] [CrossRef]
- Sanderson, C.; Paliwal, K.K. Polynomial features for robust face authentication. In Proceedings of the IEEE International Conference on Image Processing, Rochester, NY, USA, 22–25 September 2002; Volume 3, pp. 997–1000. [Google Scholar]
- Duch, W. Filter methods. In Feature Extraction: Foundations and Applications; Springer: Berlin/Heidelberg, Germany, 2006; pp. 89–117. [Google Scholar]
- Mlambo, N.; Cheruiyot, W.K.; Kimwele, M.W. A survey and comparative study of filter and wrapper feature selection techniques. Int. J. Eng. Sci. (IJES) 2016, 5, 57–67. [Google Scholar]
- Liu, H.; Zhou, M.; Liu, Q. An embedded feature selection method for imbalanced data classification. IEEE/CAA J. Autom. Sin. 2019, 6, 703–715. [Google Scholar] [CrossRef]
- Azpiroz, I.; Oses, N.; Quartulli, M.; Olaizola, I.G.; Guidotti, D.; Marchi, S. Comparison of Climate Reanalysis and Remote-Sensing Data for Predicting Olive Phenology through Machine-Learning Methods. Remote Sens. 2021, 13, 1224. [Google Scholar] [CrossRef]
- Vettoretti, M.; Di Camillo, B. A variable ranking method for machine learning models with correlated features: In-silico validation and application for diabetes prediction. Appl. Sci. 2021, 11, 7740. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Kanellopoulos, D. Association rules mining: A recent overview. GESTS Int. Trans. Comput. Sci. Eng. 2006, 32, 71–82. [Google Scholar]
- Ünvan, Y.A. Market basket analysis with association rules. Commun. Stat. Theory Methods 2021, 50, 1615–1628. [Google Scholar] [CrossRef]
- Annie, L.C.M.; Kumar, A.D. Market basket analysis for a supermarket based on frequent itemset mining. Int. J. Comput. Sci. Issues (IJCSI) 2012, 9, 257. [Google Scholar]
- Kaur, M.; Kang, S. Market Basket Analysis: Identify the changing trends of market data using association rule mining. Procedia Comput. Sci. 2016, 85, 78–85. [Google Scholar] [CrossRef]
- Gayle, S. The Marriage of Market Basket Analysis to Predictive Modeling. In Proceedings of the Web Mining for E-Commerce-Challenges and Opportunities, Boston, MA, USA, 20 August 2000; ACM: Boston, MA, USA, 2000. [Google Scholar]
- Oses, N.; Azpiroz, I.; Marchi, S.; Guidotti, D.; Quartulli, M.; Olaizola, I.G. Analysis of Copernicus’ ERA5 Climate Reanalysis Data as a Replacement for Weather Station Temperature Measurements in Machine Learning Models for Olive Phenology Phase Prediction. Sensors 2020, 20, 6381. [Google Scholar] [CrossRef]
- Piña-Rey, A.; Ribeiro, H.; Fernández-González, M.; Abreu, I.; Rodríguez-Rajo, F.J. Phenological model to predict budbreak and flowering dates of four vitis vinifera L. Cultivars cultivated in DO. Ribeiro (North-West Spain). Plants 2021, 10, 502. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Raschka, S. MLxtend: Providing machine learning and data science utilities and extensions to Python’s scientific computing stack. J. Open Source Softw. 2018, 3, 638. [Google Scholar] [CrossRef]
- Bastian, M.; Heymann, S.; Jacomy, M. Gephi: An open source software for exploring and manipulating networks. In Proceedings of the International AAAI Conference on Web and Social Media, San Jose, CA, USA, 17–20 May 2009; Volume 3, pp. 361–362. [Google Scholar]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The PageRank Citation Ranking: Bringing Order to the Web; Rech Report; Stanford InfoLab: Stanford, CA, USA, 1999; Volume 8090, p. 422. [Google Scholar]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Fruchterman, T.M.; Reingold, E.M. Graph drawing by force-directed placement. Softw. Pract. Exp. 1991, 21, 1129–1164. [Google Scholar] [CrossRef]
- Jacomy, M.; Venturini, T.; Heymann, S.; Bastian, M. ForceAtlas2, a continuous graph layout algorithm for handy network visualization designed for the Gephi software. PLoS ONE 2014, 9, e98679. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Mu, Y.; Chen, K.; Li, Y.; Guo, J. Daily activity feature selection in smart homes based on pearson correlation coefficient. Neural Process. Lett. 2020, 51, 1771–1787. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).