Abstract
The current work concerns the problem of estimating the aerodynamic forces and moments induced by the wind on the fast-erecting 63K crane by Liebherr. In the first step, scaled sectional models of the tower truss and horizontal jib truss are prepared for experimental analysis in an aerodynamic tunnel. Next, the aerodynamic forces and moments are measured in the aerodynamic tunnel. It is assumed that the direction of the wind changes from 0° to 180° in 15° steps for both of the studied sectional models. The experimental tests are carried out for two levels of turbulence intensity. In the case of the model of the vertical part of the studied crane, the turbulence intensities are assumed to be equal to 3% and 9%. In the case of the horizontal crane jib, they are 3% and 12%, respectively. In the second step, a CFD analysis is performed with the use of Ansys Fluent R22 software. The standard k-ε model with a standard wall function of the turbulent flow is utilized. The airflow around the studied structures is modeled with the use of polytetrahedral cells. A relatively good agreement between the numerical and experimental results is observed. The obtained values are compared to the appropriate standard, namely PN-ISO 4302.
1. Introduction
With the rapid change in climatic conditions, the risk of accidents due to high winds is increasing. This is particularly important in the case of cranes and different types of mobile elevating work platforms. The wind is the second most common cause of tower crane accidents [1]. Extremely tall tower cranes are particularly exposed to such dangers [2]. The entire structure, as well as the horizontal beam of the crane jib, may be damaged [3]. However, relatively lower tower cranes are also exposed to the risk of tip-over due to local strong gusts of wind. Cranes with heights of 35 to 50 m are the most commonly used cranes in the building industry. These are free-standing cranes that can be used to build a 10-story residential building. Higher structures are secured against overturning by anchoring to the building. Therefore, the authors limited themselves to free-standing crane structures. Such a structure was the scene of an accident that took place in Cracow (Poland) on 17 February 2022. A local strong whirlwind, probably created due to the interference effect caused by the surrounding buildings, was so strong that it caused the overturning of a tower crane [4]. This whirlwind is clearly visible in the video, which is available on the referenced website. Two people died because of this accident. It is worth noting that this kind of wind phenomenon is rather rare in Cracow and its surroundings areas. Moreover, it seems that all safety principles had been fully satisfied prior to the accident. Therefore, this accident is one of the main motivations for the work presented here.
Generally, according to different standards, namely the European standard, Eurocode ISO 4302:2016 [5]; British standard, BS 2573-1 [6]; American Society of Civil Engineers standard, ASCE 7-16 [7]; Japanese standard, JIS B 8830-2001 [8]; and Chinese standard, GB/T 3811-2008 [9], the load induced by wind is treated as a static load. The influence of the surroundings and adjacent structures, mainly buildings (so-called interference effect), is neglected.
However, from a practical point of view, such a simple approach could be inadequate in the case of real airflow phenomena, especially in the case of large-scale structures like tower cranes, gantry cranes, or different types of mobile elevating work platforms. Thus, there is significant value in works in which wind measurements are performed on real-scale structures [10,11,12]. Based on these results, the appropriate wind conditions can be imitated in aerodynamic tunnels, where scaled models of the real large-scale structures can be tested in order to determine the wind load (force and movement coefficients) [13,14,15,16].
On the other hand, the rapid development of computer hardware, together with specialized software based on the finite element method or finite volume method, allows for numerical simulations of the airflow and its interactions with different types of cranes or mobile elevating work platforms to be carried out [17,18,19]. Additionally, by having the distribution of the static pressure (caused by wind) on the surface of the studied structure available, it is possible to carry out further mechanical analyses based on the fluid–solid interaction in order to determine, for example, the stress distribution in the most at-risk parts of the structure [20]. Moreover, an analysis of the dynamic response of the investigated structure is also possible [21]. Nowadays, the standard approach in the case of the analysis of the impact of the wind on crane-like structures consists of two steps. Generally, in the first step, a scaled model of the studied structure is prepared, and next, the appropriate experimental analysis is performed in an aerodynamic tunnel. In the second step, numerical simulations are carried out, and the results are compared [22].
It is worth noting that the wind load, especially gusts of wind, which are very often two times greater in comparison to the mean wind speed and have a frequency of about 1 Hz [11], can also cause vibrations in structures [23]. Chen and Li [24] studied the displacement of a lattice tower using time–history analysis and a nonlinear dynamic analysis and found that the displacement was higher by about 5–28% compared to that calculated using a static analysis. Jiang and Li [25] investigated the random wind-induced response of tower cranes using the finite element method and virtual excitation method. The results indicated that the vibrations of the tower crane showed a greater response at low frequencies. Next, Takahashi et al. [26] studied the runaway of quayside container cranes subjected to transient gusty winds. They also proposed a sliding state to model the runaway and after a runaway caused by a wind gust. A linear filter autoregressive model was used by Jiang and Li [27] to simulate the time history of multi-dimensional fluctuating wind samples, and the corresponding wind load was applied to a finite element model of a tower crane to analyze the vibration response to the wind. The results showed that under the action of a wind speed of 20 m/s, the structural strength reserve of this type of tower crane was relatively sufficient. Chen et al. [21] studied the interference effect of the different segments of a tower crane subjected to wind loads. The wind coefficients of a full-scale model of a tower crane were calculated using computational fluid dynamics (CFD). Then, the time history of the wind loads, simulated through the autoregressive method, was applied to the finite element model of a tower crane. Although the maximum wind load direction of the tower crane was perpendicular to its jib, the obtained results revealed that the maximum along-wind load direction was deflected by 30°–60°, and the mean ratio of the absolute value of the across-wind coefficient to the along-wind coefficient of the tower crane was about 8.56%. Su et al. [28] studied the effect of stochastic dynamic transient gusty winds on the sliding and overturning of quayside container cranes. The main conclusion was that dynamic transient gusty-wind-induced peak responses follow a type III (Weibull) extreme value distribution. Azzi et al. [29] performed wind tunnel tests on an aeroelastic lattice tower model. The obtained results revealed that the resonance contribution could reach a maximum of 18% of the peak response of the tower. El Ouni et al. [30] performed a modal analysis using the finite element method to calculate natural frequencies and corresponding mode shapes of a tower crane. The analysis was carried out to design a decentralized active vibration control to prevent the collapse of the crane. Active damping is added to the tower crane using pairs of force actuators–displacement sensors collocated on selected elements. Finally, Oliveira and Correia [31] compared the dynamic response of the tower crane excited by seismic vibrations and wind loads.
In the last year, several interesting works, which concern the problem of the impact of wind loads on crane-like structures, were published. Lu et al. [32] took into consideration the problem of the outer-attached tower cranes installed on super-high-rise buildings and exposed to wind-induced vibrations. Numerical CFD simulations and structural FEM calculations were performed. Next, He et al. [33] presented a study on a similar problem. To avoid sophisticated finite element analysis of the main building, a modified generalized flexural–shear model (FSM-MS) was proposed to estimate the along-wind and across-wind displacement responses of the main building and the responses at the connection support of the tower crane. Yeon et al. [34] studied the lift effect on wind load estimation for a semi-submersible rig. Wind loads on the analyzed rig were calculated under the maritime atmospheric boundary layer. The obtained results matched well with those from the wind tunnel within an error of about ±20%.
The impact of the lifted load on the stability of crane-like devices has also been investigated. Here, several works can be quoted, namely Skelton et al. [35], Monteiro et al. [36], Cekus et al. [37,38], and Jin et al. [39].
At the end of this brief survey of the literature, it is also worth mentioning the wind-induced interference effect (IE). The analysis of this problem provides insights into how the neighboring structures influence the studied structure by changing the surface pressure caused by the wind. Here, the work by Wu et al. [40] can be mentioned. The authors investigated the wind load and wind-induced dynamic response of three quayside container cranes. Other similar works concerning lattice structures studied the mutual influence of a system of antennas, for example, Holmes et al. [41], Carril et al. [42], and Martín et al. [43]. The interference factor of microwave antenna dishes was found to be greater than that for some wind directions. The interference effect has also been investigated for tall buildings [44], low-rise buildings [45,46,47,48], cooling towers [49,50], and scaffoldings [51].
The main motivation for the current work is the tragic accident mentioned at the beginning of this section [4], where a relatively low tower crane tip-over due to a sudden strong gust of wind was caused by a locally formed whirlwind. As an example of such a tower crane, the fast-erecting Turmdrehkran 63K crane by Liebherr [52] is investigated. For the experimental analysis, two sectional models are prepared, namely a model for the tower truss and the truss of the horizontal jib. Next, the forces induced by the wind are estimated in an aerodynamic tunnel. A numerical analysis using CFD is also performed, and the results are compared to the Eurocode ISO 4302:2016 [5]. Based on the obtained results, the aerodynamic coefficients for the sectional models of the tower and jib are calculated. Next, select values of the aerodynamic coefficients are compared with the values from the Institute of Aviation [53] and the available literature and standards [54,55,56]. It is also worth noting that the current work is the continuation of similar studies, which concern the problem of the overturning of scissor lifts due to wind loads [57].
2. Materials and Methods
2.1. Study Object
The study object of the currently presented work is the fast-erecting Turmdrehkran 63K crane by Liebherr, which is shown in Figure 1. This type of crane is one of the most common constructions because its transport is relatively cheap and quick, and its assembly does not require much space, thus taking up little space on the construction site. This structure’s geometrical dimensions is similar to those of the crane that was destroyed during the storm in Cracow in 2022 [4].
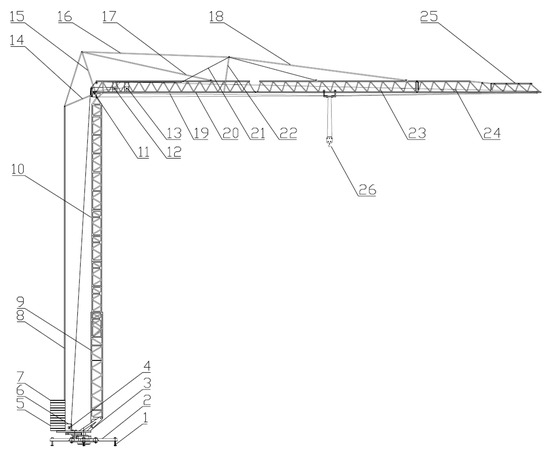
Figure 1.
Fast-erecting Turmdrehkran 63K crane by Liebherr. (1) Stationary support, (2) tower crane chassis, (3) movable platform, (4) lifting mechanism, (5) rotation mechanism, (6) switch cabinet, (7) counterweight, (8) rope immobilizing the horizontal jib, (9) lower part of the tower, (10) upper part of the tower, (11) auxiliary drive, (12) lifting winch, (13), trolley-driving mechanism, (14) rear lashing, (15) guy support I, (16) crane jib—lashing rope II, (17) crane jib—lashing rope III, (18) crane jib—lashing rope I, (19) lifting rope, (20) jib—articulated element, (21) jib—assembly rope, (22) guy support II—head, (23) jib extension, (24) jib extension, (25) jib extension, (26) hook (2/4 strand). The dimensions of the crane are listed in Table 1.
Table 1 presents the most important technical parameters of the investigated structure.

Table 1.
The technical parameters of the fast-erecting Turmdrehkran 63K crane.
2.2. Experimental Setup
In order to compare the phenomena acting on model M on a much smaller scale in an aerodynamic tunnel (sectional models of the tower and jib) and the real object N (parts of the tower and jib), the appropriate scales of the investigated phenomena should be satisfied. The appropriate dimensions and parameters, such as velocity V0, characteristic length L0 and density ρ, were chosen. Only three parameters were considered for scaling parameters; because of mechanical problems, only three quantities could be chosen to be dimension-independent, and the others should fulfill the appropriate relationships.
Taking into consideration the spatial dimensions of the aerodynamic tunnel, the model scale was equal to 1:7. Next, the other scales were estimated for both sectional models, i.e., the tower and jib. The determined scales are listed in Table 2.

Table 2.
The scales for tower and sectional models of the fast-erecting crane.
There are only three independent scales. However, in this work, there were six scales. Therefore, the following criteria will not be fulfilled:
- -
- Strouhal’s similarity criterion:
It should be mentioned that this is the only criterion that can be satisfied under the assumed scales of the dimensions (if the subject of the investigations in the aerodynamic tunnel is the aeroelastic model). For the rigid models, this criterion is not fulfilled. In our work, the studied models are rigid, openwork structures made of structural steel.
- -
- Reynold’s similarity condition:
The above discussion shows that in reality, the satisfaction of all the similarity conditions is not possible. Although some criteria are not fulfilled here, the impact of this fact on the final results of the experiments is not significant in the case of the rigid model of the fast-erecting crane because
- -
- Strouhal’s similarity criterion is satisfied for aeroelastic models and for vortex excitation;
- -
- Reynold’s similarity criterion in the laboratory environment does not have to lead to significant errors because in the case of cross-sections, which contain sharp edges or truss objects, the values of the aerodynamic coefficients do not, in fact, depend on the Reynold’s number in a wide range of Reynold’s number values.
2.2.1. Truss of the Vertical Part of the Crane
Figure 2 shows the model of the vertical part of the crane. The scale of the model is equal to 1:7. The studied part of the crane is the lattice structure with a square base with a side length of aT = 157 mm and a height of hT = 560 mm. At both ends of the model, there are circular plates installed with a diameter equal to d = 400 mm and thickness of t = 4 mm to not disturb the airflow around the model. Additionally, the plates are chamfered, as shown in Figure 2. Inside the model, there is also a part of the ladder. The structural elements of the sections are connected by welding. The ladder, due to the small dimensions of the parts from which it is made, was assembled by sealing the previously rolled rungs, and then welded to the tower structure using connectors. The entire truss structure of the model was bolted to the circular plates. Finally, the model was degreased and protected against corrosion. In Figure 3, the real object and the CAD model used in the CFD simulations are presented.
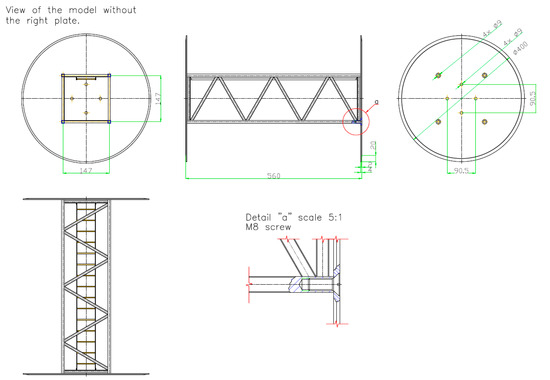
Figure 2.
Geometric dimensions of the scaled model of the truss of the tower of the crane.
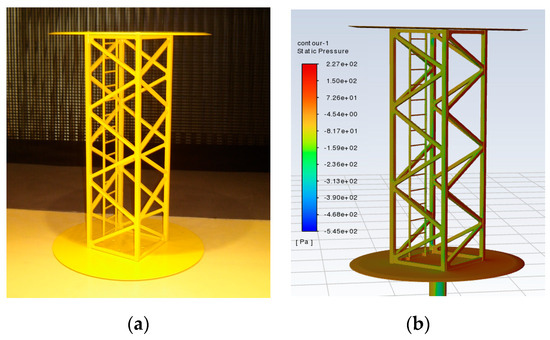
Figure 3.
Model of the truss of the tower of the crane: (a) the experimental specimen; (b) the CFD simulation.
2.2.2. Truss of the Horizontal Part of the Crane
Figure 4 represents the scaled model of the truss of the horizontal part of the investigated crane. The sectional model of the jib is a lattice (spatial structure with a triangular base). The overall dimensions of the section are as follows: height of the whole model h = 714 mm; base width composed of isosceles triangle with side aJ = 136 mm; and height hJ = 104 mm. The section, similar to the tower model, is closed on both sides with aluminum circular plates with a diameter of d = 400 mm and thickness of t = 4 mm.
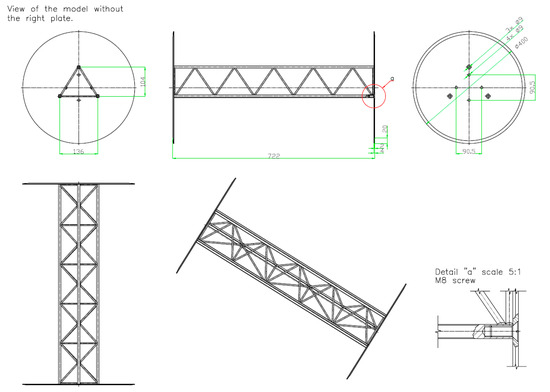
Figure 4.
Geometric dimensions of the scaled model of the truss of the horizontal jib.
The structural elements of the jib section, like the tower, were joined by welding. The entire truss structure of the model was bolted to aluminum circular plates. Figure 5 shows a sectional model of the horizontal jib of the tower crane.
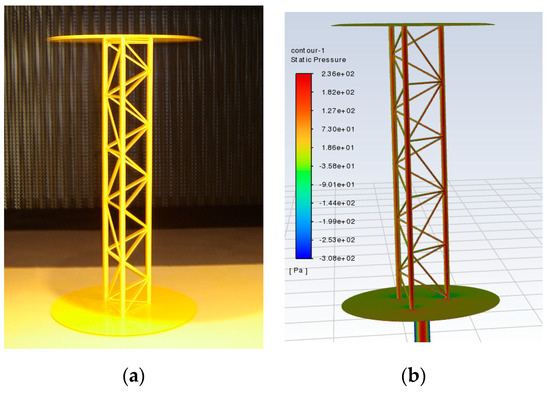
Figure 5.
Model of the truss of the horizontal jib of the crane: (a) the experimental specimen; (b) the CFD simulation.
Both models were made of the same type of structural steel and attached to the aerodynamic balance vertically using a connector (steel pipe with a flange). To prevent the air stream from exerting pressure on the element connecting the model to the balance during the test, an additional fairing was installed.
For both models, it was assumed that the wind direction varies from 0° to 180° with an increment equal to 15°. The assumed coordinate system and the way the angle of the wind direction was defined are shown in Figure 6 and Figure 7. For the tested models, the aerodynamic moment MX, MY, and MZ and aerodynamic forces FX and FY were measured using the five-component aerodynamic balance based on the electric resistance strain gauges. The orientation of the fixed x, y, z coordinate system is as follows: x—along the wind direction, y—across the wind direction, and z—vertical direction.
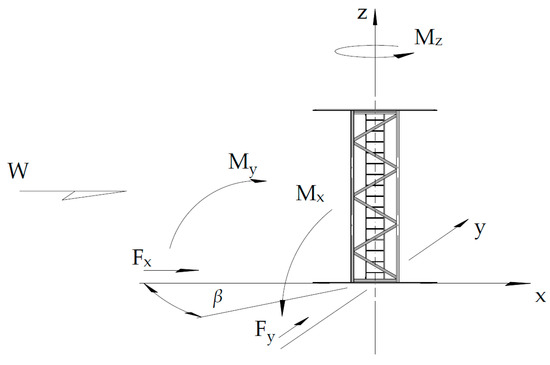
Figure 6.
The orientation of the model in the x, y, z coordinate system and the aerodynamic test conditions: the assumed wind direction W; the aerodynamic moments MX, MY, and MZ; and aerodynamic forces FX and FY.
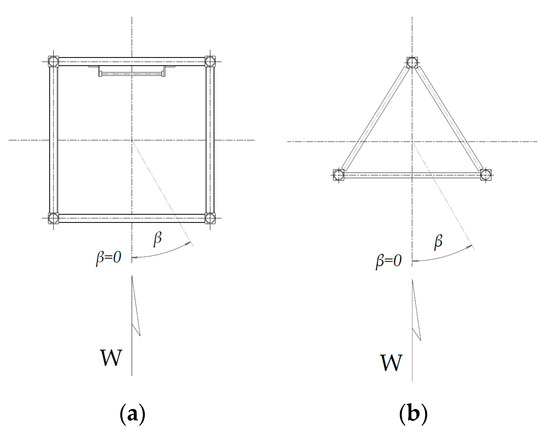
Figure 7.
Orientation of the sectional model of the tower during the test (β—wind attack angle, W—wind direction): (a) model of the tower; (b) model of the jib.
2.3. Aerodynamic Tunnel
The experimental tests were carried out in the boundary layer wind tunnel at the Wind Engineering Laboratory at the Cracow University of Technology [58]. The wind tunnel, with a length of 10 m and a measurement area of 2.2 m × 1.4 m, allowed users to conduct tests in both closed and open circuits. The wind flow was generated by an axial fan with a diameter of 2.7 m and an efficiency of 0.8–0.9, and a blade tip speed of about 100 m/s. The fan was driven by a 200 kW alternating current motor with a nominal speed of 750 rpm and was controlled by an inverter. The maximum wind speed was approximately 40 m/s (144 km/h).
2.4. The Wind Profile
The wind profile in the aerodynamic tunnel is determined for two cases, namely for “quasi-laminar” and turbulent flow. The first case mimics the flat open terrain, and the latter mimics the urban terrain. The turbulent flow was induced by the five “spires” installed at the beginning of the tunnel. The spires are 1000 mm in height and 300 mm in width at the base. Moreover, the airflow was additionally disturbed by movable wooden blocks that are 100 mm in height and installed in the tunnel floor, as shown in Figure 8.

Figure 8.
The view of the aerodynamic tunnel for (a) “quasi-laminar” flow and (b) turbulent flow. On the left side, there is a vertical rod with six thermo-anemometers for wind profile estimation.
Since the sectional models are placed 300 mm over the tunnel floor and their height does not exceed 750 mm, the wind profile was estimated at a height of 300 to 900 mm over the tunnel floor. The measurement was taken with the use of six thermo-anemometers placed at the distance of 100 mm from each other in the vertical direction (Figure 8). Mean values V(z), standard deviations σ(z), and turbulence intensities IV(z) were calculated for the series of wind speeds in each measurement. The distribution of the wind parameters along the wind tunnel height for each case of flow was estimated using the least square method. The wind profiles are described by the power law formula:
where is the reference velocity at reference height :
where pref is the reference pressure; ρ is the actual density of the air; is the power low exponent, i.e., roughness coefficient; and z is the height (spatial coordinate). The intensity of the turbulence can be estimated with the use of the following formula:
where σv is the standard deviation of the measured wind speed, The standard deviation can be computed based on the dynamic component vdyn(t) of the instantaneous velocity V(t), where V(t) = Vref + vdyn(t). The obtained wind profiles and the turbulence intensity for both investigated cases are depicted in Figure 9 and Figure 10, respectively.
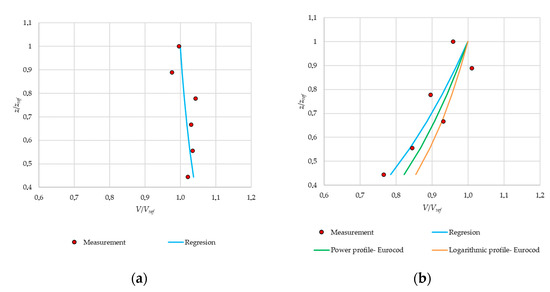
Figure 9.
The wind speed profile for (a) flat open terrain (“quasi-laminar” flow) and (b) for urban terrain (turbulent flow) according to the Eurocode standard [59].
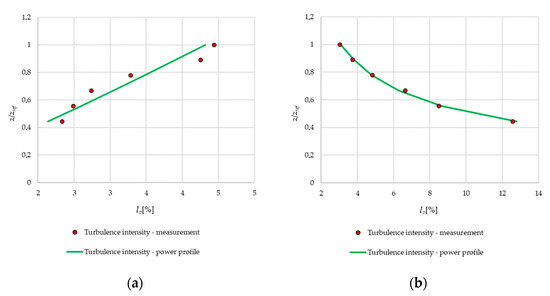
Figure 10.
The turbulent intensity profile for (a) flat open terrain (“quasi-laminar” flow) and (b) urban terrain (turbulent flow).
The sectional models of the tower and the jib were installed on the aerodynamic balance 300 mm above the aerodynamic tunnel floor. Figure 11 shows the sectional model of the tower. The sectional model of the jib was installed in the same manner.

Figure 11.
Model of the truss of the tower inside the aerodynamic tunnel during the tests.
2.5. Measurement of the Force Components Acting on the Model and Corresponding Wind Speed
The sensors for the air pressure and velocity measurements were placed in front of the model, 600 mm above the aerodynamic tunnel floor. They are visible in Figure 11 (the vertical rod installed on the movable table). The measurements of the forces and moments were performed with the use of the aerodynamic balance device that was placed under the plate of the movable table. The nominal wind speed was assumed to be equal to 15 m/s.
A diagram of the measuring system is depicted in Figure 12. The model of the studied truss (1) was installed onto the aerodynamic balance (2). The balance was wired to an amplifier module with a data acquisition system (3) that collects aerodynamic force values. The angular position of the model relative to the x, y plane was changed using a turntable with a stepper motor (4), and thus, the angle of attack of the wind was changed. The rotation of the stepper motor was controlled by a motor step control system (5). The turntable is a part of the aerodynamic balance, and its axis of rotation coincides with the axis of the balance. The wind speed was obtained based on pressure measurements provided by sensor Pitot pipes (6) located on the x, z plane, which were connected to the pressure scanner (7). The wind speed sensor (8) and thermo-anemometer AMD 2000 (9) were used for the wind speed measurements. Devices (3, 7, and 9) are linked with the multifunctional measuring card PCI DaqBoard/2000 (10), which was connected to a personal computer (11).
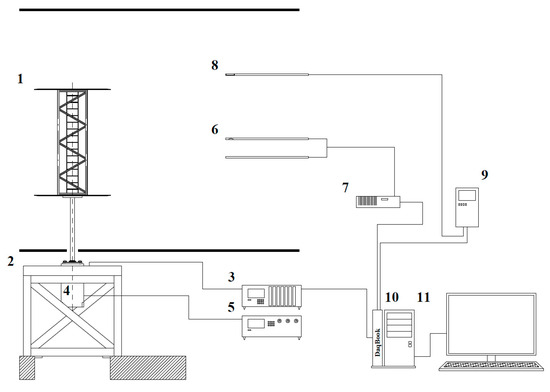
Figure 12.
Diagram of the measuring system. 1—the model of the truss; 2—the five-component aerodynamic balance, 3—amplifier module with data acquisition systems, 4—the turntable with stepper motor, 5—the motor step control system, 6—the pressure sensor Pitot pipes located on the x, z plane, 7—the pressure scanner, 8—the wind sensor, 9—thermo-anemometer AMD 2000, 10—DaqBoard/2000 card, 11—PC.
The sampling time of the wind speed measurement was equal to 5000 ms. Since the model of the investigated truss was installed 300 mm over the aerodynamic tunnel floor, it can be assumed that there was a uniform wind speed profile between the circular plates (Figure 3 and Figure 5). The turbulent air flow was introduced by the set of “spires”, which was installed at the beginning of the aerodynamic tunnel. On the other hand, the “quasi-laminar” airflow was obtained in the absence of the spires.
Below are the formulas for determining the coefficient of aerodynamic drag CX, the coefficient of the lateral aerodynamic force CY, and the aerodynamic coefficient of torque CMz:
where FX is the aerodynamic drag (N); FY is the lateral force (N); V is the average wind speed (m/s); ρ is the mass air density; Aref is the effective area of one of the supporting structures of the model, i.e., the area of the shadow normally projected by its members on a plane parallel to the wall; and bref is the conventionally accepted characteristic dimension. Table 3 shows the appropriate reference values for the force coefficients.

Table 3.
The reference values for the force coefficients.
2.6. CFD Simulation
The numerical simulations were performed with the use of the ANSYS 2022R2 Fluent with Fluent Meshing software in the Workbench environment. The main aim of the CFD simulations was the estimation of the aerodynamic forces acting on the investigated models of the crane trusses. The models of the tower truss and the jib truss (Figure 3 and Figure 5) were placed in a rectangular volume filled with air, as shown in Figure 13. The cross-section of this volume is a rectangle with geometrical dimensions of 2200 mm × 1400 mm (hydraulic diameter DH = 1.711 m). The model was placed 1500 mm from the inlet (blue wall in Figure 13) and 2000 mm from the outlet. The assumed dimensions of the aerodynamic tunnel precisely correspond to the geometric dimensions of the real aerodynamic tunnel. In the simulations, the standard air properties were assumed; therefore, ρ = 1.225 kg/m3, T = 15 °C, and p0 = 101,325.25 Pa. The walls of the aerodynamic tunnel as well as the whole surface of the studied models were assumed to be stationary boundaries and a steady state of airflow was assumed.
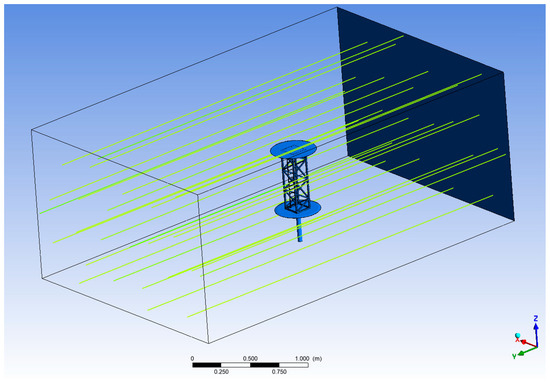
Figure 13.
Investigated model of the truss inside the volume filled with air. Blue wall is the inlet.
One of the most important problems is the appropriate choice of the turbulent model. In the current work, the three most frequently applied models were used: the Reynolds stress model, k-ω model, and k-ε model. The first model, used by Wu et al. [40], causes the computations to converge unacceptably slowly. The second model, used by He et al. [33], Yeon et al. [34], and Monteiro et al. [36], requires preparing a specific mesh at the boundary conditions. In the estimation made for the studied structure using a special calculator available online [59], the first layer of the finite volume should be about 10 × 10−5 m in height. Unfortunately, this leads to an enormous number of nodes and finite element volumes. Finally, the standard k-ε model with a standard wall function was used. It is worth noting that this model is still in use, for example, in the works of Zan et al. [19], Chen et al. [21], Lu et al. [32], and Augustyn et al. [57].
In order to generate the appropriate mesh, a relatively new approach was used, namely the shape of the elements was assumed to be polytetrahedral. Moreover, it was assumed that the approximate edge length of the faces of the elements, which cover the surface of the truss model, is equal to lc = 1.5 mm. The length of the edges of the faces of the elements that belong to the circular plates and the vertical rod is equal to lc = 3.4 mm. The maximal length of the rest cells is equal to lc = 108.867 mm. Figure 14 represents the cell mesh generated for the tower truss model.
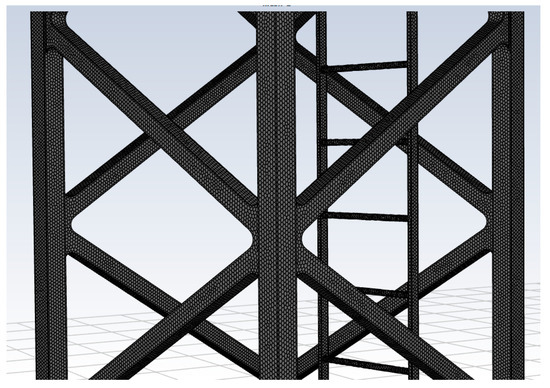
Figure 14.
The mesh of the cells generated for the tower truss model (length of the cell edge lc = 0.0015 m).
Table 4 presents the values of the aerodynamic forces and corresponding coefficients, computed according to Equation (6), for different sizes of cells. The convergence test was performed for the part of the tower truss where the angle β = 0° (Figure 7), air speed V = 15 m/s, and the turbulent intensity Iv = 9%. Table 5 shows the corresponding number of the nodes, faces, and cells. It should be noted here that the choice of the size of the cell was limited because for a cell size greater than lc = 0.002 m, the mesh on the ladder rungs would not generated properly, whereas for a cell size less than lc = 0.001 m, the number of the cells was extremely large. Moreover, for the k-ε turbulent model, and in the case where the cell size is very small, obtaining the convergent solution can be difficult. As is reported in Table 4, it is necessary to perform over 600 iterations to obtain a convergent solution. This problem is mainly connected to satisfying the continuity criterion. For other cell sizes, there were no problems with obtaining the convergent solution, and the number of necessary iterations did not exceed 50. Taking into consideration the results from Table 4, it seems that the choice of the cell size lc = 0.0015 m is reasonable. It is worth noting that for the tetrahedral elements, obtaining the converged solution would require several hundred iterations.

Table 4.
The values of the aerodynamic forces and corresponding coefficients for different mesh sizes. Wind speed V = 15 m/s, turbulent intensity Iv = 9%.

Table 5.
Total number of cells, faces, and nodes.
3. Results
3.1. Experimental Results
Table 6, Table 7, Table 8 and Table 9 show the values of the aerodynamic forces and moments that were obtained from the experimental tests on the truss models discussed in the previous sections. Table 6, Table 7, Table 8 and Table 9 also present the particular wind speed and turbulent intensity for each measurement. The experimental tests were performed with a “quasi-laminar” flow, where the average turbulent intensity was equal to Iv = 3%; for tests using turbulent airflow, the average turbulent intensity was Iv = 9% and 12% for the tower truss and jib truss models, respectively. In all investigated cases, the nominal wind speed was equal to V = 15 m/s. Moreover, it was assumed that the wind direction varied from 0° to 180° with a step of 15°. Figure 15, Figure 16, Figure 17 and Figure 18 show the profiles of the measured wind speed as a function of time. In the case of “quasi-laminar” flow, the wind speed did not change significantly. However, in turbulent flow, the wind speed varied considerably. Thus, in this case, precise wind measurements should be considered quite problematic.

Table 6.
Experimental results obtained for tower truss model with “quasi-laminar” airflow.

Table 7.
Experimental results obtained for tower truss model with turbulent airflow.

Table 8.
Experimental results obtained for jib truss model with “quasi-laminar” airflow.

Table 9.
Experimental results obtained for jib truss model with turbulent airflow.
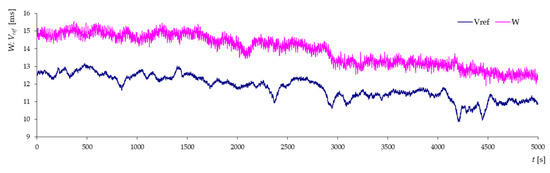
Figure 15.
Average speed and speed from the thermo-anemometer measured every 5 s for “quasi-laminar” airflow and wind direction β = 0° (tower truss model).
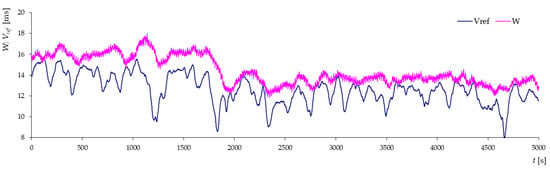
Figure 16.
Average speed and speed from the thermo-anemometer measured every 5 s for turbulent airflow and wind direction β = 0° (tower truss model).
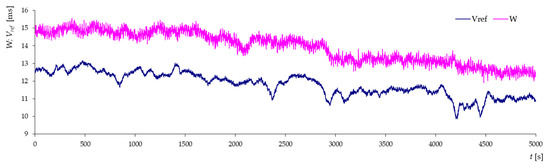
Figure 17.
Average speed and speed from the thermo-anemometer measured every 5 s for “quasi-laminar” airflow and wind direction β = 0° (jib truss model).
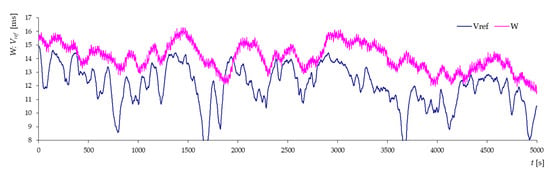
Figure 18.
Average speed and speed from the thermo-anemometer measured every 5 s for turbulent airflow and wind direction β = 0° (jib truss model).
In both studied cases of the truss models, the highest value of the aerodynamic forces was observed for the wind direction β = 45° and β = 135°. However, due to the lack of perfect symmetry of the investigated truss models, the values of the FX force components for β = 45° and β = 135° are not equal to each other. Generally, together with increasing turbulent intensity, the values of these components of the aerodynamic forces should increase. Contrary to the aerodynamic force FX components, the FY components as well as the values of the MZ moments are close to zero for both truss models.
3.2. Comparison of the Numerical and Experimental Results
The comparison of the experimental and numerical results is represented in Figure 19, Figure 20, Figure 21 and Figure 22, which show the values of the aerodynamic coefficients CX and CY as a function of the angle β. As can be observed, the results reveal a relatively good agreement.
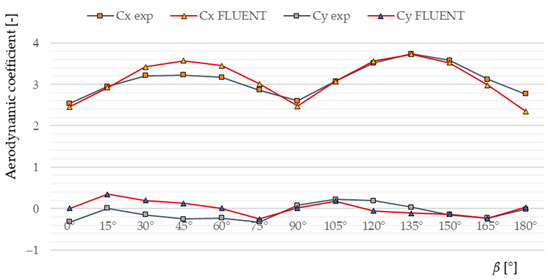
Figure 19.
Comparison of the force coefficients CX and CY for the experimental and numerical results as a function of angle of wind attack β in the tower truss model with “quasi-laminar” airflow.
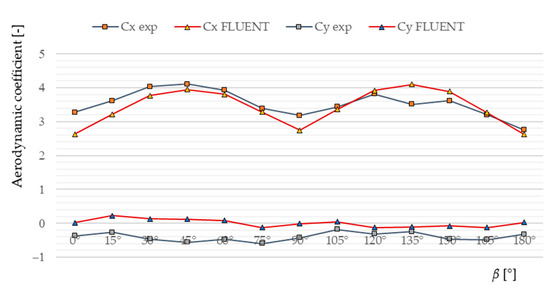
Figure 20.
Comparison of the force coefficients CX and CY for the experimental and numerical results as a function of angle of wind attack β in the tower truss model with turbulent flow.
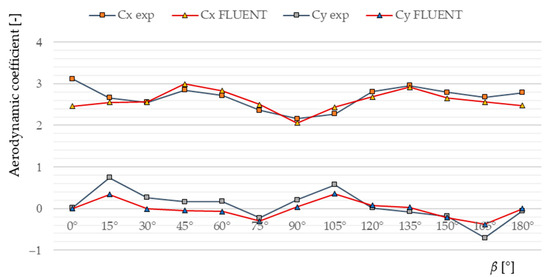
Figure 21.
Comparison of the force coefficients CX and CY for the experimental and numerical results as a function of angle of wind attack β in the jib truss model with “quasi-laminar” flow.
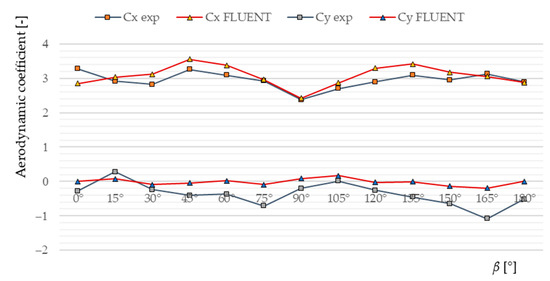
Figure 22.
Comparison of the force coefficients CX and CY for the experimental and numerical results as a function of angle of wind attack β in the jib truss model with turbulent flow.
The average errors εAVG for coefficient CX for all investigated cases are shown in Table 10. These values were estimated according to the following formula:
where CXEXP and CXNUM are the aerodynamic coefficients obtained from the experiment and numerical simulation, respectively.

Table 10.
The average error εAVG for coefficient CX.
It seems that the results of the numerical simulation slightly overestimate the value of the aerodynamic force FX, which plays an important role when the tip-over of the tower crane could happen. Moreover, the best match was obtained for the tower crane model in the case of turbulent flow. Finally, it is worth noting that in the case of the force coefficient CY, the results from the experimental tests and numerical simulations reveal noticeably worse agreement in comparison with those of the CX coefficients. This could be explained by the fact that the FY force component had values that are close to zero. Thus, it was measured during the experiment with a relatively large error.
Example distributions of the static pressure are shown in Figure 3b and Figure 5b. Here, it is worth noting that a better convergence of the numerical solution is observed in the case of turbulent flow. In this case, the number of iterations was not more than about 50, whereas in the case of “quasi-laminar” airflow, the total number of iterations was more than 80. Moreover, the main problem relates to the continuity criterion.
4. Discussion
The experimental tests carried out in the wind tunnel allowed for the comparison of the obtained results with the literature data(see Figure 23 and Figure 24).
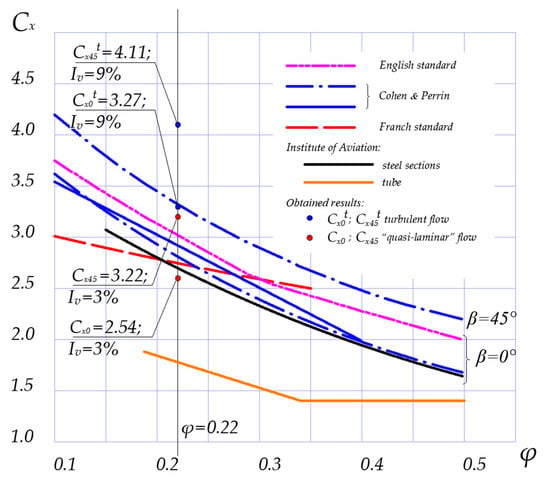
Figure 23.
Comparison of the selected aerodynamic coefficients CX in function of the solidity ratio φ of the tower truss model with the available literature and standards data (According to Institute of Aviation [53], Franch [54], Cohen & Perrin [55] and English [56] standards).
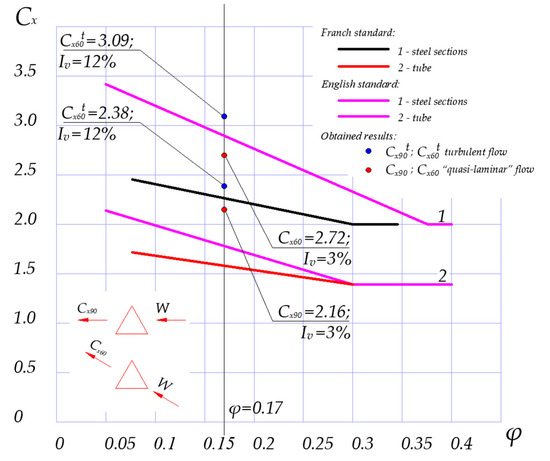
Figure 24.
Comparison of the selected aerodynamic coefficients CX in function of the solidity ratio φ of the jib model with the available literature and standards data (According to Franch [54] and English [56] standards).
Based on selected wind angles (i.e., β = 0° and β = 45° for tower, and β = 60° and β = 90° for jib), it was shown that the values obtained for the sectional models of the tower and jib are between the values of aerodynamic coefficients of trusses made of steel structural sections and trusses made of tubes that were given by Górski [56]. The obtained values were also compared with those from the available literature and standards [57,58,59]. Additionally, the effects of turbulence on the drag coefficient value for the truss of the tower and jib model are presented in Figure 23 and Figure 24.
Figure 23 shows the research results of the Institute of Aviation [53] for spatial trusses with a square base made of steel sections (black curve) and pipes (red curve).
The equation of the curve for the steel section Cx0(φ) [53] is as follows:
and the equation of curve for the tube Cx0(φ) is as follows:
In the studied case, according to the ISO-4302 standard [5], the solidity ratio φ of the tower model is given as:
where Ae is the enclosed area.
where k is the spacing ratio (relative distance between the walls of the truss structure of the tower model), and a (breadth of section across wind front) and b (depth of section parallel to window flow) are the lengths of the side walls.
Based on the above data, Cx0 is written as [53]
The findings for the truss model are as follows:
- For “quasi-laminar” flow, the value of the drag coefficient CX0 obtained from the tests was 2.54 (Figure 23), and its value is between the curves given by Górski [53]. Note that the value of CX45, which is equal to 3.22, fits the curve given by Cohen and Perrin [55]. This value is almost equal to CX0t, which is equal to 3.27.
- For turbulent flow, the drag coefficient CX0t obtained from the tests was 3.27, and CX45t was 4.11 (Figure 23). This proves the high impact of turbulence on the tested object. The CX0t coefficient is in line with the curve given by Cohen and Perrin [55] for a wind angle of attack of β = 45°.
Similarly, the selected aerodynamic coefficients CX for the jib truss model were calculated. Figure 24 shows the dependency CX = f(φ) for spatial trusses on the triangular base made of steel structural sections and tube, as recommended by French [54] and English [56] standards, and the results of the wind tunnel tests.
According to the ISO-4302 standard [5], the solidity ratio of the tested model of the jib is given by
The findings for the jib model are as follows:
- For “quasi-laminar” flow, the resistance coefficient CX90 obtained from the tests was 2.16 (Figure 24) and is close to the value from the curve given by the French standard for steel sections. This value is much higher than the values given for pipes by both the French [54] standard and the English standard [56], while CX60 has a value close to the curve given by the Polish standard for steel sections.
- For turbulent flow, the value of the drag coefficient CX90t obtained from the tests was 2.38 (Figure 24), and it indicates a high impact of turbulence on the tested object—a value above the values given by the French [54] and English [56] standards. It should be noted that the resistance coefficient CX60t is equal to 3.09.
5. Conclusions
This study was devoted mainly to the problem of determining the aerodynamic coefficients for sectional models of the two types of trusses. These types of trusses are the main parts of the tower and jib of the fast-erecting Liebherr 65K crane. The analysis consists of two steps: In the first step, experimental tests in an aerodynamic tunnel were performed. In the second step, the appropriate CFD computations were conducted, and the obtained results were compared to the experimental ones. The analysis was conducted for quasi-laminar and fully developed turbulent flow. In the case of aerodynamic coefficients CX, the average error between the numerical and experimental values did not exceed 8%.
Next, the values of the aerodynamic coefficients were compared with those available in the literature and from different standards. A significant effect of the angle of wind attack on the aerodynamic drag coefficient CX and the coefficient of lateral aerodynamic force CY was observed, as well as an increase in the value of the aerodynamic drag for the turbulent flow.
The significant relative difference between the aerodynamic drag coefficients CX for laminar and turbulent flows for a wind angle of attack of β = 0° for the tower section model made of closed profiles was 28.7%. However, in the case of the sectional model of the jib (also made of closed profiles), the relative difference between the CX values of laminar flow and turbulent flow with a wind angle of attack of 60° was 13.6%, and for an angle of 90°, it was 10.2%.
It should be stressed that the current work should be treated as an introduction to the further analysis of the phenomenon of the overturning of this kind of crane device that is caused by the wind. In the future, the authors will take other effects under consideration, for example, the influence of the load on the stability of the crane, the so-called interference effect (interaction with surrounding objects like buildings and other cranes), and the stiffness of the ground (foundation) where the crane is installed.
Author Contributions
Conceptualization, M.A.; methodology, M.A. and M.B.; software, M.B.; validation, M.A. and M.B.; numerical analysis, M.B.; experimental investigation, M.A.; data curation, M.A. and M.B.; writing—original draft preparation, M.A., M.B., M.C. and A.S.; writing—review and editing, M.A., M.B., M.C. and A.S.; visualization, M.A. and M.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weather Build. Rigging for Wind—Common Causes of Tower Crane Accidents. 2019. Available online: http://weatherbuild.co/2019/02/04/rigging-for-wind-common-causes-of-tower-crane-accidents (accessed on 28 March 2023).
- Express Web Desk. Watch: Overhead Crane Crashes on Buildings due to Cyclone Fani; Express Web Desk: New Delhi, India, 2019; Available online: https://indianexpress.com/article/india/cyclone-fani-overhead-crane-crashes-on-buildings-due-to-severe-storm-5709526/ (accessed on 28 March 2023).
- Ayub, M.; Lu, A. Investigation of the Failures of Three Hammerhead Cranes on 10 September 2017, in Miami and Fort Lauderdale in the Wake of Hurricane Irma, Office of Engineering Services Directorate of Construction. 2018. Youtube. Available online: https://www.youtube.com/watch?v=LXCj8OmAD4I (accessed on 28 March 2023).
- Wiosło, M.; Grochot, A. The Gale Overturned a Crane in Krakow. Two People Are Dead, RMF24. 2022. Available online: https://www.rmf24.pl/regiony/krakow/news-wichura-przewrocila-dzwig-w-krakowie-dwie-osoby-nie-zyja-fil,nId,5838306#crp_state=1 (accessed on 28 March 2023). (In Polish).
- ISO 4302:2016; Cranes-Wind Load Assessment. ISO Copyright Office: Geneva, Switzerland, 2016.
- BS 2573-1; British Standard. Rules for the Design of Cranes Part 1: Specifications for Classification, Stress Calculations, and Design Criteria for Structures (4th Revision). BSI: San Jose, CA, USA, 1983.
- ASCE. Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE 7: Reston, VA, USA, 2016. [Google Scholar]
- JIS B 8830-2001; Cranes-Wind Assessment. Japanese Industrial Standards Committee: Tokyo, Japan, 2001.
- GB/T 3811-2008; Design Rules for Cranes. General Administration of Quality Supervision. Inspection and Quarantine of the People’s Republic of China: Beijing, China, 2008.
- König, G.; Zilch, K.; Lappas, G. Wind loading of shipyard gantry cranes—Full scale measurements. J. Wind. Eng. Ind. Aerod. 1979, 4, 429–435. [Google Scholar] [CrossRef]
- König, G.; Zilch, K.; Lappas, G. Wind loading of shipyard gantry cranes—A comparison of full-scale measurement, wind tunnel test and gust factor approach, Wind Engineering. In Proceedings of the Fifth International Conference, Fort Collins, CO, USA, 8–13 July 1979; Volume 2, pp. 911–923. [Google Scholar]
- Farrugia, R.N.; Sant, T. Modelling wind speeds for cup anemometers mounted on opposite sides of a lattice tower: A case study. J. Wind Eng. Ind. Aerodyn. 2013, 115, 173–183. [Google Scholar] [CrossRef]
- Voisin, D.; Grillaud, G.; Solliec, C.; Beley-Sayettat, A.; Berlaud, J.-L.; Miton, A. Wind tunnel test method to study out-of-service tower crane behavior in storm winds. J. Wind Eng. Ind. Aerodyn. 2004, 92, 687–697. [Google Scholar] [CrossRef]
- Lee, S.J.; Kang, J.H. Wind load on a container crane located in atmospheric boundary layers. J. Wind Eng. Ind. Aerodyn. 2008, 96, 193–208. [Google Scholar] [CrossRef]
- Mara, T.G.; Asce, A.M. Effects of a Construction Tower Crane on the Wind Loading of a High-Rise Building. J. Struct. Eng. 2010, 136, 1453–1460. [Google Scholar] [CrossRef]
- Han, D.S.; Han, G.J. Force Coefficient at Each Support Point of a Container Crane According to the Wind Direction. Int. J. Precis. Eng. Man. 2011, 12, 1059–1064. [Google Scholar] [CrossRef]
- Hu, J.B.; Chen, D.; Ding, S.Q.; Qing, G.W. Simulation of the Wind Field of Gantry Cranes Based on FLUENT. Appl. Mech. Mater. 2012, 217–219, 1530–1534. [Google Scholar] [CrossRef]
- Wang, Y.P.; Cheng, W.M.; Du, R.; Wang, S.B.; Yang, X.Z.; Zhai, S.C. Simulation analysis of wind load response for large gantry crane. Chin. J. Eng. Des. 2020, 27, 2. [Google Scholar]
- Zan, Y.F.; Guo, R.N.; Bai, X.; Ma, Y.; Yuan, L.H.; Huasng, F.X. Wind and current loads on a pipelaying crane vessel. IOP Conf. Ser. Earth Environ. Sci. 2020, 612, 012059. [Google Scholar] [CrossRef]
- ANSYS, Inc. Fluent (Version R22), Canonsburg, PA, USA. Available online: https://www.ansys.com/products (accessed on 17 January 2023).
- Chen, W.; Qin, X.; Yang, Z.; Zhan, P. Wind-induced tower crane vibration and safety evaluation. J. Low Freq. Noise Vib. Act. Control 2020, 39, 297–312. [Google Scholar] [CrossRef]
- An, T.-W.; Lee, S.-W.; Han, D.-S.; Han, G.-J. A Study on the comparison of wind pressure on the member of container crane using wind tunnel test and CFD. In Proceedings of the Korean Institute of Navigation and Port Research Conference; Korean Institute of Navigation and Port Research: Busan, Republic of Korea, 2006; Volume 1, pp. 321–325. [Google Scholar]
- Klinder, C. Failures of cranes due to wind induced vibrations. Eng. Fail. Anal. 2014, 43, 198–220. [Google Scholar] [CrossRef]
- Chen, L.; Li, L. Investigation on dynamic response of steel tower structure under time-history wind load. Appl. Mech. Mater. 2012, 166, 699–707. [Google Scholar] [CrossRef]
- Jiang, H.; Li, S. The Wind-Induced Vibration Response for Tower Crane Based on Virtual Excitation Method. Open Mech. Eng. J. 2014, 8, 201–205. [Google Scholar] [CrossRef]
- Takahashi, K.; Abe, M.; Fujino, T. Runaway characteristics of gantry cranes for container handling by wind gust. Mech. Eng. J. 2016, 3, 15–00679. [Google Scholar] [CrossRef]
- Jiang, H.; Li, Y. Dynamic Reliability Analysis of Tower Crane with Wind Loading. IOP Conf. Ser. Mater. Sci. Eng. 2019, 677, 052031. [Google Scholar] [CrossRef]
- Su, N.; Peng, S.T.; Hong, N.N. Stochastic dynamic transient gusty wind effect on the sliding and overturning of quayside container cranes. Struct. Infrastruct. Eng. 2021, 17, 1271–1283. [Google Scholar] [CrossRef]
- Azzi, Z.; Elawady, A.; Irwin, P.; Chow, A.G.; Shdid, C.A. Aeroelastic modeling to study the wind-induced response of a self-supported lattice tower. Eng. Struct. 2021, 245, 112885. [Google Scholar] [CrossRef]
- El Ouni, M.H.; Ben Kahla, N.; Islam, S.; Jameel, M. A Smart Tower Crane to Mitigate Turbulent Wind Loads. Struct. Eng. Int. 2021, 31, 18–29. [Google Scholar] [CrossRef]
- Oliveira, C.S.; Correia, P.M.B. Comparison of the seismic and wind analyses of two tower cranes. J. Vibroengineering 2021, 23, 956–974. [Google Scholar] [CrossRef]
- Lu, Y.; Gao, M.; Liang, T.; He, Z.; Feng, F.; Pan, F. Wind-induced vibration assessment of tower cranes attached to high-rise buildings under construction. Automat. Constr. 2022, 135, 104132. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Liang, T.; Lu, Y.; Lai, X.; Pan, F. Tornado-affected safety assessment of tower cranes outer-attached to super high-rise buildings in construction. J. Build. Eng. 2022, 51, 104320. [Google Scholar] [CrossRef]
- Yeon, S.M.; Kwon, C.S.; Kim, Y.C.; Kim, K.S. Study of the lift effect on wind load estimation for a semi-submersible rig using the maritime atmospheric boundary layer model. Int. J. Nav. Arch. Ocean 2022, 14, 100419. [Google Scholar] [CrossRef]
- Skelton, I.; Demian, P.; Glass, J.; Bouchlaghem, D.; Anumba, C. Lifting Wing in Constructing Tall Buildings —Aerodynamic Testing. Buildings 2014, 4, 245–265. [Google Scholar] [CrossRef]
- Monteiro, F.A.; Moreira, R.M. A CFD Analysis of Wind Effects on Lifted Loads. Int. J. Adv. Eng. Res. Sci. 2019, 6, 365–371. [Google Scholar] [CrossRef]
- Cekus, D.; Gnatowska, R.; Kwiatoń, P. Impact of Wind on the Movement of the Load Carried by Rotary Crane. Appl. Sci. 2019, 9, 3842. [Google Scholar] [CrossRef]
- Cekus, D.; Kwiatoń, P.; Geisler, T. The dynamic analysis of load motion during the interaction of wind pressure. Meccanica 2021, 56, 785–796. [Google Scholar] [CrossRef]
- Jin, L.; Liu, H.; Zheng, X.; Chen, S. Exploring the Impact of Wind Loads on Tower Crane Operation. Hindawi Math. Probl. Eng. 2020, 2020, 2807438. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y.; Wu, Y.; Su, N.; Peng, S. The Interference Effects of Wind Load and Wind-Induced Dynamic Response of Quayside Container Cranes. Appl. Sci. 2022, 12, 10969. [Google Scholar] [CrossRef]
- Holmes, J.D.; Banks, R.W.; Roberts, G. Drag and aerodynamic interference on Microwave dish antennas and their supporting towers. J. Wind Eng. Ind. Aerodyn. 1993, 50, 263–270. [Google Scholar] [CrossRef]
- Carril, C.F., Jr.; Isyumov, N.; Brasil, R.M.L.R.F. Experimental study of the wind forces on rectangular latticed communication towers with antennas. J. Wind Eng. Ind. Aerodyn. 2003, 91, 1007–1022. [Google Scholar] [CrossRef]
- Martín, P.; Elena, V.; Loredo-Souz, A.M.; Camaño, E.B. Experimental study of the effects of dish antennas on the wind loading of telecommunication towers. J. Wind Eng. Ind. Aerodyn. 2016, 149, 40–47. [Google Scholar] [CrossRef]
- Kareem, A.; Kijewski, T.; Lu, P.C. Investigation of interference effects for a group of finite cylinders. J. Wind Eng. Ind. Aerodyn. 1998, 77–78, 503–520. [Google Scholar] [CrossRef]
- Holmes, J.D. Wind pressure on tropical housing. J. Wind Eng. Ind. Aerodyn. 1994, 53, 105–123. [Google Scholar] [CrossRef]
- Li, G.; Gan, S.; Li, Y.X.; Wang, L. Wind-induced interference effects on low-rise buildings with gable roof. J. Wind Eng. Ind. Aerodyn. 2017, 170, 94–106. [Google Scholar] [CrossRef]
- Quan, Y.; Gu, M.; Yukio, T.; Huang, P. Aerodynamic interference of wind loads on roofs of low-rise buildings. J. Tongji Univ. Nat. Sci. 2009, 37, 1576–1580. [Google Scholar]
- Pindado, S.; Meseguer, J.; Franchini, S. Influence of an upstream building on the wind-induced mean suction on the flat roof of a low-rise building. J. Wind Eng. Ind. Aerodyn. 2011, 99, 889–893. [Google Scholar] [CrossRef]
- Li, G.; Cao, W.B. Structural analysis and optimization of large cooling tower subjected to wind loads based on the iteration of pressure. Struct. Eng. Mech. 2013, 46, 735–753. [Google Scholar] [CrossRef]
- Ke, S.T.; Wang, H.; Ge, Y.J. Interference effect and the working mechanism of wind loads in super-large cooling towers under typical four-tower arrangements. J. Wind Eng. Ind. Aerodyn. 2017, 170, 197–213. [Google Scholar] [CrossRef]
- Feng, W.; Tamura, Y.; Yoshida, A. Interference effects of a neighboring building on wind loads on scaffolding. J. Wind Eng. Ind. Aerodyn. 2014, 125, 1–12. [Google Scholar]
- Liebherr. Available online: http//:www.liebherr.com/en/pol/products/construction-machines/tower-cranes/fast-erecting-cranes/k-cranes/details/71230.html (accessed on 5 April 2023).
- Augustyn, M.; Barski, M.; Chwał, M.; Stawiarski, A. Numerical and Experimental Determination of the Wind Speed Value Causing Catastrophe of the Scissor Lift. Appl. Sci. 2023, 13, 3528. [Google Scholar] [CrossRef]
- Wind Engineering Laboratory. Available online: http://www.windlab.pl/en/ (accessed on 20 February 2023).
- Fluid Mechanics 101. Available online: https://www.fluidmechanics101.com/pages/tools.html (accessed on 12 April 2023).
- Górski, S. Assumptions for the Draft Standard “Impact of Wind on the Truss Structures”; Internal Report of the Institute of Aviation: Warszawa, Poland, 1965; p. 16/TA/65. [Google Scholar]
- Collectif CSTB. Règles NV 65–Règles Définissant les Effets de la Neige et du Vent sur les Constructions et Annexes; DTU P 06-002; CSTB: Paris, France, 2009. [Google Scholar]
- Cohen, E.P.; Perrin, H. Design of Multi-Level Guyed Towers: Structural Analysis. J. Struct. Div. 1957, 83, 1–29. [Google Scholar] [CrossRef]
- EN 1991-1-4; Eurocode 1: Actions on structures–Part 1–4: General Actions–Wind Actions [Authority: The European Union Per Regulation 305/2011, Directive 98/34/EC, Directive 2004/18/EC]. CEN: Brussels, Belgium, 2005.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).