Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata
Abstract
:1. Introduction
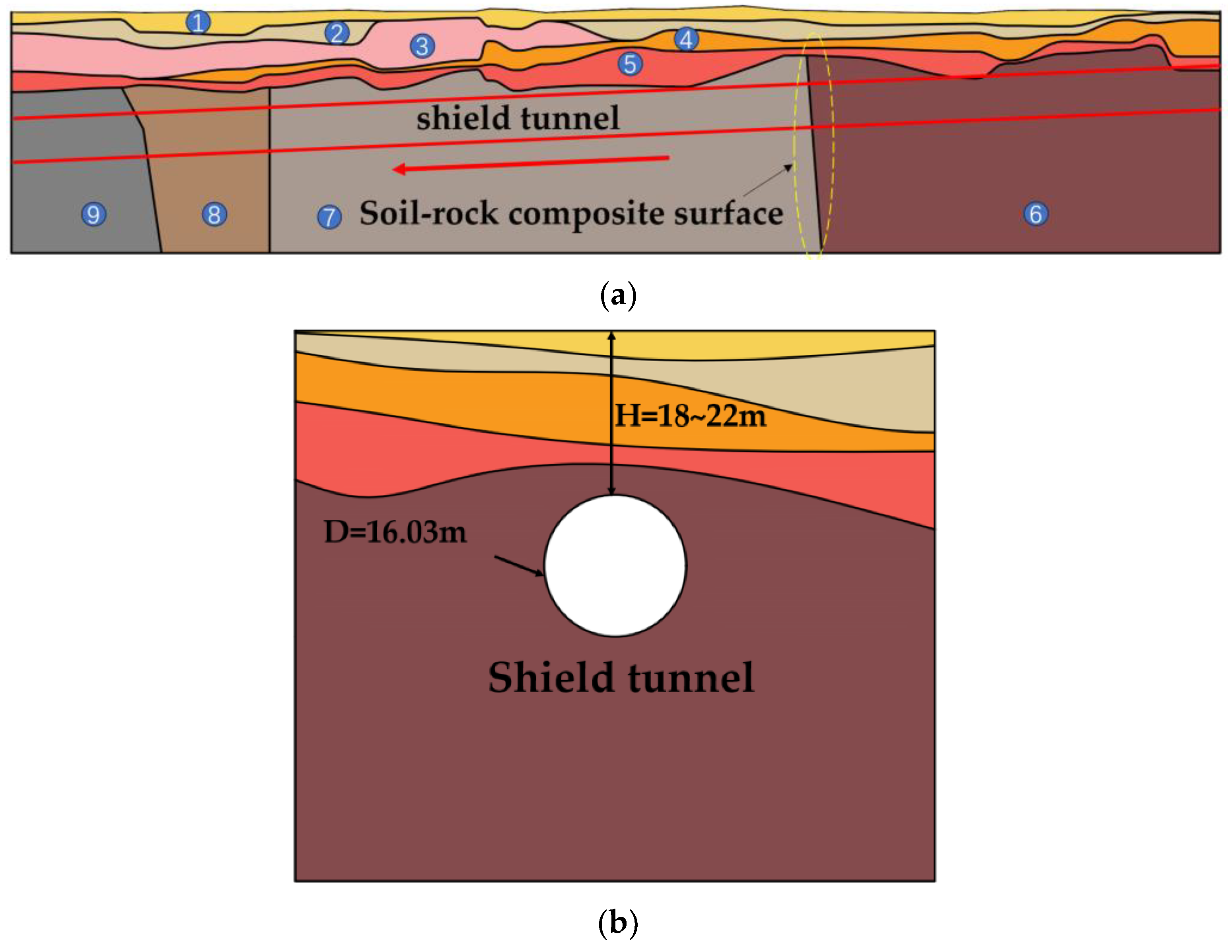
2. Engineering Background
2.1. Project Overview
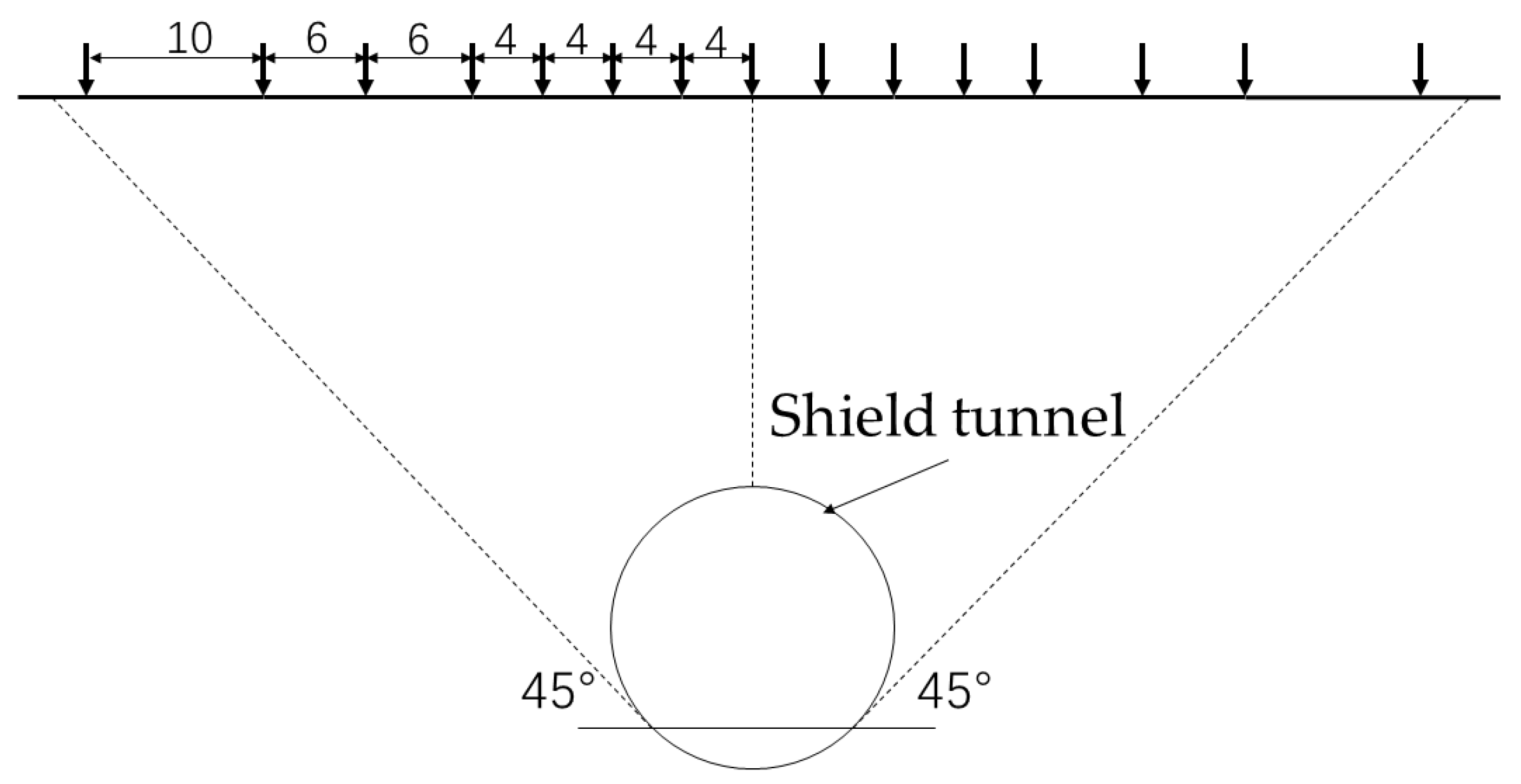
2.2. Installation of Surface Settlement Monitoring Points
3. Analysis of Compound Strata and Surface Settlement
3.1. Peck’s Empirical Formula
3.2. Regression Analysis of the Peck Formula
- (1)
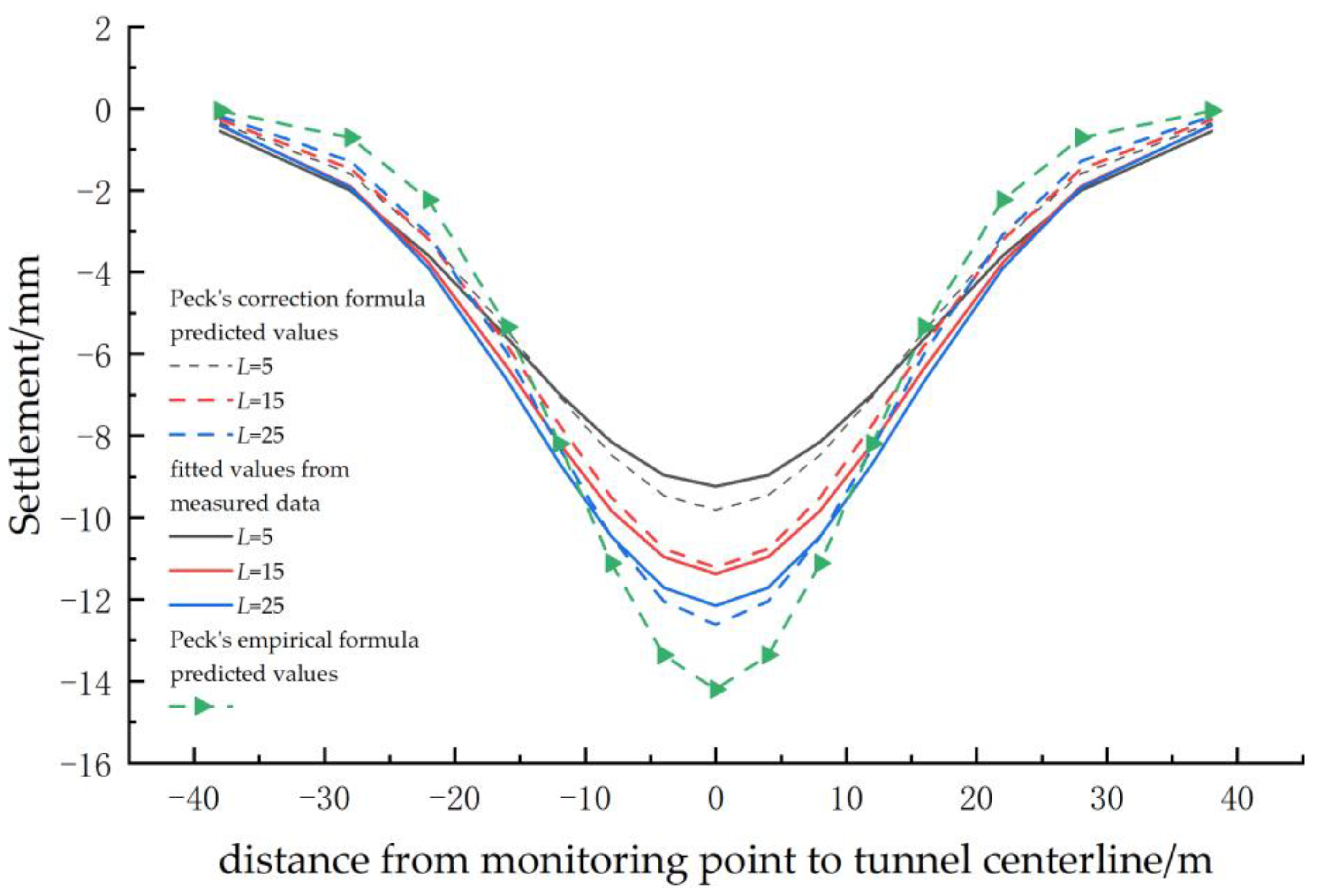
- The linear correlation coefficients (r-values) for all monitoring sections are greater than 0.8, indicating a strong correlation with the expected values from Peck’s theory. This suggests that the collected monitoring results are reliable, and the fitting curve of the Peck formula accurately reflects the actual ground settlement within the studied project area.
- (2)
- However, there is a significant discrepancy between the measured field values and the predicted results using the Peck empirical formula, indicating that the empirical formula is not capable of providing reasonable predictions for ground settlement in complex geological formations.
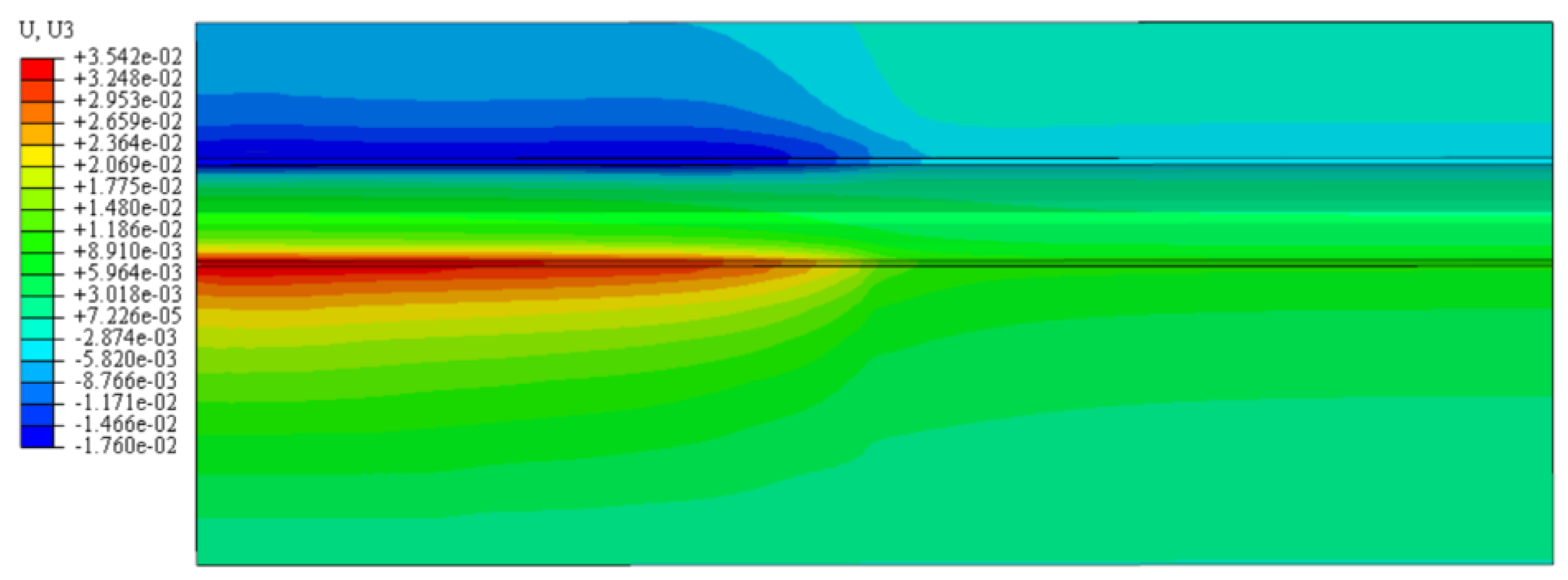
3.3. Numerical Model Establishment
4. Modification of the Peck Formula
5. Conclusions and Discussion
- (1)
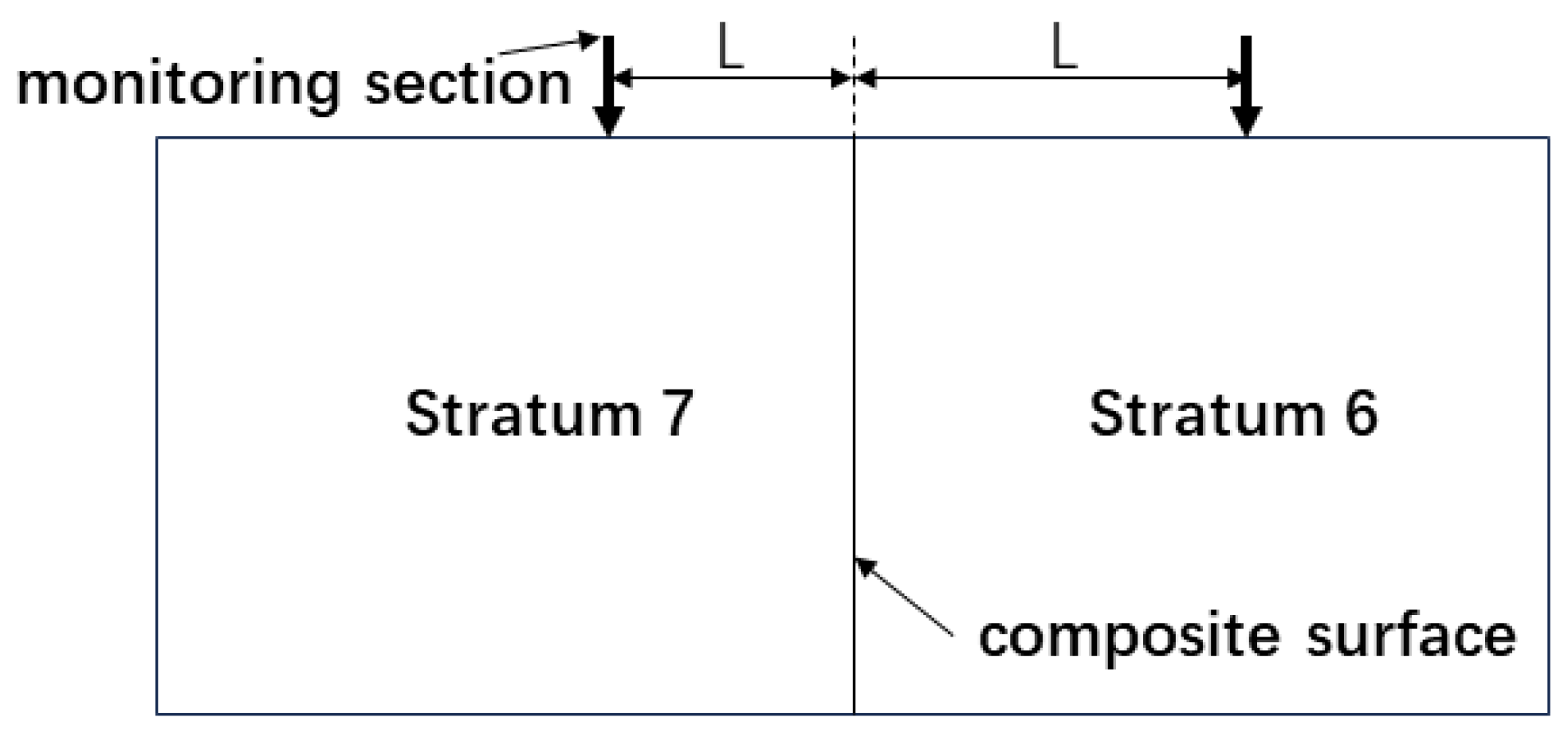
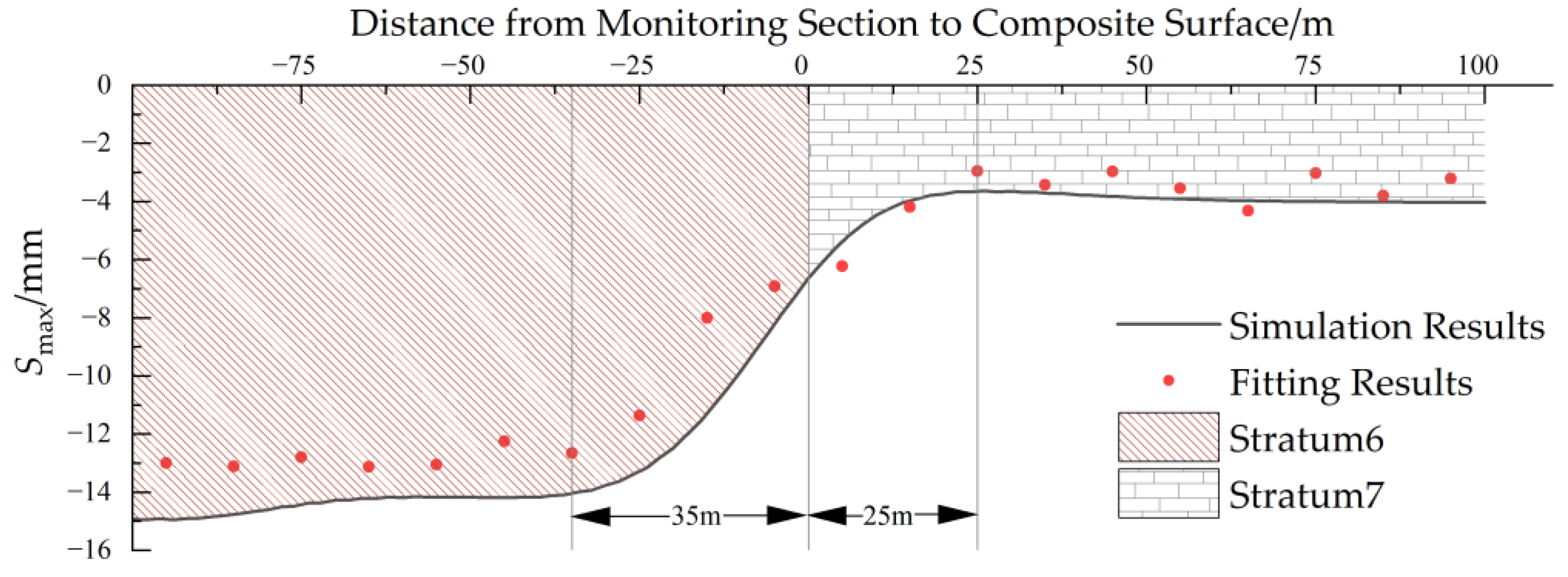
- When the shield tunnel passes through the soil–rock composite stratum, there will be large and uneven settlement near the composite interface along the direction of the shield excavation. This range is about 3.1D in the soil strata and 1.9D in the rock strata.
- (2)
- The Smax of soil strata decreases as the distance to the composite interface decreases, reaching its minimum (46% of the maximum Smax) at the interface. Conversely, the Smax of rock strata increases, reaching its maximum (approximately 1.4 times the minimum Smax) at the interface. The i value of soil strata as the distance decreases, reaching its maximum (about 1.5 times the maximum i) at the interface. Conversely, the i value of rock strata increases, reaching its minimum (88% of the maximum i) at the interface. The composite stratum has a greater influence on Smax than i, particularly in soil strata.
- (3)
- When predicting the surface settlement of the composite-stratum settlement variation intervals, considering the Peck correction formula for the distance from the monitoring section to the composite interface is more accurate than the Peck empirical formula.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Han, X.; Li, N.; Standing, J.R. An adaptability study of Gaussian equation applied to predicting ground settlements induced by tunneling in China. Yantu Lixue (Rock Soil Mech.) 2007, 28, 23–28. [Google Scholar]
- Chen, C.L.; Zhao, C.L.; Wei, G.; Ding, Z. Prediction of soil settlement induced by double-line shield tunnel based on Peck formula. Rock Soil Mech. 2014, 35, 2212–2218. [Google Scholar]
- Han, X.; Li, N.; Standing, J.R. Study on subsurface ground movement caused by urban tunneling. Yantu Lixue (Rock Soil Mech.) 2007, 28, 609–613. [Google Scholar]
- Zhu, Z.G.; Huang, S.; Zhu, Y.Q. Study of road surface settlement rule and controlled criterion for railway tunnel under crossing highway. Rock Soil Mech. 2012, 33, 558–563. [Google Scholar]
- Li, T.; Zhang, H. Meso-macro analysis of surface settlement characteristics during shield tunneling in sandy cobble ground. Rock Soil Mech. 2012, 33, 1141–1150. [Google Scholar]
- Tai, Q.M.; Zhang, D.L.; Fang, Q.; Sun, Y.; Yu, F.C.; Meng, M. Analysis of ground surface deformation induced by excavation of crossing metro tunnels in urban underground. Chinese. J. Rock Mech. Eng. 2014, 33, 2472–2480. [Google Scholar]
- Anas, S.M.; Alam, M.; Umair, M. Experimental and numerical investigations on performance of reinforced concrete slabs under explosive-induced air-blast loading: A state-of-the-art review. In Structures; Elsevier: Amsterdam, The Netherlands, 2021; Volume 31. [Google Scholar]
- Anas, S.M.; Shariq, M.; Alam, M.; Yosri, A.M.; Mohamed, A.; AbdelMongy, M. Influence of Supports on the Low-Velocity Impact Response of Square RC Slab of Standard Concrete and Ultra-High Performance Concrete: FEM-Based Computational Analysis. Buildings 2023, 13, 1220. [Google Scholar] [CrossRef]
- Quan-sheng, L.I.U.; Xing-xin, P.E.N.G.; Guang-feng, L.E.I.; Jun-tao, W.; Jing, Z.; Long-ge, X. Geomechanical model test on excavation technology of supper-large cross-section ultra-shallow tunnel with cross rock pillar method. Rock Soil Mech. 2017, 38, 2780–2788. [Google Scholar]
- Yang, S.Q.; Tao, Y.; Xu, P.; Chen, M. Large-scale model experiment and numerical simulation on convergence deformation of tunnel excavating in composite strata. Tunn. Undergr. Space Technol. 2019, 94, 103133. [Google Scholar] [CrossRef]
- Fang, Y.; Chen, Z.; Tao, L.; Cui, J.; Yan, Q. Model tests on longitudinal surface settlement caused by shield tunnelling in sandy soil. Sustain. Cities Soc. 2019, 47, 101504. [Google Scholar] [CrossRef]
- Peck, B.B. Deep excavation and tunnelling in soft ground, State of the art volume. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico; 1969; Volume 4. [Google Scholar]
- Xiaoguang, F.; Jianxi, R.; Jinhua, W. Improvement of Peck Formula for Shield Construction in Xi’an Loess Area. J. Xi’an Univ. Technol. 2012, 32, 343–347. [Google Scholar]
- Feng, L.; Wu, X.Y.; Mu, D.; Li, T.; Guo, J.; Liao, X. Parameters selection research of Peck formula for twin tunnels in sandy–pebble stratum. J. Railw. Sci. Eng. 2017, 14, 100–109. [Google Scholar]
- Zheng, X.; Fenghai, M.A. Improvement of peck formula in subway construction in Changchun. Chin. J. Undergr. Space Eng. 2017, 13, 732–736. [Google Scholar]
- Fengbo, W.U.; Huai, J.I.N.; Qiyan, Y.A.N.G.; Weiqiang, Z.H.E.N.G. Analysis of Ground Transverse Settlement Groove Parameters of Beijing Metro Tunnel. Tunn. Constr. 2020, 40, 660. [Google Scholar]
- Ding, J.; Zhang, S.; Zhang, H.; Guo, C.; Liao, Z.; Liu, H. Ground settlement caused by shield tunneling in soil-rock composite strata. J. Perform. Constr. Facil. 2021, 35, 04021057. [Google Scholar] [CrossRef]
- Hu, Y.; Lei, H.; Zheng, G.; Shi, L.; Zhang, T.; Shen, Z.; Jia, R. Ground movement induced by triple stacked tunneling with different construction sequences. J. Rock Mech. Geotech. Eng. 2022, 14, 1433–1446. [Google Scholar] [CrossRef]
- Fang, K.; Yang, Z.; Jiang, Y.; Sun, Z.; Wang, Z. Surface subsidence characteristics of fully overlapping tunnels constructed using tunnel boring machine in a clay stratum. Comput. Geotech. 2020, 125, 103679. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, J.; Zhang, M.; Yang, X. Modified Peck method of evaluating tunnelling-induced ground movements based on measured data. Arab. J. Geosci. 2022, 15, 862. [Google Scholar] [CrossRef]
- Bai, W.; Ning, M.; Guan, Z. Surface settlement characteristic of shield tunnel excavation under asymmetrical terrain condition. J. Fuzhou Univ. (Nat. Sci. Ed.) 2023, 51, 205–212. [Google Scholar]
- Fang, Q.; Wang, J.; Liu, X. Characteristics of ground deformation induced by large-diameter slurry shield construction. Mod. Tunneling Technol. 2017, 54, 120–125. [Google Scholar]
- Kang, Z.; Gong, Q.; He, C. Modified Peck equation method for shield tunnel oblique crossing upper railway. J. Tongji Univ. (Nat. Sci.) 2014, 42, 1562–1566. [Google Scholar]
- O’Reilly, M.P.; New, B.M. Settlements above Tunnels in the United Kingdom-Their Magnitude and Prediction; TRID: Ludwigsfelde, Germany, 1982. [Google Scholar]



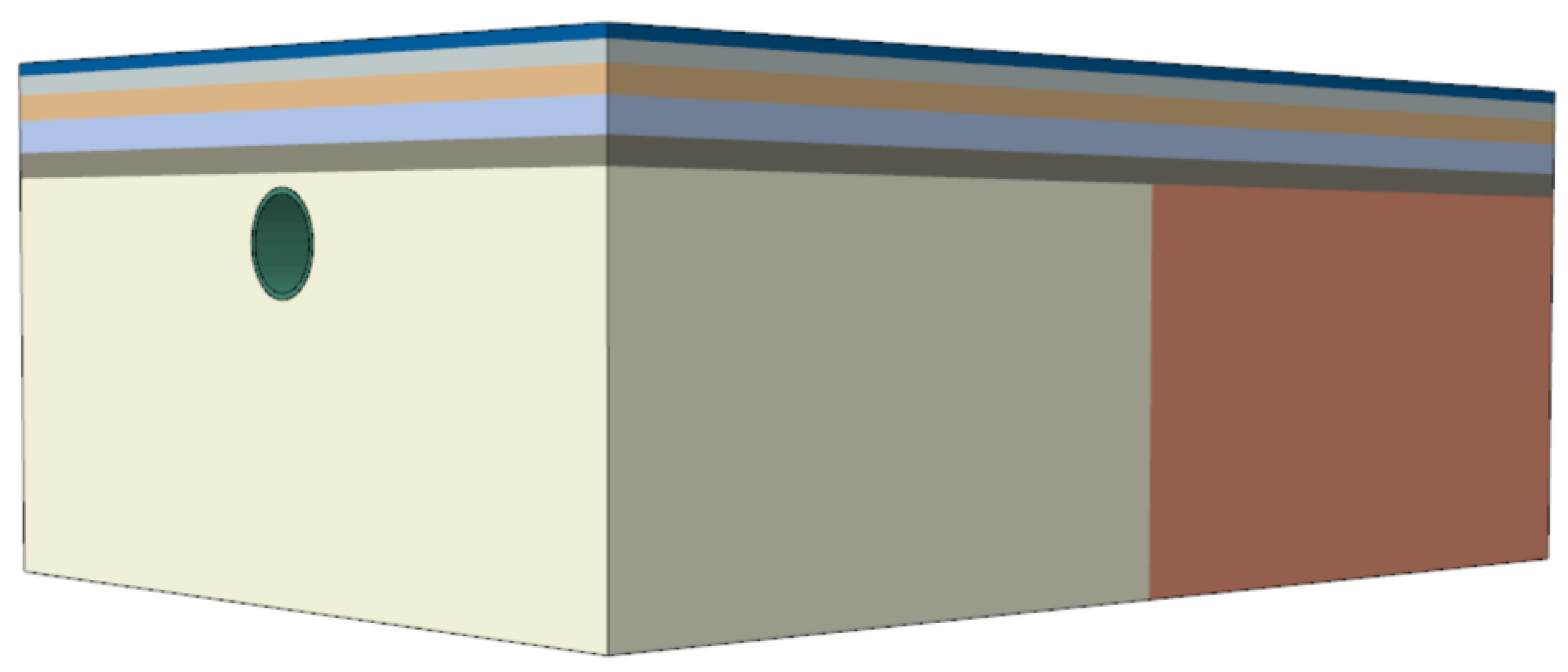



| Serial Number | Stratum | γ/ (kN·m−3) | E/MPa | v | c/kPa | φ/(°) | UCS/MPa |
|---|---|---|---|---|---|---|---|
| 1 | Mixed fill soil | 18.6 | 15.6 | 0.39 | 8 | 10 | |
| 2 | Natural fill soil | 17.5 | 12.0 | 0.37 | 5 | 15.5 | |
| 3 | Silty clay | 19.5 | 25.5 | 0.30 | 25 | 24.5 | |
| 4 | Clay with crushed stones | 19.4 | 36.0 | 0.28 | 62 | 18 | |
| 5 | Red clay | 18.7 | 28.5 | 0.33 | 43 | 17 | |
| 6 | Silty clay with loess | 19.5 | 27.6 | 0.32 | 28 | 10 | |
| 7 | Limestone | 25.7 | 15,900 | 0.25 | 6720 | 42 | 50 |
| 8 | Moderately weathered silty sandstone | 24 | 11,100 | 0.31 | 3000 | 31 | 46.7 |
| 9 | Moderately weathered fractured limestone | 25.8 | 10,690 | 0.32 | 4000 | 39 | 34.4 |
| k | Vl/% | i/m | Smax/m | |
|---|---|---|---|---|
| Stratum 6 | 0.52 | 2.0 | 11.44 | 14.02 |
| Stratum 7 | 0.88 | 0.53 | 19.36 | 3.8 |
| L | r | Smax/m | i/m |
|---|---|---|---|
| 5 m | 0.96 | 9.24 | 16.01 |
| 15 m | 0.99 | 8.5 | 14.8 |
| 25 m | 0.94 | 12.16 | 14.58 |
| 35 m | 0.98 | 12.34 | 13.75 |
| 45 m | 0.99 | 11.78 | 12.78 |
| L | r | Smax/m | i/m |
|---|---|---|---|
| 5 m | 0.97 | 5.58 | 16.78 |
| 15 m | 0.99 | 4.23 | 17.85 |
| 25 m | 0.95 | 3.02 | 18.4 |
| 35 m | 0.95 | 3.67 | 17.9 |
| 45 m | 0.97 | 3.18 | 16.8 |
| Name | γ/ (kN·m−3) | E/MPa | v |
|---|---|---|---|
| Segment lining | 25 | 34,500 | 0.2 |
| Grout material | 25 | 0.9, 4, 800 | 0.4, 0.35, 0.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liu, A.; Xing, H. Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata. Appl. Sci. 2023, 13, 10820. https://doi.org/10.3390/app131910820
Li J, Liu A, Xing H. Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata. Applied Sciences. 2023; 13(19):10820. https://doi.org/10.3390/app131910820
Chicago/Turabian StyleLi, Jinlan, Anyu Liu, and Huang Xing. 2023. "Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata" Applied Sciences 13, no. 19: 10820. https://doi.org/10.3390/app131910820
APA StyleLi, J., Liu, A., & Xing, H. (2023). Study on Ground Settlement Patterns and Prediction Methods in Super-Large-Diameter Shield Tunnels Constructed in Composite Strata. Applied Sciences, 13(19), 10820. https://doi.org/10.3390/app131910820







