Abstract
Knowledge graphs (KGs) play a crucial role in many applications, such as question answering, but incompleteness is an urgent issue for their broad application. Much research in knowledge graph completion (KGC) has been performed to resolve this issue. The methods of KGC can be classified into two major categories: rule-based reasoning and embedding-based reasoning. The former has high accuracy and good interpretability, but a major challenge is to obtain effective rules on large-scale KGs. The latter has good efficiency and scalability, but it relies heavily on data richness and cannot fully use domain knowledge in the form of logical rules. We propose a novel method that injects rules and learns representations iteratively to take full advantage of rules and embeddings. Specifically, we model the conclusions of rule groundings as 0–1 variables and use a rule confidence regularizer to remove the uncertainty of the conclusions. The proposed approach has the following advantages: (1) It combines the benefits of both rules and knowledge graph embeddings (KGEs) and achieves a good balance between efficiency and scalability. (2) It uses an iterative method to continuously improve KGEs and remove incorrect rule conclusions. Evaluations of two public datasets show that our method outperforms the current state-of-the-art methods, improving performance by 2.7% and 4.3% in mean reciprocal rank (MRR).
1. Introduction
A knowledge graph (KG) organizes knowledge as a set of interlinked triples, and a triple ((head entity, relation, tail entity), simply represented as (h, r, t)) indicates the fact that two entities have a certain relation. The availability of formalized and rich structured knowledge has emerged as a valuable resource in facilitating various downstream tasks, such as question answering [1,2] and recommender systems [3,4].
Although KGs such as DBpedia [5], Freebase [6], and NELL [7] contain large amounts of entities, relations, and triples, they are far from complete, which is an urgent issue for their broad application. To address this, researchers have introduced the concept of knowledge graph completion (KGC), which has garnered increasing interest. It utilizes knowledge reasoning techniques to automatically discover new facts based on existing ones in a KG [8].
Currently, the methods of KGC can be classified into two major categories: (1) One type of method uses explicit reasoning rules. It obtains these rules through inductive learning and then deduces new facts. (2) Another method is based on representation learning instead of directly modeling rules, aiming to learn a distributed embedding for entities and relations and perform generalization in numerical space.
Rule-based reasoning is accurate and can provide interpretability for the inference results. These rules can be hand-crafted by domain experts [9] or mined from KGs using an inductive algorithm like AMIE [10]. Traditional methods like expert systems [11,12] utilize hard logical rules for making predictions. For example, as shown in Figure 1, given the logical rule and the two facts that (Chicago, city_of, USA) and (Mary, born_in, Chicago), we can infer the fact (Mary, nationality, USA). Based on forward reasoning, it is possible to derive numerous new facts (conclusions). However, acquiring sufficient and effective reasoning rules for large-scale KGs can be a challenging and costly task. Additionally, logical rules, in many instances, may be imperfect or even self-contradictory. Therefore, it is essential to effectively model the uncertainty of logical rules.
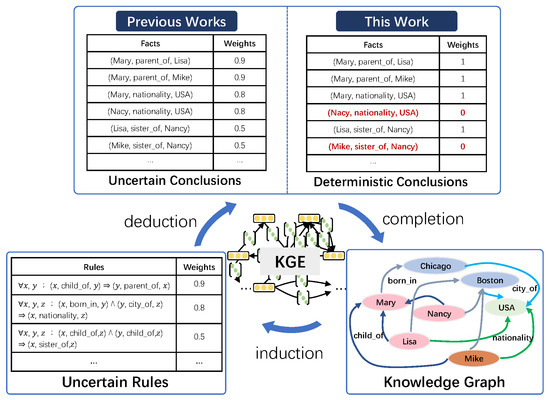
Figure 1.
We propose a novel iterative knowledge reasoning framework that fuses logical rules into a knowledge graph embedding (KGE). Previous methods associate each conclusion with a weight derived from its corresponding rule. In contrast, our method can infer the true conclusion via jointly modeling the deterministic KG and uncertain soft rules. The facts in red are erroneous conclusions filtered out by our method.
The methods used to determine knowledge graph embeddings (KGEs) learn how to embed entities and relations into a continuous low-dimensional space [13,14]. These embeddings maintain the semantic meaning of entities and relations, facilitating the prediction of missing triples. Additionally, these embeddings can be effectively trained using stochastic gradient descent (SGD). However, it is important to note that this approach does not fully capitalize on logical rules, which are instrumental in compactly encoding domain knowledge and have practical implications in various applications. It is worth mentioning that high-quality embeddings heavily rely on abundant data, making it challenging for these methods to generate meaningful representations for sparse entities [15,16].
In fact, both rule-based and embedding-based methods have advantages and disadvantages in the KGC task. Logical rules are accurate and interpretable, while embedding is flexible and computationally efficient. Recently, there has been research on combining the advantages of logical rules and KGEs to achieve more precise knowledge completion. Mixed techniques can infer missing triples effectively by exploiting and modeling uncertain logical rules. Some existing methods aim to learn KGEs and rules iteratively [16], and some other methods also utilize soft rules or groundings of rules to regularize the learning of KGEs [17,18].
The integration of logical rules and knowledge graph embeddings can achieve more efficient and accurate knowledge completion. Current methods model uncertain rules and add soft labels to conclusions by t-norm-based fuzzy logic [19]. They further utilize the conclusions to perform forward reasoning [17] or to enhance the KGE [16]. However, in most KGs, the facts are deterministic. Therefore, we believe that rules are uncertain, but conclusions are deterministic in knowledge reasoning, as shown in Figure 1; each fact is only absolutely true or false. Previous methods associate each conclusion with a weight derived from the corresponding rule. In contrast, we propose inferring that all conclusions are true (e.g., (Mary, nationality, USA)) or not (e.g., (Mike, sister_of, Nancy)) (the other fact, i.e., (Mike, gender, male), indicates that Mike is not Nancy’s sister) by jointly modeling the deterministic KG and soft rules.
Specifically, we first mine soft rules from the knowledge graph and then infer conclusions as candidate facts. Second, the KG, conclusions, and weighted rules are also used as resources to learn embeddings. Third, by defining deterministic conclusion loss, the conclusion labels are modeled as 0–1 variables, and the confidence loss of a rule is also used to constrain the conclusions. Finally, the embedding learning stage removes the noise in the candidate conclusions, and then the proper conclusions are added back to the original KG. The above steps are performed iteratively. We empirically evaluate the proposed method on public datasets from two real large-scale KGs: DBpedia and Freebase. The experimental results show that our method Iterlogic-E (Iterative using logic rule for reasoning and learning Embedding) achieves state-of-the-art results on multiple evaluation metrics. Compared to the state-of-the-art model, Iterlogic-E also achieves improvements of 2.7%/4.3% in mean reciprocal rank (MRR) and 2.0%/4.0% in HITS@1.
In summary, our main contributions are as follows:
- We propose a novel KGC method, Iterlogic-E, which jointly models logical rules and KGs in the framework of a KGE. Iterlogic-E combines the advantages of rules and embeddings in knowledge reasoning. Iterlogic-E models the conclusion labels as 0–1 variables and uses a confidence regularizer to eliminate the uncertain conclusions.
- We propose a novel iterative learning paradigm that strikes a good balance between efficiency and scalability. Iterlogic-E not only densifies the KG but can also filters out incorrect conclusions.
- Compared to traditional reasoning methods, Iterlogic-E offers better interpretability in determining conclusions. It not only knows why the conclusion holds but also knows which is true and which is false.
- We empirically evaluate the performance of Iterlogic-E with the task of link prediction on multiple benchmark datasets. The experimental results demonstrate that Iterlogic-E can outperform other methods on multiple evaluation metrics. The qualitative analysis confirms that Iterlogic-E exhibits higher robustness for rules with varying confidence levels.
2. Related Work
Knowledge reasoning aims to infer certain entities over KGs as the answers to a given query. A query in KGC is a head entity h (or a tail entity t) and a relation r. Given (or ), KGC aims to find the right tail entity t (or head entity h) in the KG that satisfies the triple . Next, we review the three most relevant classes of KGC methods.
2.1. Rule-Based Reasoning
Logical rules can encode human knowledge compactly, and early knowledge reasoning was primarily based on first-order logical rules. Existing rule-based reasoning methods have primarily utilized search-based inductive logic programming (ILP) methods, usually searching and pruning rules. Based on the partial completeness assumption, AMIE [10] introduces a revised confidence metric well suited for modeling KGs. AMIE+ [20] is optimized to expand to larger KGs by query rewriting and pruning. Additionally, AMIE+ improves the precision of the forecasts by using joint reasoning and type information. In this paper, we employ AMIE+ (https://github.com/lajus/amie, accessed on 21 September 2023) to mine Horn rules from a KG. Rule-based reasoning methods can be combined with multiple probability graph models. A typical model is a Markov logic network (MLN) [21]. Based on pre-provided rules, it builds a probabilistic graph model and then learns the weights of rules. However, due to the complicated graph structure among triples, the reasoning in an MLN is time-consuming and challenging, and the incompleteness of KGs also impacts the inference results. In contrast, Iterlogic-E uses rules to enhance KGEs with more effective inference.
2.2. Embedding-Based Reasoning
Recently, embedding-based methods have attracted much attention. These methods aim to learn distributed embeddings for entities and relations in KGs. Generally, the current KGE methods can be divided into three classes: (1) translation-based models that learn embeddings by translating one entity into another entity through a specific relation [22,23]; (2) compositional models that use simple mathematical operations to model facts, including linear mapping [24], bilinear mapping [25,26,27], and circular correlation [28]; (3) neural-network-based models that utilize a multilayer neural structure to learn embeddings and estimate the plausibility of triples with nonlinear features: for example, R-GCN [29], ConvE [30] and so on [31,32,33]. The above methods learn representations based only on the triples existing in KGs, and the sparsity of data limits them. In order to address this issue and acquire semantic-rich representations, recent studies have made efforts to incorporate additional information apart from triples. These include contextual information [34], entity type information [35,36], ontological information [37], taxonomic information [38], textual descriptions [39], commonsense knowledge [40], and hierarchical information [41]. In contrast, the proposed Iterlogic-E utilizes embeddings to eliminate erroneous conclusions derived from rules, which combines the advantages of soft rules and embeddings.
2.3. Hybrid Reasoning
Both rule-based and embedding-based methods have their own advantages and disadvantages. Recent works have integrated these two types of reasoning methods together. Guo et al. [42] tried to learn a KGE from rule groundings and triples in combination. They utilized TransE to obtain entity and relation embeddings and computed the truth value for each rule using t-norm fuzzy logic. Then, they ranked the rules by their truth values and manually filtered those ranked at the top. Nayyeri et al. [43] enhanced KGEs by injecting rules. Although their works also learned embeddings jointly, they could not support the uncertainty of soft rules. Wang et al. [44] ordered relations approximately by maximizing the margin between negative and positive logical rules to capture the transitivity and asymmetry of rules. However, it cannot directly benefit from the forward reasoning of rules and does not utilize the confidence information corresponding to the rules. Zhang et al. [17], Guo et al. [18], and Guo et al. [45] obtained KGEs with supervision from soft rules, proving the effectiveness of logical rules. Whereas, they did not consider combining KGEs to filter out erroneous facts introduced by these rules during the iteration process. Qu et al. [46] used an MLN to model logical rules and inferred new triples to enhance KGEs. One main difficulty here is the large search space in determining rule structures and searching for support groundings. Zhang et al. [16] aimed to improve sparse data representation through iterative learning and update the confidence of rules through embeddings. Nevertheless, their method evaluates sparsity based on the frequency of entities participating in triples, and only conclusions related to entities with high sparsity are injected into the original knowledge graph. This design choice is specifically tailored to address the challenges posed by sparse data in the test set but did not take into account the potentially erroneous introduced by the rules. In contrast, Iterlogic-E models the conclusion labels as 0–1 variables and uses confidence regularization loss to eliminate uncertain conclusions. Our approach employs confidence in soft rules and embedding models to evaluate conclusions inferred from soft rules. During iterative training, the embedding model learns to select the most likely true conclusion from all available conclusions. These selected conclusions are labeled as true, while the remaining facts are filtered out as potentially erroneous. This method avoids introducing erroneous facts and maintains training efficiency. Also, no extra memory is required as no additional model parameters are introduced.
3. The Proposed Method
This section presents our proposed method, Iterlogic-E. We begin by providing a comprehensive overview of our method, which entails the iterative learning process. Subsequently, we delve into the two components of Iterlogic-E: rule mining and reasoning, as well as embedding learning. Finally, we examine the space and time complexity of Iterlogic-E while also discussing its connections to related research [16,17,18].
3.1. Overview
Given a KG , , is a relation and are entities. As discussed in Section 1, on the one hand, embedding learning methods do not make full use of logical rules and suffer from data sparsity. On the other hand, high-quality rules are challenging to obtain efficiently and can only cover some facts in KGs. Our goal is to improve the embedding quality by explicitly modeling the reasoned conclusions of logical rules and discarding incorrect conclusions. Figure 2 shows the overview of Iterlogic-E given a toy knowledge graph. Iterlogic-E is a general framework that can fuse different KGE models.
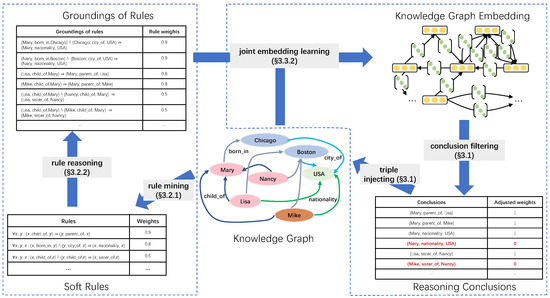
Figure 2.
The framework outlines Iterlogic-E with two iterative stages: (i) rule mining and reasoning and (ii) embedding learning. In stage (i), rules and grounding rules are generated to derive new conclusions. In stage (ii), the framework simultaneously models the conclusions derived from grounding rules and the KG for learning embeddings. After embedding learning, the conclusions are injected into the KG, and then the rule reasoning module is executed to start the next round of iterative training. The weight of a rule is its partial closed-world assumption (PCA) confidence: refer to Equation (1). The facts in red are erroneous conclusions filtered out by our method. The yellow and green spots indicate the values of entity embedding and relation embedding values, respectively.
The Iterlogic-E approach consists of two iterative steps: rule mining and reasoning, and embedding learning. The first step, rule mining and reasoning, involves two modules: rule mining and rule reasoning. The rule mining module requires input of mining configuration parameters, such as the maximum length of rules and the confidence threshold of rules, in addition to KG triples. Then, it automatically obtains the soft rules from these inputs. The KG triples and the extracted soft rules are input into the rule reasoning module to infer new triples. After that, the new triples are appended to the embedding learning step as candidate conclusions. In the embedding learning step, relations are modeled as a linear mapping operation, and triple plausibility is represented as the correlation between the head and tail entities after the operation. Finally, the incorrect conclusions are filtered out by labeling the conclusions with their scores (In the experiments, we choose the conclusion with a normalized score of more than 0.99 as the true conclusion). The true conclusion will be added back to the original KG triples, and then the rule reasoning module will be performed to start the next cycle of iterative training.
3.2. Rule Mining and Reasoning
The first step is composed of the rule mining module and the rule reasoning module. We introduce these two modules in detail below.
3.2.1. Rule Mining
Soft rules are extracted from the knowledge graph (KG) using the advanced rule mining method AMIE+ [20]. AMIE+ applies partial closed-world assumption (PCA) confidence to estimate the reliability of a rule since its partial completeness assumption is more suited to real-world KGs. The PCA confidence of a rule R in a KB is defined as the following formula:
is the body (also called premise) of rule , and the of a rule indicates the number of groundings in the knowledge base that supports the rule. Additionally, AMIE+ defines various restriction types to help extract applicable rules, e.g., the maximum length of the rule. The rule mining module takes as input the KG triples and employs the AMIE+ algorithm to generate soft rules. We execute the rule mining module only once to optimize efficiency, even though the rules could be re-mined in each iteration.
3.2.2. Rule Reasoning
The logical rule set is denoted as , where f takes the form . In this rule, x, y, and z represent variables for different entities, while , , and represent different relations. The left side of the ⇒ symbol represents the premise of the rule, which consists of multiple connected atoms. On the right side, we have a single atom representing the conclusion of the rule. These Hore rules are closed [25], meaning that the intermediate entity is shared by the continuous relations, and the first and last entities of the premise appear as the head and tail entities of the conclusion. Such rules can provide interpretive insights. A rule’s length is equal to the number of atoms in the premise. For example, is a length-2 rule. This rule reflects the reality that, most likely, a person’s nationality is the country in which he or she was born. The rule f has a confidence level of 0.8. The higher the confidence of the rule, the more likely it is to hold.
The reasoning procedure consists of instantiating the rule’s premise and obtaining a large number of fresh conclusion triples. One of the most common approaches is forward chaining, also known as the match–select–act cycle, which works in three-phase cycles. Forward chaining matches the current facts in the KG with all known rule premises to determine which rules can be satisfied in one cycle. Finally, the selected rule’s conclusions are derived, and if the conclusions are not already in the KG, they are added as new facts. This cycle should be repeated until no new conclusions are derived. However, if soft rules are used, forward reasoning will lead to incorrect conclusions. Therefore, we run one reasoning cycle in every iteration.
3.3. Embedding Learning
This section introduces a joint embedding learning approach that allows the embedding model to simultaneously learn from KG triples, conclusion triples, and soft rule confidence. First, we will examine a basic KGE model and describe how to incorporate soft rule conclusions. Finally, we detail the overall training goal.
3.3.1. A Basic KGE Model
Different KGE models have different score functions that aim to obtain a suitable function to map the triple score to a continuous true value in [0, 1], i.e., , which indicates the probability that the triple holds. We follow [17,18] and choose ComplEx [26] as a basic KGE model. It is important to note that our proposed framework can be combined with an arbitrary KGE model. Theoretically, using a better base model can continue improving performance. Therefore, we also experiment with RotatE as a base model. Below, we elaborate on the methods of ComplEx and RotatE. ComplEx assumes that the entity and relation embeddings exist in a complex space, i.e., and , where d is the dimensionality of the complex space. Using plurals to represent entities and relations can better model antisymmetric and symmetric relations (e.g., kinship and marriage) [26]. Through a multilinear dot product, ComplEx scores every triple. In contrast to ComplEx, RotatE defines the functional mapping induced by each relation r as an element-wise rotation from the head entity h to the tail entity t:
We utilize the function to extract the real part of a complex value, and ∘ is the Hadmard (or element-wise) product. Additionally, the function is employed to construct a diagonal matrix from the variable r. Furthermore, we define as the conjugate of the variable t, and is the i-th entry of a vector.
where is the sigmoid function and is the score function. By minimizing the logistic loss function, ComplEx learns the relation and entity embeddings:
where is negative triples and is the label of a triple.
3.3.2. Joint Modeling KG and Conclusions of Soft Rules
To model the conclusion label as a 0–1 variable, based on the current KGE model’s scoring function, we follow ComplEx and use the function defined in Equation (2) or Equation (3) as the scoring function for conclusion triples:
where is the set of conclusion triples derived from rule f. Aiming to regularize this scoring function so that it approaches 0 or 1 and to distinguish between true and false conclusions, we use a quadratic function with a symmetry axis of 0.5. Therefore, the conclusion score is the smallest when close to 0 or 1. Therefore, we define the deterministic conclusion loss as follows:
According to the definition of rule confidence in [10], the confidence of a rule f in a KB is the proportion of true conclusions among the true conclusions and false conclusions. Therefore, we can define the confidence loss of a rule as follows:
where is the PCA confidence of rule f. Therefore, the loss of the conclusions of all the rules can be defined as follows:
where is the set of all rules. To learn the KGE and rule conclusions at the same time, we minimize the global loss over a soft rule set and a labeled triple set (including negative and positive examples). The overall training objective of Iterlogic-E is
where the function denotes the score function, and is the Softplus activation function. In Algorithm 1, we detail the embedding learning procedure of our method. We further impose regularization on embedding to avoid overfitting. Following [18,47], we also imposed nonnegative constraints (NNE) on the entity embedding to learn more effective features.
| Algorithm 1: Iterative learning algorithm of Iterlogic-E | ||||
| ||||
| 1 | Randomly initialize relation and entity embeddings | |||
| 2 | for to N do | |||
| 3 | ||||
| 4 | if n/[N/M] == 0 then | |||
| 5 | Generate a set of conclusions by rule grounding from | |||
| 6 | ||||
| 7 | end | |||
| 8 | Sample a batch triples from | |||
| 9 | Generate negative examples | |||
| 10 | ||||
| 11 | for each to N do | |||
| 12 | ||||
| 13 | ||||
| 14 | end | |||
| 15 | Update by gradient backpropagation of Equation (10) | |||
| 16 | ||||
| 17 | for each do | |||
| 18 | if then | |||
| 19 | ||||
| 20 | end | |||
| 21 | end | |||
| 22 | ||||
| 23 | end | |||
| 24 | return | |||
3.4. Discussion
3.4.1. Complexity
In the representation learning step, relations and entities are represented as complex value vectors, following the approach of ComplEx. This results in a space complexity of , where d represents the dimensionality of the embedding space. The number of relations is denoted as , while the number of entities is denoted as . Each iteration of the learning process has a time complexity of , where and , respectively, represent the number of new conclusions or labeled triples in a batch, as illustrated in Algorithm 1.
Iterlogic-E shares similarities with ComplEx in terms of space and time complexity, as both increase linearly with d. However, the number of new conclusions in a batch is typically much smaller than the number of initial triples, specifically, . Consequently, Iterlogic-E’s time complexity is similar to ComplEx’s, which only requires per iteration.
Considering the efficiency of the rule mining module and practical constraints, such as a confidence threshold higher than 0.7 and a maximum rule length of three, the space and time complexities of the rule grounding stage are insignificant compared to that of the embedding learning stage. Hence, it can be disregarded when evaluating the space and time complexity of Iterlogic-E.
3.4.2. Connection to Related Works
IterE [16] also uses iterative learning, which defines several types of rules with OWL2. However, IterE does not modify the process of embedding learning and is limited by rules that will yield numerous noisy conclusions. IterE uses a pruning strategy that utilizes traversal and random selection to obtain rules. Furthermore, they only improve the prediction effect of sparse entities but still need to improve on standard datasets. By contrast, Iterlogic-E uses the AMIE+ rule mining system [20] to mine high-confidence rules, and the quality of the rules obtained in this way is higher because it uses the KG to evaluate the reliability of the rules thoroughly. SoLE enhances KGE by jointly modeling the groundings of rules and facts and directly utilizes uncertain rules for the forward chain without eliminating incorrect grounding.
Moreover, SoLE [17] uses t-norm-based fuzzy logic [19] to model grounding, significantly increasing the time complexity. Our proposed method avoids the abovementioned problems without increasing the number of parameters. SLRE [18] uses rule-based regularization that merely enforces the relation to satisfying constraints introduced by soft rules. However, it does not use rules for reasoning and cannot benefit from the interpretability and accuracy advantages. In addition, SLRE has strict requirements on the form of the rules, while our method can utilize various forms of rules more simply and flexibly via the rule reasoning module.
4. Experiments and Results
4.1. Datasets
Iterlogic-E is tested on two commonly used datasets: FB15K and DB100K. The FB15K dataset is based on Freebase, released by Bordes et al. [22]. The DB100K dataset, on the other hand, was obtained from DBpedia by Ding et al. [47] and consists of 99,604 entities and 470 relations. Our experiments employed fixed training, validation, and test sets for model training, hyperparameter tuning, and evaluation.
With each training dataset, we obtain soft rules and examine rules with a length of no more than two to allow efficient extraction. These rules are automatically retrieved from the training set of each dataset using the AMIE+ algorithm [20]. We only consider rules with confidence levels greater than 0.8. Shorter rules more directly capture the logical connections among relations. Therefore, we remove longer rules when all their relations also exist in shorter ones. Table 1 provides a summary of the comprehensive statistics for the datasets, and Table 2 includes several rule instances. We can observe from the statistics that the number of rules on both datasets is extremely minimal compared to the number of triples.

Table 1.
The datasets’ statistics are presented, with each column representing the quantities of training/validation/test triples, relations, entities, and soft rules. “#” indicates number.

Table 2.
Examples of rules that have been extracted. The upper part is three rules mined from the FB15K dataset, and the lower part is three rules mined from the DB100K dataset.
4.2. Link Prediction
Our method was evaluated on link prediction. This task aimed to restore a missing triple with the tail entity or with the head entity .
4.2.1. Evaluation Protocol
The standard protocol established by [22] is used for evaluation. In this protocol, we replace the head entity with each entity for every test triple , then calculate the corrupted triple score. We rank these scores in decreasing order and record the rank of the correct entity . To evaluate the ranking quality of all test triples, we use the mean reciprocal rank (MRR) and the percentage of ranks no more than N (HITS@N, where N = 1, 3, 10).
4.2.2. Comparison Settings
We compare the performance of our method to that of a number of previous KGE models, as shown in Table 3. The first batch of baselines includes the translation-based model (row 1), compositional models utilizing basic mapping operations (rows 2–10), and neural-network-based models (rows 11–13). These baselines rely only on triples seen in the KGs. The middle batch of baselines are the rule-based reasoning methods (lines 14–15). The last batch of baselines further incorporates logical rules (rows 16–26).
4.2.3. Implementation Details
On FB15K and DB100K, we compared Iterlogic-E against all of the baselines. We immediately obtained the results of a set of baselines on FB15K and DB100K from SoLR, SLRE, and CAKE. We implemented the ComplEx model using the PyTorch framework, utilizing the code provided by [24] (https://github.com/DeepGraphLearning/KnowledgeGraphEmbedding, accessed on 21 September 2023) as a basis for our implementation. Then, depending on our implementation, we provided the ComplEx result. Furthermore, we evaluated the IterE model on the FB15K-sparse dataset created by [16]. This dataset consisted of sparse entities with validation and test sets containing 18,544 and 22,013 triples, respectively. Therefore, we implemented IterE on FB15K and DB100K based on the code and hyperparameters (https://github.com/wencolani/IterE, accessed on 21 September 2023) released by the author. As a result, we compared our approach to IterE and SoLE on the FB15K-sparse dataset. Both approaches use a logistic loss and optimize in the same way (SGD with AdaGrad). The remaining baseline results were taken directly from previous literature. We conducted hyperparameter tuning during our experiments. Specifically, we varied the embedding dimensionality d within the set {100, 150, 200, 250, 300}, the number of negatives per positive triple within the set {2, 4, 6, 8, 10}, the initial learning rate within the set , and the L2 regularization coefficient within the set . For margin-based ranking loss approaches, we also tuned the margin within the set {0.1, 0.2, 0.5, 1, 2, 5, 12, 18, 24}. We selected the best hyperparameters based on maximizing the mean reciprocal rank (MRR) on the validation set. For Iterlogic-E, the best settings were , , , and on the FB15K dataset and , , , and on the DB100K dataset.

Table 3.
Link prediction results on the test sets of FB15K and DB100K. The boldface scores are the best results, and “-” indicates the missing scores not reported in the literature. The first batch of baselines includes embedding-based models, which rely only on triples seen in the KGs. The middle batch of baselines includes the rule-based reasoning methods. The last batch of baselines further incorporates logical rules and embeddings.
Table 3.
Link prediction results on the test sets of FB15K and DB100K. The boldface scores are the best results, and “-” indicates the missing scores not reported in the literature. The first batch of baselines includes embedding-based models, which rely only on triples seen in the KGs. The middle batch of baselines includes the rule-based reasoning methods. The last batch of baselines further incorporates logical rules and embeddings.
| Method | FB15K | DB100K | |||||||
|---|---|---|---|---|---|---|---|---|---|
| MRR | HITS@1 | HITS@3 | HITS@10 | MRR | HITS@1 | HITS@3 | HITS@10 | ||
| 1 | TransE [22] | 0.380 | 0.231 | 0.472 | 0.641 | 0.111 | 0.016 | 0.164 | 0.270 |
| 2 | DistMult [25] | 0.654 | 0.546 | 0.733 | 0.824 | 0.233 | 0.115 | 0.301 | 0.448 |
| 3 | HolE [28] | 0.524 | 0.402 | 0.613 | 0.739 | 0.260 | 0.182 | 0.309 | 0.4118 |
| 4 | ComplEx [26] | 0.627 | 0.550 | 0.671 | 0.766 | 0.272 | 0.218 | 0.303 | 0.362 |
| 5 | ANALOGY [27] | 0.725 | 0.646 | 0.785 | 0.854 | 0.252 | 0.143 | 0.323 | 0.427 |
| 6 | ComplEx-NNE [47] | 0.727 | 0.659 | 0.772 | 0.845 | 0.298 | 0.229 | 0.330 | 0.426 |
| 7 | ComplEx-CAS [48] | - | - | - | 0.866 | - | - | - | - |
| 8 | RotatE [24] | 0.664 | 0.551 | 0.751 | 0.841 | 0.327 | 0.200 | 0.417 | 0.526 |
| 9 | HAKE [41] | 0.408 | 0.312 | 0.463 | 0.579 | - | - | - | - |
| 10 | CAKE [40] | 0.741 | 0.646 | 0.825 | 0.896 | - | - | - | - |
| 11 | R-GCN+ [29] | 0.696 | 0.601 | 0.760 | 0.842 | - | - | - | - |
| 12 | ConvE [30] | 0.745 | 0.670 | 0.801 | 0.873 | - | - | - | - |
| 13 | DPMPN [49] | 0.764 | 0.726 | 0.784 | 0.834 | - | - | - | - |
| 14 | BLP [50] | 0.242 | 0.151 | 0.269 | 0.424 | - | - | - | - |
| 15 | MLN [21] | 0.321 | 0.210 | 0.370 | 0.550 | - | - | - | - |
| 16 | PTransE [51] | 0.679 | 0.565 | 0.768 | 0.855 | 0.195 | 0.063 | 0.278 | 0.416 |
| 17 | KALE [42] | 0.518 | 0.382 | 0.606 | 0.756 | 0.249 | 0.100 | 0.346 | 0.497 |
| 18 | ComplEx [52] | - | - | - | - | 0.253 | 0.167 | 0.294 | 0.420 |
| 19 | TARE [44] | 0.781 | 0.617 | 0.728 | 0.842 | - | - | - | - |
| 20 | RUGE [45] | 0.768 | 0.703 | 0.815 | 0.865 | 0.246 | 0.129 | 0.325 | 0.433 |
| 21 | ComplEx-NNE+AER [47] | 0.801 | 0.757 | 0.829 | 0.873 | 0.311 | 0.249 | 0.339 | 0.426 |
| 22 | IterE [16] | 0.576 | 0.443 | 0.665 | 0.818 | 0.274 | 0.215 | 0.299 | 0.386 |
| 23 | pLogicNet [46] | 0.776 | 0.706 | 0.817 | 0.885 | - | - | - | - |
| 24 | SoLE [17] | 0.801 | 0.764 | 0.821 | 0.867 | 0.306 | 0.248 | 0.328 | 0.418 |
| 25 | SLRE [18] | 0.810 | 0.774 | 0.829 | 0.871 | 0.340 | 0.261 | 0.372 | 0.490 |
| 26 | LogicENN [43] | 0.766 | - | - | 0.874 | - | - | - | - |
| Iterlogic-E(ComplEx) | 0.814 | 0.778 | 0.835 | 0.873 | 0.374 | 0.301 | 0.409 | 0.509 | |
| Iterlogic-E(RotatE) | 0.837 | 0.794 | 0.868 | 0.904 | 0.387 | 0.287 | 0.449 | 0.559 | |
4.2.4. Main Results
The results for all compared methods on the FB15K, DB100K, and FB15K-sparse test sets are presented in Table 3 and Table 4. We utilize the mean reciprocal rank or HITS@N value for each test triple, with N = 1, 3, 10, as paired data. The experimental results show that (1) Iterlogic-E outperforms numerous strong baselines in most cases. This result shows that Iterlogic-E can achieve excellent accuracy. (2) Iterlogic-E significantly outperforms the basic models that use triples alone, and the improvement comes from the ability to learn the conclusions obtained by soft rules. (3) Iterlogic-E also outperforms many baselines that incorporate logical rules, including SoLE and IterE, indicating its superiority in reducing the noise of candidate conclusions. (4) IterE can only enhance sparse entities, so the experimental results are much lower than those of other baseline models. However, Iterlogic-E is also effective on the FB15K-sparse test set. (5) In DB100K, the improvements over SLRE and SoLE are more substantial than those in FB15K. This difference is likely due to the groundings of the rules in DB100K containing more incorrect conclusions. Simple rules (length less than or equal to two) are sufficient to capture most patterns in the FB15K dataset. (6) The performance of Iterlogic-E(ComplEx) is worse than some baselines in HITS@10, and we consider that this limitation is mainly due to the shortcomings of the base model ComplEx [26]. Sun et al. [24] point out that ComplEx cannot model the composition relation. We have experimented with replacing the base model with the RotatE model(Iterlogic-E(RotatE)), which is capable of modeling four relation patterns. The experimental results have been further improved, and our method consistently achieves the best results in all evaluation metrics.

Table 4.
Results of link prediction on the test sets of FB15K-sparse. This dataset’s settings are derived from IterE. The training set is identical to FB15K, but the validation and test sets mainly consist of triples involving sparse entities. The boldface scores indicate the best results.
4.2.5. Ablation Study
To explore the influence of different constraints and iterative learning, we perform an ablation study of Iterlogic-E on DB100K with nine configurations in Table 5. Compared to the completed model Iterlogic-E, the first and second variants remove the non-negativity and -norm constraints (). The third setting is the combination setting. The fourth removes iterative learning (IL), which only uses a rule for reasoning reason once. The fifth, sixth, and seventh variants remove the additional loss item from the sixth variant. The eighth setting is another variant of the Iterlogic-E model based on the ninth setting: after the ComplEx fitting, based on the scores of the conclusions, the top n (where n is the rounded product of the number of conclusions and their confidence value) conclusions of each rule are selected and added to the KG to continue training. The ninth setting (AC) adds all conclusions inferred from the rules as positive examples, and the tenth setting (WC) uses the rule confidence as soft labels of conclusions.

Table 5.
Ablation study for different constraints used in Iterlogic-E on DB100K. The boldface scores are the best results. indicates the embedding of entities and relations, and “*” indicates replacing the soft constraints of Equations (7)–(9) to select n (where n is the rounded product of the number of conclusions and their confidence value).
As seen in Table 5, we can conclude the following: (1) When removing NNE constraints, the performance of Iterlogic-E decreases slightly. Without -norm constraints on entities, the performance of Iterlogic-E degrades by 2.3% in HITS@1 and by 5.1% in MRR. One explanation may be that -norm constraints are sufficient to constrain embedding norms on DB100K. However, the performance will suffer dramatically if no -norm constraints exist. (2) Removing iterative learning decreases performance slightly. One reason may be that the number of rules on DB100K is relatively small, so the number of conclusions added through iterative learning is relatively small. (3) Removing the additional loss item of the conclusions decreases performance slightly. The result illustrates that Iterlogic-E can filter out incorrect conclusions and dense the KG. Surprisingly, even if we directly use ComplEx to filter and learn the conclusions that can achieve such high performance, this method is not as flexible as Iterlogic-E. (4) Compared with the basic model, all variants have different degrees of improvement. The result demonstrates the critical importance of logical rules in link prediction tasks.
4.3. Influence of the Number of Iterations
To demonstrate how Iterlogic-E can enhance the embedding effect during the training process, we show the link prediction results on DB100K with different iterations. Figure 3 shows that as the number of training iterations increases, the prediction results will improve, including HITS@1, HITS@3, HITS@10, and MRR. From Figure 3, we can infer the following: (1) Iterative learning enhances embedding learning since the quality of embeddings improves with time. (2) In the first two iterations, the embedding learning module was quickly fitted to the conclusions of the rules and the triples of the training set, and the prediction accuracy rapidly improved. (3) After two iterations, as the number of new conclusions decreased, the inference results tended to be stable, and the true conclusions and the initial KG triples were well preserved in the embedding.
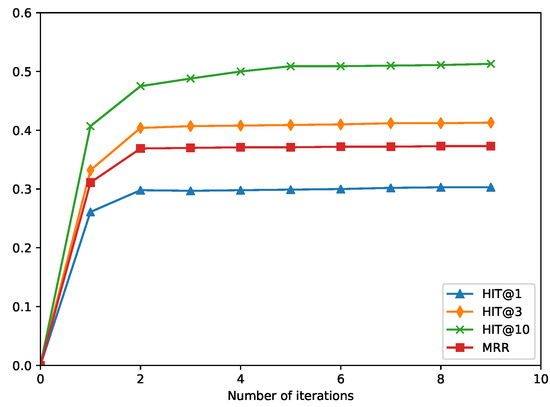
Figure 3.
Link prediction results in different iterations. On the DB100K dataset, the performance changes of Iterlogic-E on the test set as the number of iterations increases.
4.4. Influence of Confidence Levels
Additionally, we evaluate the effect of the rules’ confidence thresholds on FB15K. Since there are different rules and ComplEx does not merge rules, we refer only to their fixed results on FB15K. We set all hyperparameters to their optimum values and change the confidence threshold within [0.5, 1] in 0.05-step increments. Both SoLE and Iterlogic-E use rules with confidence levels greater than this threshold. Figure 4 displays the MRR and HITS@1 values obtained by Iterlogic-E and other baselines on the FB15K test set. We make the following observations: 1) Iterlogic-E beats both ComplEx and IterE at varying confidence levels. This demonstrates that Iterlogic-E is sufficiently robust to deal with uncertain soft rules.
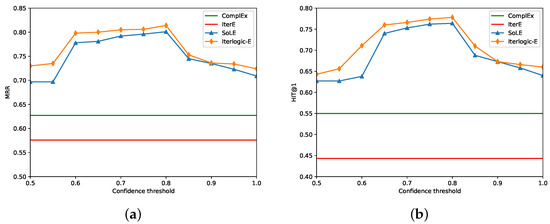
Figure 4.
Results of MRR (a) and HITS@1 (b) with different confidence thresholds on FB15K. We set all hyperparameters to their optimum values and change the confidence threshold within [0.5, 1] in 0.05-step increments.
Runtime
At last, we compared the running time of Iterlogic-E(ComplEx) and ComplEx methods. In general, the running time of the hybrid reasoning model is longer than its basic embedding model because of the addition of rule mining and the introduction of new facts (Notably, running times cannot be directly compared with other hybrid reasoning methods due to differences in code languages and deep learning frameworks. For example, SLRE is implemented in Java and only has a CPU-running version). Iterlogic-E (ComplEx) took an average of 4.6 s and 4.2 s per 100 batches on the FB15K dataset and DB100K dataset, while ComplEx took 4.6 s and 4.2 s on average. The times are very close, mainly because the method does not introduce new model parameters and only slightly increases the calculation time. Rule mining took 7.97 s and 3.63 s on those two datasets, and rule reasoning took 8.6 s and 7.98 s, respectively. Note that rule mining will only be executed once, while rule reasoning will only be executed two to five times, which is negligible compared to the total time spent training over 100,000 batches.
4.5. Case Study
In Table 6, we present a case study with four conclusions (true or false as predicted by Iterlogic-E), which are inferred with two rules during training. Table 6 shows some conclusions derived from rule inference and the score change (the average of the head entity prediction score and the tail entity prediction score) of the conclusions. Let us take the first conclusion as an example: the true conclusion is (Albany_Devils,/hockey_roster_position/posit on, Centerman), which is obtained by the rule “/sports_team_roster/position/hockey_roster _position/position”. The Albany Devils are a professional ice hockey team competing in the American Hockey League (https://en.wikipedia.org/wiki/Albany_Devils, accessed on 21 September 2023), and the centerman is the center in ice hockey. Therefore, this is indeed a true conclusion. Compared to ComplEx, Iterlogic-E increased the score of this fact from 5.48 to 9.40. Also, (San_Diego_State_Aztecs_football, /hockey_roster_position/position, Linebacker) can be inferred from the fact (San_Diego_State_Aztecs_football, /sports_team_roster/team, Linebacker) by the same rule. However, the San Diego State Aztecs are a football team, not a hockey team, and this is an incorrect conclusion. Compared to ComplEx, Iterlogic-E decreased the score of this fact from −4.65 to −8.35. This case illustrates that Iterlogic-E can distinguish whether the conclusion is true and improve prediction performance. Furthermore, Iterlogic-E has good interpretability, which allows us to understand the reason behind the inferred conclusion.

Table 6.
A case study with 4 conclusions (true or false as predicted by Iterlogic-E), which are reasoned on by 2 rules from the FB15K dataset. The score change indicates the impact on the model prediction score before and after adding rule reasoning.
5. Conclusions and Future Work
This paper proposes a novel framework that iteratively learns logical rules and embeddings, which models the conclusion labels as 0–1 variables. The proposed Iterlogic-E uses the confidence values of rules and the context of the KG to eliminate the uncertainty of the conclusion in the stage of learning embeddings. Specifically, our method is based on iterative learning, which not only supplements conclusions but also filters incorrect conclusions, resulting in a good balance between efficiency and scalability. The evaluation of benchmark KGs demonstrates that the method can learn correct conclusions and improve against a variety of strong baselines. In the future, we would like to explore how to use embeddings to learn better rules and rule confidences than AMIE+. Additionally, we will continuously explore more advanced models to integrate rules and KGEs for knowledge reasoning.
Author Contributions
Conceptualization, Y.L. and S.H.; methodology, Y.L. and S.H.; software, Y.L.; validation, Y.L.; formal analysis, Y.L., K.L. and J.Z.; investigation, Y.L.; resources, K.L. and J.Z.; data curation, Y.L.; writing—original draft preparation, Y.L.; writing—review and editing, Y.L., S.H., K.L. and J.Z.; visualization, Y.L.; supervision, K.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets in this study can be found here: https://github.com/StudyGroup-lab/SLRE/tree/master/datasets (accessed on 21 September 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Berant, J.; Chou, A.; Frostig, R.; Liang, P. Semantic parsing on freebase from question-answer pairs. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013; pp. 1533–1544. [Google Scholar]
- Huang, X.; Zhang, J.; Li, D.; Li, P. Knowledge graph embedding based question answering. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining, Melbourne, VIC, Australia, 11–15 February 2019; pp. 105–113. [Google Scholar]
- Wang, X.; Wang, D.; Xu, C.; He, X.; Cao, Y.; Chua, T.S. Explainable reasoning over knowledge graphs for recommendation. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; pp. 5329–5336. [Google Scholar]
- Cao, Y.; Wang, X.; He, X.; Hu, Z.; Chua, T.S. Unifying knowledge graph learning and recommendation: Towards a better understanding of user preferences. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 151–161. [Google Scholar]
- Auer, S.; Bizer, C.; Kobilarov, G.; Lehmann, J.; Cyganiak, R.; Ives, Z. Dbpedia: A nucleus for a web of open data. In Proceedings of the International Semantic Web Conference, Busan, Republic of Korea, 1–15 November 2007; pp. 722–735. [Google Scholar]
- Bollacker, K.; Evans, C.; Paritosh, P.; Sturge, T.; Taylor, J. Freebase: A collaboratively created graph database for structuring human knowledge. In Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data, Vancouver, BC, Canada, 10–12 June 2008; pp. 1247–1250. [Google Scholar]
- Carlson, A.; Betteridge, J.; Kisiel, B.; Settles, B.; Hruschka, E.; Mitchell, T. Toward an architecture for never-ending language learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Atlanta, GA, USA, 11–15 July 2010. [Google Scholar]
- Ji, S.; Pan, S.; Cambria, E.; Marttinen, P.; Yu, P.S. A survey on knowledge graphs: Representation, acquisition and applications. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 494–514. [Google Scholar] [CrossRef] [PubMed]
- Taskar, B.; Abbeel, P.; Wong, M.F.; Koller, D. Relational markov networks. Introd. Stat. Relational Learn. 2007, 175, 200. [Google Scholar]
- Galárraga, L.A.; Teflioudi, C.; Hose, K.; Suchanek, F. Amie: Association rule mining under incomplete evidence in ontological knowledge bases. In Proceedings of the 22nd International Conference on World Wide Web, Rio de Janeiro, Brazil, 13–17 May 2013; pp. 413–422. [Google Scholar]
- Giarratano, J.C.; Riley, G. Expert Systems; PWS Publishing: Boston, MA, USA, 1998. [Google Scholar]
- Jackson, P. Introduction to Expert Systems; Addison-Wesley Longman Publishing: Boston, MA, USA, 1986. [Google Scholar]
- Nickel, M.; Murphy, K.; Tresp, V.; Gabrilovich, E. A review of relational machine learning for knowledge graphs. Proc. IEEE 2016, 104, 11–33. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, Z.; Wang, B.; Guo, L. Knowledge graph embedding: A survey of approaches and applications. IEEE Trans. Knowl. Data 2017, 29, 2724–2743. [Google Scholar] [CrossRef]
- Pujara, J.; Augustine, E.; Getoor, L. Sparsity and noise: Where knowledge graph embeddings fall short. In Proceedings of the 2017 Conference on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, 7–11 September 2017; pp. 1751–1756. [Google Scholar]
- Zhang, W.; Paudel, B.; Wang, L.; Chen, J.; Zhu, H.; Zhang, W.; Bernstein, A.; Chen, H. Iteratively learning embeddings and rules for knowledge graph reasoning. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2366–2377. [Google Scholar]
- Zhang, J.; Li, J. Enhanced knowledge graph embedding by jointly learning soft rules and facts. Algorithms 2019, 12, 265. [Google Scholar] [CrossRef]
- Guo, S.; Li, L.; Hui, Z.; Meng, L.; Ma, B.; Liu, W.; Wang, L.; Zhai, H.; Zhang, H. Knowledge graph embedding preserving soft logical regularity. In Proceedings of the 29th ACM International Conference on Information & Knowledge Management, Shanghai, China, 3–7 November 2014; pp. 425–434. [Google Scholar]
- Hájek, P. Metamathematics of Fuzzy Logic, Volume 4 of Trends in Logic; Kluwer: Boston, MA, USA, 1998. [Google Scholar]
- Galárraga, L.; Teflioudi, C.; Hose, K.; Suchanek, F.M. Fast rule mining in ontological knowledge bases with AMIE+. VLDB J. 2015, 24, 707–730. [Google Scholar] [CrossRef]
- Richardson, M.; Domingos, P. Markov logic networks. Mach. Learn. 2006, 62, 107–136. [Google Scholar] [CrossRef]
- Bordes, A.; Usunier, N.; Garcia-Duran, A.; Weston, J.; Yakhnenko, O. Translating embeddings for modeling multi-relational data. In Proceedings of the 26th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 5–8 December 2013; pp. 1–9. [Google Scholar]
- Yang, S.; Tian, J.; Zhang, H.; Yan, J.; He, H.; Jin, Y. Transms: Knowledge graph embedding for complex relations by multidirectional semantics. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence (IJCAI-19), Macao, China, 10–16 August 2019; pp. 1935–1942. [Google Scholar]
- Sun, Z.; Deng, Z.H.; Nie, J.Y.; Tang, J. Rotate: Knowledge graph embedding by relational rotation in complex space. arXiv 2019, arXiv:1902.10197. [Google Scholar]
- Yang, B.; Yih, W.; He, X.; Gao, J.; Deng, L. Embedding entities and relations for learning and inference in knowledge bases. arXiv 2014, arXiv:1412.6575. [Google Scholar]
- Trouillon, T.; Welbl, J.; Riedel, S.; Gaussier, É.; Bouchard, G. Complex embeddings for simple link prediction. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2071–2080. [Google Scholar]
- Liu, H.; Wu, Y.; Yang, Y. Analogical inference for multi-relational embeddings. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 2168–2178. [Google Scholar]
- Nickel, M.; Rosasco, L.; Poggio, T. Holographic embeddings of knowledge graphs. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Schlichtkrull, M.; Kipf, T.N.; Bloem, P.; Van DenBerg, R.; Titov, I.; Welling, M. Modeling relational data with graph convolutional networks. In Proceedings of the Semantic Web: 15th International Conference, ESWC 2018, Heraklion, Crete, Greece, June 3–7, 2018, Proceedings 15; Springer International Publishing: Cham, Switzerland, 2018; pp. 593–607. [Google Scholar]
- Dettmers, T.; Minervini, P.; Stenetorp, P.; Riedel, S. Convolutional 2d knowledge graph embeddings. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–3 February 2018. [Google Scholar]
- Guo, L.; Sun, Z.; Hu, W. Learning to exploit long-term relational dependencies in knowledge graphs. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 10–15 June 2019; pp. 2505–2514. [Google Scholar]
- Shang, C.; Tang, Y.; Huang, J.; Bi, J.; He, X.; Zhou, B. End-to-end structure-aware convolutional networks for knowledge base completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Hilton, HI, USA, 27 January–1 February 2019; pp. 3060–3067. [Google Scholar]
- Shi, B.; Weninger, T. Proje: Embedding projection for knowledge graph completion. In Proceedings of the AAAI Conference on Artificial Intelligence, Hilton, CA, USA, 4–9 February 2017. [Google Scholar]
- Wang, Q.; Huang, P.; Wang, H.; Dai, S.; Jiang, W.; Liu, J.; Lyu, Y.; Zhu, Y.; Wu, H. Coke: Contextualized, knowledge, graph, embedding. arXiv 2019, arXiv:1911.02168. [Google Scholar]
- Guo, S.; Wang, Q.; Wang, B.; Wang, L.; Guo, L. Semantically smooth knowledge graph embedding. In Proceedings of the 53rd Annual Meeting of the Association for Computational Linguistics and the 7th International Joint Conference on Natural Language Processing, Beijing, China, 26–31 July 2015; pp. 84–94. [Google Scholar]
- Xie, R.; Liu, Z.; Sun, M. Representation learning of knowledge graphs with hierarchical types. In Proceedings of the 25th International Joint Conference on Artificial Intelligence (IJCAI-16), Palo Alto, CA, USA, 9–15 July 2016; pp. 2965–2971. [Google Scholar]
- Hao, J.; Chen, M.; Yu, W.; Sun, Y.; Wang, W. Universal representation learning of knowledge bases by jointly embedding instances and ontological concepts. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1709–1719. [Google Scholar]
- Fatemi, B.; Ravanbakhsh, S.; Poole, D. Improved knowledge graph embedding using background taxonomic information. In Proceedings of the AAAI Conference on Artificial Intelligence, Hilton, HI, USA, 27 January–1 February 2019; pp. 3526–3533. [Google Scholar]
- Veira, N.; Keng, B.; Padmanabhan, K.; Veneris, A.G. Unsupervised embedding enhancements of knowledge graphs using textual associations. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI-19), Macao, China, 10–16 August 2019; pp. 5218–5225. [Google Scholar]
- Niu, G.; Li, B.; Zhang, Y.; Pu, S. CAKE: A Scalable Commonsense-Aware Framework For Multi-View Knowledge Graph Completion; ACL: Stroudsburg, PA, USA, 2022; pp. 2867–2877. [Google Scholar]
- Zhang, Z.; Cai, J.; Zhang, Y.; Wang, J. Learning hierarchy-aware knowledge graph embeddings for link prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 3065–3072. [Google Scholar]
- Guo, S.; Wang, Q.; Wang, L.; Wang, B.; Guo, L. Jointly embedding knowledge graphs and logical rules. In Proceedings of the 2016 Conference on Empirical Methods in Natural Language Processing, Austin, TX, USA, 1–5 November 2016; pp. 192–202. [Google Scholar]
- Nayyeri, M.; Xu, C.; Alam, M.M.; Yazdi, H.S. LogicENN: A Neural Based Knowledge Graphs Embedding Model with Logical Rules. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 7050–7062. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Rong, E.; Zhuo, H.; Zhu, H. Embedding knowledge graphs based on transitivity and asymmetry of rules. In Proceedings of the Advances in Knowledge Discovery and Data Mining: 22nd Pacific-Asia Conference, PAKDD 2018, Melbourne, VIC, Australia, June 3–6, 2018, Proceedings, Part II 22; Springer International Publishing: Cham, Switzerland; pp. 141–153.
- Guo, S.; Wang, Q.; Wang, L.; Wang, B.; Guo, L. Knowledge graph embedding with iterative guidance from soft rules. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Qu, M.; Tang, J. Probabilistic logic neural networks for reasoning. In Proceedings of the Advances in Neural Information Processing Systems 32: Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Ding, B.; Wang, Q.; Wang, B.; Guo, L. Improving knowledge graph embedding using simple constraints. arXiv 2018, arXiv:1805.02408. [Google Scholar]
- Yang, J.; Ying, X.; Shi, Y.; Tong, X.; Wang, R.; Chen, T.; Xing, B. Knowledge Graph Embedding by Adaptive Limit Scoring Loss Using Dynamic Weighting Strategy. arXiv 2022, arXiv:2202.13785. [Google Scholar]
- Xu, X.; Feng, W.; Jiang, Y.; Xie, X.; Sun, Z.; Deng, Z. Dynamically pruned message passing networks for large-scale knowledge graph reasoning. arXiv 2019, arXiv:1909.11334. [Google Scholar]
- De Raedt, L.; Kersting, K. Probabilistic inductive logic programming. In Probabilistic Inductive Logic Programming: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–27. [Google Scholar]
- Lin, Y.; Liu, Z.; Luan, H.; Sun, M.; Rao, S.; Liu, S. Modeling relation paths for representation learning of knowledge bases. arXiv 2015, arXiv:1506.00379. [Google Scholar]
- Minervini, P.; Costabello, L.; Muñoz, E.; Novácek, V.; Vandenbussche, P. Regularizing knowledge graph embeddings via equivalence and inversion axioms. In Proceedings of the Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2017, Skopje, Macedonia, September 18–22, 2017, Proceedings, Part I 10; Springer International Publishing: Cham, Switzerland, 2017; pp. 668–683. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).