Accelerating Pattern Matching Using a Novel Multi-Pattern-Matching Algorithm on GPU

Abstract

Nowadays, almost all network traffic is encrypted. Attackers hide themselves using this traffic and attack over encrypted channels. Inspections performed only on packet headers and metadata are insufficient for detecting cyberattacks over encrypted channels. Therefore, it is important to analyze packet contents in applications that require control over payloads, such as content filtering, intrusion detection systems (IDSs), data loss prevention systems (DLPs), and fraud detection. This technology, known as deep packet inspection (DPI), provides full control over the communication between two end stations by keenly analyzing the network traffic. This study proposes a multi-pattern-matching algorithm that reduces the memory space and time required in the DPI pattern matching compared to traditional automaton-based algorithms with its ability to process more than one packet payload character at once. The pattern-matching process in the DPI system created to evaluate the performance of the proposed algorithm (PA) is conducted on the graphics processing unit (GPU), which accelerates the processing of network packets with its parallel computing capability. This study compares the PA with the Aho-Corasick (AC) and Wu–Manber (WM) algorithms, which are widely used in the pattern-matching process, considering the memory space required and throughput obtained. Algorithm tables created with a dataset containing 500 patterns use 425 and 688 times less memory space than those of the AC and WM algorithms, respectively. In the pattern-matching process using these tables, the PA is 3.5 and 1.5 times more efficient than the AC and WM algorithms, respectively.

1. Introduction

DPI provides an in-depth analysis of packets passing through a specific network point—usually a router or switch—and makes some decisions based on the inspection results. The method is called deep inspection because the inspection covers not only packet headers but also packet payloads. As a result of DPI, which makes it possible to detect malware signatures and network anomalies that might be attacks, the attack pattern, including the attack order, path, and techniques, can be identified [1].

The DPI process comprises two stages: recognition and action. Recognition is the process of examining the packet and discovering its hidden features. These features can be application protocols, viruses, worms, or specifically formatted data such as phone and credit card numbers. An example of the recognition process is the IDS, which compares the packet payload content with a predefined set of signatures or patterns to detect malware. DPI can serve alone in the IDS, or it can be a hybrid system component by combining with techniques such as artificial intelligence (AI). The anomaly-based IDS has an initial stage in which data are collected about typical behaviors of the observed system. The IDS alerts us according to a predetermined threshold value when it detects suspicious behavior. Unlike the DPI-based method, this AI-based technique can detect unknown attacks. As there may be deviations from the threshold value, this technique has an extremely high false-positive rate. It also has a relatively high false-negative rate, as attacks may show slight deviations within the norm. The hybrid IDS model, created by combining the anomaly-based and DPI-based techniques, aims to set a balance between the problems of the DPI-based (high storage cost and limited attack detection) and the anomaly-based (high computational costs and false-positive alarms) techniques [2]. While the DPI-based technique in the hybrid scheme is employed to detect known attacks, the anomaly-based technique detects unknown attacks [3]. The action process comes after the DPI recognition. This stage might cover operations such as keeping log records for network analysis or dropping from the network for security [4]. Unlike the IDS, the intrusion prevention system (IPS) is built for stopping or preventing an attack and represents the action process. Network traffic showing complex behavior encounters sophisticated cyberattacks. Systems developed against these attacks are generally in integrated forms, and these structures are known as intrusion detection and prevention systems (IDPSs).

Data analysis on modern communication systems and networks involves difficulties such as providing accurate analysis results and the effective processing of big data in real-time. Especially in cellular networks, the network traffic pattern exhibits complex behavior due to device mobility and network heterogeneity caused by different network architectures. In addition, the increasing number of new systems, services, and malware applications has grown the signature sets that need to be examined by DPI. As a result, large and complex signature sets, increasing the computational complexity and implementation times, reduce overall DPI performance [5].

The collection and evaluation of heterogeneous network traffic resulting from increasing network complexity require efficient mechanisms created by designing scalable and distributed applications that handle the real-time analysis of large amounts of data. However, traditional approaches using multi-core CPUs to analyze network traffic fall short of meeting processing speed requirements. Many techniques have been proposed to accelerate the processing of network packets in DPI applications. In order to achieve a high matching speed with device parallelism, hardware-based acceleration methods employ special-purpose hardware such as the field-programmable gate array (FPGA), ternary content-addressable memory (TCAM), application-specific integrated circuit (ASIC) and graphics processing unit (GPU) [6].

In DPI operations executed using the traditional deterministic finite automata (DFA), all transitions of all states in the automaton are stored in different memory entries. As the pattern set grows, the size of the state transition table used in the pattern-matching process increases. This makes the cache space useless for larger state transition tables. Also, the DPI-matching process is computationally intensive and time-consuming as each byte in the packet payload is processed individually. Accordingly, it is imperative to develop well-performing systems for DPI applications that require high computational complexity and memory space [7].

This study proposes a multi-pattern-matching algorithm that processes more than one packet byte at once to reduce the memory space and time required in the DPI pattern-matching process. Since a state can represent more than one byte in the proposed automaton, the number of states is less than that in the traditional DFA. The proposed algorithm (PA) reduces the computational density and the memory space required compared to traditional automaton-based algorithms with its ability to process multiple packet payload characters at once. In addition, a second memory reduction operation is performed by applying the P3FSM [8] approach to the proposed automaton. Instead of storing all the state transitions in different memory entries, only one entry is assigned to every state in the automaton. Thus, the memory space required to store state transitions is reduced. The contributions of this study can be listed as follows:

• Identifying GPU programming difficulties, such as memory access overhead, warp divergence, bank conflict, and misaligned or uncoalesced memory accesses to develop high-performance DPI systems;
• Proposing a multi-pattern-matching algorithm that reduces the memory space required in the pattern-matching process and shortens the pattern-matching time compared to existing DPI algorithms;
• Applying the optimization techniques determined to the created DPI system to overcome the memory access overhead difficulty arising from pattern-matching algorithms during the execution of the DPI process on the GPU platform.

Figure 1 shows the organization of the study. In this direction, the schedule in this study is as follows: Section 2 examines the DPI techniques based on pattern matching and algorithms utilizing these techniques. While the first subtitle of Section 3 details the problem discovered within the scope of the study, the following subtitle addresses the PA in line with the determined problem. Section 4 explains the GPU sensitivities that limit performance in the DPI-matching process in the subheadings. The DPI system created to evaluate the performance of the PA in the DPI-matching process is introduced in the first subtitle of Section 5. Afterward, performance analysis is performed using the Aho-Corasick (AC) [9] and Wu–Manber (WM) [10] algorithms—which are the most used in DPI processes on the GPU—and the PA. The three algorithms are compared, considering the memory space required and throughput obtained in the pattern-matching process. Section 6 compares the PA with the related studies and discusses the difficulties. Finally, Section 7 evaluates the results obtained from applying the PA to the DPI-matching process in line with the problem determined within the scope of the study.

Figure 1. Structure of the paper.

2. Pattern-Matching Algorithms Review

Pattern matching represents content-based recognition, and the recognition process is performed by matching the payload with predefined signatures. Figure 2 shows the DPI techniques based on pattern matching [4,5,11]. Algorithms applying these techniques can also accept regular expressions (REs) that can represent numerous strings as input besides a string set of predefined signatures in the pattern-matching process.

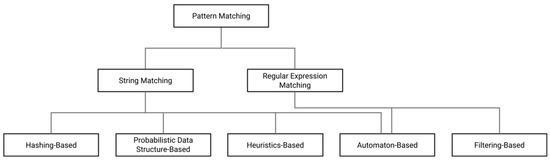
Figure 2. Pattern-matching-based DPI techniques.

2.1. Hashing-Based Technique

Hashing-based algorithms [12,13] compare the hash values instead of comparing the packet payload and the pattern character by character. In the study numbered [14], the matching performance of the hashing-based Rabin–Karp (RK) [12] algorithm on IDSs is evaluated. There are also DPI applications in which the matching performance of the parallel application of this algorithm on the GPU is assessed [15,16]. Each thread carries out the algorithm procedure for all patterns, starting from the position corresponding to the thread index in the multi-pattern-matching version of the RK algorithm performed on the GPU. An increase in the number of patterns to be examined requires additional hash calculations for the RK algorithm, and the matching speed decreases in large pattern datasets. Thus, RK is not an efficient algorithm for multi-pattern matching [16].

2.2. Probabilistic-Data-Structure-Based Technique

The bloom filter (BF) [17] is a probabilistic data structure used to represent a set in the membership check. Improved BFs exist to support deletion, provide a better location, or reduce the cost of space [18,19,20]. The quotient filter (QF) [21] that supports deletion requires additional metadata to encode each entry. This requires 10–25% more space than a standard BF. Another probabilistic data structure is the cuckoo filter (CF) [22], in which elements can be dynamically added and removed in O(1) time. The biggest challenge that CF performance comes across is using three hash functions that cause extra computations. The quotient-based cuckoo filter (QCF) [23] performs fewer computations than the standard CF, using only two hash functions.

In many DPI applications, probabilistic data structures have been used as a matching tool [23,24,25,26,27,28]. While the studies numbered [24,26] focus on increasing the system efficiency by reducing the storage space required, the study numbered [25] aims to reduce the overall power consumption of the BF. In another study numbered [27], the results obtained with the real dataset show that the QF achieves higher efficiency (30–75%) and improves the false-positive rate compared to the BF. The system developed in the study numbered [28], in which the CF is used as the DPI-matching tool, provides time savings of 93% compared to the BF and 87% compared to the QF. Another study numbered [23] tries to increase the CF performance with a new proposal called the QCF. Application results show that using the QCF as an identification tool in a DPI system results in time savings of up to 77% in the CF and up to 98% in the BF and QF.

2.3. Heuristics-Based Technique

The basic principle of the heuristic-based approach is to skip as many payload characters as possible by applying predefined rules to speed up the matching process. In this direction, the aim is to obtain a better result than the linear search that checks all the characters item by item. The single-pattern-matching algorithm Boyer-More (BM) [29] and multi-pattern-matching algorithm WM are heuristic-based matching algorithms. Besides the studies using the BM algorithm to detect known patterns of attacks [30,31,32,33], the studies focusing on reducing the number of character comparisons to improve the performance and efficiency of IDSs [34,35,36] are improved versions of the BM algorithm. An important aspect that limits the performance of the BM algorithm is that it cannot process multiple patterns in parallel. In this direction, the WM algorithm developed as an extension of the BM algorithm can simultaneously process more than one pattern.

Wu–Manber Algorithm

The tables used in pattern matching are created by performing basic calculations required for the scanning phase in the preprocessing phase of the WM algorithm. During matching, a window of length m contains the characters to be inspected, and the matching result indicates the next position to which the window should be shifted. The length of the matching window, m, is determined by the shortest pattern length, and the shift distance of the matching window is calculated using the predetermined length of character blocks (usually two or three).

The value B represents the length of the character block, the value m is the length of the matching window, and the value X is the character block at any position in the matching window. $T=t_1,t_2,\dots ,t_n$ denotes the packet payload, n is the length of the packet payload, and the $P=\{p_1,p_2,\dots ,p_n\}$ is the pattern set.

Character blocks of size B are obtained using the first m characters in each pattern. Then, the shift distance values are calculated for each character block and stored in a SHIFT table. Suppose the value X is at the ith index in a SHIFT table. Here, the value i is obtained from hash calculations performed using the character block X. The shift distance is calculated using Equation (1).

$$\mathrm{SHIFT}\left[\mathrm{i}\right]=\left\{\begin{array}{c}\mathrm{m}-\mathrm{B}+1,\mathrm{X} \mathrm{does} \mathrm{not} \mathrm{match} \mathrm{any} \mathrm{pattern}\\ \min \{\mathrm{m}-\mathrm{q}\left[\mathrm{k}\right]={\mathrm{P}}_{\mathrm{j}}\left[\mathrm{q}-\mathrm{B}+\mathrm{k}\right],1\le \mathrm{k}\le \mathrm{B},{\mathrm{P}}_{\mathrm{j}}\in \mathrm{P}\}\end{array}\right.$$

(1)

The q-value in Equation (1) denotes the location where the rightmost of the X-position is.

PREFIX tables serve to distinguish patterns with suffixes carrying identical hash values from each other. The suffix is the character block created with the last B characters of the first m characters of each pattern. The prefix of the first m characters of the patterns is employed instead of the suffix in the hash calculations in the PREFIX_value table. The values obtained as a result of hash calculations performed using the prefix of each pattern are stored in the PREFIX_value table. While the identity value of each pattern is stored in the PREFIX_index table, the PREFIX_size table keeps the number of patterns with the same suffix hash value.

The pattern detection process for the WM algorithm is as follows:

• The matching window is placed to cover the first m characters of the packet payload. In this case, the packet payload pointer t_p represents the suffix character block of the matching window.
• If the pointer value showing the last element of the packet payload is less than or equal to the value of the t_p pointer, the hash value of the suffix character block of the matching window is calculated. Otherwise, the matching process ends in the current packet.
• This hash value is used in the search operation in a SHIFT table. If the shift distance of the character block is 0, it is possible that the matching window can be the first m characters of a pattern, and, in this case, it is possible to go to Step 4 for the prefix hash calculations. Otherwise, the t_p value is increased by the shift distance, and the process returns to Step 2.
• The prefix hash values of patterns with the same suffix hash calculation are compared with the hash value of the prefix character block of T in the matching window.
• The pattern and packet payload are compared byte by byte if a correct comparison is detected in Step 4. If any match is found, the match is saved. The t_p value is increased by one, and the process returns to Step 2.

Let the N value represent the length of the scanned text, P value the number of patterns, and m value the length of the pattern. In this case, M = mP is the length of all patterns. If N ≥ M, calculations on any B-length substring of the pattern are performed once, and a SHIFT table is created in O(M) time. The scanning time of the algorithm depends on whether the shift distance value is greater or less than zero. In the first case, only shift is applied, and no additional workload is required. In the second case, in which more complex calculations occur compared to the first case, linear searches are performed on patterns with the same suffix and prefix hash values.

Strings as many as the pattern count (P = M/m) create a shift distance at the ith index. The number of all possible substrings of B-length is at least 2M. The probability that a random string of length B will generate a shift distance at the ith index is 0 ≤ i ≤ m − B + 1, ≤1/2m, and a hash function is computed in O(B) time. Accordingly, when the shift distance differs from 0, the total work is executed in O(BN/m) time. If there is no match in the hash calculations, the total amount of work is O(B). When the shift distance is 0, and a match is available, linear search is performed on patterns having the same prefix and suffix hash values. This search is performed in O(m) time for a pattern.

Studies [37,38,39,40,41] focusing on reducing the number of CPU cycles by reducing the number of unnecessary matching attempts to improve the performance and efficiency of IDSs are introduced as an improved version of the WM algorithm. In addition, the study numbered [42] is presented as an advanced version of the WM algorithm for reducing short-pattern-induced performance losses that cause short shift distances. Accordingly, it aimed to divide all patterns into different pattern sets by their lengths and to reduce the effects of the performance-reducing short patterns by sequentially processing these groups.

2.4. Automaton-Based Technique

The first step for algorithms implementing the automaton-based technique is creating a finite state machine (FSM) used in the DPI process. An FSM is generated in a pattern-specific fashion before the pattern-matching process, and is employed in the matching process. An FSM consists of a group of nodes called a state, and a set of directed edges with tags that connect the nodes. There is an initial state and a series of acceptance states. Each acceptance state represents one or more patterns. The matching process starts from the initial state and the first byte of the packet payload. When a byte is read from the payload, the process proceeds to the later state according to the edge labels formed related to the current state. If the acceptance state is reached, one or more patterns are detected in the packet payload. In the automaton-based approach, the overall DPI performance highly depends on the pattern-matching efficiency, that is, the efficiency of the FSM [4].

There are two types of FSMs—a nondeterministic finite automata (NFA) and a DFA. Figure 3 shows examples of a DFA and NFA that accept strings ending in “101” from the strings generated using the $\sum \left\{\mathrm{0,1}\right\}$ alphabet. Both FSMs are equivalent in terms of expressive power. The main difference between a DFA and NFA is that any DFA state has a single transition leading to a specific state for each character. On the other hand, any NFA state can have multiple transitions to different states for the same character. Thus, a DFA can have only one active state at any time, while an NFA can have more than one active state. As a result, a DFA has an O(1) time transaction cost while an NFA has an O(n²m) transaction cost. Here, m represents the number of REs, while n represents the average length of the RE. Accordingly, the computation required for pattern detection will be more intensive in an NFA. Also, as seen in Figure 3, there are more transitions in a DFA compared to an NFA. Conversion from an NFA to DFA increases the number of states, resulting in memory consumption as large as O(2^nm). However, memory consumption is only O(mn) for an NFA. This means more memory space is required for DPI applications, in which pattern detection is performed using the DFA structure. As a result, an NFA and DFA have opposite characteristics in their memory bandwidth requirement and computational density. A DFA requires intensive memory, whereas an NFA needs intensive computations. Most current research aims to balance storage and performance [43,44,45].

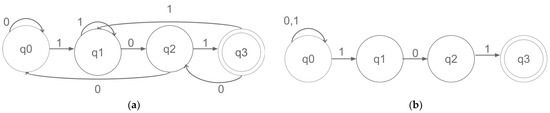
Figure 3. DFA and NFA samples: (a) DFA and (b) NFA.

(0 ∪ 1)*101 can apply as an RE for the automatons shown in Figure 3. In this direction, the DPI application uses an RE which represents strings ending in 101 during the pattern-matching process. On the other hand, a DPI application that accepts a string set with predefined signatures as input employs a pattern set consisting of strings ending in 101, such as 01101, 00101, or 11101. An RE can represent a group of strings, while a string can represent only itself [4]. Because of their powerful and flexible identification capability, REs are widely used in many open-source and commercial DPI applications [46,47]. The studies [48,49,50] focus on building memory-efficient architectures for the RE pattern-matching process. Furthermore, the study numbered [51]—aiming to improve pattern-matching accuracy and speed—has proposed a new RE-based DPI architecture that can handle unordered packets without network packet buffering and stream reassembly.

Aho–Corasick Algorithm

The automaton-based AC algorithm, which accepts fixed-size patterns as an input in the pattern-matching process, is widely used in string matching because of its easy implementation. The AC automaton is created specifically for the pattern set, and pattern detection is performed in the packet payload using this automaton. Figure 4 shows the functions that make up the AC automaton [9].

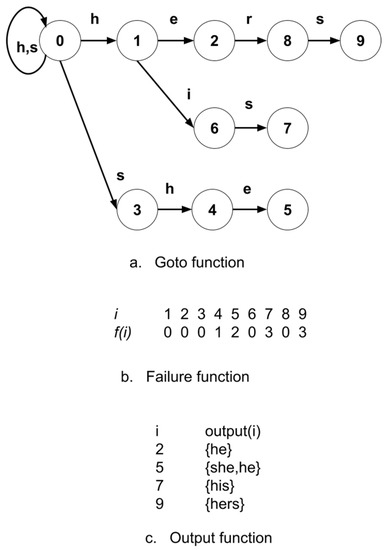
Figure 4. Aho-Corasick functions.

As shown in Figure 4, the AC automaton has three functions a, b, and c, respectively. These functions are goto (g), failure (f), and output (o). State 0 is the initial state for the AC automaton. The transition from a state-character pair to another takes place with the function g. This transition can be successful or unsuccessful. The function f is used if it is not possible to switch to another state using a state–character pair. For example, Figure 4 shows a transition from State 4 to State 5 with the character e. However, if the current character in the packet payload is not equal to e, the g(4,e) transition will not occur, and a failure transition will take place with the f(4) = 1 failure function. Function o is utilized to determine whether there is a currently detected pattern. Accordingly, the indices of all detected patterns are stored using the output function. For example, if the current state is 5, the patterns are determined using the $\mathrm{o}\left(5\right)=\{\mathrm{h}\mathrm{e},\mathrm{s}\mathrm{h}\mathrm{e}\}$ function.

Let value n be the size of the scanned text, value k the total pattern number, value m the total character number in all patterns, and value z the total pattern number in the scanned text. In this case, the AC algorithm detects all patterns in O(n + m + z) time.

The DPI-matching process is computationally intensive and time-consuming, as every byte in the packet payload is processed individually in the AC automaton. Also, storing all state transitions in different memory entries causes cache space to be useless for large state transition tables. As a result of this, the matching speed decreases in large pattern datasets. Compressing a transition table in order to use the cache efficiently is one of the research topics of the AC algorithm. While some improved AC algorithms [52,53,54,55,56,57,58] focus on reducing the memory space required for storing the automaton, some studies [59,60,61] focus on shortening the pattern-matching time. The study numbered [62] proposes a variable-stride AC automaton to reduce the number of memory accesses and energy consumption in the pattern-matching process.

2.5. Filtering-Based Technique

The filtering-based technique removes parts of the target text that do not match the patterns from the matching process. DFC [63] is a filtering-based multi-pattern-matching algorithm that improves pattern-matching performance compared to the AC algorithm by significantly reducing the memory access count and cache losses. Some studies [64,65], which conduct the pattern-matching process in the secure enclave, are examples of using the DFC algorithm. Furthermore, the study numbered [46] has employed a filtering system to exclude the flows that contain no properties of the RE from the pattern-matching process.

3. A Novel Multi-Pattern-Matching Algorithm

In this study, a multi-pattern-matching algorithm that processes more than one packet payload at once is proposed to reduce the memory space required in the pattern-matching process and to shorten the pattern-matching time. This section focuses on the reason for developing an algorithm and then defines the problem. Afterward, details of the developed algorithm are presented.

3.1. Problem Definition

In traditional DFA implementations, such as the AC algorithm, all transitions of a state are stored in different memory entries. The number of states and state transitions in the automaton increases with the growth of the pattern set. Using massive-size automatons for the pattern-matching process causes cache space to be useless for large state transition tables. Also, a transition between two states on the automaton results in the processing of a single character. Since each byte in the packet payload is processed individually, the DPI-matching process using traditional DFA is computationally intensive and time-consuming. Thus, there is a massive necessity for developing well-performing systems for DPI applications with high computational complexity and memory space requirements.

Figure 5 shows the generated AC automaton. It uses the “ABCKLMN”, “ABKXYZMNOP”, and “ABKXYZABCD” sample patterns, and failure transitions have not yet been added to automation. Each transition between states on the automaton results in single-character processing, and a state represents a single-character transition. Therefore, the number of states created for a single pattern is the same as the character length of the pattern. The automaton contains 19 states in total. Even if no failure transitions exist, the state transition table storing 19 transitions requires 19 memory entries.

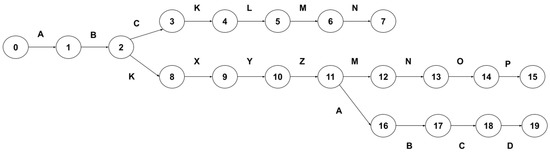
Figure 5. AC automaton created using sample patterns “ABCKLMN”, “ABKXYZMNOP”, and “ABKXYZABCD”.

3.2. Proposed Algorithm

Figure 6 shows the automaton of the pattern-matching algorithm proposed in this study. A state can represent more than one character in the automaton created using the “ABCKLMN”, “ABKXYZMNOP”, and “ABKXYZABCD” sample patterns. In this direction, the automaton created can process more than one packet payload character at once. The character block, which needs to be processed while moving from one state to another, is obtained from the subpattern table. State and character block fields in this table allow proceeding through the automaton. For example, switching from State 1 to State 3 enables the processing of the KXYZ character block (Figure 6).

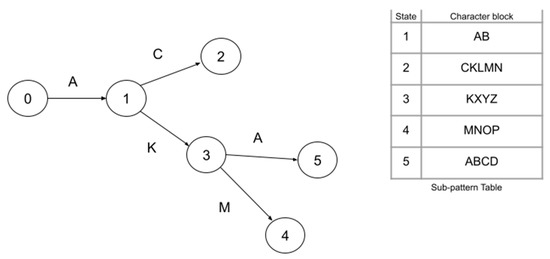
Figure 6. Automaton created using sample patterns “ABCKLMN”, “ABKXYZMNOP”, and “ABKXYZABCD”.

As seen in Figure 6, the number of characters processed in a transition between two states depends on whether the patterns that form the automaton have common roots. For instance, since the common root of the “ABCKLMN”, “ABKXYZMNOP”, and “ABKXYZABCD” patterns is “AB”, the character block consisting of two characters is processed in the transition from State 0 to 1. Again, since the common root of the “ABKXYZMNOP” and “ABKXYZABCD” patterns is “ABKXYZ”, the character block “KXYZ” comprising four characters is processed in the transition from State 1 to 3. If a pattern does not have a common root with other patterns, only one state is formed for the pattern, and the character block consisting of all the characters of the pattern is processed in the transition from State 0 to the created state.

The PA performs the memory reduction twice on the traditional automaton. The first memory reduction operation relates to the ability of the algorithm to process multiple bytes at once. Since a state can represent more than one byte in the proposed automaton, there are fewer states compared to the traditional automaton. The automatons in Figure 5 and Figure 6 are examples of this situation. While the number of states is five (Figure 6) in the PA automaton, it is 19 in the AC automaton (Figure 5) created with the same patterns. As a result, the memory requirement for storing the states in the PA automaton is less than that of the traditional one. The second memory reduction operation is to generate a code representing all the transitions for each state and apply this process to the PA. A code is generated using the P³FSM algorithm. With the P³FSM approach, only one entry is stored in memory for each state in a DFA. This entry stores the possible transitions for the state it represents and is called the state code. Storing only one entry in memory for each state in a DFA instead of storing all DFA transitions in different memory entries makes it possible to store state transitions in a minimum-level memory space. The process of generating state codes has been explained through the automaton created using the “HERS”, “HIS”, and “SHE” sample patterns (Figure 7).

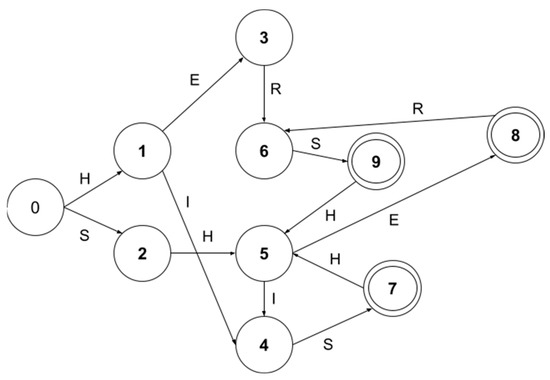
Figure 7. DFA created using sample patterns “HERS”, “HIS”, and “SHE”.

The first step in generating state codes is to obtain groups from the DFA. Groups are formed by combining states leading to the same states. In this direction, the G1[S0][H], G2[S0][S], G3[S1][E], G4[S1, S5][I], G5[S2, S7, S9][H], G6 [S3, S8][R], G7[S4][S], G8[S5][E], and G9[S6][S] groups are formed. The next step after the creation of the groups is the creation of clusters. The C1’[G1, G5][S0, S2, S7, S9][H], C2’[G2, G7, G9][S0, S4, S6][S], C3’[G3, G8][S1, S5][E], C4’[G4][S1, S5][I], and C5’[G6][S3, S8][R] clusters are formed by combining groups with the same character. The next step is to merge all clusters that do not have a common state. Accordingly, the C1[C1’, C2’, C3’, C5’][G1, G5, G2, G7, G9, G3, G8, G6][S0, S2, S7, S9, S4, S6, S1, S5, S3, S8][H, S, E, R], and C2[C4’][G4][S1, S5][I] clusters are formed.

After reducing the number of clusters to two, the next step is to generate group codes (Table 1). A character signature must be specific to each character, start with 0, and increase with each different character. A state signature should begin with 1 for each character and rise one by one for that character. When a different character comes in, it should start with 1 again. The next step after generating group codes is generating state codes (Table 2). All states from the same root are combined. Then, the character and state signatures of the destination states are combined to create a state code for each state. These codes are then used to find the next state based on the given character.

Table 1. Group coding.

Cluster	Character	Group	Char Signature	State Signature
C1	H	G1	00	01
C1	H	G5	00	10
C1	S	G2	01	01
C1	S	G7	01	10
C1	S	G9	01	11
C1	E	G3	10	01
C1	E	G8	10	10
C1	R	G6	11	01
C2	I	G4	0	1

Table 2. State codes.

State	Group	Code
S1	G3, G4	100101
S2	G5	001000
S3	G6	110100
S4	G7	011000
S5	G8, G4	101001
S6	G9	011100
S7	G5	001000
S8	G6	110100
S9	G5	001000

The final step is to create two main tables used for pattern matching. These tables are the character/cluster table (CC) (Table 3) and code table (CO) (Table 4). The index value in the CC table is the failure field. In calculating the offset value, the incrementing process is performed by character repetition. For example, since the H character is repeated twice, the S character’s offset is 2. These two tables then serve for pattern matching. Given a state and a character, Equation (2) shows the formula to calculate the next state.

$${\mathrm{S}}_{\mathrm{i}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{x}}={\mathrm{C}\mathrm{h}}_{\mathrm{o}\mathrm{f}\mathrm{f}\mathrm{s}\mathrm{e}\mathrm{t}}+{\mathrm{S}}_{\mathrm{s}\mathrm{i}\mathrm{g}}$$

(2)

Table 3. Character/cluster table (CC).

Character	Signature	Cluster	Offset	Index
H	00	1	0	1
S	01	1	2	3
E	10	1	5	0
R	11	1	7	0
I	0	2	8	0

Table 4. Code table (CO).

Index	State Code	State
1	100101	S1
2	101001	S5
3	001000	S2
4	001000	S7
5	001000	S9
6	110100	S3
7	110100	S8
8	011100	S6
9	011000	S4

In Equation (2), the S_index value represents the index field in the CO table, the Ch_offset value represents the offset field in the CC table, and the S_sig value represents the state signature in the state code. For example, let us calculate the next state at State 7 while the input character is H. First, the signature of the H character is determined as 00 from the CC table. Then, the signature of State 7 is checked on the CO table. Since equality is achieved, the addition process starts. The calculation of (00) + (10) = 2 reveals the index value in the CO table as 2. The index value of 2 corresponds to State 5 in the CO table, and, thus, a transition to State 5 occurs.

The state code length depends on the number of transitions from the current state to other states. The number of transitions depends on the presence of common roots of the patterns that form the automaton. As seen in Figure 6, since the common root of the “ABCKLMN” pattern with the “ABKXYZMNOP” and “ABKXYZABCD” patterns is “AB”, there is a transition from State 1 to two separate states. Again, since the common root of the “ABKXYZMNOP” and “ABKXYZABCD” patterns is “ABKXYZ”, there is a transition from State 3 to two separate states. A state code of the state with two transitions occurs by combining the information of two transitions. The information about a transition consists of a cluster, character signature, and state signature. If a pattern shares a common root with one or more patterns, a single transition representing all patterns with a common root is produced from State 0. For a pattern that does not share any common root with any pattern, a transition from State 0 is created, which represents only that pattern. The increase in the pattern numbers causes a large number of transitions from State 0, and the length of the code generated to store these transitions increases depending on the pattern numbers. This produces a transition to each cluster within the state code created for State 0. Therefore, identifying the next state process for State 0 differs from the procedure for other cases. The information of a transition within the state code created for State 0 comprises a character and state signature. The cluster information is obtained from the indices of the substate codes. In this respect, a linear search is not required to determine the transition information of the cluster.

Transition information must be obtained from the state code of the current state to provide a suitable transition from the current state to other states with a given character. For this reason, a linear search is performed on the code of the current state. Here, n represents the code length, and the search process over the code is conducted in O(n) time. After detecting the appropriate subcode, the next state is calculated through Equation (2). A transition from one state to another enables the processing of a character block. Therefore, consistency is imperative between the subpattern and the target text. A character block that must be processed is obtained from the subpattern table through the state number of the current state. The m value shows the length of the subpattern. In this case, the target text and subpattern are compared in O(m) time.

4. GPU Performance Issues

Traditional approaches using the CPU have fallen behind in meeting the processing rate requirements with the development of high-speed networks. Unlike the CPU, the GPU reserves more transistors for data processing, instead of the cache and flow control. Therefore, GPUs, which have superior parallel-processing power compared to CPUs, can serve in DPI applications to provide high matching rates [6]. GPU cards consist of a series of streaming multiprocessors (SM), each containing a series of streaming processors (SP). Threads operated on SMs are grouped into blocks divided into smaller units called warps, each with 32 consecutive threads. Each SM creates, manages, programs, and executes threads in warp groups. For example, if there are 128 threads in an SM, four warps can be operated in parallel in this SM. In this respect, a warp is a structure that constitutes the timing unit of the SM. Threads running concurrently on SMs are managed based on a single-instruction multiple-thread (SIMT) architecture. Each SP operates the same command by processing them into different data during any clock cycle.

Despite the computationally intensive and parallel computing capability, the GPU also has performance sensitivities. These sensitivities make it hard to develop well-performing systems for DPI applications with high computational costs and memory requirements. In this subsection, GPU sensitivities that limit performance in the DPI-matching process are explained in subheadings.

4.1. Memory Access Overhead

While threads are running, they can access data in different memory areas. Each memory area has its unique function, accessibility, and access speed. Each thread has its local memory. Each thread block has a shared memory accessible by all threads in the block and has the same lifetime as the block. All threads have access to the same global memory. As with any device memory hierarchy, local memory on the GPU is faster than global memory. Thus, executing the packet-processing process using shared memory instead of global memory shortens the packet-processing time [7]. However, shared memory has less memory capacity than global memory. Therefore, the memory space required in the matching process must not exceed the shared memory capacity so that the packet processing can proceed in shared memory.

4.2. Warp Divergence

All threads in a warp are executed based on the SIMT architecture. Namely, a warp executes a single instruction at once, and, consequently, every thread employs the same instruction in the warp. Computer resources serve efficiently when all threads in a warp execute the same command without causing different code paths to occur. If the threads of a warp are separated by a conditional code path based on the processed data, the warp executes each code path and disables any off-the-path threads. In this case, warp execution efficiency is reduced due to insufficient use of computer resources. When threads in the same warp execute different commands, it is called warp divergence. Control structures such as if, else, and switch in the source code can cause warp divergences. For example, if threads with odd-numbered IDs are forced to execute an if block and the other threads are forced to execute an else block, two code paths will arise in that source code. One of these two code paths is a divergent path. However, the presence of a control structure does not always result in warp divergence. Control structures programmed to execute all threads in a warp in the same path do not cause any warp divergence. Different warps are independently applied regardless of whether they run the same or different code paths.

4.3. Aligned and Coalesced Memory Access

Commands executed on SMs are executed at the warp level. This situation also applies to memory access instructions. All threads in a warp offer a single request containing the address requests of each thread in the warp. This request is performed as one or more memory operations, depending on how the memory address is distributed in the request. Two memory access patterns determine how many memory operations are necessary for a single memory access request. These are aligned memory access and coalesced memory access. For memory access performed using both the L1 and L2 caches, aligned memory access will occur if the first address of the memory request is a multiple of 128. In memory access performed using only the L2 cache, aligned memory access will occur if the first address of the memory request is a multiple of 32. Coalesced memory access occurs when all 32 threads in a warp access consecutive locations of a piece of memory. Ideal memory access is aligned and coalesced memory access. Organizing aligned and coalesced memory operations is critical for maximizing the global memory efficiency. In this case, memory bandwidth or bus utilization is 100%.

4.4. Bank Conflict

As with global memory accesses, access to shared memory also occurs at the warp level. In other words, every access request made by the warp to shared memory takes place in a single operation. In the worst case, each access request to shared memory is executed sequentially in 32 separate processes. Shared memory is divided into 32 equal-sized memory modules (banks) having a simultaneous access pattern to achieve high memory bandwidth. There are 32 threads in a warp, thus 32 banks. When multiple addresses in the shared memory request indicate the same bank of memory, a bank conflict occurs, causing a re-execution of the request. The system divides the memory request with a bank conflict into multiple non-conflicting processes. This situation reduces the effective use of memory bandwidth. For example, if all 32 threads in a warp access different memory locations of a single bank, this memory request is handled by 32 separate memory operations. When all addresses in the shared memory request point to different memory banks, a single memory operation executes this request. This access with no bank conflicts is a parallel access to shared memory. When all threads in a warp request access to the same memory bank, a single memory operation executes this access, and, in this case, bandwidth usage is low.

5. Experimental Results

This section first details the DPI system created to evaluate the performance of the proposed multi-pattern-matching algorithm in the DPI-matching process and then compares the PA with the AC and WM algorithms widely used in the pattern-matching process by the memory space required and throughput obtained.

5.1. Experimental Setup

A DPI system is created to evaluate the performance of the proposed multi-pattern-matching algorithm in the DPI-matching process. The pattern-matching is conducted on the GPU, which accelerated the processing of network packets with its parallel-computing capability. The pattern-matching on the GPU is performed in three steps. Figure 8 shows the steps of the pattern-matching process on the GPU.

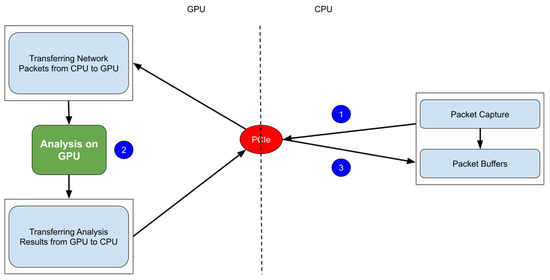
Figure 8. The steps of the pattern-matching process on the GPU.

Network packets are obtained using the libpcap packet capture library created for Unix systems. The first step of the pattern-matching process is transmitting these network packets from the CPU to the GPU memory via PCIe (1). Due to the additional overheads associated with conveying data from the CPU to the GPU, first, all packets are transferred to a buffer, and then the buffer is passed to the GPU. Next, the DPI pattern-matching is executed on the GPU (2). Finally, the pattern-matching results are transferred to the CPU memory via PCIe (3). Table 5 shows the hardware configuration used.

Table 5. Hardware configuration.

Processor	Intel Xeon E5-2640 v4
Memory	32 GB DDR4-2666 4Rx4 ECC RDIMM
GPU	RTX 2080 TI 11 G 352 Bit

The pattern sets used in the analysis are obtained from the SNORT [46] rules, which contained the patterns of network packets containing malicious activities. Table 6 shows the average lengths of the patterns in the datasets containing different numbers of patterns. The lengths of these patterns range from 10 to 171 bytes. After obtaining the patterns, the network packets containing these patterns in their payload are created to obtain a dataset. Each network packet in the dataset is 256 bytes and generated by adding a randomly chosen pattern to a random packet payload location. This dataset, consisting of network packets containing malicious activities, is used in the analysis to evaluate the performance of the PA in the DPI-matching process.

Table 6. Statistics of pattern lengths.

Pattern Count	Average Pattern Length
100	30.42
200	29.44
300	29.91
400	29.98
500	30.70

5.2. Memory Analysis

In this subsection, tables used in the pattern-matching processes of the AC algorithm, WM algorithm, and the algorithm proposed by this study are detailed, and the memory space required by these tables specially created for datasets containing different numbers of patterns is determined. Finally, the three algorithms are compared considering the memory space required in the pattern-matching process.

5.2.1. Aho-Corasick Algorithm

In order to carry out the pattern-matching process on the AC automaton, the system employs three tables in the memory: a state transition table, a failure transition table, and an output table. The state transition table determines existing transitions from the current state to another state for a given character in the AC automaton. If there is no transition to another state, the failure transition table restarts the pattern detection process. The output table serves to understand whether there is a detected pattern in the current state. Each transition in the automaton has an entry in the state transition table, while each state has a failure transition and output information in the memory. Table 7 shows the memory space required for the AC tables specially created for datasets containing different numbers of patterns.

Table 7. Memory space required for the AC tables.

Pattern Count	AC (KB)
100	2625.512
200	5181.12
300	7785.044
400	10,515.412
500	13,271.48

5.2.2. Wu–Manber Algorithm

In the pattern-matching process with the WM algorithm, the shift distance of each character block belonging to the patterns is stored in a SHIFT table. Using this distance, the character block of any pattern is searched over the target text. PREFIX tables are used to distinguish patterns containing suffixes with the same hash values. If the suffix and prefix hash values on the target text are correct for one or more patterns, the target text and candidate patterns are compared character by character to complete the pattern detection. Patterns must be held in the GPU memory to perform this comparison. All patterns have been combined within a character array on the GPU memory. The starting and ending points of each pattern in the character array must be known in order to obtain a pattern from this array. Therefore, an integer array is created, besides the character array. The number of entries in the WM tables increases with the number of patterns and the number of characters in the alphabet that form the pattern set. Table 8 shows the memory space required for the WM tables specially created for datasets containing different numbers of patterns.

Table 8. Memory space required for the WM tables.

Pattern Count	WM (KB)
100	4331.49
200	8619.935
300	12,908.622
400	17,197.241
500	21,486.196

5.2.3. Proposed Algorithm

In the pattern-matching process with the PA, the CC and CO tables must be held in the GPU memory. All state codes kept in the CO table are combined into a character array on the GPU memory. The starting and ending points of each code in the character array are kept in an integer array. Moreover, the character block that needed to be processed when moving from one state to another on the automaton is obtained from the subpattern table. All subpatterns are combined into a character array on the GPU memory so that the subpatterns in the target text and subpattern table can be compared character by character. The starting and ending points of each subpattern in the character array are kept in an integer array. Table 9 shows the memory space required for the PA tables specially created for datasets containing different numbers of patterns.

Table 9. Memory space required for the PA tables.

Pattern Count	PA (KB)
100	8.161
200	14.097
300	19.615
400	25.281
500	31.218

5.2.4. Comparison

Table 10 shows the comparison of the number of states in the automaton of the AC algorithm and the PA. The number of states in the automaton of the PA is considerably fewer than that in the AC automaton. Each transition between states in the AC automaton results in processing only a single character. That is, a single state represents a single character transition. Therefore, the number of states created for a pattern is equal to the character length of the pattern. However, the fact that a state can represent more than one byte in the automaton of the PA causes the number of states to be much fewer than that in the automaton of the AC. As a result, the memory requirement for storing the states is less in the proposed automaton. Table 11 compares the memory space required for AC, WM, and the PA in the pattern-matching process. As shown in the table, the memory space required for the PA is much less than that for the other two algorithms.

Table 10. Comparison of the number of states in the automaton of the AC algorithm and PA.

Pattern Count	AC	PA
100	2554	121
200	5040	264
300	7573	395
400	10,229	527
500	12,910	667

Table 11. Comparison of memory space required in the pattern-matching process for AC, WM, and PA.

Pattern Count	AC (KB)	WM (KB)	PA (KB)
100	2625.512	4331.49	8.161
200	5181.12	8619.935	14.097
300	7785.044	12,908.622	19.615
400	10,515.412	17,197.241	25.281
500	13,271.48	21,486.196	31.218

5.3. Throughput Analysis

Despite the GPUs’ superior parallel-processing power, the data transfer latency between the CPU and GPU hides the overall performance of the pattern-matching algorithms. For this reason, this study does not cover optimizations to minimize the data transfer costs between the CPU and GPU. The focus of the study is the throughput of the GPU core responsible for executing the pattern-matching process, and this throughput is calculated using Equation (3). Value n represents the total number of bits of the target text of n characters in length (bytes), while T_gpu indicates the execution time of the pattern-matching process on the GPU.

$$\mathrm{T}\mathrm{h}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{g}\mathrm{h}\mathrm{p}\mathrm{u}\mathrm{t}=\frac{\mathrm{n}}{{\mathrm{T}}_{\mathrm{g}\mathrm{p}\mathrm{u}}}$$

(3)

The previous subsection compares the memory space required during the pattern-matching process for AC, WM, and the PA. The memory space required for the AC and WM algorithms is too large to fit in the 64 KB shared memory of the GPU used in the pattern-matching tests (Table 11). For this reason, the necessary tables are kept in global memory in all pattern-matching tests performed with these two algorithms. However, the memory space required by the tables of the PA is large enough to fit in shared memory. Therefore, there are pattern-matching tests in which the tables required for the PA are kept in global memory, as well as the pattern-matching tests in which the tables are kept in shared memory.

In this subsection, throughputs obtained from the pattern-matching tests of AC, WM, and the PA are determined using datasets containing different numbers of patterns. Then, factors limiting the pattern-matching performance of these algorithms are discussed using the obtained results. Finally, throughputs obtained for the three algorithms in the pattern-matching tests are compared.

5.3.1. Aho-Corasick Algorithm

Algorithm 1 shows pseudo-code of the parallel implementation of the AC algorithm that executes the pattern-matching process using multiple CUDA threads. Here, InChar represents the character on the target text, cs represents the current state, and pos represents the position on the target text. Pattern-matching tests of the AC algorithm are performed in two different versions. In one of them, network packets are held in global memory (AC), while in the other, network packets are held in shared memory (AC-ps). Figure 9 and Figure 10, respectively, compare the packet-processing times and throughputs of these pattern-matching versions applied to datasets with different numbers of patterns.

Algorithm 1 Aho-Corasick algorithm

input: InChar, cs, pos

while pos is less than 256 do

GetNextState(cs, InChar);

while cs is equal -1 do

GetStateFailure(cs);

end while

GetNextState(cs, InChar);

GetOutputState(cs);

if output is greater than 0 then

UpdateDetectedPatternCount();

end if

end while

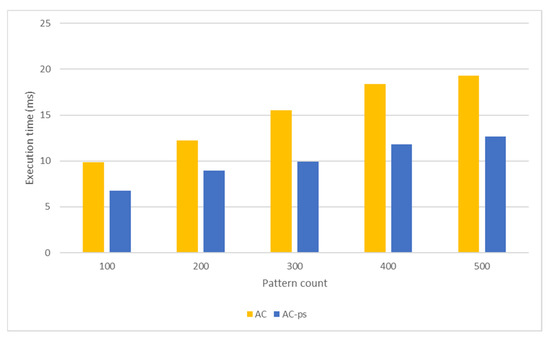
Figure 9. Comparison of the packet-processing times obtained from the pattern-matching tests performed using the AC algorithm.

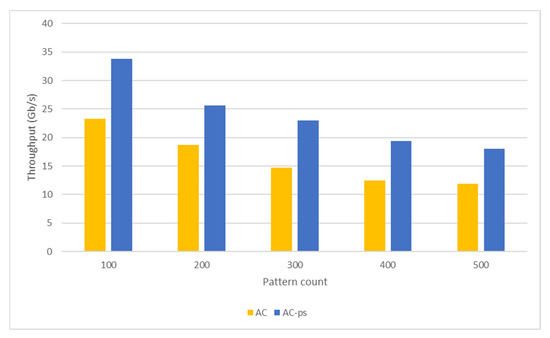
Figure 10. Comparison of the throughputs obtained from the pattern-matching tests performed using the AC algorithm.

A pattern-matching performance of the AC algorithm is associated with the memory space required by the algorithm and access overheads. An increasing number of examined patterns also increases the memory space required by the algorithm in the pattern-matching process. Therefore, applying the AC algorithm in the pattern-matching process makes the cache space useless for larger state transition tables. As a result, the pattern-matching speed drops for large pattern datasets. Local memory in the GPU have less access latency than global memory. Accordingly, processing packets in shared memory instead of global memory will reduce the packet-processing time (Figure 9). Hence, the tests produce a higher throughput when the network packets are in shared memory (Figure 10).

Coalesced memory access occurs when all 32 threads in a warp access consecutive locations of a piece of memory. While detecting the patterns using the AC algorithm, threads do not act depending on the access patterns. These threads access random locations of the AC tables to find the next state based on the character on the target text. This causes uncoalesced memory accesses. Moreover, the absence of any access pattern during the pattern detection causes bank conflicts on shared memory.

5.3.2. Wu–Manber Algorithm

Algorithm 2 shows pseudo-code of the parallel implementation of the WM algorithm that executes the pattern-matching process using multiple CUDA threads. Here, pos represents the current position on the target text, m represents the length of the shortest pattern in the pattern set, and patSize represents the number of patterns in the pattern set. Pattern-matching tests of the WM algorithm are performed in two different versions. In one of them, network packets are held in global memory (WM), while in the other version, network packets are held in shared memory (WM-ps). Figure 11 and Figure 12, respectively, compare the packet-processing times and throughputs of these pattern-matching versions applied to datasets with different numbers of patterns.

Algorithm 2 Wu–Manber algorithm

input: pos, m, patSize

if pos is greater than m-1 or equal to m-1 then

targetTextSuffixHash=ComputeTargetTextSuffixHash(pos);

GetShift(targetTextSuffixHash);

if shift is equal to 0 then

targetTextPrefixHash=ComputeTargetTextPrefixHash(pos,m);

GetNumOfPatSameSuffixHashFromPrefixSizeTable(targetTextSuffixHash);

for count value from 0 to number of patterns with the same suffix hash calculation do

GetPrefixHashFromPrefixValueTable(targetTextSuffixHash,patSize,count);

if prefix hash of target text and prefix hash from prefix value table are equal then

GetPatIndexFromPrefixIndexTable(targetTextSuffixHash,patSize,count);

if Target text and pattern text are equal then

UpdateDetectedPatternCount();

end if

end if

end for

end if

end if

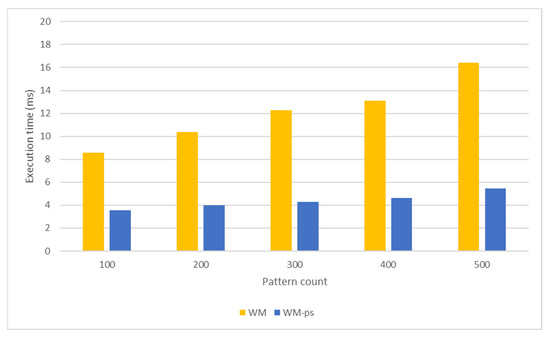
Figure 11. Comparison of the packet-processing times obtained from the pattern-matching tests performed using the WM algorithm.

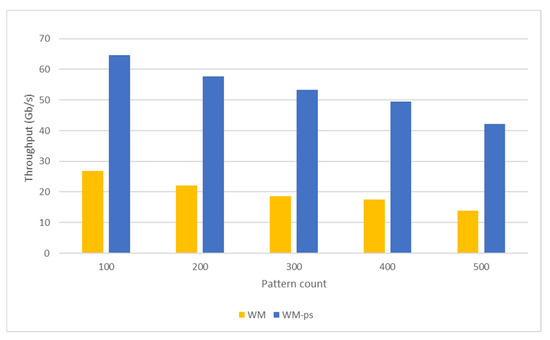
Figure 12. Comparison of the throughputs obtained from the pattern−matching tests performed using the WM algorithm.

Similar to the AC algorithm, the pattern-matching performance of the WM algorithm is also related to the memory space required by the algorithm and access overheads. In addition, an increase in the number of patterns represented by a SHIFT table also negatively affects the performance of the WM algorithm. Patterns with the same suffix hash value fall into the same address in a SHIFT table. An increasing number of the examined patterns also increases the number of patterns in the same address space in a SHIFT table. The algorithm has to sequentially compare patterns in the same address space in a SHIFT table and with the same prefix hash value with the target text to detect a match. As a result, the pattern-matching speed drops for large pattern datasets. Executing packet processing in shared memory with shorter access latency instead of global memory reduces the packet-processing time (Figure 11). As a result, the pattern-matching tests processing network packets in shared memory produce a higher throughput (Figure 12).

While detecting patterns using the WM algorithm, threads act independently of access patterns. The values in the tables are placed according to the hash values of the patterns, and the hash values calculated by the different threads differ. This causes uncoalesced memory accesses. Also, the absence of any access pattern during pattern detection causes bank conflicts on shared memory.

5.3.3. Proposed Algorithm

Algorithm 3 shows pseudo-code of the parallel implementation of the PA that executes the pattern-matching process using multiple CUDA threads. Here, InChar represents the character on the target text, cs represents the current state, and pos represents the position on the target text. The pattern-matching process performed using the PA is conducted in three different versions. In the first version, all tables and network packets are held in global memory (PA). In the second version, while network packets are held in shared memory (PA-ps), all tables are held in global memory. In the last version, all tables are held in shared memory and network packets are held in global memory (PA-s). Figure 13 and Figure 14, respectively, compare the packet-processing times and throughputs of these pattern-matching versions applied to datasets with different numbers of patterns.

Algorithm 3 Proposed algorithm

input: CC, CO, InChar, cs, pos

GetCluster(InChar,CC);

if cluster is not equal -1 then

GetCharacterSignature(CO);

GetStateSignature(CO);

GetCharacterSignature(InChar,CC);

if Character signatures of CC and CO are equal then

UpdateState(cs);

while cs is greater than 0 and pos is less than 256 do

if cs has state code then

if Target text and state text are equal then

UpdateInCharPosition(InChar,pos);

GetCluster(InChar,CC);

GetStateCodeLenght(cs);

while State code length is greater than 0 do

GetCharacterSignature(CO);

GetStateSignature(CO);

GetCluster(CO);

GetCharacterSignature(InChar,CC);

if character signatures of CC and CO are equal then

if clusters of CC and CO are equal then

UpdateState(cs);

end if

end if

end while

end if

else

if Target text and state text are equal then

UpdateDetectedPratternCount();

end if

end if

end while

end if

end if

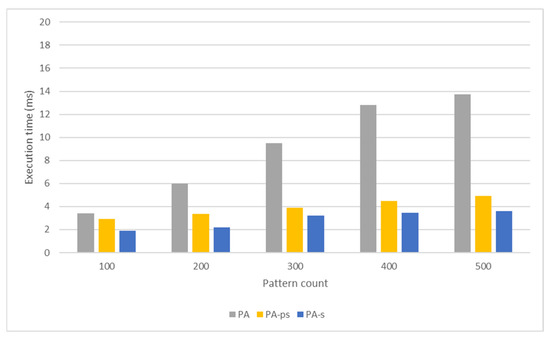
Figure 13. Comparison of the packet-processing times obtained from the pattern-matching tests performed using the PA.

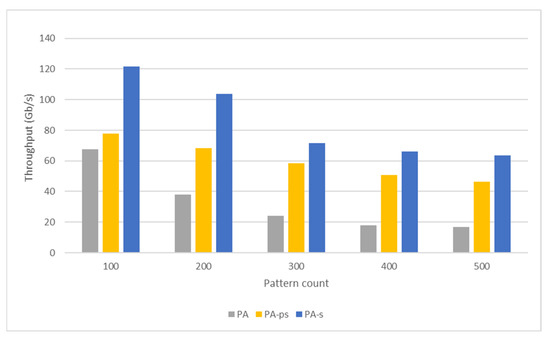
Figure 14. Comparison of the throughputs obtained from the pattern-matching tests performed using the PA.

Similar to the AC and WM algorithms, the pattern-matching performance of the PA is also related to the memory space required by the algorithm and access overheads. In addition, an increase in the number of common-rooted patterns negatively affects performance. An increase in the number of examined patterns increases the number of patterns with a common root, reducing the number of characters processed in the transition between two states. Since each byte in the packet payload is processed individually, the DPI-matching process becomes more computationally intensive and time-consuming. On the other hand, decreasing the number of characters processed in the transition between two states can increase the transition numbers in the automaton, resulting in more complex state codes. In this case, the algorithm sequentially scans all transitions in the state code to determine the appropriate subcode. As a result, the pattern-matching speed drops for large pattern datasets. Also, executing packet processing in shared memory with shorter access latency instead of global memory reduces the packet-processing time (Figure 13). Therefore, the highest throughput is obtained in tests where the tables used in the pattern-matching process are in shared memory (Figure 14). The tests in which only network packets are in shared memory have the second-highest efficiency, while the tests in which all tables and network packets are in global memory have the lowest efficiency.

Threads act independently of access patterns while detecting patterns using the PA. These threads access random positions of the CC and CO tables to determine the next state. This situation causes uncoalesced memory accesses. Also, the absence of any access pattern during the pattern detection causes bank conflicts on shared memory. An increase in the number of examined patterns increases the number of entries in the tables used in the pattern-matching process. This causes more bank conflicts in tests where tables are kept in shared memory. Increasing bank conflicts affect the pattern-matching performance negatively and decrease efficiency.

5.3.4. Comparison

The structure of the AC algorithm, WM algorithm, and the algorithm proposed by this study can cause misaligned and uncoalesced memory access operations. Also, numerous threads are inactive in the parallel region due to warp divergence. These situations decrease the number of active threads per warp and negatively affect the pattern-matching performance. In this direction, the kernel performance can be increased by using shared memory. Figure 15 and Figure 16, respectively, compare the packet-processing times and throughputs of these pattern-matching versions applied to datasets with different numbers of patterns. Shared memory located on the SM has a much lower memory processing latency than global memory. Therefore, processing packets in shared memory instead of global memory will reduce the packet-processing time (Figure 15). As a result, the highest throughput is obtained from the versions using shared memory in the pattern-matching process for all three algorithms (Figure 16).

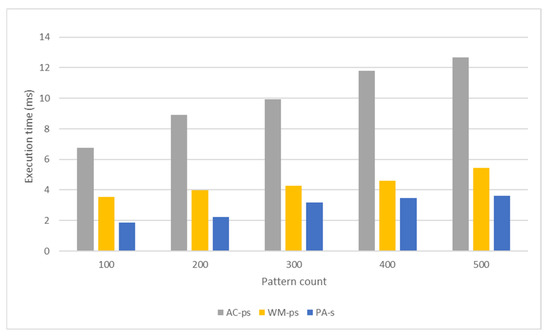
Figure 15. Comparison of the packet-processing times obtained from the pattern-matching tests performed using AC, WM, and PA.

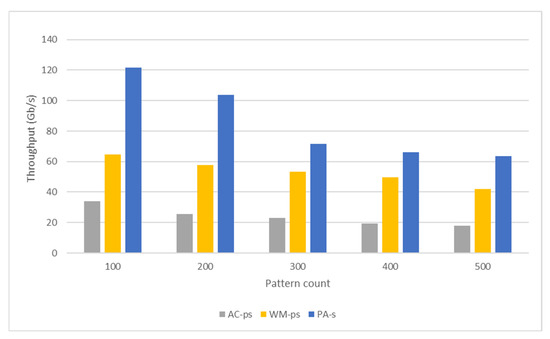
Figure 16. Comparison of the throughputs obtained from the pattern-matching tests performed using AC, WM, and PA.

As seen in Figure 16, the PA achieved the highest throughput among these three algorithms. Similar to the AC and WM algorithms, the pattern-matching performance of the PA is also related to the memory space required by the algorithm and access overheads. However, the memory space required is much less than that of the other two algorithms. This allows efficient use of the cache space and shared memory.

6. Related Work

In DPI applications in which the processing density is high and the speed factor is important, GPU usage is common because of its high computational power and suitability for parallel-computing problems [6,7,66,67,68,69,70,71,72]. GPU-based DPI applications generally emphasize the GPU’s performance sensitivities and aim to maximize the GPU’s parallel-processing capability. As well as GPU sensitivities, there are some studies examining bottlenecks in transferring packets to GPU hardware due to limited PCIe bandwidth [6,67,68,71].

While some studies [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66] have focused on reducing the memory space used, the studies numbered [6,71] aim to increase performance by reducing the processing load of the GPU through a pre-filtering mechanism on the CPU. Because network attacks are often conducted through short-packet payloads [73], long-packet payloads are less likely to be malicious. Also, payload length variety increases the load imbalance between the threads, and this situation negatively affects the DPI performance. The study numbered [71] has designed a pre-filtering mechanism that aims to reduce the payload length variety by filtering long-packet payloads owning harmless content. As an improved version of the study numbered [6] which reduces the processing density on the GPU in addition to data transfer delays, the above study aims to create a more efficient DPI mechanism by examining the performance losses caused by the payload length variety.

The study numbered [70] has removed all failure transitions in the DFA used in the AC pattern-matching process and obtained the parallel failureless AC (PFAC) automaton. In this approach, a separate thread is allocated to each byte of an input stream to identify any pattern starting from the starting position of any thread. In this case, each thread becomes responsible for detecting the pattern starting from that thread’s starting position. Therefore, when a thread cannot find any pattern starting at the starting location, it terminates without a failure transition. This situation causes a load imbalance between the threads and negatively affects the DPI performance.

Carried out using CF on the GPU, the study numbered [72] has detected the global memory parts frequently accessed by threads of the same block and transferred them to shared memory. Thus, it aimed to reduce the execution time using shared memory instead of global memory. This approach only detects memory regions that threads access frequently. Infrequently accessed memory regions are accessed through global memory. Consequently, this approach cannot guarantee that all threads only access shared memory. Therefore, the memory access latency of the study numbered [72] is much higher than that of the study numbered [7], which uses the P³FSM algorithm encoding the DFA state transition table to fit in the shared memory of the GPU.

A Comparison of the Proposed Algorithm with Related Studies

Since the experimental environments created for the DPI-matching process are different from each other, it is difficult to compare the PA with related studies. Using datasets containing different numbers of patterns in distinct structures or executing the matching process on different hardware creates different experimental environments. The study numbered [7] using the P³FSM algorithm—which encodes the AC state transition table to fit in the shared memory of the GPU—is the most relevant to the PA. Therefore, the PA is compared with the study numbered [7], considering the memory space required and throughput obtained in the DPI process.

Table 12 compares the memory space required between the PA tables and the algorithm tables of the study numbered [7]. As seen in the table, the memory space required in the matching process is similar for the two algorithms. In the study numbered [7], the AC state transition table is coded using the P³FSM algorithm, but the number of states in the automaton remained the same. In the PA, the number of states in the automaton is reduced in two memory reduction operations. However, unlike the previous study, since multiple packet payload characters are processed at once, a subpattern table must also be kept in GPU memory. This expands the memory space required by the PA in the pattern-matching process and makes this memory area similar to that in the study numbered [7].

Table 12. Comparison of the memory space required in the pattern-matching process for the PA and the algorithm proposed in the study numbered [7].

Pattern Count	PA (KB)	Study Numbered [7] (KB)
100	8.161	3.04
200	14.097	5.85
300	19.615	14.26
400	25.281	23.79
500	31.218	27.04

The pattern set used in the analysis of the study numbered [7] is obtained from the SNORT rules, and the DPI-matching process is executed using a dataset containing 20 patterns in the shared memory of the GPU. In addition, the K20 GPU hardware served in the pattern-matching process. Matching tests with the PA are performed on a pattern set containing 20 items obtained from the SNORT rules to create a similar experimental environment. The PA-s version of the PA is employed in the tests, which handled the DPI-matching process in the shared memory of the GPU.

Figure 17 compares the pattern-matching tests for the study numbered [7] (1) and this study (1). As seen in the figure, since this study performed the pattern-matching process on the GPU with more cores, and larger memory bandwidth and computing capacity, the throughput of the AC algorithm is higher. Similarly, the throughput of the PA is higher than that of the algorithm in the study numbered [7]. While the increase rate in the throughput of the AC algorithm is 13.21%, this rate is 33.52% for the proposed algorithms. This shows that the PA has a higher throughput than the algorithm in the previous study [7].

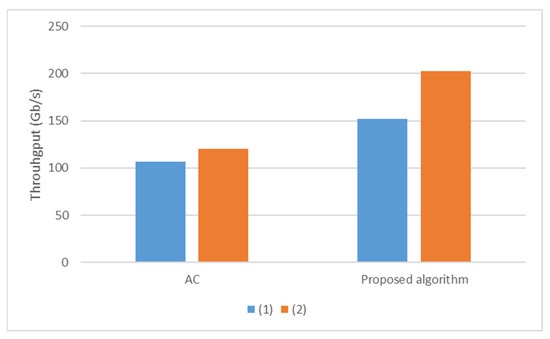
Figure 17. Comparison of the pattern-matching tests for this study and the study numbered [7].

The study numbered [7] reduced the memory space required in the matching process by coding the AC state transition table using the P3FSM approach. This improves the throughput especially for cases in which the DPI-matching process is executed in the shared memory of the GPU, and the throughput becomes higher than that of the AC algorithm. However, matching tables created for larger pattern sets will not fit the GPU’s shared memory. Since it does not change the operation of the AC algorithm, which processes a single character with a transition between two states on the automaton, the algorithm proposed in the study numbered [7] does not improve the throughput for cases where the matching process executes in global memory. However, the PA processes multiple packet payload characters at once. This also improves the throughput when the matching process executes in the global memory of the GPU, and the resulting throughput becomes higher than that of the AC algorithm.

7. Conclusions

This study proposes a multi-pattern-matching algorithm to reduce the memory space required in the pattern-matching process and to shorten the pattern-matching time. Unlike traditional automaton-based algorithms that process each byte in the packet payload, a transition between two states in the PA results in processing a block of characters, not a single character. Accordingly, more than one byte can be represented by a state in the proposed automaton. As a result, the number of states created is less than that in the traditional automaton. Processing multiple packet payload characters at once accelerates the DPI-matching process and reduces the required memory space. Also, instead of storing all state transitions in a table, a code is generated representing all transitions of each state. In this direction, memory reduction operations are performed twice on the traditional automaton through the PA.

AC, WM, and PA tables used in the pattern-matching process on the GPU are created specifically for datasets containing different numbers of patterns, and the memory space required for these tables is determined. Three algorithms are compared, considering the memory space required in the pattern-matching process. The tables of the PA, created specifically for a dataset containing 500 patterns, require 425 times less memory space than those of AC and 688 times less than those of WM. In addition, the pattern-matching test throughputs on the GPU are determined using the AC, WM, and PA datasets containing different pattern numbers. The pattern-matching test using the tables specifically created for a dataset containing 500 patterns shows that the PA is 3.5 times more efficient than AC and 1.5 times more efficient than WM.

The pattern-matching performances of AC, WM, and the PA are related to the memory space required by the algorithms and access overheads. However, the memory space required by the PA is much less than that required by the other two algorithms. This allows efficient use of the cache space and shared memory. The memory spaces required in the pattern-matching process for the AC and WM algorithms are too large to fit the shared memory of the GPU. Therefore, the necessary tables are kept in global memory in all pattern-matching tests performed with these two algorithms. However, the memory space required by the tables created to implement the PA fits in shared memory. This provides a throughput improvement when the DPI-matching process is executed in the shared memory of the GPU.

The PA and the study numbered [7], which encodes the AC state transition table to fit in the shared memory of the GPU, are compared in terms of the memory space required and throughput obtained in the DPI operation. Encoding the AC state transition table reduced the memory space required in the matching process in the study numbered [7]. This provides an improvement in the throughput when the DPI-matching process is executed in the shared memory of GPU. As a result, the throughput becomes higher than the throughput achieved by the AC algorithm. However, matching tables created for larger pattern sets do not fit in the shared memory of the GPU. Since the study numbered [7] does not change the operation of the AC algorithm—which processes each byte in the packet payload one by one—the proposed algorithm does not improve the throughput for cases where the matching process is performed in global memory. However, the PA processes multiple packet payload characters at once. This also provides an improvement in the throughput when the DPI-matching process is executed in the global memory of the GPU, and, as a result, the resulting throughput becomes higher than that of the AC algorithm.