Abstract
The aim of this paper is to analyze the transfer performance of a spacecraft whose primary propulsion system is a diffractive solar sail with active, switchable panels. The spacecraft uses a propellantless thruster that converts the solar radiation pressure into propulsive acceleration by taking advantage of the diffractive property of an electro-optically controlled (binary) metamaterial. The proposed analysis considers a heliocentric mission scenario where the spacecraft is required to perform a two-dimensional transfer between two concentric and coplanar circular orbits. The sail attitude is assumed to be Sun-facing, that is, with its sail nominal plane perpendicular to the incoming sunlight. This is possible since, unlike a more conventional solar sail concept that uses metalized highly reflective thin films to reflect the photons, a diffractive sail is theoretically able to generate a component of the thrust vector along the sail nominal plane also in a Sun-facing configuration. The electro-optically controlled sail film is used to change the in-plane component of the thrust vector to accomplish the transfer by minimizing the total flight time without changing the sail attitude with respect to an orbital reference frame. This work extends the mathematical model recently proposed by the authors by including the potential offered by an active control of the diffractive sail film. The paper also thoroughly analyzes the diffractive sail-based spacecraft performance in a set of classical circle-to-circle heliocentric trajectories that model transfers from Earth to Mars, Venus and Jupiter.
1. Introduction
Since the success of JAXA’s IKAROS spacecraft, launched on 20 May 2010 [1,2,3], the solar sail technology has demonstrated its capabilities across a range of space mission applications [4,5,6]. Although the solar sail concept dates back to about a century ago thanks to the works of the Soviet pioneers of astronautics [7,8], the manufacture of such an advanced propulsion system and its integration with the spacecraft control and navigation system [9,10,11] has been completed in the last decade only, using the lessons learned from in-flight tests [12,13,14]. In this context, the most recent example of a spacecraft propelled by a solar sail is NASA’s Near-Earth Asteroid Scout (NEA Scout) [13,15], which is a 6U CubeSat that was arranged as a secondary payload for the maiden flight of the Space Launch System (SLS) in the middle of November 2022. Unfortunately, the ground station failed to establish communications with the solar sail CubeSat after its successful separation from the SLS so that the NEA Scout is currently considered lost. The next attempt to analyze the in-flight performance of a solar sail will be at the beginning of 2025, when NASA’s Solar Cruiser will start its deep-space scientific mission for Sun observations [14,16].
One of the most delicate aspects of a solar sail-based mission, both from the trajectory design and the station-keeping viewpoint, is its attitude control [17], which requires a large reflective surface to be oriented along a given space direction [18,19] to obtain a suitable thrust vector [20,21]. The simplest solution to avoid any sail reorientation maneuver is the adoption of a Sun-facing attitude [22,23], which is a configuration where the sail nominal plane is always perpendicular to the Sun-spacecraft line (referred to as radial direction), which coincides with the direction of propagation of the Sun’s photons. It is known, in fact, that a Sun-facing attitude may be passively maintained in an orbital reference frame by means of an axially symmetric sail [24,25] with a slightly conical reflective surface, whose apex is oriented toward the Sun [26]. In that case, however, if the sail film is designed to be close to an ideal surface with specular reflection [27], a solar sail with a Sun-facing attitude is able to give only a radial thrust vector [28] and, as such, it is unable to change the spacecraft angular momentum [26]. Nevertheless, a solar sail with a Sun-facing attitude is used in important space applications such as, for example, the generation of artificial equilibrium points in the (Earth + Moon)–Sun system [29,30,31].
As far as orbit transfers are concerned, a solar sail with a Sun-facing attitude may be employed only in a few cases of two-dimensional mission scenarios, such as the transfer between two Keplerian orbits that share the same value of semilatus rectum [23,32], or the (heliocentric) deployment of a smart dust swarm [33,34,35]. However, a Sun-facing attitude is unsuited for transfers between two generic Keplerian orbits, even in the simplified case of coplanar orbits or if the propulsive acceleration magnitude is modulated during the flight. In principle, a thrust vector magnitude modulation is possible by means of electrochromic panels installed on the sail surface [36,37,38,39], or through the rotation of long reflective blades, as it happens in a Heliogyro configuration [40,41,42]. The latter concept was originally conceived about 50 years ago within the ambitious proposal of a rendezvous mission to Halley’s comet [43], and it has recently received new attention [22,44,45] due to its peculiarities in terms of thrust vector control.
A possible solution to the problem of changing the orbital angular momentum with a solar sail in a Sun-facing configuration is offered by a diffractive sail, whose concept has been recently proposed by Swartzlander [46,47,48]. This solar sail, which uses a diffractive (instead of reflective) film [49], is able to generate an in-plane thrust component even if the incoming photon direction is perpendicular to the sail nominal plane [50,51,52]; see Figure 1.
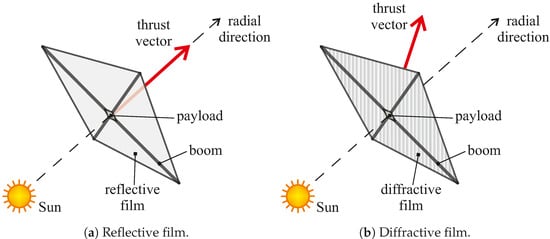
Figure 1.
Conceptual scheme of the thrust vector direction in a Sun-facing solar sail with a reflective or a diffractive film.
Exploiting the characteristics of an ideal diffractive sail, the authors [53] have recently analyzed the performance of a solar sail-based spacecraft with a Sun-facing attitude in an interplanetary mission scenario, assuming that the sail nominal plane may rotate around the Sun–spacecraft line. The trajectory design model discussed in [53] extends the preliminary results obtained by Dubill and Swartzlander [54], and it is based on the assumption that the diffractive sail-induced thrust vector belongs to a conical surface with a fixed half angle and coaxial with the Sun–spacecraft line; see Figure 2. The thrust vector orientation with respect to an orbital reference frame (that is, the azimuthal position of the thrust vector direction along the virtual cone depicted in Figure 2) can be chosen by rotating the sail nominal plane of a suitable angle around the Sun–spacecraft line.
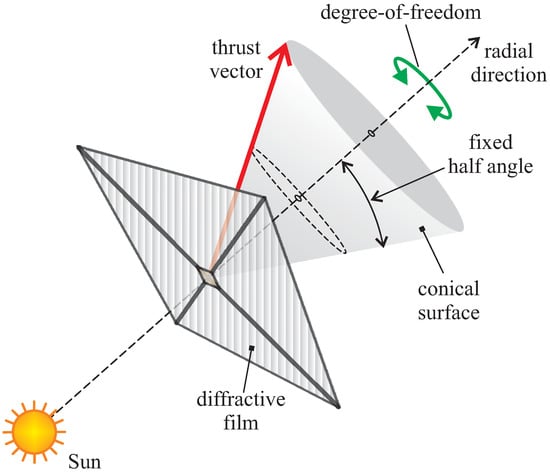
Figure 2.
Single degree-of-freedom diffractive sail considered in the trajectory analysis discussed in Ref. [53].
Using such a simplified model, Ref. [53] analyzes three-dimensional orbit-to-orbit transfers within an optimal framework, where the performance index to be minimized is the total flight time necessary for the diffractive sail to complete an assigned heliocentric transfer between two assigned Keplerian orbits.
The aim of this paper is to simplify the diffractive sail guidance scheme considered in Ref. [53], assuming a sail nominal plane with a fixed orientation relative to an orbital reference frame. The in-plane component of the diffractive sail-induced thrust vector may be changed by means of active (switchable) diffractive elements, that is, using a sail film designed with a controlled binary arrayed grating [46]. In fact, according to the conceptual propulsion system design described in Ref. [46], a diffractive sail potentially offers some interesting features that are difficult (or even impossible) to achieve with a conventional reflective solar sail, that is, with a metalized high-reflective (typically aluminum-based) thin film [55,56]. In principle, as pointed out by Swartzlander [46], the diffractive sail concept gives the opportunity: (i) to recycle photons to generate solar–electric power, using a bi-layer (or, more in general, a multi-layer) thin film containing photo-voltaic cells; and (ii) to employ electro-optically controlled binary metamaterial (either for the entire sail or for a subset of panels) to change the direction of the in-plane thrust vector component.
Actually, the use of active electro-optically controlled panels (EOCPs) is a well-known idea, which has already been exploited in solar sail design [57] since the construction of IKAROS spacecraft, which represents a milestone for solar sail technology. Indeed, during its interplanetary flight, IKAROS spacecraft was able to both generate electric power through very thin solar cells attached to the sail film and to execute attitude control maneuvers by means of advanced electro-controlled LCD panels installed near the edges of its membrane [2]; see the scheme of Figure 3.
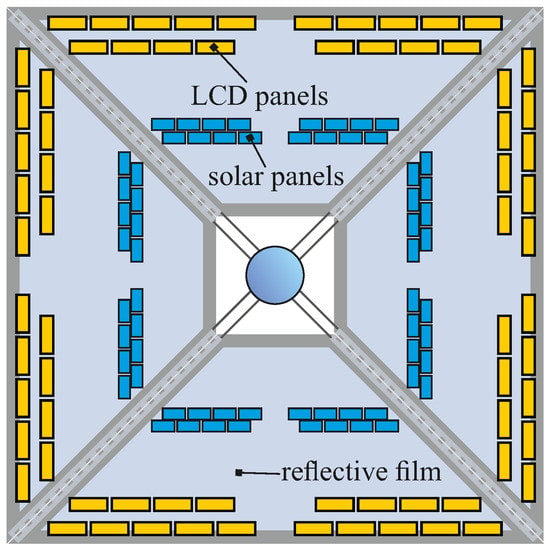
Figure 3.
Conceptual scheme of JAXA’s Interplanetary Kite-craft Accelerated by Radiation Of the Sun (IKAROS) spacecraft, showing active LCD panels to execute attitude control maneuvers.
The use of a sail film with electro-controlled and variable reflectivity panels has also been proposed as a means to (slightly) change the magnitude of the sail-induced thrust vector in order to perform missions that require a propulsive acceleration vector with a fixed (orbital) direction and a magnitude variable within a narrow range. Possible examples are the maintenance of a collinear artificial equilibrium point [58] in the Sun–planet elliptic-restricted three-body problem [59] or the guidance of a smart dust in a scientific mission aiming at an in situ study of Earth’s magnetotail [60,61].
According to Swartzlander [46], in the case of a diffractive sail, a membrane covered by EOCPs, which are switchable between two different functioning states, is potentially able to invert the direction of the in-plane component of the thrust vector while maintaining its radial component unchanged. In fact, assuming that all EOCPs change their state at the same time, the result is that the in-plane component of the thrust vector essentially flips with respect to the Sun–spacecraft line, as illustrated in Figure 4 (note that in this paper, the two states will be denoted as and ). In addition, Swartzlander [46] points out that a suitable selection of a subset of EOCPs that change their state allows the in-plane component of the thrust vector to be varied (nearly) continuously between two equal but opposite values.
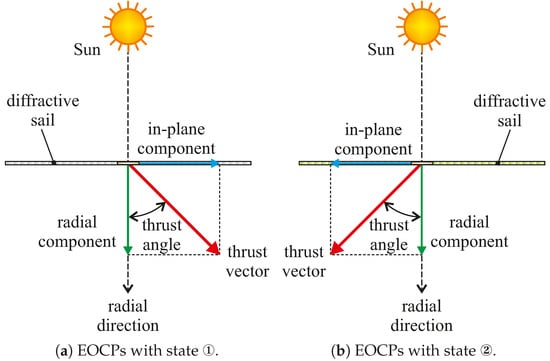
Figure 4.
Diffractive sail equipped with EOCPs: conceptual sketch of the thrust vector variation as a function of EOCPs state.
Starting from the mathematical model discussed in the recent literature [53], and assuming a Sun-facing configuration to allow the spacecraft attitude control to be passively maintained, this paper presents a simplified thrust model of a diffractive sail with EOCPs that simultaneously change their state. Using a suitable initial sail orientation in which the grating momentum unit vector (and so the thrust vector) belongs to the plane of the parking orbit, the proposed thrust model can be employed for the preliminary trajectory design of a diffractive solar sail. The transfer performance is calculated in a heliocentric mission in which a spacecraft moves between two circular and coplanar orbits. As usual, the transfer trajectory is determined by minimizing the total flight time.
This paper is organized as follows. Section 2 introduces the mathematical model used to evaluate the optimal performance of the diffractive sail-based spacecraft. It also describes the simplified thrust vector model and its integration in the two-dimensional equations of motion, which are used to optimize the transfer trajectory with an indirect approach. The optimization model is then numerically simulated, and the results are discussed in Section 3, which analyzes potential interplanetary transfers toward Mars, Venus and Jupiter. Finally, Section 4 summarizes the main results of the work.
2. Mathematical Preliminaries
This section presents the mathematical model used to evaluate the optimal performance of a diffractive sail-based spacecraft in a Sun-facing configuration. The sail membrane is equipped with a set of EOCPs that simultaneously change their state. The first part of the section describes the thrust vector model extending the mathematical description of the sail-induced acceleration recently discussed by the authors [53]. The thrust vector description used in Ref. [53] refers to a Sun-facing diffractive sail without EOCPs and is consistent with the mathematical model discussed in Ref. [54] which, in its turn, is based on the work by Swartzlander [46]. In this sense, the propulsive acceleration expression presented in this section completes the recent literature results [53], because a diffractive sail without EOCPs can be thought of as a special case of a sail entirely covered by an active (switchable) diffractive film.
2.1. Thrust Vector Mathematical Model
Consider a spacecraft propelled by a diffractive solar sail without EOCPs. Assuming a Sun-facing configuration and using the model discussed in Refs. [53,54], the spacecraft propulsive acceleration vector may be written as
where r is the Sun-spacecraft distance, is a reference distance, is the characteristic acceleration defined as the magnitude of when , is the unit vector normal to the sail nominal plane in the direction opposite to the Sun, and is the grating momentum unit vector [46]; see Figure 5. The characteristic acceleration, which is the usual performance parameter used in solar sail design, depends on the sail characteristics and the vehicle’s total mass. The direction of is considered to be fixed relative to a body reference frame when the diffractive sail is designed without EOCPs. Finally, Equation (1) states that the angle between the thrust vector direction and the radial line is 45, as illustrated in Figure 4.
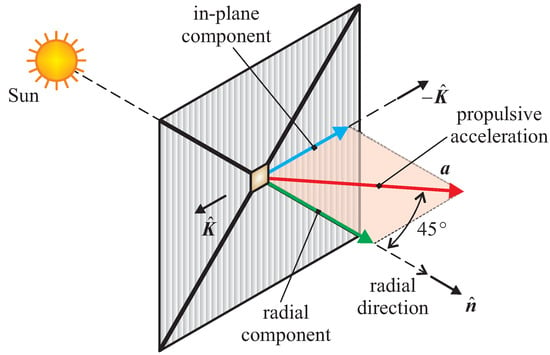
Figure 5.
Propulsive acceleration vector (and its components in a body reference frame) for an ideal diffractive sail, without EOCPs, in a Sun-facing configuration.
According to Swartzlander [46], the possible presence of a set of EOCPs allows the in-plane component of the thrust vector to be flipped (with respect to the Sun–spacecraft line) as described schematically in Figure 4. In this case, that is, in the presence of a set of EOCPs that simultaneously change their state, the diffractive sail propulsive acceleration can be simply obtained from Equation (1) by introducing a dimensionless switching parameter , which varies the direction of the in-plane components of . Accordingly, when a set of EOCPs is considered in the diffractive sail design, the expression of becomes
where
and is an auxiliary unit vector, belonging to the sail nominal plane, whose direction is fixed in a spacecraft body reference frame. In particular, the auxiliary unit vector coincides with the grating momentum unit vector when the EOCPs are on state ; see the scheme of Figure 6. According to Equation (2), the dimensionless term can be thought of as a sort of (binary) control parameter whose value can be changed during the flight in order to perform an assigned orbit transfer, as described later on in this section. Note that the assignment of in correspondence of state (and, consequently, when the EOCPs are on state ) is arbitrary. However, such a specific assumption does not affect the transfer performance in terms of total flight time, although it influences the shape of the optimal control law.
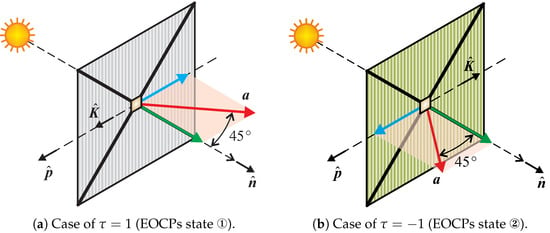
The propulsive acceleration expression given by Equation (2) can be used in a general three-dimensional mission, because the orientation of the auxiliary unit vector relative to an orbital reference frame can be varied by rotating the sail nominal plane around the Sun–spacecraft line. Note also that Equation (1) can be recovered from Equation (2) by selecting along the whole flight; compare Figure 5 and Figure 6a. In this sense, the thrust mathematical model based on Equations (2) and (3) extends and completes the model proposed in the recent literature [53].
2.2. Equations of Motion
The propulsive acceleration vector model of Equation (1) can be used to describe the two-dimensional motion of the diffractive sail in a heliocentric scenario, in which the spacecraft initially (i.e., at time ) traces a circular parking orbit of assigned radius . To that end, we introduce a heliocentric polar reference frame , whose origin coincides with the Sun’s center of mass O, where is the polar angle measured counterclockwise from the Sun–spacecraft line at time (see the scheme of Figure 7), is the radial unit vector, and is the transverse unit vector.
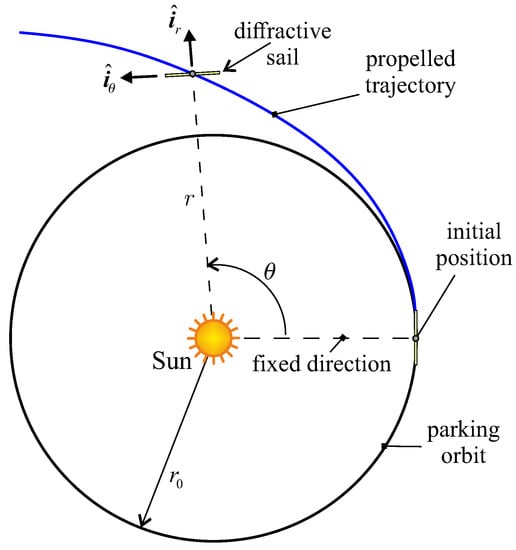
Figure 7.
Polar reference frame, parking orbit, and spacecraft state variables r and .
Assume that at the initial time, the (body-fixed) unit vector coincides with , and recall that in a Sun-facing configuration, the direction of the normal unit vector is always aligned with the Sun–spacecraft line, that is, at any time instant. In this case, for , and according to Equation (2), the propulsive acceleration vector belongs to the plane for . Note that the latter plane coincides with the parking orbit plane. Equation (2) can be therefore rewritten as
which shows that the spacecraft heliocentric motion is two-dimensional, and the vehicle’s dynamics can be described by means of a set of polar equations. More precisely, using Equation (4) to write the components of in , the spacecraft equations of motion become
where the dot symbol represents a derivative taken with respect to the time t, is the Sun’s gravitational parameter, and u (or v) is the radial (or transverse) component of the spacecraft velocity vector. The first-order differential Equations (5)–(8) are completed by four initial conditions that model the spacecraft motion along the circular parking orbit, viz.
where the initial value of the polar angle has been set equal to zero without loss of generality because of the polar symmetry of the problem.
The value of the binary-switching parameter , which appears in the last term of Equation (8), is obtained by solving an optimization problem in which the spacecraft trajectory is calculated in such a way as to minimize the time necessary for the spacecraft to reach a circular target orbit of assigned radius , starting from a circular (coplanar) parking orbit of radius . This mission scenario, which models a typical circle-to-circle orbit raising (or orbit lowering) when (or ), is a typical application of a continuous-thrust propulsion system and is analyzed in the next section.
2.3. Trajectory Optimization
The minimum time circle-to-circle orbit transfer of a diffractive sail is obtained with an indirect method [62]. The Hamiltonian function is defined as
where is that part of that explicitly depends on the control variable , that is
and are the variables adjoint to the states . The optimal control law, that is, the time variation of , is found by means of Pontryagin’s maximum principle, which requires the reduced Hamiltonian to be maximized at any time instant. Observing that the sign of Equation (11) only depends on the product , the control law that maximizes is found when , that is
where is the signum function. Equation (12) states that the spacecraft optimal transfer trajectory is a sequence of patched arcs, where is constant in each arc, and the diffractive film state change is determined by the sign of the adjoint variable . This situation is illustrated in Figure 8 in the exemplary case of four arcs.
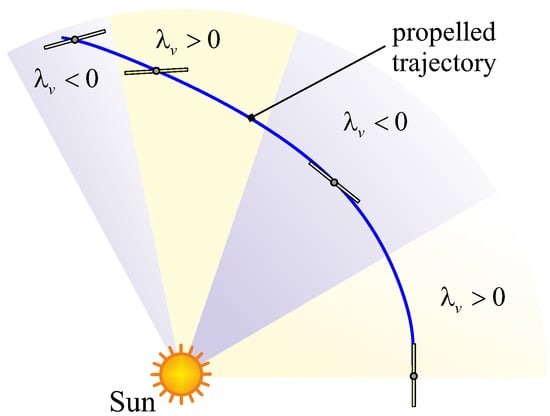
Figure 8.
Sequence of trajectory arcs related to the value of the adjoint variable .
The time variation of the adjoint variables is given by the Euler–Lagrange equations
which are completed by the four initial conditions
where are four unknowns to be found by enforcing the transversality condition [62,63] and the desired value of the spacecraft state variables at the end of the transfer. In a circle-to-circle transfer, it is required that at the final time , the spacecraft be inserted into the target circular orbit, from which
Note that the adjoint variable is a constant of motion, and the polar angle at the final time is left free, that is, the spacecraft angular position on the target circular orbit is an output of the optimization process. In a minimum time orbit transfer, the performance index J to be maximized can be written as
so that the transversality condition [62,63] gives
When Equation (14) is combined with the first of Equation (20), the result is that during the whole transfer, that is, the second of Equation (17) reads . The other three unknowns in Equation (17) and the minimum flight time are obtained by solving a two-point boundary value problem in which the three scalar (final) conditions (18) and the last of Equation (20) are numerically enforced. For an assigned set of parameters that define the diffractive sail propulsive characteristics and the mission scenario, the two-point boundary value problem has been solved through a hybrid numerical technique that combines direct methods with gradient-based routines.
3. Simulation Results
The optimization procedure described in the preceding section has been used to evaluate the diffractive sail transfer performance. A set of heliocentric canonical units [64] has been introduced to reduce the numerical sensitivity of the two-point boundary value problem, and in all of the numerical simulations, the differential Equations (5)–(8) and (13)–(16) have been integrated in double precision using a variable order Adams–Bashforth–Moulton solver [65] scheme with absolute and relative errors of .
The diffractive sail circle-to-circle transfer performance has been analyzed by selecting different possible combinations of , , and . In the remaining part of this section, the numerical results correspond to the important case when and . In fact, describes the case of a solar sail deployment along a parabolic escape orbit relative to the Earth and a heliocentric model in which the eccentricity of the Earth’s orbit is neglected. Moreover, corresponds to when the solar sail characteristic acceleration assumes a sort of canonical value, as indicated by McInnes for a reflective sail [28].
With the aim of obtaining a parametric study of the diffractive sail performance in heliocentric transfer trajectories, the target orbit radius has been selected in the range (or ) for an orbit lowering (or an orbit raising). The minimum flight time as a function of the target radius is shown in Figure 9, which also reports, for comparative purposes, the optimal transfer time obtained with a reflective solar sail assuming an ideal force model [28]. In the latter case, the trajectory optimization has been studied by adapting the procedure described in Ref. [66].
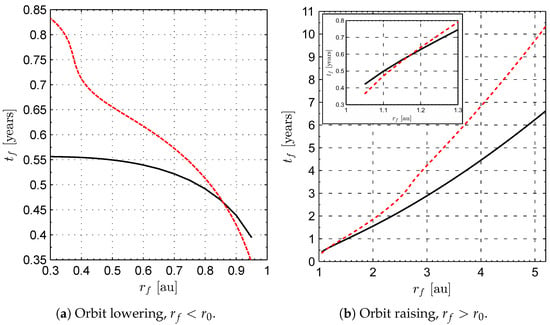
Figure 9.
Minimum flight time as a function of the target orbit radius when : comparison between an ideal and unconstrained reflective sail (red dashed line) and a Sun-facing diffractive sail with EOCPs (solid black line).
The interesting aspect that emerges from Figure 9 is that the minimum flight time of a diffractive sail is better (i.e., smaller) than that of a reflective sail of equal characteristic acceleration, provided the target radius is greater (for an orbit raising) or lower (for an orbit lowering) than a critical value, which depends on the selected . In particular, when , Figure 9 shows that a reflective sail outperforms a diffractive sail with EOCPs when . On the other hand, if or , that is, in a wide range of circle-to-circle mission cases, the flight times required by a diffractive sail with EOCPs are smaller than the reflective counterpart. Such an interesting result is related to the complex interaction between the capability of a Sun-facing diffractive sail to generate a transverse component of the propulsive acceleration greater than that obtained through an unconstrained reflective sail and the higher maneuverability of a reflective sail, which can steer the thrust vector in the half-plane . The latter consideration, which can be extended to the more general case of a three-dimensional heliocentric mission scenario, has been thoroughly analyzed in Ref. [53], where a comparison between the force bubble of the reflective sail with that of a diffractive sail is presented; see the scheme of Figure 10 which reports the force bubble comparison in the three-dimensional case.
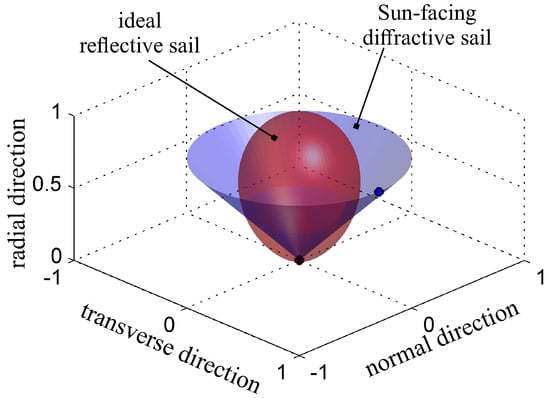
Figure 10.
Force bubble of a reflective sail without attitude constraint and a diffractive sail with a Sun-facing configuration.
Figure 11 shows the final value of the spacecraft polar angle (calculated with respect to the initial Sun–spacecraft line) as a function of the target orbit radius for the selected values of . The same figure is also useful to evaluate the number (360) of complete revolutions during the optimal transfer. The number N can be considered as a sort of metric of the geometrical complexity of the low-thrust transfer trajectory. As expected, for the reflective sail case, the value of N increases with the “distance” of the target orbit with respect to the parking one; that is, N varies with the value of the ratio . However, for the diffractive sail case, in the studied range of variation of and when , it turns out that 360 (i.e., ), which is a value that indicates a less involved transfer trajectory when compared with the reflective counterpart.
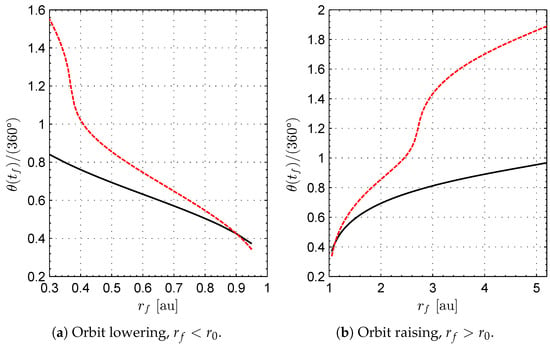
Figure 11.
Final value of the polar angle as a function of the target orbit radius for an optimal transfer using an ideal and unconstrained reflective sail (red dashed line) or a Sun-facing diffractive sail with EOCPs (solid black line) when .
This aspect is also confirmed by the graphs presented in the next subsection, which reports the results of the trajectory optimization in three important mission scenarios consistent with a transfer toward Venus, Mars, and Jupiter.
Case Study
Consider now three different cases, with ,
= 1.524 au, and
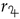 = 5.2 au, which model a simplified two-dimensional transfer from Earth to Venus, Mars, and Jupiter, respectively. Using the mathematical model described in the preceding section and a diffractive sail with a characteristic acceleration
the minimum flight time is about 189 days for the Venus case, 365 days for the Mars case, and 2420 days for the Jupiter case. In addition, according to Figure 9, for a reflective sailbased scenario of equal characteristic acceleration, the minimum flight times are about 408 days for the Mars case, 205 days for the Venus case, and 3777 days for the Jupiter case. A comparison between the optimal performance of a reflective and a diffractive sail is summarized in Table 1, where the last column highlights that the flight time saving with a diffractive sail is considerable (about 36%) in the Earth–Jupiter transfer scenario. Note that the performance improvement is about 10% for the Mars and Venus case, which is due to the reduced value (when compared with the Jupiter trans) of the typical flight time for a solar sail with
.
= 5.2 au, which model a simplified two-dimensional transfer from Earth to Venus, Mars, and Jupiter, respectively. Using the mathematical model described in the preceding section and a diffractive sail with a characteristic acceleration
the minimum flight time is about 189 days for the Venus case, 365 days for the Mars case, and 2420 days for the Jupiter case. In addition, according to Figure 9, for a reflective sailbased scenario of equal characteristic acceleration, the minimum flight times are about 408 days for the Mars case, 205 days for the Venus case, and 3777 days for the Jupiter case. A comparison between the optimal performance of a reflective and a diffractive sail is summarized in Table 1, where the last column highlights that the flight time saving with a diffractive sail is considerable (about 36%) in the Earth–Jupiter transfer scenario. Note that the performance improvement is about 10% for the Mars and Venus case, which is due to the reduced value (when compared with the Jupiter trans) of the typical flight time for a solar sail with
.

Table 1.
Minimum flight time in a classical Earth–target planet, circle-to-circle, coplanar transfer for a diffractive or a reflective sail with .
The optimal transfer trajectories are sketched in Figure 12 along with a comparison of the optimal transfer trajectories for the ideal reflective case, while Figure 13 shows the time variation of the control parameter . In particular, there exists a substantial difference between the two optimal transfer trajectories in the Earth–Jupiter mission case. The interesting aspect that emerges from Figure 13 is that in the Earth–Jupiter scenario, the control parameter is nearly constant () along the entire flight, and the state of EOCPs is equal to during the transfer; see Equation (12). Such a particular behaviour suggests a potential approach to the trajectory optimization, which could exploit an analytical, albeit approximate, method to evaluate the minimum flight time by assuming a constant value of the control parameter . The latter analysis point is beyond the scope of the current paper and represents the natural extension of the mathematical model discussed in the preceding section.
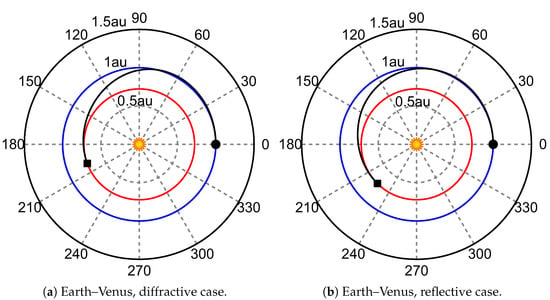
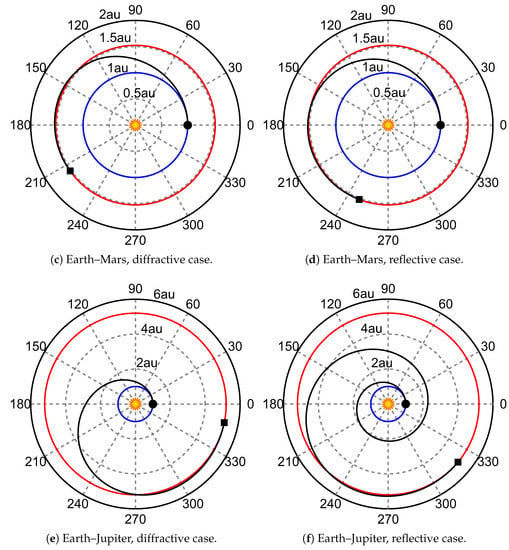
Figure 12.
Optimal transfer trajectory for the three mission scenarios. Black circle → start, black square → arrival, blue line → parking orbit, red line → target orbit, black line → optimal transfer trajectory.
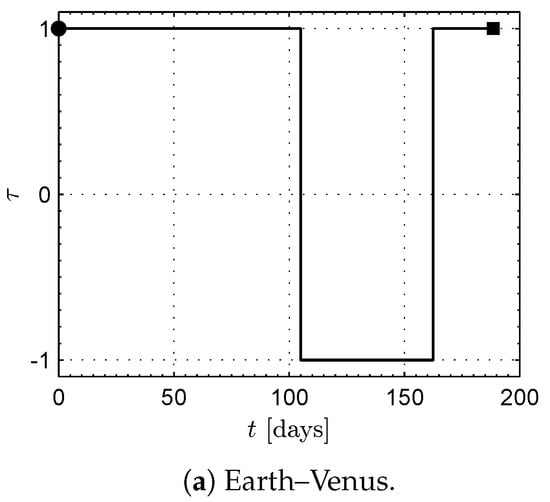
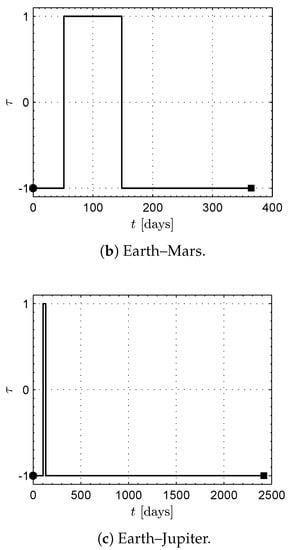
Figure 13.
Time variation of the control variable for the three mission cases using a Sun-facing diffractive sail. Black circle → start, black square → arrival.
4. Discussion and Conclusions
A diffractive sail can be considered as a sort of evolution of the classical concept of a reflecting solar sail, which received much attention in the last decade thanks to various space missions successfully flown. A solar sail with a diffractive film has interesting features; for example, it simplifies the spacecraft guidance by maintaining a Sun-facing configuration, and it guarantees good transfer performance. This paper discusses a simplified thrust model for a flat diffractive sail equipped with an electro-optically controlled panel that allows the direction of the grating momentum unit vector to be changed during the flight. Using such a feature, the in-plane component of the diffractive sail thrust vector can be easily flipped without changing the sail attitude with respect to a classical orbital reference frame. In this sense, the proposed thrust model can be thought of as a simplified version of the model for interplanetary trajectory analysis recently discussed by the authors [53].
In particular, the mathematical model proposed in this paper can be used to perform a preliminary design of an optimal interplanetary trajectory in a two-dimensional mission case, whose main limitation is related to the eccentricity of the initial and target orbits, which are both set to zero. The interesting aspect that emerges from the numerical results is that the performance of a Sun-facing diffractive sail with an active (binary) electro-controlled film is comparable or, in some cases, even better than those obtained with a more conventional reflective solar sail. More precisely, the numerical simulations have shown that the flight time saving obtainable with a diffractive sail, when compared with a reflective sail of equal (canonical) characteristic acceleration, is in the order of for a transfer toward Mars or Venus, and it increases up to in an Earth–Jupiter scenario. However, a thorough comparison between a reflective and a diffractive sail-based spacecraft cannot be confined to a simple evaluation of the optimal flight time. Indeed, although the two sails share the same concept of transforming the solar radiation pressure in propulsive acceleration without the use of propellant, the specific technology at the base of a diffractive sail concept (with electro-optically controlled panels) is different from the more conventional metalized film installed on a reflective sail surface. In this sense, a more accurate comparison between a diffractive (with active panels) and reflective sail should include a detailed mass breakdown model of the two propulsion systems. Finally, the numerical results indicate that using an optimal control law, that is, the optimal time variation of the switching parameter, a circle-to-circle orbit transfer requires a very simple guidance scheme that potentially permits finding an analytical solution to the trajectory design. The latter point is beyond the scope of this paper and is left to future research.
Author Contributions
Conceptualization, A.A.Q.; methodology, A.A.Q.; software, A.A.Q.; writing—original draft preparation, A.A.Q.; writing—review and editing, G.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partly supported by the University of Pisa, Progetti di Ricerca di Ateneo (Grant no. PRA_2022_1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| diffractive sail film states | |
| characteristic acceleration (mm/s ) | |
| propulsive acceleration vector (mm/s ) | |
| Hamiltonian function | |
| part of that depends on the controls | |
| grating momentum unit vector | |
| radial unit vector | |
| transverse unit vector | |
| J | performance index (days) |
| N | number of complete revolutions |
| sail normal unit vector | |
| O | Sun’s center of mass |
| sail-fixed unit vector | |
| r | Sun–spacecraft distance (au) |
| spacecraft position vector (au) | |
| reference distance () | |
| t | time (days) |
| polar reference frame | |
| u | radial component of the spacecraft velocity (km/s) |
| v | transverse component of the spacecraft velocity (km/s) |
| spacecraft polar angle () | |
| variable adjoint to r | |
| variable adjoint to u | |
| variable adjoint to v | |
| variable adjoint to | |
| Sun’s gravitational parameter (km /s ) | |
| dimensionless control parameter | |
| Subscripts | |
| 0 | initial, parking orbit |
| f | final, target orbit |
| ♂ | Mars |
| ♀ | Venus |
| Jupiter |
References
- Sawada, H.; Mori, O.; Okuizumi, N.; Shirasawa, Y.; Miyazaki, Y.; Natori, M.; Matunaga, S.; Furuya, H.; Sakamoto, H. Mission report on the solar power sail deployment demonstration of IKAROS. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Denver, CO, USA, 4–7 April 2011. [Google Scholar] [CrossRef]
- Tsuda, Y.; Mori, O.; Funase, R.; Sawada, H.; Yamamoto, T.; Saiki, T.; Endo, T.; Yonekura, K.; Hoshino, H.; Kawaguchi, J. Achievement of IKAROS—Japanese deep space solar sail demonstration mission. Acta Astronaut. 2013, 82, 183–188. [Google Scholar] [CrossRef]
- Mori, O.; Shirasawa, Y.; Mimasu, Y.; Tsuda, Y.; Sawada, H.; Saiki, T.; Yamamoto, T.; Yonekura, K.; Hoshino, H.; Kawaguchi, J.; et al. Overview of IKAROS Mission. In Advances in Solar Sailing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 25–43. [Google Scholar] [CrossRef]
- Montgomery, E.; Heaton, A.; Garbe, G. Places only solar sails can go. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003. [Google Scholar] [CrossRef]
- Johnson, L.; Meyer, M.; Palaszewski, B.; Coote, D.; Goebel, D.; White, H. Development priorities for in-space propulsion technologies. Acta Astronaut. 2013, 82, 148–152. [Google Scholar] [CrossRef]
- Spencer, D.A.; Johnson, L.; Long, A.C. Solar sailing technology challenges. Aerosp. Sci. Technol. 2019, 93, 105276. [Google Scholar] [CrossRef]
- Fu, B.; Sperber, E.; Eke, F. Solar sail technology—A state of the art review. Prog. Aerosp. Sci. 2016, 86, 1–19. [Google Scholar] [CrossRef]
- Gong, S.; Macdonald, M. Review on solar sail technology. Astrodynamics 2019, 3, 93–125. [Google Scholar] [CrossRef]
- Heaton, A. Solar Sail GN&C Model Verification Including Flight Data. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar] [CrossRef]
- Thomas, S.; Paluszek, M.; Wie, B.; Murphy, D. Design and Simulation of Sailcraft Attitude Control Systems Using the Solar Sail Control Toolbox. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, RI, USA, 16–19 July 2004. [Google Scholar] [CrossRef]
- Thomas, S.; Paluszek, M.; Wie, B.; Murphy, D. AOCS Performance and Stability Validation for Large Flexible Solar Sail Spacecraft. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005. [Google Scholar] [CrossRef]
- Kun, Z. Control Capability and Allocation of Solar Sail Tip Vanes over Bounded Movement. J. Guid. Control Dyn. 2015, 38, 1340–1344. [Google Scholar] [CrossRef]
- Pezent, J.B.; Sood, R.; Heaton, A. Contingency target assessment, trajectory design, and analysis for NASA’s NEA Scout solar sail mission. Adv. Space Res. 2020, 67, 2890–2898. [Google Scholar] [CrossRef]
- Pezent, J.B.; Sood, R.; Heaton, A.; Miller, K.; Johnson, L. Preliminary trajectory design for NASA’s Solar Cruiser: A technology demonstration mission. Acta Astronaut. 2021, 183, 134–140. [Google Scholar] [CrossRef]
- Lockett, T.R.; Castillo-Rogez, J.; Johnson, L.; Matus, J.; Lightholder, J.; Marinan, A.; Few, A. Near-Earth Asteroid Scout flight mission. IEEE Aerosp. Electron. Syst. Mag. 2020, 35, 20–29. [Google Scholar] [CrossRef]
- Everett, J.; Heaton, A.; Houin, A.; Miller, K. An Integrated Software Architecture for Solar Cruiser Mission Design and Navigation. In Proceedings of the IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022. [Google Scholar] [CrossRef]
- Herasimenka, A.; Dell’Elce, L.; Caillau, J.B.; Pomet, J.B. Controllability Properties of Solar Sails. J. Guid. Control Dyn. 2023, 46, 900–909. [Google Scholar] [CrossRef]
- Liu, M.; Wang, Z.; Ikeuchi, D.; Fu, J.; Wu, X. Design and Simulation of a Flexible Bending Actuator for Solar Sail Attitude Control. Aerospace 2021, 8, 372. [Google Scholar] [CrossRef]
- Gong, H.; Gong, S.; Liu, D. Attitude dynamics and control of solar sail with multibody structure. Adv. Space Res. 2022, 69, 609–619. [Google Scholar] [CrossRef]
- Murphy, D.; Trautt, T. Solar Sail Propulsion Modeling. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007. [Google Scholar] [CrossRef]
- Wie, B. Thrust Vector Control Analysis and Design for Solar-Sail Spacecraft. J. Spacecr. Rockets 2007, 44, 545–557. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Caruso, A.; Mengali, G. Optimal heliocentric transfers of a Sun-facing heliogyro. Aerosp. Sci. Technol. 2021, 119, 107094. [Google Scholar] [CrossRef]
- Bassetto, M.; Quarta, A.A.; Mengali, G.; Cipolla, V. Trajectory analysis of a Sun-facing solar sail with optical degradation. J. Guid. Control Dyn. 2020, 43, 1727–1732. [Google Scholar] [CrossRef]
- Rios-Reyes, L.; Scheeres, D.J. Generalized Model for Solar Sails. J. Spacecr. Rockets 2005, 42, 182–185. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal control laws for axially symmetric solar sails. J. Spacecr. Rockets 2005, 42, 1130–1133. [Google Scholar] [CrossRef]
- McInnes, C.R. Orbits in a generalized two-body problem. J. Guid. Control Dyn. 2003, 26, 743–749. [Google Scholar] [CrossRef]
- Wright, J.L. Space Sailing; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1992. [Google Scholar]
- McInnes, C.R. Solar Sailing: Technology, Dynamics and Mission Applications; Springer: Berlin/Heidelberg, Germany, 1999; pp. 171–196. [Google Scholar] [CrossRef]
- Mclnnes, C.R.; Simmons, J.F.L. Solar sail halo orbits. Part I—Heliocentric case. J. Spacecr. Rockets 1992, 29, 466–471. [Google Scholar] [CrossRef]
- McInnes, C.R.; Simmons, J.F.L. Solar Sail Halo Orbits Part II—Geocentric Case. J. Spacecr. Rockets 1992, 29, 472–479. [Google Scholar] [CrossRef]
- McInnes, C.R.; McDonald, A.J.C.; Simmons, J.F.L.; MacDonald, E.W. Solar sail parking in restricted three-body systems. J. Guid. Control Dyn. 1994, 17, 399–406. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal circle-to-ellipse orbit transfer for Sun-facing E-sail. Aerospace 2022, 9, 671. [Google Scholar] [CrossRef]
- Colombo, C.; McInnes, C.R. Orbital dynamics of “Smart-Dust” devices with solar radiation pressure and drag. J. Guid. Control Dyn. 2011, 34, 1613–1631. [Google Scholar] [CrossRef]
- Ren, Z.; Yuan, J.; Su, X.; Shi, Y. A novel design and thermal analysis of micro solar sails for solar sailing with chip scale spacecraft. Microsyst. Technol. 2020, 27, 2615–2622. [Google Scholar] [CrossRef]
- Niccolai, L.; Bassetto, M.; Quarta, A.A.; Mengali, G. A review of Smart Dust architecture, dynamics, and mission applications. Prog. Aerosp. Sci. 2019, 106, 1–14. [Google Scholar] [CrossRef]
- Lücking, C.; Colombo, C.; McInnes, C.R. Electrochromic orbit control for smart-dust devices. J. Guid. Control Dyn. 2012, 35, 1548–1558. [Google Scholar] [CrossRef]
- Borggräfe, A.; Heiligers, J.; Ceriotti, M.; McInnes, C. Optical Control of Solar Sails using Distributed Reflectivity. In Proceedings of the Spacecraft Structures Conference, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Mu, J.; Gong, S.; Li, J. Coupled Control of Reflectivity Modulated Solar Sail for GeoSail Formation Flying. J. Guid. Control Dyn. 2015, 38, 740–751. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A.; Denti, E. Relative Motion of Sun-pointing Smart Dust in Circular Heliocentric Orbits. J. Guid. Control Dyn. 2018, 41, 1009–1014. [Google Scholar] [CrossRef]
- Ramnath, R.V. Heliogyro Spacecraft. In Multiple Scales Theory and Aerospace Applications; Schetz, J.A., Ed.; Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010; Chapter 36; pp. 529–547. [Google Scholar] [CrossRef]
- Guerrant, D.; Lawrence, D. Tactics for Heliogyro Solar Sail Attitude Control via Blade Pitching. J. Guid. Control Dyn. 2015, 38, 1785–1799. [Google Scholar] [CrossRef]
- Heiligers, J.; Guerrant, D.; Lawrence, D. Exploring the Heliogyro’s Orbital Control Capabilities for Solar Sail Halo Orbits. J. Guid. Control Dyn. 2017, 40, 2569–2586. [Google Scholar] [CrossRef]
- Wilkie, W.K.; Warren, J.E.; Horta, L.G.; Lyle, K.H.; Juang, J.N.; Littell, J.D.; Bryant, R.G.; Thomson, M.W.; Walkemeyer, P.E.; Guerrant, D.V.; et al. Heliogyro Solar Sail Research at NASA. In Advances in Solar Sailing; Springer: Berlin/Heidelberg, Germany, 2014; pp. 631–650. [Google Scholar] [CrossRef]
- Kang, J.; Park, K.C. Flexible heliogyro solar sail under solar radiation pressure and gravitational force. Acta Astronaut. 2021, 179, 186–196. [Google Scholar] [CrossRef]
- Boni, L.; Bassetto, M.; Quarta, A.A.; Mengali, G. Nonlinear dynamics of flexible heliogyro subject to sinusoidal root pitch command. Aerosp. Sci. Technol. 2022, 130, 107920. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Radiation pressure on a diffractive sailcraft. J. Opt. Soc. Am. B Opt. Phys. 2017, 34, C25–C30. [Google Scholar] [CrossRef]
- Chu, L.J.; Swartzlander, G. Radiation pressure on a transmissive diffraction grating. In Proceedings of the Frontiers in Optics, Washington, DC, USA, 18–21 September 2017. [Google Scholar] [CrossRef]
- Swartzlander, G.A.J.; Chu, Y.J.; Srivastava, P. Beam riders and sailcraft based on diffractive light sails. In Proceedings of the Frontiers in Optics, Washington, DC, USA, 16–20 September 2018. [Google Scholar] [CrossRef]
- Chu, Y.J.; Jansson, E.M.; Swartzlander, G.A. Verification of radiation pressure on a diffraction grating. In Proceedings of the SPIE Nanoscience + Engineering, San Diego, CA, USA, 19–23 August 2018. [Google Scholar] [CrossRef]
- Swartzlander, G.A., Jr. Flying on a rainbow: A solar-driven diffractive sailcraft. JBIS J. Br. Interplanet. Soc. 2018, 71, 130–132. [Google Scholar]
- Srivastava, P.R.; Lucy Chu, Y.J.; Swartzlander, G.A., Jr. Stable diffractive beam rider. Opt. Lett. 2019, 44, 3082–3085. [Google Scholar] [CrossRef]
- Srivastava, P.R.; Swartzlander, G.A., Jr. Optomechanics of a stable diffractive axicon light sail. Eur. Phys. J. Plus 2020, 135, 570. [Google Scholar] [CrossRef] [PubMed]
- Quarta, A.A.; Mengali, G.; Bassetto, M.; Niccolai, L. Optimal interplanetary trajectories for Sun-facing ideal diffractive sails. Astrodynamics 2023, in press.
- Dubill, A.L.; Swartzlander, G.A., Jr. Circumnavigating the Sun with diffractive solar sails. Acta Astronaut. 2021, 187, 190–195. [Google Scholar] [CrossRef]
- Davoyan, A.R.; Munday, J.N.; Tabiryan, N.; Swartzlander, G.A.; Johnson, L. Photonic materials for interstellar solar sailing. Optica 2021, 8, 722–734. [Google Scholar] [CrossRef]
- Matloff, G.L. Graphene: The Ultimate Interstellar Solar Sail Material? JBIS J. Br. Interplanet. Soc. 2012, 65, 378–381. [Google Scholar]
- Kislov, N. Variable Reflectance/Transmittance Coatings for Solar Sail Altitude Control and Three Axis Stabilization. In Proceedings of the AIP Conference Proceedings, Albuquerque, NM, USA, 8–11 February 2004. [Google Scholar] [CrossRef]
- McKay, R.J.; Macdonald, M.; Biggs, J.; McInnes, C. Survey of Highly Non-Keplerian Orbits with Low-Thrust Propulsion. J. Guid. Control Dyn. 2011, 34, 645–666. [Google Scholar] [CrossRef]
- Aliasi, G.; Mengali, G.; Quarta, A.A. Artificial Lagrange Points for Solar Sail with Electrochromic Material Panels. J. Guid. Control Dyn. 2013, 36, 1544–1550. [Google Scholar] [CrossRef]
- Quarta, A.A.; Mengali, G.; Niccolai, L. Smart Dust Option for Geomagnetic Tail Exploration. Astrodynamics 2019, 3, 217–230. [Google Scholar] [CrossRef]
- Lappas, V.; Wie, B.; McInnes, C.; Tarabini, L.; Gomes, L.; Wallace, K. Microsolar Sails for Earth Magnetotail Monitoring. J. Spacecr. Rockets 2007, 44, 840–848. [Google Scholar] [CrossRef]
- Bryson, A.E.; Ho, Y.C. Applied Optimal Control; Hemisphere Publishing Corporation: New York, NY, USA, 1975; Chapter 2; pp. 71–89. ISBN 0-891-16228-3. [Google Scholar]
- Stengel, R.F. Optimal Control and Estimation; Dover Books on Mathematics; Dover Publications, Inc.: New York, NY, USA, 1994; pp. 222–254. [Google Scholar]
- Bate, R.R.; Mueller, D.D.; White, J.E. Fundamentals of Astrodynamics; Dover Publications: New York, NY, USA, 1971; Chapter 1; pp. 40–43. [Google Scholar]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM J. Sci. Comput. 1997, 18, 1–22. [Google Scholar] [CrossRef]
- Mengali, G.; Quarta, A.A. Optimal three-dimensional interplanetary rendezvous using nonideal solar sail. J. Guid. Control Dyn. 2005, 28, 173–177. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).