Abstract
Pavement maintenance and repair is a crucial part of pavement management systems. Accurate and reliable pavement performance prediction is the prerequisite for making reasonable maintenance decisions and selecting suitable repair schemes. Rutting deformation, as one of the most common forms of asphalt pavement failures, is a key index for evaluating the pavement performance. To ensure the accuracy of the commonly used prediction models, the input parameters of the models need to be understood, and the coefficients of the models should be locally calibrated. This paper investigates the prediction of the rutting development of pavements with flexible overlays based on the data of the Canadian Long-Term Pavement Performance (C-LTPP) program. Pavement performance data that may be related to rutting were extracted from the survey of Dipstick for data analysis. Then, an artificial neural network (ANN) was adopted to analyze the factors affecting the rut depth, and to establish a model for the rutting development of pavements with flexible overlays. The results of the sensitivity analysis indicate that rutting is not only affected by traffic and climatic conditions, but it is also greatly affected by the thickness of the surface layer and voids in the mixture. Finally, a rutting evaluation index was provided to describe the rutting severity, and the threshold of the pavement maintenance time was proposed based on the prediction results. These results provide a basis for predicting rut development and pavement maintenance.
1. Introduction
In China, there exist numerous pavements with long service lives and serious cumulative damage, which need to be repaired urgently [1]. At present, using a flexible overlay to repair pavement has been widely adopted in the repair of old roads. It is necessary to investigate the performance of flexible overlay for repairing pavements. Rutting is one of the most typical diseases of flexible pavement, and it affects driving safety [2]. Moreover, rutting is a significant indicator in the MEPDG to judge whether flexible pavements are going to fail. Thus, it is significant to the service performance management of pavements with flexible overlays [3].
A lot of research has been conducted to predict rutting development [4]. The simplest and most straightforward method is the empirical method, which predicts the rut depth with the pavement structure, material parameters, climate, and load using a statistical method [5]. Suh [6] obtained regression formulas for predicting the rutting depth under different traffic loads and temperatures. Considering the different factors that affect rutting, such as temperature, shear stress of the pavement structure, surface thickness, vehicle speed, loading repetitions, and dynamic stability, a multivariate regression model for rutting was established in [7].
Without considering the overall response of the pavement structure and the mechanical parameters of the materials in the model established through empirical methods, the prediction of the rutting performance is very poor. In addition, the empirical method can only be applied to specific environments. The mechanistic–empirical (M-E) method establishes the empirical relationship between the pavement rutting and material characteristics, pavement structure, and number of loads. According to the deformation characteristics of the mixture, the mechanical response of the pavement is calculated following the elastic layered system theory, or viscoelastic theory [8]. This method has been widely applied in road surface research. The most representative prediction model is the AASHTO2002 model. Based on the theory of elastic layered systems, an MEPDG mechanical–empirical design method was proposed to calculate the permanent deformation of different structural layers. The prediction model in the MEPDG needs to be calibrated using national and local data, and many researchers have calibrated models for different states. However, with the popularization of the MEPDG in North America, more and more researchers have found that its accuracy in predicting the asphalt pavement performance, especially rutting, is not high. In addition, many researchers have proposed their own calibration models. Chen [9] established a mechanical–empirical model to predict the development of rutting in different pavement structures based on data from a full-scale pavement track, and the impact of base types on rutting was analyzed. However, the influence of the asphalt mixture performance was not considered in the mechanical–empirical model.
Both the empirical model and M-E model are deterministic models, but probabilistic models can also be used for rut prediction. The Markov prediction model is the most typical probability prediction model, and it is relatively complete in predicting the asphalt pavement performance, with significant characteristics and no aftereffects [10]. Mrawira [11] and Hong [12] used Bayesian regression and Markov chains to estimate the rutting depth under different confidence levels.
With the collection and storage of a large quantity of test data, machine learning has been used in civil engineering industries [13,14,15]. Artificial neural networks (ANNs) are the most widely used. Alharbi and Smadi [16] introduced an ANN to forecast the rut depth with the input of traffic and climate parameters and the pavement thickness. Okuda et al. [17] used three years of rut-depth data to predict the rut depth in a time series for 10 years by applying a recurrent neural network (RNN) model; Cui [18] established an RNN model to predict rutting by taking traffic and climate as input variables. Based on the LTPP database, Haddad et al. [19] selected 29 input variables from 50 influencing factors and took traffic, climatic conditions, pavement thickness, and pavement material properties as inputs to establish a deep ANN model.
Neural networks have been widely used in the service performance prediction of asphalt pavement [20,21,22,23], but there is little research on applying ANNs to pavement overlay rutting prediction. Abo-Hashema [24] applied an ANN to predict the appropriate pavement overlay thickness. Abiola [25] and Wang [1] proposed an ANN model to predict the rutting depth of asphalt pavement. However, these input variables do not include the thickness of the overlay layer, the overlay material, or repave measures. Hall [26] analyzed the impact of different maintenance measures on the smoothness index, rutting, and cracks of flexible pavement. It is believed that the overlay thickness is the most important influencing factor besides climate and the axial load.
It is well known that the accumulated damage of the original pavement and the pavement repair plan have a great influence on the rutting of the pavement after repair. This article establishes an artificial neural network model based on the LTPP database to predict the rutting development of flexible overlay pavement. The features affecting the pavement performance were selected as input variables, including the overlay thickness, overlay materials, overlay measures, pavement structure, climate, and traffic. Finally, the article proposes maintenance strategies based on the curve of the rutting depth over time. The overall research scope of this study is shown in Figure 1.
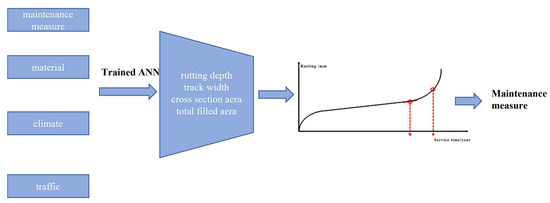
Figure 1.
Flowchart of overall research scope.
2. Data Preparation
The Canadian Long-Term Pavement Performance (C-LTPP) program is a project managed by the Canada Strategic Highway Research Program (C-SHRP), and it aims to evaluate the long-term performance of each test section after repair, and to develop flexible pavement repair procedures considering economic benefits [27,28]. The C-LTPP dataset is one of the most comprehensive datasets, in which the pavement structure of the test section is relatively uniform, and the evaluation means are relatively complete. Thus, it is suitable for studies on pavement repair and the exploration of the rutting development trends of pavements after repair with accumulated service histories.
The C-LTPP database covers 24 highway test sites in Canada’s major provincial highway systems [29]. The geographic distribution of the sites is presented in Figure 2. The test sites include from two to four different test sections that use different repair schemes. They constitute a total of 65 test sections with different pavement structures and service environments after repair. The effective length of each test section is 150 m. Meanwhile, this dataset provides many variables, including material, structure, traffic, climate, and rehabilitation, which can support various studies on the service performances of pavements repaired with flexible overlays. The data can be downloaded free from the online website (https://infopave.fhwa.dot.gov, accessed on 2003).
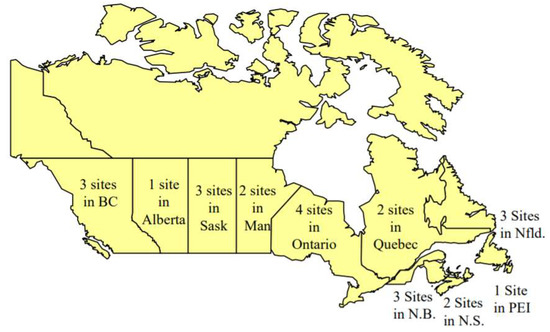
Figure 2.
Test site distribution of C-LTPP program [13].
3. Rutting Prediction
Inspired by biological neural networks, ANNs consist of many connected nodes, and they show good performances in solving linear and nonlinear problems [30,31]. At present, ANNs have been widely used in various fields [32,33,34]. In this study, a four-layer ANN was established to predict rutting after pavement repair with seven features, including the rut depth on the left and right sides, the widths of the left and right wheel tracks, the positive and negative area characteristics of the pavement cross-section, and the total filling area of the cross-section. The input variables of the ANN should be factors that affect the rut depth, such as the climatic conditions, traffic conditions, pavement material characteristics, and maintenance information. There were 4829 data samples, 70% of which were used as the training set and 30% as the test set. The constructed network architecture is shown in Figure 3.
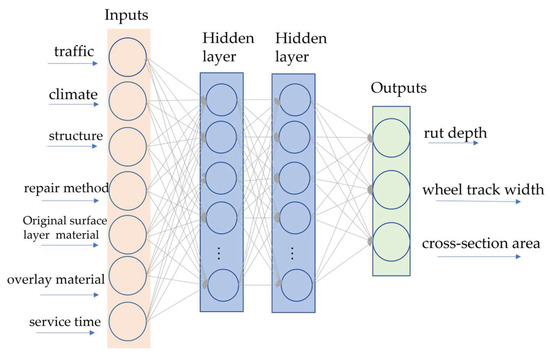
Figure 3.
Architecture of established ANN model.
The hyperparameters related to ANNs include the number of hidden layers, number of neurons in each hidden layer, activation function, learning rate, number of epochs, batch size, regularization parameter, and loss function. Among these hyperparameters, the number of neurons in each hidden layer, learning rate, and batch size are the most important ones. Searching for numerous hyperparameters is time-consuming and unnecessary. In this study, many hyperparameters, such as the number of layers and the number of neurons in each layer, were determined based on engineering background and experience. In the established ANN model, there are 7540 hidden neurons, the activation function is sigmoid, the optimizer is Adam, the learning rate is 0.4, and the number of epochs is 100.
3.1. Data Processing
Before training the model, it is necessary to preprocess the data first. The dataset needs to be cleaned by dealing with missing values and removing outliers [35,36,37]. The presence of outliers will lead to the training deviation of the model and affect the generalization. In this study, a filter based on kernel density estimation was used to detect outliers. If the estimated probability density of the dataset is lower than 0.05, then the sample data will be eliminated. Moreover, missing data need to be handled. Those items with too many missing features can be deleted directly because a lot of useful information has been lost. Thus, if there are more than seven missing features in one item, then the row will be deleted. Then, the remaining missing values are replaced with the average value of the corresponding characteristic without missing data.
Furthermore, the ranges and units of the variables vary greatly, which easily results in a deviation in the predicted output. To eliminate this impact, all inputs were standardized before being fed into the ANN. Minimum–maximum normalization was adopted in the study.
3.2. Reliability Analysis of the Model
The sample distribution and model error information of the rut model training can be obtained. The reliability of the model can be evaluated by checking the distribution of the number of samples allocated to the training set and test set, as well as the relative error between the output value and target value in the training set and test set. The results are listed in Table 1.

Table 1.
Reliability analysis of rut model.
The numbers of samples allocated to the training set and test set were 3394 and 1435, respectively, accounting for 70.3% and 29.7% of the total effective samples, respectively. The division of the sample dataset is considered reasonable. Meanwhile, the error between the output value and target value of each rut characteristic index is controlled within the range of 10%–30%, indicating that the calculation results are acceptable. Therefore, the rut prediction model obtained by training based on the above setting is considered reliable.
3.3. Sensitivity Analysis of Parameters
Unimportant variables can reduce the computational efficiency and increase the risk of overfitting. The inputs fed into ANN models should be factors that affect the output. Before being fed into ANN models, the dataset, such as the test section number and some redundant indicators, should be eliminated. Moreover, the input variables should not be correlated with each other. Feature importance can help to screen features. In this study, random forest, an integrated algorithm, was used to compute the impurity-based feature importance. A random forest is composed of many decision trees, and in this algorithm, the tree grows when the feature can make the variance of a target decrease the most [33]. The more a feature minimizes the error, the more important it is to the target. Feature importance analysis based on the random forest was carried out in this study, and the result is presented in Figure 4. The explanations of the variables in the graph are shown in Table 2.
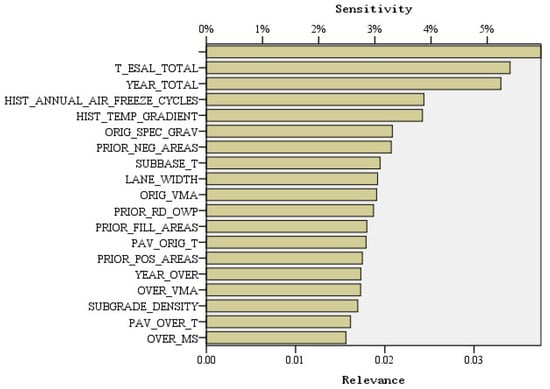
Figure 4.
Importance analysis based on random forest.

Table 2.
Explanations of variables.
According to the ranking results of the importance of the variables shown in Figure 3, the average annual number of freeze–thaw cycles and historical average daily temperature gradient have a great influence on rutting, in addition to the ESALs and service years. In addition, the structure of the surface layer and the material of the surface layer play important roles in rutting, especially the asphalt surface thickness and voids in mineral aggregate (VMA). The cumulative rut damage (PRIOR) of the original pavement also has a great impact on the pavement performance after repair. If the surface layer is not properly treated before paving, then it will provide an uneven underlayer structure to the renovated pavement. Thus, it is necessary to conduct a thickness milling treatment for the original road before overlay repair.
According to the above parameter sensitivity analysis, it is considered that the rutting of the repaired pavement is closely related to the cumulative damage of the original pavement and the repair treatment scheme, in addition to traffic and other environmental conditions.
3.4. Analysis of Predicted Results
By comparing the deviation between the measured value and predicted value and the error distribution, the prediction model’s performance for the rutting development trend of the repaired pavement can be investigated. Figure 5 shows the comparison results.
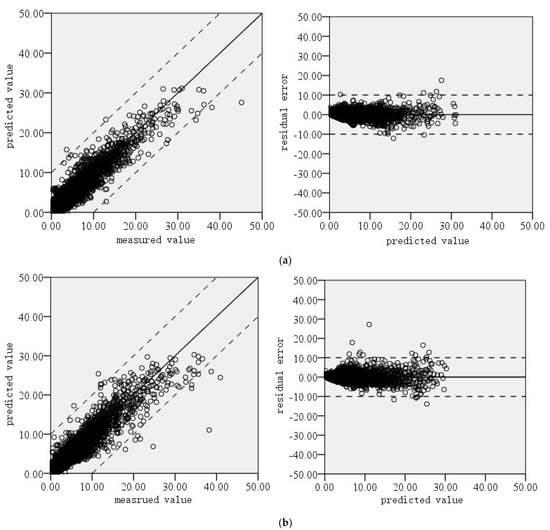
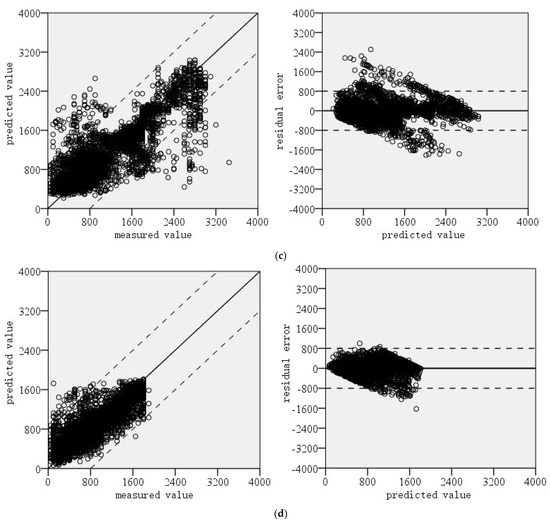
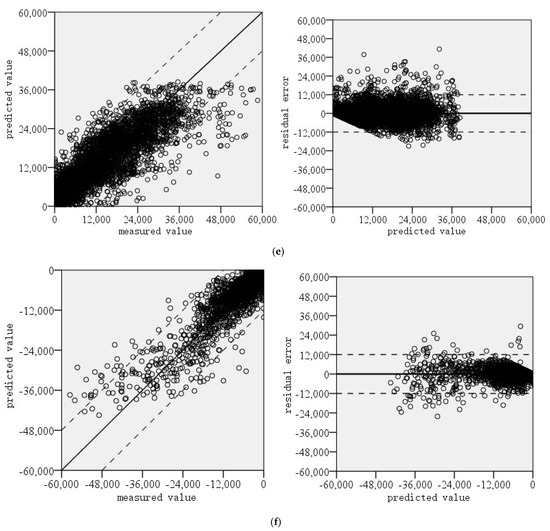
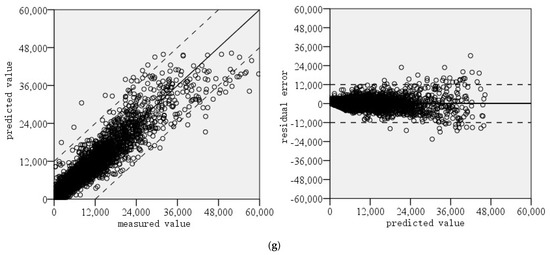
Figure 5.
Error analysis of rutting prediction: (a) left rut depth; (b) right rut depth; (c) left wheel track width; (d) right wheel track width; (e) cross-section positive area; (f) cross-section negative area; (g) cross-section total filled area.
The comparison results indicate that the model has a poor prediction performance for the width of the road wheel track and the area of the cross-section, while it has a good prediction performance for the rut depth on the left and right sides of the road and the total filling area of the road cross-section. Among the three target variables with good prediction performances, large errors mainly appear in the parts with high absolute values of sample points. The smaller the absolute value of the service time, the better the prediction result. This may be because the point with a smaller value is almost in the stage where the pavement data collection is complete, and the regularity is obvious. In the early rutting development stage, the damaging trend is linear, while in the later stage, the damaging trend is more complex, and the rutting development trend is more uncertain.
The rut depth on the left and right sides and the characteristics of the total filling area of the rut cross-section were plotted as curves over time, as shown in Figure 6. It can be seen that the rut depth generally increases with the cumulative service time, which is consistent with the actual development law.
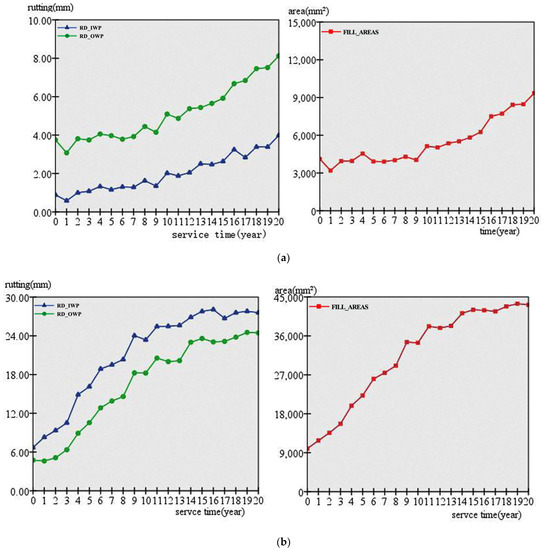
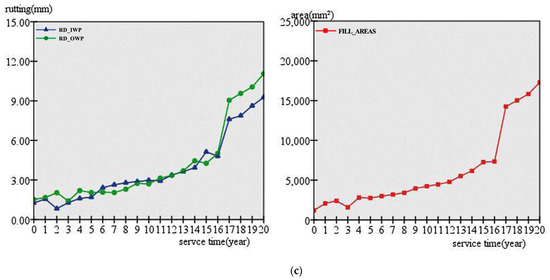
Figure 6.
Rutting prediction of each test section: (a) CSHRP_ID: 810401, SECTION: 1; (b) CSHRP_ID: 860501, SECTION: 1; (c) CSHRP_ID: 900803, SECTION: 1 (“CSHRP_ID” represents the number of test points, and “SECTION” represents the number of test sections).
The rut depths of different test sections are different. Moreover, the development trend of the rut depth is different at the same test site when different pavement repair and overlay schemes are adopted. Some sections exhibited a linear growth basically (Figure 6a,b), while some other sections exhibited an obvious accelerated growth with the service year (Figure 6c). This indicates that the development trend of pavement rutting after the repair is closely related to the selection of the repair program. In the same test section, the growth trend of the cross-section filled area is very close to that of the rut depth. The effect of using the two-dimensional surface cross-section area index is similar to that of using the one-dimensional rut-depth index to express the rut quantity on the road surface. Thus, the rut depth and total filling area of the cross-section can be taken as the characteristic indexes to describe rutting, which can better reflect the trend of the rutting changes with the service time.
4. Evaluation Index and Maintenance Management Based on Rutting
According to the rutting development trend predicted above, the rutting depth is chosen as the evaluation indicator. Figure 7presents the extraction method of the rutting index.
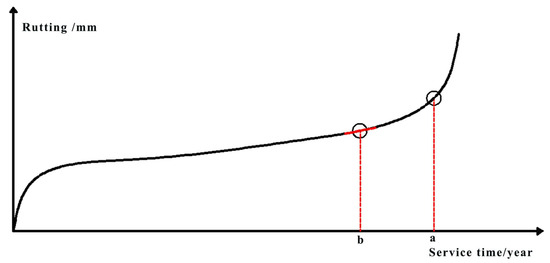
Figure 7.
Development of rutting in asphalt overlay [38].
In Figure 7, Point a represents the maintenance time based on the rut-depth accumulation, while Point b represents the maintenance time at which the rutting growth trend changes. The minimum value between a and b is taken as the actual maintenance time.
A rutting evaluation was conducted for the 65 test sections treated with different repair schemes in each test section, and the pavement maintenance time threshold was determined. The results are listed in Table 3.

Table 3.
Time threshold of pavement maintenance based on rutting prediction.
5. Conclusions
The study focused on the rutting of pavement repair with overlay. A rutting prediction model was established using an artificial neural network, and the pavement evaluation index and maintenance time were investigated based on the rutting development trend. The data used were obtained from the LTPP, with reliable data accumulated over many years of observations, making the model very reliable.
According to the results of the parameter sensitivity analysis, the rutting of the repaired pavement is not only affected by the basic service environment, such as traffic and climate, but it is also closely related to the cumulative damage of the original pavement and the pavement repair and treatment scheme. This provides a reference for selecting rutting influencing factors. Moreover, besides the axle load and time, the number of freeze–thaw cycles and daily average temperature have the greatest influence on rutting. Additionally, the surface structure and surface material have a great influence on the rutting after repair, especially the thickness of the surface layer and the voids filled in the mixture (VMA).
When describing rutting development, the characteristic indexes of the depth of the pavement ruts and the total filling area of the pavement cross-section are more representative. In this study, the evaluation index of pavement ruts was established by predicting the rutting development trend of overlay-repaired pavement and combining it with the mechanical properties of the pavement asphalt mixture. The maintenance time threshold of pavement ruts was proposed for each test section after the overlay repair, which provided a reference for the maintenance of the overlay-repaired pavement.
In addition, the results and discussion provide a reference for the optimization of rut prediction models for evaluating the performance of asphalt pavement. The prediction of rutting in this paper is based on a large amount of historical observation data, but it does not involve the mechanical mechanism of the pavement structure. In the future, the damage mechanism of pavement repair with flexible overlay can be further investigated, and the empirical analysis can be refined to scientific theory. This paper studies the rutting development of flexible asphalt pavement, and the rutting of cement concrete pavement should be explored in the future. Cement concrete pavement repaired with asphalt overlay is a common measure to improve the pavement performance and extend the pavement life. However, the modulus of the old cement panel is very different from that of asphalt concrete, and asphalt overlay concrete is more prone to rutting. It can be predicted by establishing machine learning models. The international roughness index (IRI), cracks, and texture depth, which are also important pavement performance indicators, can be downloaded from the LTTP database. Multiple machine learning methods, such as support vector machine, random forest, adaptive boosting, and other reinforcement learning for predicting them, are also going to be established in the future.
Author Contributions
Conceptualization, L.W. and H.Y.; methodology, C.Y. and C.C.; software, C.Y.; validation, C.C. and H.Y.; formal analysis, H.Y.; investigation, C.Y. and C.C.; resources, H.Y.; data curation, C.Y.; writing—original draft preparation, C.C. and C.Y.; writing—review and editing, H.Y.; visualization, C.Y.; supervision, L.W.; project administration, H.Y.; funding acquisition, L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data can be acquired by freely downloading from the online website (https://infopave.fhwa.dot.gov, accessed on 2003).
Conflicts of Interest
The authors declare that they have no conflicts of interest regarding the publication of this paper.
References
- Wang, C.; Xu, S.; Liu, J.; Yang, J.; Liu, C. Building an improved artificial neural network model based on deeply optimizing the input variables to enhance rutting prediction. Constr. Build. Mater. 2022, 348, 128658. [Google Scholar] [CrossRef]
- Chen, L.; Liu, G.; Qian, Z.; Zhang, X. Determination of allowable rutting depth based on driving safety analysis. J. Transp. Eng. 2020, 146, 04020023. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Zheng, C.; Wang, L. Optimizing asphalt mix design through predicting effective asphalt content and absorbed asphalt content using machine learning. Constr. Build. Mater. 2022, 325, 126607–126622. [Google Scholar] [CrossRef]
- Hussan, S.; Kamal, M.; Hafeez, I.; Ahmad, N.; Khanzada, S.; Ahmed, S. Modelling asphaltpavement analyzer rut depth using different statistical techniques. Road Mater. Pavement Des. 2020, 21, 117–142. [Google Scholar] [CrossRef]
- Hui, B. Failure Pattern Recognition, Multi-Dimensional Indicators Evaluation and Prediction of Rutting in Asphalt Pavement. Ph.D. Thesis, Chang’an University, Chang’an, China, 2013. [Google Scholar]
- Sun, Y.; Choand, N. Development of a rutting performance model for asphalt concrete pavement based on test road and accelerated pavement test data. KSCE J. Civ. Eng. 2014, 18, 165–171. [Google Scholar]
- Ji, X.; Zheng, N.; Niu, S.; Meng, S.; Xu, Q. Development of a rutting prediction model for asphalt pavements with the use of an accelerated loading facility. Road Mater. Pavement Des. 2016, 17, 15–31. [Google Scholar] [CrossRef]
- Wu, T.; Cao, J.; Ma, T.; Huang, W.; Zhou, Z.; Chen, B. Development of rutting forecasting models for distinct asphalt pavement structures in RIOH testing track using different approaches. Constr. Build. Mater. 2023, 368, 130483. [Google Scholar] [CrossRef]
- Liu, G.; Chen, L.; Qian, Z.; Zhang, Y.; Ren, H. Rutting prediction models for asphalt pavement with different base types based on RIOHTrack full-scale track. Constr. Build. Mater. 2021, 305, 124793. [Google Scholar] [CrossRef]
- KAbaza, A.; Ashur, S.A.; Ai-Khatib, I. Integrated Pavement Management System with a Markovian Prediction Model. J. Transp. Eng. 2004, 130, 24–33. [Google Scholar]
- Jiménez, L.; Mrawira, D. Bayesian regression in pavement deterioration modeling: Revisiting the AASHO road test rut depth model. Infraestruct. Vial 2012, 14, 28–35. [Google Scholar]
- Hong, F.; Prozzi, J.A. Estimation of pavement performance deterioration using Bayesian approach. J. Infrastruct. Syst. 2006, 12, 77–86. [Google Scholar] [CrossRef]
- Canadian Strategic Highway Research Program. Canadian Long-Term Pavement Performance (C-LTPP): Database User’s Guide, 2nd ed.; Transportation Research Board: Washington, DC, USA, 1997. [Google Scholar]
- Liu, F.; Ding, W.; Qiao, Y.; Wang, L. An artificial neural network model on tensile behaviorof hybrid steel-PVA fiber reinforced concrete containing fly ash and slag power. Front. Struct. Civ. Eng. 2020, 14, 1299–13155. [Google Scholar] [CrossRef]
- Gong, H.; Sun, Y.; Mei, Z.; Huang, B. Improving accuracy of rutting prediction for mechanistic-empirical pavement design guide with deep neural networks. Constr. Build. Mater. 2018, 190, 710–718. [Google Scholar] [CrossRef]
- Alharbi, F.; Smadi, O. Predicting pavement performance utilizing artificial neural network (ANN). Int. J. Adv. Eng. Manag. Sci. 2019, 5, 504–508. [Google Scholar] [CrossRef]
- Okuda, T.; Suzuki, K.; Kohtake, N. Proposal and evaluation of prediction of pavement rutting depth by recurrent neural network. In Proceedings of the 2017 6th IIAI International Congress on Advanced Applied Informatics (IIAI-AAI), Hamamatsu, Japan, 9–13 July 2017; pp. 1053–1054. [Google Scholar]
- Schlotjes, M.; Burrow, M.; Evdorides, H.; Henning, T. Using support vector machines to predict the probability of pavement failure. In Proceedings of the Institution of Civil Engineers-Transport; University of Birmingham: Birmingham, UK, 2015; Volume 168, pp. 212–222. [Google Scholar]
- Haddad, A.; Chehab, G.; Saad, G. The use of deep neural networks for developing generic pavement rutting predictive models. Int. J. Pavement Eng. 2021, 23, 4260–4276. [Google Scholar] [CrossRef]
- Karballaeezadeh, N.; Mohammadzadeh, S.D.; Shamshirband, S.; Hajikhodaverdikhan, P.; Mosavi, A.; Chau, K.-W. Prediction of remaining service life of pavement using an optimized support vector machine (case study of Semnan–Firuzkuh road). Eng. Appl. Comput. Fluid Mech. 2019, 13, 188–198. [Google Scholar] [CrossRef]
- Choi, S.; Do, M. Development of the road pavement deterioration model based on the deep learning method. Electronics 2019, 9, 3. [Google Scholar] [CrossRef]
- Lee, Y.; Sun, J.; Lee, M. Development of deep learning based deterioration prediction modelfor the maintenance planning of highway pavement. Korean J. Constr. Eng. Manag. 2019, 20, 34–43. [Google Scholar]
- Thube, D.T. Artificial neural network (ANN) based pavement deterioration models for low volume roads in India. Int. J. Pavement Res. Technol. 2012, 5, 115. [Google Scholar]
- Abo-Hashema, M. Artificial neural network approach for overlay design of flexible pavements. Int. Arab J. Inf. Technol. (IAJIT) 2009, 6, 204–212. [Google Scholar]
- Abiola, O.S.; Owolabi, A.O.; Sadiq, O.M. Application of dynamic artificial neural network for modelling ruts depth for lagos-ibadan expressway, Nigeria. ARPN J. Eng. Appl. Sci. 2012, 7, 987–991. [Google Scholar]
- Hall, K.T.; Correa, C.E.; Simpson, A.L. Simpson. Performance of flexible pavement maintenance treatments in the long-term pavement performance SPS-3 experiment. Transp. Res. Rec. 2003, 1823, 47–54. [Google Scholar] [CrossRef]
- Ahmed, A.; Labi, S.; Li, Z.; Shields, T. Aggregate and disaggregate statistical evaluation of the performance-based effectiveness of long-term pavement performance specific pavement study-5 (LTPP SPS-5) flexible pavement rehabilitation treatments. Struct. Infrastruct. Eng. 2013, 9, 172–187. [Google Scholar] [CrossRef]
- Dong, Q.; Huang, B. Evaluation of effectiveness and cost-effectiveness of asphalt pavement rehabilitations utilizing LTPP data. J. Transp. Eng. 2012, 138, 681–689. [Google Scholar] [CrossRef]
- Elinks, G.E.; Schmalzer, P.N.; Travis, T.; Amy, S. Long-Term Pavement Performance Information Management System: Pavement Performance Database User Reference Guide; U.S. Department of Transportation Federal Highway Administration Research, Development, and Technology Turner-Fairbank Highway Research Center: McLean, VA, USA, 2003. [Google Scholar]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Anzai, Y. Pattern Recognition and Machine Learning; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Huang, Y. Advances in artificial neural networks–methodological development and application. Algorithms 2009, 2, 973–1007. [Google Scholar] [CrossRef]
- Liu, J.; Liu, F.; Gong, H.; Fanijo, E.O.; Wang, L. Improving asphalt mix design by predicting alligator cracking and longitudinal cracking based on machine learning and dimensionality reduction techniques. Constr. Build. Mater. 2022, 354, 129162. [Google Scholar] [CrossRef]
- Alavi, A.H.; Ameri, M.; Gandomi, A.H.; Mirzahosseini, M.R. Formulation of flow number of asphalt mixes using a hybrid computational method. Constr. Build. Mater. 2011, 25, 1338–1355. [Google Scholar] [CrossRef]
- Latecki, L.J.; Lazarevic, A.; Pokrajac, D. Outlier Detection with Kernel Density Functions, International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Cham, Switzerland, 2007; pp. 61–75. [Google Scholar]
- Probst, P.; Boulesteix, A.-L.; Bischl, B. Tunability: Importance of hyperparameters of machine learning algorithms. J. Mach. Learn. Res. 2019, 20, 1934–1965. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Zhang, D.L. Asphalt Mavement; China Communications Press: Beijing, China, 1999; pp. 23–38. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).