Abstract
Optimising a swarm of many robots can be computationally demanding, especially when accurate simulations are required to evaluate the proposed robot configurations. Consequentially, the size of the instances and swarms must be limited, reducing the number of problems that can be addressed. In this article, we study the viability of using surrogate models based on Gaussian processes and artificial neural networks as predictors of the robots’ behaviour when arranged in formations surrounding a central point of interest. We have trained the surrogate models and tested them in terms of accuracy and execution time on five different case studies comprising three, five, ten, fifteen, and thirty robots. Then, the best performing predictors combined with ARGoS simulations have been used to obtain optimal configurations for the robot swarm by using our proposed hybrid evolutionary algorithm, based on a genetic algorithm and a local search. Finally, the best swarm configurations obtained have been tested on a number of unseen scenarios comprising different initial robot positions to evaluate the robustness and stability of the achieved robot formations. The best performing predictors exhibited speed increases of up to 3604 with respect to the ARGoS simulations. The optimisation algorithm converged in 91% of runs and stable robot formations were achieved in 79% of the unseen testing scenarios.
1. Introduction
Robot formations, as a part of swarm intelligence, consist of a group of robots showing a collective behaviour, which is usually achieved from emerging collaborations with the objective of performing some specific global tasks. Unmanned Aerial Vehicles (UAVs), as swarm members in a formation, can be arranged in a specific three-dimensional shape to perform different types of missions, such as surveillance [1], synchronisation of spacecrafts [2], salvage missions [3], and localisation and mapping [4], as well as representing dynamic deforming figures [5]. These types of missions usually present problems such as the unknown initial positions of the swarm members, as well as the need for path planning from these positions to the final locations. There is also a challenging adaptability to real situations, e.g., asteroid observation or escorting a rogue drone (RD) out of a restricted area, especially when there are collisions, communication losses, or robot failures. This problem cannot be accurately represented using a mathematical model where UAV iterations, such as collision avoidance manoeuvres, have to be taken into account. Therefore, a simulator is frequently used to model these real-world problems.
Simulating a UAV swarm in a 3D space often uses a high amount of computing resources (and time) to achieve high levels of accuracy, especially when using a multi-physics robot simulator, e.g., ARGoS [6]. The use of a communication layer plus an inertial model for calculating each simulation step demands from seconds to minutes, depending on the number of robots modelled [7]. Optimising these problems requiring simulations rapidly becomes unaffordable, usually due to the high number of evaluations needed to successfully obtain an optimal solution. Hence, an alternative technique, e.g., surrogate models, has been proposed to successfully complete such studies.
Bayesian optimisation, as a surrogate model [8], can be used to estimate the fitness value for the objective function during an optimisation process. It leads to an efficient reduction in the computation times required to evaluate expensive optimisation problems. Evolutionary algorithms (EAs) and gradient methods have been used in combination with surrogate models [9]. They have been applied to different problems such as modelling circuits and systems [10], forecasting wildfires [11], predicting noise emission and aerodynamic performance of propellers [12], sustainable building design [13], and modelling groundwater [14].
In previous research works [7], we have found evidence that the optimisation of UAV formations consisting of swarms of more that ten robots requires a high number of computationally expensive simulations, which makes it unaffordable in most cases. In general, the required number of UAVs to efficiently surround a rogue drone is greater than ten in such 3D formations where the virtual sphere’s radius could be several metres. We study in this article the viability of using surrogate models based on Gaussian processes (GPs) and artificial neural networks (ANNs) as predictors of the UAV swarm behaviour when arranged in formation. By doing so, we will be able to address the optimisation of a greater number of UAVs, increasing the efficiency and utility of the robot formation.
The main contributions of this paper are:
- 1.
- The study, training, and testing of six surrogate models to predict the behaviour of a UAV swarm in formation.
- 2.
- A hybrid EA (HEA) to be used as the optimisation algorithm for the parameters of our formation system, which combines simulations and predictions to balance efficiency and accuracy.
- 3.
- The evaluation of the optimised formation swarm in 150 unseen scenarios comprising up to 30 UAVs in terms of accuracy and stability.
The rest of this paper is organised as follows. A review of the state-of-the-art research related to our proposal can be found in the next section. In Section 3, we describe our UAV formation system, the simulation model, and the six proposed surrogate models. The optimisation approach is explained in Section 4, including a description of our optimisation algorithm. The experiments and results are detailed in Section 5. Finally, Section 6 presents the conclusions and future work.
2. Related Works
In this section, we analyse some recent works related to robot simulations using surrogate models. A review addressing computational time, accuracy, and problem size in surrogate models is available in [15], while in [16], the authors surveyed the use of surrogate models in optimisation algorithms.
In [17], a surrogate-based method is used to set up a parameter of the Rössler chaotic system to improve coverage of the CACOC (Chaotic Ant Colony Optimisation for Coverage). The authors proposed Bayesian optimisation to efficiently explore the parameter space, avoiding using costly simulations. Their results show that this method permitted efficient exploration of a bifurcation diagram bypassing periodic regions, providing two groups of points with excellent results in terms of coverage for the swarm.
In [18], the authors present a control system for a quadcopter using several machine learning techniques. Time series, Gaussian processes, and neural networks are proposed to calculate optimum control gains for a specific mission and overcome environmental uncertainties. These predictors are used in an optimisation process and tested using simulations. Their results show performance improvements when compared to nominal control gains due to a better exploration of the search space.
In [19], a surrogate model based on gene expression programming is proposed for the optimisation of an autonomous underwater vehicle’s shape using computational fluid dynamics. This surrogate model of resistance and surrounded volume is also compared with the response surface model. The results obtained using a multi-objective particle swarm optimisation are compared with hydrodynamic calculations. It shows that the reduced computational cost when using the surrogate model and the model’s accuracy improved the optimal shape design.
In [20], a mathematical–computational model for the control and navigation of robots is proposed. The authors use a combination of a 2D cellular automata, Tabu search, ant colonies, and greedy approaches for selecting elitist cells. Then, a genetic algorithm is used to optimise the parameters for two proposed surrogate models. The main objective of this system is the maximisation of area coverage by using a pheromone-based approach. The validation of the models was performed using Webots simulator and E-Puck robots.
In [21], the authors present a surrogate approach using the Kriging method to optimise the design of the delta wing and the canard wing of a tube–fan hybrid UAV. Moreover, a multi-objective genetic algorithm is proposed with the objective of maximising the UAVs lift and minimising the energy consumption. Computational fluid dynamics simulations were used to validate the calculated solutions.
In [22], a distributed Bayesian optimisation framework for deep neuroevolution is presented. An acquisition function is defined to mimic the actual model according to a set of input parameters. The actual model is a neural network with its training dataset and the proposed optimisation strategy, i.e., distributed swarm-based neuroevolution. The authors use the proposed method for training various feed-forward neural networks for pattern classification problems. Their results show a promising performance of the proposed method, which has a reduced computational time for large deep learning problems.
In our present work, we analyse Gaussian processes as well as other methods to calculate an accurate surrogate model for our problem, as some of the aforementioned articles also do. Conversely, we use the best performing predictor to approximate the results from simulations and speed up the optimisation of our 3D formation problem. We have proposed an optimisation algorithm, i.e., a hybrid EA, different to those used in related works, which allowed us to address bigger swarms with affordable execution times.
Summing up, in this article, we propose six surrogate models for the robot formation problem, then train them and analyse the results in terms of accuracy and execution times. After that, we optimise the UAV swarm parameters to achieve stable formations around a central point of interest, e.g., a rogue drone, and test the best configurations in a variety of different initial UAV positions. To the best of our knowledge, no previous work has proposed the comparison of these six surrogate models for robot formation simulations and their use in a hybrid evolutionary optimisation.
3. Proposal
We propose an alternative method for evaluating autonomous UAV swarm formations using surrogate models to reduce evaluation times and increase the accuracy of the optimisation algorithms. In doing so, we are able to increase the size of the UAV swarm, addressing problem instances bigger than in our previous studies. In the following sections, we describe our formation algorithm, the simulation environments, and the proposed surrogate models. After that, a hybrid evolutionary algorithm is proposed to optimise the formation’s parameters using evaluations based on predictions from the surrogate models and actual values from simulations.
3.1. Distributed Formation Algorithm3 (DFA3)
The distributed formation algorithm3 (DFA3) [7] was designed to arrange robots at the vertices of a convex polyhedron surrounding a central point of interest, e.g., a rogue drone trespassing a restricted area. Each UAV calculates its relative orientation and distance to the rest of UAVs based on the beacon signals received from each swarm member. This formation algorithm does not rely on any localisation system, such as GPS, and it works on dynamic scenarios, as the UAV positions are calculated with respect to the other UAVs and to the rogue drone (RD) using attracting and repelling forces to achieve a stable equilibrium. Figure 1a shows fourteen UAVs surrounding a central rogue drone and the attracting/repelling forces between them, while Figure 1b shows the attracting/repelling forces between the central rogue drone and the other UAVs. Only forces involving UAVs i, j, and k were explicitly named as examples, to make sure the figures are comprehensible. As the UAVs move, these forces change their orientation and intensity until the final stable positions are achieved. Hence, each UAV does not have a fixed final position in the formation that is known in advance. In our experiments, the central object is tracked using its own radio signal. However, other methods can be used such as LIDAR (light detection and ranging) or images from onboard cameras.
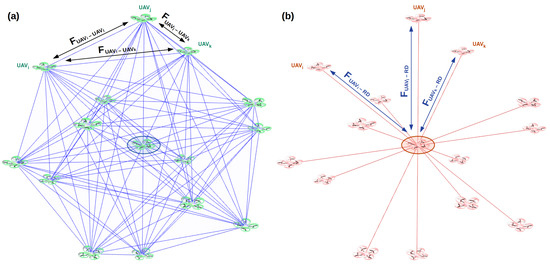
Figure 1.
Swarm of fourteen UAVs escorting the rogue drone at the centre. (a) Attracting/repelling forces between UAVs. (b) Attracting/repelling forces between UAVs in the swarm and the rogue drone. Only forces involving the UAVi, UAVj, and UAVk are represented.
The formation problem is defined by , where the distance graph is given by , where are the UAVs in the swarm, are the edges of the graph indicating the swarm connectivity, and are the distances between UAVs (). Moreover, stands for the central object, the distances between the robots and the central object are given by , and the problem’s constraint is given by , where is the desired distance to the formation centre (sphere radius).
We have observed that stable UAVs formations are frequently hard to achieve, as solving this problem implies taking into account constraints such as the absence of absolute positions, limited communication ranges, and unknown initial conditions. We have proposed in [7] four parameters for the swarm to address these difficulties: a distance threshold to control the attracting/repelling movement between UAVs, the minimum distance to the formation centre (where the rogue drone is), the intensity of the attracting/repelling force with respect to the central object, and the UAV speed, .
The block diagram of our DFA3 is detailed in Figure 2 and its pseudocode can be found in [7]. Each UAV executes the same algorithm using the swarm’s optimal parameters and formation radius, i.e., the desired distance to the rogue drone , which is a constant value. Once the vector is initialised, a calculation of the forces with respect to the other UAVs is performed based on the received beacons and the given distance threshold . In the next step, the same calculation is performed, taking into account the rogue drone at the centre of the desired spherical formation, using the values of and the extra intensity . The calculated inclination and azimuth are finally obtained from the resulting vector to be used as the new moving direction (in 3D space) for the UAV.
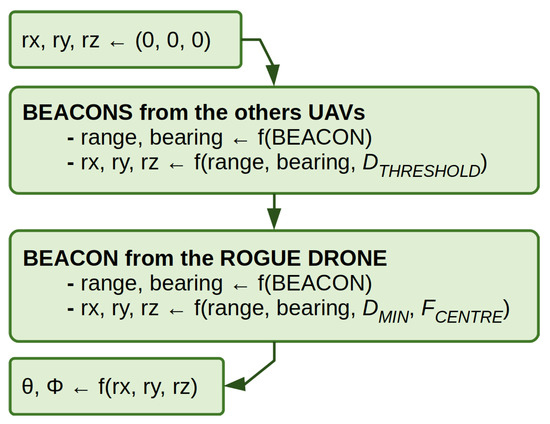
Figure 2.
Block diagram of the distributed formation algorithm3 (DFA3).
The range of the first three UAVs’ parameters depends on the desired distance , i.e., , , while the UAVs’ speed range is .
3.2. Formation Fitness
We have improved the fitness function proposed in [7] to also take into account incorrect configurations producing UAV collisions. The fitness function , shown in Equation (1), is used to evaluate the formation of N UAVs in terms of shape, distance to the centre, and how equally spread the robots are (avoiding local clusters). If there are collisions (the distance between two UAVs is lower than metre), a penalisation value () is used as a result of . Otherwise, three terms are involved in the calculation. The minimum error () and maximum error () are both calculated using the distance from every UAV in the swarm to the centre with respect to the desired distance . The last term () is present to evaluate the UAV distribution throughout a virtual sphere of radius . These terms are to be minimised to obtain accurate formations. Thus, the lower the value of the better.
3.3. ARGoS Simulations and Scenario Modelling
The formation scenarios were modelled in ARGoS [6], a robot simulator capable of efficiently simulating large-scale swarms of robots of any kind. The selected robot model was the Spiri UAV [23] (a 47 × 47 × 9-centimetre quadrotor), while the communications were implemented using the ARGoS’ Range and Bearing model (Figure 3). Each UAV only has access to the relative distances and angles to the other swarm members and to the rogue drone, calculated from the received beacon signals. The UAVs start at different initial positions and move towards the rogue drone, avoiding collisions and arranging in a stable formation. During their journey, they are subject to many iterations which make the final positions hard to calculate without using a simulator.
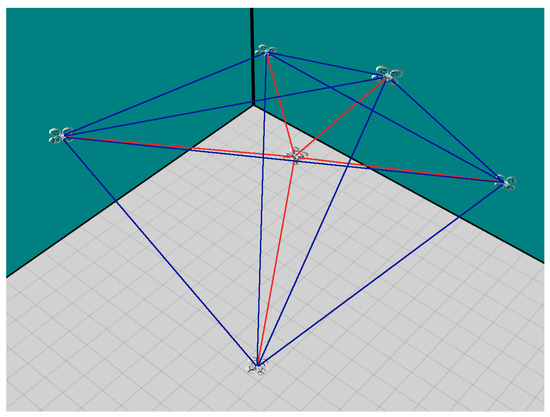
Figure 3.
Robot formation in the ARGoS simulator (swarm of five UAVs). Communications among swarm members are in blue. Rogue drone detections are in red.
The DFA3 is executed onboard each UAV and was parameterised using the aforementioned formation parameters, i.e., , , , and . Obtaining a stable formation depends on the values of these parameters, requiring an optimisation process which takes into account the distance to the centre () and the number of UAVs. In this article, we propose the study of swarms of three, five, ten, fifteen, and thirty UAVs, tripling our previous studies. This can only be possible if we use surrogate models to replace the costly simulations.
3.4. Realistic Simulations vs. Surrogate Models
We initially tested our formation algorithm in a 2D environment using E-Puck2 robots [24] and also compared it with other approaches. We then proposed an extension of the algorithm to deal with 3D formations using UAVs [7]. The inherent complexity of this problem required the use of a meta-heuristic, e.g., our HEA, to successfully calculate the optimal parameters of the formation algorithm. As aforementioned, evaluating each configuration required costly simulations using detailed dynamics. Although our HEA successfully optimised the parameters of the DFA3, we observed that the whole process was taking too long for large swarms (720 h for 30 runs optimising a swarm of 10 UAVs), limiting the number of UAVs we were able to use. Therefore, in this article, we study the use of surrogate models [25] to speed up the evaluation of the formation parameters, allowing not only having more robots in the swarm (we plan to reach 30 UAVs), but also allowing more accurate optimisations by increasing the number of evaluations and improving the optimisation algorithm’s solutions.
3.5. Surrogate Models
We propose six surrogate models to predict the result of the ARGoS simulations in order to reduce evaluation times. Five are based on Gaussian processes and the sixth uses an artificial neural network. We describe them in the following.
3.5.1. Gaussian Processes (GPs)
Bayesian optimisation aims to solve black box problems by generating surrogate models of the problems using Gaussian processes (GPs) [26]. GPs are both interpolators and smoothers of data and can be used as effective predictors when the solutions’ landscape ( in our study) is a smooth function of the parameter space. It calculates a distribution of the objective function by sampling promising zones of the solution space. The Gaussian distribution associated with the training data is given by a mean vector and a covariance matrix, calculated by a kernel function. We propose testing five different kernel functions, (linear), (squared exponential), (neural network), (Matérn ), and (Matérn ), provided by the R package “gplite” [27]. We set up 1000 maximum iterations and 100 restarts for training each of these predictors.
3.5.2. Artificial Neural Network (ANN)
Artificial neural networks (ANNs) have been used in numerous machine learning research works in recent years. We propose an artificial neural network with four neurons as inputs corresponding to our problem’s variables, one output neuron, and five neurons in the hidden layer (experimentally chosen taking into account the required training time). The activation function used was logistic, except for the output neuron, which used a linear function to fit our problem characteristics. We used resilient backpropagation (RPROP) with weight backtracking [28] during the training process, which performs a direct adaptation of the weight step based on local gradient information. We used the recommended learning rate factors and . RPROP has the advantage that for many problems, no choice of parameters is needed to obtain optimal convergence times. We used the R package “neuralnet” [29] to implement this predictor and trained it for 100 epochs to select the best calculated network (minimum error).
4. Optimisation Approach
Our optimisation algorithm is a hybrid evolutionary algorithm (HEA) whose block diagram is shown in Figure 4. It consists of a first stage where a genetic algorithm (GA) uses the first 95% of evaluations (950 in our study) to explore the solution space, converging to competitive solutions [30]. After that, a local search (LS) explores the neighbourhood of the best solution found by the GA to improve the algorithm’s result by using a high-level relay hybridisation (HRH) approach [31].
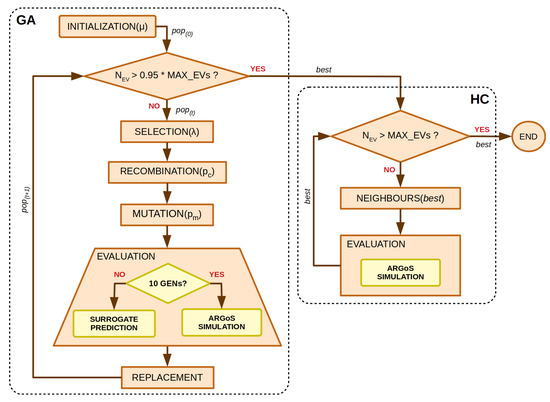
Figure 4.
Block diagram of the hybrid evolutionary algorithm (HEA).
Genetic algorithms mimic processes present in evolution such as natural selection, gene recombination after reproduction, gene mutation, and the dominance of fittest individuals over the weaker ones. Our proposed GA follows a steady-state design, where an offspring of individuals is obtained from the population , so that the auxiliary population Q contains a subset of individuals from the population .
Following the HEA diagram, first of all, the Initialisation function fills the population with random individuals. Secondly, the main loop is executed until the termination condition is fulfilled (950 evaluations). Binary Tournament [32] was used as the selection operator, Uniform Crossover [33] was used as the recombination operator (), and Integer Polynomial Mutation [34] was used as the mutation operator (), where L is the length of the solution vector. After each generation, an elitist replacement was used to update the algorithm population. Note that for the initial population and each 10 generations, ARGoS simulations were used to evaluate the individuals in order to update their fitness value if needed. Otherwise, the faster predictions provided by a surrogate model were used.
After the GA stage, the best solution obtained becomes the starting point of the hill climbing algorithm [35] (HC). It explores the best solution neighbourhood during the last 50 evaluations following the gradient of the solution with the best fitness, improving the solution found by the GA. At each iteration of the HC algorithm evaluates the solutions next to the current best one, keeping it in case of finding a better fitness. Therefore, once we first explored the search space using the GA, we exploit the best solution found using the proposed HC. The HC algorithm does not require any parameterisation other than the maximum number of evaluations.
5. Experiments and Results
In this section, we describe the proposed case studies, the experiments conducted, and their results. A schema presenting all the experimentation processes is shown in Figure 5. First, actual data are collected from the simulated scenarios to train the surrogate models. Second, once the six surrogate models have been trained, they are tested using the testing dataset to select the best performing predictor for the next stage. Third, now the optimisation of the swarm parameters is conducted using the DFA3, the selected surrogate model, and the ARGoS simulations to evaluate the individuals of the HEA. Finally, the optimal parameters are used to test our formation algorithm on 30 unseen scenarios per case study to address its robustness. The source code of the DFA3, the problem instances, surrogate models, and datasets are available at https://gitlab.uni.lu/adars/dfa3 (accessed on 9 May 2023).
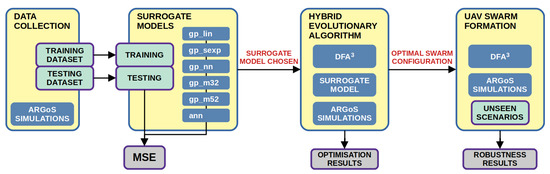
Figure 5.
Schema of the experiments proposed. First, data are collected from ARGoS simulations to train the surrogate models and test them. Second, the best surrogate model is used by the proposed hybrid EA to optimise the UAV swarm parameters. Finally, the optimal parameterisation is tested on a set of unseen scenarios to address the system robustness.
5.1. Case Studies and Scenarios
We propose five case studies comprising swarms of three, five, ten, fifteen, and thirty UAVs. We have calculated 100 scenarios per case study where the UAVs begin the simulation at different positions, away from the rogue drone at the centre, in order to address different initial conditions which also require different trajectories to achieve the desired formation. The UAVs’ initial positions for each case study are shown in Figure 6, where each scenario is represented by a different colour. In addition, a 10 metre radius sphere has been left empty at the centre to simulate the UAVs approaching the rogue drone from different distant points.
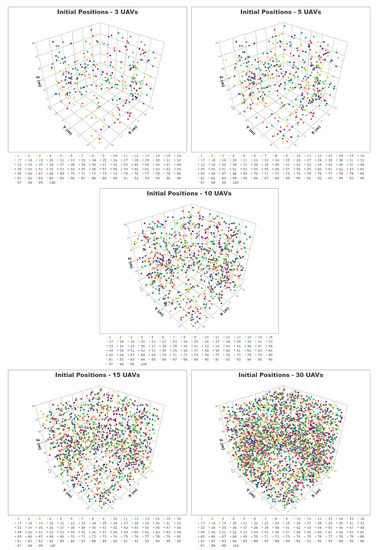
Figure 6.
UAVs’ initial positions for the five case studies (100 scenarios per case study). The UAVs in each scenario are represented by a different colour.
These scenarios were modelled in ARGoS using the Spiri UAV model. We worked in an area of 30 × 30 × 30 m. However, the system can be adapted to other area dimensions by scaling the UAVs’ parameters appropriately [24]. The formation radius () used was three metres for swarms of three, five, and ten UAVs, whereas four and five metre radii were used for swarms of fifteen and thirty UAVs, respectively. This was necessary since more UAVs require more space to form a successful formation in order to avoid collisions. The characteristics of the proposed case studies are detailed in Table 1.

Table 1.
Characteristics of the five proposed case studies.
The UAVs move in the direction provided by the DFA3 running onboard, keeping the parametrised speed (). Since the same repelling forces between UAVs prevent them from being too close to each other, no extra collision avoidance algorithm was needed, providing the swarm parameters are optimal, allowing it to work as intended.
5.2. Experimental Setup
The optimisation algorithm was implemented using the jMetalPy package [36]. Our experiments were executed in parallel runs using computing nodes of the HPC facilities of the University of Luxembourg [37], equipped with Intel Xeon Gold 6132 @ 2.6 GHz processors and 128 GB of RAM.
5.3. Data Collection
We calculated the training and testing dataset from ARGoS simulations using randomly generated parameters for each UAV swarm. The training dataset consisted of 300 configurations for each swarm and their corresponding fitness value, which was calculated as shown in Equation (1). The testing dataset was obtained from the evaluation of 2700 configurations per case study. We removed the configurations that ended up in UAV collisions, usually happening when the swarm was misconfigured. They represent discontinuities in the fitness function which unnecessarily complicate the training process and it would have been unfair if we had used them later for testing the surrogates’ accuracy.
5.4. Surrogate Training
For training the proposed predictors, we calculated the aforementioned training dataset. We propose the Mean Square Error (MSE) as a metric to evaluate the predictors’ accuracy. It is calculated as shown in Equation (5), where n is the number of data points, are the observed values (from ARGoS), and are the estimated values (from predictors).
Table 2 shows the results of the training of the six predictors using surrogate models. The number of observations is lower when the number of UAVs is higher, as collisions are more likely to happen, increasing the number of invalid parameter values. GP using neural networks as the kernel function () showed the most accurate results in terms of the MSE. ANN as a predictor showed an accuracy comparable with the rest of the GPs, although they were not the most competitive results. Note that the GP using a linear kernel did not converge for swarms of five UAVs.

Table 2.
MSE values for the training process of predictors based on GPs and an ANN. Note that (*) did not converge for five UAVs. Best values are in bold.
Table 3 shows the elapsed training times for each predictor. It can be seen that GP models are quite fast compared to the ANN (61.3 times faster on average). All models exhibit that their training speed depends on the size of the training dataset, as expected.

Table 3.
Elapsed training times in seconds for the six predictors. Note that (*) did not converge for five UAVs. Best values are in bold.
Taking into account the training times plus their accuracy during the training stage, GP models look promising as surrogate models for the simulations of UAV swarm formations. In the next section, we test all the calculated predictors on a number of unseen scenarios and configurations to address their accuracy beyond the training dataset.
5.5. Surrogate Testing
Testing the surrogate models consisted of calculating the MSE values using the predicted values and the actual fitness values obtained from ARGoS simulations. Table 4 shows the MSE values for each predictor. As we did during the training stage, the configurations producing UAV collisions were removed as they were not taken into account. It can be seen that all GP predictors (except ) performed well, with being the most promising one, despite Matérn being slightly better for swarms of ten robots. As observed during the training process, the proposed ANN predictors did not produce results good enough to compete with GPs.

Table 4.
MSE values for the predictions performed using the GP and ANN models compared with ARGoS simulations. Best values are in bold.
We also studied the time elapsed for calculating the fitness for a given configuration of a UAV swarm using the different surrogate models and compared them to simulations using ARGoS. Table 5 shows the different average execution times calculated from 30 evaluations per swarm. We can see that all the surrogate models are faster than ARGoS simulations, as expected. Moreover, the elapsed prediction times showed minimal variations with respect to the number of UAVs. This is especially interesting for 30 UAVs, where the achieved increase in speed was more than 3600.

Table 5.
Average computing times in seconds for the six predictors compared with the corresponding ARGoS simulations (30 testing scenarios). Best values are in bold.
In the following section, we use the surrogate model based on to predict the fitness value of the different configurations calculated during the optimisation of the UAV swarm using our proposed HEA.
5.6. Evolutionary Optimisation
We performed 30 runs of our proposed HEA per case study to optimise the swarm parameters using surrogate models combined with ARGoS simulations. We have optimised one new, unseen scenario (different initial conditions from all the included in the training and testing datasets) to test the surrogate model () in an unseen situation. The achieved optimisation results are shown in Table 6 which presents the minimum and mean fitness values obtained from the 30 runs and their standard deviation. Moreover, the mean elapsed time is reported, which was about one and a half hour for 10 UAVs. It shows the improvement associated with the use of surrogate models, as we spent 9 h per run in our previous work [7] based only on simulations (now it is 6.4 times faster). This also allowed us to optimise swarms of 15 and 30 UAVs in a reasonable time, e.g., 2.6 and 19.8 h on average, respectively. Given the stochastic nature of the initial population of the HEA, some optimisation runs did not converge (1 for 5 UAVs and 12 for 15 UAVs), despite beginning with 100 randomly generated individuals. In the following section, we evaluate how robust these configurations are when tested on 30 unseen scenarios.

Table 6.
Results from the optimisation of one new, unseen scenario for each case study. Best values are in bold.
5.7. Robustness Evaluation
We evaluated the optimisation process in terms of accuracy and reliability in the previous section. Now, we also want to address the robustness of HEAs solutions. Having been initially fitted to one particular scenario, now they are tested on a new set of 30 unseen scenarios per case study. To do this, we run the corresponding ARGoS simulations using the calculated swarm configuration and collected data from the formation achieved by the swarm.
Table 7 shows the evaluation of the formation through the obtained fitness values, the distance between UAVs (DUAV), and the distance to the rogue drone at the centre (DRD) for all the scenarios in which a successful formation was achieved. It can be seen that the measured DRD was always closer to the desired , i.e., 3 m for 3, 5, and 10 UAVs; 4 m for 15 UAVs; and 5 m for 30 UAVs. The distance between UAVs (DUAV) showed little variations, representing equally spaced UAVs in the formation, except for the most difficult case, i.e., 30 UAVs, although the variation is still lower than 13%. We have observed that for swarms of 10, 15, and 30 UAVs, there were some formation attempts that failed: 9, 13, and 10. Observing more than 50% successful formations is a good result, as the HEA has optimised only one particular scenario, in contrast to the 30 tested in this section. An increase in the robustness can be easily achieved by optimising not just one but several scenarios in parallel and using the average fitness values obtained to evaluate each swarm configuration, as has been previously observed in [7,24].

Table 7.
Fitness, distance between UAVs, and distance to the rogue drone in metres, all collected from the tests performed on 30 unseen scenarios per case study. Best values are in bold.
Finally, we present in Figure 7 the final positions achieved by the UAV swarm in all the working formations. Although it is not easy to appreciate how the UAVs are arranged in a virtual sphere, this figure complements the data reported in Table 7, where each colour corresponds to a different scenario. Moreover, each sphere radius is in accordance with the desired distance to the centre, i.e., 3 m for 3, 5, and 10 UAVs; 4 m for 15 UAVs; and 5 m for 30 UAVs.
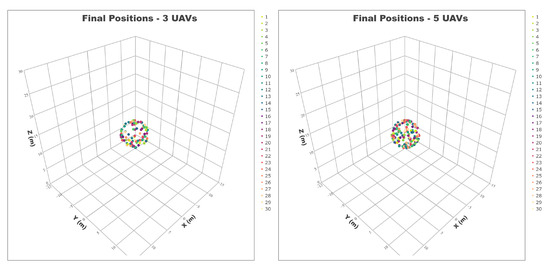
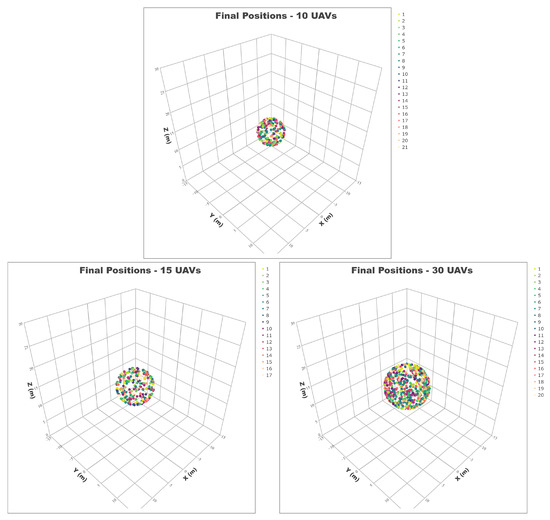
Figure 7.
UAVs’ final positions for the five case studies (scenarios ending in stable formations). The UAVs in each scenario are represented by a different colour.
6. Conclusions
In this article, we have proposed the training and testing of six surrogate models to be used as predictors of the formation accuracy of swarms of three, five, ten, fifteen, and thirty UAVs. We have defined the formation problem, described by our distributed formation algorithm (DFA3), and proposed six predictors, five based on Gaussian processes (GPs) and one based on an artificial neural network (ANN). Then, we have calculated two datasets using real ARGoS simulations. The first was used to train the predictors and the second was used to test their accuracy in terms of the median square error (MSE) and the computation time. After that, we optimised a new scenario (different initial UAV positions) using our proposed hybrid evolutionary algorithm (HEA) to obtain optimal configurations for each UAV swarm. Finally, we tested the best configurations achieved on 30 unseen scenarios per case study to evaluate the robustness of the calculated configurations.
Our results show that GP predictors using a neural network kernel achieved the best results in accuracy and they were also very competitive in terms of execution times, achieving speed increases of up to 3604 with respect to the ARGoS simulations. This allowed us to experiment with UAV swarms featuring up to 30 UAVs, which was impossible to do when we used only ARGoS simulations. During the optimisation process, the HEA converged in most of the runs (96.7% for 5 UAVs, 60% for 15 UAVs, and 100% for the rest). The main reason for not having 100% convergence was due to the lack of valid configurations in the initial population of the HEA, which were then difficult to produce during the evolutionary process. Finally, when testing the best achieved configurations, we obtained 100% successful formations for 3 and 5 UAVs, 70% for 10 UAVs, 56.7% for 15 UAVs, and 66.7% for 30 UAVs. These numbers can be further improved if needed, after optimising a higher number of scenarios simultaneously, instead of just one as we have done during our optimisation approach. However, this would require more parallel evaluations as well as longer optimisation runs. All in all, we found that in the most difficult situation (only one optimisation scenario), our formation proposal based on the DFA3, surrogate models, and ARGoS simulations plus the HEA worked on 79% of the new, unseen scenarios where it was tested, reducing optimisation times by 920% on average.
We have observed some limitations of the proposed method, including the need to train the predictors with a set of random scenarios, which may not be a good representation of the problem characteristics, the impossibility of including the scenarios that ended up in UAV collisions in the training sets, and although the majority of formations were stable, 21% of unstable formations were due to the UAVs not forming a virtual sphere around the rogue drone.
In future work, we aim to pursue this research line, trying different training strategies, e.g., implementing k-fold cross validation to increase the model accuracy. We plan to validate our proposal using real UAVs, such as Bitcraze’s Crazyflies. This would require increasing the number and diversity of optimisation scenarios to ensure that the DFA3 could be used for a variety of initial conditions.
Author Contributions
Conceptualisation, D.H.S. and G.D.; methodology, D.H.S.; software, D.H.S.; validation, D.H.S.; formal analysis, D.H.S.; investigation, D.H.S.; resources, G.D.; writing—original draft preparation, D.H.S.; writing—review and editing, D.H.S. and G.D.; visualisation, D.H.S.; supervision, G.D.; project administration, G.D.; funding acquisition, G.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Luxembourg National Research Fund (FNR)—ADARS Project, ref. C20/IS/14762457.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This work is supported by the Luxembourg National Research Fund (FNR)—ADARS Project, ref. C20/IS/14762457. The experiments presented in this paper were carried out using the HPC facilities of the University of Luxembourg [37]—see https://hpc.uni.lu (accessed on 9 May 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brust, M.R.; Danoy, G.; Stolfi, D.H.; Bouvry, P. Swarm-based counter UAV defense system. Discov. Internet Things 2021, 1, 2. [Google Scholar] [CrossRef]
- Chung, S.J.; Ahsun, U.; Slotine, J.J.E. Application of Synchronization to Formation Flying Spacecraft: Lagrangian Approach. J. Guid. Control. Dyn. 2009, 32, 512–526. [Google Scholar] [CrossRef]
- Cardona, G.A.; Calderon, J.M. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Appl. Sci. 2019, 9, 1702. [Google Scholar] [CrossRef]
- Saeedi, S.; Trentini, M.; Seto, M.; Li, H. Multiple-Robot Simultaneous Localization and Mapping: A Review. J. Field Robot. 2015, 33, 3–46. [Google Scholar] [CrossRef]
- Hauri, S.; Alonso-Mora, J.; Breitenmoser, A.; Siegwart, R.; Beardsley, P. Multi-Robot Formation Control via a Real-Time Drawing Interface. In Field and Service Robotics: Results of the 8th International Conference; Yoshida, K., Tadokoro, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 175–189. [Google Scholar] [CrossRef]
- Pinciroli, C.; Trianni, V.; O’Grady, R.; Pini, G.; Brutschy, A.; Brambilla, M.; Mathews, N.; Ferrante, E.; Di Caro, G.; Ducatelle, F.; et al. ARGoS: A modular, parallel, multi-engine simulator for multi-robot systems. Swarm Intell. 2012, 6, 271–295. [Google Scholar] [CrossRef]
- Stolfi, D.H.; Danoy, G. An Evolutionary Algorithm to Optimise a Distributed UAV Swarm Formation System. Appl. Sci. 2022, 12, 10218. [Google Scholar] [CrossRef]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Ong, Y.S.; Nair, P.B.; Keane, A.J. Evolutionary Optimization of Computationally Expensive Problems via Surrogate Modeling. AIAA J. 2003, 41, 687–696. [Google Scholar] [CrossRef]
- Yelten, M.B.; Zhu, T.; Koziel, S.; Franzon, P.D.; Steer, M.B. Demystifying Surrogate Modeling for Circuits and Systems. IEEE Circuits Syst. Mag. 2012, 12, 45–63. [Google Scholar] [CrossRef]
- Cheng, S.; Prentice, I.C.; Huang, Y.; Jin, Y.; Guo, Y.K.; Arcucci, R. Data-driven surrogate model with latent data assimilation: Application to wildfire forecasting. J. Comput. Phys. 2022, 464, 111302. [Google Scholar] [CrossRef]
- Poggi, C.; Rossetti, M.; Bernardini, G.; Iemma, U.; Andolfi, C.; Milano, C.; Gennaretti, M. Surrogate models for predicting noise emission and aerodynamic performance of propellers. Aerosp. Sci. Technol. 2022, 125, 107016. [Google Scholar] [CrossRef]
- Westermann, P.; Evins, R. Surrogate modelling for sustainable building design—A review. Energy Build. 2019, 198, 170–186. [Google Scholar] [CrossRef]
- Asher, M.J.; Croke, B.F.W.; Jakeman, A.J.; Peeters, L.J.M. A review of surrogate models and their application to groundwater modeling. Water Resour. Res. 2015, 51, 5957–5973. [Google Scholar] [CrossRef]
- Alizadeh, R.; Allen, J.K.; Mistree, F. Managing computational complexity using surrogate models: A critical review. Res. Eng. Des. 2020, 31, 275–298. [Google Scholar] [CrossRef]
- Bliek, L. A Survey on Sustainable Surrogate-Based Optimisation. Sustainability 2022, 14, 3867. [Google Scholar] [CrossRef]
- Rosalie, M.; Kieffer, E.; Brust, M.R.; Danoy, G.; Bouvry, P. Bayesian optimisation to select Rössler system parameters used in Chaotic Ant Colony Optimisation for Coverage. J. Comput. Sci. 2020, 41, 101047. [Google Scholar] [CrossRef]
- do Nascimento, R.G.; Fricke, K.; Viana, F. Quadcopter Control Optimization through Machine Learning. In AIAA Scitech 2020 Forum; American Institute of Aeronautics and Astronautics: Orlando, FL, USA, 2020. [Google Scholar] [CrossRef]
- Tang, Q.; Li, Y.; Deng, Z.; Chen, D.; Guo, R.; Huang, H. Optimal shape design of an autonomous underwater vehicle based on multi-objective particle swarm optimization. Nat. Comput. 2020, 19, 733–742. [Google Scholar] [CrossRef]
- Lopes, H.J.; Lima, D.A. Evolutionary Tabu Inverted Ant Cellular Automata with Elitist Inertia for swarm robotics as surrogate method in surveillance task using e-Puck architecture. Robot. Auton. Syst. 2021, 144, 103840. [Google Scholar] [CrossRef]
- Yue, H.; Medromi, H.; Ding, H.; Bassir, D. A novel hybrid drone for multi-propose aerial transportation and its conceptual optimization based on surrogate approach. J. Phys. Conf. Ser. 2021, 1972, 012103. [Google Scholar] [CrossRef]
- Chandra, R.; Tiwari, A. Distributed Bayesian optimisation framework for deep neuroevolution. Neurocomputing 2022, 470, 51–65. [Google Scholar] [CrossRef]
- Spiri Robotics. Spiri Mu. 2023. Available online: https://spirirobotics.com/ (accessed on 20 April 2023).
- Stolfi, D.H.; Danoy, G. Optimising Autonomous Robot Swarm Parameters for Stable Formation Design. In Proceedings of the Genetic and Evolutionary Computation Conference, GECCO’22, New York, NY, USA, 9–13 July 2022; pp. 1281–1289. [Google Scholar] [CrossRef]
- Cozad, A.; Sahinidis, N.V.; Miller, D.C. Learning surrogate models for simulation-based optimization. AIChE J. 2014, 60, 2211–2227. [Google Scholar] [CrossRef]
- Seeger, M. Gaussian Processes For Machine Learning. Int. J. Neural Syst. 2004, 14, 69–106. [Google Scholar] [CrossRef] [PubMed]
- Piironen, J. Gplite: General Purpose Gaussian Process Modelling. 2023. Available online: https://cran.r-project.org/package=gplite (accessed on 2 March 2023).
- Riedmiller, M.; Braun, H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Volume 1, pp. 586–591. [Google Scholar] [CrossRef]
- Fritsch, S.; Guenther, F.; Wright, M.N.; Suling, M.; Mueller, S.M. Neuralnet: Training of Neural Networks. 2023. Available online: https://CRAN.R-project.org/package=neuralnet (accessed on 2 March 2023).
- Holland, J.H. Adaptation in Natural and Artificial Systems; The MIT Press: Cambridge, MA, USA, 1992; p. 228. [Google Scholar] [CrossRef]
- Talbi, E.G. A Unified Taxonomy of Hybrid Metaheuristics with Mathematical Programming, Constraint Programming and Machine Learning. In Hybrid Metaheuristics; Talbi, E.G., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 3–76. [Google Scholar] [CrossRef]
- Goldberg, D.E.; Deb, K. A Comparative Analysis of Selection Schemes Used in Genetic Algorithms. Found. Genet. Algorithms 1991, 1, 69–93. [Google Scholar] [CrossRef]
- Syswerda, G. Uniform Crossover in Genetic Algorithms. In Proceedings of the Proceedings of the 3rd International Conference on Genetic Algorithms, Fairfax, VA, USA, 1 June 1989; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1989; pp. 2–9. [Google Scholar]
- Deb, K. Multi-Objective Optimization Using Evolutionary Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Lin, S. Computer solutions of the traveling salesman problem. Bell Syst. Tech. J. 1965, 44, 2245–2269. [Google Scholar] [CrossRef]
- Benítez-Hidalgo, A.; Nebro, A.J.; García-Nieto, J.; Oregi, I.; Ser, J.D. jMetalPy: A Python framework for multi-objective optimization with metaheuristics. Swarm Evol. Comput. 2019, 51, 100598. [Google Scholar] [CrossRef]
- Varrette, S.; Bouvry, P.; Cartiaux, H.; Georgatos, F. Management of an academic HPC cluster: The UL experience. In Proceedings of the 2014 International Conference on High Performance Computing & Simulation (HPCS), Bologna, Italy, 21–25 July 2014; pp. 959–967. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).