MARL-Based Dual Reward Model on Segmented Actions for Multiple Mobile Robots in Automated Warehouse Environment

Abstract

The simple and labor-intensive tasks of workers on the job site are rapidly becoming digital. In the work environment of logistics warehouses and manufacturing plants, moving goods to a designated place is a typical labor-intensive task for workers. These tasks are rapidly undergoing digital transformation by leveraging mobile robots in automated warehouses. In this paper, we studied and tested realistically necessary conditions to operate mobile robots in an automated warehouse. In particular, considering conditions for operating multiple mobile robots in an automated warehouse, we added more complex actions and various routes and proposed a method for improving sparse reward problems when learning paths in a warehouse with reinforcement learning. Multi-Agent Reinforcement Learning (MARL) experiments were conducted with multiple mobile robots in an automated warehouse simulation environment, and it was confirmed that the proposed reward model method makes learning start earlier even there is a sparse reward problem and learning progress was maintained stably. We expect this study to help us understand the actual operation of mobile robots in an automated warehouse further.

1. Introduction

In order to operate a mobile robot in an automated warehouse, the following realistic conditions must be considered. First, it is necessary to solve the Multi-Agent Path Finding (MAPF) problem, in which multiple mobile robots work simultaneously in an automated warehouse to find the optimal path for given tasks [1]. Second, we have to deal with the Multi-Agent Pickup and Delivery (MAPD) issue [1]. The actual operation of the mobile robots is not simply departure and arrival. In automated warehouses, mobile robots perform a more complex and sequential series of actions to deliver goods to a designated location.

Reinforcement learning algorithms are widely used to solve various decision making problems in complex environments. Recently, the demand for multi-agent environments has been rapidly increasing, as is interest in Multi-Agent Reinforcement Learning (MARL) algorithms [2]. In general, MARL aims to simultaneously train multiple agents to perform a given task in a shared environment [3]. In this paper, we use a Multi-Agent Reinforcement Learning (MARL) algorithm to handle additional conditions for mobile robots in a warehouse.

We simulate the environment of an automated warehouse and used a MARL algorithm to simulate multiple mobile robots. The movement of a mobile robot is not a simple operation; it is complex. We are also trying to increase the usability of training by allowing mobile robots to learn from a variety of positions rather than from a fixed position.

Reinforcement learning can proceed efficiently when the agent is smoothly rewarded for the actions performed. However, in some reinforcement learning experiments, there is no learning because of sparse rewards. In this paper, we experimentally verify that multiple mobile robots can perform realistic operations in an automated warehouse. In particular, we propose a method to improve the sparse reward problem of the learning path with multiple mobile robots in automated warehouses and named it the Dual Segmented Reward Model.

The Dual Segmented Reward Model method expects contributions to the following items:

• A reward model is proposed so that learning can proceed efficiently and stably in an environment where the sparse reward problem of reinforcement learning has become serious.
• The proposed reward model induces and supports reinforcement learning efficiently and stably by using the reward model without modifying the reinforcement learning algorithm or changing the environment.
• It is meaningful as a practical case study that confirms learning efficiently and stably despite the sparse reward problem in a simulation experiment environment similar to an actual automated warehouse.

The paper consists of the following contents. Section 2 reviews the types of reinforcement learning algorithms and briefly reviews the meaning of Model-Free, Model-Based, Value-Based, and Policy-Based. For Multi-Agent Reinforcement Learning (MARL), we review the differences between single agents and multiple agents, their algorithms, types based on agent relationship, and types of learning and execution. The algorithms to be used in the experiment are reviewed, as well. We also briefly review methods to ameliorate the sparse reward problem. In Section 3, we explain the idea and definition of the proposed “Dual Segmented Reward Model.” Section 4 describes the simulation environment, experimental methods and cases, detailed modeling information of the proposed method, the parameters to be used for the experiment, and the experimental results. Section 5 presents general conclusions and opinions, as well as directions for future research.

2. Related Work

2.1. Reinforcement Learning Types

2.1.1. Model-Based vs. Model-Free

Reinforcement learning algorithms can be classified into Model-Free and Model-Based types. These types can be classified by whether the environment model can be defined or not. If the environmental model can be defined in terms of external changes and states, a plan can be established accordingly.

The Model-Based type means planning is possible. In other words, if agents can predict how their actions will change the environment, they can anticipate changes before taking action and plan and execute optimal actions, allowing agents to act much more efficiently. Under this assumption, when an action is taken in a specific state, the algorithm form that defines the probability of the next state and probabilistically predicts the change of the environment according to the action is called the Model-Based type [4,5]. However, it is difficult to predict the exact model of the environment, and if the model does not properly reflect the environment, the agent behaves incorrectly. Model-Based reinforcement learning algorithms are Alpha Zero, Imagination-Augmented Agents (I2A), Model-Based Model-Free (MBMF), Model-Based Value Expansion (MBVE), Dyna, etc. [4,6].

In the Model-Free type, the agent seeks to find the future value of the reward as a policy function by means of its actions. Since this algorithm does not know about the environment, it passively obtains the next state and reward informed by the environment. The algorithm has to explore because it no longer knows how the environment will behave. It is a method that gradually learns policy functions by means of trial and error during such exploration [4,5]. Model-Free Reinforcement Learning can be divided into the Value-Based and Policy-Based types. We will briefly review these types.

Figure 1 and Figure 2 illustrate the Model-Free and Model-Based types.

Figure 1. Model-Free Reinforcement Learning [7].

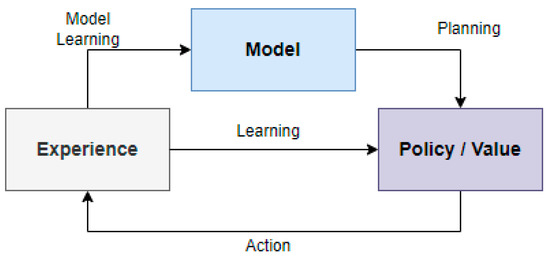
Figure 2. Model-Based Reinforcement Learning [7].

2.1.2. Value-Based vs. Policy-Based

The value function calculates the value of a specific state, and it is used when calculating the experienced state and behavior information by storing it in memory. However, this value function has limitations with storage space and operation time needed to store and manage all values, such as states and actions that are increased when the environment becomes more complex [4,5]. There are Q-Learning [4], State Action Reward State Action (SARSA) [4], Deep Q-Networks (DQN) [8,9], Double Deep Q-Networks (DDQN) [10], Dueling Double Deep Q-Networks (DDDQN) [11], Prioritized Experience Replay (PER) [12], etc., as Value-Based Reinforcement Learning algorithms.

The Policy-Based method approximates a policy by using parameters without storing all experiences. Convergence is better than that of Value-Based algorithms and can handle both discrete and continuous action spaces. However, it has disadvantages, such as large variance, which makes learning unstable, requires more samples, and is highly likely to find a local optimum [4,5]. There are REINFORCE [13], Vanilla Policy Gradient (VPG) [14], Trust Region Policy Optimization (TRPO) [15], and Proximal Policy Optimization (PPO) [16] as Policy-Based Reinforcement Learning algorithms.

Actor-Critic is a mixture of the Value-Based and Policy-Based types. The basic concept is that an Actor selects and performs an action when a state is given, and a Critic checks the action performed by the Actor and evaluates it [4,5]. It is a method to induce learning so that the Actor works better by using the Critic. Asynchronous Advantage Actor-Critic (A3C) [17], Advantage Actor-Critic (A2C) [18], and Deep Deterministic Policy Gradient (DDPG) [19] are Actor-Critic types of reinforcement learning algorithms.

2.2. Multi-Agent Reinforcement Learning (MARL)

2.2.1. Concept of Multi-Agents and MARL Algorithm

In reinforcement learning, if the agent can know everything about its environment, it can be defined as a Markov Decision Process (MDP), which consists of state S, action A, probability P, reward R, and discount factor γ, and single agent is defined based on MDP. MDP has fully observable characteristics of the state [4,20]. As the learning target of reinforcement learning expands from single to multiple, the MDP must change based on stochastic games, and the components expand with the number of agents n, state S, actions $A_{1\dots n}$, probability P, rewards $R_{1\dots n}$, and discount factor γ [19]. In stochastic games, an agent performs an action, and the agent’s combination of actions determines the next state and reward. Agents make different observations because of partially observable characteristics [20,21].

Figure 3 shows the difference between components and interactions for a single agent or multiple agents of reinforcement learning.

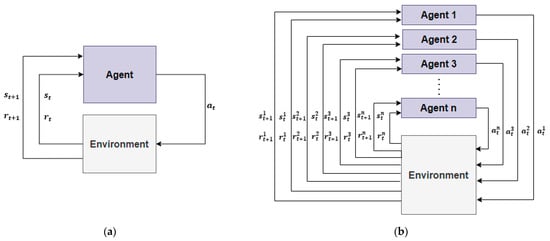
Figure 3. Components and Interactions of Reinforcement Learning: (a) Single Agent; (b) Multiple Agents [22,23].

There are Independent Q-Learning (IQL) [24,25,26,27], Advantage Actor-Critic (IA2C) [24,28], Independent Proximal Policy Optimization (IPPO) [24,29], Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [24,30], Counterfactual Multi-Agent Policy Gradients (COMA) [24,31], QMIX [24,32], and Shared Experience Actor-Critic (SEAC) [24,33] as MARL algorithms.

2.2.2. MARL Setting Types

MARL setting types can be generally divided into three types based on the task’s characteristics and the relationships between agents.

• Cooperative Type [20,34,35]

In the cooperative type, all agents work together to achieve a common goal. In general, there is a common reward model and a team-average reward model. The common reward model is described in Equation (1) and the team-average reward model is described in Equation (2) [20].

$$R^1=R^2=\cdots =R^N=R$$

(1)

$$\bar{R}\left(s,a,s^{\prime }\right):=N^{-1}·{\displaystyle \sum }_{i\in \mathcal{N}} R^i\left(s,a,s^{\prime }\right)$$

(2)

• Competitive Type [20,34,35]

The competitive type is most often described as an environment in which two agents compete against each other, where one agent gains and the other agent loses. It is usually modeled as a zero-sum game as in Equation (3) [20].

$${\displaystyle \sum }_{i\in \mathcal{N}} R^i\left(s,a,s^{\prime }\right)=0$$

(3)

• Mixed Type [20]

The mixed type is a hybrid form of cooperative and competitive types and is relatively less restrictive and more flexible [20].

2.2.3. MARL Learning and Execution Types

The MARL algorithm uses reinforcement learning techniques to train agents on multi-agent systems. MARL can be broadly classified into the following types in terms of learning and execution.

• Centralized Training Centralized Execution (CTCE)

The CTCE paradigm assumes that immediate information exchange between agents is possible without constraints. With centralized learning, a common policy is learned for all agents, and each agent can directly use the policy set for multi-agents [36]. During training, agents affect each other, which can make learning inefficient [36].

• Centralized Training Decentralized Execution (CTDE)

The CTDE paradigm allows agent-to-agent communication to exchange information during training. Agents can use the same learning model, share a common goal, and share a learning model or experience with other agents. This method is a policy method based on parameter sharing [27,36,37]. However, even if an agent owns the same policy network, different agents perceive it differently, which may result in different behavior [27,36,38].

• Distributed Training Decentralized Execution (DTDE)

In the DTDE paradigm, agents cannot see the information of other agents and are unaware that they are collaborating. From the point of view of a single agent, the environment is constantly changing and perceived as independent [36,37,38]. Distributed learning is limited in scaling the number of agents because of the complexity [36,37,38].

Figure 4 explains the training patterns of CTCE, CTDE, and DTDE.

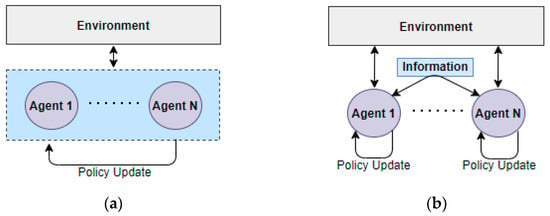
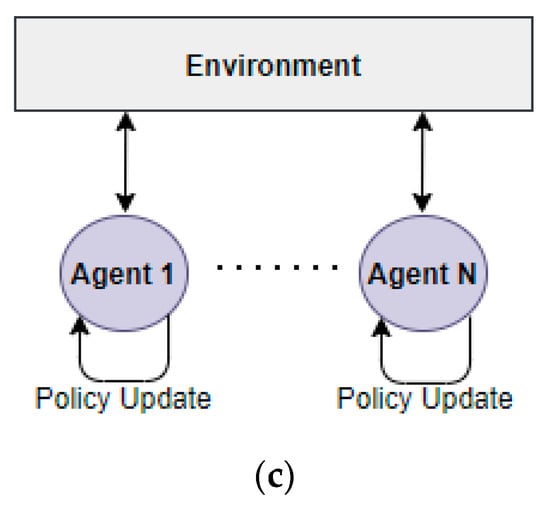
Figure 4. Training Types of Multi-Agent Environment: (a) CTCE; (b) CTDE; (c) DTDE [36].

2.3. Review of Algorithm for Experiment

2.3.1. Deep Q-Networks (DQN)

The most representative algorithm of the Value-Based method is Deep Q-Networks (DQN), which uses a deep neural network as a value function [8,9]. The optimal action-value function follows the Bellman Equation. If the optimal value Q*(s, a) for all actions is known, the optimal expected value is a method of selecting behavior a′ that maximizes r + γQ*(s′, a′) as shown in Equation (4) below [8].

$$Q^{\ast }\left(s,a\right)={\mathbb{E}}_{s^{\prime }\sim ℰ}\left[r+\gamma \underset{a^{\prime }}{max}{Q}^{\ast }\left(s^{\prime },a^{\prime }\right)\mid s,a\right]$$

(4)

Nonlinear function estimation is possible by approximating the action-value function by using a deep neural network. The neural network function approximator with weight θ, called Q-Network, learns by finding the minimum of the loss function $L_i\left({\theta }_i\right)$ [8]. y_i is the target value of iteration i and $\rho$ is the probability distribution of state s and action a as a behavior distribution.

The formula for the loss function of a Q-Network is Equation (5) [8].

$$L_i\left({\theta }_i\right)={\mathbb{E}}_{s,a\sim \rho (\cdot )}\left[{\left(y_i-Q\left(s,a;{\theta }_i\right)\right)}^2\right]$$

(5)

The optimal θ is obtained by means of learning, and this process is shown in Equation (6) [7].

$${\nabla }_{{\theta }_i}{L}_i\left({\theta }_i\right)={\mathbb{E}}_{s,a\sim \rho (·);s^{\prime }\sim ℰ}\left[\left(r+\gamma \underset{a^{\prime }}{max}Q\left(s^{\prime },a^{\prime };{\theta }_{i-1}\right)-Q\left(s,a;{\theta }_i\right)\right){\nabla }_{{\theta }_i}Q\left(s,a;{\theta }_i\right)\right]$$

(6)

2.3.2. Double Deep Q-Networks (DDQN)

If the Q-Value of the DQN becomes very large, the performance of the Q-Network may deteriorate. To solve this problem, the Double DQN algorithm uses two Q-Networks, which select an action from the current Q-Network and evaluate it using the old Q-Network [10]. The target network has the same structure as the DQN network but is composed of different parameters ${\theta }_t^{-}$.

The formula of DQN’s target network is expressed as Equation (7), and the Double DQN is changed as in Equation (8) [10].

$$Y_t^{\mathrm{DQN}}\equiv r_{t+1}+\gamma \underset{a}{max}Q\left(s_{t+1},a;{\theta }_t^{-}\right)$$

(7)

$$Y_t^{\mathrm{DoubleDQN} }\equiv s_{t+1}+\gamma Q\left(s_{t+1},\underset{a}{\mathrm{argmax}}Q\left(s_{t+1},a;{\theta }_t\right),{\theta }_t^{-}\right)$$

(8)

2.3.3. Independent Q-Learning (IQL)

The basic concept of the Independent Q-Learning (IQL) algorithm is to maximize the joint reward by observing local information, and an individual agent judges other agents as part of the environment. Early IQL was implemented, where an agent executes the Q-Learning algorithm as a value function. Recently, it has been expanded to the Deep Q-Network (DQN) or Deep Recurrent Q-Network (DRQN) by using a deep neural network [25,26,27]. When using a deep neural network, each agent calculates a loss value based on local information and updates the parameter values of the Q-Network [26].

2.4. Sparse Reward and Improvement Methods

Reinforcement learning often does not go well because of the sparse reward problem. Because the rewards are sparse, the agent spends most of its learning time on meaningless searches and is not even rewarded during any part of the training. In addition, even if an agent achieves a goal with difficulty in a sparse reward situation, if the success rate is very low, it is likely that the learning level for the final goal will not be reached.

A representative method for improving the sparse reward problem, which is a chronic problem of reinforcement learning, has been reviewed [39].

• Reward Shaping

Reward Shaping is a technique for defining an additional intermediate reward value considering the domain knowledge of the agent’s behavior and environment.

• Transfer Learning

Transfer Learning is a way to train agents with easier tasks first and transfer the knowledge learned from the training by means of a value function later.

• Curriculum Learning

In Curriculum Learning, an agent is trained in an easier environment at the beginning of learning, and then the difficulty is increased to a more complex environment to enable learning in an environment similar to the real environment.

• Curiosity-Driven Learning

Curiosity-Driven Learning efficiently explores unknown states using prediction error and visit count as intrinsic reward values. In particular, an Intrinsic Curiosity Module (ICM) is proposed to solve the exploring problem by selecting a task with a small prediction error for an agent’s curiosity.

• Hierarchical Reinforcement Learning (HRL)

When it is difficult to train directly, Hierarchical Reinforcement Learning (HRL) trains by reorganizing the task into a hierarchical agent structure. For the policy, it can be defined as a main policy and some auxiliary policies.

3. MARL Methodology in a Warehouse Environment

As seen in the latest trends in MARL algorithms discussed above, algorithms that consider various reward methods and techniques were being developed to improve the performance and efficiency of reinforcement learning algorithms in a multi-agent environment. In this paper, we propose and verify a method for improving learning performance and sparse reward problems by modeling reward values with a simple MARL algorithm that considers the behavioral characteristics of mobile robots in a warehouse.

3.1. System Architecture

Figure 5 describes the software architecture using MARL and the reward model proposed in this paper in an automated warehouse where multiple mobile robots are operated.

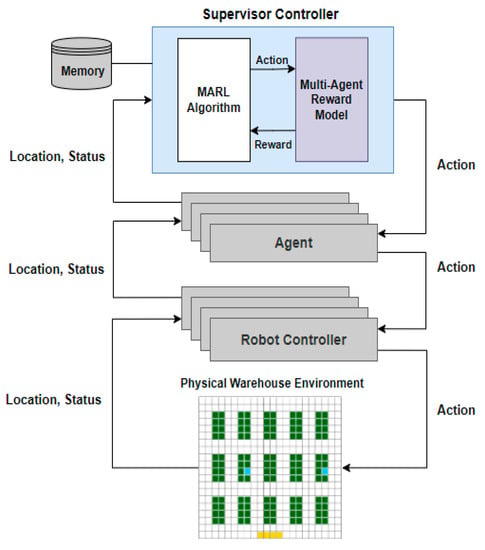
Figure 5. Multi-Agent Mobile Robot Framework Architecture in a Warehouse [22].

3.2. Proposed Reward Model

We decided to use the MARL algorithm to operate multiple mobile robots in a warehouse. However, the target experimental environment is a high-dimensional grid-type warehouse and has sparse rewards [24]. Therefore, it is necessary to ameliorate the sparse reward problem for better learning performance, and we propose a reward model to do so.

3.2.1. Basic Rules to Define the Proposed Reward Model

To define a reward model, we need the following basic rules:

• Define Full Actions and Partial Actions

The mobile robot moves to the location of the inventory pod, takes the object, and delivers it to the final destination. A mobile robot performs a series of partial actions to accomplish the complete task; that is, full actions are composed with partial actions to complete the task. Full actions and partial actions can be expressed as in Equation (9). Full actions can be Ai and are composed of n partial actions $a_{i1}$, $a_{i2}$, …, $a_{in}$.

$$A_i=a_{i1}{\displaystyle \cup }{a}_{i2}{\displaystyle \cup }{a}_{i3}{\displaystyle \cup }\dots {\displaystyle \cup }{a}_{in}$$

(9)

2.

Define the Maximum Reward Value

In order to fairly evaluate the training, one must limit the maximum reward value. The sum of the reward values of all partial actions should equal the reward values of the entire action and should not exceed the maximum reward value. The reward value for the full actions is R, and the reward value for the partial action is r, which can be expressed as Equation (10).

$$R_i={\mathrm{r}}_{i1}+{\mathrm{r}}_{i2}+{\mathrm{r}}_{i3}+\cdots +{\mathrm{r}}_{in},\left(R_i\le \mathrm{Maximum} \mathrm{Reward} \mathrm{Value} \right)$$

(10)

3.2.2. Define Reward Settings Based on Agent Relationship

Multi-agent environments can be classified into three types according to the relationships between agents: Competitive, Cooperative, and Mixed [20]. The Competitive type has zero-sum characteristics, and agents perform tasks in a competitive relationship. We considered only Cooperative and Mixed types in this paper because the Competitive type may not be suitable for the task of mobile robots in a warehouse.

• Cooperative Type [20]

In a multi-agent environment, agents work in partnership. When an agent achieves a goal, all agents receive the same reward. The Cooperative type does not deal with competition between agents for a common goal, but it is limited by not being able to distinguish between agents that have achieved the goal and agents that have not.

Figure 6 and Equation (11) explain the reward method for the Cooperative type.

$$\mathrm{Evenly} \mathrm{Divided} \mathrm{Reward} \mathrm{Value} =\frac{ \mathrm{Maximum} \mathrm{Reward} \mathrm{Value} }{ \mathrm{Number} \mathrm{of} \mathrm{Agents} }.$$

(11)

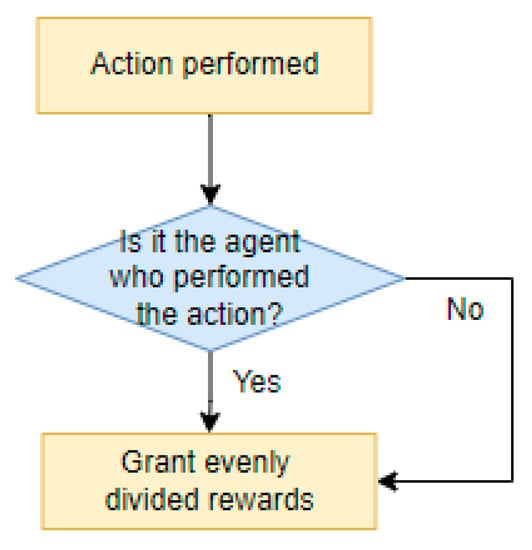
Figure 6. Reward Method Logic for the Cooperative Type.

2.

Mixed Type [20]

In a multi-agent environment, we can mix cooperative and competitive relationships between agents. When an agent achieves a goal, it gives a bigger reward to the agent who achieves the goal and a smaller reward to the agent who does not achieve the goal. This type is expected to ameliorate the learning problem when the workload is concentrated on a single agent in a competitive environment or when there is no difference in rewards between agents that achieve a goal and those that do not. The ratio of the reward given to agents that achieve the goal and those that do not are controlled by a weight w (1 ≥ w ≥ 0). Figure 7 and Equations (12) and (13) explain the reward method for the Mixed type.

$$\mathrm{Reward} \mathrm{Value} \mathrm{for} \mathrm{Achieving} \mathrm{Goal} = \mathrm{Maximum} \mathrm{Reward} \mathrm{Value} \times w,\left(0\le w\le 1\right)$$

(12)

$$\mathrm{Reward} \mathrm{Value} \mathrm{for} \mathrm{Not} \mathrm{Achieving} \mathrm{Goal} =\frac{ (\mathrm{Maximum} \mathrm{Reward} \mathrm{Value} \times \left(1-w\right))}{ \mathrm{Number} \mathrm{of} \mathrm{Agents} -1}$$

(13)

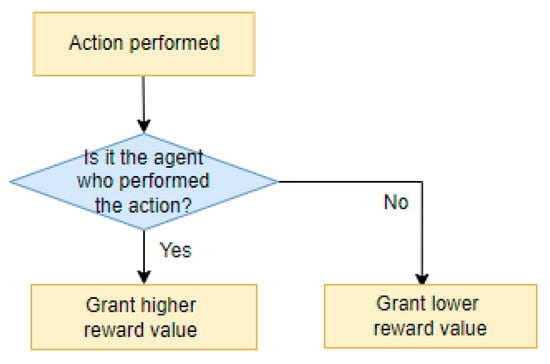
Figure 7. Reward Method Logic for the Mixed Type.

3.2.3. Proposed Reward Model Dual Segmented Reward Model

We propose the following method as a reward model for the experiment. The proposed method can be a kind of Reward Shaping to learn the optimal path of multiple mobile robots in a warehouse.

• Define Segmented Reward Model

First, it is necessary to define the Segmented Reward Model. In reinforcement learning, some studies divide the task into partial actions and distribute the reward values [40,41]. The definition of the Segmented Reward Model proceeds in a similar way. The reward value is defined by dividing the total reward value of full actions and distributing it to partial actions. Depending on the definition of the reward values for partial actions, the degree of learning can be affected.

Figure 8 shows the concept of segmented actions and distributed reward values.

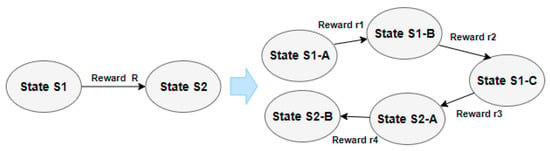
Figure 8. An Example of Splitting the Full Actions.

2.

Define Dual Reward Model based on Segmented Reward Models

By observing the behavioral patterns of agents in simulation experiments, we realized that using the same reward strategy from start to finish in a single episode might not be advantageous. Since the maximum reward value is fixed to a specific number and the reward value is divided into very small pieces for partial actions, it is difficult to improve the learning. In addition, we confirmed that the importance of partial actions may depend on the learning period. We found that important partial action can be different in the first half or the second half of an episode. In the early stage of learning, it is advantageous to increase the reward value for early partial actions. As the learning progresses gradually and the number of episodes increases, it is advantageous to increase the weight for the latter half of the partial actions to increase the number of tasks completed. Therefore, we proposed to divide the training interval of the episode in half and define the split reward model for the first half and the second half as a dual reward model, which Figure 9 describes. The two reward models are composed of the same actions, but the weight of the reward value can be different. For example, Reward Model No. 1 defines higher reward values for initial actions of entire procedure, and Reward Model No. 2 defines higher reward values for the latter actions of entire procedure.

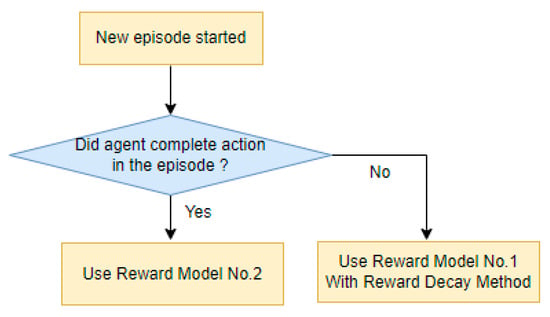
Figure 9. Dual Reward Model Logic.

We also added the Reward Decay method to maintain the learning efficiency more robustly as learning progresses by adjusting the reward weight.

Equation (14) describes the Reward Decay method. The total reward value of full actions is denoted by R, and the reward value of a partial action is denoted by r; n is the number of partial actions, m is the number of episodes currently being learned, and λ is the reward decay rate.

$$\begin{array}{c}{R}_i=r_{i,1}{\lambda }^m+r_{i,2}{\lambda }^m+\cdots +r_{i,n-1}{\lambda }^m+r_{i,n} (0<\lambda <1)\\ ={\displaystyle {\displaystyle \sum }_{j=1}^{n-1}} r_{i,j}{\lambda }^m+r_{i,n}\end{array}$$

(14)

4. Experiment and Results

4.1. Experiment Environment

The experimental environment of this paper was constructed based on the automated warehouse. The warehouse layout was the traditional type, and a simulated environment was created in a work environment in which 15 inventory pods and two mobile robots were operated. The warehouse simulation used an Open AI-based warehouse-simulation open source [3,24]. The layout of experiment warehouse environment is shown in Figure 10.

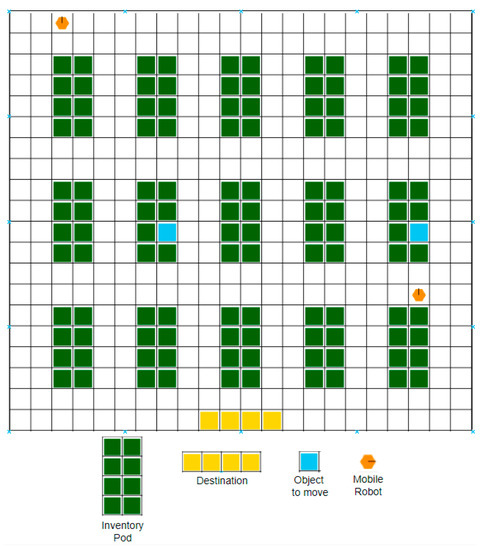
Figure 10. Warehouse Layout and Environment for Experiment [22].

We did the experiments using DQN-based and DDQN-based IQL algorithms open source as MARL algorithms [25,26].

4.2. Experiment Method

The mobile robot conducted experiments with the following scenarios:

• The mobile robot moves to find the location of the object to be transported.
• When the mobile robot arrives at the location of the object, the operator picks up the object and places it on the transport tray.
• The mobile robot moves to the final destination with the transport tray and delivers the object to the final destination. The operator gets the object from the transport tray.
• The mobile robot returns the transport tray to its initial position.

In this test method, the final destination position is fixed and does not change, but the starting position and picking position of the mobile robot are continuously changed at random, so various starting positions and picking positions of objects can be considered for learning.

4.3. Modeling of the Dual Segmented Reward Model

For reward setting based on the agent relationship, in order to consider the difference between the agent who performs the task and the agent who does not, we conducted the experiment with a Mixed type rather than a Cooperative type. However, the weight w was set to 0.6, so that the difference in reward values between agents was not too large. The definition of the reward values applied to the experiment was as follows: the agent who delivered the object received a reward of 0.6, and the agent who failed to deliver the object received a reward of 0.4, and the maximum reward value was defined as 1.

The experiment was basically based on the Mixed type and added the Dual Segmented Reward Model with reward decay. The Segmented Reward Model based on partial actions is separately defined by a Finite State Machine (FSM) technique [42].

The procedure of the Dual Segmented Reward Model is as follows (Algorithm 1).

Algorithm 1: Dual Segmented Reward Model

(a) Initialize (b) Loop for Episode: (c)  Loop for n Steps: (c-1)   Get state (c-2)   Take action and next state (c-3)   If agent does not complete action in the episode,        Get reward value via Reward Model No. 1 with Learning Decay Method     Else        Get reward value via Reward Model No. 2 (d)     Change next state to state

For the experiment, the Segmented Reward Models are defined as shown in Figure 11.

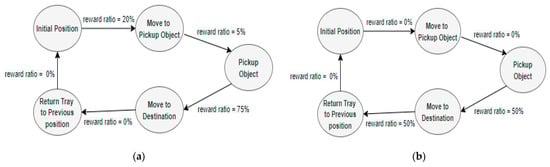
Figure 11. Segmented Reward Models: (a) Reward Model No.1; (b) Reward Model No.2.

4.4. Experiment Parameter Values

The values of the parameters applied in the test are described in Table 1.

Table 1. Parameter values for test.

Parameter	Value
Learning Rate (α)	0.00008
Discount Rate (γ)	0.99
Reward Decay Rate (λ)	0.99

4.5. Experiment Results

Two algorithms were used in the experiment, a DQN-based IQL algorithm and a DDQN-based IQL algorithm. The first experiment was conducted with the algorithm itself, and the second experiment was performed with algorithms and the proposed reward model together. We did the experiment five times for each test case and visualized the experimental results for each agent.

The experimental results of DQN and DDQN can be seen in Figure 12 and Figure 13. In the DQN experiment, rewards started to occur irregularly at various points between 100,000 and 700,000 steps, and learning began. Once the reward was created, the reward value continued to increase and learning progressed. In the DDQN experiment, rewards began to occur at various points ranging from 100,000 to 500,000 steps. Comparing the test results of DQN, the difference is that even after the reward is generated, the increase in the reward value sometimes decreases slightly and variably. By means of the experiments of DQN and DDQN, we confirmed that there are rare cases in which rewards do not occur occasionally until the end of learning.

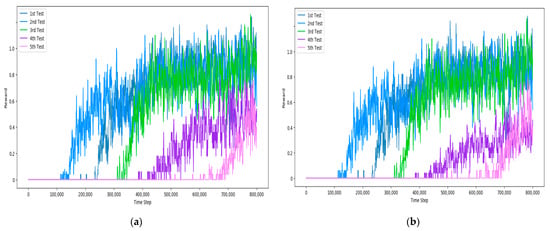
Figure 12. Test Result of DQN: (a) Agent 1; (b) Agent 2.

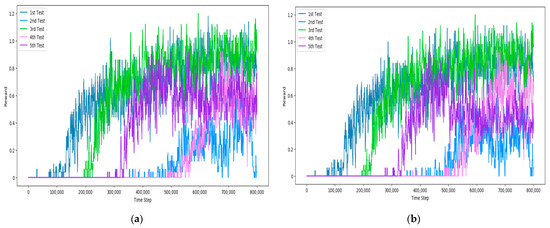
Figure 13. Test Result of DDQN: (a) Agent 1; (b) Agent 2.

The experimental results of DQN and DDQN using the proposed Dual Segmented Reward Model are shown in Figure 14 and Figure 15. The results of DQN and DDQN using the proposed reward model are very similar. The reward occurred between 100,000 and 200,000 steps, and the learning progressed stably with little deviation.

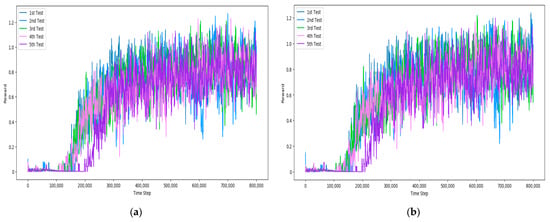
Figure 14. Test Result of DQN with Dual Segmented Reward Model: (a) Agent 1; (b) Agent 2.

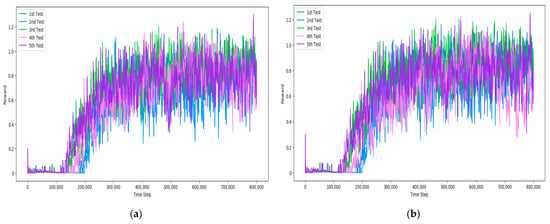
Figure 15. Test Result of DDQN with Dual Segmented Reward Model: (a) Agent 1; (b) Agent 2.

In addition, we confirmed that a small reward value was generated from the beginning. This change helped ameliorate the sparse reward problem. In addition, the proposed reward model was effective in reducing the learning deviation between each experiment and stably maintaining the learning.

In order to check more statistically, the sum of the reward values of Agent 1 and Agent 2 was calculated for the results of five experiments, and the minimum, maximum, and average reward values for each time step were visualized in Figure 16. The gray area represents the range from the minimum reward value to the maximum reward value for each step, and the orange line represents the average of five experiments. Comparing the visualization diagrams of each test case, the difference between the minimum and maximum rewards is very large and the gray area is wide in the cases of DQN and DDQN. However, when the Dual Segmented Reward Model method is applied with DQN and DDQN, the difference between the minimum and maximum rewards is significantly reduced and gray area is also narrowed.

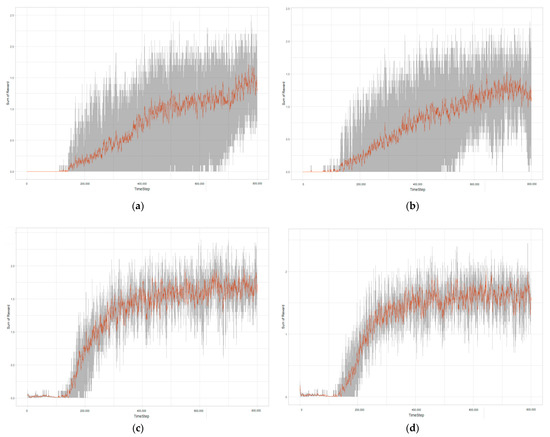
Figure 16. Reward Summation Analysis of Test Results: (a) DQN; (b) DDQN; (c) DQN with Dual Segmented Reward Model; (d) DDQN with Dual Segmented Reward Model.

The reward values of the experimental results for all test cases are compared in Figure 17. The reward values of the five experiments were averaged without any agent classification. In the experiments conducted with the DDQN algorithm, the rewards started to increase slightly faster than in the experiments conducted with the DQN, and the rewards were also slightly higher. When the proposed reward model was applied, we confirmed that the experimental results were consistent and similar regardless of the algorithm DQN or DDQN. Hence, the proposed reward model works better and more stably than did the experiment using only the DQN or DDQN algorithm in terms of timing and pattern of reward increase.

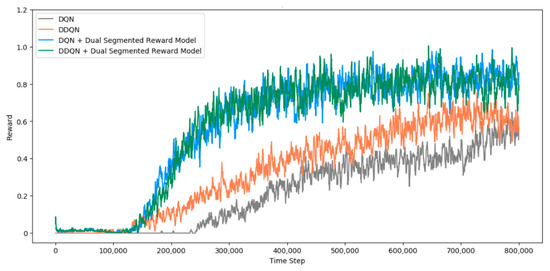
Figure 17. Comparison of Experimental Results by Test Case.

The difference between the experiment using the algorithm itself and the experiment using the Dual Segmented Reward Model is summarized as follows:

First, the reward generation pattern is different at the beginning of the experiment. For experiments on the algorithm itself, little reward occurred until the reward value increased. However, for the experiment to which the proposed reward model was applied, a small reward was continuously generated from the beginning of the experiment. Figure 18 shows the difference.

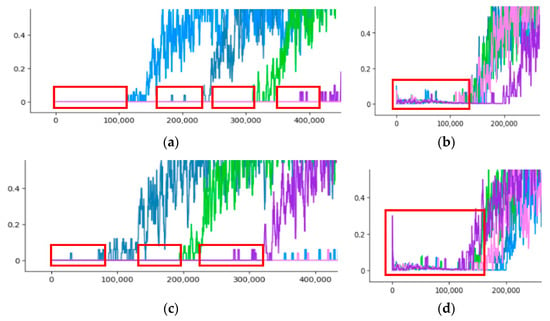
Figure 18. Comparison of Improvement #1: (a) DQN Test; (b) DQN + Dual Segmented Reward Model; (c) DDQN Test; (d) DDQN + Dual Segmented Reward Model.

Second, there is also a big difference in the time when the reward value starts to increase. For the experiment using the algorithm itself, the starting point of the increase in the reward value was not constant and there were many differences between the experiments. However, as a result of applying and testing the proposed reward model, the reward value started to increase consistently at a certain time. Figure 19 shows the changes.

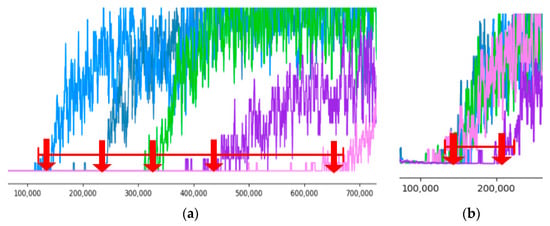
Figure 19. Comparison of Improvement #2: (a) DQN Test; (b) DQN + Dual Segmented Reward Model.

Third, there is a difference in the pattern of increase in reward value. For the experiment using the algorithm itself, the increase trend of the reward value was not constant and the reward value did not increase or decrease intermittently. However, when the proposed reward model was applied and tested, the pattern of increase in reward value was stable and consistent, and there was no decrease in the increased reward value. It can be confirmed in Figure 20.

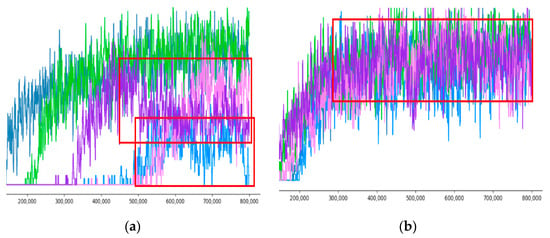
Figure 20. Comparison of Improvement #3: (a) DDQN Test; (b) DDQN + Dual Segmented Reward Model.

Given these improvements, we judged that it was helpful in improving the sparse reward problem. In the experiment using the proposed reward model, there was no case of learning failure that was intermittently observed in the experiment using the algorithm itself.

5. Conclusions

In this paper, we conducted a study considering realistically necessary conditions in an automated warehouse. Additional considerations were multiple mobile robots and complex movements. In particular, we used a MARL (Multi-Agent Reinforcement Learning) algorithm for path learning using multiple mobile robots. We did experiments with IQL algorithms based on DQN and DDQN. Although the initial experiment was successful, there was a problem in that the experimental results were not stable and the deviation was quite large. The target warehouse simulation environment basically has a characteristic of sparse reward, and it has become a poorer environment for reinforcement learning by expanding the warehouse size. It was necessary to ameliorate the sparse reward problem for better performance and stability. For this purpose, we proposed the Dual Segmented Reward Model and verified it as a reward model method optimized for warehouses. Specially, the proposed reward model is based on two separate reward models that split the entire action into partial actions. We defined two segmented reward models by observing the actual movement of mobile robots in a warehouse and understanding the characteristics of their movement. This improvement method can be a Reward Shaping method. We verified the proposed reward model by means of experiments, and the small reward value was continuously generated from the initial learning, the reward value increased in a certain time, the learning progressed, and the improvement was confirmed that the learning proceeded stably. In addition, there was almost no deviation in each experiment, thus confirming that the learning patterns of the experiments were almost identical. In this study, learning was performed using a simple MARL algorithm in a specific multi-agent environment, and positive results were confirmed with IQL algorithms based on DQN and DDQN, a distributed learning method. In the case of centralized learning, the sparse reward problem became more serious, and it was confirmed that the learning did not proceed well. The reward model method proposed in this paper has a high correlation with the operation of multiple mobile robots in an automated warehouse. It is specialized for the environment and its conditions. Therefore, as the environment and operations change, the reward model must be optimized by redefining it according to the changed environment and conditions.

Reinforcement learning is a very attractive and useful topic for solving complex problems in a variety of environments. As a future research direction, we hope to study complex decision making topics by using reinforcement learning to solve more complex realistic problems and find optimal solutions for applications or a systematical improvement method for the reward model.