Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities
Abstract
1. Introduction
- (i)
- A proposal for solving the trajectory tracking problem for an underactuated underwater vehicle moving horizontally described by equations resulting from the transformation of the inertia matrix (expressed in terms of the QV);
- (ii)
- Description with the quasi-velocities was used to detect properties of the vehicle model that are not available directly using the classical equations of motion (indication of some information that can be obtained based on the proposed vehicle dynamic equations);
- (iii)
- Controller based on transformed dynamic equations and expressed in QV;
- (iv)
- Simulation verification of the proposed control algorithm for 3-DOF planar models of 2 vehicles with different dynamics and for 2 different trajectories (this issue is important because it happens that the algorithms effectively working in the original literature do not work after changing the parameters of the model or the desired trajectory as demonstrated in [64]). Effects related to the properties of the equations are also presented.
2. Problem Formulation
3. Vehicle Model in Terms of Quasi-Velocities
- 1.
- Diagonalization of the inertia matrix instead of computing the inverse inertia matrix;
- 2.
- An insight (additional information) into the dynamics of the vehicle;
- 3.
- A heuristic algorithm in matching the QV and classical regulator gains;
- 4.
- Control signal related to the vehicle’s dynamics.
- 1.
- Norm of the matrix which determine couplings in the dynamic model of the vehicle. The matrix depend on elements of the symmetric matrix M.
- 2.
- The kinetic energy K expressed in terms of the vector for 3-DOF vehicle:Because each variable takes into account a component of the kinetic energy arising from all other velocities, which are coupled with the i-th variable, then we can examine the contribution of kinetic energy associated with each variable and the total kinetic energy of the vehicle. It is possible to determine reduced by each variable.
- 3.
- The average kinetic energy associated with each variable and the total kinetic energy:
- 4.
- Deformation of each velocity. The variables allow one to evaluate the impact of other velocities at the i-th velocity, i.e.,This result means that each takes into account a coupling between itself and the other velocities. Thus, using the controller, one can observe the effects of couplings for dynamics of the vehicle. Effect of the dynamical couplings is obtained by . As the measure of couplings we introduce the following quantity:
4. Simulation Results
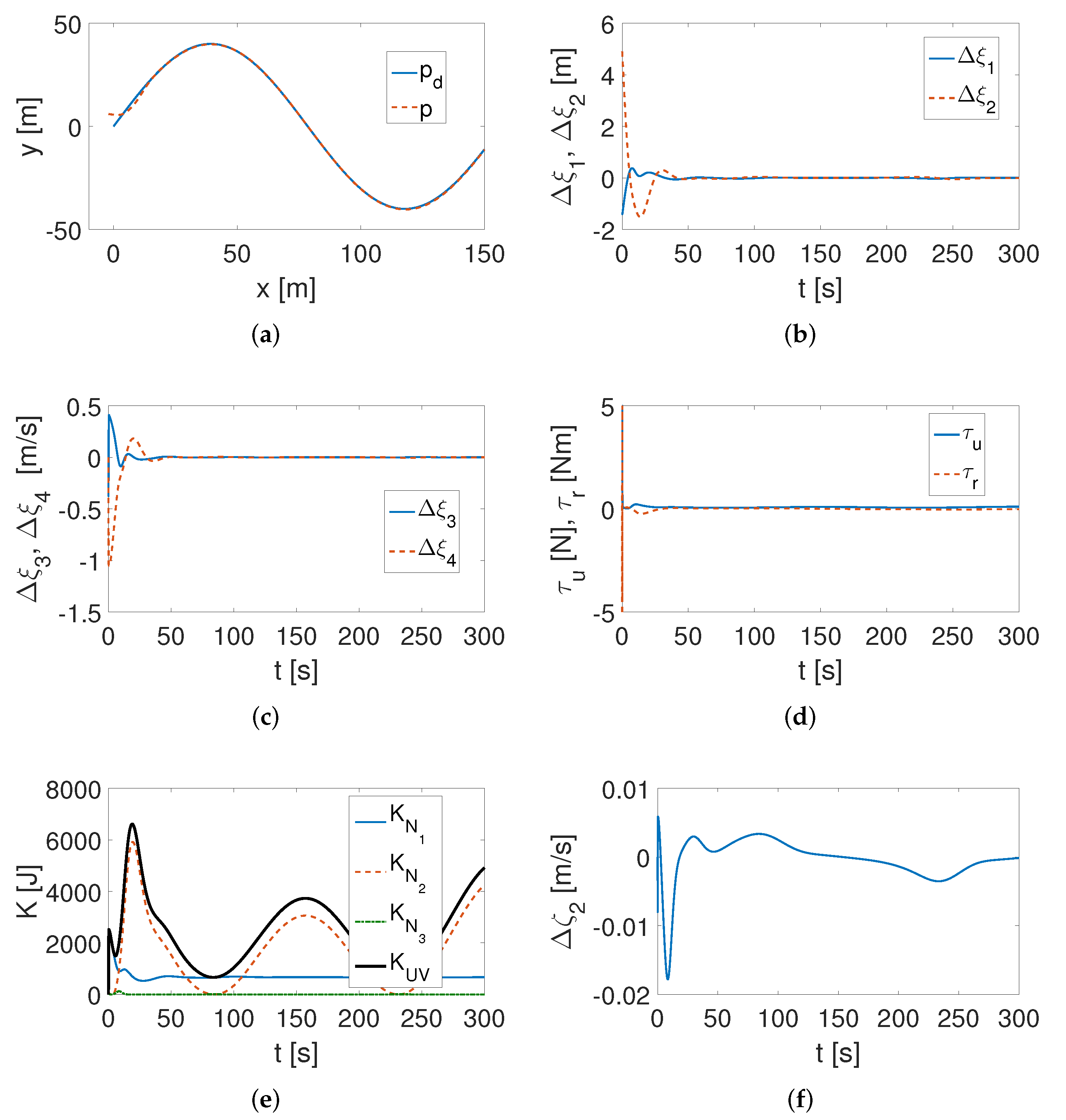
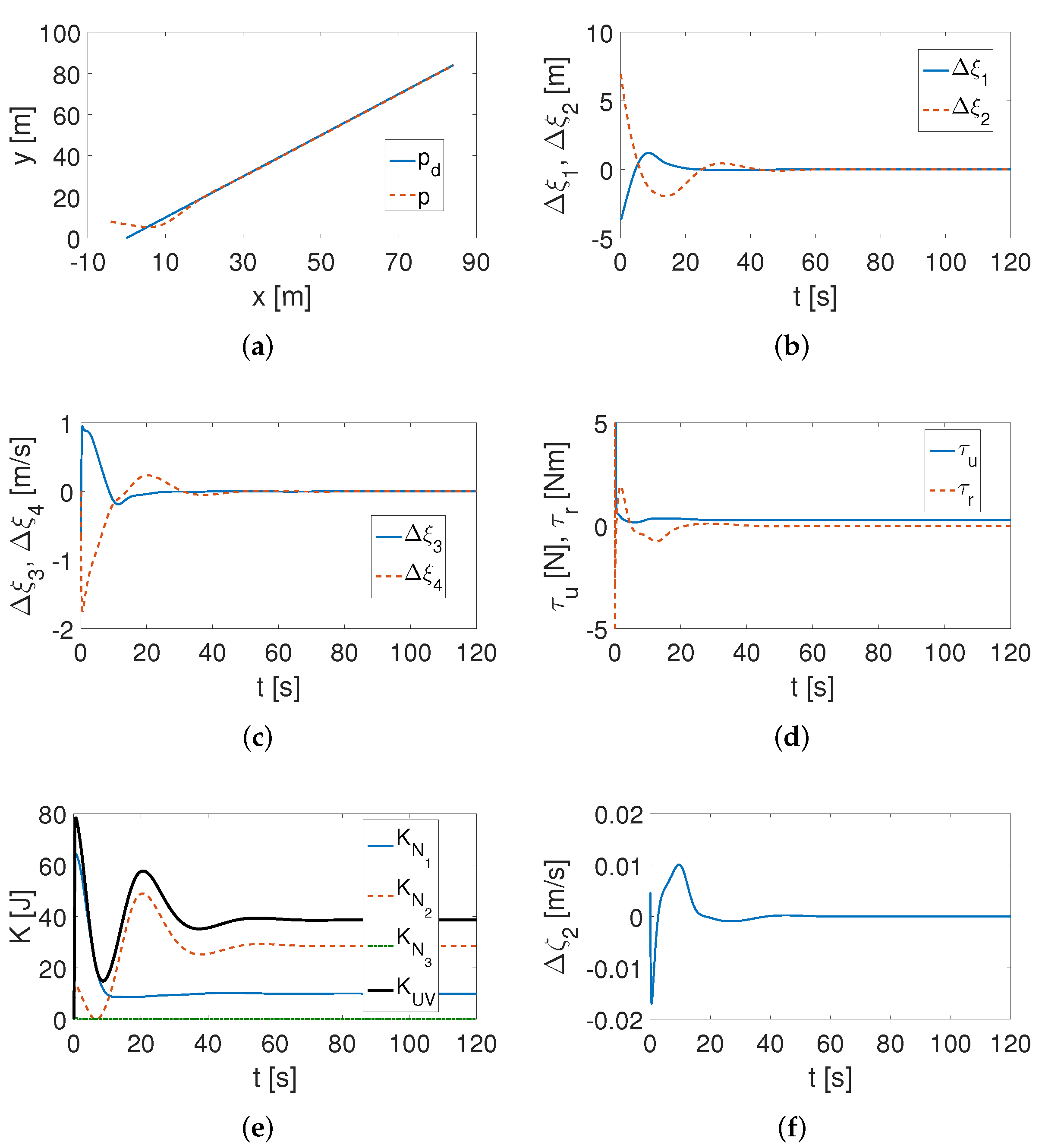
4.1. ROPOS Vehicle
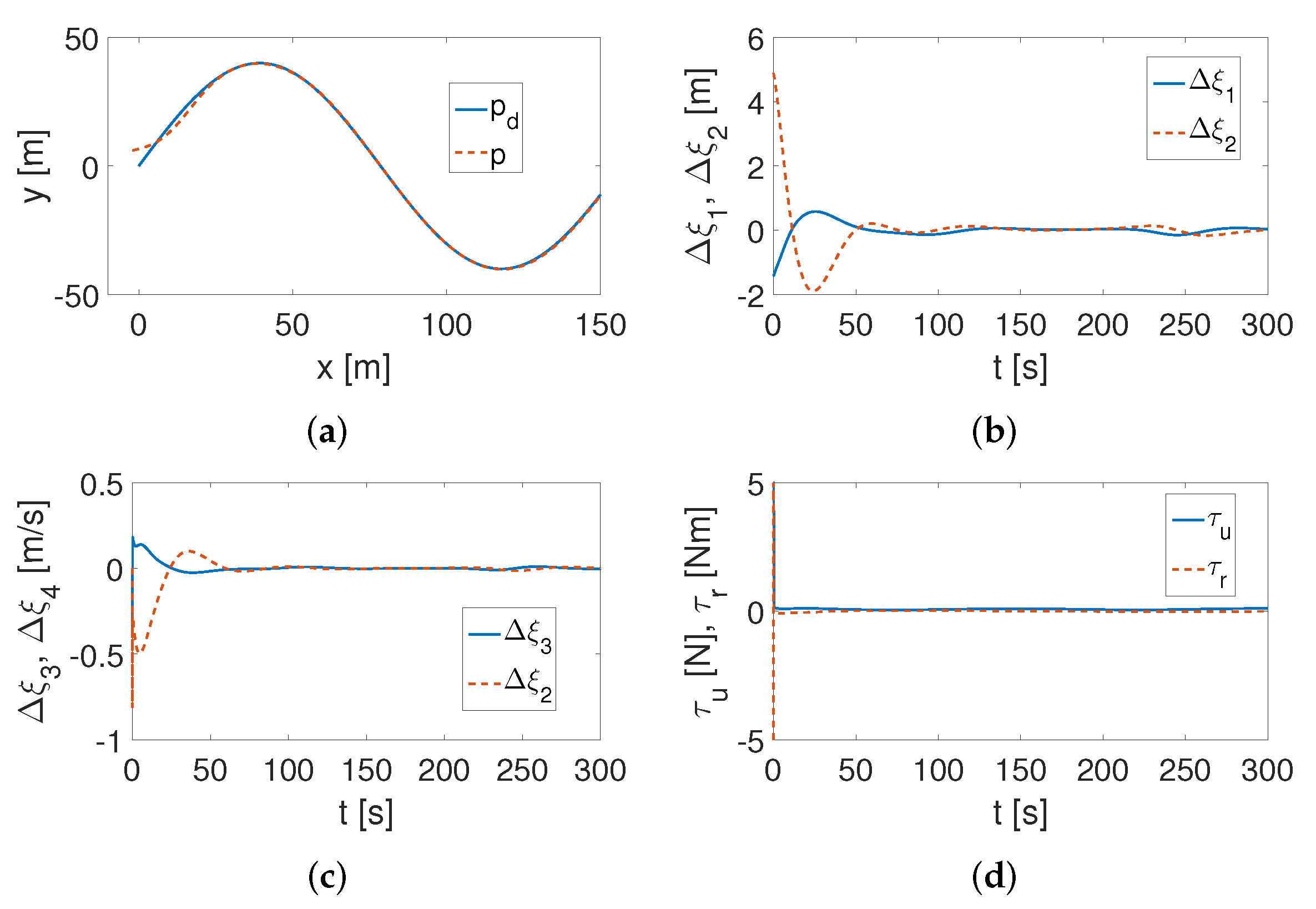
4.2. XX AUV Model Vehicle
4.3. Discussion of Results
- (1)
- It turned out that for the control algorithm in the QV version, the same set of gains allows the tracking task to be carried out for both two different trajectories and two vehicles with significantly different dynamics. Such information proves a certain universality of a correctly selected set of controller gains.
- (2)
- The coefficients that give satisfactory performance using the QV algorithms can be used to select the gains of a classic controller. For example the obtained gains set using QV , , , suggests that for ROPOS the gains for the CL algorithm may be chosen as follows: , , . For example the obtained gains set using QV , , for XX AUV model, suggests that the gains for the CL algorithm may be chosen as follows: , , , , , .
- (3)
- Both algorithms (QV and CL) make it possible to track a desired trajectory with the use of small values of applied forces and torques, which is also consistent with the results shown in [56].
- (4)
- It was found that significant changes in the vehicle dynamic parameters do not cause a significant deformation of the lateral velocity (the remaining quasi-speeds are equal to the velocities in the respective directions of movement).
5. Further Discussion on the Tracking Control Algorithm
5.1. The Proposed Controller versus Other Control Schemes
5.2. Advantages and Benefits of the Control Approach
- It is suitable for the control of asymmetric vehicles, which makes the dynamics model more realistic than the model with a diagonal inertia matrix;
- In comparison with other algorithms, after the velocity transformation from the modified controller, additional information hidden in the inertia matrix can be obtained;
- It gives ability to estimate the effect of couplings on vehicle behavior in motion (this effect can be studied for various trajectories and vehicles, e.g., to change them);
- It can be used for both diagonal and non-diagonal inertia matrix models to decide whether the simplified model is sufficient.
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Song, F.; An, E.; Folleco, A. Modeling and Simulation of Autonomous Underwater Vehicles: Design and Implementation. IEEE J. Ocean. Eng. 2003, 28, 283–296. [Google Scholar] [CrossRef]
- American Bureau of Shipping. ABS Guide for Vessel Maneuverability; American Bureau of Shipping: Houston, TX, USA, 2006; Updated February 2017. [Google Scholar]
- Do, K.D.; Pan, J. Control of Ships and Underwater Vehicles; Springer: London, UK, 2009. [Google Scholar]
- Wang, C.; Zhang, F.; Schaefer, D. Dynamic modeling of an autonomous underwater vehicle. J. Mar. Sci. Technol. 2015, 20, 199–212. [Google Scholar] [CrossRef]
- Min, F.; Pan, G.; Xu, X. Modeling of Autonomous Underwater Vehicles with Multi-Propellers Based on Maximum Likelihood Method. J. Mar. Sci. Eng. 2020, 8, 407. [Google Scholar] [CrossRef]
- Miao, J.; Wang, S.; Tomovic, M.M.; Zhao, Z. Compound line-of-sight nonlinear path following control of underactuated marine vehicles exposed to wind, waves, and ocean currents. Nonlinear Dyn. 2017, 89, 2441–2459. [Google Scholar] [CrossRef]
- Battista, T.; Woolsey, C. Control of an Underwater Vehicle in Irregular Waves. In Proceedings of the OCEANS 2015—MTS/IEEE Washington, Washingtton, DC, USA, 19–22 October 2015. [Google Scholar]
- Zhang, G.; Zhang, C.; Zhang, X.; Deng, Y. ESO-based path following control for underactuated vehicles with the safety prediction obstacle avoidance mechanism. Ocean Eng. 2019, 174, 14–30. [Google Scholar]
- Wiig, M.S.; Pettersen, K.Y.; Krogstad, T.R. Collision Avoidance for Underactuated Marine Vehicles Using the Constant Avoidance Angle Algorithm. IEEE Trans. Control. Syst. Technol. 2020, 28, 951–966. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, B.; Li, L. Collision Avoidance for Underactuated Ocean-Going Vessels Considering COLREGs Constraints. IEEE Access 2021, 9, 145943–145954. [Google Scholar] [CrossRef]
- Woods, S.A.; Bauer, R.J.; Seto, M.L. Automated Ballast Tank Control System for Autonomous Underwater Vehicles. IEEE J. Ocean. Eng. 2012, 37, 727–739. [Google Scholar] [CrossRef]
- Rosario, R.V.C.; Cunha, J.P.V.S.; Garcia-Rosa, P.B. Stabilizing Control of an Unmanned Surface Vehicle Pushing a Floating Load. Int. J. Control. Autom. Syst. 2020, 18, 3194–3203. [Google Scholar] [CrossRef]
- Behal, A.; Dawson, D.M.; Dixon, W.E.; Fang, Y. Tracking and Regulation Control of an Underactuated Surface Vessel With Nonintegrable Dynamics. IEEE Trans. Autom. Control. 2002, 47, 495–500. [Google Scholar] [CrossRef]
- Jiang, Z.P. Global tracking control of underactuated ships by Lyapunov’s direct method. Automatica 2002, 38, 301–309. [Google Scholar] [CrossRef]
- Lefeber, E.; Pettersen, K.Y.; Nijmeijer, H. Tracking Control of an Underactuated Ship. IEEE Trans. Control. Syst. Technol. 2003, 11, 52–61. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Muske, K.R.; McNinch, L.C.; Soltan, R.A. Sliding-Mode Tracking Control of Surface Vessels. IEEE Trans. Ind. Electron. 2008, 55, 4004–4012. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Trajectory tracking sliding mode control of underactuated AUVs. Nonlinear Dyn. 2016, 84, 1079–1091. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, B.; Liao, Y.; Wang, B. Finite-Time Trajectory Tracking Control for Uncertain Underactuated Marine Surface Vessels. IEEE Access 2019, 7, 102321–102330. [Google Scholar] [CrossRef]
- Elmokadem, T.; Zribi, M.; Youcef-Toumi, K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles. Ocean. Eng. 2017, 129, 613–625. [Google Scholar] [CrossRef]
- Qiao, L.; Zhang, W. Fast Trajectory Tracking Control of Underactuated Autonomous Underwater Vehicles. In Proceedings of the 8th IEEE International Conference on Underwater System Technology: Theory and Application, USYS 2018, Wuhan, China, 1–3 December 2018; pp. 1–6. [Google Scholar]
- Yan, Z.; Yu, H.; Zhang, W.; Li, B.; Zhou, J. Globally finite-time stable tracking control of underactuated UUVs. Ocean Eng. 2015, 107, 132–146. [Google Scholar] [CrossRef]
- Godhavn, J.M.; Fossen, T.I.; Berge, S.P. Non-Linear and Adaptive Backstepping Designs for Tracking Control of Ships. Int. J. Adapt. Control. Signal Process. 1998, 12, 649–670. [Google Scholar] [CrossRef]
- Repoulias, F.; Papadopoulos, E. Planar trajectory planning and tracking control design for underactuated AUVs. Ocean Eng. 2007, 34, 1650–1667. [Google Scholar] [CrossRef]
- Xie, W.J.; Ma, B.L. Universal Practical Tracking Control of Planar Underactuated Vehicle. Asian J. Control. 2015, 17, 1016–1026. [Google Scholar]
- Do, K.D. Robust adaptive tracking control of underactuated ODINs under stochastic sea loads. Robot. Auton. Syst. 2015, 72, 152–163. [Google Scholar] [CrossRef]
- Do, K.D. Global Inverse Optimal Tracking Control of Underactuated Omni-directional Intelligent Navigators (ODINs). J. Mar. Sci. Appl. 2015, 14, 1–13. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, G.; Qiao, L.; Zhang, W. Robust adaptive trajectory tracking control of underactuated surface vessel in fields of marine practice. J. Mar. Sci. Technol. 2018, 23, 950–957. [Google Scholar] [CrossRef]
- Lei, M.; Li, Y.; Pang, S. Extended state observer-based composite-system control for trajectory tracking of underactuated AUVs. Appl. Ocean. Res. 2021, 112, 102694. [Google Scholar] [CrossRef]
- Pettersen, K.Y.; Nijmeijer, H. Global practical stabilization and tracking for an underactuated ship—A combined averaging and backstepping approach. Model. Identif. Control. 1999, 20, 189–199. [Google Scholar] [CrossRef][Green Version]
- Sun, B.; Zhu, D.; Ding, F.; Yang, S.X. A novel tracking control approach for unmanned underwater vehicles based on bio-inspired neurodynamics. J. Mar. Sci. Technol. 2013, 18, 63–74. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, X.; Wang, G.; Fan, Y. Adaptive Backstepping Sliding Mode Tracking Control for Underactuated Unmanned Surface Vehicle With Disturbances and Input Saturation. IEEE Access 2021, 9, 1304–1312. [Google Scholar] [CrossRef]
- Do, K.D.; Jiang, Z.P.; Pan, J.; Nijmeijer, H. A global output-feedback controller for stabilization and tracking of underactuated ODIN: A spherical underwater vehicle. Automatica 2004, 40, 117–124. [Google Scholar] [CrossRef]
- Pan, C.Z.; Lai, X.Z.; Wang, S.X.; Wu, M. An efficient neural network approach to tracking control of an autonomous surface vehicle with unknown dynamics. Expert Syst. Appl. 2013, 40, 1629–1635. [Google Scholar] [CrossRef]
- Zhang, L.J.; Qi, X.; Pang, Y.J. Adaptive output feedback control based on DRFNN for AUV. Ocean Eng. 2009, 36, 716–722. [Google Scholar] [CrossRef]
- Mu, D.; Wang, G.; Fan, Y.; Qiu, B.; Sun, X. Adaptive Trajectory Tracking Control for Underactuated Unmanned Surface Vehicle Subject to Unknown Dynamics and Time-Varing Disturbances. Appl. Sci. 2018, 8, 547. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Wei, Y.; Wang, J. Neural-Based Command Filtered Backstepping Control for Trajectory Tracking of Underactuated Autonomous Surface Vehicles. IEEE Access 2020, 8, 42482–42490. [Google Scholar] [CrossRef]
- Zhou, J.; Zhao, X.; Chen, T.; Yan, Z.; Yang, Z. Trajectory Tracking Control of an Underactuated AUV Based on Backstepping Sliding Mode With State Prediction. IEEE Access 2019, 7, 181983–181993. [Google Scholar] [CrossRef]
- Zhu, G.; Ma, Y.; Li, Z.; Malekian, R.; Sotelo, M. Event-Triggered Adaptive Neural Fault-Tolerant Control of Underactuated MSVs With Input Saturation. IEEE Trans. Intell. Transp. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Raimondi, F.M.; Melluso, M. Fuzzy/kalman hierarchical horizontal motion control of underactuated ROVs. Int. J. Adv. Robot. Syst. 2010, 7, 139–154. [Google Scholar] [CrossRef]
- Wang, S.; Fu, M.; Wang, Y.; Tuo, Y.; Ren, H. Adaptive Online Constructive Fuzzy Tracking Control for Unmanned Surface Vessel With Unknown Time-Varying Uncertainties. IEEE Access 2018, 6, 70444–70455. [Google Scholar] [CrossRef]
- Jia, Z.; Hu, Z.; Zhang, W. Adaptive output-feedback control with prescribed performance for trajectory tracking of underactuated surface vessels. ISA Trans. 2019, 95, 18–26. [Google Scholar] [CrossRef]
- Li, J.; Du, J.; Sun, Y.; Lewis, F.L. Robust adaptive trajectory tracking control of underactuated autonomous underwater vehicles with prescribed performance. Int. J. Robust Nonlinear Control. 2019, 29, 4629–4643. [Google Scholar] [CrossRef]
- Guerreiro, B.J.; Silvestre, C.; Cunha, R.; Pascoal, A. Trajectory Tracking Nonlinear Model Predictive Control for Autonomous Surface Craft. IEEE Trans. Control. Syst. Technol. 2014, 22, 2160–2175. [Google Scholar] [CrossRef]
- Chwa, D. Global Tracking Control of Underactuated Ships With Input and Velocity Constraints Using Dynamic Surface Control Method. IEEE Trans. Control Syst. Technol. 2011, 19, 1357–1370. [Google Scholar] [CrossRef]
- Harmouche, M.; Laghrouche, S.; Chitour, Y. Global tracking for underactuated ships with bounded feedback controllers. Int. J. Control. 2014, 87, 2035–2043. [Google Scholar] [CrossRef][Green Version]
- Ye, L.; Zong, Q. Tracking control of an underactuated ship by modified dynamic inversion. ISA Trans. 2018, 83, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Serrano, M.E.; Scaglia, G.J.E.; Godoy, S.A.; Mut, V.; Ortiz, O.A. Trajectory Tracking of Underactuated Surface Vessels: A Linear Algebra Approach. IEEE Trans. Control Syst. Technol. 2014, 22, 1103–1111. [Google Scholar] [CrossRef]
- Panagou, D.; Kyriakopoulos, K.J. Viability control for a class of underactuated systems. Automatica 2013, 49, 17–29. [Google Scholar] [CrossRef]
- Chen, L.; Cui, R.; Yang, C.; Yan, W. Adaptive Neural Network Control of Underactuated Surface Vessels with Guaranteed Transient Performance: Theory and Experimental Results. IEEE Trans. Ind. Electron. 2020, 67, 4024–4035. [Google Scholar] [CrossRef]
- Dai, S.L.; He, S.; Lin, H. Transverse function control with prescribed performance guarantees for underactuated marine surface vehicles. Int. J. Robust Nonlinear Control. 2019, 29, 1577–1596. [Google Scholar] [CrossRef]
- Park, B.S. Neural Network-Based Tracking Control of Underactuated Autonomous Underwater Vehicles With Model Uncertainties. J. Dyn. Syst. Meas. Control. Trans. ASME 2015, 137, 021004. [Google Scholar] [CrossRef]
- Qiu, B.; Wang, G.; Fan, Y.; Mu, D.; Sun, X. Adaptive Sliding Mode Trajectory Tracking Control for Unmanned Surface Vehicle with Modeling Uncertainties and Input Saturation. Appl. Sci. 2019, 9, 1240. [Google Scholar] [CrossRef]
- Dong, Z.; Wan, L.; Liu, T.; Zeng, J. Horizontal-plane Trajectory-tracking Control of an Underactuated Unmanned Marine Vehicle in the Presence of Ocean Currents. Int. J. Adv. Robot. Syst. 2016. [Google Scholar] [CrossRef]
- Zhang, Z.; Wu, Y. Further results on global stabilisation and tracking control for underactuated surface vessels with non-diagonal inertia and damping matrices. Int. J. Control. 2015, 88, 1679–1692. [Google Scholar] [CrossRef]
- Ashrafiuon, H.; Nersesov, S.; Clayton, G. Trajectory Tracking Control of Planar Underactuated Vehicles. IEEE Trans. Autom. Control. 2017, 62, 1959–1965. [Google Scholar] [CrossRef]
- Paliotta, C.; Lefeber, E.; Pettersen, K.Y.; Pinto, J.; Costa, M.; de Figueiredo Borges de Sousa, J.T. Trajectory Tracking and Path Following for Underactuated Marine Vehicles. IEEE Trans. Control Syst. Technol. 2019, 27, 1423–1437. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, K.; Li, Y.; Xu, G.; Xiang, X. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation. Ocean Eng. 2019, 174, 14–30. [Google Scholar] [CrossRef]
- Wang, N.; Xie, G.; Pan, X.; Su, S.F. Full-State Regulation Control of Asymmetric Underactuated Surface Vehicles. IEEE Trans. Ind. Electron. 2019, 66, 8741–8750. [Google Scholar] [CrossRef]
- Wang, N.; Su, S.F.; Pan, X.; Yu, X.; Xie, G. Yaw-Guided Trajectory Tracking Control of an Asymmetric Underactuated Surface Vehicle. IEEE Trans. Ind. Inform. 2019, 15, 3502–3513. [Google Scholar] [CrossRef]
- Wang, C.; Xie, S.; Chen, H.; Peng, Y.; Zhang, D. A decoupling controller by hierarchical backstepping method for straight-line tracking of unmanned surface vehicle. Syst. Sci. Control. Eng. 2019, 7, 379–388. [Google Scholar] [CrossRef]
- Loduha, T.A.; Ravani, B. On First-Order Decoupling of Equations of Motion for Constrained Dynamical Systems. Trans. ASME J. Appl. Mech. 1995, 62, 216–222. [Google Scholar] [CrossRef]
- Herman, P. Velocity tracking controller for simulation analysis of underwater vehicle model. J. Mar. Eng. Technol. 2020, 19, 229–239. [Google Scholar] [CrossRef]
- Herman, P. Application of nonlinear controller for dynamics evaluation of underwater vehicles. Ocean Eng. 2019, 179, 59–66. [Google Scholar] [CrossRef]
- Herman, P. Numerical Test of Several Controllers for Underactuated Underwater Vehicles. Appl. Sci. 2020, 10, 8292. [Google Scholar] [CrossRef]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; John Wiley and Sons: Chichester, UK, 1994. [Google Scholar]
- Lesniak, J.; Stachowiak, M. Simulation Analysis of Selected Vehicle Control Methods with Incomplete Input Signals. Engineering Thesis, Poznan University of Technology, Poznań, Poland, 2020. [Google Scholar]
- Soylu, S.; Buckham, B.J.; Podhorodeski, R.P. A chattering-free sliding-mode controller for underwater vehicles with fault-tolerant infinity-norm thrust allocation. Ocean Eng. 2008, 35, 1647–1659. [Google Scholar] [CrossRef]
- Dong, Z.; Wan, L.; Li, Y.; Liu, T.; Zhuang, J.; Zhang, G. Point Stabilization for an Underactuated AUV in the Presence of Ocean Currents. Int. J. Adv. Robot. Syst. 2015, 12, 1. [Google Scholar] [CrossRef]
- Pan, B.; Chen, C.; Zhu, G.; Su, Y. Event-Triggered Composite Learning Finite-Time Trajectory Tracking Control for Underactuated MSVs Subject to Uncertainties. IEEE Access 2022, 10, 14440–14449. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, Y.; Huang, B.; Su, Y. Finite-time trajectory tracking control for under-actuated unmanned surface vessels with saturation constraint. Ocean Eng. 2022, 249, 110745. [Google Scholar] [CrossRef]
- Zhang, J.X.; Chai, T. Singularity-Free Continuous Adaptive Control of Uncertain Underactuated Surface Vessels With Prescribed Performance. IEEE Trans. Syst. Man Cybern. Syst. 2021, 1–10. [Google Scholar] [CrossRef]
- Park, B.S.; Yoo, J.Y. Robust trajectory tracking with adjustable performance of underactuated surface vessels via quantized state feedback. Ocean Eng. 2022, 246, 110475. [Google Scholar] [CrossRef]
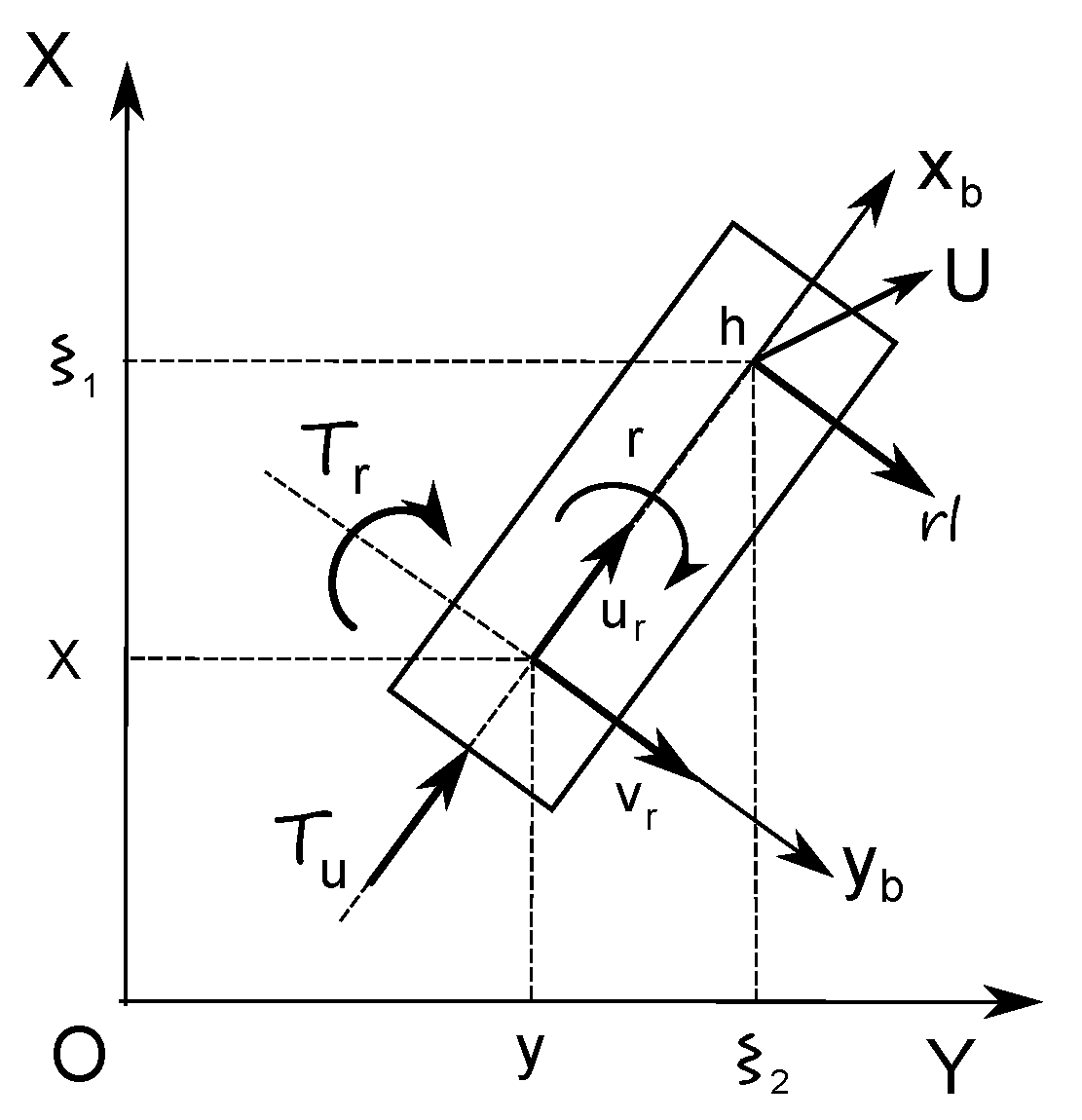




| ROPOS | ||
|---|---|---|
| Symbol | Value | Unit |
| L | 1.75 | m |
| W | 2.6 | m |
| H | 1.45 | m |
| m | 2268 | kg |
| J | 2457 | kg·m |
| −4380 | kg | |
| −9518 | kg | |
| −5000 | kg·m | |
| 6648 | kg | |
| 11,786 | kg | |
| −1134 | kg·m | |
| 7457 | kg·m | |
| 725 | kg/s | |
| 1240 | kg/s | |
| 1804 | kg·m/s |
| XX AUV Model | ||
|---|---|---|
| Symbol | Value | Unit |
| L | approx. 1.2 | m |
| m | approx. 45 | kg |
| 47.5 | kg | |
| 94.1 | kg | |
| 5.2 | kg·m | |
| 5.2 | kg·m | |
| 13.6 | kg·m | |
| 13.5 | kg/s | |
| 50.2 | kg/s | |
| 41.4 | kg·m/s | |
| 17.3 | kg·m/s | |
| 27.2 | kg·m/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herman, P. Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities. Appl. Sci. 2022, 12, 3496. https://doi.org/10.3390/app12073496
Herman P. Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities. Applied Sciences. 2022; 12(7):3496. https://doi.org/10.3390/app12073496
Chicago/Turabian StyleHerman, Przemyslaw. 2022. "Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities" Applied Sciences 12, no. 7: 3496. https://doi.org/10.3390/app12073496
APA StyleHerman, P. (2022). Application of a Trajectory Tracking Algorithm for Underactuated Underwater Vehicles Using Quasi-Velocities. Applied Sciences, 12(7), 3496. https://doi.org/10.3390/app12073496





