Abstract
Lanthanide hydrogen-rich materials have long been considered as one of the candidates with high-temperature superconducting properties in condensed matter physics, and have been a popular topic of research. Attempts to investigate the effects of different compositions of lanthanide hydrogen-rich materials are ongoing, with predictions and experimental studies in recent years showing that substances such as LaH, CeH, and LaH exhibit extremely high superconducting temperatures between 150–250 GPa. In particular, researchers have noted that, in those materials, a rise in the f orbit character at the Fermi level combined with the presence of hydrogen vibration modes at the same low energy scale will lead to an increase in the superconducting transition temperature. Here, we further elaborate on the effect of the ratios of lanthanide to hydrogen in these substances with the aim of bringing more clarity to the study of superhydrides in these extreme cases by comparing a variety of lanthanide hydrogen-rich materials with different ratios using the dynamical mean-field theory (DMFT) method, and provide ideas for later structural predictions and material property studies.
1. Introduction
Recently, hydrogen-rich materials have attracted great attention as potential candidates for high-temperature superconductivity, which is referred to as the holy grail of condensed matter physics. Since hydride causes high-frequency vibrations of hydrogen atoms at high pressure, it leads to stronger electron-phonon coupling, making it a potential high-temperature superconducting material [1,2]. Almost 90 years ago, theoretical physicists E. Wigner and H. B. Huntington predicted that hydrogen, the lightest element in nature, would be extremely likely to metalize in a high pressure environment [3]. An early study in the 1960s on metallic hydrogen found superconductivity at temperatures close to or even above room temperature, which suggests that of molecular hydrogen under high pressure is about 100–240 K, and that of atomic hydrogen can reach 300–350 K also under high pressure [4,5]. However, it is currently still difficult to perform relevant experiments due to the stringent synthesis requirements and ultra-sensitivity of metallic hydrogen under high pressure [6,7]. As a result of development of computational tools for predicting crystal structures and calculating properties of materials, ultra-high pressure generators have emerged. Nowadays, theoretical and experimental research on hydrogen-rich compounds covers binary hydride materials formed by almost all elements, which also includes the lanthanum-based high-temperature superconducting material LaH [8], as well as CeH [9,10,11], CeH, and YbH [12,13]. Research on these materials has found that binary lanthanide superconducting materials with high hydrogen content at high pressure are characterized by high symmetry and that they exhibit a space group structure of hexagonal and cubic crystal systems under 200–300 GPa. In addition to lanthanide superconducting materials, there are also hydrogen-rich superconducting materials with yttrium elements, which are chemically similar to lanthanides and often classified as rare earth metals YH, YH, and YH [14,15]. Among the transition elements, many actinide-related superconducting materials have also been found, such as AcH, AcH, AcH, and ThH [16,17,18].
Furthermore, some common metal elements have been found to form hydrogen-rich materials with superconducting properties, which include CaH [19,20,21,22], MgH [23], MgH [24], to name a few.
In addition to the hydrogen-rich superconducting materials containing metallic elements, hydrogen-rich materials with nonmetals have also attracted much attention. In recent research, Ranga P. Dias reported the superconductivity of a C-S-H system with a maximal superconducting transition temperature of 287.7 ± 1.2 K (approximately 15 degrees Celsius) at 267 ± 10 GPa [25]. Besides, it was predicted that values of PbH, SbH, and AsH would be 178 K, 150 K, and 100 K above 200 Gpa, 350 GPa, and 150 GPa respectively, as covalent hydrogenates [26,27].
It has been found that LaH with face-centered cubic structure is a good metal, forming high electron-density energy bands at the Fermi level. The finite occupancy of the La- orbitals, which are successively pushed at the Fermi level as the external pressure increases [28], ensures a particularly high in La-H systems. The localized La-4f orbitals become more stable compared to the La-6s and La-5d orbitals due to the pressure of the external environment, which leads to new prominent quantum states originating from strong electronic correlations [28].
Therefore, in order to more accurately describe the properties and physical laws of hydrogen-rich high-temperature superconductors at high pressures, the quantitative theoretical calculations were used in our research. The interaction between the localized electrons and the strong lattice vibrations of the hydrogen atoms facilitates superconductivity in these materials. A thorough description of the electrical properties is required for a precise analysis of this interaction, which brings notorious difficulties for f-systems correlation, as it requires that both mobile and localized electrons are treated on the same basis [29].
Here, we present a study of the superconducting properties of two members of lanthanum hydrates family LaH and LaH in order to learn the effect of the hydrogen content on and to find out if the many-body corrections to the DFT results are equally important for lanthanides with different hydrogen content. We employ a practical first-principles computationally consistent platform that uses a many-body correction of electron spectral weights and then feeds back into ’s estimate. In the present work, we limit ourselves to the DMFT corrections of the electronic spectrum only.
This paper proves that many-body correction in f-orbital systems may lead to changes occurring in spectral weights on the order of an eV. Our research presents an assessment of the physical properties of two La-H systems for different quantities of hydrogen atoms, paying particular attention to the influence of related factors on the spectral properties. It was found that LaH and LaH have stable crystal structures at pressures up to 400 GPa, while LaH is unstable at lower pressure; hence, we focus this investigation on modeling the materials at 400 GPa, as our aim is to compare the correction validity for different hydrogen compositions.
2. Discussion
Electron-phonon interactions are thought to be the origin of superconductivity in lanthanide hydrides. According to the Migdal–Eliashberg theory, there are four factors to define : the characteristic phonon frequency , the electron-phonon coupling strength , the density of states at the Fermi level , and the Coulomb pseudopotential, . Density functional theory (DFT), which uses standard pseudo-potentials and exchange correlation functionals, e.g., PBE, to explain lattice dynamics, is universally considered to be correct. It is generally acknowledged that DFT struggles to describe systems possessing strong electronic correlations with strongly localized d and f shells, and the use of many-body corrections are necessary.
In the following analysis, we used DFT combined with DMFT. In order to capture the local paramagnetic moment in lanthanide elements, one has to correct for local charge and spin fluctuations captured by DMFT. Changes in the orbital character at the Fermi surface produced by spectral weight transfer linked to Hubbard f band splitting are accounted for using DMFT. In accordance to the Allen–Dynes formalism, this affects low-energy electron-electron scattering processes via transfer of phonon momentum, which will be indicated in the following section.
In Table A1 are given the structural parameters of Fm3m-LaH and Fmmm-LaH, which show hardly any correlation at 400 GPa. In addition, quantities involved in the calculations, namely, and , are summarized in Table A2. was taken to be . We compared the effect of different DMFT electronic charge self-consistency schemes. A comparison is shown in Figure 1 between (i) PBE DFT and (ii) DFT + DMFT with full charge self-consistent formalism (DFT + DMFT + CSC). According to our research, we found that the Eliashberg function, , was significantly influenced by the correlation effects, which is defined in Equation (2). We utilized the Koster–Slater interaction vertex for the La correlated manifold, with values of eV and eV. From Figure 2 we can conclude that the DFT + DMFT + CSC method enables an increase in the superconducting temperature, which confirms the large contribution of the many-body effect to the prediction of the superconducting temperature of lanthanide hydrides, and justifies the need for more detailed correction models.
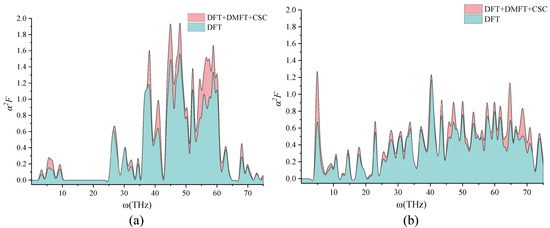
Figure 1.
Eliashberg function for (a) LaH and (b) LaH; the spectral weight at the Fermi level is calculated with different extents of approximation: (i) DFT and (ii) with the full-charge self-consistent formalism (DFT + DMFT + CSC).
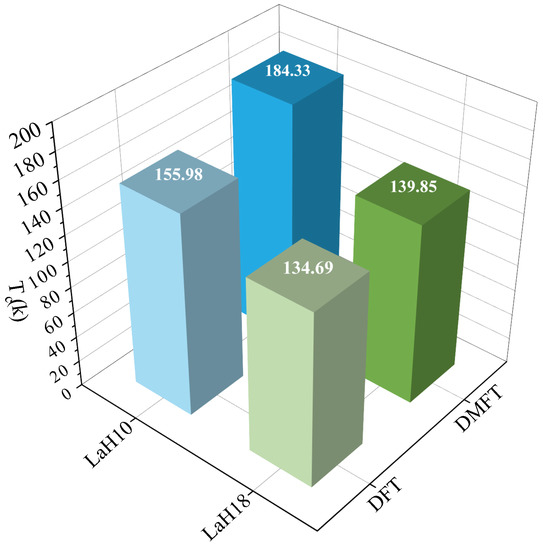
Figure 2.
The superconducting temperature obtained by the Allen and Dynes formalism for LaH and LaH at 400 GPa. We obtained a theoretical estimation for LaH of K by DFT and K by DMFT, and a theoretical estimation for LaH of K by DFT and K by DMFT. We have used values of eV and eV. All these calculations have been carried out using Fm3m-LaH and Fmmm-LaH at 400 GPa.
We noted that for the higher composition of hydrogen, LaH, the correction to the critical temperature is less significant compared to the lower hydrogen composition case. Figure 1 shows that the latter has a few well determined peaks that are enhanced by the DMFT + CSC correction, whilst in the LaH case, the Eliashberg function has a more evenly spread character with lower height of the peaks. Consequently, for the many-body corrections, we obtained an approximately correction to LaH critical temperature compared to just under for LaH, as can be seen from Figure 2. Note that eV and eV are used in the following section of this paper.
As shown in Figure 3a, the La compound is represented by a two-band system in the absence of a long-range magnetic order in DFT calculation. DFT formalism uses a single Slater determinant model and consequently fails to capture any paramagnetic effects, with an associated magnetic multiplet (fluctuating magnetic moment). These effects usually cause a splitting of spectral features into satellites, as seen in Figure 3b,c, with a resulting enforcement of the f character at the Fermi level. We established that since sharp La features exist at the Fermi level, a greater degree of theoretical modeling is necessary to correctly reflect the superconducting characteristics. In the conducted analysis, for example, the one-shot (DFT + DMFT) and the full-charge self-consistent method (DFT + DMFT + CSC) generate a minor shift of the acute La feature at the Fermi level, which reduces the f character weight at the Fermi level.
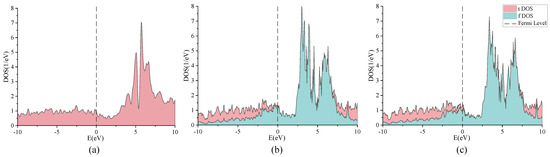
Figure 3.
(a) Density of states produced by DFT calculations. In (b,c), we show the density of states, obtained within the oneshot DFT + DMFT and within the full-charge self-consistent DFT + DMFT + CSC, respectively. and signify the density of states corresponding to the lattice and f impurity Green’s function, respectively. All calculations were carried out in the Fm3m phase of LaH at 400 GPa.
According to our results, f orbitals seem to be particularly significant for the superconducting characteristics of rare-earth hydrates. However, the impact of the quantity of the atoms for hydrogen in hydrate with the same f-element is unknown. Hence, in addition to LaH, we also studied stable LaH structures at 400 GPa with the aim to distinguish any notable tendencies.
A comparison between Figure 4a–c shows that the one-shot (DFT + DMFT) and the full-charge self-consistent method (DFT + DMFT + CSC) barely change the -La spectral weight at the Fermi level. This leads to similar results for the superconducting temperature of LaH within DFT, one-shot DFT + DMFT, and DFT + DMFT + CSC approaches. By looking at Figure 3 and Figure 4, it can be seen that the f orbital DOS modifications within DMFT with respect to DFT are different for different hydrogen content. For LaH, DFT significantly overestimates the -La weight at the Fermi level, while for LaH, the -La weight is low both in DFT and DMFT, leading to a lower .
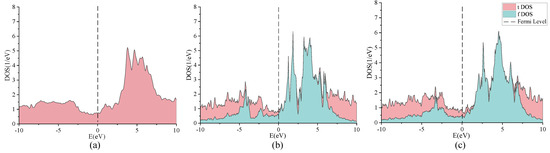
Figure 4.
(a) Density of states produced by DFT calculations. In (b,c), we show the density of states, obtained within the one-shot DFT + DMFT and within the full-charge self-consistent DFT + DMFT + CSC, respectively. and signify the density of states corresponding to the lattice and f impurity Green’s function, respectively. All calculations were carried out in the Fmmm phase of LaH at 400 GPa.
3. Methods
Our theoretical approach is sketched in Figure 5. We provide a diagrammatic outline of the main elements of the proposed theoretical platform, as well as their inter-relations. Our technique creates a modular structure for the screening of high-pressure materials.
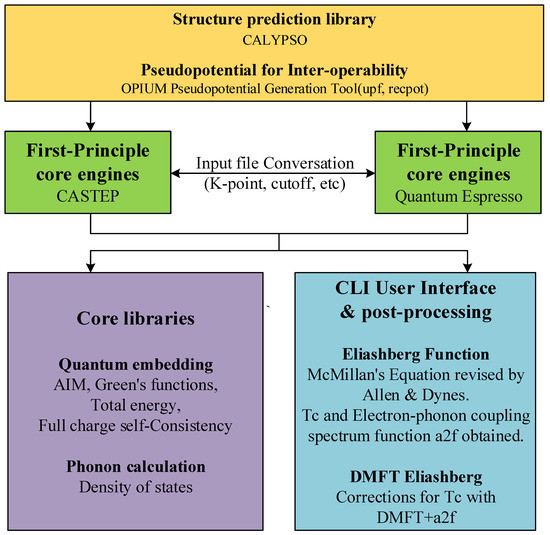
Figure 5.
Schematic of the workflow for DFT + DMFT interfaced with Allen–Dynes. Outline of the theoretical platform’s core modules and their interrelationships. To begin with, structures are modeled by crystal structure analysis by particle swarm optimization (CALYPSO), and the pseudopotentials are generated with OPIUM. The main core engines are CASTEP and QE DFT software. We have used format conversion of input files, pseudo-potentials, and K-point grids to ensure interoperability between QE and CASTEP. We employed core libraries to provide many-body corrections using quantum embedding, which also provides updated values for the forces and energies. During the post-processing phase, we used the DMFT + a2F approach to obtain values for the Eliashberg function and superconducting temperature . As a final step, data was archived for future usage using HDF5.
Structural predictions. Crystal structure investigation by particle swarm optimization (CALYPSO) [30,31], based on PSO algorithm [32,33], provides stoichiometric compositions via Gibbs enthalpies for the equation of state and convex hull. The structure searches were carried out at 400 GPa with primitive cells of LaH and LaH for more than 600 structures.
Ab initio calculations. Structural optimization and computations of enthalpy were performed using VASP code [34]. Electronic structures were calculated by QUANTUM ESPRESSO (QE) [35] code.
EPC calculations. We performed the electron-phonon coupling (EPC) calculation using QE with a kinetic energy cutoff of 90 Ry. In order to perform reliable calculation of the electron-phonon coupling in metallic systems, we have employed k-meshes of for the electronic Brillouin zone integration and q-meshes of for LaH and LaH compounds.
Methods. We combined the use of QE and CASTEP [36,37] by using input file format conversion, pseudopotentials, and K-point grids. Core libraries for DMFT quantum embedding were used for the many-body corrections, which provided the total free energies, electronic densities, and Kohn–Sham levels occupancies [9,38].
Norm-conserving pseudopotentials by OPIUM were adopted for describing the core electrons and their effects on the valence orbitals [39]. Reference electronic configurations of for the La atoms and for the H atoms were used.
Post-processing. For estimating the superconducting transition temperature, we used the Allen–Dynes modified McMillan equation [40]:
where is the Coulomb pseudopotential. Formulas for the electron-phonon coupling strength and were taken from Ref. [9]. In the post-processing stage, we have followed the procedure outlined by [9]; the reader interested in the computation details could refer to this paper for more exhaustive explanations of the steps, equations, and definitions of the relevant terms. Below, we quote the main equations that we used in our calculations of .
The Allen–Dynes analysis models the Eliashberg function as a sum at the Fermi level over all scattering processes, mediated by phonon momentum transfer [41]:
where is the DOS at Fermi level, is the phonon spectrum of a branch at momentum , and are electronic band energies, referred to the Fermi level, while are the electron-phonon coupling matrix elements. When many-body corrections are taken into account, there is a shift of the spectral character at the Fermi level. Furthermore, the electronic correlations lead to a mass enhancement and induce a finite lifetime, due to incoherence. Following onto the DMFT scissors, the DFT bands are supplied with the renormalized DMFT spectral density:
where is the total and is the -momentum resolved spectral weight at the Fermi level. This method is indicated as DMFT + a2F in the model diagram. We would like to point out that, unlike the Allen–Dynes method using DFT eigenvalues, which suffers from the double-broadening issue, within our approach, the broadening is given by the finite lifetime from the many-body Green’s function and, therefore, our approach is free from the double broadening issue.
The DFT Kohn–Sham Eigenstates are employed in the derivation of the DMFT Green’s function in the DFT + DMFT quantum embedding approach [41]. The Anderson Impurity Model (AIM) is defined using atomic projectors and solved sequentially inside the Hubbard-I approximation. Furthermore, TRIQS open-source platform [42] provides a wide range of quantum solvers through an interface to DMFT inside CASTEP. The Kohn–Sham potential is computed using the DMFT electronic density, which is generated from the DMFT occupancies, in the complete charge self-consistent technique (DFT + DMFT + CSC). Total energies and forces are determined using Green’s function and self-energy after DMFT convergence.
4. Conclusions
We used many-body adjustments to predict the superconducting temperature in lanthanide hydrides and explored the significance of this model under different compositions with the same elements. To reestablish a consistent theoretical framework, the DMFT charge self-consistency method was utilized, including many-body corrections to the local charge density in first-principles calculations. Our methodology is free, flexible, and simple to implement, providing interaction of first- principles software with modular foundation. The software includes QE, CASTEP, and CASTEP + DMFT.
We found that an increase in the spectral weight of the f states at the Fermi level led to an increase in the estimated superconducting temperature. In this research, within the DFT + DMFT + CSC method, was changed by 18% for LaH and by 3% for LaH at 400 GPa pressure. Furthermore, we discovered that the adjustment of the superconducting temperature of lanthanide materials within DFT + DMFT + CSC is more significant in symmetric structures and when the fraction of hydrogen elements is not excessively large.
Author Contributions
The calculations have been carried out by Y.W. The data is analyzed by Y.W., E.C. and E.P. All of the authors wrote this paper. This investigation was outlined by C.W. All authors have read and agreed to the published version of the manuscript.
Funding
Y.W. is grateful for the funding from China Scholarship Council. E.C. is a self-funded student. The Engineering and Physical Sciences Research Council of the United Kingdom funded C.W., N.B. and E.P. with Grant EP/R02992X/1.
Data Availability Statement
The following link is an endpoint to provide the code used in the investigation: dmft.ai (accessed on 23 February 2022).
Acknowledgments
Y.W. is thankful to Ying Sun (Jilin University) for valuable discussions. The research was conducted on resources supplied by the ARCHER U.K. National Supercomputing Service and the Cambridge Service for Data Driven Discovery (CSD3) which is operated by the University of Cambridge Research Computing Service.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
The structural parameters of LaH and LaH were calculated and the results are shown below.
Table A1.
The structural parameters of LaH and LaH were calculated and the results are shown below.
| Space Group | Lattice Parameters (Å) | Atoms | Atomic Coordinates (Fractional) | |||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| LaH (400 GPa) | Fm-3m | a = b = c = 4.59461 = = = 90° | H(32f) | 0.62021 | 0.62021 | 0.62021 |
| H(8c) | 0.25000 | 0.25000 | 0.25000 | |||
| La(4a) | 0.00000 | 0.00000 | 0.00000 | |||
|
LaH (400 GPa) | Fmmm | a =5.78715 b = 7.06134 c = 3.33380 = = = 90° | H(16o) | 0.32905 | 0.27446 | 0.00000 |
| H(16l) | 0.08379 | 0.25000 | 0.25000 | |||
| H(16k) | 0.25000 | 0.38271 | 0.25000 | |||
| H(16o) | 0.33762 | 0.07756 | 0.00000 | |||
| La(8h) | 0.00000 | 0.61864 | 0.00000 | |||
| La(4a) | 0.00000 | 0.00000 | 0.00000 | |||

Table A2.
Calculated variation of , and for LaH and LaH compounds in Fm-3m and Fmmm phase at 400 GPa, respectively.
Table A2.
Calculated variation of , and for LaH and LaH compounds in Fm-3m and Fmmm phase at 400 GPa, respectively.
| Method | (States/eV/f.u.) | |||
|---|---|---|---|---|
| LaH | DFT | 1.35 | 1536 | 0.80 |
| DMFT | 1.76 | 1405 | 1.23 | |
| LaH | DFT | 1.65 | 1083 | 0.75 |
| DMFT | 2.22 | 909 | 0.83 |
References
- McMahon, J.M.; Ceperley, D.M. High-temperature superconductivity in atomic metallic hydrogen. Phys. Rev. B 2011, 84, 144515. [Google Scholar] [CrossRef] [Green Version]
- Borinaga, M.; Errea, I.; Calandra, M.; Mauri, F.; Bergara, A. Anharmonic effects in atomic hydrogen: Superconductivity and lattice dynamical stability. Phys. Rev. B 2016, 93, 174308. [Google Scholar] [CrossRef] [Green Version]
- Wigner, E.; Huntington, H. On the possibility of a metallic modification of hydrogen. J. Chem. Phys. 1935, 3, 764. [Google Scholar] [CrossRef]
- Cudazzo, P.; Profeta, G.; Sanna, A.; Floris, A.; Continenza, A.; Massidda, S.; Gross, E. Ab initio description of high-temperature superconductivity in dense molecular hydrogen. Phys. Rev. Lett. 2008, 100, 257001. [Google Scholar] [CrossRef] [Green Version]
- McMahon, J.M.; Morales, M.A.; Pierleoni, C.; Ceperley, D.M. The properties of hydrogen and helium under extreme conditions. Rev. Mod. Phys. 2012, 84, 1607. [Google Scholar] [CrossRef]
- Eremets, M.I.; Drozdov, A.P.; Kong, P.; Wang, H. Semimetallic molecular hydrogen at pressure above 350 gpa. Nat. Phys. 2019, 15, 1246. [Google Scholar] [CrossRef]
- Loubeyre, P.; Occelli, F.; Dumas, P. Synchrotron infrared spectroscopic evidence of the probable transition to metal hydrogen. Nature 2020, 577, 631. [Google Scholar] [CrossRef]
- Sun, W.; Kuang, X.; Keen, H.D.; Lu, C.; Hermann, A. Second group of high-pressure high-temperature lanthanide polyhydride superconductors. Phys. Rev. B 2020, 102, 144524. [Google Scholar] [CrossRef]
- Plekhanov, E.; Zhao, Z.; Macheda, F.; Wei, Y.; Bonini, N.; Weber, C. Computational materials discovery for lanthanide hydrides at high pressure for high temperature superconductivity. Phys. Rev. Res. 2022, 4, 013248. [Google Scholar] [CrossRef]
- Wang, C.; Liu, S.; Jeon, H.; Yi, S.; Bang, Y.; Cho, J.-H. Effect of hole doping on superconductivity in compressed ceh 9 at high pressures. Phys. Rev. B 2021, 104, L020504. [Google Scholar] [CrossRef]
- Li, B.; Miao, Z.; Ti, L.; Liu, S.; Chen, J.; Shi, Z.; Gregoryanz, E. Predicted high-temperature superconductivity in cerium hydrides at high pressures. J. Appl. Phys. 2019, 126, 235901. [Google Scholar] [CrossRef]
- Wei, Y.; Macheda, F.; Zhao, Z.; Tse, T.; Plekhanov, E.; Bonini, N.; Weber, C. High-temperature superconductivity in the lanthanide hydrides at extreme pressures. Appl. Sci. 2022, 12, 874. [Google Scholar] [CrossRef]
- Kruglov, I.A.; Semenok, D.V.; Song, H.; Szczsniak, R.; Wrona, I.A.; Akashi, R.; Esfahani, M.M.D.; Duan, D.; Cui, T.; Kvashnin, A.G.; et al. Superconductivity of lah 10 and lah 16 polyhydrides. Phys. Rev. B 2020, 101, 024508. [Google Scholar] [CrossRef] [Green Version]
- Kong, P.; Minkov, V.S.; Kuzovnikov, M.A.; Drozdov, A.P.; Besedin, S.P.; Mozaffari, S.; Balicas, L.; Balakirev, F.F.; Prakapenka, V.B.; Chariton, S.; et al. Superconductivity up to 243 k in the yttrium-hydrogen system under high pressure. Nat. Commun. 2021, 12, 1. [Google Scholar] [CrossRef] [PubMed]
- Struzhkin, V.; Li, B.; Ji, C.; Chen, X.-J.; Prakapenka, V.; Greenberg, E.; Troyan, I.; Gavriliuk, A.; Mao, H.-K. Superconductivity in la and y hydrides: Remaining questions to experiment and theory. Matter Radiat. Extrem. 2020, 5, 028201. [Google Scholar] [CrossRef] [Green Version]
- Semenok, D.V.; Kvashnin, A.G.; Kruglov, I.A.; Oganov, A.R. Actinium hydrides ach10, ach12, and ach16 as high-temperature conventional superconductors. J. Phys. Chem. Lett. 2018, 9, 1920. [Google Scholar] [CrossRef] [Green Version]
- Semenok, D.V.; Kvashnin, A.G.; Ivanova, A.G.; Svitlyk, V.; Fominski, V.Y.; Sadakov, A.V.; Sobolevskiy, O.A.; Pudalov, V.M.; Troyan, I.A.; Oganov, A.R. Superconductivity at 161 k in thorium hydride thh10: Synthesis and properties. Mater. Today 2020, 33, 36. [Google Scholar] [CrossRef] [Green Version]
- Kvashnin, A.G.; Semenok, D.V.; Kruglov, I.A.; Wrona, I.A.; Oganov, A.R. High-temperature superconductivity in a th–h system under pressure conditions. ACS Appl. Mater. Interfaces 2018, 10, 43809. [Google Scholar] [CrossRef]
- Wang, H.; John, S.T.; Tanaka, K.; Iitaka, T.; Ma, Y. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 2012, 109, 6463. [Google Scholar] [CrossRef] [Green Version]
- Shao, Z.; Duan, D.; Ma, Y.; Yu, H.; Song, H.; Xie, H.; Li, D.; Tian, F.; Liu, B.; Cui, T. Unique phase diagram and superconductivity of calcium hydrides at high pressures. Inorg. Chem. 2019, 58, 2558. [Google Scholar] [CrossRef]
- Ma, L.; Wang, K.; Xie, Y.; Yang, X.; Wang, Y.; Zhou, M.; Liu, H.; Yu, X.; Zhao, Y.; Wang, H.; et al. High-Tc superconductivity in clathrate calcium hydride CaH6. arXiv 2021, arXiv:2103.16282. [Google Scholar]
- Li, Z.; He, X.; Zhang, C.; Zhang, S.; Feng, S.; Wang, X.; Yu, R.; Jin, C. Superconductivity above 200 K observed in superhydrides of calcium. arXiv 2021, arXiv:2103.16917. [Google Scholar]
- Szczesniak, R.; Durajski, A. Superconductivity well above room temperature in compressed mgh 6. Front. Phys. 2016, 11, 1. [Google Scholar] [CrossRef]
- Lonie, D.C.; Hooper, J.; Altintas, B.; Zurek, E. Metallization of magnesium polyhydrides under pressure. Phys. Rev. B 2013, 87, 054107. [Google Scholar] [CrossRef] [Green Version]
- Snider, E.; Dasenbrock-Gammon, N.; McBride, R.; Debessai, M.; Vindana, H.; Vencatasamy, K.; Lawler, K.V.; Salamat, A.; Dias, R.P. Room-temperature superconductivity in a carbonaceous sulfur hydride. Nature 2020, 586, 373. [Google Scholar] [CrossRef]
- Fu, Y.; Du, X.; Zhang, L.; Peng, F.; Zhang, M.; Pickard, C.J.; Needs, R.J.; Singh, D.J.; Zheng, W.; Ma, Y. High-pressure phase stability and superconductivity of pnictogen hydrides and chemical trends for compressed hydrides. Chem. Mater. 2016, 28, 1746. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Conway, L.; Sun, W.; Kuang, X.; Lu, C.; Hermann, A. Phase stability and superconductivity of lead hydrides at high pressure. Phys. Rev. B 2021, 103, 035131. [Google Scholar] [CrossRef]
- Fedorov, A.; Laubschat, C.; Starke, K.; Weschke, E.; Barholz, K.-U.; Kaindl, G. Surface shift of the unoccupied 4f state in la metal. Phys. Rev. Lett. 1993, 70, 1719. [Google Scholar] [CrossRef]
- Pfleiderer, C. Superconducting phases of f-electron compounds. Rev. Mod. Phys. 2009, 81, 1551. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Calypso: A method for crystal structure prediction. Comput. Phys. Commun. 2012, 183, 2063. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference on Neural Networks Proceedings, Perth, Australia, 27 November–1 December 1995; Volume 4. [Google Scholar]
- Eberhat, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Piscataway, NJ, USA, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using castep. Z. Für Krist.-Cryst. Mater. 2005, 220, 567. [Google Scholar] [CrossRef] [Green Version]
- Plekhanov, E.; Hasnip, P.; Sacksteder, V.; Probert, M.; Clark, S.J.; Refson, K.; Weber, C. Many-body renormalization of forces in f-electron materials. Phys. Rev. B 2018, 98, 075129. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.; Plekhanov, E.; Blackbourn, D.; Acharya, S.; Weber, C. The mott to kondo transition in diluted kondo superlattices. Commun. Phys. 2019, 2, 1. [Google Scholar] [CrossRef]
- Rappe, A.M.; Rabe, K.M.; Kaxiras, E.; Joannopoulos, J. Optimized pseudopotentials. Phys. Rev. B 1990, 41, 1227, Erratum in Phys. Rev. B 1991, 44, 13175. [Google Scholar] [CrossRef]
- Dynes, R. Mcmillan’s equation and the tc of superconductors. Solid State Commun. 1972, 10, 615. [Google Scholar] [CrossRef]
- Allen, P.B.; Dynes, R. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 1975, 12, 905. [Google Scholar] [CrossRef]
- Parcollet, O.; Ferrero, M.; Ayral, T.; Hafermann, H.; Krivenko, I.; Messio, L.; Seth, P. Triqs: A toolbox for research on interacting quantum systems. Comput. Phys. Commun. 2015, 196, 398. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).