Explicit Solution to Large Deformation of Cantilever Beam by Improved Homotopy Analysis Method II: Vertical and Horizontal Displacements

Abstract

Explicit solutions to vertical and horizontal displacements are derived for large deformation of a cantilever beam under point load at the free end by an improved homotopy analysis method (IHAM). Quadratic and cubic nonlinear differential equations are adopted to construct more proficient nonlinear equations for vertical and horizontal displacements respectively combined with their currently available nonlinear displacement equations. Higher-order nonlinear iterative homotopy equations are established to solve the vertical and horizontal displacements by combining simultaneous equations of the constructed nonlinear equations and the auxiliary linear equations. The convergence range of vertical displacement is extended by the homotopy-Páde approximation. The explicit solutions to the vertical and horizontal displacements are in favorable agreements with the respective exact solutions. The convergence ranges for a relative error of 1% by the improved homotopy analysis method for vertical and horizontal displacements increases by 60% and 7%, respectively. These explicit formulas are helpful in practical engineering design for very slender structures, such as high-rise buildings and long bridges.

1. Introduction

In view of the shortage of land worldwide, especially in metropolitan areas, high-rise building is a prioritized land-efficient architectural form developed more than 100 years ago. High-rise building is the product of the comprehensive application of modern sciences and engineering technologies. Smooth construction and sustainability of this new structural form depends on more accurate calculation theory and method than those for non-high-rise structures in light of that the extrusion of high-rise building into space could be as high as 800 m plus, and slight artefacts could be exaggerated into intractable unpredictability. Since the 21st century, beam-like structures have achieved overwhelming popularity, such as in high-rise buildings [1,2], long-span bridges [3,4], robots and aerospace; however, analysis methods for this form of structure are still those conventional Euler-Bernoulli laws for large deflection beams, which contain implicit integral to hinder general engineering application. An explicit higher-resolution analysis method is expected to tackle the high nonlinearity in high-rise buildings or long bridges.

The general theory of elastic deflection is called Elastica. To solve a general problem of elastic large deflection, the equivalent load, deflection and longitudinal displacement can be expressed by an analytic expression of elliptic integrals with free-end rotation angle as parameters [5]; indeed, the results have been reported extensively in the classical works of elastic mechanics [6,7,8]. For a cantilever beam subject to point load, the solution to this elastic problem is still an implicit solution with an elliptic integral.

In this study, the high-rise building is simplified as a large deformation of a cantilever beam subject to point load at the free end, for example, of a loading extremity, as shown in Figure 1. Given that the traditional analytical methods for solving nonlinear equations such as perturbation [9], methods introduced in [10,11], Adomian decomposition method [12], and $\delta$-expansion method [13], in addition to the elliptical integrals mentioned above, cannot provide accurate, convergent and simple solutions, we aim to derive an explicit and accurate expression for rotation angle ${\theta }_b$, vertical displacement ${\delta }_v$ and horizontal displacement ${\delta }_h$ to minimize the potential unpredictability in the large deformation of the long cantilever-like building.

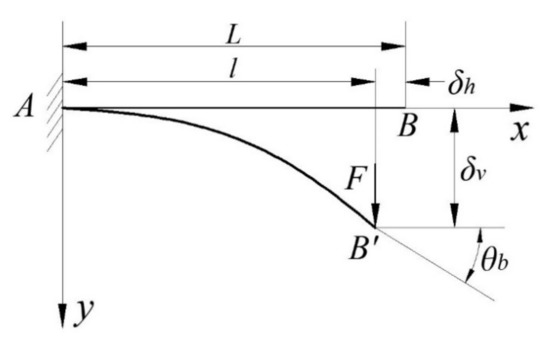
Figure 1. Large deformation of beam under point load at the free end.

Unlike the perturbation technique, the homotopy analysis method (HAM) is independent of any small/large physical parameters. HAM provides us great freedom to choose equation-type and solution expression of the high order approximation equations. A convergence-control parameter $ħ$ is introduced into the series solutions to guarantee the convergence. HAM distinguishes itself from other analytic approaches to be applied to complicated problems with strong nonlinearity [14,15,16,17,18,19,20,21,22,23,24,25,26,27]. The Föppl–Von Kármán’s plate equations were solved by HAM [28,29]. Especially, the steady-state resonant waves were firstly predicted by the HAM in theory [21,22,30,31], which were then confirmed experimentally [30].

Ji Wang et al. derived an explicit solution to the large deformation of a cantilever beam under point load at the free end with HAM [32]. However, the improficiency of this method is identified to be a low convergence rate due to the step-by-step iteration of solutions of linear differential equations to approximate the exact solutions of complex non-linear differential equations; moreover, it fails to serve explicit solutions of vertical and horizontal displacements for large deformation of the beam.

In our previous paper, “Explicit Solution to Large Deformation Cantilever Beam by Improved Homotopy Analysis Method I: ROTATION ANGLE”, an improved homotopy analysis method (IHAM) was proposed. In IHAM, an auxiliary nonlinear operator $\epsilon$ is introduced to improve the convergence rate and extend the convergence range. The improved homotopy analysis method was used to obtain the explicit solution to the rotation angle for the large deformation of a cantilever beam under point load at the free end.

For small deflection, the horizontal displacement of the cantilever beam is neglected and only the deflection and rotation angle are calculated. For large deflection, horizontal displacement is signified not to be neglected. Based on the explicit solution to the rotation angle obtained in our previous paper, explicit expressions for the deflection and horizontal displacement are derived using the improved homotopy analysis method in this paper.

2. Improved Homotopy Analysis Method

2.1. Problem Description

The bending equations of a uniform cross-section beam with large deformation are [5,6,7,8]

$$\frac{\mathrm{d}\theta \left(s\right)}{\mathrm{d}s}=\frac{F}{EI}\left[l-x\left(s\right)\right]$$

(2.1a)

$$\frac{\mathrm{d}v\left(s\right)}{\mathrm{d}s}=\sin \left[\theta \left(s\right)\right]$$

(2.1b)

$$\frac{\mathrm{d}x\left(s\right)}{\mathrm{d}s}=\cos \left[\theta \left(s\right)\right]$$

(2.1c)

subject to boundary conditions

$$\theta \left(0\right)=0, {\theta }^{\prime }\left(L\right)=0$$

(2.2a)

$$v\left(0\right)=0$$

(2.2b)

$$x\left(0\right)=0$$

(2.2c)

where $s$ is the arc-coordinate of the neutral axis of the beam; $x$ denotes the horizontal coordinate from the fixed end; $L$ represents the length of the beam; $F$ stands for the point load at the free end; $EI$ is the bending stiffness of the beam; $\theta$ specifies the rotation angle of cross-section of the beam; and $l$ is the horizontal distance of two ends and is unknown.

Differentiating the equation with respect to $s$ and then using the dimensionless variables $\xi =s/L$, $\alpha =F{L}^2/\left(EI\right)$, $X=x/L$, $V=v/L$, ${\mathrm{\Theta }}_b={\theta }_b/\left(\pi /2\right)$, $V_b={\delta }_v/L$ and $U_b={\delta }_h/L$, the original equations become

$${\theta }^{″}\left(\xi \right)+\alpha \cos \left[\theta \left(\xi \right)\right]=0$$

(2.3a)

$$V^{\prime }\left(\xi \right)=\sin \left[\theta \left(\xi \right)\right]$$

(2.3b)

$$X^{\prime }\left(\xi \right)=\cos \left[\theta \left(\xi \right)\right]$$

(2.3c)

subject to boundary conditions

$$\theta \left(0\right)=0, {\theta }^{\prime }\left(1\right)=0$$

(2.4a)

$$V\left(0\right)=0$$

(2.4b)

$$X\left(0\right)=0$$

(2.4c)

where the prime denotes the differentiation with respect to $\xi$.

For infinitesimal deformation, the below linear equations are sufficiently accurate

$${\theta }^{″}\left(\xi \right)+\alpha =0$$

(2.5a)

$$V^{\prime }\left(\xi \right)=\theta \left(\xi \right)$$

(2.5b)

$$X^{\prime }\left(\xi \right)=1$$

(2.5c)

subject to boundary conditions

$$\theta \left(0\right)=0, {\theta }^{\prime }\left(1\right)=0$$

(2.6a)

$$V\left(0\right)=0$$

(2.6b)

$$X\left(0\right)=0$$

(2.6c)

Accordingly, the solutions are

$$\theta \left(\xi \right)=\frac{\alpha }{2}\left(2-\xi \right)\xi$$

(2.7a)

$$V\left(\xi \right)=\frac{\alpha }{6}{\xi }^2\left(3-\xi \right)$$

(2.7b)

$$X\left(\xi \right)=\xi$$

(2.7c)

The rotation angle, vertical and horizontal displacement of cross-section plane at end as denoted by ${\theta }_b=\theta \left(1\right)$, $V_b=V\left(1\right)$, $U_b=1-X\left(1\right)$, are calculated to be

$${\theta }_b=\frac{\alpha }{2}$$

(2.8a)

$$V_b=\frac{\alpha }{3}$$

(2.8b)

$$U_b=0$$

(2.8c)

In our previous paper, “Explicit Solution to Large Deformation Cantilever Beam by Improved Homotopy Analysis Method I: ROTATION ANGLE”, the improved homotopy analysis method was proposed to solve Equations (2.3a) and (2.4a), and a series of solutions to the rotation angle are derived as [27]:

$$\theta \left(\xi \right)={\theta }_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{\theta }_n\left(\xi \right)}$$

(2.9)

where

$${\theta }_n\left(\xi \right)={\displaystyle \sum _{k=1}^{+\infty }{a}_k{\xi }^k},n=1,2,\cdots$$

(2.10)

In this paper, we apply the improved homotopy analysis method to derive the explicit expressions of deflection and horizontal displacement using Equations (2.3b), (2.4b), (2.3c), and (2.4c) on the basis of the derived explicit expressions of rotation angle in Equations (2.9) and (2.10).

2.2. Fundamentals of Improved Homotopy Analysis Method

For quick reference, the new improved homotopy analysis method (IHAM) is briefed. The IHAM is essentially different from the HAM. Table 1 compares the formulations of IHAM and HAM.

Table 1. Comparison of improved homotopy analysis method against homotopy analysis method.

Homotopy Analysis Method (HAM)	Improved Homotopy Analysis Method (IHAM)
Original $\mathrm{N}\left(\xi \right)=0$ and Auxiliary $\mathrm{L}\left(\xi \right)=0$ $\Rightarrow$ Higher order $\mathcal{H}\left(\xi ;q\right)=0$	① Original $\mathrm{N}\left(\xi \right)=0$ and Auxiliary ${\mathrm{N}}_0\left(\xi \right)=0$ $\Rightarrow$ New $\overline{\mathrm{N}}\left(\xi ;q\right)=0$
	② New $\overline{\mathrm{N}}\left(\xi ;q\right)=0$ and Auxiliary $\mathrm{L}\left(\xi \right)=0$ $\Rightarrow$ Higher order $\overline{\mathcal{H}}\left(\xi ;q\right)=0$

Notes: $\mathrm{N}$—nonlinear operator, $\mathrm{L}$—linear operator, ${\mathrm{N}}_0$—auxiliary nonlinear operator, $\overline{\mathrm{N}}$—new nonlinear operator, $\mathcal{H}$—homotopy operator, $\xi$—independent variable, $q$—embedding parameter.

Substantial difference lies in the different construction methods. HAM constructs a higher order nonlinear iterative homotopy differential equation by the selected linear differential equation and the original non-linear differential equation. However, IHAM builds up a higher-order nonlinear iterative homotopy differential equation using the selected linear differential equation, the selected simple non-linear differential equation and the original non-linear differential equation (See Table 1).

Generalized Equation (2.3b) or Equation (2.3c) have the form of

$$\mathrm{N}\left[v\left(\xi \right)\right]=0: v^{\prime }\left(\xi \right)=f\left[w\left(\xi \right)\right],\xi \in \left[0,1\right]$$

(2.11)

where in $f\left(w\right)$ is a derivable function in compliance with the boundary conditions of $f_w\left(0\right)=c_0$, $f_w^{\prime }\left(0\right)=c_1$, $\frac{1}{2!}{f}_w\left(0\right)=c_2$, $\frac{1}{3!}{f}_w^{‴}\left(0\right)=c_3$; $w\left(\xi \right)$ is the selected polynomial function of an independent variable in Equations (2.9) and (2.10). The boundary condition in Equation (2.4b) or Equation (2.4c) can be expressed as

$$v\left(0\right)=0$$

(2.12)

Note that it is unnecessary to assume the existence of any small or large parameters in Equation (2.11). Thus, the proposed approach is general.

Linearizing original Equation (2.11) yields

$$\mathrm{L}\left[v\left(\xi \right)\right]=0: v^{\prime }\left(\xi \right)=c_0+c_{1}w\left(\xi \right),\xi \in \left[0,1\right]$$

(2.13)

which complies to the boundary condition of

$$v\left(0\right)=0$$

(2.14)

We choose the simplest auxiliary nonlinear equations of

$${\mathrm{N}}_0\left[v\left(\xi \right)\right]=0: v^{\prime }\left(\xi \right)=c_0+c_{1}w\left(\xi \right)+c_2{\epsilon }_2{w}^2\left(\xi \right)+c_3{\epsilon }_1{w}^3\left(\xi \right), \xi \in \left[0,1\right]$$

(2.15)

herein, $c_0$, $c_1$, $c_2$ and $c_3$ are undetermined coefficients; and ${\epsilon }_1\in \left[0,1\right]$, ${\epsilon }_2\in \left[0,1\right]$, ${\epsilon }_1^2+{\epsilon }_2^2\ne 0$. which satisfies the boundary condition of

$$v\left(0\right)=0$$

(2.16)

Detailed formulation for the improved homotopy analysis method could be found in our previous paper titled “Explicit Solution to Large Deformation Cantilever Beam by Improved Homotopy Analysis Method I: ROTATION ANGLE”.

3. Vertical Displacement of Cantilever Beam by IHAM

3.1. Zero Order Deformation Equation

The nonlinear boundary value Equations (2.3b) and (2.4b) are then solved by IHAM to derive explicit form for $V_b$. To start with, $V\left(\xi \right)$ is expressed by power series of $\xi$, i.e.,

$$V\left(\xi \right)={\displaystyle \sum _{k=1}^{+\infty }{b}_k{\xi }^k}$$

(3.1)

where $b_k$ is a constant coefficient. Since Equation (2.7b) from linear equation is an appropriate initial guess, we choose

$$V_0\left(\xi \right)=\frac{\alpha }{6}{\xi }^2\left(3-\xi \right)$$

(3.2)

The equivalent nonlinear Equation (2.3b) becomes

$$V^{\prime }-\theta +\frac{{\epsilon }_1}{3!}{\theta }^3=0$$

(3.3)

subject to boundary condition

$$V\left(0\right)=0$$

(3.4)

where ${\epsilon }_1$ is the coefficient, and ${\epsilon }_1\in \left[0,1\right]$.

When ${\epsilon }_1=0$, Equation (3.3) becomes linear Equation (2.5b), so that

$$V^{\prime }-\theta =0$$

(3.5)

When ${\epsilon }_1=1$, Equation (3.3) becomes

$$V^{\prime }-\theta +\frac{1}{3!}{\theta }^3=0$$

(3.6)

Equation (3.6) is an approximate expression of the second-order Taylor expansion of sine function in view of that

$$\sin \theta \approx \theta -\frac{1}{3!}{\theta }^3$$

(3.7)

According to the original Equation (2.3b) and the equivalent Equation (3.3), we define a nonlinear operator as

$${\mathrm{N}}_v\left[\nu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_1\right]=\frac{\mathrm{d}\nu \left(\xi ;q\right)}{\mathrm{d}\xi }-\sin \left[q\cdot \psi \left(\xi ,q\right)\right]$$

$$-\left(1-q\right)\psi \left(\xi ,q\right)+\frac{{\epsilon }_1}{3!}\left(1-q^3\right){\left[\psi \left(\xi ,q\right)\right]}^3$$

(3.8)

where $q\in \left[0,1\right]$ is an embedding parameter; $\nu \left(\xi ;q\right)$, $\psi \left(\xi ;q\right)$ are dependent on $\xi$ and $q$; ${\epsilon }_1$ is a control parameter to represent the convergent region, and ${\epsilon }_1\in \left[0, 1\right]$.

When $q=0$, there is

$${\mathrm{N}}_v\left[\nu \left(\xi ;0\right),\psi \left(\xi ,0\right),0,{\epsilon }_1\right]=\frac{\mathrm{d}\nu \left(\xi ;0\right)}{\mathrm{d}\xi }-\psi \left(\xi ,0\right)+\frac{{\epsilon }_1}{3!}{\left[\psi \left(\xi ,0\right)\right]}^3$$

(3.9)

If $q=1$, it yields

$${\mathrm{N}}_v\left[\nu \left(\xi ;1\right),\psi \left(\xi ,1\right),1,{\epsilon }_1\right]=\frac{\mathrm{d}\nu \left(\xi ;1\right)}{\mathrm{d}\xi }-\sin \left[\psi \left(\xi ,1\right)\right]$$

(3.10)

Letting

$${\mathrm{L}}_v\left[\nu \left(\xi ;q\right)\right]=\frac{\partial \nu \left(\xi ;q\right)}{\partial \xi }$$

(3.11)

be an auxiliary linear operator, and $ħ\in \left[-1,0\right)$ denotes a nonzero auxiliary parameter (called convergence-control parameter), a homotopy is then constructed as

$${\mathcal{H}}_v\left[\nu \left(\xi ;q\right),q\right]:=\left(1-q\right){\mathrm{L}}_v\left[\nu \left(\xi ;q\right)-V_0\left(\xi \right)\right]$$

$$-q{ħ}_1{\mathrm{N}}_v\left[\nu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_1\right]$$

(3.12)

When $q=0$, we have

$${\mathcal{H}}_v\left[\nu \left(\xi ;0\right),0\right]:={\mathrm{L}}_v\left[\nu \left(\xi ;0\right)-V_0\left(\xi \right)\right]$$

(3.13)

If $q=1$, there is

$$\begin{array}{c}{\mathcal{H}}_v\left[\nu \left(\xi ;1\right),1\right]:=-{ħ}_1{\mathrm{N}}_v\left[\nu \left(\xi ;1\right),1,{\epsilon }_1\right]\\ =-{ħ}_1\left\{\frac{\mathrm{d}\nu \left(\xi ;1\right)}{\mathrm{d}\xi }-\sin \left[\psi \left(\xi ,1\right)\right]\right\}\end{array}$$

(3.14)

Thus, by enforcing

$${\mathcal{H}}_v\left[\nu \left(\xi ;q\right),q\right]=0$$

we have a family of equations

$$\left(1-q\right){\mathrm{L}}_v\left[\nu \left(\xi ;q\right)-V_0\left(\xi \right)\right]=q{ħ}_1{\mathrm{N}}_v\left[\nu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_1\right]$$

(3.15)

subject to the boundary condition of

$$\nu \left(0;q\right)=0$$

(3.16)

When $q=0$, we have

$$\nu \left(\xi ;0\right)=V_0\left(\xi \right),\psi \left(\xi ;0\right)={\theta }_0\left(\xi \right)$$

(3.17)

When $q=1$, Equations (3.15) and (3.16) are equivalent to the original Equations (2.3b) and (2.4b), provided that

$$\nu \left(\xi ;1\right)=V\left(\xi \right),\psi \left(\xi ;1\right)=\theta \left(\xi \right)$$

(3.18)

Thus, as $q$ increases from 0 to 1, $\nu \left(\xi ;q\right)$ evolves smoothly from the specified initial guess $V_0\left(\xi \right)$ to the solution $V\left(\xi \right)$ of Equations (2.3b) and (2.4b).

With reference to Equation (3.17), by expanding $\nu \left(\xi ;q\right)$ into Taylor series of the embedding parameter $q$, we have

$$\nu \left(\xi ;q\right)=V_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{V}_n\left(\xi \right)q^n}$$

(3.19a)

$$\psi \left(\xi ;q\right)={\theta }_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{\theta }_n\left(\xi \right)q^n}$$

(3.19b)

where

$$V_n={\left.\frac{1}{n!}\frac{{\partial }^n\nu \left(\xi ;q\right)}{\partial q^n}\right|}_{q=0}, {\theta }_n={\left.\frac{1}{n!}\frac{{\partial }^n\psi \left(\xi ;q\right)}{\partial q^n}\right|}_{q=0}$$

It is worth noting that the zero order deformation Equation (3.15) contains auxiliary parameters ${\epsilon }_1$, ${ħ}_1$. Auxiliary function $H_1\left(\xi ;q,{\epsilon }_1\right)$ has the form of

$$H_1\left(\xi ;q,{\epsilon }_1\right)=-\left(1-q\right)\psi \left(\xi ,q\right)+\frac{{\epsilon }_1}{3!}\left(1-q^3\right){\left[\psi \left(\xi ,q\right)\right]}^3$$

Assuming that ${ħ}_1$ and ${\epsilon }_1$ are properly chosen, so that Equation (3.18) is convergent at $q=1$. Thus, we have

$$V\left(\xi \right)=V_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{V}_n\left(\xi \right)}$$

(3.20a)

$$\theta \left(\xi \right)={\theta }_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{\theta }_n\left(\xi \right)}$$

(3.20b)

The governing equations of $V_n\left(\xi \right)$ can be deduced from the 0th-order deformation Equations (3.15) and (3.16).

3.2. High Order Deformation Equations

Substituting Equation (3.19) into Equation (3.15) and differentiating Equation (3.15) $n$ times with respect to the embedding parameter $q$, then dividing by $n!$ and setting $q=0$, we have the $n$ th-order deformation equation as below,

$${\mathrm{L}}_v\left[V_n\left(\xi \right)-{\chi }_n{V}_{n-1}\left(\xi \right)\right]={ħ}_1{R}_n^v\left(V_0,V_1,\cdots ,V_{n-1};{\theta }_0,{\theta }_1,\cdots ,{\theta }_{n-1}\right)$$

(3.21)

Equation (3.21) is subject to boundary conditions of

$$V_n\left(0\right)=0$$

(3.22)

where

$$R_n^v={\left.\frac{1}{\left(n-1\right)!}\frac{{\partial }^{n-1}{\mathrm{N}}_v\left[\nu \left(\xi ;q\right),\psi \left(\xi ;q\right),q,{\epsilon }_1\right]}{\partial q^{n-1}}\right|}_{q=0}$$

(3.23)

and

$${\chi }_n=\left\{\begin{array}{c}0,n\le 1\\ 1, n>1\end{array}\right.$$

(3.24)

Combining Equations (3.8) and (3.23), we have

$$R_1^{\nu }={V^{\prime }}_0\left(\xi \right)-{\theta }_0\left(\xi \right)+\frac{{\epsilon }_1}{6}{\theta }_0^3\left(\xi \right)$$

(3.25a)

$$R_2^v={V^{\prime }}_1\left(\xi \right)-{\theta }_1\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0^2\left(\xi \right){\theta }_1\left(\xi \right)$$

(3.25b)

$$R_3^v={V^{\prime }}_2\left(\xi \right)-{\theta }_2\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0^2\left(\xi \right){\theta }_2\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0\left(\xi \right){\theta }_1^2\left(\xi \right)$$

(3.25c)

$$\begin{array}{c}{R}_4^v={V^{\prime }}_3\left(\xi \right)-{\theta }_3\left(\xi \right)+\frac{1}{6}{\theta }_0^3\left(\xi \right)-\frac{{\epsilon }_1}{6}{\theta }_0^3\left(\xi \right)\\ +\frac{{\epsilon }_1}{6}{\theta }_1^3\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0^2\left(\xi \right){\theta }_3\left(\xi \right)+{\epsilon }_1{\theta }_0\left(\xi \right){\theta }_1\left(\xi \right){\theta }_2\left(\xi \right)\end{array}$$

(3.25d)

$$\begin{array}{c}{R}_5^v={V^{\prime }}_4\left(\xi \right)-{\theta }_4\left(\xi \right)+\frac{1}{2}{\theta }_0^2\left(\xi \right){\theta }_1\left(\xi \right)\\ -\frac{{\epsilon }_1}{2}{\theta }_0^2\left(\xi \right){\theta }_1\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0^2\left(\xi \right){\theta }_4\left(\xi \right)+\frac{{\epsilon }_1}{2}{\theta }_0\left(\xi \right){\theta }_2^2\left(\xi \right)\\ +\frac{{\epsilon }_1}{2}{\theta }_1^2\left(\xi \right){\theta }_2\left(\xi \right)+{\epsilon }_1{\theta }_0\left(\xi \right){\theta }_1\left(\xi \right){\theta }_3\left(\xi \right) \end{array}$$

(3.25e)

These equations can be solved by symbolic calculation software such as Maple, Matlab, etc. Thereafter, the linear high-order deformation Equations (3.21) and (3.22) can be solved explicitly.

The solutions given by the IHAM contains auxiliary parameters ${\epsilon }_1$ and ${ħ}_1$, which control and adjust the convergence region and rate of IHAM solution series.

3.3. Vertical Displacement at Free end of Cantilever Beam

3.3.1. Accurate Solution of Vertical Displacement

From Equation (2.3), the transcendental equation used to solve $V_b$ is as follows

$$V_b=1-\frac{2}{\sqrt{\alpha }}\left[E\left(\mu \right)-E\left(\varphi ,\mu \right)\right]$$

(3.26)

where

$$E\left(\mu \right)={\displaystyle {\int }_0^{\pi /2}\frac{\mathrm{d}t}{\sqrt{1-{\mu }^2{\sin }^{2}t}}}$$

(3.27a)

$$E\left(\varphi ,\mu \right)={\displaystyle {\int }_0^{\varphi }\frac{\mathrm{d}t}{\sqrt{1-{\mu }^2{\sin }^{2}t}}}$$

(3.27b)

herein $E\left(\mu \right)$ is complete elliptic integral of the second kind; $E\left(\varphi ,\mu \right)$ is the elliptic integral of the second kind; and

$$\varphi =\arcsin \frac{1}{\sqrt{2} \mu }$$

(3.28)

$$\mu =\sqrt{\frac{1+\sin {\theta }_b}{2}}$$

(3.29)

From Equation (2.8b), the linear solution of the vertical displacement at the free end is

$$V_b=\frac{\alpha }{3}$$

(3.30)

When the relative error $\Delta \le 1\%$, the convergent region of the linear solution is

$$\alpha \in \left[0,0.29\right], V_b\in \left[0,0.097\right], 0\le {\delta }_v\le 0.097L$$

(3.31)

3.3.2. Control Parameter ${\epsilon }_1\in \left[0,1\right]$ for Convergent Region

Combining Equation (2.3b) with Equation (3.3) gives

$$\sin \theta =\theta -\frac{{\epsilon }_1}{3!}{\theta }^3$$

(3.32)

When $\theta =\frac{\pi }{2}$, we have

$$1=\frac{\pi }{2}-\frac{{\epsilon }_1}{3!}{\left(\frac{\pi }{2}\right)}^3$$

(3.33)

Accordingly, the optimal convergence parameter for the full coverage is derived as

$${\epsilon }_1=\frac{24\left(\pi -2\right)}{{\pi }^3}$$

(3.34)

When $n=2$, $ħ=-1$, $\epsilon =8/{\pi }^2$, the 2nd-order approximation of $V_b$ by IHAM is

$$\begin{array}{c}{V}_b=\frac{1}{3}\alpha +2.3159 \times {10}^{-2}{ħ}_1{\alpha }^3+1.9048\times {10}^{-3}{ħ}_1{\epsilon }_1{\alpha }^3\\ +9.5238\times {10}^{-3}{ħ}_1^2{\epsilon }_1{\alpha }^3-2.0430\times {10}^{-3}{ħ}_1{\epsilon }_1{\alpha }^5\end{array}$$

(3.35)

For example, the 2nd-order approximation of $V_b$ with ${ħ}_1=-1$, ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$ is

$$V_b=\frac{1}{3}\alpha -3.1575\times {10}^{-2}{\alpha }^3+1.8053\times {10}^{-3}{\alpha }^5$$

(3.36)

When the relative error $\Delta \le 1\%$, the convergent region of the 2nd-order approximation by IHAM is

$$\alpha \in \left[0,1.5\right], V_b\in \left[0,0.41\right], 0\le {\delta }_v\le 0.41L$$

(3.37)

Table 2 shows 2nd order numerical solutions $V_b^{\left[n=2\right]}$ by IHAM with different values ${\epsilon }_1$ compared with exact solutions $V_b$. The relative error in Table 2 is calculated by

$$\Delta =\frac{\left|V_b^{\left[n=2\right]}-V_b\right|}{V_b}\times 100\%$$

(3.38)

Table 2. 2st-order numerical solutions $V_b^{\left[n=2\right]}$ by IHAM (${ħ}_1=-1$) with different values ${\epsilon }_1$ compared with exact solutions $V_b$.

$\mathit{a}$	Exact Solution	${\mathbf{\epsilon }}_1=0$ (HAM)		${\mathbf{\epsilon }}_1=24\left(\mathbf{\pi }-2\right)/{\mathbf{\pi }}^3$ (IHAM)		${\mathbf{\epsilon }}_1=1$ (IHAM)
	${\mathit{V}}_{\mathit{b}}$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$
0	0	0	0	0	0	0	0
0.1	0.033295	0.033310	0.0446%	0.033302	0.0194%	0.033301	0.0161%
0.2	0.066364	0.066481	0.176%	0.066414	0.0756%	0.066405	0.0623%
0.3	0.098991	0.099375	0.388%	0.099152	0.163%	0.099123	0.133%
0.4	0.13098	0.13185	0.669%	0.13133	0.272%	0.13126	0.219%
0.5	0.16214	0.16377	1.00%	0.16278	0.390%	0.16265	0.309%
0.6	0.19235	0.19500	1.38%	0.19332	0.504%	0.19310	0.389%
0.7	0.22148	0.22539	1.76%	0.22281	0.599%	0.22247	0.445%
0.8	0.24945	0.25481	2.15%	0.25109	0.658%	0.25060	0.461%
0.9	0.27621	0.28312	2.50%	0.27805	0.666%	0.27738	0.425%
1.0	0.30172	0.31017	2.80%	0.30356	0.611%	0.30269	0.322%
1.1	0.32598	0.33584	3.02%	0.32755	0.480%	0.32646	0.145%
1.2	0.34901	0.35998	3.14%	0.34993	0.264%	0.34861	0.115%
1.3	0.37082	0.38245	3.14%	0.37067	0.0427%	0.36911	0.461%
1.4	0.39147	0.40312	2.97%	0.38973	0.442%	0.38797	0.892%
1.5	0.41098	0.42184	2.64%	0.40714	0.933%	0.40521	1.40%
1.6	0.42941	0.43847	2.11%	0.42293	1.51%	0.42089	1.99%
1.7	0.44682	0.45289	1.36%	0.43717	2.16%	0.43510	2.62%
1.8	0.46326	0.46494	0.361%	0.44997	2.87%	0.44800	3.30%
1.9	0.47879	0.47448	0.899%	0.46146	3.62%	0.45975	3.98%
2	0.49346	0.48139	2.44%	0.47184	4.38%	0.47058	4.64%
$\infty$	1	1	0	1	0	1	0

After two iterations, when ${\epsilon }_1=0$, the convergence region of $V_b$ is $0<\alpha \le 0.5$. When ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, the convergence region of $V_b$ is $0 < \alpha \le 1.5$, whence the convergence region is expanded by $200\%$ compared to the case with ${\epsilon }_1=0$.

When $0<\alpha \le 0.5$, ${\epsilon }_1$ increases from 0 to 1, the series of solutions of vertical displacement converge to the exact solution with relative error to the exact solution is less than 1%, so that the effective region of ${\epsilon }_1$ is identified to be $R_{{\epsilon }_1}=\left[0,1\right]$.

Thus, the optimal control parameters for the convergence region of the improved homotopy analysis method is identified to be ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$.

3.3.3. Control Parameters ${ħ}_1\in \left[-1,0\right)$ for Convergence Rate

By IHAM, when $\epsilon =8/{\pi }^2$, $ħ=-0.5$, ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, ${ħ}_1=-0.5$, the 10th-order approximation of $V_b$ is

$$\begin{array}{l}{V}_b=\frac{1}{3}\alpha -3.7639\times {10}^{-2}{\alpha }^3+7.5564\times {10}^{-3}{\alpha }^5\\ -1.6013\times {10}^{-3}{\alpha }^7+2.9034\times {10}^{-4}{\alpha }^9-4.1074\times {10}^{-5}{\alpha }^{11}\\ +4.3984\times {10}^{-6}{\alpha }^{13}-3.5126\times {10}^{-7}{\alpha }^{15}+2.0566\times {10}^{-8}{\alpha }^{17}\\ -8.2692\times {10}^{-10}{\alpha }^{19}+1.7210\times {10}^{-11}{\alpha }^{21}\end{array}$$

(3.39)

When the relative error $\Delta \le 1\%$, the convergent regions of the 10th-order approximation by IHAM are

$$\alpha \in \left[0,3.3\right], V_b\in \left[0,0.63\right], 0\le {\delta }_v\le 0.63L$$

(3.40)

Table 3 compares the 10th-order numerical solutions with the exact solutions. The relative error in Table 3 is calculated by

$$\Delta =\frac{\left|V_b^{\left[n=10\right]}-V_b\right|}{V_b}\times 100\%$$

(3.41)

Table 3. 10th-order numerical solutions $V_b^{\left[n=10\right]}$ by IHAM with different values of ${ħ}_1$ (${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$) compared with exact solutions $V_b$.

$\mathit{\alpha }$	Exact Solution	${\mathbf{h}}_1=1$		${\mathbf{h}}_1=-0.5$		${\mathbf{h}}_1=-0.3$
	${\mathit{V}}_{\mathit{b}}$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$
0	0	0	0	0	0	0	0
0.2	0.066364	0.066365	0.000951%	0.066368	0.00522%	0.066385	0.0316%
0.4	0.13098	0.13098	0.00286%	0.13100	0.0183%	0.13113	0.120%
0.6	0.19235	0.19236	0.00418%	0.19241	0.0339%	0.19283	0.252%
0.8	0.24945	0.24946	0.00464%	0.24957	0.0480%	0.25047	0.410%
1.0	0.30172	0.30174	0.00486%	0.30190	0.0602%	0.30348	0.583%
1.2	0.34901	0.34902	0.00369%	0.34926	0.0713%	0.35168	0.765%
1.4	0.39147	0.39145	0.00312%	0.39178	0.0803%	0.39519	0.950%
1.6	0.42941	0.42933	0.0201%	0.42977	0.0829%	0.43429	1.14%
1.8	0.46326	0.46305	0.0457%	0.46361	0.0750%	0.46936	1.32%
2.0	0.49346	0.49313	0.0665%	0.49374	00572%	0.50082	1.49%
2.2	0.52042	0.52014	0.0539%	0.52061	0.0371%	0.52908	1.66%
2.4	0.54455	0.54472	0.0319%	0.54471	0.0296%	0.55457	1.84%
2.6	0.56619	0.56745	0.222%	0.56646	0.0475%	0.57767	2.03%
2.8	0.58567	0.58846	0.476%	0.58610	0.0741%	0.59864	2.21%
3	0.60325	0.60709	0.636%	0.60340	0.0243%	0.61745	2.35%
3.2	0.61918	0.62601	1.10%	0.61870	0.0777%	0.63428	2.44%
3.4	0.63365	0.68393	7.94%	0.64405	1.64%	0.65542	3.44%
3.6	0.64684	—	—	0.76181	17.8%	0.72504	12.1%
3.8	0.65890	—	—	—	—	—	—
4.0	0.66996	—	—	—	—	—	—
$\infty$	1	1	0	1	0	1	0

After $n=10$ iterative calculations, when ${ħ}_1=-1$, the convergence region of $V_b$ is $0 < \alpha \le 3$. When ${ħ}_1=-0.5$, the convergence region of $V_b$ is $0 < \alpha \le 3.2$. When ${ħ}_1=-0.3$, the convergence region of $V_b$ is $0<\alpha \le 1.4$. It is seen that when ${ħ}_1=-0.5$, the convergence region is $128\%$ larger than that with ${ħ}_1=-0.3$, while it is $6.7\%$ larger than that with ${ħ}_1=-1$ (See Table 3).

Accordingly, the optimal control parameters ${ħ}_1$ of convergence rate for the 10th-order approximation solution to the vertical displacement is identified to be ${ħ}_1=-0.5$.

3.3.4. 30th-Order Approximation Solution of Vertical Displacement

When $\epsilon =8/{\pi }^2$, $ħ=-0.1$, the 30th-order approximation of ${\theta }_b$ by IHAM is

$$\begin{array}{l}{\theta }_b=\frac{\alpha }{2}-4.3804\times {10}^{-2}{\alpha }^3+7.2872\times {10}^{-3}{\alpha }^5-1.3299\times {10}^{-3}{\alpha }^7\\ +2.2991\times {10}^{-4}{\alpha }^9-3.5481\times {10}^{-5}{\alpha }^{11}+4.7492\times {10}^{-6}{\alpha }^{13}\\ -5.4234\times {10}^{-7}{\alpha }^{15}+5.2245\times {10}^{-8}{\alpha }^{17}-4.2081\times {10}^{-9}{\alpha }^{19}\\ +2.8138\times {10}^{-10}{\alpha }^{21}-1.5540\times {10}^{-11}{\alpha }^{23}+7.0725\times {10}^{-13}{\alpha }^{25}\\ -2.6561\times {10}^{-14}{\alpha }^{27}+8.2720\times {10}^{-16}{\alpha }^{29}-2.1528\times {10}^{-17}{\alpha }^{31}\\ +4.7252\times {10}^{-19}{\alpha }^{33}-8.8286\times {10}^{-21}{\alpha }^{35}+1.4162\times {10}^{-22}{\alpha }^{37}\\ -1.9643\times {10}^{-24}{\alpha }^{39}+2.3681\times {10}^{-26}{\alpha }^{41}-2.4891\times {10}^{-28}{\alpha }^{43}\\ +2.2824\times {10}^{-30}{\alpha }^{45}-1.8213\times {10}^{-32}{\alpha }^{47}+1.2569\times {10}^{-34}{\alpha }^{49}\\ -7.4143\times {10}^{-37}{\alpha }^{51}+3.6656\times {10}^{-39}{\alpha }^{53}-1.4683\times {10}^{-41}{\alpha }^{55}\\ +4.4741\times {10}^{-44}{\alpha }^{57}-9.1359\times {10}^{-47}{\alpha }^{59}+9.2009\times {10}^{-50}{\alpha }^{61}\end{array}$$

(3.42)

When the relative error $\Delta \le 1\%$, the convergent region of the 30th-order approximation by IHAM is

$$\alpha \in \left[0,5.1\right], {\mathrm{\Theta }}_b\in \left[0,0.79\right], 0\le {\theta }_b\le 70.6°$$

(3.43)

When ${\epsilon }_1=0$, ${ħ}_1=-0.3$, the 30th-order approximation of $V_b$ by HAM is

$$\begin{array}{l}{V}_b=\frac{1}{3}\alpha -3.6198\times {10}^{-2}{\alpha }^3+6.5568\times {10}^{-3}{\alpha }^5\\ -1.2305\times {10}^{-3}{\alpha }^7+2.1160\times {10}^{-4}{\alpha }^9-3.1714\times {10}^{-5}{\alpha }^{11}\\ +4.0427\times {10}^{-6}{\alpha }^{13}-4.3197\times {10}^{-7}{\alpha }^{15}+3.8284\times {10}^{-8}{\alpha }^{17}\\ -2.7902\times {10}^{-9}{\alpha }^{19}+1.6610\times {10}^{-10}{\alpha }^{21}-8.0436\times {10}^{-12}{\alpha }^{23}\\ +3.1678\times {10}^{-13}{\alpha }^{25}-1.0188\times {10}^{-14}{\alpha }^{27}+2.6964\times {10}^{-16}{\alpha }^{29}\\ -5.9333\times {10}^{-18}{\alpha }^{31}+1.0971\times {10}^{-19}{\alpha }^{33}-1.7218\times {10}^{-21}{\alpha }^{35}\\ +2.3130\times {10}^{-23}{\alpha }^{37}-2.6772\times {10}^{-25}{\alpha }^{39}+2.6808\times {10}^{-27}{\alpha }^{41}\\ -2.3258\times {10}^{-29}{\alpha }^{43}+1.7456\times {10}^{-31}{\alpha }^{45}-1.1275\times {10}^{-33}{\alpha }^{47}\\ +6.2040\times {10}^{-36}{\alpha }^{49}-2.8576\times {10}^{-38}{\alpha }^{51}+1.0708\times {10}^{-40}{\alpha }^{53}\\ -3.0973\times {10}^{-43}{\alpha }^{55}+6.1662\times {10}^{-46}{\alpha }^{57}-6.2456\times {10}^{-49}{\alpha }^{59}\end{array}$$

(3.44)

Table 4 compares the above numerical solution with the exact solution. The relative error in Table 4 is calculated by

$$\Delta =\frac{\left|V_b^{\left[n=30\right]}-V_b\right|}{V_b}\times 100\%$$

(3.45)

Table 4. 30th-order numerical solutions $V_b^{\left[n=30\right]}$ by IHAM ($\epsilon =8/{\pi }^2$, $ħ=-0.1$, ${ħ}_1=-0.3$) compared with exact solutions $V_b$.

$\mathit{\alpha }$	Exact Solution	${\mathbf{\epsilon }}_1=0$ (HAM)		${\mathbf{\epsilon }}_1=24\left(\pi -2\right)/{\pi }^3$ (IHAM)
	${\mathit{V}}_{\mathit{b}}$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$
0	0	0	0	0	0
0.3	0.098991	0.099038	0.0481%	0.099038	0.0482%
0.6	0.19235	0.19266	0.160%	0.19266	0.162%
0.9	0.27621	0.27697	0.275%	0.27699	0.282%
1.2	0.34901	0.35025	0.355%	0.35030	0.370%
1.5	0.41098	0.41262	0.400%	0.41271	0.422%
1.8	0.46326	0.46522	0.423%	0.46534	0.449%
2.1	0.50732	0.50953	0.437%	0.50966	0.462%
2.4	0.54455	0.54699	0.449%	0.54709	0.467%
2.7	0.57618	0.57883	0.459%	0.57888	0.467%
3.0	0.60325	0.60609	0.470%	0.60605	0.464%
3.3	0.62658	0.62959	0.479%	0.62945	0.457%
3.6	0.64684	0.65001	0.490%	0.64975	0.450%
3.9	0.66455	0.66794	0.510%	0.66746	0.438%
4.2	0.68014	0.68338	0.475%	0.68282	0.393%
4.5	0.69397	0.69274	0.177%	0.69571	0.251%
4.8	0.70629	0.68406	3.15%	0.70724	0.135%
5.1	0.71735	0.65758	8.33%	0.72349	0.856%
5.4	0.72731	0.76120	4.66%	0.73988	1.73%
5.7	0.73635	—	—	0.68583	6.86%
6.0	0.74457	—	—	0.44959	39.6%
$\infty$	1	1	0	1	0

When the relative error $\Delta \le 1\%$, the convergent regions of the 30th-order approximation by HAM (${\epsilon }_1=0$) are

$$\alpha \in \left[0,4.6\right], V_b\in \left[0,0.70\right], 0\le {\delta }_v\le 0.70L$$

(3.46)

When ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, ${ħ}_1=-0.3$, the 30th-order approximation of $V_b$ by IHAM is

$$\begin{array}{l}{V}_b=\frac{1}{3}\alpha -3.6198\times {10}^{-2}{\alpha }^3+6.6118\times {10}^{-3}{\alpha }^5-1.2700\times {10}^{-3}{\alpha }^7\\ +2.2683\times {10}^{-4}{\alpha }^9-3.5802\times {10}^{-5}{\alpha }^{11}+4.8726\times {10}^{-6}{\alpha }^{13}\\ -5.6396\times {10}^{-7}{\alpha }^{15}+5.5006\times {10}^{-8}{\alpha }^{17}-4.4899\times {10}^{-9}{\alpha }^{19}\\ +3.0512\times {10}^{-10}{\alpha }^{21}-1.7202\times {10}^{-11}{\alpha }^{23}+8.0374\times {10}^{-13}{\alpha }^{25}\\ -3.1168\times {10}^{-14}{\alpha }^{27}+1.0073\times {10}^{-15}{\alpha }^{29}-2.7301\times {10}^{-17}{\alpha }^{31}\\ +6.2517\times {10}^{-19}{\alpha }^{33}-1.2190\times {10}^{-20}{\alpha }^{35}+2.0389\times {10}^{-22}{\alpha }^{37}\\ -2.9432\times {10}^{-24}{\alpha }^{39}+3.6841\times {10}^{-26}{\alpha }^{41}-4.0095\times {10}^{-28}{\alpha }^{43}\\ +3.7952\times {10}^{-30}{\alpha }^{45}-3.1164\times {10}^{-32}{\alpha }^{47}+2.2056\times {10}^{-34}{\alpha }^{49}\\ -1.3297\times {10}^{-36}{\alpha }^{51}+6.6933\times {10}^{-39}{\alpha }^{53}-2.7186\times {10}^{-41}{\alpha }^{55}\\ +8.3645\times {10}^{-44}{\alpha }^{57}-1.7196\times {10}^{-46}{\alpha }^{59}+1.7421\times {10}^{-49}{\alpha }^{61}\end{array}$$

(3.47)

When the relative error $\Delta \le 1\%$, the convergent regions of the 30th-order approximation by IHAM (${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$) are

$$\alpha \in \left[0,5.1\right], V_b\in \left[0,0.72\right], 0\le {\delta }_v\le 0.72L$$

(3.48)

From Table 4, the improved homotopy analysis method extends the convergence region from $\alpha \in \left[0,4.6\right]$ by the homotopy analysis method [32] to $\alpha \in \left[0,5.1\right]$, which is an $11\%$ increase.

From the above comparison, it can be seen that the expansion rate of the convergence region for vertical displacement by IHAM against that by HAM increases with the increasing iterations.

3.3.5. Homotopy-Páde Approximation

By application of the homotopy-Páde acceleration technique [27], the convergence region can be greatly enlarged. For example, when $n=30$, ${\epsilon }_1=0$, ${ħ}_1=-0.3$, the $Pade\left[11,11\right]$ homotopy-Páde approximation of $V_b$ in Equation (3.44) by HAM can be written as

$$V_b=\frac{\alpha }{3}\frac{f\left(\alpha \right)}{g\left(\alpha \right)}$$

(3.49a)

$$\begin{array}{c}f\left(\alpha \right)=1+0.31708{\alpha }^2+6.1434\times {10}^{-2}{\alpha }^4+6.0404\times {10}^{-3}{\alpha }^6\\ +4.1539\times {10}^{-4}{\alpha }^8+5.5063\times {10}^{-6}{\alpha }^{10}\end{array}$$

(3.49b)

$$\begin{array}{c}g\left(\alpha \right)=1+0.42567{\alpha }^2+8.7988\times {10}^{-2}{\alpha }^4+1.0914\times {10}^{-2}{\alpha }^6\\ +8.0640\times {10}^{-4}{\alpha }^8+2.8143\times {10}^{-6}{\alpha }^{10}\end{array}$$

(3.49c)

When the relative error $\Delta \le 1\%$, the convergent regions of the $Pade\left[11,11\right]$ homotopy-Páde approximation by HAM are

$$\alpha \in \left[0,5\right], V_b\in \left[0,0.71\right], 0\le {\delta }_v\le 0.71L$$

(3.50)

When $n=30$, ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, ${ħ}_1=-0.3$, the $Pade\left[15,15\right]$ homotopy-Páde approximation of $V_b$ in Equation (3.47) by IHAM are

$$V_b=\frac{\alpha }{3}\frac{f\left(\alpha \right)}{g\left(\alpha \right)}$$

(3.51a)

$$\begin{array}{c}f\left(\alpha \right)=1+0.33026{\alpha }^2+7.1207\times {10}^{-2}{\alpha }^4+8.9035\times {10}^{-3}{\alpha }^6+9.2792\times {10}^{-4}{\alpha }^8\\ +5.3226\times {10}^{-5}{\alpha }^{10}+2.5321\times {10}^{-6}{\alpha }^{12}+1.9082\times {10}^{-8}{\alpha }^{14}\end{array}$$

(3.51b)

$$\begin{array}{c}g\left(\alpha \right)=1+0.43885{\alpha }^2+9.9028\times {10}^{-2}{\alpha }^4+1.4763\times {10}^{-2}{\alpha }^6+1.5584\times {10}^{-3}{\alpha }^8\\ +1.1572\times {10}^{-4}{\alpha }^{10}+5.5647\times {10}^{-6}{\alpha }^{12}+1.3297\times {10}^{-7}{\alpha }^{14}\end{array}$$

(3.51c)

When the relative error $\Delta \le 1\%$, the convergent regions of the $Pade\left[15,15\right]$ homotopy-Páde approximation by IHAM are

$$\alpha \in \left[0,8.1\right], V_b\in \left[0,0.79\right], 0\le {\delta }_v\le 0.79L$$

(3.52)

Table 5 shows that numerical solutions $V_b^{\left[P\right]}$ of homotopy-Páde approximation by IHAM compares with exact solutions $V_b$. The relative error in Table 5 is calculated by

$$\Delta =\frac{\left|V_b^{\left[P\right]}-V_b\right|}{V_b}\times 100\%$$

(3.53)

Table 5. Numerical solutions $V_b^{\left[P\right]}$ of homotopy-Páde approximation by IHAM. ($n=30$, $\epsilon =8/{\pi }^2$, $ħ=-0.1$, ${ħ}_1=-0.3$) compared with exact solutions $V_b$.

$\mathit{\alpha }$	Exact Solution	${\mathbf{\epsilon }}_1=0$ (HAM) $\mathit{P}\mathit{a}\mathit{d}\mathit{e}\left[\mathbf{11},\mathbf{11}\right]$		${\mathbf{\epsilon }}_1=24\left(\mathit{\pi }-2\right)/{\mathit{\pi }}^3$ (IHAM) $\mathit{P}\mathit{a}\mathit{d}\mathit{e}\left[\mathbf{15},\mathbf{15}\right]$
	${\mathit{V}}_{\mathit{b}}$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$	${\mathit{V}}_{\mathit{b}}$	$\mathbf{\Delta }$
0	0	0	0	0	0
0.5	0.16214	0.16234	0.120%	0.16234	0.121%
1	0.30172	0.30265	0.307%	0.30267	0.315%
1.5	0.41098	0.41262	0.400%	0.41271	0.422%
2	0.49346	0.49559	0.433%	0.49572	0.459%
2.5	0.55566	0.55817	0.452%	0.55826	0.468%
3	0.60325	0.60610	0.471%	0.60605	0.463%
3.5	0.64039	0.64360	0.501%	0.64325	0.446%
4	0.66996	0.67379	0.571%	0.67272	0.412%
4.5	0.69397	0.69899	0.723%	0.69645	0.358%
5	0.71379	0.72096	1.00%	0.71587	0.292%
5.5	0.73042	0.74102	1.45%	0.73214	0.235%
6	0.74457	0.76007	2.08%	0.74616	0.213%
6.5	0.75676	0.77877	2.91%	0.75867	0.252%
7	0.76737	0.79754	3.93%	0.77024	0.374%
7.5	0.77670	0.81664	5.14%	0.78132	0594%
8	0.78498	0.83624	6.53%	0.79222	0.922%
8.5	0.79239	0.85642	8.08%	0.80319	1.36%
9	0.79906	0.87725	9.79%	0.81439	1.92%
9.5	0.80510	0.89871	11.6%	0.82593	2.59%
10	0.81061	0.92080	13.6%	0.83788	3.36%
$\infty$	1	1	0	1	0

From Equations (3.50) and (3.52), the improved homotopy analysis method extends the convergence region from $\alpha \in \left[0,5\right]$ to $\alpha \in \left[0,8.1\right]$ for the homotopy-Páde approximate solution compared with the homotopy analysis method [32], which is a $62\%$ increase.

Figure 2 compares the 30th-order iteration solution and the exact solution of the vertical displacement. From Figure 2, it can be observed that

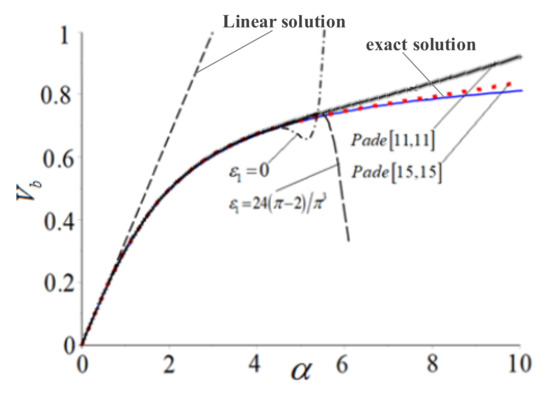
Figure 2. Comparison of vertical displacement at the free end $V_b$ with $n=30$.

• the difference between the linear solution and the exact solution is remarkable;
• the 30th-order improved homotopy analysis solution for ${\epsilon }_1=24(\pi -2)/{\pi }^3$ is much closer to the exact solution than does the 30^th-order homotopy analysis solution for ${\epsilon }_1=0$;
• the convergence range and rate have been greatly improved by the expression by homotopy-Páde approximation;
• the Páde approximation solution $Pade\left[15,15\right]$ by IHAM is more approximating to the exact solution than does the Páde approximation solution $Pade\left[11,11\right]$ by HAM.

4. Horizontal Displacement of Cantilever Beam by IHAM

4.1. Zero Order Deformation Equation

The nonlinear boundary value Equations (2.3c) and (2.4c) are then solved by IHAM to give explicit expression for $U_b$. To start with, $X\left(\xi \right)$ is expressed by the power series of $\xi$, so that

$$X\left(\xi \right)={\displaystyle \sum _{k=1}^{+\infty }{c}_k{\xi }^k}$$

(4.1)

where $c_k$ is a constant coefficient. Linear Equation (2.7c) is specified as initial guess. Accordingly, we choose

$$X_0\left(\xi \right)=\xi$$

(4.2)

The equivalent nonlinear equation of Equation (2.3c) is

$$X^{\prime }-1+\frac{{\epsilon }_2}{2!}{\theta }^2=0$$

(4.3)

subject to boundary condition of

$$X\left(0\right)=0$$

(4.4)

where ${\epsilon }_2$ is the correction coefficient of the convergent region, and ${\epsilon }_2\in \left[0,1\right]$.

When ${\epsilon }_2=0$, Equation (4.3) becomes the linear Equation (2.5c), so that

$$X^{\prime }-1=0$$

(4.5)

When ${\epsilon }_2=1$, Equation (4.3) becomes

$$X^{\prime }-1+\frac{1}{2!}{\theta }^2=0$$

(4.6)

Approximation expression of the second-order Taylor expansion of cosine function can be written as

$$\cos \theta \approx 1-\frac{1}{2!}{\theta }^2$$

(4.7)

According to the original Equation (2.3c) and the equivalent Equation (4.3), we define a nonlinear operator as

$$\begin{array}{c}{\mathrm{N}}_u\left[\mu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_2\right]=\frac{\mathrm{d}\mu \left(\xi ;q\right)}{\mathrm{d}\xi }-\cos \left[q\cdot \psi \left(\xi ,q\right)\right]\\ +\frac{{\epsilon }_2}{2!}\left(1-q^2\right){\left[\psi \left(\xi ,q\right)\right]}^2\end{array}$$

(4.8)

where $q\in \left[0,1\right]$ is an embedding parameter; $\mu \left(\xi ;q\right)$, $\psi \left(\xi ;q\right)$ are the functions dependent on $\xi$ and $q$; ${\epsilon }_2$ is a control parameter for the convergent region, and ${\epsilon }_2\in \left[0,1\right]$.

When $q=0$, there is

$${\mathrm{N}}_u\left[\mu \left(\xi ;0\right),\psi \left(\xi ,0\right),0,{\epsilon }_2\right]=\frac{\mathrm{d}\mu \left(\xi ;0\right)}{\mathrm{d}\xi }-1+\frac{{\epsilon }_2}{2!}{\left[\psi \left(\xi ,0\right)\right]}^2$$

(4.9)

If $q=1$, it yields

$${\mathrm{N}}_u\left[\mu \left(\xi ;1\right),\psi \left(\xi ,1\right),1,{\epsilon }_2\right]=\frac{\mathrm{d}\mu \left(\xi ;1\right)}{\mathrm{d}\xi }-\sin \left[\psi \left(\xi ,1\right)\right]$$

(4.10)

Specifying

$${\mathrm{L}}_u\left[\mu \left(\xi ;q\right)\right]=\frac{\partial \mu \left(\xi ;q\right)}{\partial \xi }$$

(4.11)

as an auxiliary linear operator, and denoting ${ħ}_2\in \left[-1,0\right)$ as a nonzero auxiliary parameter (convergence-control parameter), a homotopy is constructed as

$${\mathcal{H}}_u\left[\mu \left(\xi ;q\right),q\right]:=\left(1-q\right){\mathrm{L}}_u\left[\mu \left(\xi ;q\right)-X_0\left(\xi \right)\right]$$

$$-q{ħ}_2{\mathrm{N}}_u\left[\mu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_2\right]$$

(4.12)

Accordingly, when $q=0$, we have

$${\mathcal{H}}_u\left[\mu \left(\xi ;0\right),0\right]:={\mathrm{L}}_u\left[\mu \left(\xi ;0\right)-X_0\left(\xi \right)\right]$$

(4.13)

If $q=1$, it becomes

$$\begin{array}{c}{\mathcal{H}}_u\left[\mu \left(\xi ;1\right),1\right]:=-{ħ}_2{\mathrm{N}}_u\left[\mu \left(\xi ;1\right),1,{\epsilon }_2\right]\\ =-{ħ}_2\left\{\frac{\mathrm{d}\mu \left(\xi ;1\right)}{\mathrm{d}\xi }-\cos \left[\psi \left(\xi ,1\right)\right]\right\}\end{array}$$

(4.14)

Thus, by enforcing

$${\mathcal{H}}_u\left[\mu \left(\xi ;q\right),q\right]=0$$

(4.15)

we have a family of equations

$$\left(1-q\right){\mathrm{L}}_u\left[\mu \left(\xi ;q\right)-X_0\left(\xi \right)\right]=q{ħ}_2{\mathrm{N}}_u\left[\mu \left(\xi ;q\right),\psi \left(\xi ,q\right),q,{\epsilon }_2\right]$$

(4.16)

subject to boundary conditions

$$\mu \left(0;q\right)=0$$

(4.17)

When $q=0$, we have

$$\mu \left(\xi ;0\right)=X_0\left(\xi \right), \psi \left(\xi ;0\right)={\theta }_0\left(\xi \right)$$

(4.18)

When $q=1$, Equations (4.16) and (4.17) are equivalent to the original Equations (2.3c) and (2.4c), provided that

$$\mu \left(\xi ;1\right)=X\left(\xi \right), \psi \left(\xi ;1\right)=\theta \left(\xi \right)$$

(4.19)

Thus, as $q$ increases from 0 to 1, $\mu \left(\xi ;q\right)$ evolves from the known initial guess solution $X_0\left(\xi \right)$ to the exact solution $X\left(\xi \right)$ of Equations (2.3c) and (2.4c).

With reference to Equation (4.10), by expanding $\mu \left(\xi ;q\right)$ into Taylor series of the embedding parameter $q$, we have

$$\mu \left(\xi ;q\right)=X_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{X}_n\left(\xi \right)q^n}$$

(4.20a)

$$\psi \left(\xi ;q\right)={\theta }_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{\theta }_n\left(\xi \right)q^n}$$

(4.20b)

where

$$X_n={\left.\frac{1}{n!}\frac{{\partial }^n\mu \left(\xi ;q\right)}{\partial q^n}\right|}_{q=0}, {\theta }_n={\left.\frac{1}{n!}\frac{{\partial }^n\psi \left(\xi ;q\right)}{\partial q^n}\right|}_{q=0}$$

(4.21)

It is worth noting that the zero order deformation Equation (4.16) contains auxiliary parameters ${\epsilon }_2$, ${ħ}_2$. And the auxiliary function $H_2\left(\xi ;q,{\epsilon }_2\right)$ has the form of

$$H_2\left(\xi ;q,{\epsilon }_2\right)=\frac{{\epsilon }_2}{2!}\left(1-q^2\right){\left[\psi \left(\xi ,q\right)\right]}^2$$

(4.22)

Assuming that ${ħ}_2$ and ${\epsilon }_2$ are properly chosen, so that Equation (4.19) is convergent at $q=1$, thus, we have

$$X\left(\xi \right)=X_0\left(\xi \right)+{\displaystyle \sum _{n=1}^{+\infty }{X}_n\left(\xi \right)}$$

(4.23)

The governing equations $X_n\left(\xi \right)$ can be deduced from 0th-order deformation Equations (4.16) and (4.17).

4.2. High Order Deformation Equations

Substituting Equation (4.20) into Equation (4.16) and differentiating (4.16) $n$ times with respect to the embedding parameter $q$, then dividing by $n!$ and setting $q=0$, we have the $n$ th-order deformation equation as below

$${\mathrm{L}}_u\left[X_n\left(\xi \right)-{\chi }_n{X}_{n-1}\left(\xi \right)\right]={ħ}_2{R}_n^u\left(X_0,X_1,\cdots ,X_{n-1};{\theta }_0,{\theta }_1,\cdots ,{\theta }_{n-1}\right)$$

(4.24)

Equation (4.24) is subject to boundary condition of

$$X_n\left(0\right)=0$$

(4.25)

where

$$R_n^u={\left.\frac{1}{\left(n-1\right)!}\frac{{\partial }^{n-1}{\mathrm{N}}_u\left[\mu \left(\xi ;q\right),\psi \left(\xi ;q\right),q,{\epsilon }_2\right]}{\partial q^{n-1}}\right|}_{q=0}$$

(4.26)

and

$${\chi }_n=\left\{\begin{array}{c}0,n\le 1\\ 1, n>1\end{array}\right.$$

(4.27)

Combining Equations (4.8) and (4.26), we have

$$R_1^u={X^{\prime }}_0\left(\xi \right)-1+\frac{{\epsilon }_2}{2}{\theta }_0^2\left(\xi \right)$$

(4.28a)

$$R_2^u={X^{\prime }}_1\left(\xi \right)+{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_1\left(\xi \right)$$

(4.28b)

$$R_3^u={X^{\prime }}_2\left(\xi \right)+\frac{1}{2}{\theta }_0^2\left(\xi \right)-\frac{{\epsilon }_2}{2}{\theta }_0^2\left(\xi \right)+\frac{{\epsilon }_2}{2}{\theta }_1^2\left(\xi \right)+{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_2\left(\xi \right)$$

(4.28c)

$$\begin{array}{c}{R}_4^u={X^{\prime }}_3\left(\xi \right)+{\theta }_0\left(\xi \right){\theta }_1\left(\xi \right)\\ -{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_1\left(\xi \right)+{\epsilon }_2{\theta }_1\left(\xi \right){\theta }_2\left(\xi \right)+{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_3\left(\xi \right)\end{array}$$

(4.28d)

$$\begin{array}{c}{R}_5^u=X_4^{\prime }\left(\xi \right)+{\theta }_0\left(\xi \right){\theta }_2\left(\xi \right)+\frac{1}{2}{\theta }_1^2\left(\xi \right)-\frac{1}{24}{\theta }_0^4\left(\xi \right)\\ -{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_2\left(\xi \right)+{\epsilon }_2{\theta }_1\left(\xi \right){\theta }_3\left(\xi \right)+{\epsilon }_2{\theta }_0\left(\xi \right){\theta }_4\left(\xi \right)\\ -\frac{{\epsilon }_2}{2}{\theta }_1^2\left(\xi \right)+\frac{{\epsilon }_2}{2}{\theta }_2^2\left(\xi \right)\end{array}$$

(4.28e)

The right-hand side term $R_n^u$ of the above equations can be derived by symbolic calculation software such as Maple, Matlab, etc. Thereafter, explicit form of solution to the linear high-order deformation Equations (4.24) and (4.25) have been derived.

4.3. Horizontal Displacement at Free End of Cantilever Beam

4.3.1. Accurate Solution to Horizontal Displacement

Accordingly, in Equation (2.3c), the transcendental equation to solve $U_b$ is as follows

$$U_b=1-\sqrt{\frac{2\sin {\theta }_b}{\alpha }}$$

(4.29)

With reference to Equation (2.8c), the linear solution of the horizontal displacement at the free end is

$$U_b=0$$

(4.30)

4.3.2. Explicit Solution to Horizontal Displacement by IHAM

The solutions by IHAM contains two auxiliary parameters ${\epsilon }_2$ and ${ħ}_2$, which control and adjust the convergence region and rate of IHAM solution series.

For example, the 10th-order approximation of $U_b$ with $n=10$, $\epsilon =8/{\pi }^2$, $ħ=-0.5$, ${\epsilon }_2=8/{\pi }^2$, ${ħ}_2=-0.4$ is derived as

$$\begin{array}{l}{U}_b=6.6128\times {10}^{-2}{\alpha }^2-1.2132\times {10}^{-2}{\alpha }^4+2.6029\times {10}^{-3}{\alpha }^6\\ -5.0108\times {10}^{-4}{\alpha }^8+7.4259\times {10}^{-5}{\alpha }^{10}-8.1166\times {10}^{-6}{\alpha }^{12}\\ +6.5090\times {10}^{-7}{\alpha }^{14}-3.7900\times {10}^{-8}{\alpha }^{16}+1.5743\times {10}^{-9}{\alpha }^{18}\\ -3.4811\times {10}^{-11}{\alpha }^{20}\end{array}$$

(4.31)

When the relative error $\Delta \le 1\%$, the convergent regions of the 10th-order approximation by IHAM are

$$\alpha \in \left[0,2.8\right], U_b\in \left[0,0.24\right], 0\le {\delta }_h\le 0.24L$$

(4.32)

The 20th-order approximation of $U_b$ with $n=20$, $\epsilon =8/{\pi }^2$, $ħ=-0.3$, ${\epsilon }_2=8/{\pi }^2$, ${ħ}_2=-0.4$ is expressed as

$$\begin{array}{l}{U}_b=6.6663\times {10}^{-2}{\alpha }^2-1.2647\times {10}^{-2}{\alpha }^4+3.0553\times {10}^{-3}{\alpha }^6\\ -7.8913\times {10}^{-4}{\alpha }^8+1.9565\times {10}^{-4}{\alpha }^{10}-4.2939\times {10}^{-5}{\alpha }^{12}\\ +7.8795\times {10}^{-6}{\alpha }^{14}-1.1689\times {10}^{-6}{\alpha }^{16}+1.3828\times {10}^{-7}{\alpha }^{18}\\ -1.3058\times {10}^{-8}{\alpha }^{20}+9.9286\times {10}^{-10}{\alpha }^{22}-6.1404\times {10}^{-11}{\alpha }^{24}\\ +3.1142\times {10}^{-12}{\alpha }^{26}-1.3002\times {10}^{-13}{\alpha }^{28}+4.4587\times {10}^{-15}{\alpha }^{30}\\ -1.2419\times {10}^{-16}{\alpha }^{32}+2.7429\times {10}^{-18}{\alpha }^{34}-4.5778\times {10}^{-20}{\alpha }^{36}\\ +5.1643\times {10}^{-22}{\alpha }^{38}-2.9055\times {10}^{-24}{\alpha }^{40}\end{array}$$

(4.33)

When the relative error $\Delta \le 1\%$, the convergent region of the 20th-order approximation by IHAM is

$$\alpha \in \left[0,3.4\right], U_b\in \left[0,0.29\right], 0\le {\delta }_h\le 0.29L$$

(4.34)

The 30th-order approximation of $U_b$ with $n=30$, $\epsilon =8/{\pi }^2$, $ħ=-0.1$, ${\epsilon }_2=8/{\pi }^2$, ${ħ}_2=-0.3$ is

$$\begin{array}{l}{U}_b=6.6665\times {10}^{-2}{\alpha }^2-1.1891\times {10}^{-2}{\alpha }^4+2.4037\times {10}^{-3}{\alpha }^6\\ -4.6144\times {10}^{-4}{\alpha }^8+7.8466\times {10}^{-5}{\alpha }^{10}-1.1452\times {10}^{-5}{\alpha }^{12}\\ +1.4110\times {10}^{-6}{\alpha }^{14}-1.4525\times {10}^{-7}{\alpha }^{16}+1.2395\times {10}^{-8}{\alpha }^{18}\\ -8.7140\times {10}^{-10}{\alpha }^{20}+5.0250\times {10}^{-11}{\alpha }^{22}-2.3731\times {10}^{-12}{\alpha }^{24}\\ +9.1975\times {10}^{-14}{\alpha }^{26}-2.9421\times {10}^{-15}{\alpha }^{28}+7.8331\times {10}^{-17}{\alpha }^{30}\\ -1.7531\times {10}^{-18}{\alpha }^{32}+3.3309\times {10}^{-20}{\alpha }^{34}-5.4217\times {10}^{-22}{\alpha }^{36}\\ +7.6171\times {10}^{-24}{\alpha }^{38}-9.2885\times {10}^{-26}{\alpha }^{40}+9.8639\times {10}^{-28}{\alpha }^{42}\\ -9.1295\times {10}^{-30}{\alpha }^{44}+7.3481\times {10}^{-32}{\alpha }^{46}-5.1117\times {10}^{-34}{\alpha }^{48}\\ +3.0383\times {10}^{-36}{\alpha }^{50}-1.5131\times {10}^{-38}{\alpha }^{52}+6.1056\times {10}^{-41}{\alpha }^{54}\\ -1.8743\times {10}^{-43}{\alpha }^{56}+3.8564\times {10}^{-46}{\alpha }^{58}-3.9126\times {10}^{-49}{\alpha }^{60}\end{array}$$

(4.35)

When the relative error $\Delta \le 1\%$, the convergent regions of the 30th-order approximation by IHAM are

$$\alpha \in \left[0,4.6\right], U_b\in \left[0,0.37\right], 0\le {\delta }_h\le 0.37L$$

(4.36)

Table 6 compares the above numerical solutions with the exact solutions. The relative error in Table 6 is calculated by

$$\Delta =\frac{\left|U_b^{\left[n=30\right]}-U_b\right|}{U_b}\times 100\%$$

(4.37)

Table 6. 30th-order numerical solutions $U_b^{\left[n=30\right]}$ by IHAM ($\epsilon =8/{\pi }^2$, $ħ=-0.1$, ${ħ}_2=-0.3$) compared with exact solutions $U_b$.

$\mathit{\alpha }$	Exact Solution	${\mathbf{\epsilon }}_2=0$ (HAM)		${\mathbf{\epsilon }}_2=8/{\pi }^2$ (IHAM)
	${\mathbf{U}}_{\mathbf{b}}$	${\mathbf{U}}_{\mathbf{b}}$	$\mathbf{\Delta }$	${\mathbf{U}}_{\mathbf{b}}$	$\mathbf{\Delta }$
0	0	0	0	0	0
0.3	0.0058994	0.0059063	0.116%	0.0059052	0.0993%
0.6	0.022488	0.022578	0.402%	0.022563	0.335%
0.9	0.047034	0.047359	0.690%	0.047300	0.565%
1.2	0.076400	0.077065	0.870%	0.076933	0.696%
1.5	0.10794	0.10894	0.923%	0.10872	0.723%
1.8	0.13981	0.14104	0.886%	0.14076	0.681%
2.1	0.17085	0.17223	0.804%	0.17190	0.610%
2.4	0.20046	0.20188	0.705%	0.20153	0.531%
2.7	0.22835	0.22973	0.603%	0.22939	0.456%
3.0	0.25442	0.25570	0.504%	0.25540	0.387%
3.3	0.27870	0.27985	0.411%	0.27961	0.324%
3.6	0.30128	0.30226	0.324%	0.30210	0.270%
3.9	0.32228	0.32316	0.274%	0.32310	0.257%
4.2	0.34180	0.34334	0.448%	0.34302	0.356%
4.5	0.35999	0.36371	1.03%	0.36042	0.121%
4.8	0.37695	0.37525	0.449%	0.36186	4.00%
5.1	0.39279	0.31920	18.7%	0.30447	22.5%
5.4	0.40762	0.027011	93.4%	0.14924	63.4%
5.7	0.42153	—	—	0.10903	74.1%
6.0	0.43459	—	—	—	—
$\infty$	1	1	0	1	0

From Table 6, IHAM extends the convergence regions from $\alpha \in \left[0,4.2\right]$ by HAM to $\alpha \in \left[0,4.6\right]$, which is $7.1\%$ increase.

Figure 3 shows the relationship between horizontal displacement and concentrated force at the free end. From Figure 3, it is observed that

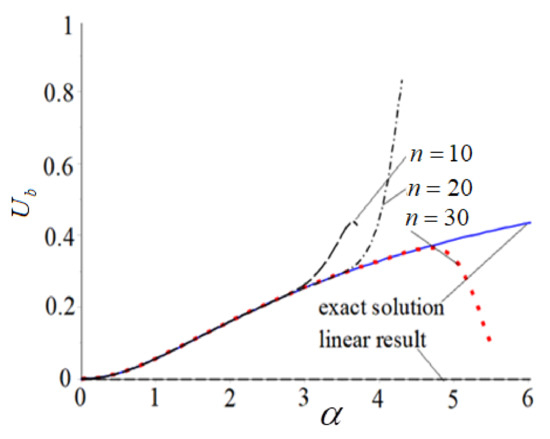
Figure 3. Horizontal displacement at free end.

• the difference between the linear solution and the exact solution is remarkable;
• from $n=10$ result of Equation (4.32), $n=20$ result of Equation (4.34) and n = 30 result of Equation (4.37), the convergence regions of horizontal displacement increases with increasing iterations.

5. Discussions and Conclusions

5.1. Error Analysis of Vertical Displacement

The influence of the control parameters ${\epsilon }_1$ and ${ħ}_1$ on the error of vertical displacement after $n=5$ iterations with $\alpha =2.0$ is then discussed.

After five iterations, the improved homotopy analysis method is adopted to solve the Equations (3.21) and (3.22) to yield the solution to the original Equations (2.3b) and (2.4b) as below

$$\begin{array}{l}{V}_b=0.33333\alpha +0.096738{ħ}_1{\alpha }^3+0.10197{ħ}_1^2{\alpha }^3\\ +0.052108{ħ}_1^3{\alpha }^3+0.011580{ħ}_1^4{\alpha }^3+0.028571{\epsilon }_1{ħ}_1{\alpha }^3\\ +0.085714{\epsilon }_1{ħ}_1^2{\alpha }^3+0.095238{\epsilon }_1{ħ}_1^3{\alpha }^3+0.047619{\epsilon }_1{ħ}_1^4{\alpha }^3\\ +9.5238\times {10}^{-3}{\epsilon }_1{ħ}_1^5{\alpha }^3-6.1695\times {10}^{-3}{ħ}_1{\alpha }^5-3.3120\times {10}^{-3}{ħ}_1^2{\alpha }^5\\ -8.2799\times {10}^{-4}{ħ}_1^3{\alpha }^5-5.8320\times {10}^{-3}{\epsilon }_1{ħ}_1{\alpha }^5-8.1553\times {10}^{-3}{\epsilon }_1{ħ}_1^2{\alpha }^5\\ -4.5967\times {10}^{-3}{\epsilon }_1{ħ}_1^3{\alpha }^5-1.0215\times {10}^{-3}{\epsilon }_1{ħ}_1^4{\alpha }^5+2.5955\times {10}^{-4}{ħ}_1{\alpha }^7\\ +7.4156\times {10}^{-5}{ħ}_1^2{\alpha }^7+6.8257\times {10}^{-4}{\epsilon }_1{ħ}_1{\alpha }^7+4.3913\times {10}^{-4}{\epsilon }_1{ħ}_1^2{\alpha }^7\\ +1.0978\times {10}^{-4}{\epsilon }_1{ħ}_1^3{\alpha }^7-7.4415\times {10}^{-6}{ħ}_1{\alpha }^9-4.2843\times {10}^{-5}{\epsilon }_1{ħ}_1{\alpha }^9\\ -1.2241\times {10}^{-5}{\epsilon }_1{ħ}_1^2{\alpha }^9+1.4103\times {10}^{-6}{\epsilon }_1{ħ}_1{\alpha }^{11}\end{array}$$

(5.1)

When $\alpha =2.0$, Equation (5.1) becomes

$$\begin{array}{l}{V}_b=0.66667+0.60589{ħ}_1+0.71928{ħ}_1^2+0.39037{ħ}_1^3\\ +0.092637{ħ}_1^4+0.11027{\epsilon }_1{ħ}_1+0.47469{\epsilon }_1{ħ}_1^2\\ +0.62886{\epsilon }_1{ħ}_1^3+0.34826{\epsilon }_1{ħ}_1^4+0.076190{\epsilon }_1{ħ}_1^5\end{array}$$

(5.2)

When $\alpha =2.0$, the exact solution is $V_b=0.49346$. When the iteration is five times, the relative error between the result by IHAM and the exact solution can be expressed as

$${\Delta }_V=\frac{\left|V_b^{\left[n=5\right]}-V_b\right|}{V_b}\times 100\%$$

(5.3)

When ${ħ}_1=-0.68$, Equation (5.2) becomes

$$V_b=0.48432+0.010163{\epsilon }_1$$

(5.4)

According to Equations (5.3) and (5.4), the relative error curve of control parameter ${\Delta }_V-{\epsilon }_1$ is a broken line. When the relative error is less than ${\Delta }_V\le 1\%$, the convergence interval is $R_{{\epsilon }_1}=\left[0.4,1\right]$, which is the effective region of ${\epsilon }_1$.

Figure 4 shows the relative errors curve ${\Delta }_V-{\epsilon }_1$ of Equation (2.3b) when $\alpha =2.0$, ${ħ}_1=-0.68$. From Figure 4, when ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, the relative error is the minimum.

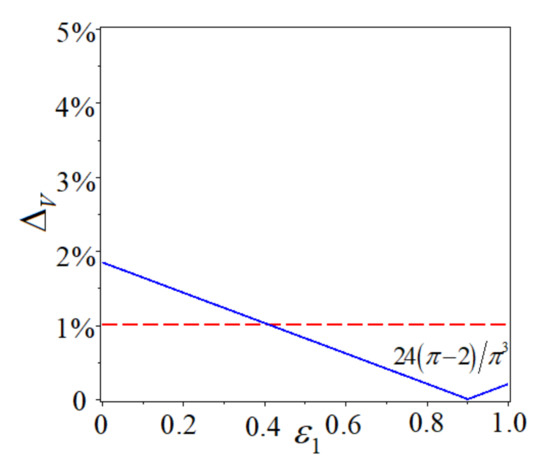
Figure 4. Relative errors curve ${\Delta }_V-{\epsilon }_1$ of Equation (2.3b) when $\alpha =2.0$, ${ħ}_1=-0.68$.

When ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$, Equation (5.2) becomes

$$\begin{array}{l}{V}_b=0.66667+0.70333{ħ}_1+1.1387{ħ}_1^2\\ +0.94605{ħ}_1^3+0.40038{ħ}_1^4+0.067325{ħ}_1^5\end{array}$$

(5.5)

According to Equations (5.3) and (5.5), the relative error curve of control parameter ${\Delta }_V-{ħ}_1$ is a quintic power function. When the relative error is less than ${\Delta }_V\le 1\%$, the convergence interval is $R_{{ħ}_1}=\left[-1,-0.58\right]$, which is the effective region of ${ħ}_1$.

Figure 5 gives the relative errors curve ${\Delta }_V-{ħ}_1$ of Equation (2.3b) when $\alpha =2.0$, ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$. From Figure 5, when ${ħ}_1=-0.68$, the relative error is the minimum.

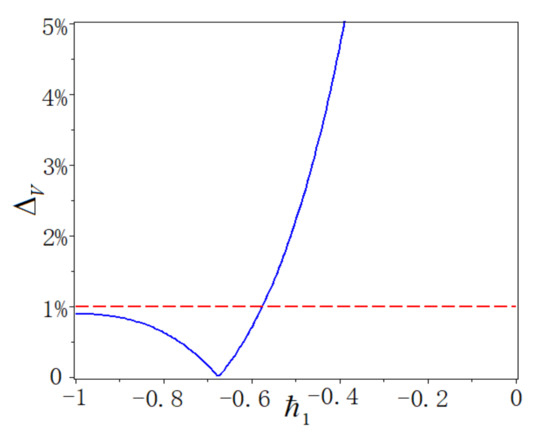
Figure 5. Relative errors curve ${\Delta }_V-{ħ}_1$ of Equation (2.3b) when $\alpha =2.0$, ${\epsilon }_1=24\left(\pi -2\right)/{\pi }^3$.

5.2. Error Analysis of Horizontal Displacement

The influence of the control parameter ${\epsilon }_2$ and ${ħ}_2$ on the error of horizontal displacement after 5 iterations when $\alpha =2.0$ is then discussed.

After five iterations, the improved homotopy analysis method is adopted to solve the Equations (4.24) and (4.25) to derive the solution to the original Equations (2.3c) and (2.4c). Thus,

$$\begin{array}{l}{U}_b=-0.20000{ħ}_2{\alpha }^2-0.20000{ħ}_2^2{\alpha }^2-0.066667{ħ}_2^3{\alpha }^2\\ -0.13333{\epsilon }_2{ħ}_2{\alpha }^2-0.46667{\epsilon }_2{ħ}_2^2{\alpha }^2-0.60000{\epsilon }_2{ħ}_2^3{\alpha }^2\\ -0.33333{\epsilon }_2{ħ}_2^4{\alpha }^2-0.066667{\epsilon }_2{ħ}_2^5{\alpha }^2+0.010871{ħ}_2{\alpha }^4\\ +3.7741\times {10}^{-3}{ħ}_2^2{\alpha }^4+0.017903{\epsilon }_2{ħ}_2{\alpha }^4+0.027904{\epsilon }_2{ħ}_2^2{\alpha }^4\\ +0.017361{\epsilon }_2{ħ}_2^3{\alpha }^4+3.7741\times {10}^{-3}{\epsilon }_2{ħ}_2^4{\alpha }^4-2.6973\times {10}^{-4}{ħ}_2{\alpha }^6\\ -1.6042\times {10}^{-3}{\epsilon }_2{ħ}_2{\alpha }^6-1.1329\times {10}^{-3}{\epsilon }_2{ħ}_2^2{\alpha }^6\\ -2.6973\times {10}^{-4}{\epsilon }_2{ħ}_2^3{\alpha }^6+8.2194\times {10}^{-5}{\epsilon }_2{ħ}_2{\alpha }^8\\ +2.1630\times {10}^{-5}{\epsilon }_2{ħ}_2^2{\alpha }^8-1.8596\times {10}^{-6}{\epsilon }_2{ħ}_2{\alpha }^{10}\end{array}$$

(5.6)

When $\alpha =2.0$, Equation (5.6) becomes

$$\begin{array}{l}{U}_b=-0.64333{ħ}_2-0.73961{ħ}_2^2-0.26667{ħ}_2^3\\ -0.33042{\epsilon }_2{h}_2-1.4872{\epsilon }_2{ħ}_2^2-2.1395{\epsilon }_2{ħ}_2^3\\ -1.2729{\epsilon }_2{ħ}_2^4-0.26667{\epsilon }_2{ħ}_2^5\end{array}$$

(5.7)

When $\alpha =2.0$, the exact solution is $U_b=0.16064$. After 5 time iterations, the relative error between the results by IHAM method and the exact solution can be written as

$${\Delta }_U=\frac{\left|U_b^{\left[n=5\right]}-U_b\right|}{U_b}\times 100\%$$

(5.8)

When ${ħ}_2=-0.465$, Equation (5.7) becomes

$$U_b=0.16603-0.0065196{\epsilon }_2$$

(5.9)

According to Equations (5.8) and (5.9), the relative error curve of control parameter ${\Delta }_U-{\epsilon }_2$ is a broken line. When the relative error is less than ${\Delta }_U\le 1\%$, the convergence region is $R_{{\epsilon }_2}=\left[0.58,1\right]$, which is the effective region of ${\epsilon }_2$.

Figure 6 shows the relative errors curve ${\Delta }_U-{\epsilon }_2$ of Equation (2.3c) when $\alpha =2.0$, ${ħ}_2=-0.465$. From Figure 6, when ${\epsilon }_2=8/{\pi }^2$, the relative error is the minimum.

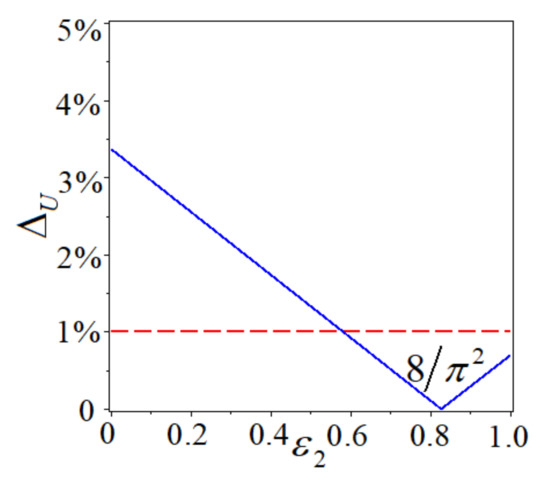
Figure 6. Relative errors curve ${\Delta }_U-{\epsilon }_2$ of Equation (2.3c) when $\alpha =2.0,$ ${ħ}_2=-0.465$.

When ${\epsilon }_2=8/{\pi }^2$, Equation (5.7) becomes

$$\begin{array}{l}{U}_b=-0.91116{ħ}_2-1.9451{ħ}_2^2-2.0009{ħ}_2^3\\ -1.0318{ħ}_2^4-0.21615{ħ}_2^5\end{array}$$

(5.10)

According to Equations (5.8) and (5.10), the relative error curve of control parameter ${\Delta }_U-{ħ}_2$ is a quintic polynomial curve. When the relative error is less than ${\Delta }_U\le 1\%$, the convergence interval is $R_{{ħ}_2}=\left[-0.75,-0.42\right]$, which is the effective region of ${ħ}_2$.

Figure 7 depicts the relative errors curve ${\Delta }_U-{ħ}_2$ of Equation (2.3c) when $\alpha =2.0$, ${\epsilon }_2=8/{\pi }^2$. From Figure 7, when ${ħ}_2=-0.465$ or ${ħ}_2=-0.66$, the relative error is the minimum.

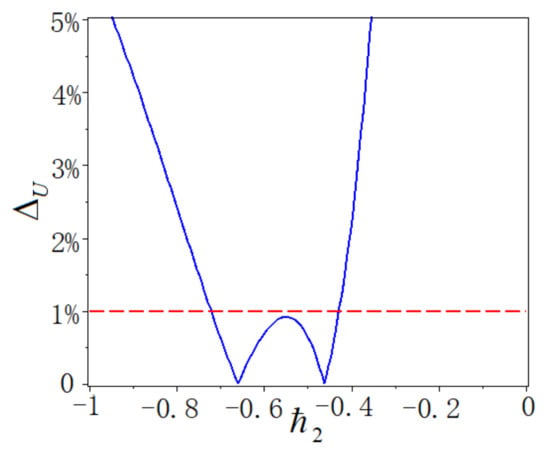
Figure 7. Relative errors curve ${\Delta }_U-{ħ}_2$ of Equation (2.3c) when $\alpha =2.0$, ${\epsilon }_2=8/{\pi }^2$.

5.3. Conclusions

In this paper, an improved homotopy analysis method (IHAM) is applied to derive complete expressions of vertical and horizontal displacements of a cantilever beam under point load at the free end. In fact, the proposed method is a semi-analytical method since many numerical algorithms are used.

The linear solution is only valid for small $\alpha$. For large $\alpha$, the nonlinear effect of the equation cannot be neglected. A family of the explicit solutions of the rotation angle, the vertical and horizontal displacements of a cantilever beam under a point load at the free end are obtained by IHAM, which are summarized in Table A1 for 30th-order approximation. The current explicit solutions with different parameters and solution schemes match well with the exact solutions from elliptical integrals; however, our solutions for the current problem by the proposed IHAM, especially Equations (3.36) and (4.31), are explicit and simple compared with the exact solution from the elliptical integrals which requires solving a transcendental equation. The current solution is easy to calculate with the explicit polynomial expressions, which should be, thus, prioritized for practical engineering applications with minimal requirements on the calculation and computation.

By solving the exact bending equation of a cantilever beam, we demonstrate the superior proficiency of IHAM over a class of existing equations in solid mechanics. The improved homotopy analysis method has great superiority compared over the traditional homotopy analysis method in view of the very much increased rate and precision of convergence as well as the substantially enlarged convergence range.

The convergence ranges of the rotation angle and vertical displacement are extended by the homotopy-Páde approximation, whereas it does not avail horizontal displacement.

In summary, the 30th-order improved homotopy analysis solutions and exact solutions of the angular, vertical and horizontal displacements of large deflection cantilever beams by Equations (3.42), (3.47) and (4.35) are compared in the following Appendix A table. It can be concluded from this study that the proposed IHAM can be applied to solve a general strong nonlinear problem in structural analysis.