Abstract
This paper presents a modification to the dingo optimization algorithm (mDOA) to solve the non-linear set of equations of the selective harmonic elimination (SHE) control technique widely applied in multilevel inverters. In addition, said modification is conducted to the survival criteria by including a local search to provide a better balance when replacing vectors (dingoes) with a low survival rate. The proposed method is also benchmarked with some unimodal functions to illustrate its better exploitation capabilities. Finally, the SHE optimization results were calculated and compared with three well-known state-of-the-art metaheuristics, where the modified version of the dingo optimization algorithm showed very competitive results. The significant difference between the mDOA results and the rest of the algorithms is determined by the Wilcoxon rank-sum non-parametric statistical test with a 5% degree of significance. The p-values confirm the meaningful advantage of the mDOA compared to other bio-inspired algorithms for many modulation indexes. Experimentally, the proposed algorithm is validated through the implementation of a three-phase 11-level inverter.
1. Introduction
Due to the incremental use of renewable energy systems, (photovoltaics arrays, wind, fuel cells, just to mention a few), there is a need for power conversion systems that can transform their electrical output to the specific characteristics needed for a load to work [1]. Inverters are power electronic devices capable of transforming a direct current (DC) power source to an alternative current (AC) at a desired electrical characteristics output [2]. A multilevel inverter (MLI) is an inverter-type capable of generating a staircase output waveform synthesized at different voltage levels, where the levels are controlled by the correct angle switching of the MLI power switching devices. Due to their better electromagnetic compatibility, high power quality, low switching losses, and lower total harmonic distortion, they have been extensively used as industrial drivers, compensators, medium and high voltage inverters, and as an interface to renewable energy systems [3].
The multilevel inverters main advantage lies in the use of separate DC sources that are ideal for fuel cells and photovoltaics arrays applications. They can be classified in three basic types, cascaded H-bridge, diode clamped, and capacitor clamped inverters. Cascaded H-bridge inverters (CHBMLI) consist of a series of H-bridge cells connected in series, where the addition of each cell voltage is used to synthesize the desired output waveform [4]. Continuous research has aimed to reduce the MLIs harmonic content and to improve their structure by designing new topologies [5,6]. On the operation of an MLI, the harmonic reduction mostly depends on the modulation strategy selected to control the inverter [6]. Selective harmonic elimination [4,7,8] (SHE) is a pulsed modulation (PWM) control strategy aimed to suppress low-order harmonics by determining the angles to control the switching sequence of the MLI power semiconductor devices. Then, the typical staircase output waveform is generated. The SHE-PWM formulation relies on the Fourier decomposition of this periodic output voltage waveform, giving a series of non-linear equations as a function of the inverter’s switching angles for each level of the DC voltages [9,10]. Finding the solution of these equations has been conducted by applying several methods such as iterative [11], stochastics [9], and metaheuristics [12,13,14], with the latter being highly used due to their ability to find the local optima and to avoid stagnation. On the metaheuristics side, many of them have been developed in recent years and can be classified as swarm-based, evolutionary, physics-based, human-based, and maths-based algorithms [15]. Several metaheuristics have been applied to solve the SHE-PWM formulation. Prasad et al. in [16] compared the flower pollination algorithm against particle swarm optimization (PSO), teaching learning-based optimization (TLBO), and cuckoo search algorithm (CSA) to establish the effectiveness of FPA in solving the selective harmonic elimination problem. Similarly, in [17,18], the whale optimization (WOA) and modified version of the grey wolf optimization (GWO) were applied to solve the SHE formulation. In [19], they show that bio-inspired intelligent algorithms can effectively eliminate the undesired lower harmonics from the SHE-PWM control strategy. Researchers in [20] applied the asynchronous particle swarm optimization to solve the SHE-PWM formulation. Nowadays new optimization algorithms such as the black widow [21], harmony search [22], and the bacterial foraging algorithm [23] have been proposed to solve the SHE set of non-linear equations.
Currently, no algorithm can efficiently and effectively solve every optimization problem in all engineering and research fields. The scientific community is still searching for new algorithms, which are then compared to those existing in the literature to prove their reliability. Good results can be achieved in a particular application but fail to find the global optimum in others [24,25]. The main difference between metaheuristics algorithms lies in the recombination functions. Said recombination functions are calculated based on the bio-inspired mathematical model inspiration. In order to show the advantages of the proposed method compared with the WOA, GWOA, and the BWOA algorithm, the Wilcoxon rank-sum non-parametric statistical test with a 5% degree of significance was implemented. This work proposes a modification to the standard dingo optimization algorithm (mDOA), where the main advantage lies in the dingo survival evaluation criterion, a procedure not available in the remainder of the algorithms part of this study. It gives an opportunity to substitute vectors with low dingoes’ survival rate (fitness with worse values) before moving to the next iteration. The modified algorithm is used to solve the SHE set of equations for a three-phase 11-levels symmetric cascaded H-bridge MLI.
2. Materials and Methods
2.1. Selective Harmonic Elimination Method
In cascaded H-bridge inverters, the staircase voltage output is a consequence of the addition of each DC source () from each H-bridge cell (m), where the number of cells are equal to the numbers of sources (s). The relationship between the number of levels (n) and number of sources is given by . Figure 1 shows an ideal single phase sine voltage waveform () and the multilevel inverter staircase voltage output for un period (T). Where, the peak phase voltage is equal to and the angles, defined for a quarter-wave symmetry are subjected to:
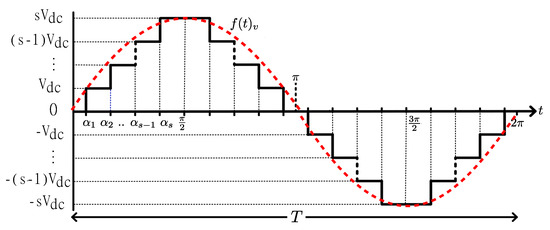
Figure 1.
MLI staircase phase voltage output (black lines) and its relationship with an ideal pure sine waveform (red-dashed lines).
By applying Fourier analysis [10], the MLI staircase output showed in Figure 1 is defined as follows:
SHE aims for the elimination of low-order harmonics as it keeps the fundamental component equal to a given amplitude. In a three-phase system, as in this study, the triplen harmonics are canceled out. Thus, Equation (2) is solved to eliminate the fifth, seventh, eleventh, and thirteenth harmonics while keeping the amplitude of the fundamental component equal to M. Then, Equation (2) can be rewritten as:
where is defined as the modulation index for and is equal to the desired fundamental component [26]. Then, subjected to Equation (1), Equation (3) can be expressed as an optimization problem [10,17] as follows:
Once the objective function is defined, and previous to the definition of the modified dingo optimization algorithm (mDOA), the standard DOA is described in the next section.
2.2. Standard Dingo Optimization Algorithm (DOA)
The dingo optimization algorithm (DOA) is a novel bio-inspired algorithm for global optimization that mimics dingoes hunting strategies. These strategies are attacking by persecution, grouping tactics, and scavenging behavior [27]. The Australian dingo dog is at risk of extinction. So, in this algorithm, dingoes’ survival probability is also considered. The overall flow is shown in Figure 2.
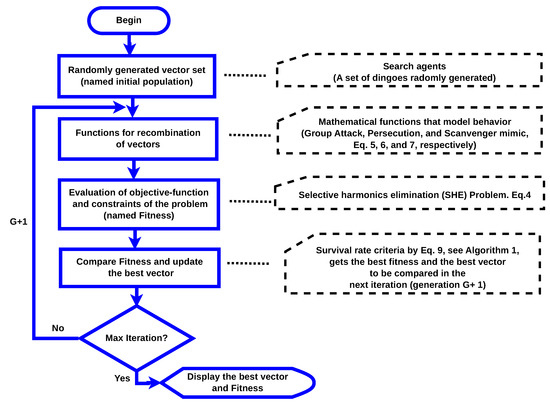
Figure 2.
DOA flowchart.
The mathematical models taken from [27], are described as follow:
Strategy 1: Group attack. Dingoes usually gather in groups when hunting. Dingoes can find the location of the prey and surround it. This behavior is represented by Equation (5):
where is the new position of a search agent (indicates dingoes’ movement), is a random integer number generated in the invertal of , where is the total size of the population of dingoes. , is a sub-set of search agents (dingoes that will attack) where , X is the dingoes’ population randomly generated, is the current search agent, is the best search agent found from the previous iteration, and is a random number uniformly generated in the interval of , it is a scale factor that changes the magnitude and sense of the dingoes’ trajectories [27].
Strategy 2: Persecution. Dingoes usually hunt small prey, and chased until the prey is caught individually. The following Equation models this behavior [27]:
where indicates the dingoes’ movement, is the current search agent, is the best search agent found from the previous iteration, has the same value as in Equation (5), is a random number uniformly generated in the interval of , is the random number generated in the interval from 1 to the size of maximum of search agents (dingoes), and is the -th search agent selected, where .
Strategy 3: Scavenger. Scavenger behavior is defined as the action when dingoes find carrion to eat, when they are randomly walking in their habitat. Equation (7) is used to model this behavior [27].
where indicates the dingoes’ movement, has the same value as in Equation (6), is the random number generated in the interval from 1 to the size of maximum of search agents (dingoes), is the -th search agent selected, is the current search agent, where , and is a binary number randomly generated.
Strategy 4: Dingoes’ survival rates. The dingoes’ survival rate value is provided by Equation (8).
where, and are the worst and the best fitness value in the current generation, respectively, whereas is the current fitness value of the i-th search agent. The survival vector in Equation (8), contains the normalized fitness in the interval of . Equation (9) is applied for low survival rates, e.g. for survival rates values equal or less than 0.3 [27].
where is the search agent with low survival rates that will be updated, and are random numbers generated in the interval from 1 to the maximum size of search agents (dingoes), with , and , are the , -th search agents selected, is the best search agent found from the previous iteration, and is a binary number randomly generated.
2.3. Modified Dingo Optimization Algorithm (mDOA)
In this paper, an improved algorithm is proposed for the features of the standard DOA algorithm. The main improvement is an incorporation of a local search procedure in the survival criteria. The local search is associated with an exploitation mechanism in the search space of solutions. It consists of enhancing the best solution obtained so far by looking for other alternatives around it. All bio-inspired algorithms must have a good balance between exploitation (local search) and exploration (global search). So, Equation (9), proposed in [27], is associated to global search whilst Equation (10) is associated to local search.
where is the search agent with low survival rates that will be updated, is the best search agent found from the previous iteration, and is a pseudo-random number uniformly distributed in the interval (−2, 2). Whereas, is a normally distributed pseudo-random number in the interval of (0, 1).
The proposed criterion consists of: If the content of the indexed vector has a survival rate less than 0.3 and if the index number is even, then a global search will be applied; otherwise, for odd index numbers, a local search will then be used. The survival criteria is summarized in Algorithm 1 and depicted in Figure 3. In all of the benchmark functions, the mDOA overtops the classic DOA in the majority of the tests.

Figure 3.
Survival rate proposal.
The proposed approach was benchmarked with four unimodal functions associated with exploitation (local search), shown in Equation (11), and compared with the standard DOA algorithm. All functions have a dimension of 30 (number of variables) and each variable in the interval [−100, 100] with the best known value = 0:
The importance of the survival criterion is that it replaces (repairs) vectors with low fitness by incorporating a local search strategy in addition to the global search it previously had to improve the standard DOA algorithm. The result of these tests are summarized in Figure 4.
| Algorithm 1 Survival procedure |
| 1: Begin procedure 2: for to sizePopulation do 3: if then 4: if i is Even then 5: Strategy 4: search agent updated by Equation (9). 6: else 7: Strategy 4: search agent updated by Equation (10). 8: end if 9: end if 10: end for 11: End procedure |
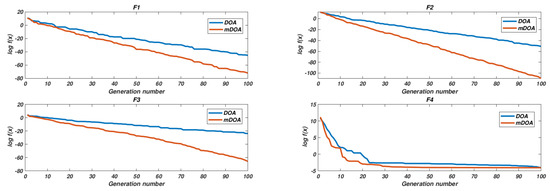
Figure 4.
DOA and mDOA unimodal functions ( convergence graph.
Pseudo Code for mDOA
The pseudo code of the mDOA is described below (Algorithm 2).
| Algorithm 2 Modified Dingo Optimizer Algorithm (mDOA) |
| 1: procedure DOA Taken from [27] and updated with our approach 2: Initialization of parameters 3: , probability of hunting or scavenger strategy 4: , probability of Strategy 1 (group attack) or Strategy 2 (persecution attack) 5: Generate the initial population 6: while iteration < Max Number of Iterations do 7: if then 8: if then 9: Strategy 1: Group Attack Procedure, Equation (5). 10: else 11: Strategy 2: Persecution, Equation (6). 12: end if 13: else 14: Strategy 3: Scavenger, Equation (7). 15: end if 16: Update search agents that have low survival value, Algorithm 1, Equation (9) or (10). 17: Calculate , the fitness value of the new search agents 18: if then 19: 20: end if 21: 22: end while 23: Display , the best optimal solution 24: end procedure |
3. Experimental Setup
Previously, the modified version of the dingo optimization algorithm (mDOA) upgraded capabilities were tested with four unimodal testbench functions from the literature, showing superior results than the classic DOA. The selective harmonic elimination formulation is tested and compared with the whale optimization (WOA) [17], modified gray wolf (GWOA) [18], black widow optimization algorithm (BWOA) [21], and the mDOA. All tests were conducted with a population size of 100 and 250 iterations. The best optimal computed angles are then fed to a Simulink program to determine the correct elimination of the desired harmonics, following the methodology illustrated in Figure 5 and described in [21]. Once the best angles are calculated, they are fed to control the triggering of the IGBTs of a three-phase 11-levels cascaded H-bridge multilevel inverter simulated in Simulink. Once the staircase output waveform is determined, Fourier analysis is conducted to determine the harmonic content and the total harmonic distortion, see Figure 6.
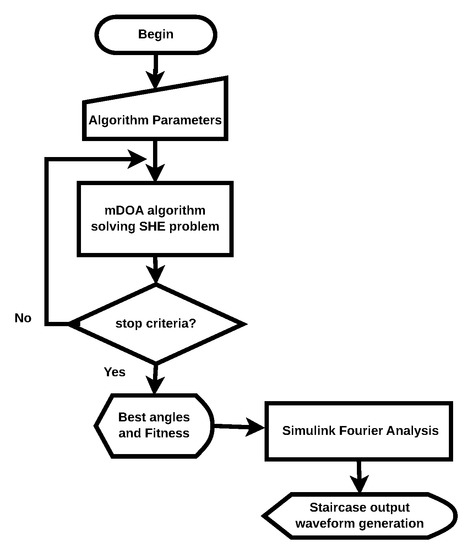
Figure 5.
Selective harmonic elimination formulation and Fourier analysis flowchart.
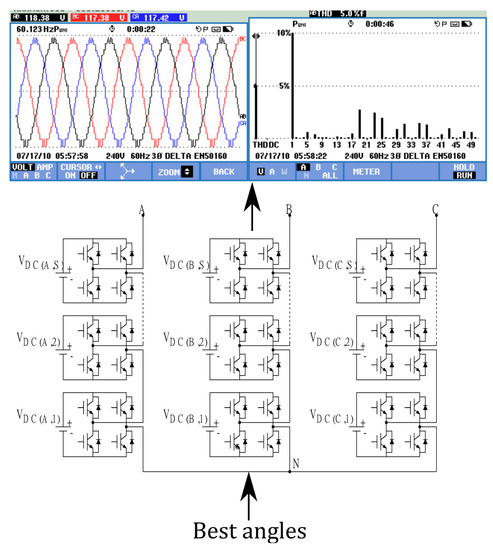
Figure 6.
Simulink simulation workflow.
4. Results
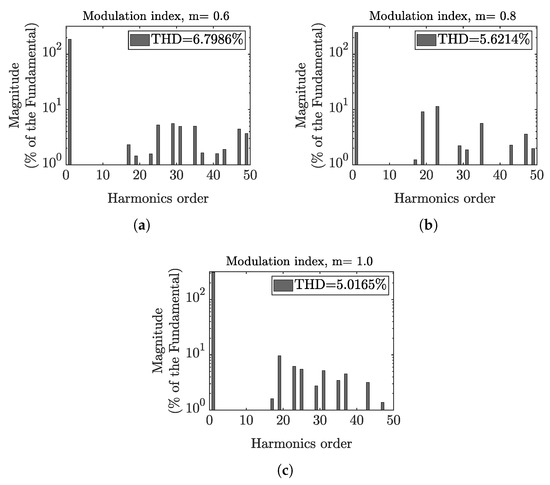
In order to verify the mDOA capabilities to solve the non-linear set of equations of the selective harmonic elimination technique, three tests were conducted for each of the selected algorithms. As stated in Equation (4), the modulation index M can vary between 0 and 1. Thus, three modulation index analysis at 0.6, 0.8, and 1 are then proposed. It is worth emphasizing that say values are widely used in multilevel inverters. As previously mentioned, all tests were run for a population size of 100 and 250 iterations. Table 1, Table 2 and Table 3, summarize the experimental tests conducted, where the modified version of the dingo optimization algorithm outperforms the other algorithms by obtaining the best fitness for all of the selected modulation indexes. The near-optimal obtained angles are then used in a Fourier analysis to determine the total harmonic distortion and the corrected elimination of the fifth, seventh, eleventh, and thirteenth harmonics for the three selected modulation indexes. As the mDOA algorithm showed the best fitness, Figure 7 shows the Fourier spectrum calculated by using the mDOA angles summarized in Table 1, Table 2 and Table 3, where the correct elimination of the selected low order harmonics is appreciated.

Table 1.
Algorithms results for modulation index = 1.

Table 2.
Algorithms results for modulation index = 0.8.

Table 3.
Algorithms results for modulation index = 0.6.
In order to show the advantages of the proposed method compared with the WOA, GWOA, and the BWOA algorithm, the Wilcoxon rank-sum non-parametric statistical test with a 5% degree of significance was implemented at 21 modulation indexes running from 0.5 to 1, see Table 4. This test returns a p-value that establishes the significance level of the two algorithms. In this work analysis, an algorithm is statistically significant if and only if the p-values are less than 0.05. For many cases (bold numbers), the Wilcoxon rank-sum test p-values obtained confirm the meaningful advantage against the WOA and GWOA. Specifically at modulation indexes ranging from 0.65 to 0.8 and from 0.875 to 0.95 when compared with the WOA. Whereas when compared to the GWOA, it shows statistical advantage for modulation indexes between 0.65 and 0.9. Moreover, the Wilcoxon analysis against the BWOA shows competitive results at modulation indexes of 0.5, 0.55, and 0.7. It is to be noted that at a modulation index of 1, the mDOA results are statistically significant compared with the BWOA, WOA, and GWOA.

Table 4.
The p-values of the Wilcoxon rank-sum test with 5% significance for mDOA vs. BWOA, WOA, and GWOA. p-values ≤ 0.05 are shown in bold.
On the other hand, from the convergence graph, it is confirmed that the mDOA outperforms the rest of the algorithms part of this work by minimizing the objective function more optimally, see Figure 8. The near-to-optimal firing angles calculated using the mDOA at different modulation indexes typically used in multilevel inverters are shown in Figure 9.
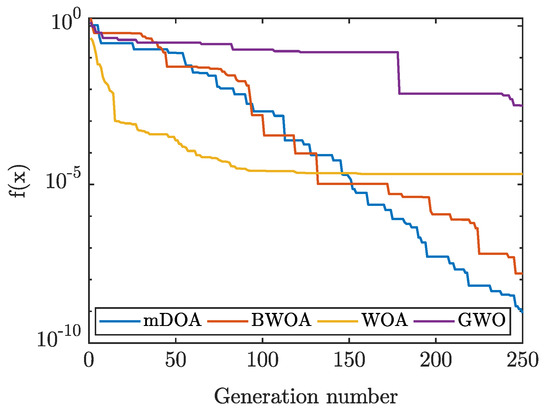
Figure 8.
Convergence graph for a modulation index of 1.
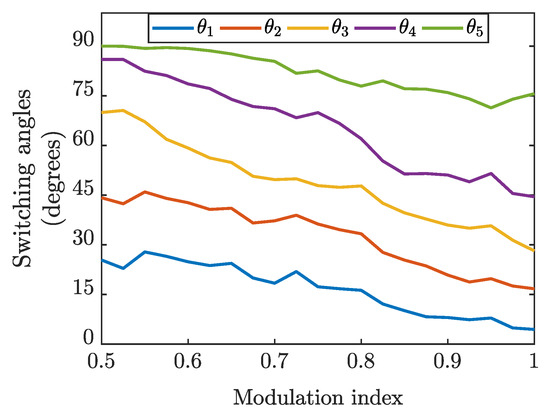
Figure 9.
Optimized firing angles as a function of the modulation index.
The experimental results are summarized in Figure 10, where the harmonic spectrum and output waveform for an 11-level inverter at three modulation indexes are illustrated. Each of the Fourier spectrum is shown at 10% of the magnitude of the fundamental component. The mDOA angles used for the experimentation are summarized in Table 1, Table 2 and Table 3. The agreement between the theoretical and experimental total harmonic distortion and the minimization of the desired harmonics can be seen. The instantaneous waveforms and harmonic spectrum of the output voltage were obtained using a Fluke 427 series II Power Quality and Energy Analyzer, see Figure 11 for the experimental setup.
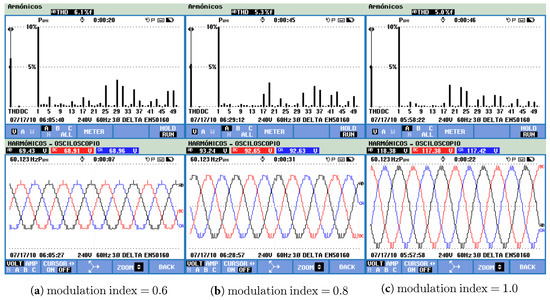
Figure 10.
Sub-figure a to c show the experimental output waveform and harmonic spectrum of a three-phase eleven-level inverter at modulation index of 0.6, 0.8 and 1.

Figure 11.
Three-phase 11-level inverter experimental setup.
5. Conclusions
This paper proposed a modification to the dingo optimization algorithm, which incorporates a local search procedure in the survival criteria to improve the exploitation abilities over the solution search space. This modification was tested with some unimodal benchmark functions, where the upgraded version gained better results than the standard dingo optimization algorithm. From statistical analysis, the Wilcoxon rank-sum test p-values confirmed the advantage of the mDOA for a modulation index equal to 1 over the rest of the algorithms that were a part of this study. In terms of the BWOA, it shows competitive results at modulation indexes of 0.5, 0.55, and 0.7. Whereas when compared to the GWOA, it also showed a statistical advantage for modulation indexes between 0.65 and 0.9. Additionally, a meaningful advantage against the WOA at modulation indexes ranging from 0.65 to 0.8 and from 0.875 to 0.95 was identified. The mDOA was applied to solve the non-linear equations of the selective harmonic elimination control strategy. Specifically, it was used to eliminate the fifth, seventh, eleventh, and thirteenth harmonics for modulation indexes of 0.6, 0.8, and 1.0, finding a better global minima solution than the rest of the algorithms. Moreover, the calculated and experimental total harmonic distortion are in close agreement. These results confirm that the mDOA can effectively be used to solve the SHE mathematical formulation.
Author Contributions
Conceptualization, J.H.A.-C.; methodology, J.H.A.-C.; software, J.H.A.-C., H.P.-V. and A.F.P.-D.; validation, H.P-V. and A.F.P.-D.; formal analysis, J.H.A.-C., H.P.-V. and A.F.P.-D.; investigation, J.H.A.-C.; data curation, J.H.A.-C.; writing—original draft preparation, J.H.A.-C.; writing—review and editing, H.P.-V. and A.F.P.-D.; visualization, A.F.P.-D. and H.P.-V.; supervision, H.P.-V., P.M.G.-V. and A.F.P.-D.; project administration, P.M.G.-V. and A.F.P.-D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by Programa Para el Desarrollo Profesional Docente (PRODEP), para el tipo superior (Grant no. 511–6/18–8171). The article processing charge was funded by Universidad Tecnológica de Altamira.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moeed Amjad, A.; Salam, Z. A review of soft computing methods for harmonics elimination PWM for inverters in renewable energy conversion systems. Renew. Sustain. Energy Rev. 2014, 33, 141–153. [Google Scholar] [CrossRef]
- José, R.; Franquelo, L.G.; Samir, K.; León, J.I.; Portillo, R.C.; Prats, M.Á.M.; Pérez, M.A. 03 Multilevel converters: An enabling technology for high-poer applications. Proc. IEEE 2009, 97, 1786–1817. [Google Scholar] [CrossRef] [Green Version]
- Vijeh, M.; Rezanejad, M.; Samadaei, E.; Bertilsson, K. A General Review of Multilevel Inverters Based on Main Submodules: Structural Point of View. IEEE Trans. Power Electron. 2019, 34, 9479–9502. [Google Scholar] [CrossRef]
- Dahidah, M.S.; Konstantinou, G.; Agelidis, V.G. A Review of Multilevel Selective Harmonic Elimination PWM: Formulations, Solving Algorithms, Implementation and Applications. IEEE Trans. Power Electron. 2015, 30, 4091–4106. [Google Scholar] [CrossRef]
- El-Hosainy, A.; Hamed, H.A.; Azazi, H.Z.; El-Kholy, E.E. A review of multilevel inverter topologies, control techniques, and applications. In Proceedings of the 2017 Nineteenth International Middle East Power Systems Conference (MEPCON), Cairo, Egypt, 19–21 December 2017; pp. 1265–1275. [Google Scholar]
- Colak, I.; Kabalci, E.; Bayindir, R. Review of multilevel voltage source inverter topologies and control schemes. Energy Convers. Manag. 2011, 52, 1114–1128. [Google Scholar] [CrossRef]
- Guan, E.; Song, P.; Ye, M.; Wu, B. Selective harmonic elimination techniques for multilevel cascaded H-bridge inverters. In Proceedings of the International Conference on Power Electronics and Drive Systems, Kuala Lumpur, Malaysia, 28 November–1 December 2005; Volume 2, pp. 1441–1446. [Google Scholar] [CrossRef]
- Siddique, M.D.; Mekhilef, S.; Padmanaban, S.; Memon, M.A.; Kumar, C. Single-Phase Step-Up Switched-Capacitor-Based Multilevel Inverter Topology with SHEPWM. IEEE Trans. Ind. Appl. 2021, 57, 3107–3119. [Google Scholar] [CrossRef]
- El-Naggar, K.; Abdelhamid, T.H. Selective harmonic elimination of new family of multilevel inverters using genetic algorithms. Energy Convers. Manag. 2008, 49, 89–95. [Google Scholar] [CrossRef]
- Al-Othman, A.K.; Abdelhamid, T.H. Elimination of harmonics in multilevel inverters with non-equal dc sources using PSO. Energy Convers. Manag. 2009, 50, 756–764. [Google Scholar] [CrossRef]
- Sun, J.; Grotstollen, H. Solving nonlinear equations for selective harmonic eliminated PWM using predicted initial values. In Proceedings of the 1992 International Conference on Industrial Electronics, Control, Instrumentation, and Automation, San Diego, CA, USA, 9–13 November 1992; Volume 1, pp. 259–264. [Google Scholar] [CrossRef]
- Kavousi, A.; Vahidi, B.; Salehi, R.; Bakhshizadeh, M.K.; Farokhnia, N.; Fathi, S.H. Application of the Bee Algorithm for Selective Harmonic Elimination Strategy in Multilevel Inverters. IEEE Trans. Power Electron. 2012, 27, 1689–1696. [Google Scholar] [CrossRef]
- Patil, S.D.; Kadwane, S.G.; Gawande, S.P. Ant Colony Optimization applied to selective harmonic elimination in Multilevel inverters. In Proceedings of the 2016 2nd International Conference on Applied and Theoretical Computing and Communication Technology (iCATccT), Bangalore, India, 21–23 July 2016; pp. 637–640. [Google Scholar]
- Routray, A.; Singh, R.K.; Mahanty, R. Modified Particle Swarm Optimization Based Harmonic Minimization in Hybrid Cascaded Multilevel Inverter. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, ECCE 2018, Portland, OR, USA, 23–27 September 2018; Volume 15, pp. 5573–5578. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.; Ranjan, P.; Barde, C.; Choubey, A.; Morales-Cepeda, A.B. A Bio-Inspired Method for Mathematical Optimization Inspired by Arachnida Salticidade. Mathematics 2022, 10, 102. [Google Scholar] [CrossRef]
- Panda, K.P.; Bana, P.R.; Panda, G. FPA Optimized Selective Harmonic Elimination in Symmetric-Asymmetric Reduced Switch Cascaded Multilevel Inverter. IEEE Trans. Ind. Appl. 2020, 56, 2862–2870. [Google Scholar] [CrossRef]
- Kar, P.K.; Priyadarshi, A.; Karanki, S.B. Selective harmonics elimination using whale optimisation algorithm for a single-phase-modified source switched multilevel inverter. IET Power Electron. 2019, 12, 1952–1963. [Google Scholar] [CrossRef]
- Routray, A.; Member, S.; Singh, R.K.; Member, S.; Mahanty, R. Harmonic Reduction in Hybrid Cascaded Multilevel Inverter Using Modified Grey Wolf Optimization. IEEE Trans. Ind. Appl. 2019, 56, 1827–1838. [Google Scholar] [CrossRef]
- Memon, M.A.; Mekhilef, S.; Mubin, M.; Siddique, M.D.; Dardeer, M. Comparative Analysis of Optimal and Fixed Input DC Sources with Selective Harmonic Elimination Pulse Width Modulation. In Proceedings of the IEEE Conference on Power Electronics and Renewable Energy, CPERE 2019, Aswan, Egypt, 23–25 October 2019; pp. 94–98. [Google Scholar] [CrossRef]
- Memon, M.A.; Siddique, M.D.; Saad, M.; Mubin, M. Asynchronous Particle Swarm Optimization-Genetic Algorithm (APSO-GA) based Selective Harmonic Elimination in a Cascaded H-Bridge Multilevel Inverter. IEEE Trans. Ind. Electron. 2021, 69, 1477–1487. [Google Scholar] [CrossRef]
- Peña-Delgado, A.F.; Peraza-Vázquez, H.; Almazán-Covarrubias, J.H.; Torres Cruz, N.; García-Vite, P.M.; Morales-Cepeda, A.B.; Ramirez-Arredondo, J.M. A Novel Bio-Inspired Algorithm Applied to Selective Harmonic Elimination in a Three-Phase Eleven-Level Inverter. Math. Probl. Eng. 2020, 2020, 8856040. [Google Scholar] [CrossRef]
- Xin, Y.; Yi, J.; Zhang, K.; Chen, C.; Xiong, J. Offline Selective Harmonic Elimination With (2N+1) Output Voltage Levels in Modular Multilevel Converter Using a Differential Harmony Search Algorithm. IEEE Access 2020, 8, 121596–121610. [Google Scholar] [CrossRef]
- Ram, J.P.; Rajasekar, N. Investigation of Bacterial Foraging Algorithm Applied for PV Parameter Estimation, Selective Harmonic Elimination in Inverters and Optimal Power Flow for Stability. In Nature-Inspired Methods for Metaheuristics Optimization: Algorithms and Applications in Science and Engineering; Bennis, F., Bhattacharjya, R.K., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 135–167. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Ho, Y.C.; Pepyne, D.L. Simple Explanation of the No-Free-Lunch Theorem and Its Implications. J. Optim. Theory Appl. 2002, 115, 549–570. [Google Scholar] [CrossRef]
- Haghdar, K. Optimal DC Source Influence on Selective Harmonic Elimination in Multilevel Inverters Using Teaching—Learning Based Optimization. IEEE Trans. Ind. Electron. 2019, 67, 942–949. [Google Scholar] [CrossRef]
- Peraza-Vázquez, H.; Peña-Delgado, A.F.; Echavaria-Castillo, G.; Morales-Cepeda, A.B.; Velasco-Alvarez, J.; Ruiz-Perez, F. A Bio-Inspired Method for Engineering Design Optimization Inspired by Dingoes Hunting Strategies. Math. Probl. Eng. 2021, 2021, 9107547. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).