Stochastic Strength Analyses of Screws for Femoral Neck Fractures
Abstract
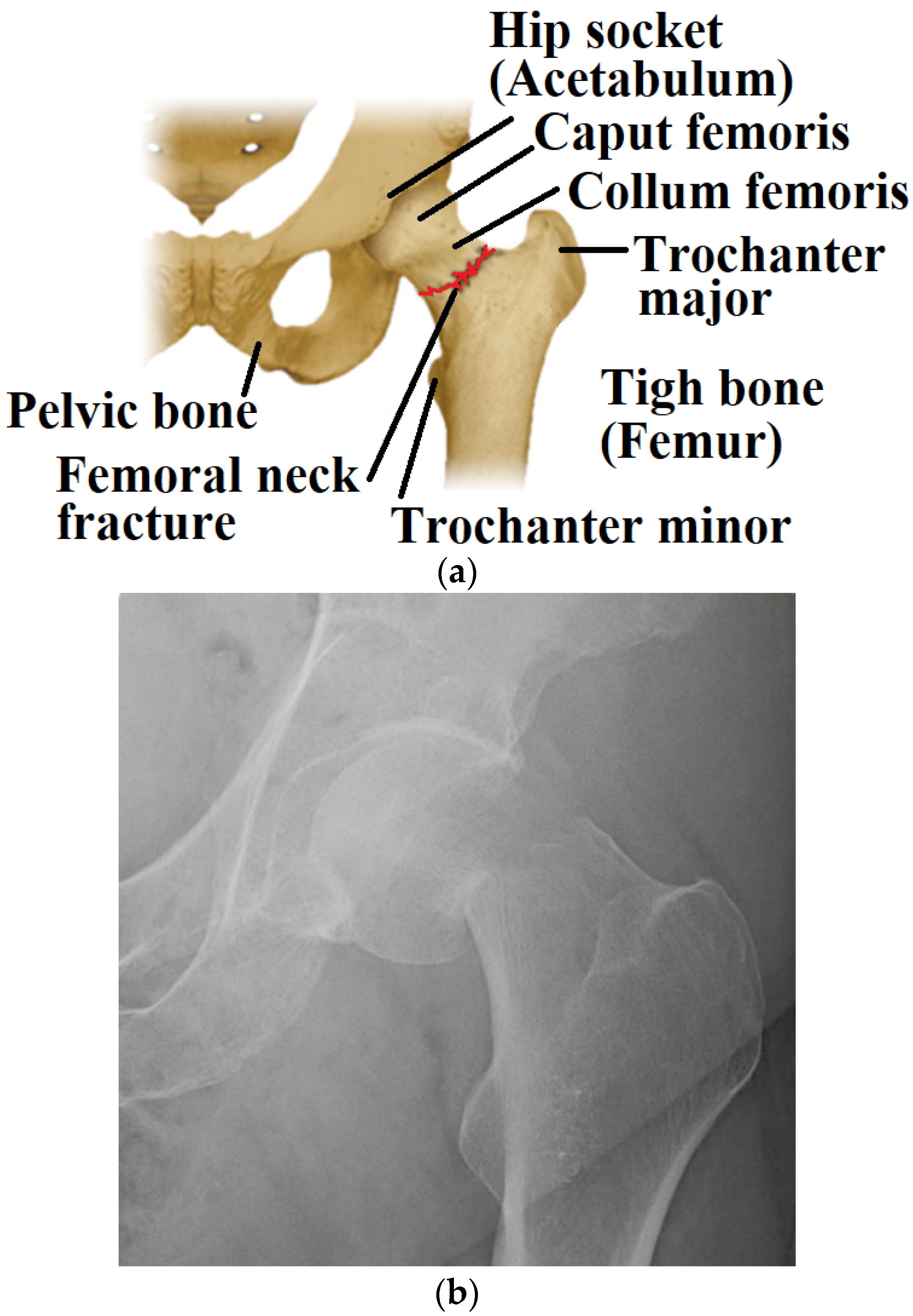
1. Introduction
2. Limitations
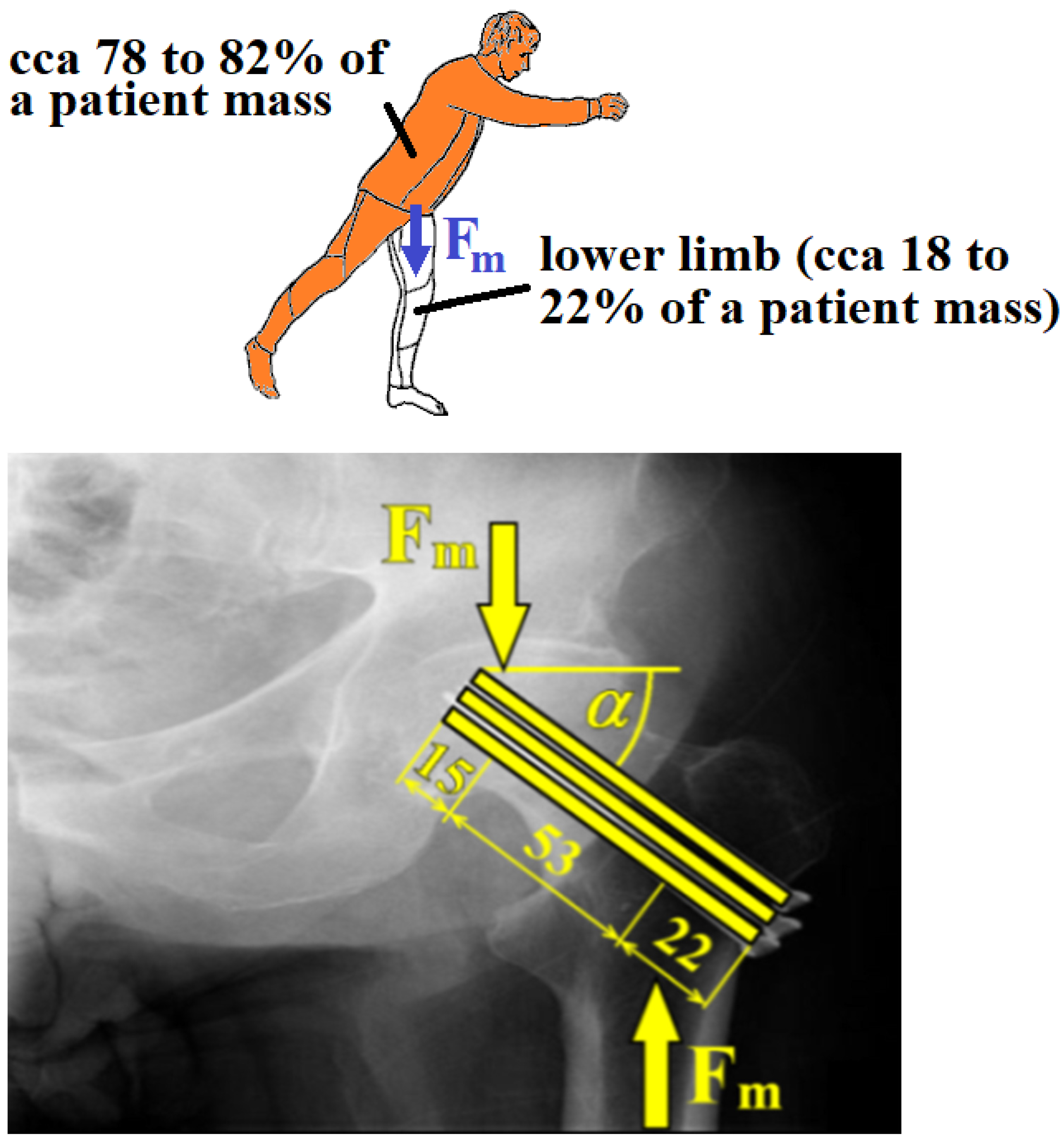
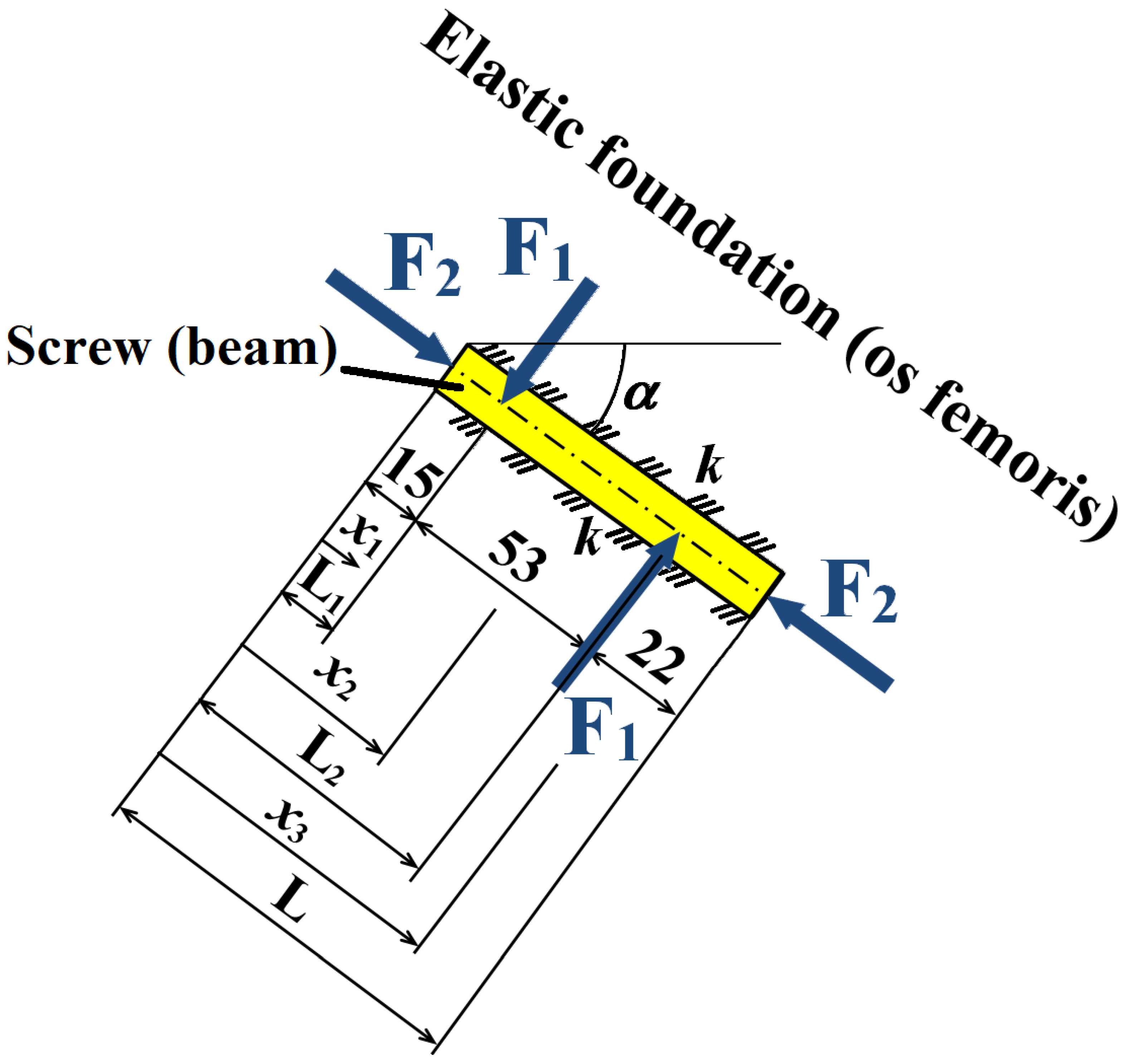
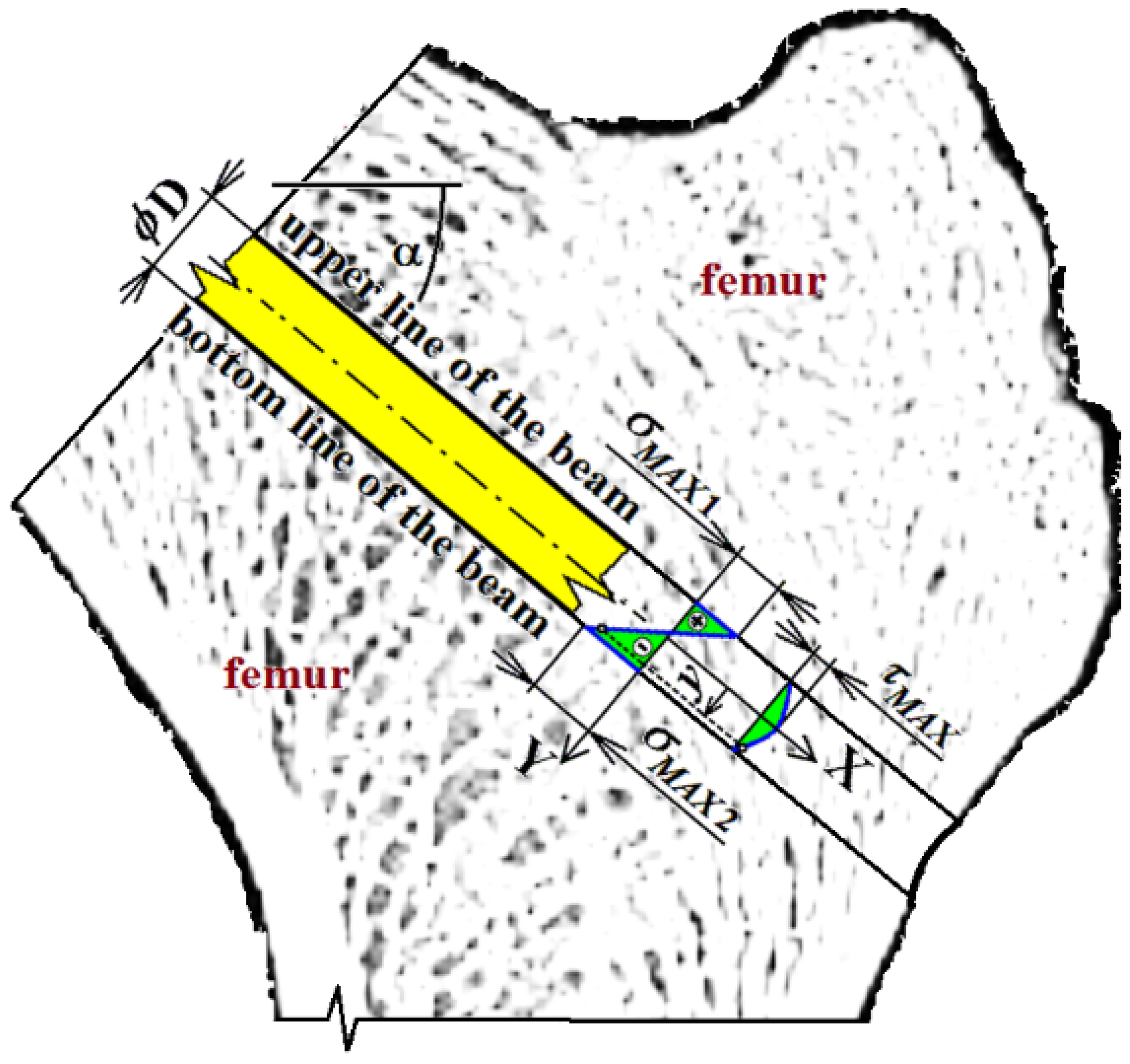
3. Materials and Methods
4. Probabilistic Inputs
5. Probabilistic Solution and Probabilistic Reliability Assessment
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| A1i, …, A4i, {A} | Integral constants and vector of integral constants (m). They are related to boundary conditions. |
| {B} | Vector of the left side (1) |
| D, d | Outer (shank) and inner (cannulation) diameter of cancellous screw (m) (input variables) |
| E | Elastic modulus of cancellous screw material (Pa) (input variable) |
| F | Quasi-dynamic force acting on one cancellous screw (N) |
| Fm | Total loading quasi-dynamic force acting in caput femoris (N) |
| F1, F2 | Tangential and axial force acting in one cancellous screw (N) |
| g | Gravitational acceleration (ms−2) (input variable) |
| i = 1, 2 and 3 | Index of a section of the cancellous screw |
| JZT | Principal quadratic moment of the cross-sectional area of cancellous screw (m4) |
| k | Elastic foundation stiffness, i.e., femoral bone stiffness (Nm−2) (input variable) |
| kdyn, km | Dynamic force and mass reduction coefficients (1) (input variables) |
| L, L1, L2 | Total length and local lengths of cancellous screws (m) (input variables) |
| [M] | Matrix of equations (1) |
| Moi, MoMAX | Internal bending moments in sections of the screw and the absolute value (Nm) of the maximal bending moment in the screw |
| m | Patient mass (kg) (input variable) |
| N | Internal normal (axial) force in the cancellous screw (N) |
| n | Coefficient of inequality in the division of force (F) (1) (input variable) |
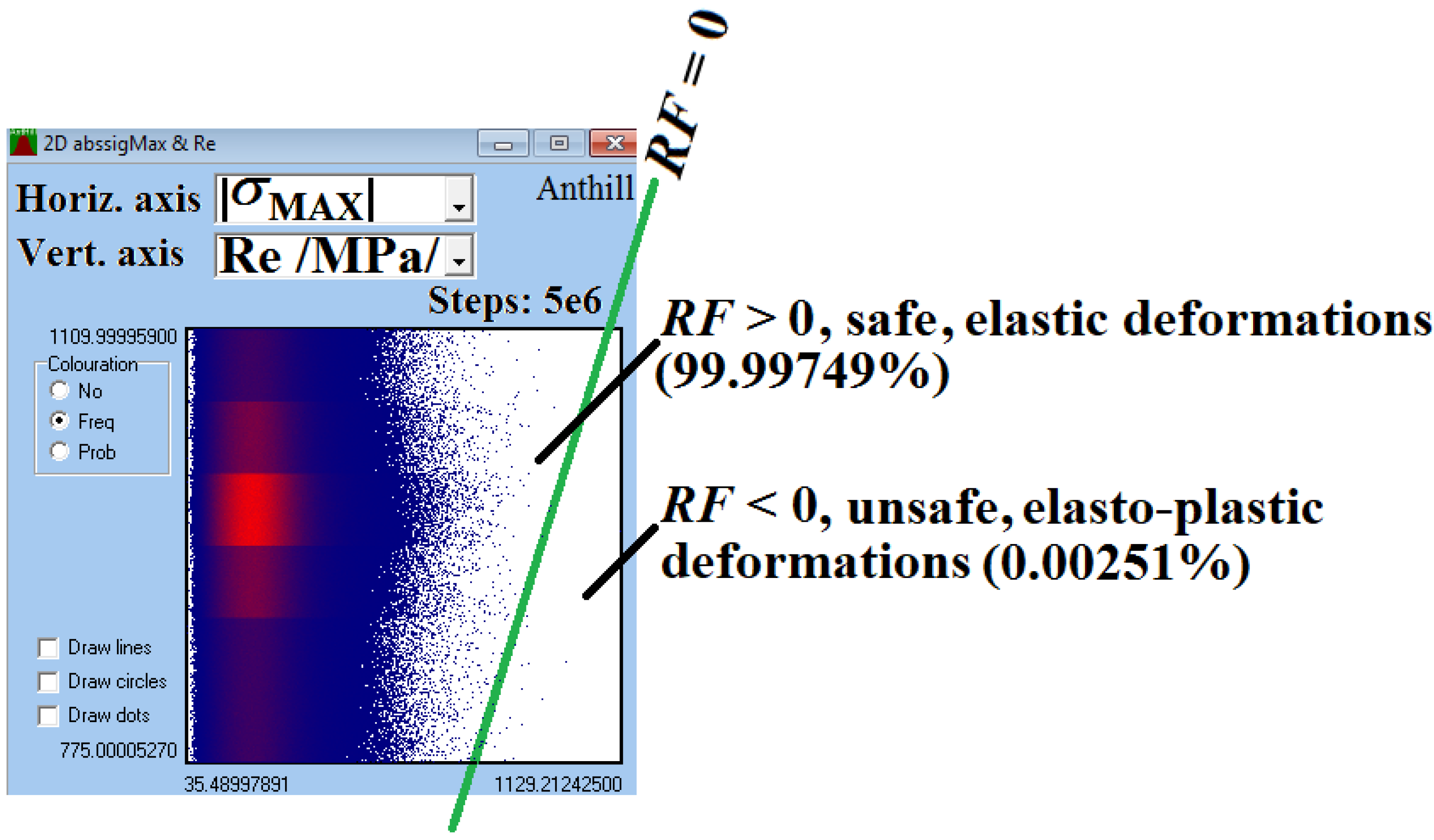
| PRF≤0 | Probability of biomechanical failure |
| Punsuccessful | Probability of unsuccessful treatment |
| PFN | Proximal femoral neck |
| Re | Yield stress of the material of cancellous screws (MPa) (input variable) |
| RF | Probabilistic (stochastic) reliability function (MPa) |
| Ti, TMAX | Internal shearing forces in sections of the cancellous screw and absolute value (N) of the maximal shearing force |
| vi, vMAX | Deflections (i.e., vertical displacements) in sections of the cancellous screw and their maximum (m) |
| Slope of the cancellous screw (rad) | |
| x1, x2, x3, xi | Cartesian coordinates in sections (m) |
| ∝ | Cancellous screw angle (deg)(input variable) |
| σMAX, σMAX1, σMAX2 | Global maximal and maximal normal mechanical stresses in the cancellous screw (MPa) |
| τMAX | Maximal shear mechanical stress in the cancellous screw (MPa) |
| ω, ωR, ωI | Parameters of the numerical solutions (m−1) |
References
- Frydrýšek, K.; Šír, M.; Pleva, L. Strength Analyses of Screws for Femoral Neck Fractures. J. Med. Biol. Eng. 2018, 38, 816–834. [Google Scholar] [CrossRef]
- Kellam, J.F.; Meinberg, E.G.; Agel, J.; Karam, M.D.; Roberts, C.S. Fracture and Dislocation Classification Compendium—2018. J. Orthop. Trauma 2018, 32 (Suppl. 1), S1–S10. [Google Scholar] [CrossRef]
- Shen, M.; Wang, C.; Chen, H.; Rui, Y.; Zhao, S. An update on the Pauwels classification. J. Orthop. Surg. Res. 2016, 11, 161. [Google Scholar] [CrossRef]
- Embden, D.V.; Rhemrev, S.J.; Genelin, F.; Meylaerts, S.A.G.; Roukema, G.R. The reliability of a simplified Garden classification for intracapsular hip fractures. Orthop. Traumatol. Surg. Res. 2012, 98, 405–408. [Google Scholar] [CrossRef]
- Bartoníček, J.; Džupa, V.; Skála-Rosenbaum, J.; Pazdírek, P. Femoral Neck Fractures of Adults—Summary, (Zlomeniny krčku femuru u dospělých- souhrnný referát). Úrazová Chir. 2003, 11, 10–23. [Google Scholar]
- Hawks, M.A.; Kim, H.; Strauss, J.E.; Oliphant, B.W.; Golden, R.D.; Hsieh, A.H.; Nascone, J.W.; O’Toole, R.V. Does a trochanteric lag screw improve fixation of vertically oriented femoral neck fractures? A Biomechanical Analysis in Cadaveric Bone. Clin. Biomech. 2013, 28, 886–891. [Google Scholar] [CrossRef] [PubMed]
- Leonard, M.; Alao, U.; Glynn, A.; Dolan, M. Hip fractures: Failure of fixation and outcome of salvage arthroplasty. Eur. J. Orthop. Surg. Traumatol. 2009, 19, 553–558. [Google Scholar] [CrossRef]
- Skála–Rosenbaum, J.; Bartoníček, J.; Říha, D.; Waldauf, P.; Džupa, V. Single-Centre Study of Hip Fractures in Prague, Czech Republic, 1997–2007. Int. Orthop. 2011, 35, 587–593. [Google Scholar] [CrossRef]
- Takano, E.; Ozaki, K.; Satoh, K.; Kawamura, K. Effects of a Balance Exercise Assist Robot on Older Patients with Hip Fracture: A Preliminary Study. J. Med. Biol. Eng. 2020, 40, 783–789. [Google Scholar] [CrossRef]
- Özkal, F.M.; Cakir, F.; Sensoz, E. Schematization of Cannulated Screw Fixations in Femoral Neck Fractures Using Genetic Algorithm and Finite Element Method. J. Med. Biol. Eng. 2020, 40, 673–687. [Google Scholar] [CrossRef]
- Frydrýšek, K.; Pleva, L.; Pompach, M.; Učeň, O.; Fojtík, F.; Kubín, T.; Theisz, G.; Žilka, L.; Poruba, Z. External and internal fixators for treatment of complicated fractures in traumatology and orthopaedics. In Engineering Mechanics 2014, 20th International Conference; University of Technology, Institute of Solid Mechanics, Mechatronics and Biomechanics: Brno, Czech Republic, 2014; pp. 180–183. [Google Scholar]
- Kubíček, J.; Tomanec, F.; Černý, M.; Vilímek, D.; Kalová, M.; Oczka, D. Recent Trends, Technical Concepts and Components of Computer-Assisted Orthopedic Surgery Systems: A Comprehensive Review. Sensor 2019, 19, 5199. [Google Scholar] [CrossRef] [PubMed]
- Bone Screws. MEDIN a.s. Available online: https://www.medin.cz/7--1 (accessed on 7 April 2021).
- Frydrýšek, K. Strength Analyses of Full and Cannulated Femoral Screws Made Up from Stainless Steel and Ti6Al4V, Calculation Report; Book, Department of Applied Mechanics, FME, VŠB-Technical University of Ostrava: Ostrava, Czech Republic, 2014; pp. 1–43. [Google Scholar]
- Li, J.; Wang, M.; Li, L.; Zhang, H.; Hao, M.; Li, C.; Han, L.; Zhou, J.; Wang, K. Finite element analysis of different configurations of fully threaded cannulated screw in the treatment of unstable femoral neck fractures. J. Orthop. Surg. Res. 2018, 13, 272. [Google Scholar] [CrossRef]
- Xia, Y.; Zhang, W.; Zhang, Z.; Wang, J.; Yan, L. Treatment of femoral neck fractures: Sliding hip screw or cannulated screws? A meta-analysis. J. Orthop. Surg. Res. 2021, 16, 54. [Google Scholar] [CrossRef] [PubMed]
- Začal, J.; Jančar, L. Effect of Temperature on Bolt WorkingLoad of Pressure Vessels. Current Methods of Construction Design, Lecture Notes in Mechanical Engineering; Springer: Cham, Switzerland, 2020. [Google Scholar] [CrossRef]
- Joszko, K.; Gzik, M.; Wolański, W.; Gzik-Zroska, B.; Kawlewska, E. Biomechanical evaluation of human lumbar spine in spondylolisthesis. J. Appl. Biomed. 2018, 16, 51–58. [Google Scholar] [CrossRef]
- Michenková, Š.; Frydrýšek, K.; Nikodým, M. Straight beams rested on nonlinear elastic foundations—Part 2 (numerical solutions, results and evaluation). Appl. Mech. Mater. 2014, 684, 21–29. [Google Scholar] [CrossRef]
- Morávkova, Z.; Tomečková, I.; Frydrýšek, K. Beam rested on unilateral elastic foundation—(Theory, experiments and finite element approach). In Proceedings of the 23rd International Conference on Engineering Mechanics 2017, Svratka, Czech Republic, 15–18 May 2017; pp. 670–673, ISBN 978-80-214-5497-2. [Google Scholar]
- Frydrýšek, K.; Tvrdá, K.; Jančo, R. Handbook of Structures on Elastic Foundation; VŠB—Technical University of Ostrava: Ostrava, Czech Republic, 2013; pp. 1–1691. ISBN 978-80-248-3238-8. [Google Scholar]
- Pérez-González, A.; Fenollosa-Esteve, C.; Sancho-Bru, J.L.; Sánchez-Marín, F.T.; Vergara, M.; Rodríguez-Cervantes, P.J. A modified elastic foundation contact model for application in 3D models of the prosthetic knee. Med. Eng. Phys. 2008, 30, 387–398. [Google Scholar] [CrossRef]
- Frydrýšek, K. Probabilistic approaches applied in the solution of problems in mining and biomechanics. In Proceedings of the 17th International Conference ENGINEERING MECHANICS 2011, Svratka, Czech Republic, 9–12 May 2011; pp. 151–154, ISBN 978-80-87012-33-8. [Google Scholar]
- Marek, P.; Brozetti, J.; Guštar, M.; Tikalsky, P. Probabilistic Assessment of Structures Using Monte Carlo Simulation, 2nd ed.; Institute of Theoretical and Applied Mechanics, Academy of Sciences of the Czech Republic: Prague, Czech Republic, 2003; pp. 1–471. ISBN 80-86246-08-6. [Google Scholar]
- Tvrdá, K. Foundation Plate on the Elastic Half-Space, Deterministic and Probabilistic Approach. In Proceedings of the Conference on Dynamics of Civil Engineering and Transport Structures and Wind Engineering Dyn-Wind’2017, MATEC Web of Conferences, Bratislava, Slovakia, 21–25 May 2017; Volume 107. no. 00058. Available online: https://www.matec-conferences.org/articles/matecconf/abs/2017/21/matecconf_dyn2017_00058/matecconf_dyn2017_00058.html (accessed on 7 April 2021). [CrossRef]
- Lokaj, A.; Vavrušová, K.; Rykalová, E. Application of Laboratory Tests Results of Dowel Joints in Cement-Splinter Boards VELOX into the Fully Probabilistic Methods (SBRA Method). Appl. Mech. Mater. 2012, 137, 95–99. [Google Scholar] [CrossRef]
- Le, T.D.; Lehner, P.; Konečný, P. Probabilistic modeling of chloride penetration with respect to concrete heterogeneity and epoxy-coating on the reinforcement. Materials 2019, 12, 4068. [Google Scholar] [CrossRef]
- Chen, X.L.; Yang, Q.H.; Ding, J.P. Mechanical Characterization of Beams on Tensionless Foundation Materials. Mater. Sci. Forum 2016, 867, 152–156. [Google Scholar] [CrossRef]
- Chen, X.L.; Tian, Z.; Ding, J.P. Mechanical Analysis of Three Kinds of Beams on Non-Linear Elastic Foundation. Mater. Sci. Forum 2016, 867, 147–151. [Google Scholar] [CrossRef]
- Famfulík, J.; Richtář, M.; Řehák, R.; Šmiraus, J.; Dresler, P.; Fusek, M.; Miková, J. Application of hardware reliability calculation procedures according to ISO 26262 standard. Qual. Reliab. Eng. Int. 2020, 36, 1822–1836. [Google Scholar] [CrossRef]
- Famfulík, J.; Miková, J.; Lanská, M.; Richtář, M. A stochastic model of the logistics actions required to ensure the availability of spare parts during maintenance of railway vehicles. Proc. Inst. Mech. Eng. Part F 2014, 228, 85–92. [Google Scholar] [CrossRef]
- Filipov, O. Biplane double-supported screw fixation (F-technique): A method of screw fixation at osteoporotic fractures of the femoral neck. Eur. J. Orthop. Surg. Traumatol. 2011, 21, 539–543. [Google Scholar] [CrossRef] [PubMed]
- Čada, R.; Frydrýšek, K.; Sejda, F.; Demel, J.; Pleva, L. Analysis of locking self-taping bone screws for angularly stable plates. J. Med. Biol. Eng. 2017, 37, 612–625. [Google Scholar] [CrossRef]
- Losertová, M.; Štamborská, M.; Lapin, J.; Mareš, V. Comparison of Deformation Behavior of 316L Stainless Steel and Ti6Al4V Alloy Applied in Traumatology. Metalurgija 2016, 55, 667–670. [Google Scholar]
- Engelhardt, L.; Niemeyer, F.; Christen, P.; Müller, R.; Stock, K.; Blauth, M.; Urban, K.; Ignatius, A.; Simon, U. Simulating Metaphyseal Fracture Healing in the Distal Radius. Biomechanics 2021, 1, 29–42. [Google Scholar] [CrossRef]
- Hrabovský, L. Tension force equalizer in a rope system using a proximity sensor. Sci. J. Sil. Univ. Technol. Ser. Transp. 2021, 110, 35–44. [Google Scholar] [CrossRef]
- Frydrýšek, K.; Jořenek, J.; Učeň, O.; Kubín, T.; Žilka, L.; Pleva, L. Design of External Fixators Used in Traumatology and Orthopaedics—Treatment of Fractures of Pelvis and its Acetabulum. Procedia Eng. 2012, 48, 164–173. [Google Scholar] [CrossRef][Green Version]
- Frydrýšek, K.; Michenková, S.; Pleva, L.; Koutecký, J.; Dědková, K.P.; Madeja, R.; Trefil, A.; Krpec, P.; Halo, T.; Hrabovský, L.; et al. Mechanics of Screw Joints Solved as Beams Placed in a Tangential Elastic Foundation. Appl. Sci. 2021, 11, 5616. [Google Scholar] [CrossRef]
- Murčinková, Z.; Adamčík, P.; Živčák, J. Re-Design of Machine Tool Joint Components Based on Polymer Fillings for High-Speed Performance. Materials 2021, 14, 6913. [Google Scholar] [CrossRef]

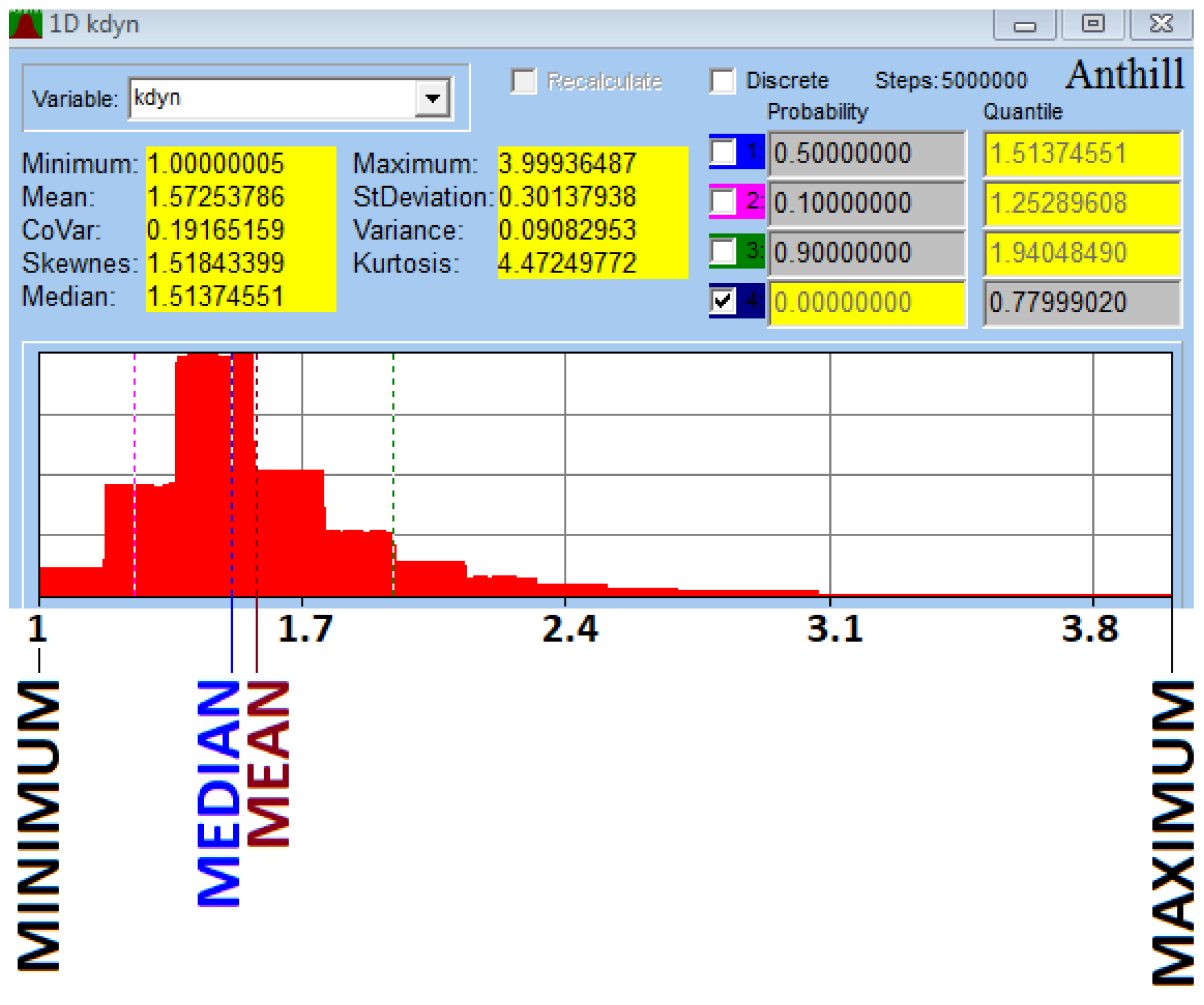


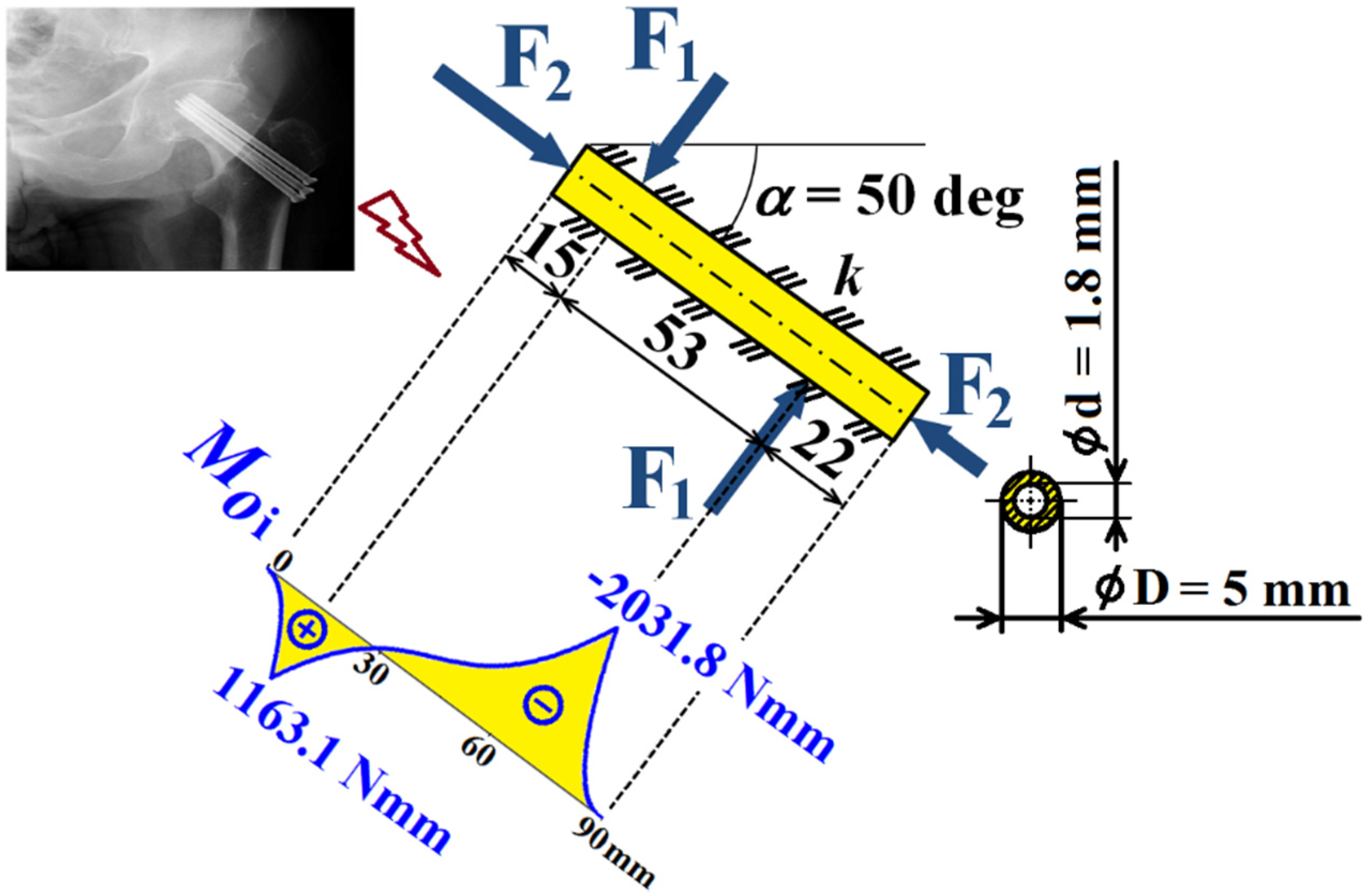

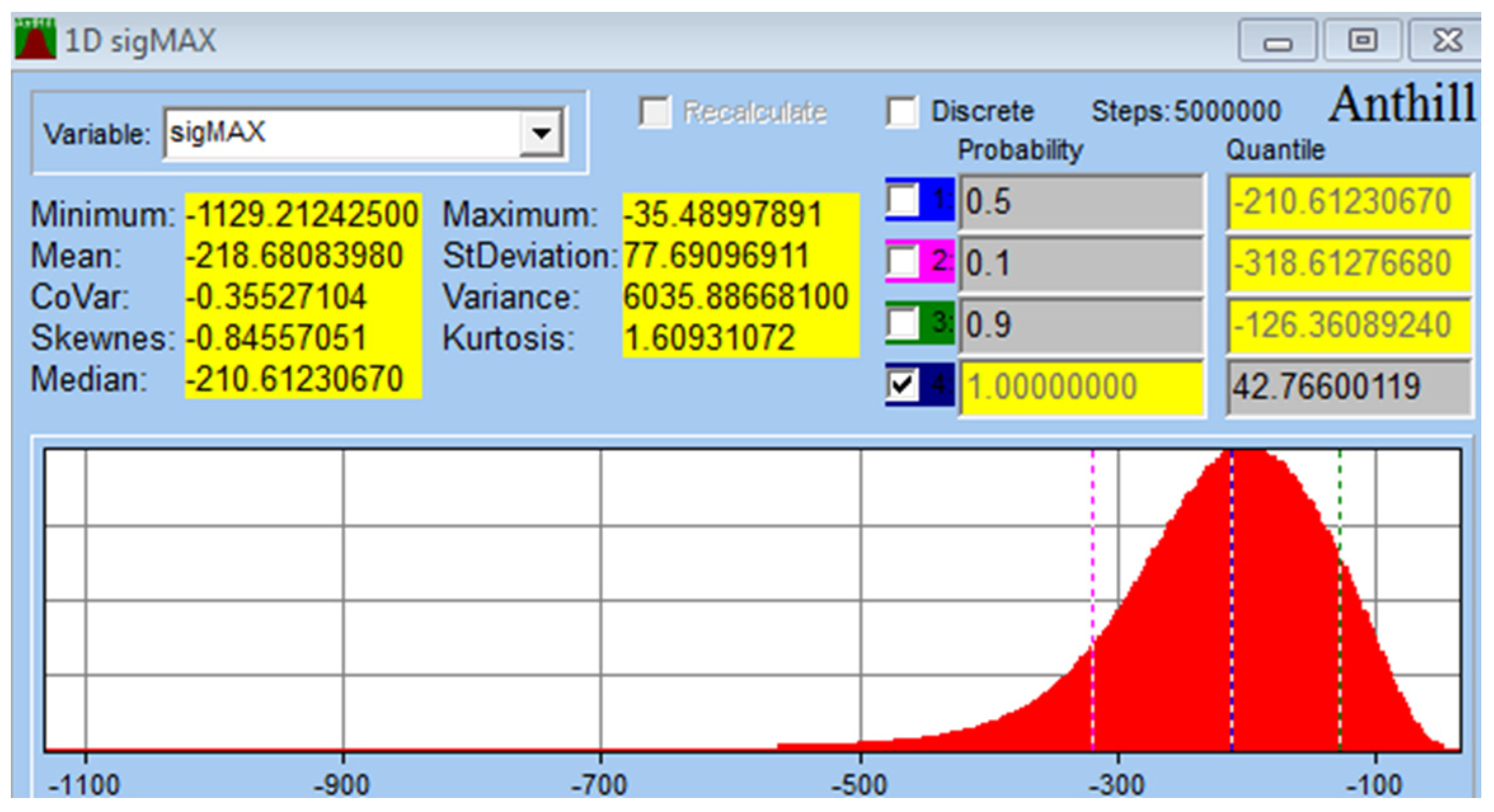
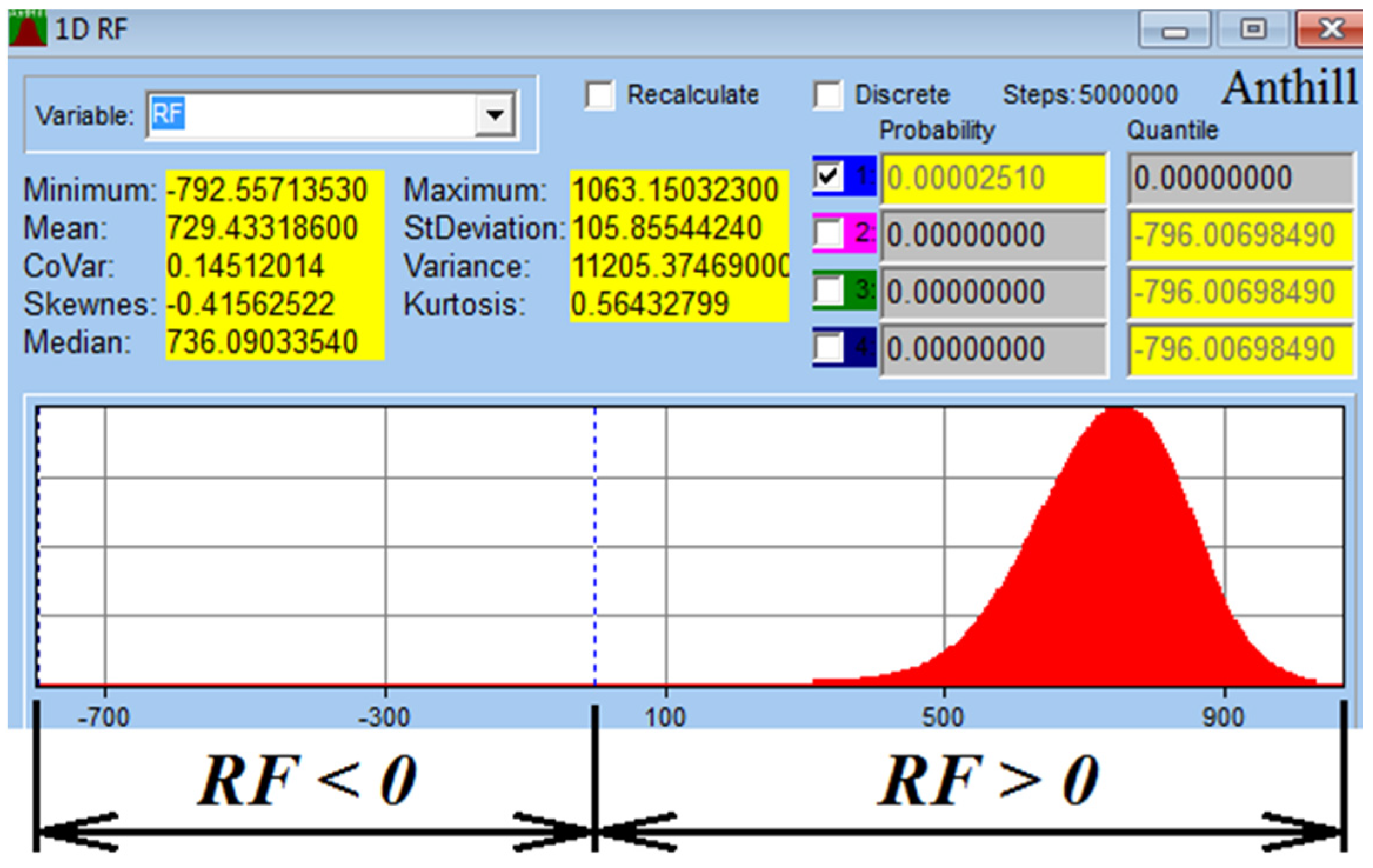


| Input Parameters (for Figure 7, Figure 8 and Figure 9) | D = 0.005 m, d = 0.0018 m, E = 2.1 × 1011 Pa, g = 9.807 ms−2, k = 2.2222 × 107 Pa, kdyn = 1.4, km = 0.814, L = 0.09 m, L1 = 0.015 m, m = 120 kg, L2 = 0.068 m, n = 3, Re = 103 MPa, ∝ = 50 deg |
| Input Variable | Minimum | Maximum | Mean | Median | Standard Deviation | Bounded (Truncated) Histogram |
|---|---|---|---|---|---|---|
| ∝/deg/ Cancellous screw angle | 5 | 80 | 45.94 | 46.71 | 16.45 |  |
| /kg/ Entire mass of a patient | 70 | 145 | 107.50 | 107.50 | 12.33 |  |
| /1/ Mass reduction coefficients | 0.78 | 0.82 | 0.80 | 0.80 | 6.57 × 10−3 | 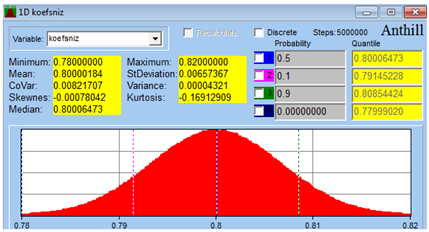 |
| /1/ Dynamic force coefficient | 1 | 4 | 1.57 | 1.51 | 0.301 | 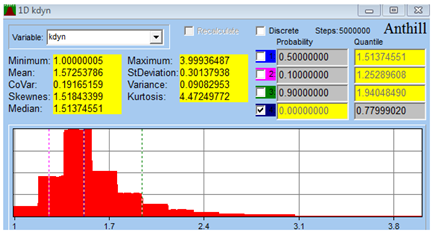 |
| n/1/ Coefficient of inequality in the division of force F | 2 | 3 | 2.5 | 2.5 | 0.289 | 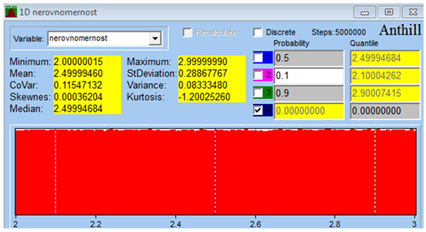 |
| /MPa/ Yield stress of Ti6Al4V material of cancellous screws | 775 | 1110 | 948.07 | 956.47 | 71.84 | 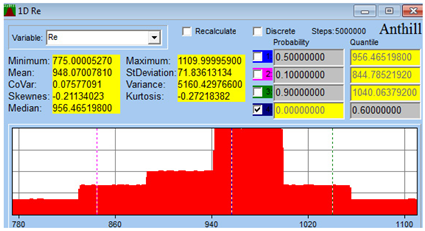 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frydrýšek, K.; Šír, M.; Pleva, L.; Szeliga, J.; Stránský, J.; Čepica, D.; Kratochvíl, J.; Koutecký, J.; Madeja, R.; Dědková, K.P.; et al. Stochastic Strength Analyses of Screws for Femoral Neck Fractures. Appl. Sci. 2022, 12, 1015. https://doi.org/10.3390/app12031015
Frydrýšek K, Šír M, Pleva L, Szeliga J, Stránský J, Čepica D, Kratochvíl J, Koutecký J, Madeja R, Dědková KP, et al. Stochastic Strength Analyses of Screws for Femoral Neck Fractures. Applied Sciences. 2022; 12(3):1015. https://doi.org/10.3390/app12031015
Chicago/Turabian StyleFrydrýšek, Karel, Milan Šír, Leopold Pleva, Jiří Szeliga, Jan Stránský, Daniel Čepica, Jiří Kratochvíl, Jan Koutecký, Roman Madeja, Kateřina Peterek Dědková, and et al. 2022. "Stochastic Strength Analyses of Screws for Femoral Neck Fractures" Applied Sciences 12, no. 3: 1015. https://doi.org/10.3390/app12031015
APA StyleFrydrýšek, K., Šír, M., Pleva, L., Szeliga, J., Stránský, J., Čepica, D., Kratochvíl, J., Koutecký, J., Madeja, R., Dědková, K. P., & Stančeková, D. (2022). Stochastic Strength Analyses of Screws for Femoral Neck Fractures. Applied Sciences, 12(3), 1015. https://doi.org/10.3390/app12031015







