Abstract
This paper presents a modified model for hand–eye calibration based on dual quaternion algebra. By using dual quaternions to represent the rotations and translations of a rigid body simultaneously in the task space, the formulation is elegant for the analysis of the hand–eye equation. The hand–eye transformation derived in this study is represented in a compact manner, which uses a combination of the dual part and the real part of the dual quaternion. Although the hand–eye equation can be solved by using six elements of a dual quaternion without using its scalar parts, the scaler numbers in both the real and dual parts of a dual quaternion contain part of the pose information. The originality is based on the derivation of the construct of the identification algorithm of external parameters of the camera by using all eight elements of a dual quaternion. Then, the data transformation between the cameras of the dual-arm hand–eye robot system is presented. The corresponding results demonstrate that the proposed hand–eye calibration algorithm can process measurement data with noise and can also improve the identification accuracy to verify its efficiency.
1. Introduction
Designing a robot system to operate like a human being requires mimicking the basic human ability of obtaining environmental information, and a camera can provide the vision function for the robot. For example, a medical robot system can provide an intraperitoneal view for doctors in order to perform minimally invasive medical surgery [1], and image-guided systems can form a material sorting system [2]. The robotic hand–eye system usually needs a calibration procedure which includes the determination of the internal and the external parameters of the camera. There are many different methods that can be adopted to solve hand–eye calibration problems in different application environments [3,4,5]. Most of these methods need the consideration of transformation constraints that contain the parameters of the camera and the characteristics of the corresponding pictures. The model of a hand–eye system can be established through known reference points or geometric features of the targets in view of the camera, and then, the equations can be solved by numerical methods or learning methods in order to identify the parameter values [6,7].
1.1. Brief Overview of the Hand–Eye Equation
Many previous studies have shown that the hand–eye calibration problem can be summarized as the solution of the equation AX = XB, such as the classic Faugeras method, Tsai’s two-step method, and Zhang Zhengyou’s calibration method [8,9,10]. In 1989, Shiu summarized the basic transformation equation among the camera coordinate, the world coordinate, and the end-effector coordinate. Since then, many other researchers have studied different ways to summarize this topic. Tsai and Lenz used Rodrigues’ formula to transform a rotation matrix into a rotation vector, and the calibration matrix could be solved by the geometric transformation algorithm but may have encountered the problem of pose singularity [11]. Malti proposed a robust way of solving the hand–eye equation, and it can be used for medical robots [12]. Shah used the Kronecker product to solve the hand–eye calibration problem in a convenient way [13]. Faugeras proposed a method to derive a linear model from the transformation matrix of the scene points and the coordinates in order to construct a combination of the internal and external parameters so that the results could be estimated by using the extended Kalman filter [14]. Tsai’s two-step method was proposed in 1987, and it considers radial distortion. This method can obtain some external parameters by using radial permutation constraints; then, the internal parameters and the remaining parameters can be obtained by solving the nonlinear equations [15]. Heller studied the properties of hand–eye and robot–world transformation matrixes and proposed an effective global polynomial optimization way to solve this problem [16]. Pachtrachai studied the remote centre of motion during a robot control procedure and presented a practical and effective method of hand–eye calibration to be applied in medical robots [17]. Zhang Zhengyou proposed the method of calculating the homography matrix from the image feature data of the target, and then, the parameters could be calculated by using the maximum likelihood estimation [18]. In 1989, Wei proposed a calibration method using blanking points in three-dimensional Euclidean space in the deduction and derived the direction information of blanking points in the projective space in order to solve the calibration equation; then, the camera parameters could be obtained by using the projective geometry [19]. Hartley and Faugeras proposed a self-calibration method for a hand–eye robot system without using specific targets and the information of robot motion in 1992. This method makes use of the conversion relationship between camera parameters and image data so that the parameter results can be obtained by nominal numerical methods [20,21]. In 1993, Basu and Du proposed an algorithm to derive the estimation solution of the internal and external parameters of the camera by using the rotation transformation of itself [22]. Wang studied the coupling factors of rotation and translation during the pose transformation of a hand–eye robot system and proposed an effective optimal calibration method for robot–world and hand–eye calibration [23].
1.2. Dual Quaternion Algebra and Hand–Eye Calibration
From a certain point of view, there are two forms of hand–eye robot systems, such as the eye-in-hand systems and the eye-to-hand systems. The difference between the two is whether the relative pose of the camera changes with the movement of the end-effector. Normally, the hand–eye calibration procedure contains the steps of extracting the pose information of image data from the camera coordinate to the robot coordinate. After hand–eye calibration, the robot system can transform image information extracted from the camera into the representation of that with respect to the base coordinate so that the robot operation can be processed into the motion control instruction of the system, which is expressed in a unified coordinate [24]. Moreover, based on the classification of the camera mode, the hand–eye system can also be divided into three types, such as monocular, binocular, and the multi-ocular. From another point of view, the main work of hand–eye calibration is to find the transformation matrix between the camera coordinate and the robot coordinate. Furthermore, the equivalence relationship of the basic transformation matrix can be deduced by analyzing the robot vision system as well. Chen studied dual quaternion algebra and proposed an effective regularization-patching optimization method for hand–eye calibration based on dual quaternion [25]. Huang and Wang studied the camera projection matrix by analyzing the constraints step by step in order to identify the internal and external parameters of the camera, and then, the corresponding transformation matrix could be obtained by using the quaternion algebra [26,27]. Park proposed an algorithm for analyzing the hand–eye equation by using the properties of the Euclidean groups; then, the equation could be decomposed based on the special orthogonal group SO(3) and the special Euclidean group SE(3) in Lie algebra so that the transformation matrix could also be solved by using multiple groups of the measured data and the least square method [28]. Furthermore, the nonlinear calibration equation could be established by collecting the information of the feature points among multiple images. The corresponding parametric results could be obtained by the optimization algorithm or the intelligent algorithm [29].
As mentioned above, early researchers such as Tsai and Shui have summarized the methods of hand–eye calibration to obtain the hand–eye equation which can be solved by traditional algorithms. More importantly. this can elicit more researchers to study a variety of specific ways that can also solve this problem [30,31]. Furthermore, most of these methods need the intrinsic parameters of the target in space and its image data in different directions in the camera view. Horaud and Dornaika used quaternions to represent the rotation variables and vectors to describe the displacement of an object in space, and then, the calibration results could be obtained by nominal nonlinear algorithms [28]. Chou and Kamel used quaternions to represent the pose transformation of the rigid body motion in space so that the rotation matrix and the displacement vector could be separated. Then, the corresponding identification model could be established and used for obtaining the calibration results [32]. However, the combination concept of quaternion and dual numbers, that is called dual quaternion, has been used repeatedly in robotics recently. Furthermore, dual quaternion algebra has its own calculating characteristics, and it is not similar to the homogeneous transformation, but also combines the characteristics of screw axes. This concept has been used as a mathematical tool to deal with robotic problems and is considered to be the most efficient and compact way of representing the transformations of a rigid body in coordinates [33,34]. This could be the main factor that the calibration problem in robotics can also be solved by using dual quaternion algebra. Zhongtao Fu presented an algorithm for calibrating the transformation parameters of robot–robot and tool–flange based on dual quaternions, simultaneously, and modified the accuracy of coordinate calibration in robot collaborative motion [35,36]. Daniilidis used dual quaternion algebra to decompose the constraint equation of the hand–eye rotation matrix and obtained the displacement matrix by using the characteristics of screw axes as well. Then, the classical numerical solution method, which is a singular-value decomposition, was used to obtain the corresponding identification results [14]. Furthermore, the method based on dual quaternion algebra can not only express the rotation and translation changes in a rigid body, simultaneously, but can also obtain more accurate calibration results. The identification method proposed by Daniilidis uses the characteristics of screw axes and a 6 × 1 dimensional matrix, which represents the rigid body in three-dimensional space. However, the two elements ignored in this method contain some information on the transformation matrix of hand–eye coordination, which means all of the eight elements should be analyzed for the complete pose information of transformation. More specifically, the corresponding dual quaternion can be integrated into an 8 × 1 dimensional matrix, and the scalar parts of the real part and the dual part may not be equivalent to zero always. The dual quaternion contains eight elements, and all of them can be calculated by its own algebra. Furthermore, it can be seen from the kinematic model of the hand–eye robot system that the scalar part of the real part of a dual quaternion does not belong to the null space, but the real number space, and the dual part does as well. The eight elements of a dual quaternion contain all of the information on the position and orientation of the rigid body in space. Most hand–eye calibration methods based on dual quaternion ignore the scalar parts of the real part and the dual part of the dual quaternion. Therefore, research on the calibration of hand–eye robot systems using eight elements of a dual quaternion should be carried out. Furthermore, the extrinsic parameters of the camera are the main consideration during hand–eye calibration [35]. In addition, this paper mainly considers the modified solution of hand–eye calibration based on dual quaternion, which provides full information on the transformation between the robot coordinate and the camera coordinate. Thus, the improved hand–eye calibration algorithm based on dual quaternion includes full information on the pose transformation. It can include considerations of the uncertainty of the pose representation of the camera relative to the robot in the hand–eye system, and a complete form of hand–eye calibration using dual quaternion is formed. This is very useful for constituting a robot visual system as well as vision savoring control in further studies.
In the rest of the paper, the full model for hand–eye calibration based on dual quaternion is presented in an explicit form. In addition, this paper is organized as follows: Section 2 briefly introduces the kinematic analysis of a dual-arm hand–eye robot based on dual quaternion and shows the derivation of the identification algorithm for each dual part and scalar part of the dual quaternion. Section 3 presents a computer simulation example of the corresponding algorithm. The hand–eye identification experiment is conducted on a dual-arm robot (the robot type is SDA5F) in Section 4. Section 5 concludes the paper.
2. Methodology
2.1. Kinematic Analysis of the Dual-Arm Hand–Eye Robot Based on Dual Quaternion
Generally speaking, there are two ways to set up the vision system of the hand–eye robot. More importantly, different hand–eye systems can be selected according to different operation tasks and control objectives. The first one is the eye-to-hand system, in which the camera is fixed near the workspace of the robot. In this kind of system, the relative pose between the camera and the end-effector of the robot is not fixed, so that the system can observe local image details. The second one is the eye-in-hand system, in which the camera is also fixed on the robot body. In this kind of system, the camera can follow the movement of the end-effector of the robot in the world coordinate. Even though different installation ways have different features, all of them have to determine the pose constraints among the world coordinate, the robot coordinate, the end-effector coordinate, the camera coordinate, and the picture coordinate, etc., so that the vision system can describe and express the target information using pictures in the three-dimensional space accurately.
Generally, the pictures captured by commercial cameras are corrected or compensated according to the internal parameters of the camera itself provided by the manufacturers. However, usually it is necessary to identify the external parameters of the camera in order to construct the transformation model between the corresponding coordinates in the hand–eye system. This paper mainly considers the identification of the external parameters of the camera, which is important in the hand–eye calibration procedure. The dual-arm robot contains two normal manipulators, and both of them share some common workspace, while the system has more flexible operation ability. The dual-arm robot can also use the vision system to acquire a picture of the external environment in order to expand the system function. For example, the vision system can acquire data on the moving object in order to derive the relative pose of that expressed in the robot coordinate for further control commands. As mentioned above, many papers have proposed effective methods to calibrate the constraint model of hand–eye systems so that the premise of the robot vision ability can be obtained for further development. In addition, among the classical hand–eye calibration solutions up to now, Tsai and Shui have summarized the methods and the procedure of that in order to obtain the equation AX = XB and also have studied the corresponding solutions earlier. In addition, Horn presented an online identification algorithm for the extrinsic parameters of the camera based on dual quaternion and solved the corresponding numerical equation by using the globally fast optimization method [34]. Pachtrachai presented a solution for the trocar limitation which may cause ill-conditioned constraints during the procedure of hand–eye calibration based on dual quaternion and solved the problem by using the Levenberg–Marquardt algorithm [7]. These subtle methods use the operational derivation of dual quaternion algebra but are also not the same as that presented by Daniilidis [14]. The main purpose of this section is to deduce the procedure of identifying the external parameters of the hand–eye equation by using the eight elements of the dual quaternion.
Assuming that, first, in the example of eye-to-hand systems, the camera is mounted near the base of the dual-arm robot, so that it mimics the human view, the relative position and orientation of the object or the end-effectors of the robot can be obtained from the image data.
For the general analysis, Figure 1 shows the example setup of the coordinate systems for a dual-arm robot equipped with two cameras. is the dual quaternion representation of the coordinate of camera 1 with respect to the coordinate of camera 2, is the dual quaternion representation of the robot coordinate with respect to the coordinate of camera 1, is the dual quaternion representation of the coordinate of camera 2 with respect to the robot coordinate , is the dual quaternion representation of the robot coordinate with respect to the end-effector coordinate of arm 1, is the dual quaternion representation of the robot coordinate with respect to the end-effector coordinate of arm 2, is the dual quaternion representation of the calibration plate of arm 1 with respect to the end-effector coordinate of arm 1, and is the dual quaternion representation of the calibration plate of arm 2 with respect to the end-effector coordinate of arm 2. These coordinates construct the hand–eye robot coordinate system.
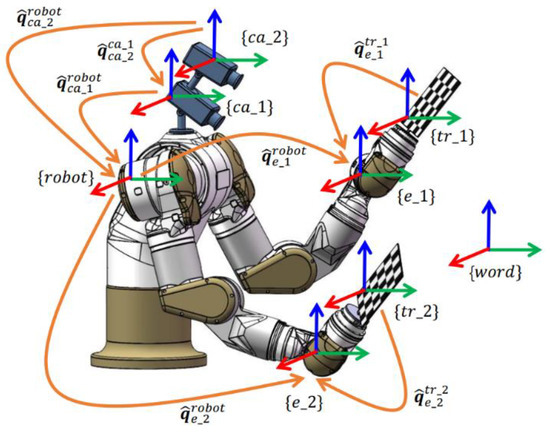
Figure 1.
Example setup of the coordinate systems in the dual-arm hand–eye calibration.
There are two cameras in Figure 1 in order to show the example of the relative transformation between the robot and different cameras, which capture pictures used by the dual-arm robot system. Two or more cameras can offer the robot system a greater range of visual perception, which can extend the functionality of the dual-arm robot in further usages. The procedure of hand–eye calibration not only requires the optical information, which is determined by the pictures, but also obtains the external parameters of the camera. Furthermore, it was necessary to determine the transformation model of the output from the nonlinear model, which was formed by the pixel coordinate of the picture in the two-dimensional sensor space and the world coordinate in the three-dimensional scene state. The pictures of the calibration board contain the information of that with respect to the system coordinates as the robot moved to different poses so that the constraints could be constructed from the data of multiple two-dimensional pictures, which were captured by the cameras, and the external parameters of the cameras could be obtained.
As Figure 1 is a dual-arm hand–eye robot system, it was necessary to perform a hand–eye calibration procedure on each of the two cameras and to construct the relative transformation between the two cameras. The equation of the two camera coordinates could be formed as:
Nevertheless, the hand–eye calibration of one end-effector and one camera should be carried out first. In general, one arm in the example shown in Figure 1 is chosen for further derivation. The relative pose constraint between the end-effector coordinate of the one arm and the other coordinate should mainly be considered. Two-dimensional hand–eye calibration boards with known geometric parameters were fixed to the end-effectors of the robot in Figure 1, and the cameras captured the different poses of the target as the robot’s arm pose changed.
According to the picture data of the calibration board, the constraint equation of the camera coordinate, the robot coordinate, and the end-effector coordinate could be established as:
where is the end-effector of arm 1 or arm 2, is the -frame picture of the calibration board, is camera 1 or camera 2, is the dual quaternion representation of the coordinate with respect to the end-effector coordinate , is the dual quaternion representation of the robot coordinate with respect to the end-effector coordinate , is the dual quaternion representation of the camera coordinate with respect to the robot coordinate , and is the dual quaternion representation of the coordinate with respect to the camera coordinate .
2.2. Identification Algorithm of Each Dual Part and Scalar Part of the Dual Quaternion
Using Equation (2) and the differences among different pictures, the following equations were obtained:
On the other hand, the homogeneous transformation matrixes , , and were directly converted into the corresponding dual quaternion forms by using the basic equation of the hand–eye calibration, and the similar form of the basic equation was obtained as:
where is the dual quaternion form of , is the dual quaternion form of , and is the dual quaternion form of .
Furthermore, there is the equation:
where is the matrix form of when it used left multiplication, is the matrix form of when it used right multiplication, is an dimensional matrix, and is an dimensional matrix.
The matrix can be written in a partitioned matrix form as:
The matrix can also be written in a partitioned matrix form as:
The first rows of , , and in Equation (7) do not belong to the zero vectors, and the scalar parts of the real and dual parts of in Equation (8) do not belong to the null space either. In addition, the matrix is not fully ranked so that the block matrices of and could be identified, respectively.
The formulas that were obtained from Equations (6)–(8) are:
It was necessary and convenient to solve Equation (9) using the singular-value decomposition (SVD) method first and then to obtain the real part result of the rotation information contained in the dual quaternion . The dual part of the dual quaternion includes the combination information of the rotation and the translation, and it is not an intuitive representation form of the position vector. Therefore, it was necessary to substitute the result of Equation (9) into Equation (10), and the dual result of was obtained by using the SVD method so that a complete representation of the identification result was formed finally.
In order to improve the accuracy and the precision of the calibration results, it was necessary to acquire data of multiple pictures in order to form a combined identification algorithm during the specific implementation procedure of the hand–eye calibration so that there would be equations expressed as follows:
where is the number of the measurement, and is the serial number of the -th picture.
Using the SVD method to identify Equations (11) and (12), successively, can obtain more reasonable results than that identified by using Equations (9) and (10). Furthermore, based on the dual quaternion , which is the camera coordinate with respect to the robot coordinate , the dual quaternion contains the same transformation information as the homogeneous transformation matrix of the actual robot system. Otherwise, the rotation angle and the translation value contained in the dual quaternion can represent the intuitive numerical meaning in the corresponding coordinate.
From the above analysis and derivation, the steps of the modified hand–eye calibration algorithm based on dual quaternion algebra can be concluded as follows: First, fix the two-dimensional calibration board at the end-effector of one arm, and use the camera to capture different poses of the board. Second, compute the real part of by using the SVD method to solve the combination of Equations (6) and (11). Third, compute the dual part of by using Equations (6) and (12) and the result of the second step. Therefore, complete the overall result of . After following these steps of the procedure, the relative transformation between the two cameras can be obtained by using Equation (1).
Furthermore, the dual-arm hand–eye robot system discussed in Figure 1 has two arms, and the relative position and orientation between the two end-effectors and the two cameras should be obtained in order to complete the procedure so that the kinematic equation of these two end-effectors and the corresponding two cameras can be written as:
From the discussion above, the modified hand–eye calibration for the dual-arm robot system based on dual quaternion can be summarized in Algorithm 1. In addition, an abbreviation is used to express the corresponding algorithm as MDQ, which means the modified hand–eye calibration using dual quaternion.
| Algorithm 1: Modified hand–eye calibration for the dual-arm robot system using dual quaternion |
| Input: The pictures captured by cameras; the poses data of end-effectors; the corresponding dual quaternions , . 1: Compute the real part and the dual part of based on Equations (6), (11), and (12). 2: initial the first solution in step 1; 3: while , do Form solution based on Equations (11) and (12); ; 4: Form kinematic equation of robot system based on Equations (15) and (16); end while Output: |
3. Simulation and Discussion
In this section, the initial observation data of the hand–eye robot are set in the simulation in order to verify the hand–eye calibration algorithm proposed above. This simulation was conducted on a model of the dual-arm hand–eye robot system, which contains a dual-arm robot SDA5F and two monocular cameras. Moreover, it was important to make the basic assumption that the eye-to-hand robot system in the simulation included one manipulator and one monocular camera typically.
Multiple sets of dual quaternions that represented the transformations between the robot base coordinate and the camera coordinate were set. The simulation data included the information of translation vectors and rotation angles of the camera coordinate with respect to the robot coordinate. Furthermore, the dual quaternions that contained the information on the measurement data of the corresponding hand–eye equation were set as random quantities at the same time. For the comparison, the method proposed by Lu in reference [21] was used to process the sets of the same data in this simulation. Furthermore, the norm values of the position were set in the range (50, 500) mm, and random noise was added in the angle data which was in the range (−0.01, 0.01). In general, the errors between the sets of the nominal pose data and the sets of the pose results that were obtained by the identification were greatly affected by interference. MATLAB was used for algorithm simulation and discussion using the Windows operating system in this part.
As a result, the quadratic norm of its position vector error was changed according to the quadratic norm of the nominal position vector in the simulation. In addition, the orientation error changed with the random characteristic to some extent.
Figure 2 shows the root mean square (RMS) relative errors in translation between the simulation results and the nominal values without noise interference, and the RMS errors in translation are less than 0.33 mm. Figure 3 shows the RMS errors in rotation between the simulation results and the nominal values without noise interference, and the RMS errors in rotation are less than 0.02 rad.
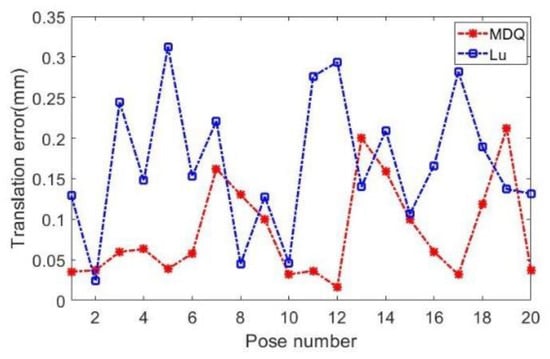
Figure 2.
The RMS errors in translation without noise interference.
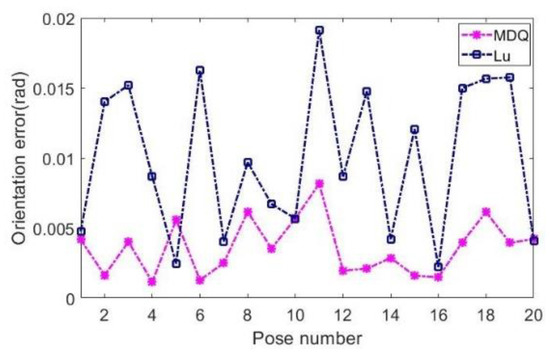
Figure 3.
The RMS errors in rotation without noise interference.
It can be seen from Figure 2 and Figure 3 that the results of the hand–eye calibration algorithm proposed in this paper are very close to the nominal values without interference. In addition, the results have a smaller error range compared with the method proposed by Lu mentioned in the reference [21].
Furthermore, Figure 4 shows the RMS relative errors in translation between the simulation results and the nominal values interfered with random noise, and the RMS errors in translation are less than 0.36 mm. Figure 5 shows the RMS errors in rotation between the simulation results and the nominal values interfered with random noise, and the RMS errors in rotation are less than 0.025 rad. It can be seen from Figure 4 and Figure 5 that the results obtained by the MDQ algorithm proposed in this paper have RMS relative errors in translation less than 0.23 mm and RMS errors in rotation less than 0.01 rad. The scales of the results of the simulation are small, and the MDQ algorithm has smaller errors than that. These results mean that the MDQ algorithm can also improve the anti-interference ability with respect to the compared method. Moreover, the simulation results can verify the effectiveness of the MDQ algorithm proposed in this paper.
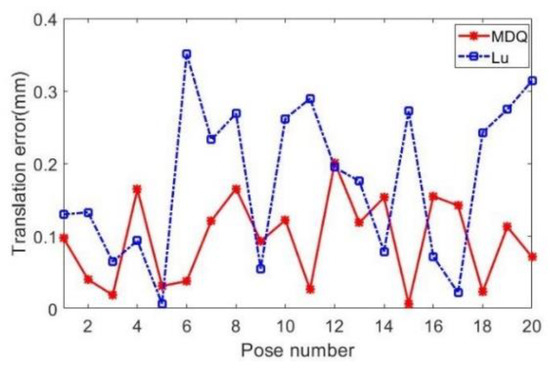
Figure 4.
The RMS errors in translation interfered with random noise.
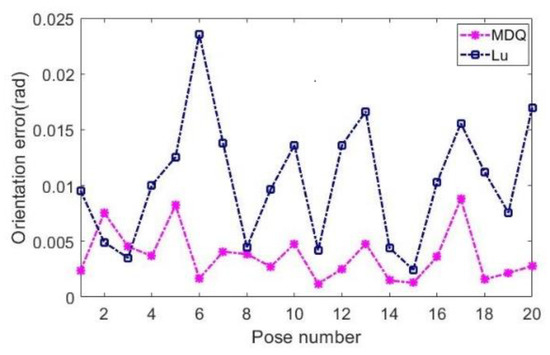
Figure 5.
The RMS errors in rotation interfered with random noise.
4. Experiment and Analysis
In order to further verify the hand–eye calibration algorithm described above, an experiment was conducted on a real dual-arm hand–eye robot system, which contains a dual-arm robot SDA5F and two monocular cameras.
The SDA5F is a kind of humanoid robot made by Yaskawa Electric for scientific research, and the two monocular cameras were used for mimicking the different views of a human being. Both of the cameras were calibrated in the experiment. As shown in Figure 6, the two cameras were fixed near the rotational axis of the dual-arm robot base, and both of them were monocular RGB cameras. Camera 1 looked up at an angle from the horizon plane in order to mimic the upward view of a human being, and camera 2 looked down at an angle from the horizontal plane in order to mimic the downward view of a human being.

Figure 6.
Setup of the two cameras in the dual-arm hand–eye robot system.
The two monocular cameras have the ability to sense the body, and the main properties of them are RGB image acquisition functions with adjustable frequencies. During the experiment, the software platforms were running in the Windows operating system, and C++ was used to carry out the secondary development of the robot control programs, including the hand–eye calibration and result analysis of the dual-arm robot. The model of the robot control cabinet is FS100, which is a type of processing center manufactured by Yaskawa Electric Co., Ltd. in Kitakyushu, Fukuoka, Japan. The control cabinet can connect to the PC in order to obtain the predetermined instructions from the host computer.
The hand–eye calibration algorithm proposed in this paper mainly considers the identification of the external parameters of the cameras and requires multiple pictures with the known two-dimensional board as the target.
Figure 7 shows the setup of the hand–eye calibration of the dual-arm hand–eye robot system during the experiment, and the external parameters of the two cameras were identified. Figure 7a shows the calibration setup of the left arm of the SDA5F robot and camera 1. Figure 7b shows the calibration setup of the right arm of the SDA5F robot and camera 2.

Figure 7.
Calibration of the dual-arm hand–eye robot system.
It is necessary to calibrate the two arms and cameras to describe them in a unified coordinate system at last. The data extracted from the pictures describe the movement of the target that is useful for further processing such that that the two-dimensional board is fixed at the end-effector of one arm of the dual-arm robot, and its orientation is close to that of the end-effector coordinate. Although the simulation of the MDQ algorithm proposed could obtain better results with added random noise, it is also affected by the accuracy of the poses or other factors which would be difficult to model in this experiment. Therefore, in order to make the adverse effects on the observed data as acceptable as possible, it was necessary to use a calibration board with a flat surface and a suitable accuracy so that more groups of experimental data for calibration could be collected and conveniently processed. In order to obtain better experimental results, approximately random poses of each end-effector were selected in different areas of the robot workspace. The cameras captured multiple sets of pictures and collected reasonable data. For the comparison, the same data were identified by the method mentioned in the reference [21]. The two arms of the dual-arm robot and the two cameras were calibrated in the experiment, and the results were processed with the same set of the measurements as the two arms have the same structure.
Figure 8 shows some pictures of the calibration board captured by the two cameras in the experiment, and each camera was calibrated separately.

Figure 8.
Some pictures captured by the cameras.
Figure 9 and Figure 10 show the results of the RMS errors in translation and rotation after hand–eye calibration by the two methods within the distance range of 1 m. Due to the measurement, position, and orientation errors of the end-effectors and other unmolded nonlinear factors, the experimental data are interfered and have more errors than that of the single-factor methods.
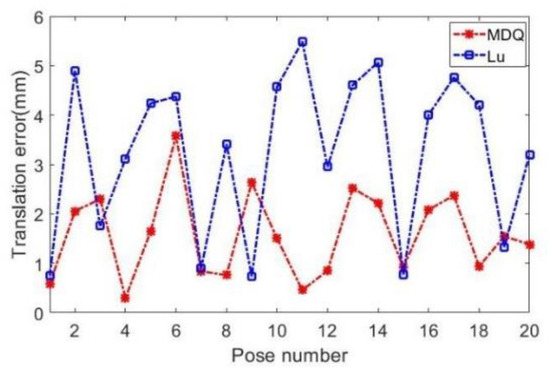
Figure 9.
Comparison of the RMS errors in translation of the calibration results.
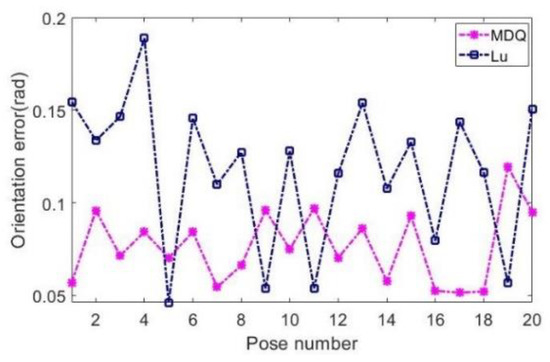
Figure 10.
Comparison of the RMS errors in rotation of the calibration results.
Otherwise, it can be seen from Figure 9 and Figure 10 that the actual effects are different from the results of the simulation above, but the results are still reasonable. As the scale and unit of the translation are different from the rotation, the threshold ranges of them are also different. It can be seen from the resulting curves in Figure 9 and Figure 10 that the RMS relative errors in translation using MDQ are within 3.7 mm. This means MDQ can obtain better results for translation during the hand–eye calibration in the real experiment. The RMS relative errors in rotation using MDQ are within 0.13 rad. This means MDQ can obtain better results for rotation during the hand–eye calibration in the real experiment. After the steps of the hand–eye calibration for each camera and each arm, the relative pose data of the arbitrary target captured by one camera can be transformed to the other camera by using Equation (15) or Equation (16). The calibration procedure was repeated several times, and the last results of the linear offsets of camera 1 along the x, y, and z axes were 24.51, 9.67, and 45.32, respectively, in millimeters; the rotational offsets of camera 1 along the x, y, and z axes are 0.005, 0.062 and 0.003, respectively, in rad. The last results of the linear offsets of camera 2 along the x, y, and z axes are 34.92, 11.86, and 463.75, respectively, in millimeters; the rotational offsets of camera 1 along the x, y, and z axes are 0.006, 0.102, and 0.007, respectively, in rad. Moreover, Figure 11 shows the test of the movement after the hand–eye calibration of the dual-arm robot, which can be used in real applications and in further studies using a robot to hit a Ping-Pong ball.

Figure 11.
The test of the movement after the hand–eye calibration of the dual-arm robot.
The full procedure of the dual-arm hand–eye calibration was completed and was necessary for further applications of the dual-arm robot. The comparison between the two methods shows that the MDQ algorithm has a better performance than the reference one, which means the effectiveness of the MDQ algorithm proposed in this paper can be illustrated.
5. Conclusions
Based on the analysis of the hand–eye equation, a modified hand–eye calibration algorithm based on a dual quaternion was proposed. A modified identification matrix and the steps derived from the hand–eye equation for identifying the external parameters of the camera were presented. The simulation task, summarized in MATLAB, was performed to deal with the comparison of this modified algorithm and the other algorithm. The real hand–eye calibration experiment was carried out on a dual-arm robot, and the data of the calibration plate were measured by the real cameras and were calculated for the comparisons. The corresponding calibration algorithm for the dual-arm hand–eye robot system was also constructed, and it can deal with the problem of data transformation between the two cameras. Meanwhile, the results of the simulation and experiment show that this algorithm considers the scalar parts of the real part and the dual part of the dual quaternion, and it can obtain more accurate results. Furthermore, the corresponding calibration results of the simulation and experiment were improved by the proposed algorithm, and it could be the modified solution for the hand–eye calibration problem based on dual quaternion.
Author Contributions
G.L. designed this study, supervised and led the experimental process, and wrote the original draft; S.Z. reviewed and revised the manuscript and provided funding for the experiments; S.D. surveyed the background of this research; B.Q. collected and analyzed the experimental data. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Director Foundation of Guangxi Key Laboratory of Automatic Detection Technology and Instrument (Grant No. YQ21110).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, Z. Estimating Motion and Structure from Correspondences of Line Segments Between Two Perspective Images. In Proceedings of the IEEE International Conference on Computer Vision, Cambridge, MA, USA, 20–23 June 1995; pp. 257–262. [Google Scholar]
- Olagoke, A.S.; Ibrahim, H.; Teoh, S.S. Literature Survey on Multi-Camera System and Its Application. IEEE Access 2020, 8, 172892–172922. [Google Scholar] [CrossRef]
- Li, H.; Ma, Q.; Wang, T.; Chirikjian, G.S. Simultaneous Hand-Eye and Robot-World Calibration by Solving the AX = YB Problem Without Correspondence. IEEE Robot. Autom. Lett. 2016, 1, 145–152. [Google Scholar] [CrossRef]
- Pan, H.; Wang, N.L.; Qin, Y.S. A closed-form solution to eye-to-hand calibration towards visual grasping. Ind. Robot Int. J. 2014, 41, 567–574. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, X.; Wen, K.; Zhou, Y.; Yue, Y.; Yang, J. A simple and rapid calibration methodology for industrial robot based on geometric constraint and two-step error. Ind. Robot Int. J. 2018, 45, 715–721. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Song, H. Simultaneous robot–world and hand–eye calibration based on a pair of dual equations. Measurement 2021, 181, 109623. [Google Scholar] [CrossRef]
- Pachtrachai, K.; Vasconcelos, F.; Edwards, P.; Stoyanov, D. Learning to Calibrate—Estimating the Hand-eye Transformation Without Calibration Objects. IEEE Robot. Autom. Lett. 2021, 6, 7309–7316. [Google Scholar] [CrossRef]
- Zhao, Z. Simultaneous robot-world and hand-eye calibration by the alternative linear programming. Pattern Recognit. Lett. 2019, 127, 174–180. [Google Scholar] [CrossRef]
- Zhang, Y.; Qiu, Z.; Zhang, X. A Simultaneous Optimization Method of Calibration and Measurement for a Typical Hand–Eye Positioning System. IEEE Trans. Instrum. Meas. 2021, 70, 5002111. [Google Scholar] [CrossRef]
- Pedrosa, E.; Oliveira, M.; Lau, N.; Santos, V. A General Approach to Hand–Eye Calibration Through the Optimization of Atomic Transformations. IEEE Robot. Autom. Lett. 2021, 37, 1619–1633. [Google Scholar] [CrossRef]
- Peters, A.; Schmidt, A.; Knoll, A.C. Extrinsic Calibration of an Eye-In-Hand 2D LiDAR Sensor in Unstructured Environments Using ICP. IEEE Robot. Autom. Lett. 2020, 5, 929–936. [Google Scholar] [CrossRef]
- Abed, M.; Barreto, J.P. Robust hand-eye calibration for computer aided medical endoscopy. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation, Anchorage, AK, USA, 3–7 May 2010; pp. 5543–5549. [Google Scholar]
- Mili, S. Solving the robot-world/hand-eye calibration problem using the Kronecker product. J. Mech. Robot. 2013, 5, 031007. [Google Scholar]
- Maybank, S.J.; Faugeras, O.D. A theory of self-calibration of a moving camera. Int. J. Comput. Vis. 1992, 8, 123–151. [Google Scholar] [CrossRef]
- Chen, E.C.; Morgan, I.; Jayarathne, U.; Ma, B.; Peters, T.M. Hand-eye calibration using a target registration error model. Healthc. Technol. Lett. 2017, 4, 157–162. [Google Scholar] [CrossRef] [PubMed]
- Jan, H.; Henrion, D.; Pajdla, T. Hand-eye and robot-world calibration by global polynomial optimization. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 3157–3164. [Google Scholar]
- Pachtrachai, K.; Vasconcelos, F.; Dwyer, G.; Hailes, S.; Stoyanov, D. Hand-eye calibration with a remote centre of motion. IEEE Robot. Autom. Lett. 2019, 4, 3121–3128. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 22, 1330–1334. [Google Scholar] [CrossRef]
- Wei, G.; Ma, S. Camera Calibration by Vanishing Point and Cross Ratio. Int. Conf. Acoust. Speech Signal Process. 1989, 3, 1630–1633. [Google Scholar]
- Boudine, B.; Kramm, S.; El Akkad, N.; Bensrhair, A.; Saaidi, A.; Satori, K. A flexible technique based on fundamental matrix for camera self-calibration with variable intrinsic parameters from two views. J. Vis. Commun. Image Represent. 2016, 39, 40–50. [Google Scholar] [CrossRef]
- Zou, Y.; Chen, X. Hand–eye calibration of arc welding robot and laser vision sensor through semidefinite programming. Ind. Robot Int. J. 2018, 45, 597–610. [Google Scholar] [CrossRef]
- Faraji, M.; Basu, A. Simplified Active Calibration. Image Vis. Comput. 2019, 91, 103799. [Google Scholar] [CrossRef]
- Xiao, W.; Song, H. Optimal robot-world and hand-eye calibration with rotation and translation coupling. Robotica 2022, 40, 1–16. [Google Scholar]
- Li, J.; Liu, F.; Liu, S.; Wang, Z. Optical Remote Sensor Calibration Using Micromachined Multiplexing Optical Focal Planes. IEEE Sens. J. 2017, 17, 1663–1672. [Google Scholar]
- Chen, Z.; Lin, C.; Qi, L.; Yan, H. A regularization-patching dual quaternion optimization method for solving the hand-eye calibration problem. arXiv 2022, arXiv:2209.07870. [Google Scholar]
- Grossmann, B.; Krüger, V. Continuous hand-eye calibration using 3D points. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics (INDIN), Emden, Germany, 24–26 July 2017; pp. 311–318. [Google Scholar]
- Xiao, W.; Huang, J.; Song, H. Robot-world and hand–eye calibration based on quaternion: A new method and an extension of classic methods, with their comparisons. Mech. Mach. Theory 2023, 179, 105127. [Google Scholar]
- Radu, H.; Dornaika, F. Hand-eye calibration. Int. J. Robot. Res. 1995, 14, 195–210. [Google Scholar]
- Park, F.C.; Martin, B.J. Robot sensor calibration: Solving AX = XB on the Euclidean group. IEEE Trans. Robot. Autom. 1994, 10, 717–721. [Google Scholar] [CrossRef]
- Yan, M.; Li, A.; Kalakrishnan, M.; Pastor, P. Learning Probabilistic Multi-Modal Actor Models for Vision-Based Robotic Grasping. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 4804–4810. [Google Scholar]
- Basu, A. Active Calibration: Alternative Strategy and Analysis. In Proceedings of the Computer Vision and Pattern Recognition, New York, NY, USA, 15–17 June 1993; pp. 495–500. [Google Scholar]
- Bai, Y.; Wang, D. On the Comparison of Fuzzy Interpolations and Neural Network Fitting Functions in Modeless Robot Calibrations. In Proceedings of the 2019 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), New Orleans, LA, USA, 23–26 June 2019; pp. 1–6. [Google Scholar]
- Deniz, C.; Cakir, M. A solution to the hand-eye calibration in the manner of the absolute orientation problem. Ind. Robot Int. J. 2018, 45, 64–77. [Google Scholar] [CrossRef]
- Horn, M.; Wodtko, T.; Buchholz, M.; Dietmayer, K. Online Extrinsic Calibration Based on Per-Sensor Ego-Motion Using Dual Quaternions. IEEE Robot. Autom. Lett. 2021, 6, 982–989. [Google Scholar] [CrossRef]
- Adorno, B.V.; Marinho, M.M. DQ Robotics: A Library for Robot Modeling and Control. IEEE Robot. Autom. Mag. 2021, 28, 102–116. [Google Scholar] [CrossRef]
- Fu, Z.; Pan, J.; Spyrakos-Papastavridis, E.; Chen, X.; Li, M. A Dual Quaternion-Based Approach for Coordinate Calibration of Dual Robots in Collaborative Motion. IEEE Robot. Autom. Lett. 2020, 5, 4086–4093. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).