Abstract
The size of datasets is growing exponentially as information technology advances, and it is becoming more and more crucial to provide efficient learning algorithms for neural networks to handle massive amounts of data. Due to their potential for handling huge datasets, feed-forward neural networks with random weights (FNNRWs) have drawn a lot of attention. In this paper, we introduced an efficient feed-forward neural network scheme (FNNS) for processing massive datasets with random weights. The FNNS divides large-scale data into subsets of the same size, and each subset derives the corresponding submodel. According to the activation function, the optimal range of input weights and biases is calculated. The input weight and biases are randomly generated in this range, and the iterative scheme is used to evaluate the output weight. The MNIST dataset was used as the basis for experiments. The experimental results demonstrate that the algorithm has a promising future in processing massive datasets.
1. Introduction
Feed-forward neural networks (FNNs) have gained increasing attention in recent years because of their flexible structural design and strong representational capacity. Feed-forward neural networks [1], which have adaptive characteristics and universal approximation characteristics, have been widely used in regression and classification. In addition, they offers study models for a wide range of natural and artificial processes, and it has been used in numerous technical and scientific domains [2]. In the traditional neural network theory, all the parameters of FNNs, such as input weight, bias, and output weight, need to be adjusted under specific conditions. The hierarchy of the network structure, however, makes this process complex and ineffective. The usual method is a gradient-based optimization method, such as the BP algorithm, but this method usually has some problems such as local minimum, slow convergence speed, sensitive learning speed, and so on. In addition, some parameters, such as the hidden node count or the learning algorithm parameters, need to be manually adjusted. In order to solve this series of problems, as the times require, Schmidt, Kraaijveld, and Duin first proposed the FNNRW in 1992 [3]. The output weights may be evaluated and estimated using the well-known least-square approach since the input weights and biases’ random distribution are uniformly distributed in [−1, 1]. Many simulation results in the literature show that the randomization model has higher performance than the fully adaptive model, and provides simpler implementation and faster training speed [4].
Theoretically, it is clear that the capability of global approximation cannot be guaranteed by the random distribution of input weights and biases [5,6]. For a variety of reasons, many random learning algorithms emerge endlessly. Ref. [7] suggested a feed-forward neural network learning method with random weights. Ref. [8] studied the sparse algorithm of random weight networks and its applications. Ref. [9] presented a random single hidden layer feed-forward neural network metaheuristic optimization research. The authors of [10] carried out a study on distributed learning of random vector function chain networks. Ref. [11] proposed a probability learning algorithm based on a random weight neural network for robust modeling.
In addition, Ref. [12] provided a complete discussion of the randomization method of neural networks. In order to ensure the universal approximation property, the development of neural network randomization methods is promoted for the constraints of random weights and biases [13]. However, data are in a period of rapid expansion due to the ongoing advancement of information technology. The resulting problem is that the number of data samples or neural network hidden layer nodes in the NNRW model becomes very large so the method of calculating the output weight is very time-consuming. In response to this problem, there have been many studies on large-scale data modeling problems in the past few decades. Ref. [14] explained how to efficiently train language models using neural networks on big datasets. Ref. [15] provided a kernel framework for energy-efficient large-scale classification and data modeling. Ref. [16] examined a population density method that makes large-scale neural network modeling possible. Ref. [17] presented a framework for parallel computing to train massive neural networks. Ref. [18] presented a multiprocessor computer for simulating neural networks on a huge scale. Reducing the size of the datasets by subsampling is perhaps the easiest method for dealing with enormous datasets. Osuna E, Freund R, and Girosi F were the first to suggest using this decomposition technique [19,20]. Bao-Liang Lu and Ito, M. (1999) also proposed this method [21], which is used to solve the problem of pattern classification. However, the method used for large-scale data processing in this paper is similar to the method of dealing with large-scale data by the Bayesian committee SVM proposed by Tresp et al. [22,23]. In this approach, the datasets are split into equal-sized parts, and models are generated from each subset. Each submodel is trained independently, and a summary is used to get the final determination.
This study examines a feed-forward neural network model for big datasets that uses random weights and a decomposition approach. In this study, the data were divided into tiny subsets of the same size at random, and each subset was then utilized to generate the associated submodel. The weights and biases of the hidden nodes that determine the nonlinear feature mapping are set randomly and are not learned in the feed-forward neural network with random weights. It is crucial to pick the right interval when selecting the weights and deviations. This topic has not been fully discussed in many studies. The method used in this paper calculates the optimal range of input weights and biases according to the activation function, and each submodel initializes the same input weight and biases within the optimal range. At the same time, an iterative scheme is adopted to evaluate the output weight.
The rest of this article is divided into the following sections. Section 1 introduces the traditional random weight feed-forward neural network learning algorithm. Section 2 details the work related to this paper. Section 3 describes in detail the optimized random weight feed-forward neural network learning algorithm proposed in this paper. In Section 4, the experimental simulation results are shown, the algorithm’s performance is examined and appraised, and the possibility of an engineering application is discussed. In Section 4, the experimental simulation results are given, and the performance of the algorithm is analyzed and evaluated, as well as the prospect of engineering applications. Section 5 is the conclusion of this paper and the planning for the future work.
2. The Related Work
This section introduces the development of feed-forward neural networks (FNN) and related works. This paper first discusses the history of artificial neural networks (ANNS) and the use of feed-forward neural networks in real-world applications. It next discusses random weight feed-forward neural networks, their optimization, and ultimately our optimization strategy. This paper first introduces the origin of artificial neural networks (ANNS) and the practical application of feed-forward neural networks, then introduces the optimization and application of random weight feed-forward neural networks, and finally presents our optimization scheme.
An artificial neural network (ANN), also referred to as a neural network (NN), is a mathematical model of hierarchically distributed information processing by imitating the behavior characteristics of animal brain neural network [24], through the relationship between various neurons, mainly by regulating the relationship between a large number of internal nodes, to achieve the purpose of data processing [25]. The logician W. Pitts and psychologist W.S. Macculloch created the mathematical MP models and neural networks in 1943. The age of artificial neural network research began when they proposed the formal mathematical description of neurons and the network structure approach through the MP model, and demonstrated that a single neuron can carry out logical functions [26]. Artificial neural networks have many model structures, and feed-forward neural networks are only one of them [27].
Frank Rosenblatt created the perceptron, an artificial neural network, in 1957. The perceptron is a simple neural network in which each neuron is arranged in layers and is only connected to the previous layer. The output of the previous layer is received and exported to the next layer, and there is no feedback between neurons in each layer. This is the earliest form of a feed-forward neural network (FNN). The feed-forward neural network is one of the most popular and rapidly evolving artificial neural networks due to its straightforward construction. The study of feed-forward neural networks started in the 1960s, and both theoretical and practical advancements have been made. The FNN can be regarded as a multilayer perceptron. With all the links between layer and layer, it is a kind of typical deep learning model. The performance of the traditional model, with large data samples and outstanding performance, can solve the problems that some traditional machine learning models cannot understand. However, deep learning models with small data samples are complex, making the process difficult to explain. The FNN also shares these characteristics, so it is mainly used in scenarios with large datasets. A feed-forward neural network-based approach for creating rocket trajectories online is presented in [28], and the trajectory is roughly estimated utilizing the neural network’s nonlinear mapping capability. In [29], the study of source term inversion of nuclear accidents uses deep feed-forward based neural networks. The Bayesian MCMC technique is used to examine the DFNN’s prediction uncertainty when the input parameters are unclear. In [30], with the chaotic encryption of the polarization division multiplexing OFDM/OQAM system, the feed-forward neural network is used to increase data transmission security and realize a huge key space. In [31], a feed-forward backpropagation artificial neural network is used to predict the force response of linear structures, which helps researchers understand the mechanical response properties of complex joints with special nonlinearities. In [32], the initial weight approach and the construction algorithm are combined to form a novel method of feed-forward neural network multi-class classification that can achieve high success rates. In [33], hybrid MVO and FNN were improved for fault identification of WSN cluster head data. It is clear that feed-forward neural networks are used in a variety of industries.
Feed-forward neural networks demonstrate the superiority of mathematical models in a variety of applications, but as the size of the dataset keeps growing, the feed-forward neural network’s original performance cannot keep up with the demands of engineering. As a result, many researchers have focused on developing improved feed-forward neural networks to deal with large-scale datasets. The feed-forward neural network is optimized primarily from two aspects: on the one hand, random weighting by weight set in selected is used to enhance the performance of the algorithm, as mentioned in [33,34,35,36,37]; on the other hand, large datasets are processed by using the method of sample selection, as described in [38,39], in order to enhance the algorithm’s performance. The method of random weight optimization is commonly used by scholars. Because it offers effective learning capabilities, feed-forward neural networks are frequently employed in mathematical modeling [34]. Recently, some advanced stochastic learning algorithms have been developed slowly, a feed-forward neural network with a random hidden nodes approach was proposed in [34]. Weights and bias are generated randomly depending on the input data and kinds of activation functions, allowing the model’s level of generalization to be controlled. In [35], a training iterative solution for large-scale datasets is developed, and the regularization model is used to initially generate a learning model with improved generalization ability. When dealing with large-scale datasets, good applicability and effectiveness are achieved. In [36], a distributed learning algorithm of a feed-forward neural network with random weights is proposed by using an event-triggered communication scheme. To reduce needless transmission overhead, the method adopts a discrete-time zero-gradient and strategy solution and introduces an event-triggered communication approach. In [37], a new feed-forward neural network method for initializing weights is proposed, which linearizes the whole network at the equilibrium point, especially the initial weights and deviations. Ref. [40] offered a linear algebraic approach based on the Cauchy inequality that guaranteed the output of neurons in the active area, sped up convergence, and drastically decreased the number of algorithm iterations for sample extraction. Many scholars discuss hot topics [38] such as combining Monte Carlo simulations (MCSs) and implementing efficient sampling of feed-forward neural networks (FNNs). The authors of [39] put forward a kind of incremental learning method based on a hybrid fuzzy neural network framework from the angle of the dataset to improve the performance of the algorithm.
Feed-forward neural network optimization has drawn a lot of interest in the era of big data. To lower the sample size, feed-forward neural network optimization now primarily uses the processing of random weights, although researchers have only been able to increase the performance of these networks in isolation. In order to handle enormous datasets, this research suggests a random weighting feed-forward neural network scheme based on a decomposition approach. This scheme not only ensures the network’s integrity but also the random performance of feed-forward neural networks. However, the sample feature extraction’s actual applicability is not exhaustive; large-scale datasets only use random weights, which have poor feed-forward neural network performance.
3. Our Proposed FNNS
3.1. FNNRW Learning Algorithm
Feed-forward neural networks have been widely used in many fields. FNNRWs are generally described as:
where N is the number of hidden nodes; is the input; and are the input and output weights connecting the i th hidden node and the output node, respectively; is the bias; is the activation function; and the activation function generally adopts the common sigmoid function, as shown in Equation (2).
Presented with a collection of practice data , satisfies expression , where
is the hidden-layer output matrix, is the output weights, and are the target vectors.
In FNNRWs, as shown in Figure 1, input weights and biases are distributed uniformly at random, , . The well-known least-squares approach may be used to analytically compute the output weights:
which gives . The least squares issue is typically poorly phrased, though. So we can use the regularization method to solve this kind of problem, i.e.,
where is a regularization factor. If is given such that is invertible, then the minimizer of Equation (5) is easily described as:
where I represents the identity matrix.
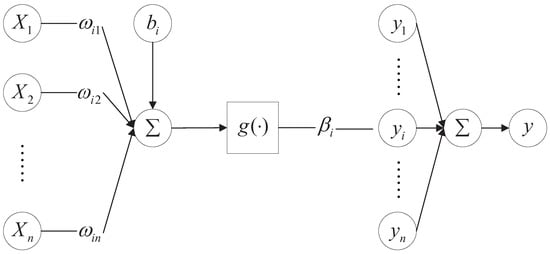
Figure 1.
Mathematical model of FNNRWs. The convergence of the output weights of the unified learning model is provided by the FNNRW, which divides the whole training sample into many tiny subsets and utilizes each subset to create a local learning model to integrate the unified classifier.
3.2. Improved FNNRW Learning Algorithm
In large-scale data, as shown in Figure 2, the sample is randomly divided into m parts, . For each subset , derive the corresponding submodel and initialize the same input weights and biases. Calculate the hidden layer output matrix , and is a positive definite matrix. The whole problem can be described as:
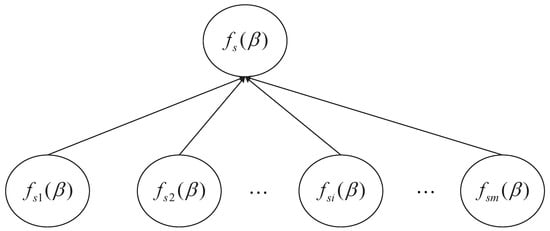
Figure 2.
General organization. The link between the local model and the global model is depicted in the picture. A big data collection may be broken up into smaller subsets, each of which is made up of , and m submodels that are derived from each subset.
The ith local model’s hidden output matrix and target output, respectively, are denoted by the symbols and .
In this algorithm, the most common sigmoid function is used for the activation function. For convenience, the activation function can be denoted as:
The parameters and b are used to govern the movement of the picture on the x axis. The derivative of the activation function is shown in Equation (10). When , the derivative is also greater than zero, so the slope of is greater than zero. Similarly, when , the slope of the activation function is less than zero, so can be used as the slope parameter of . According to Figure 3, when , ; when , .
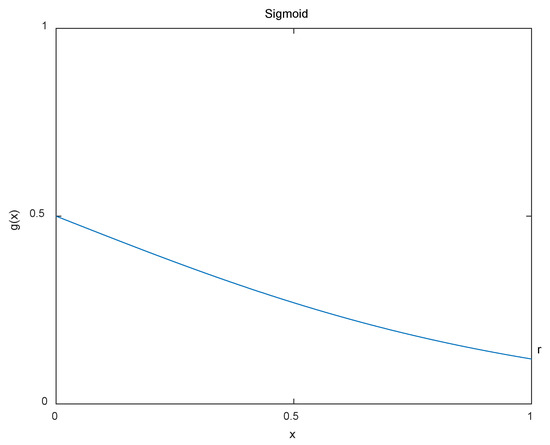
Figure 3.
The flatter fragments of the activation function. The figure corresponds to the range when the activation function’s value range is [0, 1].
When , , and , we get:
After transformations we obtain:
Assuming that the fitting curve of the activation function is not as flat as that of the sigmoid function, then:
In order to determine the range of parameters more accurately, let , where is used to define the maximum input weight and the steepest part of the activation function. The ranges may be used to calculate the slope parameter of the i-th activation function:
Parameter s determines the steepest part of the activation function, whose specific value is determined by the target function.
Following transformations, we get:
For we get the first boundary of b:; for , we get the second boundary of b:. It can be seen that bias b depends on the input weight , so the range of bias b can be obtained:
The formula above illustrates the best decision range in the process of determining input weights and biases at random.
In the process of determining the output weight, randomly initialize the output matrix as and, respectively, calculate the local and global gradients:
At the same time, calculate:
Each local model is locally optimized during each iteration:
The idea of Bregman divergence is presented in order to better comprehend this local model:
In this algorithm, for each , there is
The regularization parameter is . Accordingly, the Bregman divergence is
According to the above equation, Equation (22) can be be changed to:
Taylor’s extension, however, transforms the Bregman divergence into:
Thus, Equation (22) can be further transformed into:
The ultimate output weight may be calculated using the preceding derivation as follows:
These are a few of the approaches for improvement this study employed. Algorithm 1 displays the particular FNNS algorithm, and Figure 4 displays the flowchart of algorithm development.
| Algorithm 1 Improved FNNRW learning algorithm. |
| Step 1: Divide the sample randomly into m parts, . For each subset , derive the corresponding submodel. |
| Step 2: Determine the range of input weights and biases that the activation function deems to be optimum,
|
| Step 3: Randomly initialize the same input weights and biases within the range of values. |
| Step 4: Calculate the hidden layer output matrix and initialize the output matrix at random. |
| Step 5: Calculate the required components such as local gradients and global gradients.
|
| Step 6: Calculate the output weight,
|
| Step 7: if or reach the maximum number of iterations, then break; else go on Step 5 and Step 6. |
| Step 8: Train the network using the calculated weights. |
| Step 9: Return result. |
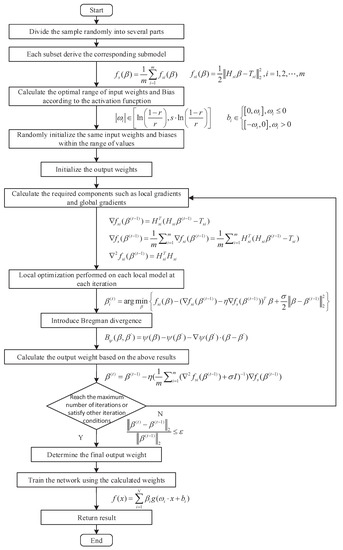
Figure 4.
An optimized FNNRW learning algorithm flowchart. The graphic depicts each phase of the FNNRW optimization process, and the chosen approach corresponds to that step specifically. The flow chart may be used to more clearly illustrate the improved FNNRW algorithm’s execution process, condition judgment at its start, and condition at its conclusion.
4. Performance Analysis
4.1. Results and Discussion
The effectiveness of the suggested algorithm is tested in this section. A Pentium (R) dual-core E5400 processor clocked at 2.70 GHz and operating with 2 Gb of memory was used for all tests in the MATLAB 7.10.0 (2010a) environment. The activation function used by the algorithm is the sigmoid function . Because it is for large-scale data processing, the dataset used in this paper is the MNIST dataset. The Mixed National Institute of Standards and Technology database, also known as the MNIST dataset, is a sizable collection of handwritten digits that the National Institute of Standards and Technology has collected and organized. It includes a training set of 60,000 examples and a test set of 10,000 examples. In comparison to other types of datasets, MNIST, a publicly accessible handwritten digital dataset, has small image pixels, relatively low computing power, the ability to build a neural network with fewer layers, is amenable to computer arithmetic, and the dataset has sufficient quantity, high discrimination, and low noise. Consequently, it was selected as the experiment’s dataset. The samples are initially separated into m equal subgroups and all samples are normalized in order to test the algorithm’s efficacy. During the experiment, the parameters and were selected in the process of calculating the input weights and biases. Additionally, take the regularization parameter , learning rate , the threshold . The following charts intuitively show the performance of the optimized algorithm.
When the number of subsets m is 10 or 20, respectively, Table 1 and Table 2 compare the accuracy of the FNNRWs learning algorithm and the improved FNNRWs learning method. As shown in Table 1 and Table 2, the accuracy of the optimized FNNRWs learning algorithm is greater than the accuracy of the FNNRWs learning algorithm as sample size or the number of hidden layer nodes increases. Figure 5 and Figure 6 compare the training accuracy and test accuracy while displaying the accuracy of the optimized FNNRWs learning algorithm and the accuracy of the FNNRWs learning algorithm as the number of training rises, respectively. In the figure, the advantages of the optimized FNNRWs learning algorithm in terms of accuracy can be seen very intuitively. Figure 7 and Figure 8 show the performance advantages of the optimized FNNRWs learning algorithm from the aspect of relative error by calculating the relative error.

Table 1.
Training accuracy and test accuracy of the FNNRW learning algorithm and the optimized FNNRW learning algorithm when samples are divided into 10 subsets. We partitioned the entire huge dataset into 10 smaller datasets, using the training set and test set to examine how well the improved method performed. The accuracy of each dataset is displayed in the table.

Table 2.
Training accuracy and test accuracy of the FNNRW learning algorithm and the optimized FNNRWs learning algorithm when samples are divided into 20 subsets. We partitioned the entire huge dataset into 20 smaller datasets, using the training set and test set to examine how well the improved method performed. The accuracy of each dataset is displayed in the table.
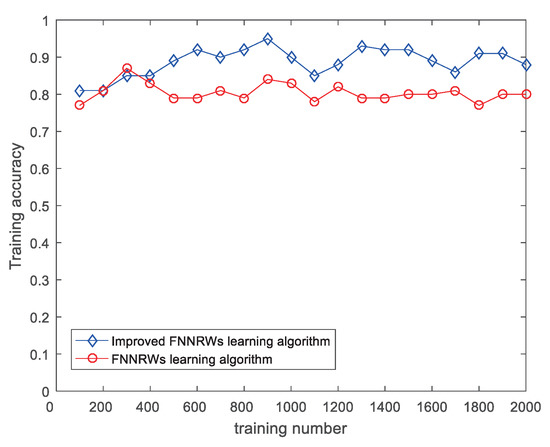
Figure 5.
Comparison of the learning algorithms used by the FNNRW for training accuracy. The accuracy of the improved FNNRW method is superior to the FNNRW algorithm in the training dataset in terms of different training durations.
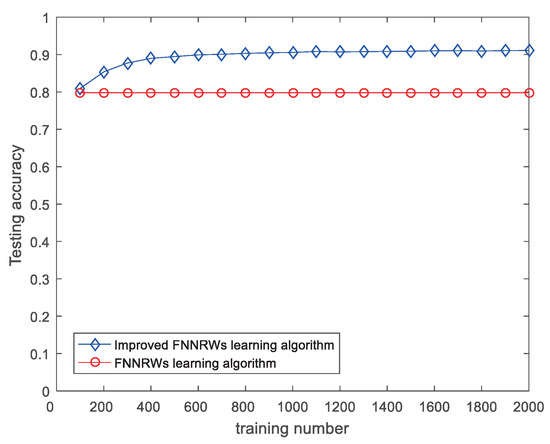
Figure 6.
Test accuracy comparison of learning algorithms for the FNNRW. The accuracy of the improved FNNRWs method is superior to the FNNRW algorithm in the test dataset in terms of various training durations.
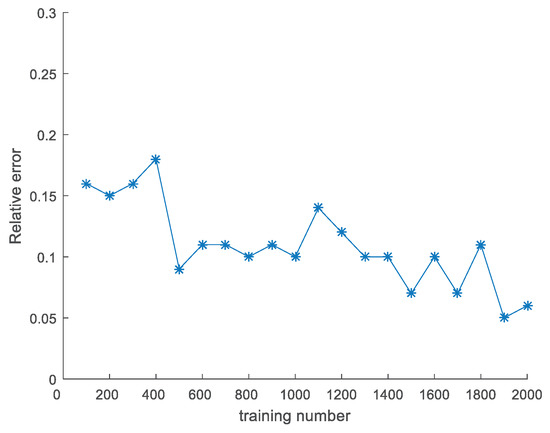
Figure 7.
Algorithm for learning the FNNRW’s relative error. While the error of the optimized FNNRW learning algorithm is typically lower than 0.05, the relative error of the FNNRW learning algorithm drops with the number of training repetitions but stays around 0.1.
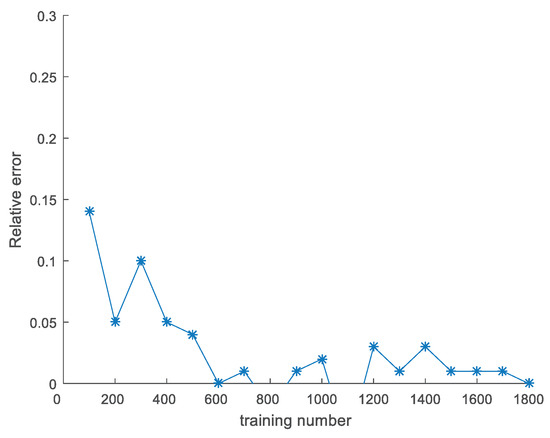
Figure 8.
Relative inaccuracy of the FNNRW learning method that has been improved. The optimized FNNRW learning algorithm’s relative errors show a downward trend as training times increase, and the majority of them are lower than 0.05, which is much lower than the FNNRW learning algorithm’s relative error of 0.1, demonstrating the optimized FNNRW algorithm’s superior performance.
4.2. Engineering Applications
Data have grown more quickly as science and technology have advanced. In the big data era, people may find a ton of pertinent information. For instance, environmental factors that are regularly studied offer a significant dataset in coal mine safety. The feed-forward network random weighting algorithm presented in this paper is based on the decomposition method, which is more adaptable, divides a large dataset into local datasets rather than using sampling to reduce it, preserves the integrity of the original dataset, and is thus better suited for use in real-world engineering applications.
5. Conclusions and the Future Work
In this paper, a feed-forward neural network model with random weights based on decomposition technology is examined for large-scale datasets. It is based on the feed-forward neural network with random weights (FNNRW). Each subset of the data is used to create the associated submodel once the samples are separated into subsets of the same size. The technical contribution of this study is to optimize the three parameter generating process in order to increase overall performance. The input weights and biases in FNNRWs are set arbitrarily and are not learned. The choice of the proper interval is crucial. The best value range is computed in this study using the activation function. Starting with a variety of input weights and biases will boost performance as a whole. In addition, an iterative approach is employed to get over the challenge of assessing the output weights of the random model. The MNIST dataset was used as the basis for experiments. The outcomes of the experiments demonstrate the algorithm’s efficacy.
The algorithm performance of the suggested feed-forward neural network model with random weights for large-scale datasets based on decomposition technology has greatly improved; however, the following has to be done in the future: (a) Despite a minor flaw, the suggested method can still be made better. The improved approach will be used in further work to boost the algorithm’s performance even more. The experimental data used in the paper are two-dimensional, and the subsequent work will start from the dimensionality to improve the algorithm’s adaptability, filter the dataset to improve its quality in order to indirectly improve algorithm performance, and continue to improve the algorithm structure in order to satisfy more application requirements. (b) Only the MINIST dataset will be tested since the future data will be enormous and the dataset utilized in the experiment will be small. The performance of the method will be examined in the subsequent study using a bigger dataset. (c) Every algorithm update is eventually used in everyday life, and our original goal was to use high-performing algorithms in actual situations. In our upcoming work, we will concentrate on applying algorithms to many technical domains in addition to improving the algorithm’s performance.
Author Contributions
Writing—original draft, Z.Z., F.F., T.H.; Writing—review & editing, Z.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Ningxia Key Research and Development project grant number: 2022BEG02016, and Ningxia Natural Science Foundation Key Project grant number: 2021AAC02004.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The MNIST database is available from http://yann.lecun.com/exdb/mnist/ (accessed on 20 November 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Han, F.; Jiang, J.; Ling, Q.H.; Su, B.Y. A survey on metaheuristic optimization for random single-hidden layer feedforward neural network. Neurocomputing 2019, 335, 261–273. [Google Scholar] [CrossRef]
- Li, F.-j.; Li, Y. Randomized algorithms for feedforward neural networks. In Proceedings of the 2016 35th Chinese Control Conference, Chengdu, China, 27–29 July 2016; pp. 3664–3668. [Google Scholar]
- Scardapane, S.; Wang, D.; Panella, M.; Uncini, A. Distributed learning for random vector functional-link networks. Inf. Sci. 2015, 301, 271–284. [Google Scholar] [CrossRef]
- Tang, S.; Chen, L.; He, K.; Xia, J.; Fan, L.; Nallanathan, A. Computational intelligence and deep learning for next-generation edge-enabled industrial IoT. IEEE Trans. Netw. Sci. Eng. 2022. [Google Scholar] [CrossRef]
- Li, M.; Wang, D. Insights into randomized algorithms for neural networks: Practical issues and common pitfalls. Inf. Sci. 2017, 382, 170–178. [Google Scholar] [CrossRef]
- Xia, F.; Hao, R.; Li, J.; Xiong, N.; Yang, L.T.; Zhang, Y. Adaptive GTS allocation in IEEE 802.15. 4 for real-time wireless sensor networks. J. Syst. Archit. 2013, 59, 1231–1242. [Google Scholar] [CrossRef]
- Dudek, G. A method of generating random weights and biases in feedforward neural networks with random hidden nodes. arXiv 2017, arXiv:1710.04874. [Google Scholar]
- Cao, F.; Tan, Y.; Cai, M. Sparse algorithms of Random Weight Networks and applications. Expert Syst. Appl. 2014, 41, 2457–2462. [Google Scholar] [CrossRef]
- Wu, C.; Luo, C.; Xiong, N.; Zhang, W.; Kim, T.H. A greedy deep learning method for medical disease analysis. IEEE Access 2018, 6, 20021–20030. [Google Scholar] [CrossRef]
- Schmidt, W.F.; Kraaijveld, M.A.; Duin, R.P.W. Feed forward neural networks with random weights. In Proceedings of the 11th IAPR International Conference on Pattern Recognition. Vol. II. Conference B: Pattern Recognition Methodology and Systems, The Hague, The Netherlands, 30 August–3 September 1992. [Google Scholar]
- Ye, H.; Cao, F.; Wang, D.; Li, H. Building feedforward neural networks with random weights for large scale datasets. Expert Syst. Appl. 2018, 106, 233–243. [Google Scholar] [CrossRef]
- Scardapane, S.; Wang, D. Randomness in neural networks: An overview. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2017, 7, e1200. [Google Scholar] [CrossRef]
- Wang, D.; Li, M. Stochastic Configuration Networks: Fundamentals and Algorithms. IEEE Trans. Cybern. 2017, 47, 3466–3479. [Google Scholar] [CrossRef] [PubMed]
- Mikolov, T.; Deoras, A.; Povey, D. Strategies for training large scale neural network language models. In Proceedings of the 2011 IEEE Workshop on Automatic Speech Recognition & Understanding, Waikoloa, HI, USA, 11–15 December 2012. [Google Scholar]
- Yoo, P.D.; Ng, J.W.; Zomaya, A.Y. An Energy-Efficient Kernel Framework for Large-Scale Data Modeling and Classification. In Proceedings of the 25th IEEE International Symposium on Parallel and Distributed Processing Workshops and Phd Forum, Anchorage, AK, USA, 16–20 May 2011. [Google Scholar]
- Nykamp, D.Q.; Tranchina, D. A Population Density Approach That Facilitates Large-Scale Modeling of Neural Networks: Extension to Slow Inhibitory Synapses. Neural Comput. 2001, 13, 511–546. [Google Scholar] [CrossRef] [PubMed]
- Gu, R.; Shen, F.; Huang, Y. A parallel computing platform for training large scale neural networks. In Proceedings of the 2013 IEEE International Conference on Big Data, Silicon Valley, CA, USA, 6–9 October 2013; pp. 376–384. [Google Scholar]
- Elias, J.G.; Fisher, M.D.; Monemi, C.M. A multiprocessor machine for large-scale neural network simulation. In Proceedings of the IEEE Ijcnn-91-seattle International Joint Conference on Neural Networks, Seattle, WA, USA, 8–12 July 1991. [Google Scholar]
- Osuna, E.; Freund, R.; Girosi, F. An Improved Training Algorithm for Support Vector Machines. In Proceedings of the Neural Networks for Signal Processing Vii-IEEE Workshop, Amelia Island, FL, USA, 24–26 September 1997. [Google Scholar]
- Osuna, E.; Freund, R.; Girosi, F. Training Support Vector Machines: An Application to Face Detection. In Proceedings of the IEEE Computer Society Conference on Computer Vision & Pattern Recognition, Quebec City, QC, Canada, 6 August 2002. [Google Scholar]
- Lu, B.L.; Ito, M. Task decomposition and module combination based on class relations: A modular neural network for pattern classification. IEEE Trans. Neural Netw. 1999, 10, 1244–1256. [Google Scholar]
- Schwaighofer, A.; Tresp, V. The Bayesian Committee Support Vector Machine. In Artificial Neural Networks—ICANN 2001; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Tresp, V. A Bayesian committee machine. Neural Comput. 2000, 12, 2719–2741. [Google Scholar] [CrossRef] [PubMed]
- Cheng, H.; Xie, Z.; Shi, Y.; Xiong, N. Multi-step data prediction in wireless sensor networks based on one-dimensional CNN and bidirectional LSTM. IEEE Access 2019, 7, 117883–117896. [Google Scholar] [CrossRef]
- Yao, Y.; Xiong, N.; Park, J.H.; Ma, L.; Liu, J. Privacy-preserving max/min query in two-tiered wireless sensor networks. Comput. Math. Appl. 2013, 65, 1318–1325. [Google Scholar] [CrossRef]
- Jain, A.K.; Mao, J.; Mohiuddin, K.M. Artificial neural networks: A tutorial. Computer 1996, 26, 31–44. [Google Scholar] [CrossRef]
- Krogh, A. What are artificial neural networks? Nat. Biotechnol. 2008, 26, 195–197. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Dai, P.; Cheng, X.; Liu, Y.; Cui, J.; Zhang, L.; Feng, D. An online generation method of ascent trajectory based on feedforward neural networks. Aerosp. Sci. Technol. 2022, 128, 107739. [Google Scholar] [CrossRef]
- Cui, W.; Cao, B.; Fan, Q.; Fan, J.; Chen, Y. Source term inversion of nuclear accident based on deep feedforward neural network. Ann. Nucl. Energy 2022, 175, 109257. [Google Scholar] [CrossRef]
- Xiao, L.; Fang, X.; Zhou, Y.; Yu, Z.; Ding, D. Feedforward neural network-based chaos encryption method for polarization division multiplexing optical OFDM/OQAM system. Opt. Fiber Technol. 2022, 72, 102942. [Google Scholar] [CrossRef]
- Mouloodi, S.; Rahmanpanah, H.; Gohari, S.; Burvill, C.; Davies, H.M. Feedforward backpropagation artificial neural networks for predicting mechanical responses in complex nonlinear structures: A study on a long bone. J. Mech. Behav. Biomed. Mater. 2022, 128, 105079. [Google Scholar] [CrossRef] [PubMed]
- Fontes, C.H.; Embiruçu, M. An approach combining a new weight initialization method and constructive algorithm to configure a single Feedforward Neural Network for multi-class classification. Eng. Appl. Artif. Intell. 2021, 106, 104495. [Google Scholar] [CrossRef]
- Dudek, G. Generating random weights and biases in feedforward neural networks with random hidden nodes. Inf. Sci. 2019, 481, 33–56. [Google Scholar] [CrossRef]
- Cao, F.; Wang, D.; Zhu, H.; Wang, Y. An iterative learning algorithm for feedforward neural networks with random weights. Inf. Sci. 2016, 328, 546–557. [Google Scholar] [CrossRef]
- Ai, W.; Chen, W.; Xie, J. Distributed learning for feedforward neural networks with random weights using an event-triggered communication scheme. Neurocomputing 2017, 224, 184–194. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Srivastava, G.; Gupta, G.P.; Tripathi, R.; Gadekallu, T.R.; Xiong, N.N. PPSF: A privacy-preserving and secure framework using blockchain-based machine-learning for IoT-driven smart cities. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2326–2341. [Google Scholar] [CrossRef]
- Yam, J.Y.; Chow, T.W. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; Xiao, P.; Zhou, J.; Armaghani, D.J. Intelligent rockburst prediction model with sample category balance using feedforward neural network and Bayesian optimization. Underground Space 2022, 7, 833–846. [Google Scholar] [CrossRef]
- Deng, X.; Wang, X. Incremental learning of dynamic fuzzy neural networks for accurate system modeling. Fuzzy Sets Syst. 2009, 160, 972–987. [Google Scholar] [CrossRef]
- Makantasis, K.; Georgogiannis, A.; Voulodimos, A.; Georgoulas, I.; Doulamis, A.; Doulamis, N. Rank-r fnn: A tensor-based learning model for high-order data classification. IEEE Access 2021, 9, 58609–58620. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).