Abstract
In electrical machinery, the rotor windings’ internal short-circuit faults are addressed by the instantaneous over-current protection of the power electronic excitation device, which has low sensitivity and has difficulty meeting the safety requirements. In this paper, a rotor windings’ internal short-circuit fault protection method is proposed based on the harmonic characteristics of the circulating current between stator branches. The magnetomotive force distribution of the short-circuit coils in the rotor windings is theoretically deduced, and the characteristic frequencies of the circulating current between stator branches are analyzed. On this basis, the protection criterion of the rotor windings’ internal short-circuit fault is constructed by using the harmonic component of the circulating current. Then, an analytic model of the variable-speed pumped storage unit is established based on the multi-loop method, and the finite element method is used to verify the correctness of the proposed modeling method. An actual large variable-speed pumped storage unit is taken as an example, and the possible faults under different slip ratios are simulated. In the simulation results, the stator branch circulation has the obvious characteristic frequency harmonic components, which is consistent with the theoretical analysis. It verifies the effectiveness of the proposed protection method. Finally, it is analyzed and verified that the proposed protection has a strong maloperation prevention ability under other kinds of faults.
1. Introduction
New power systems with renewable energy as the main body have the problem of large random fluctuations of power generation; thus, they have a huge demand for energy storage devices represented by pumped storage. The variable-speed pumped storage unit is different from the traditional constant-speed pumped storage unit, which can be used not only for planned peak regulation but also for dynamic peak regulation with system power fluctuation. It will be an important device for future power systems.
Variable-speed pumped storage units adopt a doubly fed AC excitation structure, which has the characteristics of variable rotor speed, multi-branch rotor winding structure, and dense distribution of rotor windings [1]. Under high-speed operation conditions, the probability of internal short-circuit faults of the rotor windings is high; not only inter-turn short-circuit faults, but inter-phase short-circuit faults may occur. It will cause an unbalanced force on the rotor, partial overheating, and severe vibration of the unit [2,3]. If left unchecked, it may evolve into serious faults such as large-scale short circuits and rotor core damage [4]. However, AC excitation system protection of variable-speed pumped-storage units is also used as the rotor windings’ internal short-circuit fault protection in engineering, which lacks pertinence and has low sensitivity. Only a few short-circuit faults with large phase currents can be covered, which is difficult to sensitively reflect the inter-turn short-circuit faults with weak fault characteristics. Therefore, special protection should be provided to detect the fault in the early stage and avoid causing significant economic losses [5].
At present, there have been several studies [6,7,8] on the internal short-circuit fault of synchronous generators. There are two kinds of methods based on non-electrical quantities and electrical quantities. The methods based on non-electrical quantities mainly include the vibration signal analysis method [9] and temperature measurement method [10]. Those based on the electrical quantities mainly include the detection coil-based method [11,12,13], recurrent surge oscillography method [14,15], flux linkage difference vector-based method [16], machine learning method [17,18,19] and circulating current between stator branches-based method [20,21]. The essence of the circulating current between stator branches-based method is to use the stator windings as the detection coil to monitor the distorted air-gap magnetic field caused by the rotor windings’ internal short-circuit faults. This has the advantage of no additional equipment installation.
However, the rotor winding of a variable speed pumped storage unit is in the form of three-phase AC excitation, while the excitation circuit of the conventional synchronous unit is single-phase DC excitation, which is completely different. When an internal short-circuit fault of a rotor winding occurs, the fault type and characteristics of variable-speed units are more complex and are completely different from those of a synchronous speed unit, which makes the existing inter-turn short-circuit protection of the excitation circuit no longer applicable. Variable-speed pumping storage units and doubly fed wind generators both use doubly fed AC excitation [22]. In [23], two measuring coils are used to obtain the magnetic field difference value. The short-circuited fault of the rotor windings is detected by analyzing the induced voltage difference of the measuring coils. In [24], the variation law of the flux linkage difference vector before and after the short-circuit fault of rotor windings is analyzed, then the inter-turn short-circuit fault can be easily identified. In [25,26], the armature reaction mechanism of the air gap magnetic field is studied when the rotor windings of a doubly fed wind generator are short-circuited, and the characteristic frequencies of the electrical quantities on the stator side are summarized. In [27], the low-frequency band component of the circulating current between stator branches is extracted to determine whether a rotor windings’ internal short-circuit fault occurs; but, the sensitivity and maloperation prevention ability of the proposed protection are not analyzed. However, the capacity and winding structure of variable-speed pumped storage units are quite different from those of the doubly fed wind generator. It is necessary to carry out further research based on the characteristics of variable-speed pumped storage units. In Japan and Germany, a small number of variable-speed pumped storage units have been put into commercial operation. These units do not specially configure the rotor winding short-circuit fault protection, but use the instantaneous over-current protection of the converter (power electronic excitation device) as the rotor winding short-circuit fault protection. This lacks pertinence and cannot reflect some rotor winding short-circuit faults with weak fault characteristics.
A rotor windings’ internal short-circuit fault protection method for variable-speed pumped storage units is proposed in this paper. Through the derivation of the magnetomotive force generated by the short-circuited coil, it is found that the circulating current between stator branches will produce characteristic harmonic components related to the slip ratio and pole-pairs number when a rotor winding is short-circuited. On this basis, a protection method for the rotor windings’ internal short-circuit fault is proposed by using the harmonic characteristics. A practical variable-speed pumped storage unit is taken as an example to verify the proposed protection method. Simulation results show that the method has strong practicability at different rotor speeds and has strong maloperation prevention ability under other kinds of faults.
2. The Harmonic Circulating Current between Stator Branches-Based Protection Method
When the variable-speed pumped storage unit is in normal operation, the magnetomotive force of a single coil is a rectangular wave that can be decomposed into the superposition of multiple fractional and integer harmonic (including the fundamental wave) magnetomotive forces. However, for the whole branch of stator and rotor windings, the fractional and low-order harmonic (excluding fundamental wave) magnetomotive force components of each coil in the branch offset each other, and the total magnetomotive force of the branch exhibits the fundamental wave characteristic. Therefore, the current flowing through the single-turn rotor coil only contains the fundamental frequency component during normal operation, which can be denoted as . is the electric angular frequency of the rotor.
After a short-circuit fault occurs in rotor windings, a large short-circuit current flows through the short-circuit coils, which can be recorded as . According to Fourier series decomposition, the magnetomotive force of the short-circuit coils can be decomposed into:
where N is the turn number of short-circuit winding, is the harmonic winding factor of the short-circuit winding, is the space electrical angle of the rotor, P is the number of pole pairs, and k is the harmonic order.
Assuming that represents the stator space electrical angle, then:
where s is the slip ratio. Since there is a relationship between the electric angular frequency of stator and rotor: , where is the stator electric angular frequency. Then, Equation (3) can be expressed as:
Substituting Equation (4) into Equation (1), the magnetomotive force of the short-circuit coils can be expressed in the stator space electric angle as:
According to Equation (5), the characteristic frequency of the induced potential corresponding to the harmonic magnetic field with order k is:
where fs is the fundamental wave frequency of the stator side, equal to 50 Hz.
The fractional and integer harmonic magnetic fields generated by the short-circuit current are known. For the integer harmonic magnetic field, k = 1, 2..., since the amplitude and phase of the overall induced potential of each stator in-phase branch are equal, there will be no circulating current between the stator branches. For the fractional harmonic magnetic fields, k = 1/P…, (P − 1)/P, (P + 1)/P, … since the different phases of the overall induced potential of each stator in-phase branch, the circulating current will be generated between the stator branches. The theoretical characteristic frequency of the circulating current is:
The circulating current can be measured directly by the split-phase transverse differential protection without additional installation of a measurement device.
When an internal short-circuit fault occurs in rotor windings, the circulating current between stator branches has the characteristic harmonic frequency as shown in Equation (7). Therefore, the protection criterion for rotor windings’ internal short-circuit faults can be designed as follows:
where is the protection setting value, is the protection action value, which represents the comprehensive effective value of characteristic harmonics. The greater the calculated value of is, the more serious the corresponding fault is. , and are the amplitudes corresponding to characteristic frequency fk of the circulating current of phase A, phase B, and phase C transformed by FFT respectively.
Due to the large measurement error of electromagnetic current transformers for low-frequency current, only the characteristic frequency greater than 5 Hz is selected in Equation (8). In addition, the frequency resolution of FFT transformation results is limited, so it is impossible to obtain exactly , and corresponding to the characteristic frequency fk. Therefore, the larger amplitude values on both sides of fk in FFT transformation results should be selected as , and for calculation. This processing method can also overcome the adverse effect of slight rotational speed measurement error.
When the unit is in normal operation, the split-phase transverse differential current (circulating current between stator branches) is obtained by the difference of two current transformers with the same type, which contains a weak unbalanced current, and the unbalanced current only contains the fundamental frequency component. Therefore, the protection setting value can be set very small. In Section 3 and Section 4, the actual variable-speed pumped storage unit mentioned above is taken as an example; the proposed protection method simulated to verify the effectiveness when rotor windings’ internal short-circuit fault occurs and the maloperation prevention ability when other kinds of faults occur will be discussed.
3. Model of the Variable-Speed Pumped Storage Unit
At present, the main method to analyze the fault characteristics of variable-speed pumped storage units is simulation analysis. It is difficult to use an actual unit for short-circuit tests directly because of the huge capacity and high cost of variable-speed pumped storage units. The economic loss of the real machine destructive test is unbearable. In addition, the small capacity doubly fed wind generator cannot be used to replace variable-speed pumped storage units in the tests. The main reason is that the rotor windings of the variable-speed pumped storage unit are a structure with multi-branches, while the rotor windings of doubly fed wind generators are a structure with a single branch. Additionally, field tests of the doubly fed wind generator have difficulty in accurately reflecting the fault characteristics of a variable-speed pumped storage unit.
In this paper, the multi-loop modeling method is used to simulate the variable-speed pumped storage unit. This modeling method has been successfully applied to large hydraulic generators and steam generators and has been verified by practical application [28,29,30,31]. In recent years, this modeling method has also been used to analyze the internal fault characteristics of variable-speed pumped storage units and verified by dynamic simulation tests [32]. This paper is mainly concerned with the protection of rotor windings from internal short-circuit faults. Therefore, the following is only a brief description of the modeling process. Since the modeling details are lengthy, the authors have written another article to explain.
Both the stator and rotor of a variable-speed pumped storage unit are of the winding form. The branches of a stator and rotor can be equivalent to the series connection of inductance and resistance, as shown in Figure 1. In the figure, m and n are the numbers of branches per phase of the stator and rotor windings, i and u are the branch current and voltage, respectively, and the upper corner symbols s and r represent the electrical quantities of stator and rotor sides, respectively.
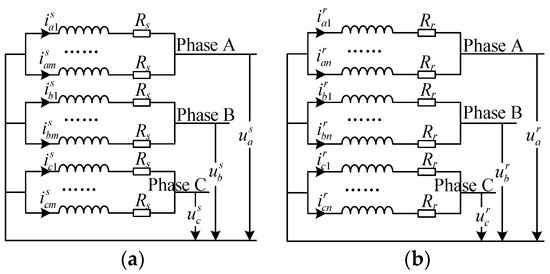
Figure 1.
Equivalent circuit diagram of stator and rotor windings; (a) stator windings; (b) rotor windings.
The voltage equations of each branch are:
where p is a differential operator, Us and Ur are the branch voltage matrices of stator and rotor, respectively, Is and Ir are the branch current matrices of stator and rotor, respectively, Rs and Rr are the branch resistance matrices of stator and rotor, respectively, and and are the branch flux linkage matrices of stator and rotor, respectively, which can be expressed as:
where Lss is 3 m × 3 m stator inductance matrix, Lrr is 3 n × 3 n rotor inductance matrix, and Lsr and Lrs are mutual inductance matrices of stator and rotor. Since the relative motion is between the coils of stator and rotor, the mutual inductance matrices Lsr and Lsr are time-varying function matrices. Combining Equation (11) and Equation (9), Equation (9) is transformed into a time-varying ordinary differential equation system:
Considering the stator and rotor current constraints, Equation (12) can be further reduced. When the internal short-circuit fault occurs in rotor windings, the voltage equation of the faulty loop should be added to Equation (12). Then, the simulation can be realized by solving the modified equation system.
The calculation methods of inductance matrices Lss, Lsr, Lsr, and Lrr are as follows.
Assume that the air gap is uniform. According to the analysis of air-gap permeance and taking the single-turn coil as the research object, the mutual inductance coefficient between the stator coil i and the coil j is
where ws is the number of turns of a single stator coil, is the pole pitch, l is the core length, is the permeability of vacuum, P is the number of pole-pairs, k is the harmonic order, , is the equivalent air gap length, is the stator electric angle, and is the stator side short distance coefficient of kth harmonic.
In particular, when i = j, Equation (13) is converted to the self-inductance coefficient of the coil i, which is expressed as:
If is used to represent the mutual inductance between the coil x of the loop H and the coil t of the loop J, then the mutual inductance between the stator loop H and the loop J is expressed as:
where m is the number of coils in loop H, and n is the number of coils in loop J. When loop H and loop J are the same loop, the calculation result is the self-inductance coefficient of this loop.
Since the rotor is also winding, the calculation method of the inductance coefficient of the rotor side is similar to that of the stator side. The mutual inductance coefficient between the rotor coil i and coil j is:
where wr is the number of turns of a single rotor coil, is the rotor electric angle, and is the rotor side short distance coefficient of kth harmonic. Similarly, the mutual inductance coefficient between the rotor loop H and loop J is expressed as:
where m is the number of coils in loop H, and n is the number of coils in loop J.
Similarly, the mutual inductance between stator coil i and rotor coil j is:
where is the rotor position angle, which varies with the rotor rotation. The mutual inductance coefficient between the stator loop H and the rotor loop J is expressed as:
The above inductance parameters , and are the elements in the inductance matrices Lss, Lsr, Lsr, and Lrr.
Take a 300 MW variable-speed pumped storage unit with seven pairs of poles (P = 7) as an example. The basic parameters of the unit are shown in Table 1, and the stator branch wiring diagram is shown in Figure 2. Each phase of the stator consists of four branches in parallel. In the figure, A, B, and C are phases, 1, 2, 3, 4 are branch numbers. CT represents a current transformer. CT2 measures the sum current of branch A1 and branch A2, and CT3 measures the sum current of branch A3 and branch A4. The current difference between CT2 and CT3 is the circulating current of Phase A, and the split-phase transverse difference current of Phase A. At present, the stator internal CT of the large generator is mainly the TPY type. TPY is a current transformer considering transient characteristics for protection applications; its core has an air gap. The core of the TPY current transformer has an air gap, so the reluctance is large, and the saturation time is prolonged; that is, there is a longer time to maintain the linear transformation, which greatly improves the transient characteristics. Therefore, a TPY current transformer has a strong anti-saturation ability, which can effectively avoid transient maloperation. The error of the TPY current transformer under rated primary current should be less than ±1%. The measurement accuracy is high. In addition, CT2 and CT3 are the same type current transformers, which can overcome the measurement error caused by non-fault factors to a certain extent.

Table 1.
The basic parameters of a variable-speed pumped storage unit.
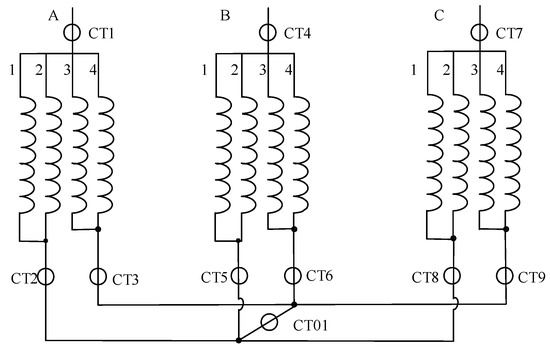
Figure 2.
Stator winding branch wiring diagram.
The protection object of split-phase transverse differential protection is the short-circuit fault of the stator winding, and the fundamental frequency effective value of circulating current is extracted as the action quantity of split-phase transverse differential protection. However, the protection object of the proposed method is the rotor winding short-circuit fault, and the comprehensive effective value of the characteristic frequency components of the circulating current is extracted as the protection action. In summary, this method does not need additional measurement devices in the industrial environment and only needs to add a set of protection algorithms in the microcomputer protection device to realize the protection of the rotor winding short-circuit fault of the variable speed pumped storage unit. When the slip ratio s is 0.1, the theoretical characteristic frequency of the circulating current between stator branches can be calculated according to Equation (7), and the calculation results are shown in Table 2.

Table 2.
The theoretical characteristic frequency of the circulating current between stator branches.
It is assumed that a short-circuit fault occurs in the 32nd turn coil of branch A2 (the second branch of phase A in rotor winding) and the 34th turn coil of branch A2; the turn difference is 2 turns, and the fault time is 35 s. The analytic model constructed by the multi-loop method is used for simulation calculation, and the transient current waveforms of stator branches are obtained as shown in Figure 3. The abscissa of Figure 3 is time, and the ordinate is the normalized unit value of the current. The reference value of current normalization is the amplitude of the 50 Hz stator phase current. In normal operation, the amplitude of the normalized current of each stator branch is about 0.25 p.u (the stator winding is a four-branch structure in each phase, 1/4 = 0.25 p.u). p.u is the abbreviation of per unit, which is a numerical labeling method used in power system analysis and engineering calculation. It represents the relative value of a physical quantity or a parameter that can be considered dimensionless. Since the physical position of each stator branch winding is different, the transient current of each stator branch is different.
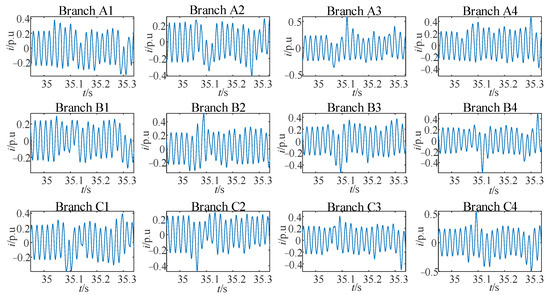
Figure 3.
The transient current of waveform stator branches (the inter-turn short circuit fault occurs at t = 35.0 and in rotor branch A2).
It can be found that the stator branch current distortion is obvious, with a large number of harmonic components after the fault occurs. At this point, the transient circulating current of each phase measured by the split-phase transverse differential protection is as shown in Figure 4. Taking phase A as an example, FFT transformation is performed on the circulating current of phase A to obtain the spectrum diagram, as shown in Figure 5. In Figure 4 and Figure 5, the normalized reference values are both the amplitude of the 50 Hz stator phase current. The characteristic frequencies are consistent with the theoretical analysis values in Table 2.
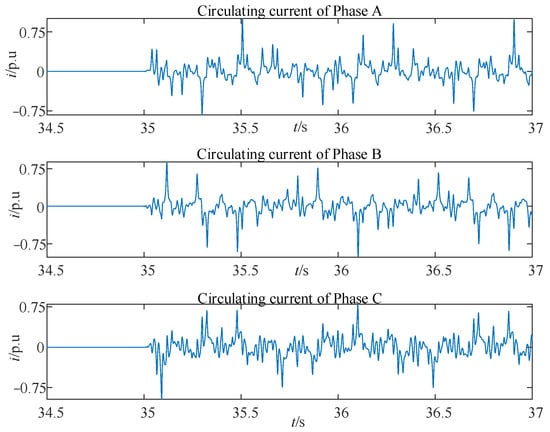
Figure 4.
The transient circulating current of each stator phase (the inter-turn short circuit fault occurs at t = 35.0 and in rotor branch A2).
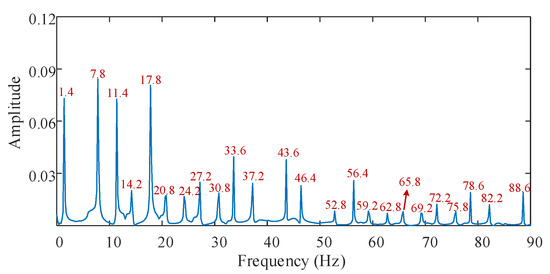
Figure 5.
Spectrum diagram of the circulating current of phase A obtained by the multi-loop method.
The finite element method is another recognized effective simulation method that is different from the multi-loop method used in this paper. The finite element analysis method is used to model the actual variable-speed pumped storage unit. Considering the boundary conditions, the equation for solving the nonlinear time-varying electromagnetic field is:
where is the z-axis component of the vector magnetic potential, is the source current density, is the permeability of the material, is the electrical conductivity of the material, and S is the outer diameter of the stator core.
The stator winding has four branches in each phase that are connected by double-layer winding. The rotor winding is connected by double-layer wave winding with two branches per phase. The winding connection form is complex, not symmetrical. In addition, the short-circuit fault destroys the symmetry of the magnetic field when the rotor winding short-circuit fault occurs. Therefore, the entire electrical machine must be simulated; it cannot be decomposed into 1/2 units or 1/4 units for simulation. To ensure that the coil connection sequence of stator and rotor windings in the simulation model is consistent with the actual unit, the Maxwell circuit design is used to set the coil connection sequence of stator and rotor windings. In addition, the rotor winding short-circuit fault is also based on the switch element setting in Maxwell circuit design. The materials of stator and rotor cores are silicon steel sheets, and the model is “DW315_50”. The materials of stator and rotor windings are copper, and the model is “copper_75C”. The material of the air gap is the vacuum, and the model is “vacuum”. The solution algorithm is Backward Euler, which is an implicit solution method with better convergence. The nonlinear residual is 0.0001, which ensures that the simulation results have higher accuracy. During the normal operation of the variable-speed pumped storage unit, the distribution of magnetic density and the magnetic force line is as shown in Figure 6a. It is obvious that the unit has seven pairs of poles, and the magnetic field is symmetrically distributed on the circumference. After the rotor winding has a short-circuit fault, the distribution of magnetic density and magnetic force line is as shown in Figure 6b. The short-circuit fault is located in the upper right corner of Figure 6b. It can be found that the magnetic field at the short circuit will cause serious distortion, and the magnetic line is no longer symmetrical.
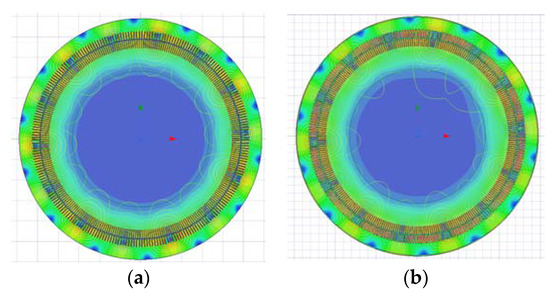
Figure 6.
The finite element analysis model; (a) the distribution of magnetic density and magnetic force line during normal operation; (b) the distribution of magnetic density and magnetic force line after the rotor winding has a short-circuit fault.
Take a short-circuit fault occurring in the 32nd turn coil of branch A2 and the 34th turn coil of branch A2 as an example. Using the finite element method for modeling and simulation, the spectrum diagram of the circulating current of phase A is obtained by FFT transform, as shown in Figure 7. Comparing Figure 5 and Figure 7, it can be found that the characteristic frequencies of the two simulation results are the same, which is consistent with the theoretical analysis. The characteristic frequency amplitudes obtained by the two simulation methods are compared, as shown in Table 3. The maximum relative error of each harmonic component amplitude is −14.0553%.
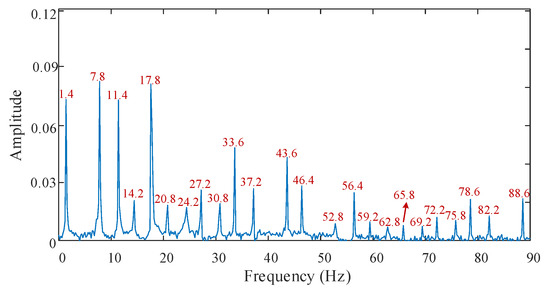
Figure 7.
Spectrum diagram of the circulating current of phase A obtained by finite element method.

Table 3.
Characteristic frequency amplitude obtained by multi-loop simulation method and finite element simulation method.
The accuracy of the multi-loop method is not as good as that of the finite element method, but we still chose the multi-loop method for the following considerations. According to the statistics of the number of rotor winding short-circuit faults, there are as many as thousands or even tens of thousands possible faults for an actual unit. It is inevitable to consider the time cost required for simulation when simulating these faults. The computer configuration for simulation included an Intel Core i7-11700 processor and 16.0 GB of RAM. For the multi-loop method, it takes about 34 s to simulate a fault. For the finite element method, it takes about 2812 s to simulate a fault. In addition, each fault simulated by the finite element method needs to change the wiring of the fault location in the Maxwell circuit design, which requires the participation of personnel. It can be estimated that it is difficult to simulate all faults by the finite element method.
The influence of the simulation error of the multi-loop method on the proposed protection is further analyzed. Combined with the data shown in Table 3, the protection action values corresponding to the two simulation methods are calculated by Equation (8). The protection action value corresponding to the multi-loop method is 0.163 p.u, and that corresponding to the finite element method is 0.169 p.u. The relative error is −3.55%, and the error is small. In addition, the protection action value of the multi-loop method is smaller than that of the finite element method, which makes the analysis result of the multi-loop method more conservative than that of the finite element method. In the multi-loop method, the calculation formulas of the inductance parameters of stator and rotor windings are Equations (13)–(19). The inductance parameter is inversely proportional to the equivalent air gap length. In the modeling, the actual air gap length is set as the equivalent air gap length. That is, the multi-loop method ignores the core reluctance and only considers the air gap reluctance. However, both the core reluctance and air gap reluctance are considered in the finite element method. This makes the equivalent air gap length in the multi-loop method smaller, which leads to the calculated inductance parameters being larger. According to Equation (12), when the inductance parameter is larger, the calculation results of the stator and rotor currents are smaller due to the constant voltage parameter on the right side of the equation. Therefore, the protection action value of the multi-loop method is less than that of the finite element method. More faults shown in Table 4 are simulated, and the protection action values obtained by the multi-loop method and finite element method are compared. The relative errors are calculated with “the protection action values obtained by the finite element method” as the reference value. In the table, A1_13 and A1_30 indicate that the 13th turn coil of branch A1 and the 30th turn coil of branch A1 have a short circuit fault. It can be found that the maximum relative error does not exceed −5%, which verifies the correctness of the simulation results of the multi-loop method.

Table 4.
Protection action values obtained by the multi-loop method and finite element method under various faults.
4. Batch Simulation and Verification
4.1. Effectiveness Analysis and Verification of the Proposed Protection Method
An internal short-circuit fault in rotor windings is mainly caused by insulation damage. It can be divided into in-slot and end faults according to the fault position. For the in-slot fault, as the name implies, the short-circuit fault occurs on two bar conductors in the same slot. The number of possible short-circuit faults is equal to the total number of slots in the rotor, denoted as Z. For the end faults, a specific connection form of the rotor double-layer wave windings needs to be considered, as shown in Figure 8. A single-turn coil is composed of the upper bar conductor in slot n and the lower bar conductor in slot n + y1. The upper connecting line of the upper bar conductor in slot n is overlapped with the upper connecting line of the lower bar conductor in slot (n + 1) − (n + y1 − 1), which may lead to a total of (y1 − 1) short-circuit faults. The lower connecting line of the upper bar conductor in slot n is overlapped with the lower connecting line of the lower bar conductor in the slot (n − 1) − (n − y2 + 1), which may lead to a total of (y2 − 1) short-circuit faults. There are (y1 + y2 − 2) faults in total. Therefore, the number of possible short-circuit faults at the end of the whole rotor winding is (y1 + y2 − 2) Z.
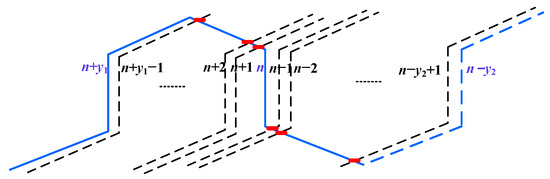
Figure 8.
Position of the possible end short-circuit faults.
For the actual variable speed unit in Table 1, the number of possible internal short-circuit faults in rotor windings is shown in Table 5. Various faults can be simulated by using the modeling method described in Section 3.

Table 5.
The number of possible internal short-circuit faults in rotor windings.
When the slip ratio is 0.1, the simulation results of all possible faults in Table 5 are as shown in Figure 9, which are divided into four parts: in-slot faults, end faults in the same branch with different short turns, end faults between two branches in the same phase, and end faults between phases. In the figure, each scattered point represents a fault situation, the abscissa is the turn difference of the short-circuit fault, and the ordinate is the simulation calculation result of the protection action value obtained by Equation (8). The number of end faults is huge and the overlap of scattered points is serious. Therefore, a scatter density diagram is used in the display, and the scatter color changes are proportional to the scatter density. Figure 9a corresponds to the calculation results of in-slot faults, and the minimum protection action value is 0.1678 p.u. Figure 9b corresponds to the calculation results of end faults in the same branch with different short turns, and the minimum protection action value is 0.1281 p.u. Figure 9c corresponds to the calculation results of end faults between two branches in the same phase, and the minimum protection action value is 0.0535 p.u. Figure 9d corresponds to the calculation results of end faults between phases, and the minimum protection action value is 0.0473 p.u. Among them, 0.0473 p.u is the minimum value of the above protection action value. Therefore, the minimum protection action value can be determined to be 0.0473 p.u. In addition, the protection action value of most faults is greater than 0.1 p.u., indicating obvious fault characteristics.
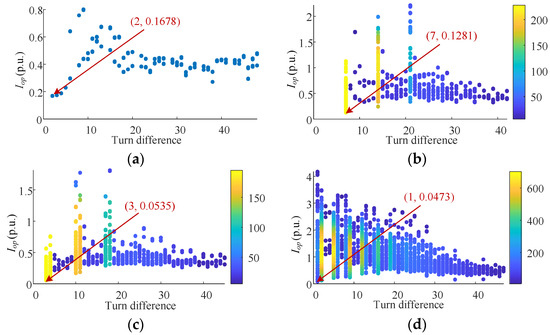
Figure 9.
When s = 0.1, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
Consider that the rotor speed of a variable-speed pumped storage unit has a certain range of variation, usually [32]. Therefore, all possible faults with slip ratios s of −0.1, 0.05, −0.05, 0.01 and −0.01 are simulated. The simulation calculation results are shown in Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14. The overall distribution trend of calculation results of protection action values is almost the same under different slip ratios. In general, the minimum value of the protection action value in all faults is 0.0368 p.u. in Figure 13d. However, the protection action value of most faults is still greater than 0.1 p.u.; the number of faults whose action value is greater than 0.1 p.u. is shown in Table 6. It can be found that most faults with different rotor speeds have obvious fault characteristics. Therefore, the protection setting value can be selected flexibly, which verifies the effectiveness of the protection method. The protection action value is positively correlated with the fault degree. Even if the protection action value of a very few faults is less than the setting value and cannot be applied, the fault degree of this kind of rejection fault is extremely weak and will not cause serious harm to the unit in a short time. Therefore, it is acceptable to set the protection value to 0.1 p. u.
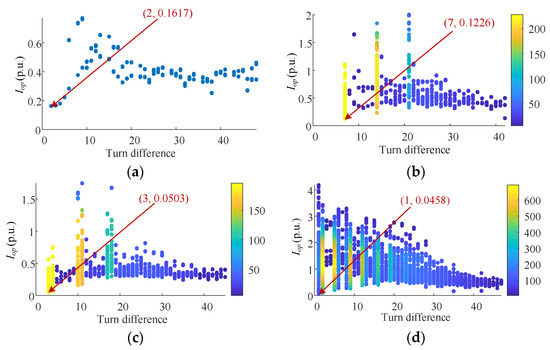
Figure 10.
When s = −0.1, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
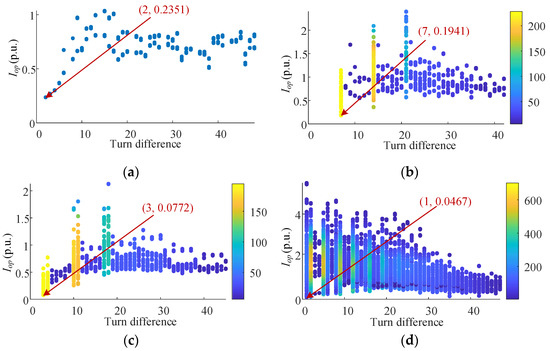
Figure 11.
When s = 0.05, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
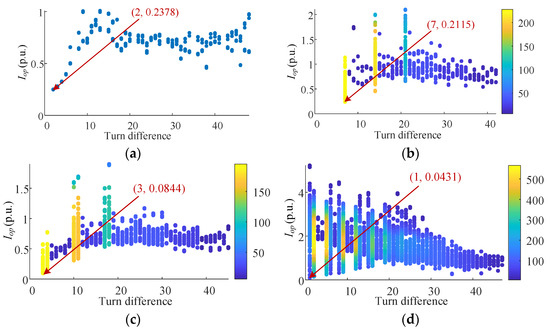
Figure 12.
When s = −0.05, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
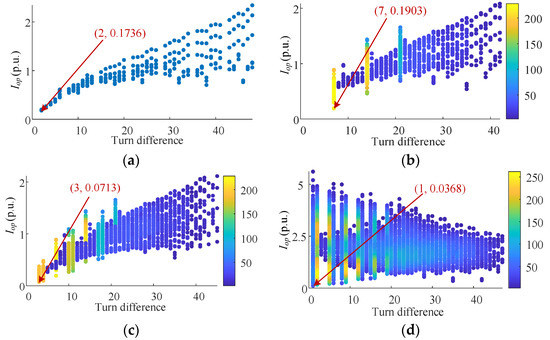
Figure 13.
When s = 0.01, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
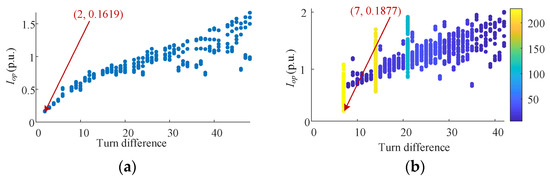
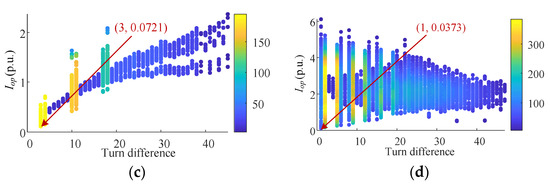
Figure 14.
When s = −0.01, the simulation results of all possible internal short-circuit faults in rotor windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.

Table 6.
The number of faults whose action value is greater than 0.1 p.u.
It is worth mentioning that the fault corresponding to the protection action value 0.0368 p.u. in Figure 13d is a short-circuit fault between the 2nd turn coil of branch A2 and the 1st turn coil of branch B2, as shown in Figure 15. That is, the short-circuit fault occurs between F1 and F2. F2 is the equipotential with the neutral point o. Therefore, although this fault is a fault between phases, the fault characteristic is consistent with the characteristic of a small turn difference inter-turn short-circuit fault. Currently, the short-circuit fault current in rotor windings is small, and the amplitude of the harmonic characteristic circulating current induced on the stator side is also very weak.
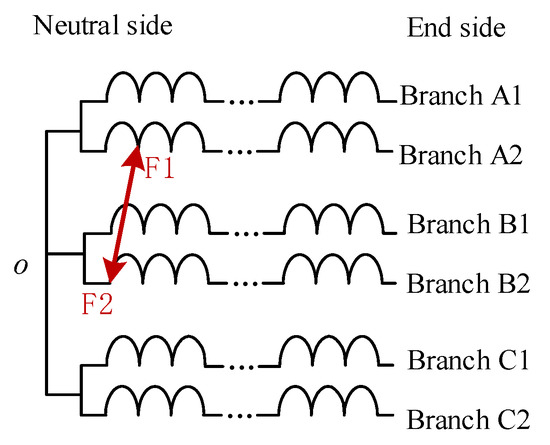
Figure 15.
Diagram of the short-circuit fault in rotor windings.
4.2. Analysis and Verification of Protection Method against Maloperation
In this section, the maloperation prevention ability of the proposed protection method is mainly analyzed.
For the stator single-phase grounding fault, since the neutral point of the stator winding is grounded by high resistance, the fault characteristics are weak, and only the change characteristics of fundamental frequency zero-sequence voltage and third harmonic voltage ratio will appear. The current of each branch is almost unchanged, which will not cause protection maloperation.
For the rotor one-point grounding fault, since the neutral point of the rotor winding is not grounded, there is no current path, thus the air-gap magnetic field distribution generated by rotor windings will not be changed, and the circulating current between stator branches will not be induced.
For the internal short-circuit faults in stator windings, the stator short-circuit current will distort the air-gap magnetic field, and then fault current with some specific frequencies will be induced in rotor windings. The above-induced current will also in turn generate a fault current with some characteristic frequencies on the stator side. However, the amplitude of this fault current is very weak after secondary induction, and the characteristic frequencies are different from that in Equation (8). Therefore, the protection action value will not reach the setting value. Still taking the above variable-speed pumped storage unit as an example, all possible internal short-circuit faults in stator windings are simulated. When the slip ratio s = 0.1, the calculation results of the action value of the proposed protection are as shown in Figure 16. In the figure, the abscissa is the turn difference of the short-circuit fault in stator windings, and the ordinate is the calculation result of the protection action value . It can be found that the maximum protection action value is only 0.00164 p.u. in all fault cases, which is close to 0. Therefore, the protection setting value can be flexibly selected to ensure that the proposed protection does not malfunction when other kinds of faults occur.
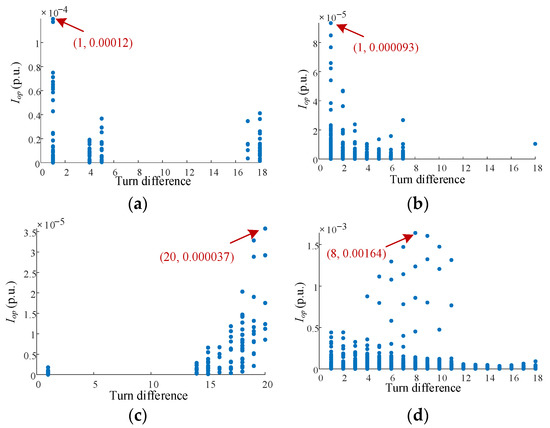
Figure 16.
When s = 0.1, the simulation results of all possible internal short-circuit faults in stator windings: (a) in-slot faults; (b) end faults in the same branch with different short turns; (c) end faults between two branches in the same phase; (d) end faults between phases.
5. Conclusions
In this paper, a rotor winding internal short-circuit fault protection method for variable-speed pumped storage units is proposed. The harmonic characteristic frequencies of the circulating current between stator branches were analyzed when the rotor winding was short-circuited, and it was verified that the characteristic frequencies matched the simulation results. Then, the protection criterion for the rotor windings’ internal short-circuit faults was proposed based on the harmonic characteristics, and a large variable-speed pumped storage unit was taken as an example to verify the proposed method. All possible rotor winding internal short-circuit faults had large protection action values under different slip ratios, which could reliably reflect the inter-turn and inter-phase short-circuit faults of the rotor windings. In addition, when other kinds of faults occurred, the action value of the proposed protection was close to 0, which has a strong maloperation prevention ability.
In summary, the advantages of the proposed method are that a protection criterion for rotor winding short-circuit faults in a variable speed pumped storage unit is proposed explicitly, and a calculation method is provided for the reasonable selection of the protection setting value and the evaluation of the protection coverage rate.
Author Contributions
Conceptualization, R.H. and J.Q.; methodology, X.Y.; software, Y.P.; validation, Y.W., R.H. and J.Q.; formal analysis, H.Z.; investigation, W.W.; resources, R.H.; data curation, J.Q.; writing—original draft preparation, Y.P.; writing—review and editing, X.Y.; visualization, Y.W.; supervision, H.Z.; project administration, W.W.; funding acquisition, R.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Key technology project of China Southern Power Grid Co., LTD, grant number STKJXM20210102.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Deng, Y.; Wang, P.; Morabito, A. Dynamic analysis of variable-speed pumped storage plants for mitigating effects of excess wind power generation. Int. J. Electr. Power Energy Syst. 2022, 135, 1–17. [Google Scholar] [CrossRef]
- Orchuk, S. Synchronous motors: Methods for quantifying rotor condition. IEEE Ind. Appl Mag. 2019, 25, 44–54. [Google Scholar] [CrossRef]
- Sahoo, S.; Rodriguez, P.; Sulowicz, M. Evaluation of different monitoring parameters for synchronous machine fault diagnostics. Electr. Eng. 2017, 99, 551–560. [Google Scholar] [CrossRef]
- Luo, W.; Yonggang, L.; Junqing, L. Diagnosis of inter-turn short circuit of synchronous generator rotor winding based on Volterra kernel identification. Energies 2018, 11, 1–15. [Google Scholar]
- Bouzida, M.B.K.; Champenois, G. Reliable stator fault detection based on the induction motor negative sequence current compensation. Int. J. Electr. Power Energy Syst. 2018, 95, 490–498. [Google Scholar] [CrossRef]
- Henaoet, H. Trends in fault diagnosis for electrical machines: A review of diagnostic techniques. IEEE Ind. Electron. Mag. 2014, 8, 31–42. [Google Scholar] [CrossRef]
- Ehya, H.; Nysveen, A.; Skreien, T.N. Performance Evaluation of Signal Processing Tools Used for Fault Detection of Hydro generators Operating in Noisy Environments. IEEE Trans. Ind. Appl. 2021, 57, 3654–3665. [Google Scholar] [CrossRef]
- Doorwar, A.; Bhalja, B.; Malik, O.P. A New Internal Fault Detection and Classification Technique for Synchronous Generator. IEEE Trans. Power Del. 2020, 34, 739–749. [Google Scholar] [CrossRef]
- Cuevas, M.; Romary, R.; Lecointe, J.P. Non-invasive detection of rotor short-circuit fault in synchronous machines by analysis of stray magnetic field and frame vibrations. IEEE Trans. Magn. 2016, 52, 8105304. [Google Scholar] [CrossRef]
- Junqing, L.; Luo, W.; Yonggang, L. Calculation of Rotor Temperature Field for Inter-turn Short Circuit of Hydro-generator Excitation Winding. J. North China Electr. Power Univ. 2018, 45, 58–66. [Google Scholar]
- Afrandideh, S.; Milasi, M.E.; Haghjoo, F. Turn to Turn Fault Detection, Discrimination, and Faulty Region Identification in the Stator and Rotor Windings of Synchronous Machines Based on the Rotational Magnetic Field Distortion. IEEE Trans. Energy Convers. 2020, 35, 292–301. [Google Scholar] [CrossRef]
- Yucai, W.; Minghan, M. A New Detection Coil Capable of Performing Online Diagnosis of Excitation Winding Short-Circuits in Steam-Turbine Generators. IEEE Trans. Energy Convers. 2018, 33, 106–115. [Google Scholar] [CrossRef]
- Venikar, P.A.; Ballal, M.S.; Umre, B.S. Search Coil Based Online Diagnostics of Transformer Internal Faults. IEEE Trans. Power Del. 2017, 32, 2520–2589. [Google Scholar] [CrossRef]
- Kulkarni, A.S.; El-Sharkawi, M.A.; Marks, R.J. Development of a technique for on-line detection of shorts in field windings of turbine-generator rotors: Circuit design and testing. IEEE Trans. Energy Convers. 2000, 15, 8–13. [Google Scholar]
- Tianhui, L.; Ming, T.; Boyan, J. Modeling Simulation and Diagnosis Analysis of Inter-turn Short Circuits Fault in Generator Rotor. High Volt. Eng. 2019, 45, 3932–3940. [Google Scholar]
- Shurong, W.; Zixu, R.; Yang, F. Early Stage Inter-Turn Faults Detection Technique for the Rotor Windings of Offshore Wind DFIGs Based on the Differential Value of Two-side Linkage’s Observation. Pro. CSEE 2019, 39, 1470–1479. [Google Scholar]
- Ehya, H.; Skreien, T.; Nysveen, A. Intelligent Data-driven Diagnosis of Incipient Inter-turn Short Circuit Fault in Field Winding of Salient Pole Synchronous Generators. IEEE Trans. Ind. Inform. 2021, 18, 3286–3294. [Google Scholar] [CrossRef]
- Ince, T. Real-time broken rotor bar fault detection and classification by shallow 1D convolutional neural networks. Electr. Eng. 2019, 101, 599–608. [Google Scholar] [CrossRef]
- Monaro, R.M.; Vieira, J.C.M.; Coury, D.V. A Novel Method Based on Fuzzy Logic and Data Mining for Synchronous Generator Digital Protection. IEEE Trans. Power Del. 2015, 30, 1487–1494. [Google Scholar] [CrossRef]
- Salomon, C.P.; Santana, W.C.; Lambert-Torres, G. Discrimination of Synchronous Machines Rotor Faults in Electrical Signature Analysis Based on Symmetrical Components. IEEE Trans. Ind. Appl. 2017, 53, 3146–3155. [Google Scholar] [CrossRef]
- Valavi, M.; Jorstad, K.G.; Nysveen, A. Electromagnetic Analysis and Electrical Signature-Based Detection of Rotor Inter-Turn Faults in Salient-Pole Synchronous Machine. IEEE Trans. Magn. 2018, 54, 8104309. [Google Scholar] [CrossRef]
- Rehman, A.U.; Chen, Y.; Zhang, M. Fault detection and fault severity calculation for rotor windings based on spectral, wavelet and ratio computation analyses of rotor current signals for a doubly fed induction generator in wind turbines. Electr. Eng. 2020, 102, 1091–1102. [Google Scholar] [CrossRef]
- Elez, A.; Car, S.; Tvorić, S. Rotor Cage and Winding Fault Detection Based on Machine Differential Magnetic Field Measurement (DMFM). IEEE Trans. Ind. Appl. 2017, 53, 3156–3163. [Google Scholar] [CrossRef]
- Fu, Y.; Ren, Z.; Wei, S. Using Flux Linkage Difference Vector in Early Inter-turn Short Circuit Detection for the Windings of Offshore Wind DFIGs. IEEE Trans. Energy Convers. 2021, 36, 3007–3015. [Google Scholar] [CrossRef]
- Lebaroud, A.; Medoued, A. Online computational tools dedicated to the detection of induction machine faults. Int. J. Electr. Power Energy Syst. 2013, 44, 752–757. [Google Scholar] [CrossRef]
- Stefani, A.; Yazidi, A.; Rossi, C. Double fed induction machines diagnosis based on signature analysis of rotor modulating signals. IEEE Trans. Ind. Appl. 2008, 44, 1711–1721. [Google Scholar] [CrossRef]
- Jun, C.; Hong, Y. Research on Protection of Internal Short Circuit in Rotor Winding of Variable Speed Pumped-Storage Generator-Motor. Electr. Power 2021, 54, 121–127. [Google Scholar]
- Shiyong, X.; Baojun, G.; Zhihui, L. Multi-loop model for fractional pole-path ratio synchronous generators with stator winding internal faults. IET Electr. Power Appl. 2020, 14, 2687–2696. [Google Scholar]
- Yuguang, S.; Wang, S. Analysis of armature inter-turn fault in the multiphase synchronous generator-rectifier system. IET Electr. Power Appl. 2019, 13, 871–880. [Google Scholar]
- Yuguang, S.; Liangliang, H.; Xiangheng, W. Calculation of the Multi-loop Inductances for Inter-turn Short Circuits of Field Windings in Non-salient Pole Synchronous Machine. Auto. Elec. Power Sys. 2010, 13, 55–60. [Google Scholar]
- Rawicki, S. Damages of windings of a three-phase slip-ring induction machine having parallel paths in the stator or in the rotor. Electr. Eng. 1988, 71, 257–267. [Google Scholar]
- Huamin, N.; Lin, G.; Yuguang, S. Simulation and Experimental Research on Stator Winding Internal Faults of AC Excitation Machine Based on Multi-Loop Theory. Pro. CSEE 2019, 39, 3666–3684. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).