Defect Shape Classification Using Transfer Learning in Deep Convolutional Neural Network on Magneto-Optical Nondestructive Inspection

Abstract

To implement a magneto-optic (MO) nondestructive inspection (MONDI) system for robot-based nondestructive inspections, quantitative evaluations of the presence, locations, shapes, and sizes of defects are required. This capability is essential for training autonomous nondestructive testing (NDT) devices to track material defects and evaluate their severity. This study aimed to support robotic assessment using the MONDI system by providing a deep learning algorithm to classify defect shapes from MO images. A dataset from 11 specimens with 72 magnetizer directions and 6 current variations was examined. A total of 4752 phenomena were captured using an MO sensor with a 0.6 mT magnetic field saturation and a 2 MP CMOS camera as the imager. A transfer learning method for a deep convolutional neural network (CNN) was adapted to classify defect shapes using five pretrained architectures. A multiclassifier technique using an ensemble and majority voting model was also trained to provide predictions for comparison. The ensemble model achieves the highest testing accuracy of 98.21% with an area under the curve (AUC) of 99.08% and a weighted F1 score of 0.982. The defect extraction dataset also indicates auspicious results by increasing the training time by up to 21%, which is beneficial for actual industrial inspections when considering fast and complex engineering systems.

1. Introduction

With improvements in manufacturing technology, nondestructive testing (NDT) has become an asset for supporting quality control and maintenance inspection processes. NDT is a noninvasive approach for providing actual results to determine the integrity and safety of an engineering system [1]. By implementing NDT assessments, the inspection process can be completed without destroying the target object, thereby increasing the economic and resource benefits. These advantages have led NDT to become the backbone of maintenance inspections in critical engineering industries such as aerospace, marine, railroad, and nuclear systems, as these industries require surface inspections to analyze and evaluate the defect risks for preventive and overhaul maintenance decisions [2,3,4,5,6].

In current NDT techniques, there are several methods of surface inspection commonly used to inspect material defects, including penetrant testing (PT), magnetic-particle inspection (MPI), and magnetic flux leakage (MFL) [7]. The PT method considers a capillary action based on filling a perforated surface with a penetrant based on a liquid or dye [8,9]. When the penetrant is cleaned from the target surface, the penetrant filling the defect stacks inside the defect and can be quickly observed using visual or UV assessments, depending on the type of penetrant. The most significant advantages of PT are its high portability and high applicability to most materials [10]. Another approach (and one of the oldest) to NDT visual surface inspections is the MPI method, which uses a magnetization process with tiny magnetic particles as a coating to observe material defects [11,12,13]. MPI is widely used for detecting surface defects in ferromagnetic materials. This inspection utilizes an induction magnetic flux based on a permanent magnet or direct-current electromagnetic field. When a specimen containing a defect is magnetized, a magnetic flux leakage (MFL) appears around the crack gap [14], and the defect can be detected when powders containing ferromagnetic particles are applied to the material. The magnetic leak attracts the powder to form the defect shape [15]. However, MPI inspection has a lower reputation compared to advanced electromagnetic techniques, as it requires a subjective decision from a highly experienced observer and is strongly dependent on inspector concentration [11]. Aiming to improve on the MPI weaknesses, MFL-based inspections have been further developed by utilizing inductive magnetic sensors such as giant magnetoresistance, Hall, and magneto-optic (MO) sensors as the observers. The MFL is widely used to inspect material defects owing to volume losses caused by corrosion or erosion. One approach to MLF inspection comprises an MO nondestructive inspection (MONDI) system, which promises a high-sensitivity assessment with a magnetic domain width of approximately 3–50 µm and a defect detection ability at up to 0.4 mm [14,16,17,18]. The MONDI system works based on a principle of the Faraday rotation effect on the behavior of light propagation through a magnetized medium. An MO sensor is used to detect the MFL distribution around a crack, with a high spatial resolution. The defects can be observed by implementing an optical polarity system based on the Faraday effect. Furthermore, to increase the assessment efficiency and reliability, robotics-based nondestructive inspection systems have been developed to address fast and complex engineering systems in actual industrial inspections (Figure 1).

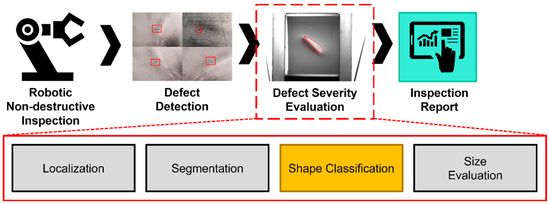
Figure 1. Future implementation of robotics-based nondestructive inspection.

To implement autonomous NDT inspections, a quantitative evaluation of the presence, locations, shapes, and sizes of defects must be performed. This capability is essential for training NDT robots to track material defects and evaluate defect severity. Several image processing algorithms have been proposed to address these challenges. Nguyen et al. (2012) proposed crack image extraction by using radial basis functions based on an interpolation technique [19]. By applying a Gaussian filtering process as preprocessing, a region-based speed function based on the Chan–Vase model could easily track the presence of a defect and extract the crack image. Lee et al. (2021) developed a boundary extraction algorithm based on image binarization to track the locations of metal grains [20]. In addition to the extraction processing algorithm, 67% of the image extraction is finished by a machine learning process [21], e.g., according to the recent advances in deep convolutional neural networks (CNN), which can achieve human-level accuracy in analyzing and segmenting an image. Table 1 summarizes the CNN application methods for NDT assessments. Both the image processing algorithms and machine learning approaches are excellent for extracting the presence and location of defects. However, the defect extraction is generally insufficient for observing the severity of defects on a metal surface. Defect severity can be inspected by evaluating the defect size and particularly the defect depth [22]. However, directly evaluating a defect’s size is a highly complex task. The defect size is strongly related to the defect geometry; thus, recognizing defect shapes is essential for tracking defect sizes. The MONDI system has advantages in complex crack inspection, including its high defect observation sensitivity, precise transcription for complex crack geometries, and independent orientation [22]. These characteristics allow the MONDI system to precisely indicate the geometry of a complex crack, and the implementation of this system using a vertical magnetizer increases the possibility of accurately tracking the defect shape. Unfortunately, an algorithm for identifying the shape of a defect from MO images has not yet been proposed. Still, the CNN promises a robust image classification performance that could support severity evaluation by providing defect shape classification tools.

Table 1. Surface defect evaluation based on a deep convolutional neural network (CNN) model.

Ref.	CNN Dataset	Method	Research Objectives	Data Acquisition	Results	Novelty
[23]	2068 images 1024 × 1024 pixels	CNN, atrous convolution, atrous spatial pyramid pooling (ASPP), deep-wise separable	Bridge crack detection	Phantom 4 Pro’s CMOS surface array camera	Accuracy: 96.37% Precision: 78.11% Specificity: 95.83% F1 score: 0.8771	Random center crop operation and integrated CNN convolution
[24]	2000 images 1024 × 1024 pixels	Transfer learning CNN models, YOLOv3 model	Structural crack detection	Manual photo collection and augmentation	Performance comparison and auto crack tracking with max. acc of 98.8%	YOLOv3 for crack location tracking
[25]	10,000 images (4 K and 6 K)	U-Net sematic segmentation, CNN	Steel defect type, severity segmentation	Constructing manual real-life industrial dataset	Improve defect segmentation by 2.5% and severity assessment by 3%	Integrated CNN branch network
[26]	12,568 images 256 × 1600 pixels	Transfer learning CNN models	Automatic steel defect detection	Public dataset	Improve defect initialization by 5% and segmentation by 26% (relatively)	Transfer learning U-Net (TLU-Net) framework for the assessment
[27]	900 images 256 × 256 pixels	3D-shadow modeling (SM), CNN	Pipelines crack identification	3D-SM	Accuracy: 93.53% Regression rate: 92.04%	3D-SM for pipeline defect detection
This study	4752 images 676 × 676 pixels	Transfer learning CNN models	Defect shape classification	Magneto-optic nondestructive inspection (MONDI) system	Comparison of each transfer learning, ensemble, and majority voting model performance and score mapping analysis	Defect shape classification method using MONDI dataset

The current project aims to develop an efficient defect shape classification method for supporting severity inspections based on the MONDI system. In this framework, the transfer learning approach of a deep CNN is adopted, using five pretrained architectures. Multiclassifier training techniques using ensemble and majority voting models are also trained to provide a comparison. The multiclassifier network promises more collaborative prediction for classifying the defect shape, thereby potentially achieving a higher prediction accuracy than a single model classifier. Three variations of image preprocessing are processed to evaluate the model performance and understand the network behavior. Ultimately, comparing all of the models allows for the formation of a potential defect classification method based on the transfer learning in a deep CNN, with promising results.

The main contribution of this research is in providing an algorithm for correctly classifying the defect shapes. This improvement is expected to support evaluations of defect severity for future implementations of robotics-based nondestructive inspections.

2. Materials and Methods

In this study, a defect shape classification algorithm was used to perform defect severity evaluation in a MONDI system. Experiments were conducted on dataset acquisition, image preprocessing, data augmentation, and transfer learning in a deep CNN to achieve the desired goals. Figure 2 summarizes the research methodology.

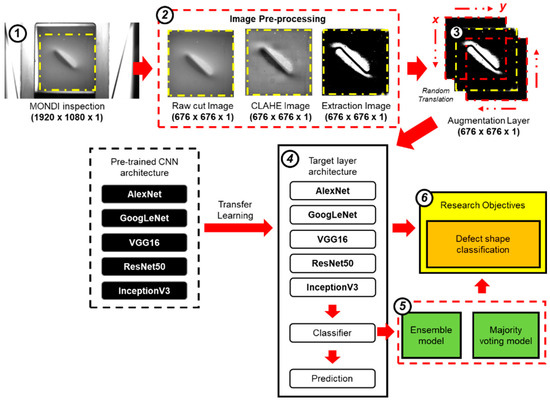
Figure 2. Outline research methodology for magneto-optic nondestructive inspection (MONDI) system with pretrained convolutional neural network (CNN).

2.1. Data Acquisition

The dataset used in this study was prepared by utilizing a novel MONDI system that reflected light, as discussed by Lee et al. [28]. Figure 3a shows the inspection process using the MONDI system. The MONDI system inspected the specimen with a 15.5 × 20.5 mm MO sensor with 0.6 mT of magnetic field saturation, a measurement range of approximately 0.03 to 5.0 kA/m, and a spatial resolution up to 1 μm, over a magnetized specimen with an artificial defect. Magnetic flux leaks (MFLs) appeared around the defect when the specimen contained a defect, owing to the corresponding discontinuities [29]. Each MFL distorted the magnetic domain distribution of the MO sensor and made the domain unstable, following the distribution of the MFL, which duplicated the defect geometry [22]. A polarized optical system was used to observe the MO sensor based on the Faraday rotation effect. In general, when linearly polarized light propagates through a medium in the direction parallel to the applied magnetic field, the polarization plane is rotated by an angle (${\theta }_F$) in proportion to the magnetic field ($B$) and sample thickness ($d$). The angle also depends on the Verdet constant ($V$), i.e., the strength coefficient of the Faraday effect in a particular material, as described by Equation (1) [30].

$${\theta }_F=V\cdot B\cdot d$$

(1)

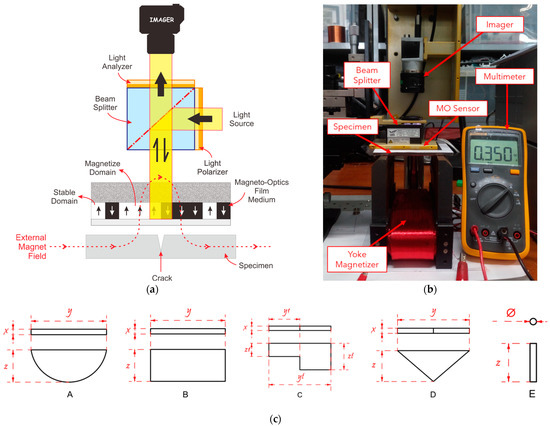
Figure 3. Data acquisition process by capturing 4752 images from 11 specimens in 72 different directions of magnetizer and six current variations using MONDI system. (a) Visualization of MONDI system; (b) experimental setup; (c) geometry of the defect: A (semioval), B (rectangular), C (combination), D (triangle), and E (hole).

This study utilized the polarized optical system by flashing 12 volts of polarized white light to a beam splitter that deflected light parallel to the MOF. The polarized light is influenced by the magnetic domain of the magneto-optical film (MOF) and rotated based on the Faraday rotation effect. The rotating plane light is reflected by the mirror layer of the MO sensor and reformed by an analyzer. Furthermore, the strength and direction of the magnetization can be obtained by estimating the rotation angle of the beam. The propagation of the light intensity through the polarizer, sample, and analyzer is defined mathematically by Equation (2), where $I_0$ is the intensity of the incident light, and ${\alpha }_0$ is the angle between the polarizer and analyzer [30]. The reflected light forms bright and dark areas according to the intensity of the rotation; these represent the crack geometry [22]. The reflection intensity can be described by analyzing the ratio of the upward and downward magnetized areas in the magnetic domain of the MO sensor [17] as explained by Equation (3), where $H$ is the external magnetic field intensity, $Hs$ is the intensity of the magnetic field saturating the MO sensors, and $E$ is the electric field of the light transmitted to the analyzer.

$$I=I_0{\cos }^2\left({\theta }_F+{\alpha }_0\right)$$

(2)

$$I_{output}=\frac{1}{2}\left[\frac{Hs+H}{Hs}{E}^2{\cos }^2\left({\alpha }_0-{\theta }_F\right)+\frac{Hs-H}{H_0}{E}^2{\cos }^2\left({\alpha }_0+{\theta }_F\right)\right]$$

(3)

The inspection in this study attempted to duplicate an actual industrial inspection process by involving variations in the magnetizer direction to determine the critical magnetizer angle, which is very important for understanding the distribution of the MFLs. The experiment was conducted using a carbon steel plate (ASTM A36) widely used for bridge structures and the marine industry, owing to its advantage of an increased service lifetime [31]. All of the specimens had a unique defect shape and dimensions; the specimens were classified as semioval, rectangular, combination shape, triangle, and hole defects (Figure 3c). In particular, 11 specimens with different artificial defect shapes and dimensions were manufactured using an electrical discharge machining (EDM) method. The machining of complex defect shapes can be completed with high precision using EDM. Table 2 lists the specimen properties and defect geometries.

Table 2. Properties of the specimen and geometry of the defect for the MONDI experiment.

Part Number	Defect Shape	Depth (z) (mm)	Length (y) (mm)	Width (x) (mm)	Diameter (⌀) (mm)	Class	Total Image
A1	Semioval	1	4.93	0.5	-	A	432
A2	Semioval	2	6.37	0.5	-	A	432
A3	Semioval	3	7	0.5	-	A	432
B1	Rectangle	1	7	0.5	-	B	432
B2	Rectangle	2	7	0.5	-	B	432
B3	Rectangle	3	7	0.5	-	B	432
C	Combination	1–3	3.5–7	0.5	-	C	432
D	Triangle	3	7	0.5	-	D	432
E1	Hole	1	-	-	0.5	E	432
E2	Hole	2	-	-	0.5	E	432
E3	Hole	3	-	-	0.5	E	432

Part number ‘C’ is a combination of 1 × 3.5 mm and 3 × 7.5 mm rectangular defect.

Furthermore, the magnetic field was induced using a yoke-type magnetizer with 2200 turns of 0.4 mm enameled copper wire in the center of the magnetizer (Figure 3b). Six variations of currents were supplied to the coil, starting from 0.2 to 0.45 A, and 72 different magnetizer directions were captured using the MONDI system. Using this configuration, the MONDI dataset contained specific geometric properties, owing to the variations in the magnetic lift-off distribution captured by the MONDI system. In addition to these advantages, inspecting defects with different current and magnetizer angles increased the number of data varieties, which is beneficial for a feature extraction process using a CNN. A total of 4752 images were captured in this experiment (Figure 4). This dataset is open for academic use. Corresponding email: jinyilee@chosun.ac.kr.

Figure 4. Magneto-optical image from MONDI system experiments.

2.2. Image Preprocessing and Data Augmentation

After completing the experiment, a dataset with 4752 elements was obtained. Three preprocessing image variations were employed to evaluate the model performance and understand the network behavior. The first dataset was processed using a simple cutting algorithm to resize the MONDI dataset to 676 × 676 pixels. This process was performed to remove unnecessary parts, thereby increasing the training efficiency.

The second dataset was processed by using the contrast-limited adaptive histogram equalization (CLAHE) algorithm to improve image clarity, which helps in feature extraction in the CNN algorithm. CLAHE is a contrast-limit equalization process; it uses an enhancement function applied to all neighborhood pixels. The process is then completed by deriving a transformation function [32,33]. The CLAHE algorithm utilizes histogram equalization to measure the intensity level of the MONDI image, thereby enhancing the image quality by increasing the contrast level to address excessive shadows and provide better defect details. Equation (4) shows the gray-level mapping and clipped histogram using the average number of pixels ($N_{avg})$, where $N_{CR-xp}$ and $N_{CR-yp}$ are the number of pixels in the X and Y directions, respectively, and $N_{gray}$ is the number of gray levels. CLAHE also has distinct advantages as a noise image limiter, i.e., by, using the cliplimit function to increase the image clarity and accuracy of the image extraction process. Equation (5) shows the function for calculating the actual number of cliplimit pixels ($N_{CL}$), where $N_{CLIP}$ is the actual current pixel in the target image.

$$N_{avg}=\frac{N_{CR-xp} . N_{CR-yp} }{N_{gray}}$$

(4)

$$N_{CL}=N_{CLIP}\cdot N_{avg}$$

(5)

The third dataset was processed by using a histogram brightness transformation (HBT) to extract the defect images. The HBT method works in a manner similar to that of a filter, by transforming matrix values unsuitable for the filter threshold. However, directly extracting the raw data causes a defect to lose some critical parts, especially on the edges. Degradation occurs during extraction because the raw image contains a foggy edge that confuses the extraction algorithm. The CLAHE dataset was used in this extraction dataset to address these challenges. The filter threshold was set to one-third of the maximum and minimum image intensities. The algorithm transformed each image pixel with a brightness between the threshold to 0 (black) and those with brightness suitable on the threshold to 255 (white). This method efficiently extracted the defect shapes. The MONDI system depends on the reflection intensity; thus, using the image pixel intensity as the threshold promises high accuracy and reduces biased results. Figure 5 shows a histogram analysis of each preprocessing step.

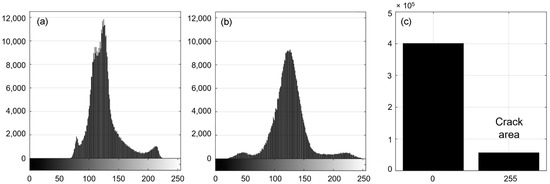
Figure 5. Image histogram analysis: (a) raw image, (b) contrast-limited adaptive histogram equalization (CLAHE) image, and (c) extraction image.

After completing the preprocessing and defect extraction, the three variation datasets were trained using a transfer learning method. However, directly processing this dataset increased the potential for overfitting the training. Overfitting can be a severe problem in a prediction model, especially if there is a weak relationship between the research outcome and predictor set variable [34]. Accordingly, an image augmentation layer was applied to generate random transformations in the datasets to prevent this condition. The augmented layer performed a random translation from −3% to 3% of the image size in the x- and y-directions. This process increased the relationship among the features and reduced the possibility of overfitting training (Figure 2).

2.3. Deep Convolutional Neural Network and Transfer Learning Pretrained Neural Network

CNNs, widely known as “convnets,” have shown tremendous improvements in image or video data prediction, reaching human-level accuracy. Essentially, a CNN is a classification structure for classifying an image into particular labeled classes by reconstructing the image features and sharing the weights of each pixel for neurons to respond [35]. A CNN has a computation process similar to other deep learning algorithms, such as the multilayer perceptron. However, a CNN makes an explicit assumption for a dataset with a specific structure, such as with image data [36]. This process makes the proposed CNN robust in image classification.

The CNN process for image classification is divided into two main processes: image extraction (convolution layer, nonlinearity, layer subsampling or pooling process) and image classification or perceptron. The convolution layer preserves the relationship of all pixel matrices by extracting a feature using a small square transformation matrix called a filter (or kernels) across the height and width (strides) of the target image. After the convolution process, negative values may appear. An additional nonlinearity operation is applied to replace the negative values with zero. This process is necessary to prevent biased results in the matrix-polling process. This process has several nonlinear operation functions, such as tanh, sigmoid, and the rectified linear unit (ReLU). However, the ReLU performs better in most situations [37]. The extraction process is completed by implementing a pooling process to reduce the dimensions of the feature map. The most common pooling process is max pooling, which separates the target data using a small filter and determines the maximum value as the final weight. The polling process reduces the number of parameters, makes the feature dimension more manageable, and controls overfitting by using fewer parameters. The polling process improves the network invariant to decrease the transformation, distortions, and translation, and automatically scales the invariant of the image representation to detect the target location. The CNN completes the training process using a weight classifier called a fully connected layer (FC). The FC represents a traditional perceptron method and provides a softmax activation function to classify an input image into various classes based on the training input. In addition, implementing the FC is the cheapest method for learning linear combinations [38].

Furthermore, when working with a similar computer vision task, implementing a tested pretrained model can promise a more efficient process than training the CNN architecture from scratch. This approach is called a transfer learning method. This method transfers the image extraction architecture of the tested model by reusing the network layer weights. Transfer learning is a powerful technique, particularly for initial benchmarking studies. The transfer learning method has proven its ability to achieve significant performance in computer vision and other research fields such as medical image computing, robotics, chemical engineering, and NDT [26,35,36,39]. In this study, five different pretrained architectures (AlexNet [40], GoogLeNet [41], VGG16 [42], ResNet50 [43], and InceptionV3 [44]) were trained using the transfer learning method by adding the image augmentation layer of the MONDI dataset as the input dataset. By analyzing all training results using the pretrained architecture, the softmax function classified them into five defect categories: semioval (A), rectangular (B), combination (C), triangle (D), and hole (E). Figure 6 summarizes the transfer learning process conducted in this study.

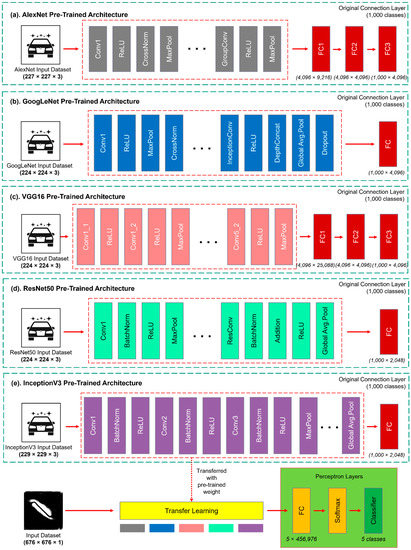
Figure 6. Transfer learning of five pretrained architectures using MONDI dataset.

3. Experimental Results

To predict the defect shape using the MONDI system, the classifier requires a deeper understanding of the visible defect features. The MONDI system has successfully shown a high sensitivity in defect observation and precise transcription for complex crack geometry, which is very beneficial for the feature extraction process in CNNs. MO images seem to look different from the true defect shape because instead of imaging the physical shape, the polarizing optical system captures the rotation intensity of the light plane corresponding to the Faraday rotation effect represented by the image intensity on each pixel, thereby very beneficial for the feature extraction process on CNN. The main goal of implementing the transfer learning method is to correctly predict the shape of a defect material during a surface inspection using the MONDI system. From the 4752 image datasets captured during the experiment, 60% of the dataset was allocated as the training dataset, and 20% was allocated as the validation dataset. Then, the last 20% was stored separately as the testing dataset, i.e., to evaluate the network performance after finishing the training. The training and validation datasets were transformed in the augmentation layer via a random translation to prevent overfitting during training. The convolution neural network was trained on MATLAB R2021a using five pretrained architectures: AlexNet, GoogLeNet, VGG16, ResNet50, and InceptionV3. As mentioned above, this study compared three variations of image preprocessing (the raw cut dataset, CLAHE dataset, and extraction dataset) to evaluate the performance and efficiency of each transfer learning model, majority voting model, and ensemble model (Figure 7). All of the computation processes, training, validating, testing, and network analysis were performed using a Dell ALIENWARE PC with an Intel^® Core™ i9-9900HQ 3.6 GHz of CPU and 32 GB of RAM. The model was trained with a 3 × 10^–4 learning rate and 150 maximum epochs. The early stop training method was applied to obtain the best parameter performance and prevent overfitting during training. The patience value for the early stop method was set at 25, meaning that if the validation loss did not decrease within 25 epochs, the training process would stop automatically. The computer was turned off for two hours after finishing the training to subside the system heat before continuing with the following models, to prevent uncertain results owing to a drop in computation performance. In particular, a performance drop could occur during training because of thermal throttling, causing the GPU or CPU to decrease the clock speed linearly with the increasing temperature.

Figure 7. Three variation datasets: raw cut image, CLAHE image, and extraction image.

Several positive results were obtained in this study by successfully preventing overfitting, underfitting, and performance drops during the training, thereby ensuring the validity of the testing results for further research. Figure 8 compares the network performance with the average training variance and training and validation accuracy plots during the network training using the transfer learning approach in the deep CNN. The training process was completed with the 15 network models without indicating either overfitting or underfitting, by maintaining an average variance between the training accuracy and validation accuracy of approximately 4.98 ± 0.4%. Overfitting is a condition in which the training and validation performance have a low bias and high variance, whereas underfitting is when they have a high bias and low variance. The average testing accuracy of each transfer learning model gave a relatively higher performance than the validation accuracy during network testing, indicating that the testing dataset was easier to predict.

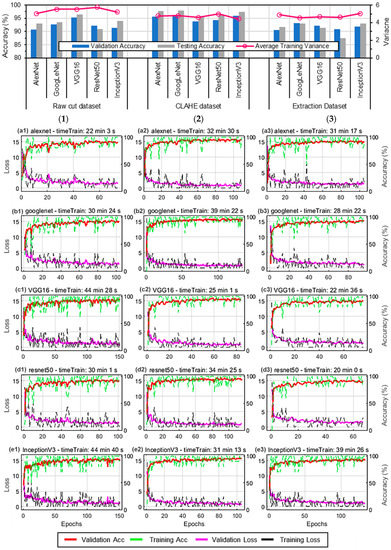
Figure 8. Plots of training and validation performance from three variation dataset on five pretrained architecture using transfer learning approach in deep CNN: (1) raw image dataset, (2) CLAHE image dataset, and (3) extraction image dataset.

This result confirmed that the transformation of the training and validation datasets using the augmentation layer was performed effectively. From the five transfer learning models, the VGG16 model obtained the best results for the raw cut dataset with a validation accuracy of 95.37%, whereas GoogLeNet showed the best results for the CLAHE and extraction datasets with 96.32% and 93.17% validation accuracies, respectively.

After analyzing the five transfer learning models, the ensemble model was trained using all of the models, and the majority voting classifier was trained for comparison. Table 3 shows the performance of each transfer learning model and comparisons with ensemble and majority voting models. From 150 maximum epochs, the average early stop training of each dataset was 115 epochs with 17.94 ± 0.13 s/epoch for computation speed for the raw cut dataset, 109 epochs with 17.84 ± 0.05 s/epoch for the CLAHE dataset, and 95 epochs with 17.84 ± 0.07 s/epoch for the extraction dataset. The model accuracy was provided in three forms: testing, network, and weighting. The testing accuracy indicates the model performance in predicting the testing dataset, whereas the network accuracy and weighted accuracy indicate the average model performance for every defect class. Measuring the model accuracy in every class provides a better understanding of model performance. The weighted accuracy obtained higher results than the network accuracy, indicating that the classifier struggled to predict the testing model correctly in several defect classes. The F1 score clearly describes the uncertainty value in each class, and reflects the difficulties experienced by the classifier. After analyzing all of the models, the ensemble model consistently gave the highest testing results for each dataset compared with the average testing accuracy from the transfer learning and majority voting models. The ensemble model achieved the highest results on the CLAHE dataset with 98.21% testing accuracy, an area under the receiver operating characteristic curve of 99.08%, and a weighted F1 score of 0.982. In contrast, the lowest testing accuracy was achieved by the ResNet50 model on the extraction dataset, with 87.46% accuracy. Except for the majority voting model combining every transfer learning prediction, all models on each dataset performed with a relatively stable classification time, with an average of 2.57 ± 0.02 s from 949 testing images.

Table 3. Comparison of the performance for each transfer learning model.

Dataset	Model	Epoch	Testing Accuracy (%)	Network Accuracy (%)	Weighted Accuracy (%)	Area under the Curve (AUC) (%)	F1_Score					Classification Time (s)
							A	B	C	D	E
Raw cut Image	AlexNet	73	93.05	97.22	97.53	97.88	0.960	0.934	0.796	0.824	0.981	2.570
	GoogLeNet	102	93.57	97.43	97.39	98.12	0.952	0.939	0.891	0.816	0.965	2.565
	VGG16	150	96.42	98.57	98.70	98.70	0.975	0.972	0.901	0.901	0.987	2.570
	ResNet50	100	90.94	96.38	97.44	97.20	0.967	0.947	0.688	0.635	0.990	2.566
	InceptionV3	150	93.99	97.60	98.49	98.41	0.977	0.983	0.758	0.701	0.998	2.574
	Majority Voting	-	94.94	97.98	98.43	98.84	0.979	0.970	0.824	0.819	0.985	-
	Ensemble	-	95.68	98.27	98.70	98.84	0.979	0.976	0.837	0.849	0.992	2.608
Contrast-limited adaptive histogram equalization (CLAHE) Image	AlexNet	109	97.68	99.07	99.43	99.32	0.989	0.996	0.900	0.889	1	2.567
	GoogLeNet	133	97.89	99.16	99.43	99.06	0.985	0.996	0.907	0.916	1	2.565
	VGG16	84	95.47	98.19	98.26	94.98	0.947	0.963	0.904	0.880	0.996	2.554
	ResNet50	116	96.31	98.52	98.74	98.60	0.979	0.970	0.914	0.846	0.992	2.563
	InceptionV3	105	97.37	98.95	99.16	98.31	0.981	0.985	0.908	0.912	0.998	2.563
	Majority Voting	-	98.10	99.24	99.41	98.89	0.986	0.989	0.931	0.935	1	-
	Ensemble	-	98.21	99.28	99.48	99.08	0.988	0.990	0.937	0.929	1	2.598
Extraction Image	AlexNet	105	91.78	96.71	96.74	96.11	0.909	0.928	0.810	0.802	0.990	2.567
	GoogLeNet	96	93.05	97.22	97.41	95.41	0.933	0.938	0.840	0.815	0.994	2.561
	VGG16	76	91.36	96.54	96.71	95.65	0.910	0.922	0.797	0.771	0.996	2.560
	ResNet50	67	87.46	94.98	95.25	94.47	0.876	0.886	0.680	0.663	0.994	2.567
	InceptionV3	133	92.94	97.18	97.57	96.09	0.936	0.963	0.822	0.740	0.986	2.564
	Majority Voting	-	93.15	97.26	97.34	96.38	0.919	0.945	0.854	0.811	0.996	-
	Ensemble	-	94.20	97.68	97.82	96.91	0.934	0.958	0.869	0.828	0.996	2.603

Figure 9, Figure 10 and Figure 11 show the confusion matrices of the best and weakest models and their comparisons with the majority voting and ensemble models on each dataset. Comparing all network models, it can be seen that the ensemble and majority voting models achieve relatively more balanced prediction results in each dataset, i.e., by successfully reducing the bias from each transfer learning model and proposing more collaborative predictions for classifying defect shapes. From analyzing model performance on every dataset, the raw cut dataset as performed by the ResNet50 model has a problem predicting the combination and triangle defect classes with the lowest F1 scores of 0.688 and 0.635, respectively. In contrast, the VGG16 model using the CLAHE dataset successfully improves the classification bias by increasing the network performance for the combination and triangle defect classes by 31.4% and 38.5%, respectively. Unfortunately, ambiguous prediction results were detected in the extraction dataset. Thus, it not only failed to improve the prediction performance in the combination and triangle defect classes, but the extraction dataset also indicated a new problem regarding predicting the semioval and triangle defect classes. The weighted F1 score of the weakest extraction model with ResNet50 decreased by 9.3% relative to the CLAHE dataset and by 4.4% relative to the raw cut dataset. However, the training time of the extraction dataset showed a successful and auspicious performance by extracting the image features with an average training time of 28 min and 20 s, improving the training time of the CLAHE and the raw cut dataset by 15% and 21%, respectively. Training and classification time improvements are beneficial in actual industrial inspections, as they commonly involve fast and complex systems. Fortunately, the hole defect class has a relatively consistent performance, as it maintains an F1 score above 0.96 for each dataset and network model. Furthermore, understanding how a network model makes a particular decision is essential to providing check-and-balance control of CNN models and recording model weaknesses for further training. Figure 12 shows a score activation map plotted using occlusion sensitivity, with the aim of further understanding the network behavior [45]. The red area of the score map indicates the area that positively influences the classifier when predicting the defect class. The causes of bias in each dataset were identified using this approach. The bias in the raw cut dataset was caused by an excessive shadow that interfered with the classifier. The CLAHE dataset can reduce the bias caused by unnecessary shadows. The CLAHE dataset uniforms the minority shadow and reduces complexity by sharpening the specific shadows of the defect shapes. This ability increases the testing accuracy for the CLAHE dataset relative to the other two datasets. Moreover, the score map analysis successfully identifies ambiguous predictions in the extraction dataset. The strange prediction from the extraction dataset was a consequence of an extraction process using a fixed threshold filter. A fixed threshold makes the extraction process suboptimal because the defect loses some critical parts, especially on the edges. Figure 13 shows an analysis of the bias for every dataset.

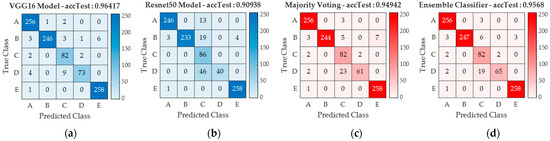
Figure 9. Confusion matrix: (a) best, (b) weakest, (c) voting, and (d) ensemble, of raw cut dataset.

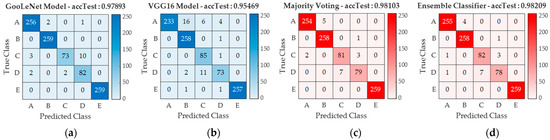
Figure 10. Confusion matrix: (a) best, (b) weakest, (c) voting, and (d) ensemble, of CLAHE dataset.

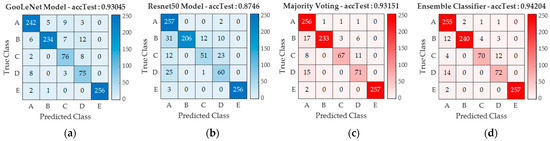
Figure 11. Confusion matrix: (a) best, (b) weakest, (c) voting, and (d) ensemble, of extraction dataset.

Figure 12. Score activation map for analyzing network behavior using occlusion sensitivity.

Figure 13. Bias analysis: (a) raw cut dataset, (b) CLAHE dataset, and (c) extraction dataset.

4. Conclusions

In this study, the main concern was to propose a deep CNN technique for classifying defect shapes during surface inspections using a MONDI system. This framework adopted a transfer learning approach with five pretrained architectures: AlexNet, GoogLeNet, VGG16, ResNet50, and InceptionV3. An experimental study using the MONDI system was conducted to provide a dataset using five defect shape variations on 11 specimens: semioval, rectangular, combination, triangle, and hole defects. In total, 4752 phenomena were captured using the MO sensor. Then, 60% of the dataset was allocated as the training dataset, 20% was allocated as the validation dataset, and the last 20% was stored separately as the testing dataset to evaluate the network performance after finishing the training. To train the deep CNN model, the MONDI dataset was processed based on the feature extraction of the respective pretrained models, and the output was classified using a softmax function classifier. Ensemble and majority voting models using the five pretrained models were employed for comparison. The model performance was observed by evaluating the network performance for three variations of image preprocessing: raw cut images, CLAHE images, and extraction images.

Several positive results were obtained in this study by successfully preventing overfitting, underfitting, and performance drops during network training, thereby ensuring the validity of the testing results for further research. The investigation of network behavior successfully identified the causes of bias in each dataset by plotting a score activation map using occlusion sensitivity. After analyzing all of the models, the ensemble model gave the highest testing results for each network model, by proposing more collaborative predictions for classifying the defect shape. The ensemble model performed the best on the CLAHE dataset with a 98.21% testing accuracy, AUC value of 99.08%, and weighted F1 score of 0.982. The extraction dataset indicated promising results by increasing the training time by up to 21%. Improvements in training and classification time are beneficial in real industrial inspections, as these commonly must manage fast and complex systems. The extraction dataset can be improved by adding a more sophisticated defect extraction algorithm with a dynamic threshold filter (rather than a fixed threshold filter). This function will track the maximum and minimum thresholds of every defect image, thereby making the processes more independent.

Another limitation was owing to the unbalanced dataset in every class, which reduced the prediction accuracy. Training a deep CNN without a balanced dataset can increase the possibility of overfitting during training and lead to weak network generalization. An imbalanced dataset can be improved by adding an oversampling or undersampling algorithm to increase the number of minority datasets via random sampling. It sounds straightforward to implement but is very challenging in practice, because the MONDI system dataset is very sensitive to image transformations. Careless transformation and augmentation will cause the dataset to lose essential features of the defect shape.

Future research directions include improving the image preprocessing and data augmentation techniques to improve the accuracy, e.g., by reducing the extraction error while avoiding overfitting during training. This improvement is expected to support evaluations of defect severity for future implementations of robotics-based nondestructive inspections.