Research on Interface Slip Characteristics of Heritage Composite Timber Columns under Inclined Deformation

Abstract

In order to study the mechanical performance and friction slip mechanism of the interface of a composite timber column under inclined deformation, the unilateral contact mechanical model of an ancient composite timber column under inclined deformation is proposed in this paper. According to the limit of the inclination angle of slip point and the limit of the inclination angle of slip surface, the failure modes of the combination’s interface can be divided into three stages: the fully sticky stage, the partially sticky stage and the sliding stage. The theoretical results of the sliding displacement and shear stiffness of the combination’s interface under the effect of iron hoops were obtained by using the elastic mechanics method. Based on the shear sliding test of a composite timber column’s interface under the effect of iron hoops, the influences of different parameters on the shear sliding performance of the combination’s interface were investigated. The test results show that the number and the spacing of the iron hoops and the inclination angle of the interface are important factors affecting the shear strength of the combination’s interface. The shear strength of the interface increased with the increase in the number of iron hoops and the inclination angle of the interface. Since hoop spacing that is too large or too small cannot effectively improve the shear capacity of the interface, there is an optimal value for the hoop spacing.

1. Introduction

In the heritage timber structures of ancient Chinese buildings, the column is the most important bearing component in the stress system. Most of the beams, columns and other components of Chinese heritage timber structures are directly made of logs. However, as early as in Yingzaofashi [1], the concept of the composite column has been put forward, which is the practice of assembling large pieces of materials with small pieces when there were not enough logs available. The garlic petal columns of Baoguo Temple in Ningbo are the earliest masterpiece preserved in the case of composite columns and a polyprism structure with a similar composite form also exists in the Potala Palace in Tibet, as shown in Figure 1. The practice of the creation of the garlic petal columns of Baoguo Temple and Tibetan polyprism use are differently from that of the composite column that was recorded in Yingzaofashi, but the basic principle of them is the same. All of them used built-in mortise and tenon joints, external hoops or nails to combine small pieces of wood into larger pieces, so as to improve the bearing capacity and utilization rate of the materials.

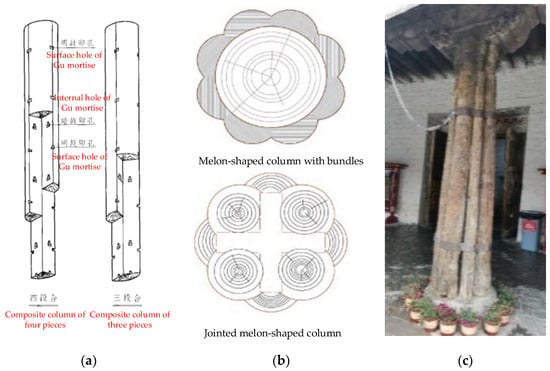
Figure 1. Schematic diagrams of the composite column. (a) The composite column in Yingzaofashi; (b) garlic petal column of Baoguo Temple in Ningbo; (c) Tibetan polyprism.

Due to the effects of the surrounding environment and the upper structure over thousands of years, the composite timber columns have undergone different degrees of inclined deformation. The existence of inclined damage will affect the mechanical performance and friction slip characteristics of the combined interface and, therefore, affect the bearing capacity of the composite timber column and the whole heritage timber structure. Therefore, it is significant to study the sliding characteristics of interface in order to protect and develop the heritage timber structure by focusing on the inclined deformation of the components.

At present, scholars have done a lot of work on the study of composite timber columns and most of the research has focused on modern glulam columns. Yang et al. [2] conducted axial compression tests on a glulam wood column in order to study its deformation and its stability-bearing capacity and it was found that the bearing capacity increased by 4.3% compared to the results of tests that were carried out on a log column with the same cross-sectional area. Zeng et al. [3] considered the influence of different slenderness ratios on the ultimate bearing capacity of a glulam wood column and proposed an empirical formula for the reduction coefficient of the ultimate bearing capacity of long columns by the use of regression analysis. There are a few reports of research on the mechanical properties of traditional composite timber columns. Chen et al. [4] obtained the internal structure of the bearing melon-shaped column in the grand hall of Ningbo Baoguo Temple through non-destructive testing technology, providing basic data support for the protection and repair of the grand hall. Chen et al. [5] studied the mechanical properties of a composite column that is connected by nails under axial compression and analyzed the influences of the slenderness ratio, nail spacing, steel hoop and hoop spacing on the stability-bearing capacity of the composite column. An [6] explored the influence of the diameter, spacing, number of rows of compressed wood pins and slenderness ratio of the components on the stability-bearing capacity of a compressed timber pin composite column by numerical modeling and proposed an adjustment coefficient formula for the stability-bearing capacity, considering the influence of the slenderness ratio.

The majority of the research on the mechanical properties of ancient wooden columns has focused on the bearing capacity or stability of a single wooden column, while the initial inclined deformation of the wooden column has been considered to a lesser extent. Considering the second-order bending effect and the elastic–plastic bending of members, Zhou [7] derived the ultimate bearing capacity formula of biased timber components and the theoretical expression of failure deflection at the central span of a rectangular section timber member. Chang et al. [8] used the method of elasticity to simplify the cumulative deformation of the column and they then deduced the analytical results of the stress, displacement and yield load of the wooden column under the axial load. Lam et al. [9] analyzed the lateral support capacity of wooden columns under bi-axial eccentric pressure in terms of the stability-bearing capacity and they proposed a numerical model for columns undergoing initial bending. Matthias et al. [10] proposed a theoretical model of the wood frame considering strain and material nonlinearity under an eccentric load in order to analyze the nonlinear deformation of wood columns under axial compression and bending.

The amount of research on the friction slip characteristics of an interface is abundant and it mainly focuses on the shearing–bonding–sliding mechanism and bearing capacity of steel–steel, steel–concrete or steel–wood combination interfaces. Schnal [11,12] has analyzed the influence of boundary conditions and axial deformation on the critical buckling load of geometrically elastic double-layered composite columns with interlayer slip. On this basis, Kryžanowski et al. [13] proposed a mathematical model of sliding buckling for a double-layer composite column with an inelastic material and nonlinear interlaminar displacement and obtained accurate results. Girhammar et al. [14,15] carried out first-order and second-order analyses of uniform composite beams and columns with interlaminar sliding under a static load, provided ordinary differential equations and general solutions for their deflection and internal action and derived accurate characteristic equations and corresponding buckling length coefficients under four different Euler boundary conditions. Research on the friction slip characteristics of a wood–wood combination interface needs to be further carried out by scholars. Cao [16] considered the friction sliding shear effect between a two-layer wooden beam and established a nonlinear analytical model of a two-layer wooden beam that is based on Euler–Bernoulli beam theory. Kroflič et al. [17] proposed a new mathematical model and finite element formula for the non-linear analysis of the mechanical properties of double-layer timber beams. Yang [18] and other scholars [19,20,21] have conducted single shear or double shear tests on the combined interfaces of different forms of composite structures and have carried out parameter analysis on the effective bonding length of the combined interface in order to explore the variation in the law of bonding stress and strain on the interface.

Given the current status of the literature, this paper aims to study the mechanical performance and friction slip mechanism of the interface of a composite timber column under inclined deformation, it then puts forward a unilateral contact mechanical model of ancient composite timber columns and deduces the formula of the sliding amount and the expression of the shear stiffness of the interface under the effect of iron hoops. Through an experiment on the interface slip characteristics of the composite timber column, this paper explores the influence of the number and the spacing of the iron hoops and the inclination angle of the interface on the shear sliding performance, so as to more clearly and accurately analyze the bearing capacity of the interface of a composite timber column that is in a damaged state, and it finally applies these findings to the state evaluation of ancient timber structures that are in a damaged state.

2. Mechanical Performance of a Unilateral Combined Interface under Inclined Deformation

In this section, based on the most basic shape and connection mode of the composite timber columns that are found in Yingzaofashi, the mechanical model of the unilateral contact of a composite timber column with a square section in ancient buildings is proposed and the calculation formula for the stress distribution of the composite’s interface is derived. By analyzing the sliding mechanism of the composite’s interface under the effect of iron hoops, a three-stage sliding failure mode is proposed and the limit of this failure mode is able to be obtained.

2.1. Stress State of the Unilateral Contact Interface of a Composite Timber Column

Due to the long-term influences of the upper structure and the environment, the wooden column will tilt to a certain extent, resulting in a lateral displacement of the top of the column. At this time, the included angle between the wooden column and the ground is less than 90°. Figure 2a shows a schematic diagram along the height and length when a composite timber column inclines under a vertical load. The left portion of the composite timber column is column A, and the right portion is column B. Column A and column B have the same height but different sizes. The vertical action of the upper structure on the composite timber column is simplified into a vertical concentrated load N and applied to the center of the top of the column. θ is the included angle between the edge of the composite timber column and the vertical direction when the column inclines. ∆ is the horizontal lateral displacement of the column’s top.

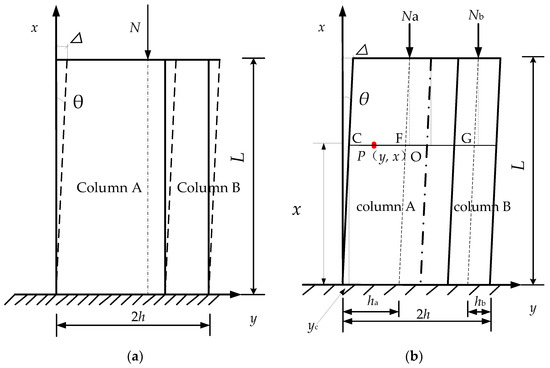
Figure 2. Inclined composite timber column. (a) Schematic diagram of tilting; (b) diagram of force analysis, where P (y, x) is any point in the composite timber column.

2.1.1. Basic Assumptions

In order to simplify the calculation, the following basic mechanical assumptions were made:

• The interaction between the dowel pin and mortise–tenon joint in the ancient timber structure is not considered.
• Each component material is in the linear elastic range under tension and compression.
• Shear stress along the interface direction and normal stress perpendicular to the interface direction will be generated on the interface of the timber column.
• The positive pressure that is produced by the iron hoops and applies to the interface is in a sinusoidal distribution and varies with the position and number of hoops.
• Under the action of a vertical load, N, there is only friction slip along the interface but no displacement that is perpendicular to the interface.
• On the non-sliding stage, the wood conforms to the plane section assumption.

2.1.2. Vertical Stress Distribution at Any Point

Each cross section along the column’s height still remains in a planar state when the composite column is inclined. It is assumed that the vertical stress on the cross section is linearly distributed in the y direction and uniformly distributed along the width direction. The force analysis diagram of a composite timber column in an inclined state is shown in Figure 2b. P (y, x) is any point in the composite timber column. The values h_A and h_B are the distance from the central axis of column A and column B to the edge of the column, respectively, and these meet the requirement of h = h_A + h_B. The following relations can be obtained from the geometric relationship: $\tan \theta ={{\displaystyle y}}_c/x$, ${{\displaystyle y}}_O={{\displaystyle y}}_{\mathrm{c}}+h$.

According to the relative magnitude of the compressive stiffness of the two columns, ${{\displaystyle N}}_A$ and ${{\displaystyle N}}_B$ can be obtained by distributing the vertically concentrated load N to the centers of the tops of column A and column B.

$${{\displaystyle N}}_A=\frac{{{\displaystyle EA}}_A}{{{\displaystyle EA}}_A+{{\displaystyle EA}}_B}N$$

(1)

$${{\displaystyle N}}_B=\frac{{{\displaystyle EA}}_B}{{{\displaystyle EA}}_A+{{\displaystyle EA}}_B}N$$

(2)

where E represents the modulus of the elasticity of the wood and ${{\displaystyle A}}_A$ and ${{\displaystyle A}}_B$ are the sectional areas of column A and column B, respectively.

According to the basic assumptions, the vertical stress of the plane at P satisfies the linear distribution in the y direction, so the expression of the vertical stress at P can be assumed as:

$${\sigma }_x(y)=ky+c$$

(3)

The force analysis of the body above P can then be carried out and the following equation can be obtained from the static equilibrium equation ${{\displaystyle \sum F}}_x=0$:

$$b{\displaystyle {\int }_{y_{\mathrm{c}}}^{y_{\mathrm{c}}+2h}(ky+c)dy-\left({{\displaystyle N}}_A+{{\displaystyle N}}_B\right)=}0$$

(4)

where b represents the width of the column.

Equation (5) can be obtained from the moment equilibrium equation ${\displaystyle \sum M_{(\mathrm{O})}}=0$. Note that $N_A+N_B=N$ and $N_B{h}_A-N_A{h}_B=M^{\prime }$ are specified in advance.

$$-N_A(y_c-L\tan \theta +h_B)+N_B(L\tan \theta +h_A-y_c)+b{\displaystyle {\int }_{y_{\mathrm{c}}}^{y_{\mathrm{c}}+2h}(ky+c)(y_c+h-y)dy}=0$$

(5)

According to Equations (4) and (5), the coefficients k and c can be expressed as:

$$k=\frac{3\left[N(L\tan \theta -y_c)+M^{\prime }\right]}{2b{h}^3}$$

(6)

$$c=\frac{N}{2bh}-\frac{3(y_c+h)\left[N(L\tan \theta -y_c)+M^{\prime }\right]}{2b{h}^3}$$

(7)

By substituting Equations (6) and (7) into Equation (3), the vertical stress at P can be calculated as:

$${\sigma }_x(y)=\frac{3\left[N(L-x)\tan \theta +M^{\prime })\right]}{2b{h}^3}y+\frac{N}{2bh}-\frac{3(x\tan \theta +h)\left[N(L-x)\tan \theta +M^{\prime }\right]}{2b{h}^3}$$

(8)

2.1.3. Stress Distribution on the Interface

When the composite timber column is inclined, the stress on any inclined section can be obtained according to the unidirectional stress state at any point in the interface. The stress distribution on any inclined section is shown in Figure 3.

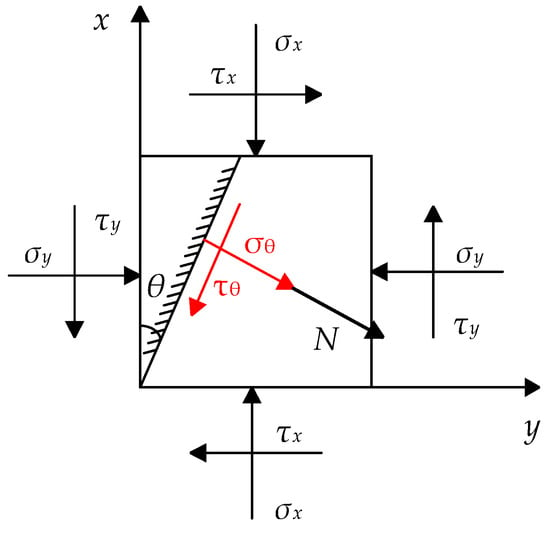
Figure 3. Stress distribution on any inclined section.

According to material mechanics, the stress of any inclined section under the plane stress state is:

$$\{\begin{array}{l}{\sigma }_{\theta }=\frac{{\sigma }_x+{\sigma }_y}{2}+\frac{{\sigma }_x-{\sigma }_y}{2}\cos 2\theta -{\tau }_x\sin 2\theta \\ {\tau }_{\theta }=\frac{{\sigma }_x-{\sigma }_y}{2}\sin 2\theta +{\tau }_x\cos 2\theta \end{array}$$

(9)

The stress on the interface satisfies ${\sigma }_x=-{\sigma }_y$ and ${\tau }_x={\tau }_y=0$. The y coordinate of any point of the interface satisfies the relation: $y=\tan \theta x+2h_{\mathrm{a}}$. By substituting Equation (8) into Equation (9), the distribution of the shear stress ${\tau }_{\theta }$ and normal stress ${\sigma }_{\theta }$ on the inclined section at any point in the composite timber column can be obtained:

$$\{\begin{array}{l}{\sigma }_{\theta }=-\{\frac{N}{2bh}-\frac{3[N(L-x)\tan \theta +M^{\prime }](h_A-h_B)}{2b{h}^3}\}{\sin }^2\theta \\ {\tau }_{\theta }=-\{\frac{N}{2bh}-\frac{3[N(L-x)\tan \theta +M^{\prime }](h_A-h_B)}{2b{h}^3}\}\sin \theta \cos \theta \end{array}$$

(10)

2.2. Mechanical Model of Unilateral Contact on the Interface under the Effect of Iron Hoops

The stress that manifests in the normal direction outside the interface and the stress of the peripheral iron hoops are related to the normal stress that is caused by the inclination. It is assumed that the force that is generated by the peripheral iron hoops is in a sinusoidal distribution, as shown in Figure 4. The stress in the normal direction, outside of the interface, can be calculated as:

$$r(x)=a\sin \frac{(2n-1)\pi x}{L}+a+{\sigma }_{\theta }$$

(11)

$$x=\frac{(4i-3)L}{4n-2}$$

(12)

where n is the number of peripheral iron hoops, i represents the ith hoop, and a represents the amplitude of the normal stress on the interface at the position of the iron hoops.

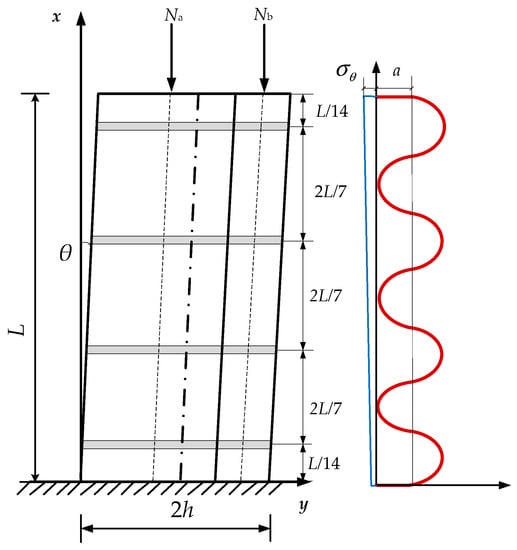
Figure 4. The normal force on the interface.

2.2.1. The Sticky Stage

When the inclination angle of the composite timber column is small, the maximum shear stress of the interface is less than that of the maximum sliding friction. At this time, the interface is in the sticky stage and the axial deformation of the two columns is coordinated. The shear stress of the interface will increase with the increase in the inclination angle. When the inclination angle increases to the point where the maximum shear stress of the interface is greater than that of the maximum sliding friction, the interface will slip. At this angle, the shear stress of the interface is equal to that of the maximum sliding friction, which is defined as the boundary inclination angle between the sticky stage and the sliding stage, namely the limit inclination angle of the slip point ${\theta }_1$.

In this state, the shear stress and friction force of the interface are calculated by Equations (13) and (14), respectively, and ${\theta }_1$ can be solved by making the two equations equal.

$$\tau (x)={\tau }_{\theta }=-\{\frac{N}{2bh}-\frac{3[N(2L-x)\tan \theta +M^{\prime }](h_A-h_B)}{2b{h}^3}\}\sin \theta \cos \theta$$

(13)

$${\tau }_m={\mu }_{f}r{(x)}_{\max }$$

(14)

where ${\mu }_f$ is the friction coefficient of the interface.

When the value of the shear stress at the interface is equal to the value of the maximum sliding friction, the whole interface will slip and the inclination angle, at this time, is defined as the limit inclination angle of slip surface ${\theta }_2$.

In this case, the value of the shear stress and the value of the maximum sliding friction of the interface can be calculated from Equations (15) and (16), respectively.

$$F_{\tau }(x)=b{\displaystyle \int {\tau }_{\theta }(x)dx}=-\{[\frac{N}{2h}-\frac{3(2NL\tan \theta +M^{\prime })(h_A-h_B)}{2h^3}]x+\frac{3N(h_A-h_B)\tan \theta }{4h^3}{x}^2\}\sin \theta \cos \theta +C_1$$

(15)

$$\begin{array}{l}{F}_r(x)=b{\displaystyle \int r(x)dx}=\frac{-aL}{(2n-1)\pi }\cos \frac{(2n-1)\pi x}{L}\\ -\{\frac{N}{2h}-\frac{3\left(2NL\tan \theta +M^{\prime }\right)(h_A-h_B)}{2h^3}x+\frac{3N(h_A-h_B)\tan \theta }{4h^3}{x}^2\}{\sin }^2\theta +C_2\end{array}$$

(16)

where C₁ and C₂ are constants.

According to $F_{\tau }(x)={\mu }_f{F}_r(x)$, ${\theta }_2$ can be obtained.

2.2.2. The Sliding Stage

Because the trigonometric value of any given angle is a constant, the shear stress of the interface is linearly distributed along the height of the column. It is assumed that the shear stress that is acting on the interface is equal to the maximum sliding friction when the slip displacement of the interface is ∆L, therefore the shear stress of the interface satisfies the following equation:

$$\{\begin{array}{l}\tau (x)=\{\begin{array}{ll}{b}_{1}x+c_1& (0\le x\le L-\Delta L)\\ {\tau }_m& (L-\Delta L<x\le L)\end{array}\\ r(x)=a\sin \frac{(2n-1)\pi x}{L}+b_{2}x+c_2\end{array}$$

(17)

where $b_1=-\frac{3(NL\tan \theta +M^{\prime })(h_A-h_B)\sin \theta \cos \theta }{2h^3}$, $c_1=-\frac{[N{h}^2-3\left(NL\tan \theta +M^{\prime }\right)\left(h_A-h_B\right)]\sin \theta \cos \theta }{2h^3}$, $b_2=\frac{3(NL\tan \theta +M^{\prime })(h_A-h_B){\sin }^2\theta }{2h^3}$, $c_2=\frac{[N{h}^2-3\left(NL\tan \theta +M^{\prime }\right)\left(h_A-h_B\right)]{\sin }^2\theta }{2h^3}$.

Furthermore, in order to calculate the slip displacement of the interface, any micro-element dx is taken along the column’s height direction for analysis, as is shown in Figure 5.

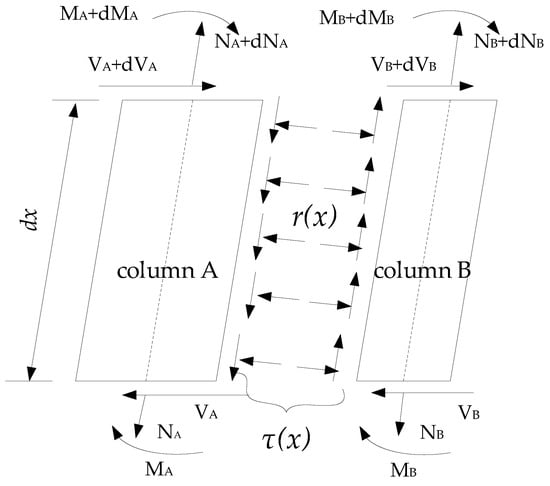
Figure 5. The force exerted on any micro-element.

Equation (18) can be obtained from the equilibrium equation.

$$\{\begin{array}{l}\frac{d{N}_i(x)+dVi(x)\sin \theta }{dx}\mp \tau (x)=0\\ \frac{d{V}_i(x)\cos \theta }{dx}\mp r(x)=0\\ \frac{d{M}_i(x)}{dx}+V_i(x)+\tau (x)h_i=0\end{array}$$

(18)

where $N_i(x)$, $V_i(x)$ and $M_i(x)$ (i = a, b) represent the axial force, shear force and bending moment at the center of the mass of the column. The value $\tau (x)$ represents the shear stress per unit length x away from the bottom of the timber column.

Equation (19) can be obtained from the geometric equation:

$${\epsilon }_i(x)=u_i(x)$$

(19)

where ${\epsilon }_i(x)$ and $u_i(x)$ (i = a, b) represent the strain and axial displacement at the centroidal axis. Then, the relative axial displacement difference along the interface (i.e., the slip displacement of the interface) can be expressed as:

$$g(x)=u_a(x)-u_b(x)$$

(20)

Equation (21) can be obtained from the physical equation:

$$\{\begin{array}{l}{N}_i(x)=E_i{A}_i{\epsilon }_i(x)\\ \tau (x)=k_f(x)g(x)\end{array}$$

(21)

where $k_f(x)$ is the shear stiffness of the interface.

According to Equations (18) through (21), the axial displacement difference of the interface can be calculated as:

$$g(x)=\frac{1}{EA}[{\tau }_m{x}^2+(N_a-N_b-{\tau }_{m}L)x-\frac{2b_1}{3}{(L-\Delta L)}^3+({\tau }_m-c_1){(L-\Delta L)}^2]$$

(22)

The shear stiffness of the combination’s interface can be calculated by:

$$k_f(x)=\frac{{\tau }_m}{g(x)}=\frac{{\tau }_{m}EA}{{\tau }_m{x}^2+(N_a-N_b-{\tau }_{m}L)x-\frac{2b_1}{3}{(L-\Delta L)}^3+({\tau }_m-c_1){(L-\Delta L)}^2}$$

(23)

3. The Shear Sliding Test of the Composite Timber Column’s Interface

3.1. Specimens’ Design

In this test, the side blocks were chamfered in order to simulate the initial inclined deformation of the specimens. When the horizontal lateral displacement ∆ of the top of the column was 7 mm, the inclination angle of the component was 2.67°. When the horizontal lateral displacement ∆ of the top of the column was equal to 9.3 mm, the inclination angle of the component was 3.43°. The structure and dimensions of the typical specimens are shown in Figure 6. The height of the side block and middle block was 360 mm, the section size of the side block was 35 mm × 95 mm and the section size of the middle block was 80 mm × 80 mm. The test was divided into 10 groups with 3 specimens in each group. The geometric parameters and the grouping of the specimens are shown in Table 1. The wood that was used in the test was larch (Larix principis-rupprechtii), which is commonly used in the wooden structures of ancient buildings in northern China, as shown in Figure 7a. According to the Wooden Structure Design Manual [22], the bending modulus of elasticity of larch (Larix principis-rupprechtii) is 1.29 × 10⁴ N/mm² and the compressive modulus of elasticity along the grain is 1.17 × 10⁴ N/mm². The iron hoops were made of Q235 steel, with a width of 10 mm and a thickness of 5 mm, as is shown in Figure 7b. The elastic modulus of the Q235 steel was taken as 200 GPa. The iron hoops were connected by bolts with a diameter of 5 mm.

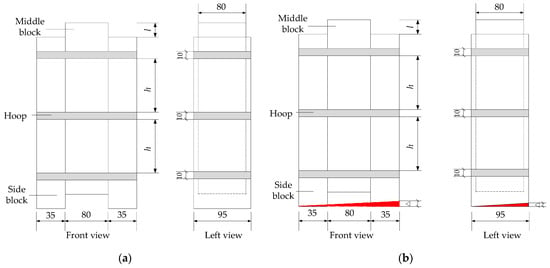
Figure 6. Specimen structure, unit: mm. (a) Non inclined specimen; (b) inclined specimen. Where Δ represents the chamfering height of the side block; l represents the initial distance between the top of the middle block and the top of the side block, which was taken as 20 mm in this test; h represents the distance between iron hoops.

Table 1. Grouping of tests.

Test Group Number	Parameter	Number of Iron Hoops	Number of Specimens	Spacing of Iron Hoops	Inclination Angle/°
1-1	Number of iron hoops	1	3 *	/	0
1-2		2	3	260 mm	0
1-3		3	3	125 mm	0
1-4		4	3	80 mm	0
2-1	Spacing of iron hoops	2	3	0 mm	0
2-2		2	3	170 mm	0
2-3		2	3	260 mm	0
3-1	Inclination angle	3	3	125 mm	0
3-2		3	3	125 mm	2.79
3-3		3	3	125 mm	3.55

* Each test group included three specimens, which are represented by (a), (b) and (c), respectively.

Figure 7. Material used for specimen. (a) Wood used for the composite timber column; (b) Q235 steel used for the iron hoop.

The test was carried out in the Mechanical Laboratory of Beijing Jiaotong University. The equipment that was used is a universal press with a range of 100 kN. The specimen was placed on the pedestal of the universal press during the test loading and it was ensured that the actuator of the universal press was located in the center of the top of the middle block, as is shown in Figure 8a. The test loading system adopts displacement control loading and the loading rate was 0.5 mm/min. A preload was performed before the test in order to ensure that the actuator of the press was in close contact with the specimen. Loading was continued until the sliding displacement of the interface exceeded 10 mm. The vertical displacement at the loading point, vertical load at the loading point and the positive pressure of the iron hoops on the combined interface were measured. The vertical displacement and vertical load at the loading point were obtained from a computer that was connected to the universal press. The positive pressure of the iron hoops on the interface was obtained by measuring the strain in the strain gauges that were arranged on the iron hoops. Figure 8b shows the arrangement of the strain gauges on the iron hoops.

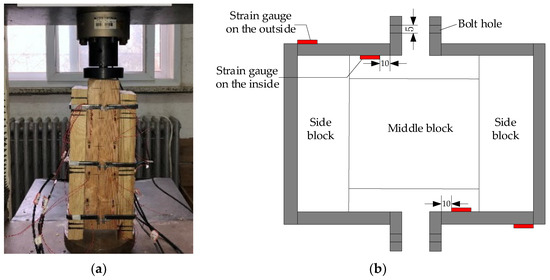
Figure 8. Schematic diagram of the test. (a) Test loading setup; (b) the arrangement of strain gauges on the iron hoop, unit: mm.

3.2. Test Results and Discussion

3.2.1. Failure Mechanism

The failure mechanism of the interface was analyzed by the shear stress–displacement curves that were obtained from the sliding characteristic test. The shear stress within the interface was obtained by dividing the shear load, as measured by the universal press, by the sum of the areas of the shear surface. The shear stress–displacement curves of all of the test groups had similar variation trends in this test. The test groups with different numbers of iron hoops were taken as examples for the analysis of the change in the shear stress–displacement curves during the loading process, as shown in Figure 9.

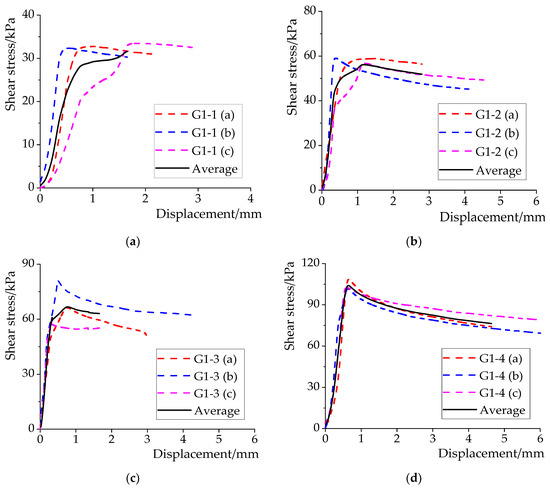
Figure 9. Shear stress–displacement curves of test groups with different numbers of iron hoops. (a) G1-1; (b) G1-2; (c) G1-3; (d) G1-4.

From the Figure 9, it can be seen that the shear stress–displacement curves of the interface increased monotonically and almost linearly during the initial loading stage. The large slope of the curves indicates that the shear stress of the interface increased rapidly, but the growth rate of the displacement was low. At this stage, the interface was in the sticky stage with the trend of sliding. The static friction and shear stress of the interface were balanced and their values gradually and synchronously increased. With the continuation of the loading process, the curves increased monotonically in the convex direction. The slope of the curves decreased, showing that the growth rate of the displacement sped up, and the shear stress increased slowly until reached its peak value, which is equal to the maximum sliding friction of the interface. That value is exactly the boundary between the partially sticky stage and the sliding stage.

Following this, uniform sliding occurred at the interface. The shear stress of the interface should, in theory, have remained unchanged and been in balance with the maximum sliding friction. However, by observing the shear stress–displacement curves of the specimen in the test, it can be found that the shear stress dropped after reaching its peak. The main reasons for this are as follows: first, the friction coefficient of the interface does not remain constant due to the size error (i.e., the surfaces of the interface are not always in close contact, as is shown in Figure 10a), operation error and material defects (i.e., there were initial shrinkage cracks and knots in the wood, as are shown in Figure 10b). Second, when the interface slid, the iron hoops were no longer parallel to the interface (Figure 10c). There is a certain included angle between them that reduces the positive pressure of the iron hoops on the interface. Based on the above reasons, the sliding friction (i.e., the shear stress) of the interface decreased after reaching its peak.

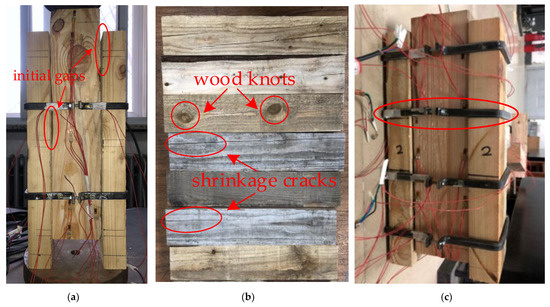
Figure 10. Test errors. (a) Initial gaps between the interface surfaces; (b) initial shrinkage cracks and knots in the wood; (c) inclined iron hoop at end of loading.

3.2.2. Parameter Analysis

The peak load, as measured by the universal press, is defined as the ultimate load of the shear sliding of the interface. The shear strength of the interface is calculated by the application of Equation (24):

$$\tau =\frac{P}{A}$$

(24)

where P is the ultimate load of the shear sliding of the interface and A is the sum of the areas of the interface.

The shear strengths of the interfaces of the different test groups are shown in Table 2. The average value curves of the shear stress–displacement curve of each group of test results were used to represent this group. The shear stress–displacement curves of the interfaces of the different test groups are shown in Figure 11. Figure 12a shows the fitting curves between the number of iron hoops and the shear strength of the interfaces. Figure 12b shows the fitting curves between the inclination angles and the shear strength of the interfaces.

Table 2. Shear strength of the interfaces.

Parameter	Specimen Number	Parameter Value	Ultimate Shear Load P/kN	$\mathbf{Shear} \mathbf{Strength} \mathit{\tau }/\mathbf{kPa}$	$\mathbf{Average} \mathbf{Shear} \mathbf{Strength} \overline{\mathit{\tau }}/\mathbf{kPa}$
Number of iron hoops	G1-1 (a)	1	1.651	32.474	33.975
	G1-1 (b)		1.762	34.657
	G1-1 (c)		1.769	34.795
	G1-2 (a)	2	2.896	56.962	58.424
	G1-2 (b)		3.004	59.086
	G1-2 (c)		3.011	59.224
	G1-3 (a)	3	4.569	89.868	85.751
	G1-3 (b)		4.385	86.249
	G1-3 (c)		4.125	81.135
	G1-4 (a)	4	5.183	101.945	104.574
	G1-4 (b)		5.232	102.909
	G1-4 (c)		5.535	108.869
Spacing of iron hoops	G2-1 (a)	0 mm	2.389	46.990	56.398
	G2-1 (b)		2.898	57.001
	G2-1 (c)		3.315	65.203
	G2-2 (a)	170 mm	3.196	62.863	65.360
	G2-2 (b)		3.309	65.085
	G2-2 (c)		3.464	68.134
	G2-3 (a)	260 mm	2.896	56.962	58.424
	G2-3 (b)		3.004	59.086
	G2-3 (c)		3.011	59.224
Inclination angle	G3-1 (a)	0°	4.125	81.135	85.751
	G3-1 (b)		4.385	86.249
	G3-1 (c)		4.569	89.868
	G3-2 (a)	2.79°	4.280	84.184	89.245
	G3-2 (b)		4.467	87.862
	G3-2 (c)		4.865	95.690
	G3-3 (a)	3.55°	4.452	87.567	91.684
	G3-3 (b)		4.567	89.829
	G3-3 (c)		4.965	97.657

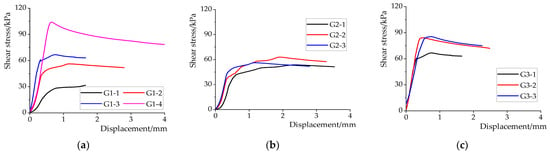
Figure 11. Shear stress–displacement curves of different test groups. (a) The number of iron hoops; (b) the spacing of iron hoops; (c) the inclination angle of the interface.

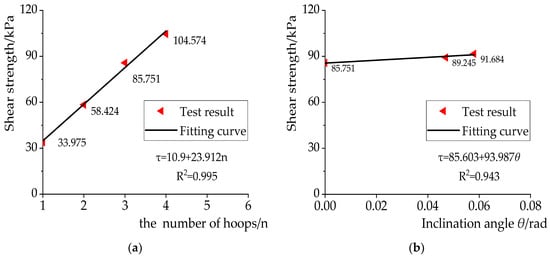
Figure 12. Fitting curves of shear strength. (a) The number of iron hoops; (b) the inclination angle of the interface.

(1)

The Effect of the Number of Iron Hoops

It can be seen from Figure 11a that the shear stress of the interface increased with the increase in the number of iron hoops under the same displacement. At the beginning of loading, the shear stress of the interface increased linearly, but with the increase in the number of iron hoops, the shear strength of the interface did not increase by any multiple. By analyzing the data that are provided in Table 2, it was found that when the number of iron hoops n = 2, 3 and 4, the average shear strength of the interface was 1.72 times, 2.52 times and 3.10 times that of when the number of iron hoops n = 1, respectively, indicating that increasing the number of iron hoops can effectively improve the shear strength of the interface. The average shear strength of G1-3 (n = 3) is the sum of that of the G1-1 (n = 1) and G1-2 (n = 2), with an error of 7.8%. Therefore, the specimen with 3 iron hoops can be regarded as the superposition of the specimen with 1 and 2 iron hoops. The reason for the above is that the effect of the iron hoops on the interface is related to its position. When the spacing of the iron hoops is within a certain range, the effect of each iron hoop can be superimposed independently. When the spacing exceeds this range, the effect of the iron hoops on the interface will not increase.

Figure 12a shows that the shear strength of the interface is positively correlated with the number of iron hoops. When there is a greater number of iron hoops there is a greater level of shear strength in the interface. The fitting equation between the number of iron hoops and the shear strength of the interface can be expressed by Equation (25).

$$\tau =10.9+23.912n$$

(25)

where τ is the shear strength of the interface and n is the number of iron hoops.

(2)

The Effect of the Spacing of the Iron Hoops

According to the data in Table 2, when the iron hoop spacing d = 170 mm (i.e., G2-2), the average shear strength of the interface increased by 15.9% compared with that of G2-1 (d = 0 mm), while that of G2-3 (d = 260 mm) increased only by 3.6% compared with G2-1 (d = 0 mm). This indicates that, when the spacing is less than 170 mm, the effect of the iron hoops on the interface increases with the increase in the iron hoops’ spacing, but it is opposite when the spacing is more than 170 mm. Compared with G1-1, the average shear strength of the interface of G2-1 (d = 0 mm), G2-2 (d = 170 mm) and G2-3 (d = 260 mm) had increased by 66.0%, 92.4% and 72.0%, respectively. When the iron hoop spacing d = 170 mm (G2-2) was used, the shear strength of the interface increased the most, this is a result which can be regarded as the most reasonable arrangement of the iron hoops. The reason of this is that the iron hoop is too close to the edge of the wooden column when the iron hoop spacing exceeds 170 mm and the constraint range of the iron hoops on the interface is narrower than the width of the side block, which leads to the decline of the constraint effect of the iron hoops. Therefore, it can be considered that there is a most reasonable spacing of the iron hoops and that the shear strength of the interface cannot be effectively improved when the spacing is too large or too small.

(3)

The Effect of the Inclination Angle of the Interface

The shear stress–displacement curves of the interface under different inclination angles are shown in Figure 11c. Figure 11c demonstrates that, under the same displacement, the shear stress of the interfaces of G3-2 (θ = 2.79°) and G3-3 (θ = 3.55°) were greater than that of G3-1 (θ = 0°), indicating that the existence of the inclination angle increases the shear strength of an interface.

Figure 12b pinpoints that the shear strength is positively correlated with the inclination angle of the interface. The shear strength of the interface increases with the increase in the inclination angle. The fitting equation between the inclination angle and the shear strength of the interface can be expressed by Equation (26).

$$\tau =85.603+93.987\theta$$

(26)

where θ is the inclination angle of the interface.

4. Verification and Comparison of Theoretical and Experimental Results

According to the above theoretical analysis, it is known that the shear stress of the interface is related to the vertical load, the number of iron hoops and the inclination angle of the interface. In order to verify the theoretical formula, the parameters of the different inclination angle groups that were used in the test were substituted into the derived formula and the theoretical results were compared with the test results. The specific verification process and results are as follows.

4.1. Comparison of Results

By substituting the parameters of G3-2 and G3-3 into Equations (15) and (16) and making them equal, the limit inclination angle of surface slip can be obtained. These results were compared with the test, as shown in Table 3.

Table 3. Comparison of theoretical and test results.

Group Number	$\mathbf{Shear} \mathbf{Strength} \mathit{\tau }/\mathbf{kPa}$		Error	${\mathit{\theta }}_2$		Error
	Test Result	Theoretical Result		Test Setting	Theoretical Result
3-2	89.245	79.372	11.1%	2.79	3.21	15.1%
3-3	91.684	80.843	11.8%	3.55	3.84	8.2%

The data in Table 3 show that the theoretical results are in good agreement with the test results and that the relative error of the results was controlled within 15%. In addition, with the same number of iron hoops, the shear strength and the limit inclination angle of the interface gradually increased with the increase in the vertical load.

4.2. Error Analysis

The main reasons for the error between the theoretical results and test results are as follows:

• In the actual ancient composite timber columns, the effect of the iron hoops on the interface is discontinuous. However, in the process of theoretical analysis, it is assumed that the positive pressure from the iron hoops on the interface is applied in a continuous sinusoidal distribution, an assumption which inevitably expands the influence range of the iron hoops on the interface, making the theoretical results of the positive pressure from the iron hoops greater than the test results. Thus, the inclination angle of the theoretical results is greater than that of the test results.
• The actual ultimate shear load of the interface is less than that of the theoretical result due to the size error (the gap between the interfaces) of the specimen and the material defects (the initial shrinkage cracks and knots of the wood).

5. Conclusions

In this paper, a unilateral contact mechanics model of the composite interface of an ancient timber column was proposed and the formula of the stress distribution of that composite interface was deduced. Furthermore, based on the hypothesis, the stress distribution of the interface under the effect of iron hoops was obtained and the correctness of the theoretical model was verified by comparing it with the shear sliding test results of interfaces. According to these test results, the expressions and curves between the shear strength of the interface, the number of iron hoops and the inclination angle of the interface are able to be fitted, respectively. On this basis, the influences of the number and the spacing of the iron hoops and the inclination angle of the interface on the shear sliding performance of the interface were studied. The main conclusions are as follows:

• Based on the analysis of the slip characteristics of the interface, the limit inclination angle of the point slip and the limit inclination angle of the surface slip of the interface were obtained. According to this, a three-stage slip failure mode of the interface has been proposed: the fully sticky stage, the partially sticky stage and the sliding stage;
• Using the elastic mechanics equation, the sliding displacement in the sliding stage of the interface can be calculated by Equation (22) and the shear stiffness of the interface can be expressed by Equation (23);
• The number and the spacing of the iron hoops and the inclination angle of the interface were found to be the important factors affecting the shear strength of the interface. When the number of iron hoops n = 2, 3 and 4, the interfacial shear strength was 1.72 times, 2.52 times and 3.10 times that which was found when the number of iron hoops n = 1, respectively, indicating that increasing the number of iron hoops can improve the shear strength of the interface significantly. There is an optimal value of hoop spacing. If the spacing of the iron hoops is too large or too small, the shear strength of the interface cannot be improved effectively. Within a certain range of the inclination angle, the shear strength is positively correlated with the inclination angle of the interface.