An Image-Encryption Algorithm Based on Stage-Merging Bit Scrambling

Abstract

At present, the existing single-pixel position-scrambling technique is not sensitive to the chaotic sequence used, and adjacent-pixel position scrambling has difficulty ensuring a good scrambling effect and speed at the same time. In this paper, a stage-merging scrambling algorithm is proposed, which combines the two-stage scrambling process and can complete the dual scrambling of pixel position and pixel value at the same time. It not only improves the scrambling speed, but also greatly improves the scrambling effects. Then, a complete image encryption and decryption scheme was designed based on stage-merging bit scrambling combined with DNA coding. Security analysis shows that the algorithm can resist various means of attack such as exhaustive attack and differential attack. The research in this paper extends the existing bit-scrambling algorithms and is suitable for practical applications.

1. Introduction

With the advancement of technology and society, people’s demand for information has exploded, and the channel of information exchange also tends to be transmitted through the internet. As one of the main carriers of information transmission, digital images are frequently used in sensitive fields such as personal life, medical care, and military affairs. Due to the virtual and open nature of the internet, there is a risk of theft or tampering during the transmission of digital images. Bit scrambling is an image-encryption method that changes the pixel value by scrambling the bits of the pixel value. It has been paid growing attention by scholars in recent years.

In 2014, Deng et al. [1] proposed an image-encryption algorithm with dual scrambling of the pixel position and bit. The algorithm first scrambles the pixel position, then extracts the eight decimal places of the chaotic value to generate a sorting index sequence, and scrambles the 8 bits of each pixel value in turn. Since the algorithm uses the sum of the pixel values as the connection between the chaotic sequence and the plain image, the correlation is not strong. In 2016, Xie et al. [2] proposed a different bit-scrambling algorithm. After the pixel position is scrambled, the pixel bits are scrambled by comparing the size of two adjacent numbers in the chaotic sequence. If the former is greater than the latter, the first 4 bits and the last 4 bits of the current pixel value are exchanged; otherwise, the odd and even bits are exchanged in turn. The algorithm uses three chaotic sequences, but only one is associated with the sum of the pixel values of the plain image, while the other two sequences are generated independently of the plain image, and the diffusion process only uses forward diffusion, which is not secure. It has been deciphered in [3]. In 2018, the authors of [4,5] proposed different position-scrambling methods, and the binary cycle shift for each pixel value to achieve bit scrambling. The difference between them lies in the addition of DNA coding, DNA replacement operations, and DNA decoding before positive diffusion. In 2020, Tian et al. [6] proposed a new multi-chaotic image-encryption algorithm based on cyclic shift, which designed a new position-scrambling process and replaced pixels by an index matrix obtained by chaotic sequence sorting. After that, a cyclic shift and forward diffusion were carried out. Since the generation of the chaotic sequence of the algorithm has no relationship with the plain image, the ability to resist differential attack is weak.

The bit-scrambling algorithms mentioned above are different from each other, but have a common point, that is, they all perform bit scrambling for a single pixel. In the above algorithm, the proportion of 0 bit and 1 bit of a single pixel does not change before and after bit scrambling, which also causes the bit-scrambling stage to be insensitive to the chaotic sequences used. During decryption, except the bit-scrambling stage, the rough outline of the plain image can be recognized from the decrypted image.

In response to this problem, Guo et al. [7] designed an image-encryption algorithm based on adjacent-pixel bit scrambling in 2020. The algorithm first converts the image into a one-dimensional sequence and performs global position scrambling, and then iterates through the sequence, swapping the specific bits of adjacent pixels. It designs two exchange methods, selects with a chaotic value of 0.5 as the threshold, and finally diffuses the pixel value in both directions. The bit-scrambling stage of the algorithm is sensitive to chaotic sequences, but the information entropy of the intermediate cipher image obtained by bit scrambling is not ideal. In 2022, Niu et al. [8] proposed another adjacent-pixel bit scrambling method, which uses a newly-designed fill curve to complete the position scrambling, and uses an improved Joseph traversal to scramble the adjacent four pixels. The scrambling effect is favorable, but the scrambling speed is slow. The diffusion process of the algorithm described in [7,8] adopts forward and reverse diffusion, which is realized by the XOR of the pixel value with the previous pixel value and the chaotic value in turn. This diffusion method has been proven to create security problems, and attackers can obtain equivalent keys by constructing special images [9,10].

It can be seen from the above analysis that single-pixel bit scrambling is less sensitive to the chaotic sequence used, and adjacent-pixel bit scrambling suffers from difficulties ensuring a good scrambling effect and speed at the same time. Additionally, these two scrambling processes are divided into two stages of position scrambling and bit scrambling. The two stages are executed serially. It would be considered an improvement to this process to increase the scrambling speed. In this regard, this paper proposes a stage-merging scrambling method. Compared with the two-stage scrambling process, this method merges the two stages and can simultaneously complete the double scrambling of pixel position and pixel value. While the scrambling effect is excellent, the scrambling time is shortened.

2. Materials and Methods

2.1. Chaotic System

2.1.1. Kent Chaos

Kent chaos is a one-dimensional chaotic system whose equations of motion are as follows [1]:

$$x_{n+1}=\{\begin{array}{l}\frac{x_n}{a},0<x_n\le a\\ \frac{1-x_n}{1-a},a<x_n<1\end{array}$$

(1)

where $a$ is the control parameter and $x$ is the state variable.

Figure 1 shows the bifurcation diagram of Kent chaos. When the parameter value is $0<a<1$ and the initial value is $0<x_1<1$, Kent chaos is in a chaotic state.

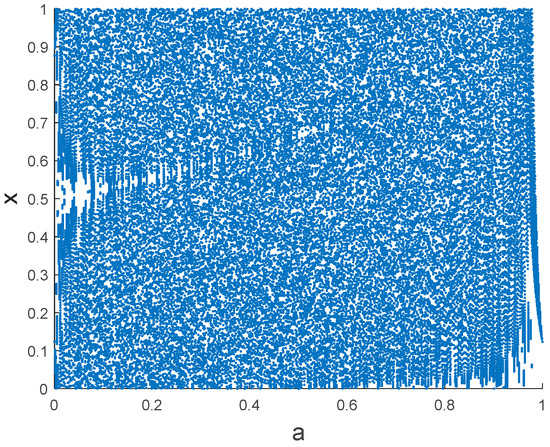
Figure 1. Bifurcation diagram of Kent chaos.

2.1.2. Calculating 2D Logistic Chaos

The equation of motion of two-dimensional logistic chaos is as follows [11]:

$$\{\begin{array}{l}{x}_{n+1}=u_1{x}_n(1-x_n)+{\lambda }_1{y}_n^2\\ y_{n+1}=u_2{y}_n(1-y_n)+{\lambda }_2(x_n^2+x_n{y}_n)\end{array}$$

(2)

where $u_1$, $u_2$, ${\lambda }_1$, and ${\lambda }_2$ are control parameters, $x_n$ and $y_n$ are state variables. When the parameter values are $2.75<u_1\le 3.4$, $2.75<u_2\le 3.45$, $0.15<{\lambda }_1\le 0.21$, $0.13<{\lambda }_2\le 0.15$, and the initial values are $0<x_1\le 1$, $0<y_1\le 1$, 2D logistic chaos is in a chaotic state.

The parameters are set to $u_2=3.1$, ${\lambda }_1=0.18$, ${\lambda }_2=0.14$, the initial values are set to $x_1=0.123$, $y_1=0.567$ to draw the bifurcation diagram of the system, and then $u_1=3.0$ is set to draw the attractor phase diagram, as shown in Figure 2 and Figure 3 respectively. The chaotic sequences are randomly distributed in the value interval, and there are fewer period-doubling bifurcations. The chaotic characteristics are outstanding.

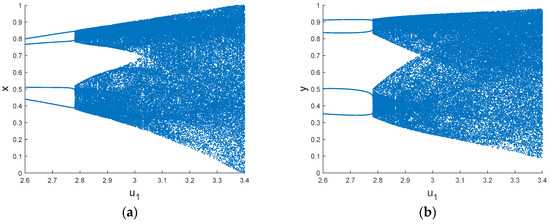
Figure 2. Bifurcation diagram of 2D logistic chaos (a) $u_1$ and $x$; (b) $u_1$ and $y$.

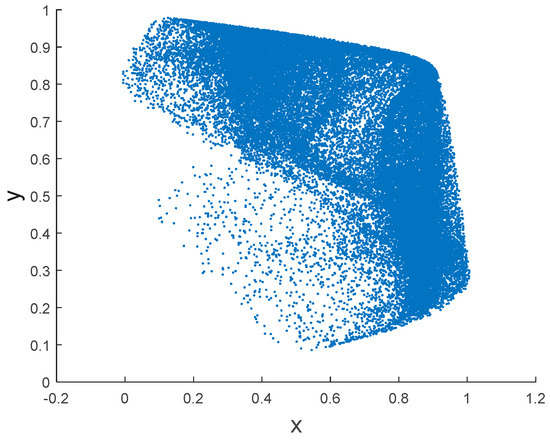
Figure 3. Attractor phase diagram of 2D logistic chaos.

2.2. Knuth Shuffle Algorithm

The Knuth shuffle algorithm [12] can realize in-situ shuffling when the length of the array is known. It only needs one traversal to randomly shuffle the elements in the array, and its time complexity is $O(n)$. Since there is no need to open up additional space, the space complexity is only $O(1)$. The shuffle process is as follows:

(1)

Enter data, numbered $1~n$;

(2)

Randomly generate an integer $k_1$ in the range $1~n$, and exchange $k_1$ and $n$;

(3)

Randomly generate an integer $k_2$ in the range $1~n-1$, and exchange $k_2$ and $n-1$;

(4)

Randomly generate an integer $k_i$ in the range $1~n-i+1$, and exchange $k_i$ and $n-i+1$;

(5)

Continue until $i=n-1$, the shuffle process is complete.

The Knuth shuffle algorithm divides the array into two parts: the head and the tail, which store the unprocessed data and the processed data respectively. Each time, one datum is randomly selected from the unprocessed data and exchanged to the tail of the array without opening up additional storage space. This shuffle process is mainly divided into two processes: card selection and card exchange. Take step (4) as an example, card selection corresponds to the process of generating an integer $k_i$, and card exchange corresponds to the process of exchanging $k_i$ and $n-i+1$. The algorithm in this paper redesigns the card selection and card exchange processes, and uses improved card selection as the selection strategy for bit-scrambled pixels. In the improved card exchange, the selected three pixels are bit scrambled each time.

2.3. DNA Coding

DNA molecules contain different nitrogenous bases, namely adenine (A), guanine (G), cytosine (C), and thymine (T). The bases A and T, C and G have a one-to-one correspondence [13]. In binary, 00 and 11, 01 and 10 also have a one-to-one correspondence. When using bases for coding, there are a total of 24 coding rules, of which only 8 rules satisfy the complementation mechanism of bases, as shown in Table 1. There are also addition, subtraction, and XOR operations in binary between DNA codes. Table 2 shows the operation rules corresponding to the second encoding rule.

Table 1. The rules of DNA encoding and decoding.

	1	2	3	4	5	6	7	8
00	A	A	T	T	G	G	C	C
01	C	G	C	G	A	T	A	T
10	G	C	G	C	T	A	T	A
11	T	T	A	A	C	C	G	G

Table 2. The rules of DNA operation.

	Addition				Subtraction				XOR
	A	T	C	G	A	T	C	G	A	T	C	G
A	A	T	C	G	A	G	C	T	A	T	C	G
T	T	C	G	A	T	A	G	C	T	A	G	C
C	C	G	A	T	C	T	A	G	C	G	A	T
G	G	A	T	C	G	C	T	A	G	C	T	A

2.4. Encryption Process

Figure 4 shows the encryption process.

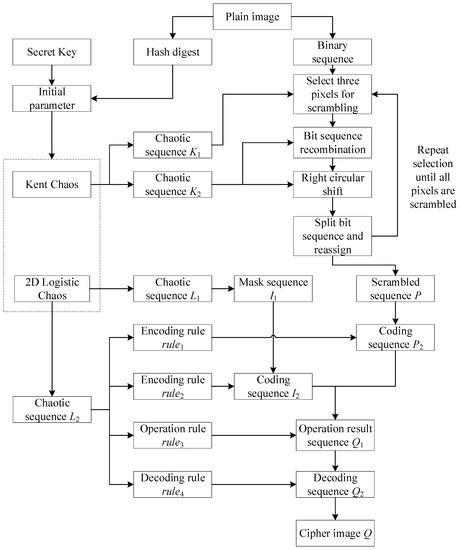
Figure 4. Flow chart of the image-encryption algorithm.

2.4.1. Key Handling

In order to prevent differential attacks, this algorithm uses a hash algorithm to calculate the plain image, generates a hash digest that is highly sensitive to the plain image, and associates it with the key-processing process. In this way, different initial parameters can be generated for each different plain image, thereby generating completely different cipher images.

This paper uses the MD5 hash algorithm to calculate the plain image, and obtains a hexadecimal string with a length of 32 bits, denoted as, $hash$ and evenly splits it into four strings with a length of 8 bits, denoted as $has{h}_1$, $has{h}_2$, $has{h}_3$, and $has{h}_4$. The key of this algorithm is a hexadecimal string with a length of 48 bits, denoted as $key$, which is evenly divided into four strings with a length of 12 bits, denoted as $ke{y}_1$, $ke{y}_2$, $ke{y}_3$, and $ke{y}_4$.

The initial parameters of Kent chaos and 2D logistic chaos are calculated by Equation (3) and Equation (4) respectively:

$$\{\begin{array}{l}{x}_1=\mathrm{mod}(\frac{\mathrm{hex}2\mathrm{dec}(ke{y}_1)}{2^{48}}+\frac{\mathrm{hex}2\mathrm{dec}(has{h}_1)}{2^{32}},1)\\ a=\mathrm{mod}(\frac{\mathrm{hex}2\mathrm{dec}(ke{y}_2)}{2^{48}}+\frac{\mathrm{hex}2\mathrm{dec}(has{h}_2)}{2^{32}},1)\end{array}$$

(3)

$$\{\begin{array}{l}{x}_1{}^{\prime }=\mathrm{mod}(\frac{\mathrm{hex}2\mathrm{dec}(ke{y}_3)}{2^{48}}+\frac{\mathrm{hex}2\mathrm{dec}(has{h}_3)}{2^{32}},1)\\ y_1{}^{\prime }=\mathrm{mod}(\frac{\mathrm{hex}2\mathrm{dec}(ke{y}_4)}{2^{48}}+\frac{\mathrm{hex}2\mathrm{dec}(has{h}_4)}{2^{32}},1)\end{array}$$

(4)

where $\mathrm{hex}2\mathrm{dec}(key)$ represents the conversion of the hexadecimal string $key$ to a decimal value, $\mathrm{mod}$ represents the modulo operation, and $\mathrm{mod}(x,1)$ returns the remainder of dividing $x$ by 1.

Mark the plain image to be encrypted as $I$ and its size as $M\times N$. Iteratively calculate the Kent chaos. In order to eliminate the influence of the transient effect of the chaotic system, the first 1000 iterations are discarded and two chaotic sequences with length $MN-2$ are obtained, which are denoted as $K_1$ and $K_2$. The 2D logistic chaotic system is iteratively calculated $1000+MN$ times, and the first 1000 calculation results are discarded, and two sequences $L_1$ and $L_2$ of length $MN$ are obtained.

2.4.2. Stage-Merging Bit Scrambling

In this part, through the redesign of the card-selection and card-exchange processes of the Knuth shuffle algorithm, the two-stage scrambling process can be merged to accomplish the double scrambling of pixel position and pixel value, with a better performance of encryption compared to single- and adjacent-pixel scrambling. The steps are as follows:

(1)

Rearrange the image $I$ in columns and rows, and convert all pixel values to binary to obtain a one-dimensional sequence $I^{\prime }$.

(2)

Select the three pixels $f$, $s$, and $t$ that will be bit scrambled each time as follows:

$$K_1^{\prime }(i)=\mathrm{mod}(\mathrm{floor}(K_1(i)\times {10}^{14}),MN-i-1)+1$$

(5)

$$f=I^{\prime }(MN-i)$$

(6)

$$s=I^{\prime }(K_1^{\prime }(i))$$

(7)

$$t=I^{\prime }(MN-i+1)$$

(8)

where $\mathrm{floor}$ represents rounding down, $i=1,2,\dots ,MN-2$.

(3)

After each selection of pixels $f$, $s$, and $t$, the binary bits will be recombined. The 8 bits of pixel $f$ are recorded as $f_1{f}_2{f}_3{f}_4{f}_5{f}_6{f}_7{f}_8$, $s$ and $t$ are similar. In addition, the method of recombination is shown in Figure 5, which is divided into four types. Choose the corresponding method for recombination. The calculation of $K_2^{\prime }(i)$ is as follows:

$$K_2^{\prime }(i)=\mathrm{mod}(\mathrm{floor}(K_2(i)\times {10}^{10}),4)+1$$

(9)

where $i=1,2,\dots ,MN-2$.

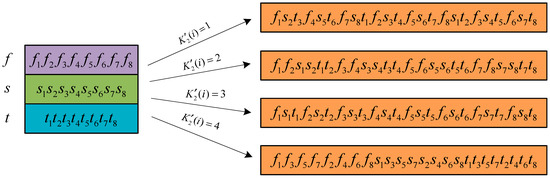Figure 5. Schematic diagram of the way of bit recombination.

(4)

Perform a right cyclic shift on the recombined bit sequence $bitSt{r}_1$ to obtain a bit sequence $bitSt{r}_2$:

$$bitSt{r}_2=\mathrm{circshift}(bitSt{r}_1,K_2^{″}(i))$$

(10)

where $\mathrm{circshift}$ represents the right circular shift, which moves the sequence to the right, and the shifted low bits are repositioned to the high bits. $K_2^{″}(i)$ represents the number of shift bits from 1 to 7, expressed as:

$$K_2^{″}(i)=\mathrm{mod}(\mathrm{floor}(K_2(i)\times {10}^{14}),7)+1$$

(11)

where $i=1,2,\dots ,MN-2$.

(5)

Divide the bit sequence $bitSt{r}_2$ into three blocks every 8 bits, and reassign $f$, $s$, and $t$ respectively. Thus far, the three pixels selected in this round have completed the bit-scrambling operation.

(6)

Repeat steps (2) to (5) until the entire sequence is scrambled, and then convert to a decimal sequence $P$.

Figure 6 shows the whole process of stage-merging bit scrambling for image sequences.

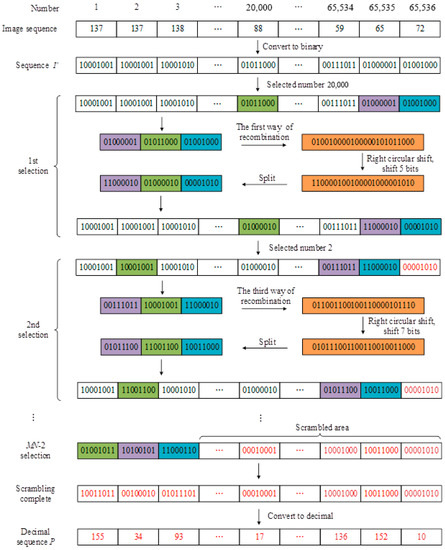
Figure 6. Schematic diagram of the stage-merging bit-scrambling process.

2.4.3. DNA Dynamic Coding and Operation

(1)

The chaotic sequence $L_1$ is converted into an integer sequence $I_1$ with a value of 0~255 by Formula (12). $I_1$ is used as a mask sequence.

$$I_1(i)=\mathrm{mod}(\mathrm{floor}(L_1(i)\times {10}^{14}),255)$$

(12)

where $i=1,2,\dots ,MN$.

(2)

Calculate the DNA encoding rules $rul{e}_1$ and $rul{e}_2$, the DNA operation rule $rul{e}_3$, and the DNA decoding rules $rul{e}_4$; the calculation methods are as follows:

$$rul{e}_1(i)=\mathrm{mod}(\mathrm{floor}(L_2(i)\times x_1\times {10}^{14}),8)+1$$

(13)

$$rul{e}_2(i)=\mathrm{mod}(\mathrm{floor}(L_2(i)\times a\times {10}^{14}),8)+1$$

(14)

$$rul{e}_3(i)=\mathrm{mod}(\mathrm{floor}(L_2(i)\times x_1{}^{\prime }\times {10}^{14}),3)+1$$

(15)

$$rul{e}_4(i)=\mathrm{mod}(\mathrm{floor}(L_2(i)\times y_1{}^{\prime }\times {10}^{14}),8)+1$$

(16)

where $i=1,2,\dots ,MN$.

(3)

Traverse the sequences $P$ and $I_1$, and select the coding rules of $rul{e}_1(i)$ and $rul{e}_2(i)$ to encode the DNA for $P(i)$ and $I_1(i)$ respectively. The coding sequences $P_2$ and $I_2$ are obtained. Perform DNA operations on sequences $P_2$ and $I_2$ to obtain the coding sequence $Q_1$. If $rul{e}_3(i)=1$, perform an addition operation. If $rul{e}_3(i)=2$, perform a subtraction operation. Otherwise, perform an XOR operation. Traverse the coding sequence $Q_1$, take every four bases as a group, and decode according to the decoding rule of $rul{e}_4(i)$ to obtain the sequence.

(4)

The sequence $Q_2$ is recombined into an image $Q$ of size $M\times N$ in the order of columns and rows. $Q$ is the final cipher image.

2.5. Decryption Process

The decryption scheme is the reverse process. Specific steps are as follows:

(1)

Perform key processing to obtain chaotic sequences $K_1$, $K_2$, $L_1$, and $L_2$.

(2)

Perform the reverse process of the DNA dynamic encoding operation. First perform steps (1) and (2) of Section 2.4.3 to obtain the mask sequence $I_1$ and four rule sequences $rul{e}_1$, $rul{e}_2$, $rul{e}_3$, and $rul{e}_4$. The cipher image is rearranged into a one-dimensional sequence in the order of columns first and then rows, and the sequence $Q_1$ is obtained by encoding with the coding rule of $rul{e}_4(i)$, and the sequence $I_2$ is obtained by encoding the mask sequence $I_1$ with the coding rule of $rul{e}_2(i)$. The DNA inverse operation is performed between the sequences $Q_1$ and $I_2$ to obtain the coding sequence $P_2$. If $rul{e}_3(i)=2$, the addition operation is performed. If $rul{e}_3(i)=1$, the subtraction operation is performed. Otherwise, the XOR operation is performed. Traverse the coding sequence $P_2$, and decode according to the decoding rule of $rul{e}_1(i)$ to obtain the scrambled sequence $P$.

(3)

Perform the inverse process of stage-merging bit scrambling. Convert the sequence $P$ to a binary sequence, then select the three pixels, the selection process is the reverse step of step (2) in Section 2.4.2. Then, the reverse process of right circular shift and bit sequence recombination is carried out. Finally, the selected pixels are revalued.

(4)

When all the scrambled pixels are revalued, convert the sequence back to decimal and reassemble into an image $I$ of size $M\times N$, which is the final decrypted image.

3. Security Analysis

The simulation environment is as follows: the hardware environment is AMD Ryzen 7 5800H CPU, 16GB RAM, and the programming environment is MATLAB R2019b which opens the parallel computing toolbox. The standard images Lena, text, fruits, and peppers of size $256\times 256$ are used as test images, and the key used is “CD8C10890E0ABC357C6061F9D01EC890322C9769F0123456”. The experimental results are shown in Figure 7. Under the naked eye, no feature of the plain image can be found from the cipher image, and the decrypted image is consistent with the plain image.

Figure 7. Image encryption and decryption results: (a) plain, cipher, and decrypted image of Lena; (b) plain, cipher, and decrypted image of text; (c) plain, cipher, and decrypted image of fruits; (d) plain, cipher, and decrypted image of peppers.

3.1. Sensitivity Analysis of Chaotic Sequences

In order to test the sensitivity of bit scrambling to chaotic sequences, cipher images are decrypted except for the bit-scrambling stage. Figure 8 shows the results of the tests for the image of peppers. The algorithms proposed in [1,2,4] can recognize the approximate outline of the original image from the decrypted image, and the sensitivity is poor. In addition, it is difficult to get the original information from the decrypted image by the algorithm proposed in this paper and in [7,8]. The results show that stage-merging bit scrambling and adjacent-pixel bit scrambling are both sensitive to the chaotic sequences used.

Figure 8. Peppers decryption diagram except for the bit-scrambling stage: (a) ours; and those algorithms proposed in (b) [1]; (c) [2]; (d) [4]; (e) [7]; and (f) [8].

3.2. Histogram Analysis

An algorithm with an outstanding encryption effect is supposed to make the number of pixels corresponding to each pixel value after encryption relatively average, which can hide the statistical information of pixel values and improve security. Figure 9 shows the histogram comparison of Lena’s plain image, scrambled intermediate cipher image, and cipher image. The pixel value distribution of the plain image is concentrated in a specific interval. After bit scrambling, the pixel value distribution becomes smooth and uniform, which hides the original information.

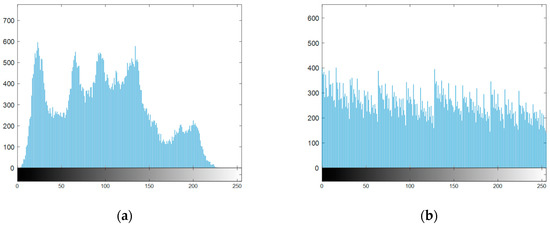
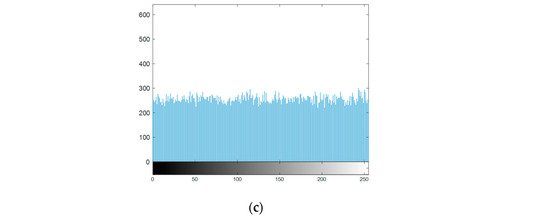
Figure 9. Histogram comparison of Lena: (a) plain image; (b) scrambled intermediate cipher image; (c) cipher image.

3.3. Information Entropy Analysis

The information entropy can be used to measure the randomness of the images. For grayscale images, the ideal information entropy is 8 [14]. The definition of information entropy is given as [15]:

$$H=-{\displaystyle \underset{i=0}{\overset{255}{\Sigma }}{p}_i}{\log }_2(p_i)$$

(17)

where $p_i$ represents the frequency of occurrence of pixel value $i$.

Table 3 and Table 4 show the results of the information entropy test. It should be noted that the scrambled intermediate cipher image of this algorithm is a one-dimensional sequence of length $MN$. For the convenience of comparison, it is rearranged into an image with a size of $M\times N$ for processing. Compared with the algorithm put forth in [4] that uses single-pixel bit scrambling and those described in [7,8] that use adjacent-pixel bit scrambling, the information entropy of the scrambled intermediate cipher image and final cipher image is closer to the ideal value 8. After encryption by the algorithm in this paper, the pixel value has an excellent random distribution characteristic.

Table 3. Information entropy test results of scrambled intermediate cipher image.

Image	Plain Image	Ours	Ref. [4]	Ref. [7]	Ref. [8]
Lena	7.5683	7.9691	7.9261	7.7532	7.9674
Text	0.4912	7.1349	2.9977	2.8157	6.9499
Fruits	7.4782	7.9650	7.8868	7.6300	7.9635
Peppers	7.5701	7.9499	7.8984	7.8290	7.9499

Table 4. Information entropy test results of cipher image.

Image	Plain Image	Ours	Ref. [4]	Ref. [7]	Ref. [8]
Lena	7.5683	7.9974	7.9969	7.9973	7.9973
Text	0.4912	7.9971	7.9961	7.9969	7.9967
Fruits	7.4782	7.9973	7.9970	7.9972	7.9972
Peppers	7.5701	7.9976	7.9973	7.9972	7.9971

3.4. Correlation Analysis

The strong correlation between adjacent pixels is one of the characteristics of image data. It is necessary to make adjacent pixels as irrelevant as possible. The correlation coefficient can reflect the degree of association between adjacent pixels. A correlation coefficient close to 0 represents a weak correlation between adjacent pixels, and it is difficult for attackers to use this information to conduct statistical attacks. The correlation coefficient is computed as follows [16,17]:

$$E(x)=\frac{1}{K}{\displaystyle \underset{i=1}{\overset{K}{\Sigma }}{x}_i}$$

(18)

$$D(x)=\frac{1}{K}{\displaystyle \underset{i=1}{\overset{K}{\Sigma }}{\left(x_i-E(x)\right)}^2}$$

(19)

$$cov(x,y)=\frac{1}{K}{\displaystyle \underset{i=1}{\overset{K}{\Sigma }}\left(x_i-E(x)\right)\left(y_i-E(y)\right)}$$

(20)

$$H=-{\displaystyle \underset{i=0}{\overset{255}{\Sigma }}{p}_i}{\log }_2(p_i)$$

(21)

where $r_{xy}$ represents the correlation coefficient, $x$ and $y$ represent the pixel values of adjacent pixels, and $K$ represents the number of randomly selected pixel pairs; $K=5000$ is set in this paper.

The correlation coefficients are divided into the horizontal direction, vertical direction, and diagonal direction according to the different ways of taking adjacent pixels. Table 5 shows the test results. The correlation coefficients of the cipher image are close to 0 in three directions, indicating that the correlation degree of adjacent pixels can be effectively reduced.

Table 5. Correlation coefficient test results.

Images	Plain Image			Cipher Image
	Horizontal	Vertical	Diagonal	Horizontal	Vertical	Diagonal
Lena	0.9391	0.9682	0.9232	0.0035	0.0028	−0.0045
Text	0.2385	0.3664	0.0500	−0.0094	0.0053	0.0082
Fruits	0.9523	0.9578	0.9288	−0.0022	−0.0095	−0.0170
Peppers	0.9675	0.9723	0.9451	0.0064	−0.0110	−0.0088

Figure 10 shows the correlation of Lena in different directions. The pixel value of adjacent points of plain images are all clustered near $y=x$, which has a strong correlation. The pixel value of the adjacent points of the cipher image are uniformly distributed in the rectangular region, which shows that the distribution of the pixel value of the cipher image is discrete and the correlation degree of the adjacent pixels is weak.

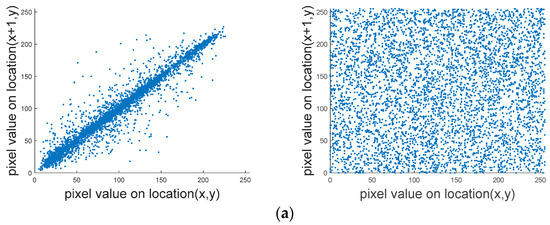
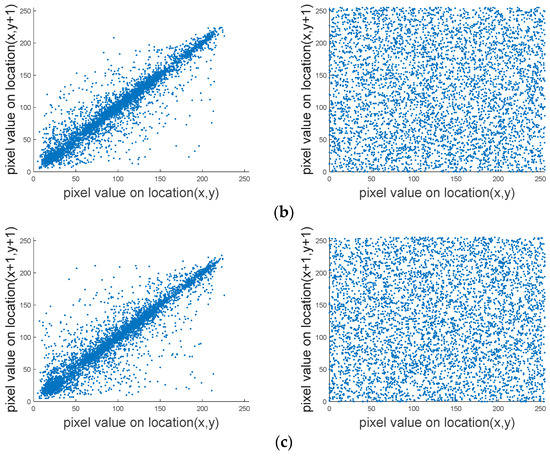
Figure 10. The correlation of Lena in different directions: (a) horizontal direction of plain image and cipher image; (b) vertical direction of plain image and cipher image; (c) diagonal direction of plain image and cipher image.

3.5. Differential Attack

Differential attack means that the attacker encrypts two plain images with only slight differences, and cracks them by the difference between the ciphertext images [18]. In order to resist differential attacks, it is required that even if the plain image changes slightly, the cipher image needs to be greatly different. NPCR (number of pixels change rate) and UACI (unified average changing intensity) are usually used to measure the degree of difference, where NPCR represents the proportion of different pixel values at the same location in the two images, and UACI represents the difference in pixel values at the same location. The ideal values of the two are 99.6094% and 33.4635% respectively, and the calculation formulas are defined as [19,20]:

$$\mathrm{NPCR}=\frac{{\displaystyle \underset{i=1}{\overset{M}{\Sigma }}{\displaystyle \underset{j=1}{\overset{N}{\Sigma }}D(i,j)}}}{M\times N}\times 100\%$$

(22)

$$\mathrm{UACI}=\frac{{\displaystyle \underset{i=1}{\overset{M}{\Sigma }}{\displaystyle \underset{j=1}{\overset{N}{\Sigma }}\left|C_1(i,j)-C_2(i,j)\right|}}}{255\times M\times N}\times 100\%$$

(23)

$$D(i,j)=\{\begin{array}{l}0,C_1(i,j)=C_2(i,j)\\ 1,C_1(i,j)\ne C_2(i,j)\end{array}$$

(24)

where $C_1$ and $C_2$ represents the two images used to test the difference.

Randomly select a pixel value of the plain image and add 1 to encrypt it. If the selected pixel value is 255, decrease it by 1. Calculate the NPCR and UACI between the new and old cipher images, and repeat 500 times to calculate the average value. The test results are shown in Table 6.

Table 6. Differential attack test results.

Image	NPCR/%	UACI/%
Ours	99.6086	33.4635
Ref. [4]	51.0727	10.0694
Ref. [7]	99.6087	33.4652
Ref. [8]	99.6085	33.4617

The NPCR and UACI of this algorithm are very close to the ideal value, which can effectively resist differential attack. The NPCR and UACI values of the algorithm described in [4] are quite different from the ideal values, because the initial chaotic value of the algorithm is not associated with the plain image. The generation of the chaotic initial value of the algorithm in this paper and those described in [7,8] is linked to the hash digest of the plain image, so it is extremely sensitive to the plain image.

3.6. Key Sensitivity Analysis

Image-encryption algorithms should be highly sensitive to keys [21]. To ensure security, even if the key used is only slightly different from the correct key, it should have a completely different encryption and decryption result.

The key used in this algorithm is a hexadecimal string, which is split into four equal-length parts to calculate the initial value and parameters of the chaotic system. In order to verify the sensitivity of the key, only the last digit of one of the segments is changed each time, and it is added by 1. The key is divided into an encryption key and decryption key. Additionally, the encryption key sensitivity test uses the key before and after the change for encryption and the difference between the two cipher images is calculated. The decryption key sensitivity test uses the changed key for decryption, and the difference between the decrypted image and the original image is calculated. The test results are shown in Table 7. Both the NPCR and UACI are close to their ideal values, indicating that the key sensitivity is excellent.

Table 7. Key sensitivity test results.

Key	Key after Change	Encryption Key		Decryption Key
		NPCR/%	UACI/%	NPCR/%	UACI/%
CD8C10890E0A	CD8C10890E0B	99.5270	33.2301	99.6155	29.2486
BC357C6061F9	BC357C6061FA	99.5712	33.4940	99.5789	29.5203
D01EC890322C	D01EC890322D	99.6063	33.2062	99.6170	30.6404
9769F0123456	9769F0123457	99.6414	33.4769	99.5667	30.6010

3.7. Encryption Time

For image-encryption algorithms, on the basis of ensuring security, encryption time is also a significant indicator to measure the quality of the algorithm.

In the simulation environment of this paper, the encryption time test is carried out on the same image with the size of 256 $\times$ 256, and the average value of multiple test results is taken. Table 8 shows the results. Compared with single- and adjacent-pixel bit scrambling, stage-merging bit scrambling significantly shortens the scrambling time, and the scrambling speed is faster.

Table 8. Encryption time test results.

Process	Ours	Ref. [4]	Ref. [7]	Ref. [8]
Scrambling	0.53s	0.73s	0.80s	2.81s
Total	0.77s	0.87s	0.94s	2.95s

3.8. Key Space

Exhaustive attack means that the attacker brute-forces the algorithm by trying every possible key combination, so the encryption algorithm needs to have a key space large enough to prevent brute force enumeration. If the key space is larger than $2^{100}$, it means that the brute force attack can be resisted [22].

The key used in this algorithm is a hexadecimal string with a length of 48, which is equivalent to 192 binary bytes. Therefore, the key space is 2¹⁹², which is much larger than 2¹⁰⁰, indicating that this algorithm can resist exhaustive attacks.

3.9. Robustness

During the transmission of cipher images, there may be data loss or noise pollution. If the robustness of the image-encryption algorithm is not strong, the corresponding decrypted image may lose the original information completely. In order to test the robustness of the proposed algorithm, the cropping attack and noise attack on cipher images are tested.

The cipher image is decrypted after 1/8, 1/4, and 1/2 regions are cropped, and the results are shown in Figure 11. The first row shows the cropped cipher images of different regions, and the second row shows the corresponding decrypted images. Although the cipher images have different degrees of data loss, the decryption images can still restore some information, indicating that the algorithm can resist cropping attacks to a certain extent.

Figure 11. The results of a cropping attack: (a) cipher images with 1/8, 1/4, and 1/2 data loss; (b) decrypted images of (a).

Cipher images of Lena were processed with different intensities of salt and pepper noise (SPN), speckle noise (SN), and Gaussian noise (GN), and then decrypted, as shown in Figure 12. With the increase in noise intensity, the decoded images become less clear. Among them, the decrypted images processed by SPN have only a few noise points, and the decryption quality is good. In addition, SN and GN have a great influence on the decryption quality, but the rough outline of the original image can still be recognized.

Figure 12. The results of a noise attack (a) SPN with density = 0.001; (b) SN with variance = 0.00001; (c) GN with mean = 0 and variance = 0.00001; (d) SPN with density = 0.01; (e) SN with variance = 0.0001; (f) GN with mean = 0 and variance = 0.0001.

The peak signal-to-noise ratio (PSNR) between the plain image and the decrypted image can be used to evaluate the strength of the robustness. Its formula is as follows [23]:

$$\mathrm{PSNR}=10\times {\log }_{10}(\frac{{255}^2}{\mathrm{MSE}})$$

(25)

$$\mathrm{MSE}=\frac{1}{M\times N}{\displaystyle \underset{i=1}{\overset{M}{\Sigma }}{\displaystyle \underset{j=1}{\overset{N}{\Sigma }}{\left[C_1(i,j)-C_2(i,j)\right]}^2}}$$

(26)

where $\mathrm{MSE}$ represents the mean square error, $C_1$ represents the plain image, and $C_2$ represents the decrypted image after the attack.

Figure 13 shows the PSNR test results of Lena under different intensity cropping and noise attacks. In the cropping attack, the PSNR of this algorithm is higher than that in [4] and lower than that in [7,8], but the gap is small. In the noise attack, this algorithm has the highest PSNR and the best ability to resist SPN, SN, and GN attacks.

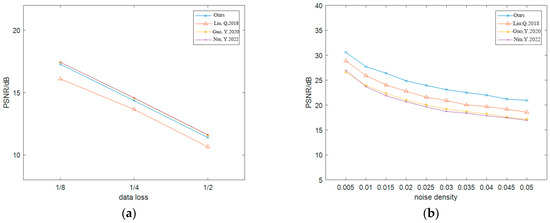
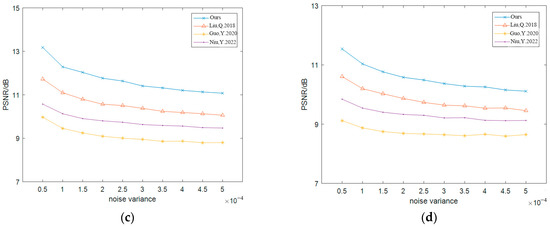
Figure 13. The PSNR test results of Lena (a) cropping attack; (b) SPN [4]; (c) SN [7]; (d) GN [8].

4. Conclusions

At present, single-pixel position scrambling is not sensitive to the chaotic sequences used, and adjacent pixel position scrambling still needs to be improved in scrambling speed and scrambling effect. To solve this problem, this paper proposes a stage-merging position-scrambling algorithm, which combines the two-stage scrambling process, and can complete the dual scrambling of pixel position and pixel value at the same time. Compared with the two-stage scrambling process, this method effectively improves the scrambling speed and information entropy of the scrambled intermediate encrypted image. This paper also introduces the Knuth shuffle algorithm, and redesigns its card selection and replacement. DNA dynamic encoding is also used to dynamically select specific rules in the process of encoding, operation, and decoding, which further improves the security of the algorithm. After testing, the encrypted image pixels are evenly distributed, and the correlation between adjacent pixels is weak. The algorithm can effectively resist statistical attacks, differential attacks, exhaustive attacks, and other common attacks. In the future, we can further explore the use of stage merging to design encryption schemes for different types of images (such as color images).