Radiative Lifetimes for the A and C¹Σ⁺ States of the (SrK)⁺ Ion Molecular

Abstract

We have investigated, in a previous work, the transition dipole moments (TDM) of the 13 ¹Σ⁺ states of the (SrK)⁺ molecular ion by using the ab initio method based on the pseudo-potential approach. The radiative lifetimes for all vibrational levels of A and C¹Σ⁺ have been calculated by using such transition dipole moments curves. We have included the bound-free emissions probabilities further to the bound–bound transitions. The bound-free emissions probabilities have been determined exactly, using the Franck–Condon approach, and then included in the total radiative lifetime. An important change has been observed for the higher excited vibrational levels in these lifetimes when the approximate evaluation breaks down. For the first time, the radiative lifetimes associated with the Aand C¹Σ⁺ excited state have been studied here.

1. Introduction

It is well-known that the radiative lifetimes of diatomic molecules [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32] are very important in diverse fields of physicsandhave been observed in plasmas and in spectroscopic observations of interstellar clouds, where there are a huge number of molecular ions and molecules. Several ab initio and dynamical works have carried out to determine the potential energy curves and the spectroscopic properties of various states and to test developed techniques and methods by determining the non-adiabatic effects such as the radial coupling, the adiabatic correction, pre-dissociation and the vibronic shifts.

The Fermi model is used to process the interaction between a Rydberg electron and an atom in its ground state, thereby producing potential curves for various excited and long inter-nuclear molecules. A specific attentiveness is paid to cases of degeneration or asymptotic quasi-degeneration. Exhaustive comparisons are made with recent ab initio calculations for very excited ¹Σ⁺ and ³Σ⁺ and adiabatic and diabatic states of the SrK⁺ system. Overall, we see good qualitative agreement, and sometimes the agreement even becomes quantitative. For isolated electronic states, the potential ripples reflect the nodal structure of the Rydberg state involved and their amplitude is given, in the Fermi method, by the diffusion length of an electron by the atom in its fundamental state. For several close energy states, due to the particular product structure of the interaction, in the Fermi model, a single non-zero potential emerges from a set of flat potentials. This clarifies the presence in the ab initio potentials of high-energy barriers at a great interatomic distance for the ^1,3Σ⁺ 4f states of SrK⁺. For systems involving H, the Fermi model gives better results for weak interactions in particular for triplets rather than singlets and especially in the case of quasi-degeneration. We show that the Fermi model provides a good description of the physics of the excited diabatic states of diatomic molecules and their couplings, allowing an in-depth understanding of the unusual forms of adiabatic potential curves. The limitations of the model are also discussed.

In this study, we have carried out a dynamic study that allowed us to understand the interactions between dipole moments and electromagnetic radiations by considering transitions with emission or absorption. Using the exploited results of Potential Dipole Moments (PDM) and Transition Dipole Moment (TDM) [1], we have determined the absorption spectra of level v = 0 from state X to all levels v of each of the A and C¹Σ⁺ states. We have also presented the radiative lifetimes at the vibrational levels of states A and C for the SrK⁺ systems with two exact and Franck–Condon methods.

2. Radiative Processes

In this section, we present the absorption and emission spectra as well as the lifetimes of the SrK⁺ molecular ion associated with X¹Σ⁺ and with the first excited states A¹Σ⁺ and C¹Σ⁺. The determination of these physical quantities is based on adiabatic and diabatic results and using Fermi’s Model.

2.1. The Fermi Model

To determine the transitions between a vibrational level and another level of a bound state, it is necessary to perform a calculation of the transition probability.

Consider a system withunperturbed Hamiltonian H₀ Eigen values E_n and Eigen states $|{\psi }_n⟩$. The transition probability of a bound vibrational state $|{\psi }_n⟩$ towards a continuum state $|{\psi }_m⟩$, under the effect of a disturbance W (external field), is given by Fermi’s Golden Rule:

$$p_{nm}(t)=\frac{2\pi }{\hslash }{\left|W_{nm}\right|}^2\rho (E_m=E_n)t$$

(1)

where ρ(E) is the density of states in the continuum such that ρ(E)dE is the number of states in an energy interval dE, and $W_{mn}=⟨{\psi }_n|W|{\psi }_m⟩$ is the matrix element of the disturbance W.

The probability of transition per unit time is written:

$$\frac{d{p}_{nm}(t)}{dt}=\frac{2\pi }{\hslash }{\left|W_{nm}\right|}^2\rho (E_m=E_n)$$

(2)

The transition probability makes sense when the perturbation is applied for a sufficient interval of time ($t\succ \succ \frac{2\pi \hslash }{\Delta E}$) for the system to feel the disturbance.

2.2. Absorption and Emission Spectrum

The term “spectrum” usually denotes a curve thatrepresents the variations of an atomic or molecular property as a function of a parameter. Spectroscopy is the set of methods allowing the determination of these spectra and their analyses.

When an atom is heated or even undergone an electric discharge, one of its electrons in its peripheral layer (more rarely the internal layers) goes from the fundamental level to a higher energy level called the excited state level. This phenomenon is called absorption. When the electron goes down, it re-emits energy in a light form (photon): this is the emission.

In classical physics, there can be an energy exchange between an electromagnetic wave of frequency n and a system having certain mechanical energy due to a periodic movement of frequency n₀ (see Figure 1) of the general form, Q = Q₀ cos 2pnt.

Figure 1. Classic diagram of the absorption of electromagnetic energy converted into mechanical energy.

2.3. Radiative Lifetime

The oscillator strength of transition between two vibrational states i and j is given as a function of Einstein’s coefficients by:

$$f_{ij}=\frac{{\mu }_e\hslash c^3}{\pi {}_{}e{}^2}\overline{v_{ij}}{B}_{ij}$$

(3)

where ${\overline{\nu }}_{ij}$ is the wave-number associated with the transition, μ and e are the mass and the charge, and the magnitude υ =E/2π is defined such that:

$$E=h\nu ={\hslash }_{}2\pi \nu =2\pi \nu \stackrel{}{}(\hslash =1{}_{}in\stackrel{}{}a.u)$$

(4)

$$B_{ij}=\frac{8{\pi }^3{|D_{ij}|}^2}{3h^{2}c}$$

(5)

where $D_{ij}=⟨{\Psi }_i\left|D\right|{\Psi }_j⟩$ is the matrix element of the electric dipole moment. There are two possible transitions: bound–bound transition and bound-free transition.

• Bound–Bound Transition

The radiative lifetime of a vibration level v’ through a bound–bound transition is given by:

$${\tau }_{{\nu }^{\prime }}=\frac{1}{{\displaystyle {\sum }_{n=0}^{n_{\nu }}{A}_{\nu {\nu }^{\prime }}}}$$

(6)

where v is a vibration level belonging to a lower electronic state, and the Einstein coefficient $A_{\nu {\nu }^{\prime }}$ is given by:

$$A_{\nu {\nu }^{\prime }}=2.141986\ast {10}^{10}{E}^3|⟨{\chi }_{\nu }|\mu ||{\chi }_{{\nu }^{\prime }}⟩{|}^2$$

(7)

• Bound-Free Transition

This is the transition from one level of vibration v’ linked to all states of the continuum. Its contribution to the lifetime is τ_ν’ such that: ${\tau }_{{\nu }^{\prime }}=\frac{1}{{\mathrm{\Gamma }}_{\nu }}$

$${\mathrm{\Gamma }}_{\nu }=2.141986\ast {10}^{10}{}_{}{\displaystyle \underset{Eas}{\overset{E_{{}^{\nu \prime }}}{\int }}{\nu }^{\prime }}{E}^3|⟨{\chi }_{\nu }|\mu ||{\chi }_{{\nu }^{\prime }}⟩{|}^{2}dE$$

(8)

E_as is the energy of the asymptotic limit of the electronic state corresponding to the continuum v.

3. Results

3.1. Transition Dipole Moment (TDM)

For the first time, the TDM functions for all states were investigated in the previous work [2]. The most obvious transition is between adjacent states (i, i + 1), and the forms of these functions have extrema at different positions.

In Figure 2, we have presented the selected transitions from states (X-A), (X-C) and (A-C) ¹Σ⁺ symmetry. The other states wereinvestigated before in our work of Souissi et al. [1]. The (X-A), (X-C) and (A-C) ¹Σ⁺ transition shows a peak around 10 a.u, 18 a.u and 14.1 a.u, respectively, which coincide with an avoided crossing position (ACP) in their PECs [1].

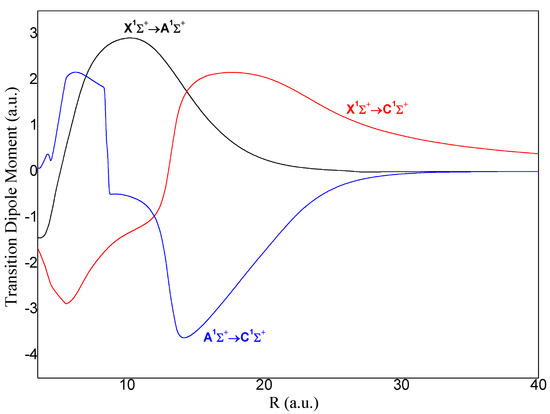
Figure 2. Adiabatic transition dipole moment of: (X-A), (X-C) and (A-C)¹Σ⁺ of (SrK)⁺.

3.2. Electronic Spectrum

Based on the method of Franck–Condon, the vertical transition is the most probable, and this corresponds to the most probable intensity. In Figure 3a–f, we have presented the absorption and emission spectra as a function of the excitation energy of the SrK⁺ molecular ion. These spectra have the same shapes as the absorption spectra. Note that the absorption spectra of X (v = 0) → A of the molecular ion SrK⁺ have a peak of maximum intensity (I = 1.299× 10⁻⁶⁵ a.u) at energy E = 15,870 cm⁻¹for the quantum number v’= 51 (Figure 3a). For the transition from X (v = 0) to C, the most intense peak (I = 1.123 × 10⁻⁴ a.u) takes place at an energy of E = 22,338 cm⁻¹ for the level v’= 4, and we noticed that this transition is more intense than that of the transition X → A. Table 1 contains the intensities of the most intense peaks of absorption spectra from level v = 0 to level v’. Likewise, the most probable peak intensities and the most corresponding energy for all transitions between the first three electronic states X, A and C of the (SrK)⁺ ion are given in this same table.

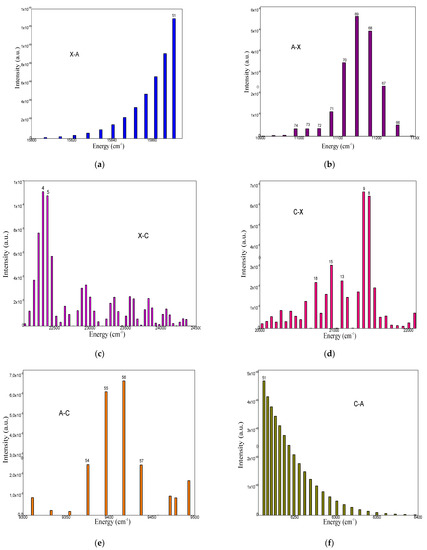
Figure 3. (a) Absorption Spectra X (v = 0) ➔ A (v = 0,…,52) for SrK⁺. (b) Emission Spectra A (v = 0) ➔ X (v = 0,…,28) for SrK⁺. (c) Absorption Spectra X (v = 0) ➔ C (v = 0,…,141) for SrK⁺. (d) Emission Spectra C (v = 0) ➔ A (v = 0,…,52) for SrK⁺. (e) Absorption Spectra A (v = 0) ➔ C (v = 0,…,141) for SrK⁺. (f) Emission Spectra C (v = 0) ➔ X (v = 0,…, 28) for SrK⁺.

Table 1. Energypositions of the maximum intensities for each absorption and emission transition for (SrK)⁺.

Transition	v	${\mathit{v}}_{\mathbf{S}\mathbf{r}{\mathbf{K}}^{+}}^{\prime }$	ISrK+(u.a)	ESrK+(cm−1)
Absorption
X→A	0	51	1.299 × 10−65	15,870
X→C	0	4	1.123 × 10−4	22,338
A→C	0	56	6.723 × 10−6	9417
Emission
A→X	0	69	5.699 × 10−6	11,148
C→A	0	51	4.747 × 10−48	6212
C→X	0	9	6.706 × 10−6	21,397

3.3. Infrared Spectrum

We have determined the infrared absorption spectra of the states X, A and C ¹Σ⁺ of the SrK⁺ molecular ion. In Figure 4, we have represented the transitions between neighboring and non-neighboring vibrational levels (Δv = v − v’ = 1, 2 and 3).

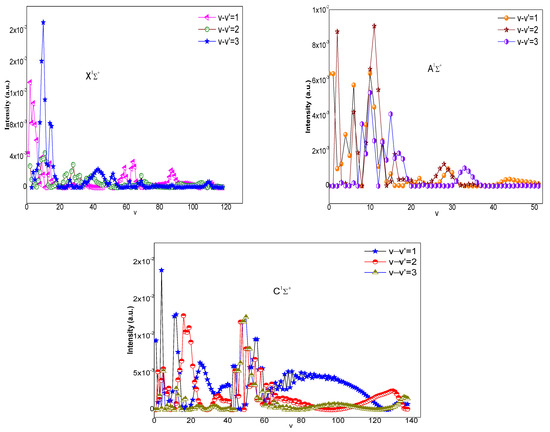
Figure 4. Transition between the non-neighboring vibrational states of the X, A and C of SrK⁺.

We note that, contrary to the rules for the selection of the harmonic oscillator, we can have non-negligible transitions between non-neighboring vibrational levels [3,4], but the transitions between neighboring levels are generally greater.

3.4. Radiative Lifetime

In this last part, we are interested in the determination of the radiative lifetimes associated with the first two excited states of the sigma symmetry for the molecular ion SrK⁺, which were calculated using the approximate approach of Franck–Condon and the exact calculation.

In literature, we found theoretical works that have been interested in the calculation of the lifetime of several diatomic systems with two valence electrons [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32].

Table 2, Table 3 and Table 4 show the bound–bound contributions as well as the radiative lifetime without correction of the electron affinity for the X, A and C¹Σ⁺ states for SrK⁺. Remember that the radiative lifetime of state C, for example, is given by:

$$\frac{1}{{\tau }_c}=\frac{1}{\tau {}_{c\to x}}+\frac{1}{\tau {}_{c\to A}}$$

(9)

$${\tau }_c=\frac{{\tau }_{c\to x}\ast {\tau }_{c\to A}}{{\tau }_{c\to x}+{\tau }_{c\to A}}$$

(10)

Table 2. Radiativelifetimes associated with the A → X emission of the ion (SrK)⁺.

v	Bound–Bound (106 ×S−1)	Bound-Free F.C. (106×S−1)	Bound-Free Exact (106 ×S−1)	Total F.C (106 ×S−1)	Total Exact (106×S−1)
0	86.0200	0.00000	0.00000	86.0200	86.0200
1	91.0063	0.00000	0.00000	91.0063	91.0063
2	106.574	0.00000	0.00000	106.574	106.574
3	118.649	0.00000	0.00000	118.649	118.649
4	107.895	0.00000	0.00000	107.895	107.895
5	122.825	0.00000	0.00000	122.825	122.825
6	123.396	0.00000	0.00000	123.396	123.396
7	125.298	0.00000	0.00000	125.298	125.298
8	132.575	0.00000	0.00000	132.575	132.575
9	134.261	0.00000	0.00000	134.261	134.261
10	142.069	0.00000	0.00000	142.069	142.069
11	148.531	0.00000	0.00000	148.531	148.531
12	149.446	0.00000	0.00000	149.446	149.446
13	166.148	0.00000	0.00000	166.148	166.148
14	162.660	0.00000	0.00000	162.660	162.660
15	171.311	0.00000	0.00000	171.311	171.311
16	182.630	28.1527	0.00000	154.4773	182.630
17	183.503	27.8199	0.15887	155.6831	183.34413
18	189.114	28.2431	0.15369	160.8709	188.96031
19	195.335	27.9084	0.14743	167.4266	195.18757
20	201.828	27.6343	0.14142	174.1937	201.68658
21	208.495	27.9382	0.13633	180.5568	208.35867
22	210.789	27.7882	0.13142	183.0008	210.65758
23	215.295	27.7246	0.12719	187.5704	215.16781
24	224.447	28.2721	0.12241	196.1749	224.32459
25	231.470	28.6801	0.11814	202.7899	231.35186
26	236.621	28.9141	0.11401	207.7069	236.50699
27	245.169	29.7375	0.11000	215.4315	245.05900
28	255.618	31.0485	0.10612	224.5695	255.51188
29	263.444	32.1135	0.10286	231.3305	263.34114
30	270.164	32.9228	0.09934	237.2412	270.06466
31	280.713	33.9901	0.09567	246.7229	280.61733
32	295.988	35.4501	0.09205	260.5379	295.89595
33	311.966	37.0031	0.08901	274.9629	311.87699
34	324.868	38.2842	0.08580	286.5838	324.78220
35	335.409	39.5255	0.08236	295.8835	335.32664
36	347.013	41.4138	0.07996	305.5992	346.93304
37	362.045	44.0120	0.07699	318.0330	361.96801
38	380.475	46.5438	0.07415	333.9312	380.40085
39	400.858	48.4931	0.07163	352.3649	400.78637
40	421.969	50.2775	0.06894	371.6915	421.90006
41	443.600	52.4300	0.06630	391.1700	443.5337
42	466.174	55.0002	0.06387	411.1738	466.11013
43	490.087	57.9621	0.06154	432.1249	490.02546
44	515.371	61.0145	0.04907	454.3565	515.32193
45	541.936	64.4507	0.03655	477.4853	541.89945
46	570.253	68.3283	0.03622	501.9247	570.21678
47	601.263	72.2775	0.02351	528.9855	601.23949
48	635.026	76.3719	0.01024	558.6541	635.01576
49	671.341	80.7716	0.00825	590.5694	671.33275
50	710.292	85.1271	0.00197	625.1649	710.29003
51	750.449	89.8953	0.00000	660.5537	750.44900
52	780.030	93.5021	0.00000	686.5279	780.03000

Table 3. Radiative lifetimes associated with the C → A emission of the ion (SrK)⁺.

v	Bound–Bound (106 ×S−1)	Bound-Free F.C. (106 ×S−1)	Bound-Free Exact (106 ×S−1)	Total Exact (106 ×S−1)	Total F.C. (106 ×S−1)
0	37.9892	0.00000	0.00000	37.9892	37.9892
1	41.1484	0.00000	0.00000	41.1484	41.1484
2	43.6414	0.00000	0.00000	43.6414	43.6414
3	46.4402	0.00000	0.00000	46.4402	46.4402
4	48.9569	0.00000	0.00000	48.9569	48.9569
5	51.7851	0.00000	0.00000	51.7851	51.7851
6	54.2838	0.00000	0.00000	54.2838	54.2838
7	56.7512	0.00000	0.00000	56.7512	56.7512
8	59.5366	0.00000	0.00000	59.5366	59.5366
9	62.2937	0.00000	0.00000	62.2937	62.2937
10	64.8818	0.00000	0.00000	64.8818	64.8818
11	67.9425	0.00000	0.00000	67.9425	67.9425
12	70.5524	0.00000	0.00000	70.5524	70.5524
13	73.7978	0.00000	0.00000	73.7978	73.7978
14	76.7052	0.00000	0.00000	76.7052	76.7052
15	79.6894	0.00000	0.00000	79.6894	79.6894
16	82.9077	0.65136	0.01535	82.89235	82.25634
17	86.0519	0.57220	0.01748	86.03442	85.4797
18	89.2754	0.59421	0.01683	89.25857	88.68119
19	92.7504	0.64026	0.01562	92.73478	92.11014
20	96.3155	0.54542	0.01833	96.29717	95.77008
21	99.6056	0.60202	0.01661	99.58899	99.00358
22	103.339	0.52154	0.01917	103.31983	102.81746
23	106.771	0.61323	0.01631	106.75469	106.15777
24	110.440	0.51845	0.01929	110.42071	109.92155
25	114.305	0.64096	0.01560	114.2894	113.66404
26	118.029	0.59326	0.01685	118.01215	117.43574
27	120.901	0.60323	0.01657	120.88443	120.29777
28	123.090	0.60095	0.01663	123.07337	122.48905
29	124.072	0.58559	0.01706	124.05494	123.48641
30	122.949	0.63775	0.01567	122.93333	122.31125
31	121.159	0.60272	0.01658	121.14242	120.55628
32	119.678	0.70056	0.01422	119.66378	118.97744
33	120.265	0.69248	0.01426	120.25074	119.57252
34	123.659	0.68695	0.01426	123.64474	122.97205
35	126.933	0.69783	0.01410	126.9189	126.23517
36	127.981	0.72656	0.01358	127.96742	127.25444
37	127.330	0.72380	0.01319	127.31681	126.6062
38	128.698	0.68990	0.01339	128.68461	128.0081
39	132.495	0.72629	0.01305	132.48195	131.76871
40	133.936	0.82697	0.01165	133.92435	133.10903
41	133.509	0.75787	0.01243	133.49657	132.75113
42	0.00000	4.03374	0.00000	4.03374	1
43	0.00000	4.03374	0.00000	4.03374	1.00023
44	0.00000	3.89376	0.00000	3.89376	1.00026
45	0.00000	4.04197	0.00000	4.04197	2.00005
46	0.00000	4.04197	0.00000	4.04197	1.00846
47	0.00000	4.16380	0.00000	4.1638	1.2703
48	0.00000	4.25301	0.00000	4.25301	2.21109
49	0.00000	4.25301	0.00000	4.25301	1.2195
50	0.00000	4.26168	0.00000	4.26168	1.36818
51	0.00000	4.27002	0.00000	4.27002	2.2281
52	0.00000	4.27002	0.00000	4.27002	1.23651
53	0.00000	4.27124	0.00000	4.27124	1.37774
54	0.01181	4.24682	0.00000	0.01181	0.00079
55	0.01189	4.24682	0.00000	0.01189	0.00107
56	0.02898	4.24497	0.00000	0.02898	0.01401
57	17.2919	4.30959	0.00000	17.2919	12.98231
58	17.4233	4.30959	0.00000	17.4233	13.11371

Table 4. Radiative lifetime associated with the C → X emission of the ion (SrK)⁺.

v	Bound–Bound (106 ×S−1)	Bound-Free F.C. (106 ×S−1)	Bound-Free Exact (106 ×S−1)	Total Exact (106 ×S−1)	Total F.C. (106 ×S−1)
0	15.5833	0.00000	0.00000	15.5833	15.5833
1	15.6567	0.00000	0.00000	15.6567	15.6566
2	15.9250	0.00000	0.00000	15.9250	15.9249
3	16.2872	0.00000	0.00000	16.2872	16.2872
4	15.9554	0.00000	0.00000	15.9554	15.9553
5	15.6539	0.00000	0.00000	15.6539	15.6539
6	16.6202	0.00000	0.00000	16.6202	16.6202
7	16.2943	0.00000	0.00000	16.2943	16.2943
8	16.4717	0.00000	0.00000	16.4717	16.4716
9	17.3941	0.00000	0.00000	17.3941	17.3941
10	17.7805	0.00000	0.00000	17.7805	17.7804
11	17.9315	0.00000	0.00000	17.9315	17.9315
12	16.2405	0.00000	0.00000	16.2405	16.2405
13	18.4025	0.00000	0.00000	18.4025	18.4025
14	17.7258	0.00000	0.00000	17.7258	17.7258
15	18.9324	0.00000	0.00000	18.9324	18.9323
16	17.7166	0.00000	0.00000	17.7166	17.7166
17	16.9305	0.00000	0.00000	16.9305	16.9305
18	18.5192	0.00000	0.00000	18.5192	18.5192
19	18.6292	0.00000	0.00000	18.6292	18.6292
20	18.6425	0.00000	0.00000	18.6425	18.6425
21	18.4598	0.00000	0.00000	18.4598	18.4598
22	18.0091	0.00000	0.00000	18.0091	18.0091
23	18.4431	0.00000	0.00000	18.4431	18.4431
24	19.3574	0.00000	0.00000	19.3574	19.3574
25	18.4619	0.00000	0.00000	18.4619	18.4619
26	19.0309	0.00000	0.00000	19.0309	19.0309
27	19.1000	0.00000	0.00000	19.1000	19.0999
28	21.1174	0.00000	0.00000	21.1174	21.1174
29	19.9818	0.00000	0.00000	19.9818	19.9819
30	19.3688	0.00000	0.00000	19.3688	19.3688
31	19.2693	0.00000	0.00000	19.2693	19.2693
32	19.7974	0.00000	0.00000	19.7975	19.7975
33	19.4599	0.00000	0.00000	19.4599	19.4598
34	20.4417	0.00000	0.00000	20.4417	20.4417
35	19.1984	0.00000	0.00000	19.1984	19.1984
36	20.7021	0.00000	0.00000	20.7021	20.7021
37	20.0228	0.00000	0.00000	20.0228	20.0228
38	20.6207	0.00000	0.00000	20.6207	20.6206
39	20.6388	0.00114	0.00000	20.6388	20.6383
40	21.0813	0.00554	0.00000	21.0809	21.0789
41	21.3171	0.03080	0.00405	21.3153	21.3031
42	3205.322	2360.19	3205.01	0.31201	0.42369
43	3205.321	2398.19	3205.01	0.31201	0.41698
44	7160.209	4443.17	7160.07	0.13966	0.22506
45	6484.534	4542.33	6484.38	0.15422	0.22015
46	6484.534	4627.04	6484.38	0.15422	0.21612
47	4250.365	4712.43	4250.13	0.23529	0.21220
48	3747.907	4809.56	3747.64	0.26683	0.20792
49	3747.907	4886.03	3747.64	0.26683	0.20467
50	3157.377	4968.57	3157.06	0.31675	0.20127
51	3073.305	5057.45	3072.98	0.32542	0.19773
52	3073.305	5091.10	3072.98	0.32542	0.19642
53	2677.963	5152.83	2677.59	0.37347	0.19407
54	2553.892	5208.97	2553.50	0.39162	0.19198
55	2553.892	5243.22	2553.50	0.39162	0.19072
56	2325.930	5294.10	2325.50	0.43002	0.18888
57	2037.810	5188.71	2037.32	0.49028	0.19264
58	2037.320	5228.11	2037.32	0.49028	0.19119
59	2078.160	5411.56	2078.16	0.48109	0.18477

In Table 5, we have displayed the exact total lifetimes and Franck–Condon of state C of the SrK⁺ molecular ion.

Table 5. Total radiative lifetime of the C-state of the ion (SrK)⁺.

v	Total Exact (106 ×S−1)	Total F.C (106 ×S−1)
0	15.582	9.7885
1	15.655	9.5220
2	15.923	9.3953
3	16.285	9.2732
4	15.953	8.9579
5	15.651	8.6455
6	16.617	8.7373
7	16.291	8.4658
8	16.468	8.3162
9	17.390	8.3483
10	17.776	8.2560
11	17.927	8.0834
12	16.237	7.5685
13	18.397	7.8041
14	17.721	7.5120
15	18.927	7.5466
16	17.712	7.1761
17	16.925	6.8909
18	18.513	6.9797
19	18.624	6.8292
20	18.636	6.6686
21	18.454	6.5029
22	18.003	6.2946
23	18.438	6.2115
24	19.350	6.1695
25	18.457	5.9358
26	19.025	5.8625
27	19.094	5.7718
28	21.109	5.8670
29	19.975	5.7432
30	19.363	5.7281
31	19.263	5.7785
32	19.792	5.8758
33	19.454	5.8257
34	20.436	5.7945
35	19.193	5.5859
36	20.697	5.6726
37	20.017	5.6409
38	20.615	5.6435
39	20.633	5.5264
40	21.075	5.5134
41	21.309	5.5417
42	0.3120	0.4237
43	0.3120	0.4169
44	0.1397	0.2251
45	0.1542	0.2201
46	0.1542	0.2161
47	0.2353	0.2122
48	0.2668	0.2079
49	0.2668	0.2047
50	0.3167	0.2013
51	0.3254	0.1977
52	0.3254	0.1964
53	0.3735	0.1941
54	0.3916	0.1919
55	0.3916	0.1907
56	0.4300	0.1889
57	0.4903	0.1920
58	0.4903	0.1906
59	0.4811	0.1846

The bound and continuum states and the vibrational levels were determined by means of the Numerov algorithm.

However, a first trial set of approximate energy levels has been determined by diagonalizing a tridiagonal matrix and provided to the Numerov propagator. This matrix corresponds to the numerical derivative of the nuclear Schrödinger equation on a radial grid of N points (N is taken larger than the last vibrational level). All quantities used, such as the potential energy curve, the transition dipole moment, and the bound and free wave functions were determined for a radial grid of 30 000 points. The grid used in the integration of the bound-free contribution wasof 1000 energy points. Tests were carried out to ensure the convergence of the radiative lifetime for integration on the radial as well as the energy grids.

4. Conclusions

In this study, we wereinterested in the determination of radiativelifetime effects. First, we determined the transitions dipole moments and of the SrK⁺ molecular ion in the adiabatic representation. Next, we determined the absorption and emission spectra, depending on the vibrational level and its energy, for the first ¹Σ⁺ symmetry states for SrK⁺ system. Subsequently, we represented the transition spectra, within the same electronic state, between vibrational levels having v = 1, 2 and 3. Using the dipole moments of transition, determined beforehand, we calculated the radiative lifetimes of the vibrational levels of the molecular states A¹Σ⁺ and C¹Σ⁺ of the molecular ion SrK⁺. These lifetimes were calculated by two methods:

-

Exact method based on an exact calculation of the integral of the bound-free contribution.

-

Approximate method based on the Franck–Condon approximation.

The two methods give results of the same order of magnitude for the first vibrational levels, but this concordance does not persist for the excited levels, and the divergence is greater and greater as the vibrational level becomes more and more excited. The radiative lifetimes obtained from this molecular system for the first excited state are of the order of a nanosecond.

To the best of our knowledge, the lifetimes for the studied system have not been studied in the literature. Our results would clearly be of interest for physicists working in atomic physics, plasma physics and astrophysics.