Abstract
This study is the second part of the theoretical study of “Modeling and Simulation of a Two-Stage Air-Cooled Adsorption Chiller with Heat Recovery”, which is based on developing a theoretical model for a two-stage adsorption chiller with an activated carbon/methanol pair. The following models were conducted numerically using MATLAB. The model was based on 10th order differential equations; six of them were used to predict bed, evaporator and condenser temperatures, while the other four equations were used to calculate adsorption isotherm and adsorption kinetics. In this second part, bed heat exchangers and evaporator and condenser heat exchangers are studied by varying the parametric design of a chiller. This includes but is not limited to activated carbon mass inside a single bed, overall heat transfer coefficient for the bed and evaporator and the mass flow rates of all components comprising the chiller. The optimum values increased the COP from 0.35 to 0.4, while the cooling capacity was slightly changed. The COP is 95% of a Carnot cycle working at hot water temperatures as low as 60 °C, and 90% at hot water temperatures as high as 90 °C. It was found that the simulation model results for the two-stage air-cooled chiller agreed well with the experimental data in terms of cooling capacity (6.7 kW for the model against 6.14 kW for the experimental result at 30 °C cooling water temperature). The model optimized the adsorption/desorption time, switching time and heat recovery time to maximize both cooling capacity and COP. Moreover, the model is used to study the effect of activated carbon mass, size of beds and mass flow rates of cooling, heating, chiller and condenser on both cooling capacity and COP.
1. Introduction
The work in this paper is conducted to continue the research work submitted for applied science [1], for the modeling and simulation of a two-stage adsorption chiller with heat recovery.
Since the 1980s, due to projected energy shortages, many researchers have investigated the performance and operation of adsorption in air conditioning, freezing and heat pump applications for solar energy because of the near coincidence of peak of cooling load and available solar load [2,3,4,5,6,7,8,9]. The subject was handled experimentally and mathematically from basic fundamentals, number of stages, working pairs, mass and heat recovery and cycle time optimization, in addition to many parametric studies for chiller components, such as adsorption bed and heat exchangers [10]. Dynamic modeling for optimizing the half-cycle time of adsorption at a different solar intensity was presented and showed remarkable improvements in cooling capacity [11]. Two of the pioneering researchers were (Sakoda and Suzuki, 1983) who carried out many fundamental experiments on the solar-powered adsorption cooling system. A simple model that takes into account both adsorption properties and apparatus characteristics was used to interpret experimental results. The heat and mass transfer were also interpreted by this model. They studied quantitatively the effect of regeneration temperature on the cooling performance [12]. Parametric analysis studied a two-stage adsorption chiller using reheat demonstrating the effect of the overall thermal conductance and adsorbent mass on system performance [13,14,15]. Bed and heat exchanger configurations to reduce heat-transfer resistance and improve performance were reviewed for a single-stage and a multistage adsorption chiller [16,17,18]. Finally, Ahmad, R.M. Rezk and Raya. K. Aldadah studied, using MATLAB, the performance of a silica gel adsorption chiller at different operating and physical conditions [19]. A parametric study of the influence of many system parameters on the performance is accomplished and discussed [19]. Many studies showed that system performance (cooling capacity and COP) is strongly affected by the number of transfer units of an adsorber/desorber, and the number of transfer units of a condenser is the least sensitive parameter [20,21]. Some researchers studied the effect of particle diameter and adsorbent bed thickness on bed thermal conductivity and how this lead to a dramatic improvement in specific cooling power (SCP) [22]. The performance of three different solar cooling systems is examined by a solar electrical, a solar thermal and a hybrid solar electrical–thermal cooling system for different regional climates [22,23]. The performance of silica gel/water adsorption chiller for the Jordan climate was evaluated experimentally and theoretically against ambient temperature, global solar radiation, relative humidity, wind speed and temperatures of the solar adsorption system at different locations of the experimental setup [24,25].
The novelty of this work includes the enhancement of the performance of a transient models’ medium capacity for an air-cooled adsorption chiller that could work at near-ambient temperature and a humidity higher than any other chillers ever built (up to 50 °C) by applying mass and heat recovery and optimizing for operating conditions and cyclic time. The results of the models will be used for predicting the cooling capacity of larger sizes and different operating conditions.
2. Physical and Mathematical Models
2.1. Physical Model
The two-stage chiller is composed of four beds, two stages (desorption/adsorption), an evaporator, a condenser, circulating pipes and valves and pressure- and temperature-monitoring instruments. In a two-stage adsorption chiller, the evaporating pressure is divided into two consecutive temperature lifts to exploit low-heat source temperature by introducing four beds. This configuration makes it possible to run the chiller at high ambient temperature ranges (up to 50 °C) and hot water temperatures as low as 60 °C to produce chilled water as low as 7 °C. A schematic for the two-stage adsorption chiller is shown in Figure 1. The working principles of this chiller were discussed in part I of this study.
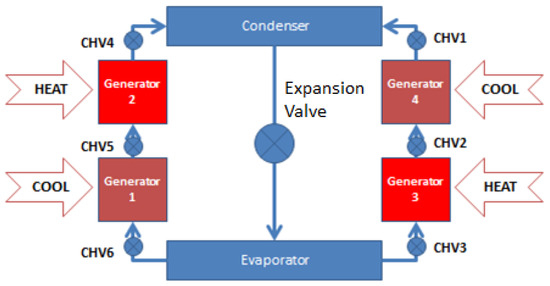
Figure 1.
Schematic for two-stage adsorption chiller.
Modes of Operation for Two-Stage Adsorption Chiller
Table 1 shows the operation modes for the two-stage chiller with mass and heat recovery. The two-stage chiller with mass and heat recovery has six modes, Modes A, B, C, D, E and F.

Table 1.
Operation modes for the two-stage chiller with mass and heat recovery.
2.2. Mathematical Model
Assumptions for the model and energy balance during the operation, switching time and heat recovery were discussed in Part I of this study. The governing equations during the operation are briefly mentioned hereafter.
For G1 and G4: Adsorption
The energy balance equation is:
The outlet temperature of the cooling water is calculated by log mean temperature difference (LMTD):
For G2 and G3: desorption
The energy balance equation is:
The outlet temperature of the heating water is calculated by LMTD:
For the evaporator:
The outlet temperature of the chilled water is calculated by LMTD:
For the condenser:
The outlet temperature of the condenser water is calculated by LMTD:
For cooling capacity and COP:
3. Results and Discussion
In this study, the bed heat exchangers and evaporator and condenser heat exchangers are studied by varying the parametric design of the chiller. This includes but is not limited to activated carbon mass inside a single bed, the overall heat transfer coefficient for the bed and evaporator and the mass flow rates of all components comprising the chiller. The optimum values are determined by designs that give maximum cooling capacity and maximum COP.
3.1. Effect of the Mass of Activated Carbon
Figure 2 shows that as the mass of activated carbon increases, the cooling capacity and COP increases, taking into account that a larger bed size is required. The cooling capacity and COP increase with the increasing activated carbon mass in the adsorption/desorption bed, since with increased mass, more methanol is adsorbed in the beds, and as a result, more cooling capacity is obtained. Moreover, more activated carbon mass required more heat input, and therefore, the COP was no further improved, as shown at a mass of 50 kg.
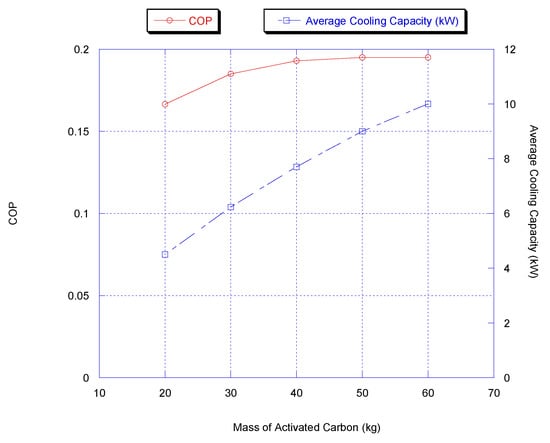
Figure 2.
Effect of activated carbon mass on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
3.2. Effect of Evaporator Overall Heat Transfer Coefficient
Figure 3 shows the effect of the evaporator’s overall heat transfer coefficient value on the chiller average cooling capacity COP. Both the chiller’s average cooling capacity and COP decrease with the evaporator’s increasing overall heat transfer coefficient.
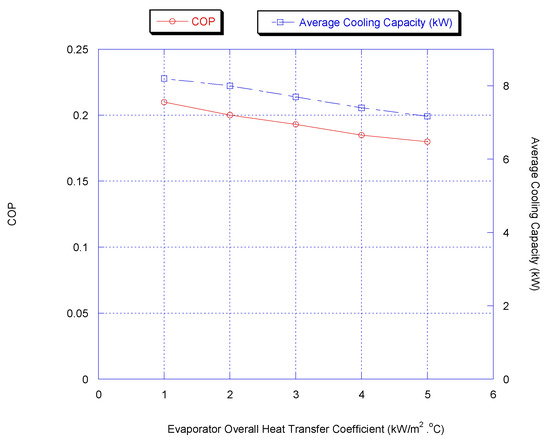
Figure 3.
Effect of evaporator’s overall heat transfer coefficient on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
3.3. Effect of Bed’s Overall Heat Transfer Coefficient
Figure 4 shows the effect of the bed’s overall heat transfer coefficient value on the chiller average cooling capacity and COP.
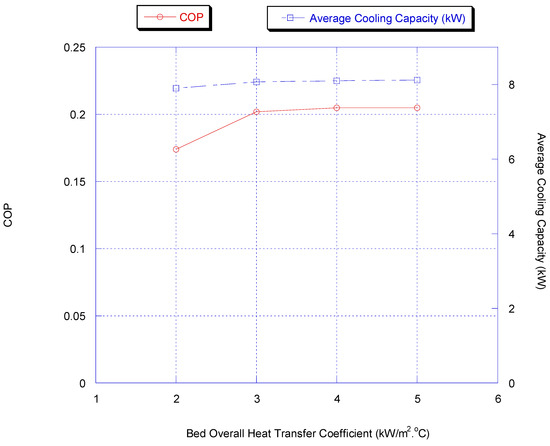
Figure 4.
Effect of bed’s overall heat transfer coefficient on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
It can be seen that both the cooling capacity and COP increase with the overall heat transfer coefficient of the adsorption/desorption bed since the increase in the overall heat transfer coefficient means a more steady heat exchange to heat and cool water, leading to a higher cooling capacity and COP. It is very clear that the rate of change for cooling capacity and COP is small when the overall heat transfer coefficient is greater than 3 kW/m2·°C.
3.4. Effect of Chilled Water Mass Flow Rate
Figure 5 shows the effect of chiller flow rate on chiller average cooling capacity and COP.
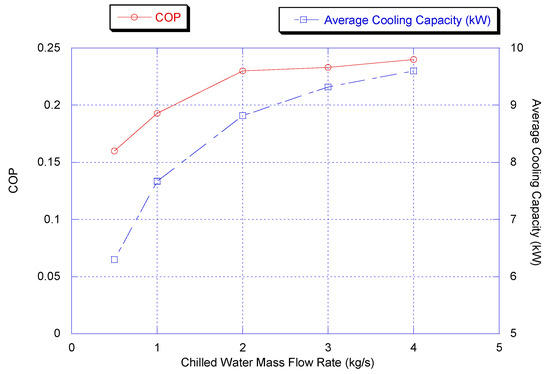
Figure 5.
Effect of chiller flow rate on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
Figure 5 shows that the higher the mass flow rate of chilled water, the higher the cooling capacity and COP. The mass flow rate of chilled water can control the chiller outlet temperature, as shown in Figure 6. Therefore, to compare between chillers, the chilled water inlet temperature must be the same.
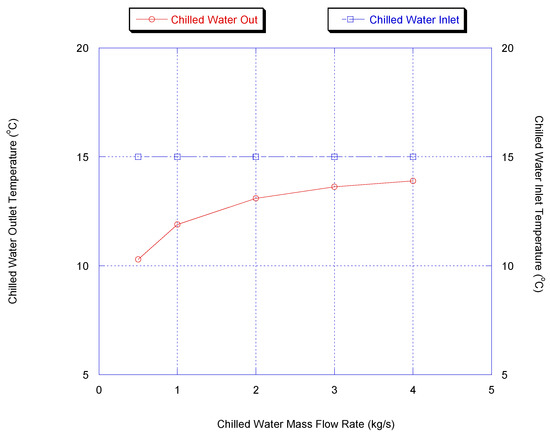
Figure 6.
Effect of chiller flow rate on chiller outlet temperature (results are at chiller nominal operating conditions, shown in Appendix B).
3.5. Effect of Cooling Water Mass Flow Rate
Figure 7 shows the effect of the cooling water flow rate on the chiller’s average cooling capacity and COP.
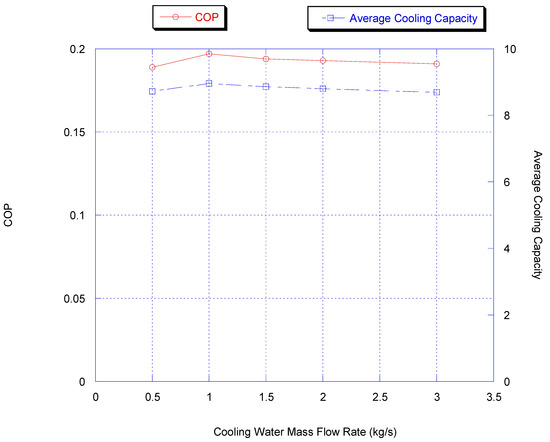
Figure 7.
Effect of cooling water flow rate on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
For this chiller, it is shown that the cooling water mass flow rate of 1 kg/s is the optimum, and so there is no need to increase it during the chiller operation.
3.6. Effect of Hot Water Mass Flow Rate
Figure 8 shows the effect of hot water flow rate on the chiller’s average cooling capacity and COP, while Figure 9 shows the effect of hot water flow rate on the hot water outlet temperature. The optimum hot water mass flow rate is 1.5 kg/s, which gives a maximum average cooling capacity of around 8 kW and a maximum COP of 0.26.
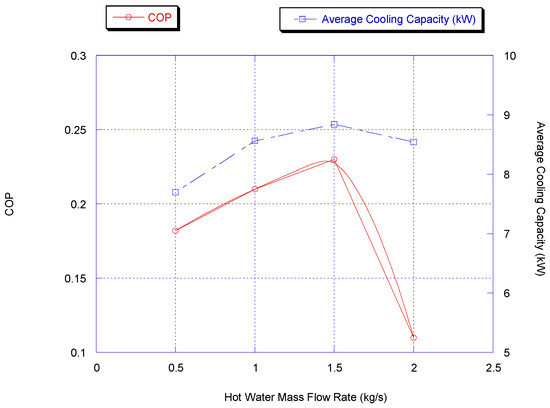
Figure 8.
Effect of hot water flow rate on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
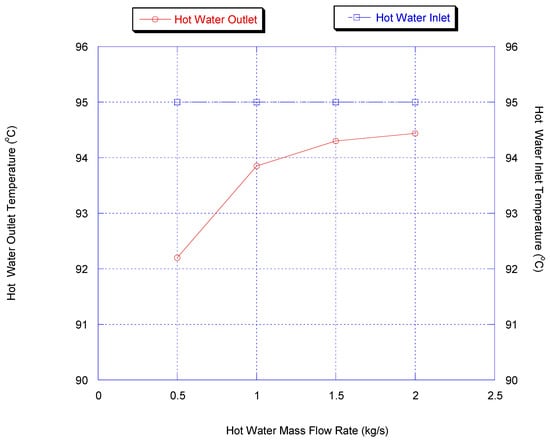
Figure 9.
Effect of hot water flow rate on hot water outlet temperature (results are at chiller nominal operating conditions, shown in Appendix B).
For this chiller, it is shown that the hot water mass flow rate of 1.5 kg/s is optimal, and it gives the maximum COP, while the cooling capacity is slightly influenced.
3.7. Effect of Condenser Water Mass Flow Rate
Figure 10 shows the effect of condenser water flow rate on the chiller average cooling capacity and COP, while Figure 11 shows the effect of condenser water flow rate on the condenser outlet temperature.
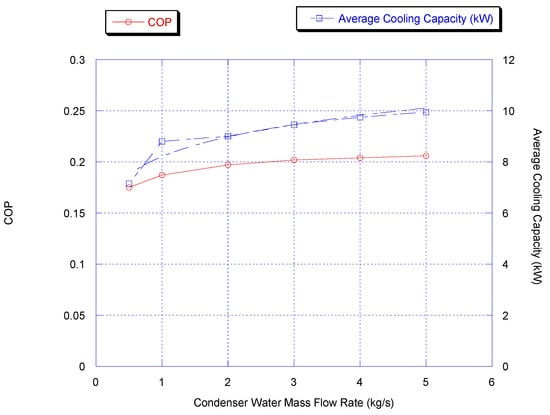
Figure 10.
Effect of condenser water flow rate on chiller average cooling capacity and COP (results are at chiller nominal operating conditions, shown in Appendix B).
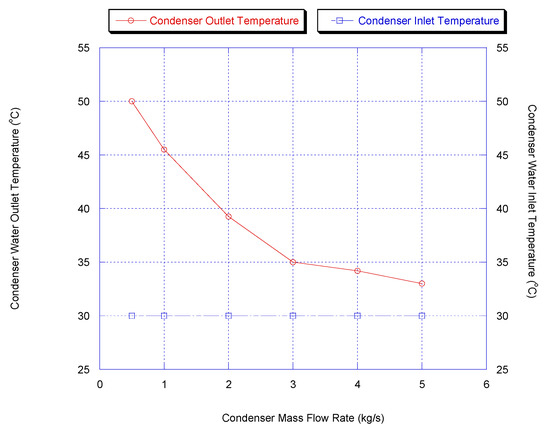
Figure 11.
Effect of condenser water flow rate on condenser outlet temperature (results are at chiller nominal operating conditions, shown in Appendix B).
3.8. Effect of Cooling Water Inlet Temperature
The influence of varying cooling temperature is studied by changing the inlet temperature of the cooling water. The cooling water is important factor for both condensation and adsorption process. Figure 12 shows the effect of changing inlet cooling water temperature on cooling capacity and COP for two stage chiller without heat recovery cycle while Figure 13 shows the same effect for chiller with heat recovery scheme.
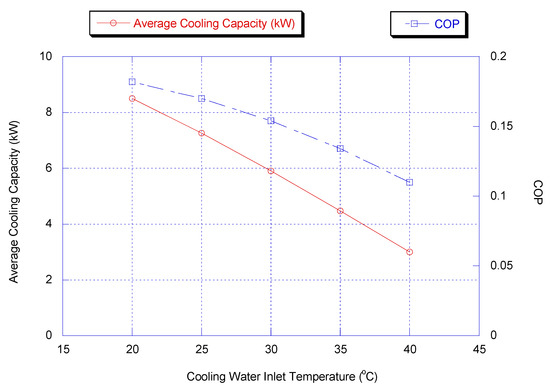
Figure 12.
Effect of cooling water inlet temperature on chiller average cooling capacity and COP without heat recovery (results are at optimum parametric values, shown in Appendix B).
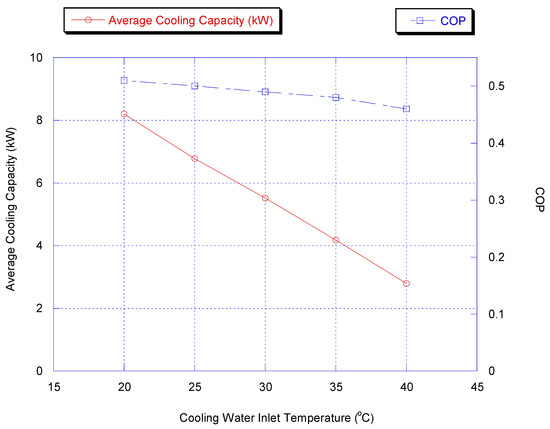
Figure 13.
Effect of cooling water inlet temperature on chiller average cooling capacity and COP with heat recovery (results are at optimum parametric values, shown in Appendix B).
3.9. Comparison with Carnot Cycle COP
Carnot cycle COP was used to evaluate the model results.
The chiller allows for running at optimum parameters for cycle time, switching time, heat recovery time, mass flow rates and activated carbon mass and optimum heat transfer coefficients for beds and evaporator heat exchangers. These results are compared with a Carnot cycle COP at different operating conditions, as shown in Table 2. All results are at nominal operating chiller conditions except hot water inlet temperature; the chiller without heat recovery mode operated at a very low COP when compared with the Carnot COP, while the heat recovery mode results are very close to the Carnot COP, as shown in the last column of Table 2.

Table 2.
Carnot cycle COP at different heating source input temperature.
3.10. Model Results at Optimum Parametric Values
The optimum values obtained from the parametric study are used to calculate the average cooling capacity and COP. The optimum values are shown in Appendix C.
3.11. Preliminary Study for the Extension of the Models for Larger Chiller Capacity
The models are used for the preliminary design of a larger capacity and different operating conditions. The size of the chiller was increased from 6.8 kW to 13.7 kW by increasing the area and mass flow rates for the beds, evaporator and condenser.
Figure 14 shows the average cooling capacity for the chiller when area and mass flow rates for the beds, evaporator and condenser are doubled.
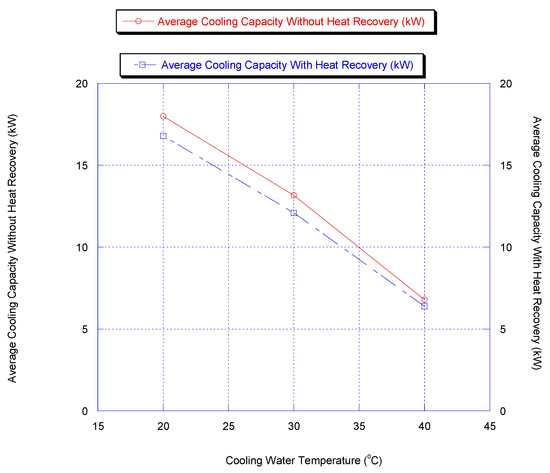
Figure 14.
Average cooling capacity for double-sized chiller (results are at chiller nominal operating conditions, shown in Appendix B).
4. Conclusions
- The dynamic model could predict all sizes for the two-stage chiller using an activated carbon/methanol pair, and easily could be adapted for any working pairs at variable operating conditions.
- The two-stage chiller could be operated by using low-grade waste heat at low COP or at a high temperature heat source with moderate to high COP.
- The proposed model could predict the COP for any chiller size with 90–95% of a Carnot cycle chiller working the same as an operating chiller at temperatures as low as 60 °C with heat recovery between beds.
- The model is a useful tool to predict the effect of the changing of mass of activated carbon mass and the heat transfer coefficient of beds, evaporator and condenser.
- The model is a useful tool to predict the effect of the flow rate of cooling and heating water in addition to the effect of chiller and condenser flow rates on chiller cooling capacity and COP.
- The model is a useful tool to predict the effect of inlet temperature of cooling and heating water on chiller cooling capacity and COP.
- The two-stage air-cooled adsorption chiller has a significant market potential, and the model used in this study could be used as a base for prototype scaling or series production.
Subscript
| ac | activated carbon |
| ad | adsorption |
| Al | Aluminum |
| b | bed |
| ci | cooling inlet |
| co | cooling outlet |
| cw | cold water |
| chw | chilled water |
| conw | condenser water |
| con | condenser |
| des | desorption |
| eva | evaporator |
| fg | vaporization |
| g | gas |
| hw | hot water |
| i | inlet |
| o | outlet |
| recw | recalculated water |
| s | solid |
| sat | saturation |
| st | storage |
Author Contributions
Data curation, F.M.M. and A.A.A.-M.; Investigation, A.A.B. and A.A.; Methodology, F.M.M. and A.A.B.; Resources, A.A.; Supervision, H.A.; Writing—original draft, A.A.B.; Writing—review & editing, H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
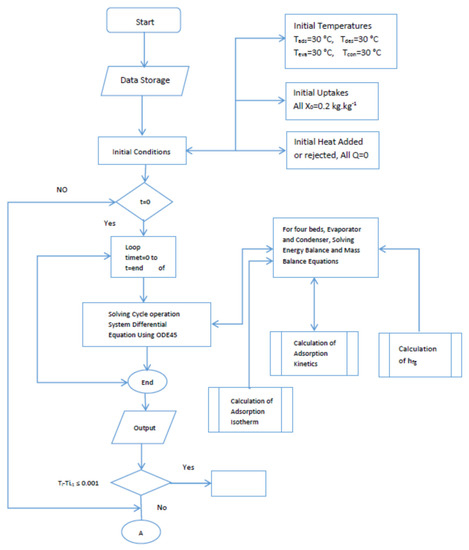
Figure A1.
Flow chart for the simulation.
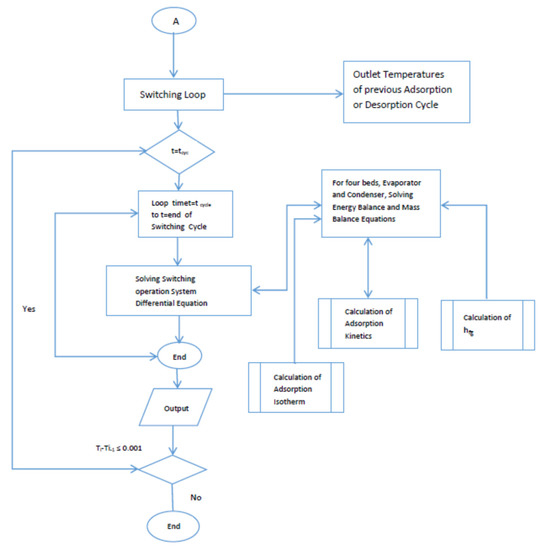
Figure A2.
Flow chart for the simulation, Continue.
Appendix B

Table A1.
Parameters Used in Simulation.
Table A1.
Parameters Used in Simulation.
| Symbol | Value | Unit |
|---|---|---|
| Abed | 4.5 | m2 |
| Aeva | 3 | m2 |
| Acon | 3 | m2 |
| Ubed | 3 | kW/m2·°C |
| Ueva | 2 | kW/m2·°C |
| Ucon | 4 | kW/m2·°C |
| Cpeva | 0.65 | kJ/kg·°C |
| Cpcon | 0.65 | kJ/kg·°C |
| Cpw | 4.18 | kJ/kg·°C |
| Cpac | 1 | kJ/kg·°C |
| Cpm | 2.6 | kJ/kg·°C |
| ρ (activated carbon) | 2000 | Kg/m3 |
| kac (activated carbon) | 0.63 | W/m·k |
| Meva | 20 | kg |
| Mcon | 30 | kg |
| hfg | 1200 | kJ·kg−1 |
| Mac | 40 | kg |
| Meva,m | 20 at time = 0 | kg |
| Mcon,m | 5 | kg |
| (E/R) Methanol | 978 | K |
| (15 Dso/R) Methanol | 7.35 × 10−2 | S−1 |
| xo | 0.284 | kg·kg−1 |
| n | 1.39 | Non Dimensional |
| K | 10.21 | Non Dimensional |
| R1 | 260 | Non Dimensional |
| Q | 4.666 | Non Dimensional |
| A | 20.84 | Non Dimensional |
| B | 4696 | Non Dimensional |
Appendix C

Table A2.
Chiller Nominal Operating Conditions.
Table A2.
Chiller Nominal Operating Conditions.
| Symbol | Value | Unit |
|---|---|---|
| Thi | 95 | °C |
| Tci | 30 | °C |
| Tconi | 30 | °C |
| Tchi | 15 | °C |
| Mchw | 2 | kg·s−1 |
| Mcw | 1 | kg·s−1 |
| Mhw | 1.5 | kg·s−1 |
| Mconw | 2 | kg·s−1 |
| Mrecw | 1 | kg·s−1 |
| Adsorption time | 300 | s |
| Desorption time | 300 | s |
| Switching time | 50 | s |
| Heat recovery time | 30 | s |
Appendix D

Table A3.
Chiller Optimum Parametric Conditions.
Table A3.
Chiller Optimum Parametric Conditions.
| Symbol | Value | Unit |
|---|---|---|
| Thi | 95 | °C |
| Ub | 3 | kW/m2·°C |
| Ueva | 1 | kW/m2·°C |
| Tchi | 15 | °C |
| Mchw | 3 | kg·s−1 |
| Mcw | 1 | kg·s−1 |
| Mhw | 1.5 | kg·s−1 |
| Mconw | 2 | kg·s−1 |
| Mrecw | 1 | kg·s−1 |
| Adsorption time | 300 | s |
| Desorption time | 300 | s |
| Switching time | 50 | s |
| Heat recovery time | 30 | s |
Appendix E

Table A4.
Nomenclature.
Table A4.
Nomenclature.
| Symbol | Description | Unit |
|---|---|---|
| Abed | Bed area | (m2) |
| Aeva | Evaporator area | (m2) |
| Acon | Condenser area | (m2) |
| Cp | Specific heat capacity | (kJ/kg·°C) |
| CC | Cooling Capacity | (kW) |
| COP | Coefficient of Performance | (Cooling capacity/input power) |
| Dso | Surface specific heat | (m2·s−1) |
| Ea | Activation energy | (kJ) |
| hfg | Latent heat of vaporization | (kJ·kg−1) |
| H | Enthalpy | (kJ·kg−1) |
| K | Constant in D-A equation | Non dimensional |
| Meva | Evaporator mass | (kg) |
| Mcon | Condenser mass | (kg) |
| Mac | Mass of activated carbon in each bed | (kg) |
| Meva,m | Mass of methanol in evaporator at t = 0 | (kg) |
| Mcon,m | Mass of methanol in condenser | (kg) |
| N | Constant in D-A equation | Non dimensional |
| P | Pressure | (Bar) |
| Qst | Adsorption heat | (kJ·kg−1) |
| R | Universal gas constant | (kJ/mol·K) |
| T | Temperature | (°C) |
| T | Time | (S) |
| Ubed | Bed overall heat transfer coefficient | (kW/m2·°C) |
| Ueva | Evaporator overall heat transfer coefficient | (kW/m2·°C) |
| Ucon | Condenser overall heat transfer coefficient | (kW/m2·°C) |
| X | Methanol concentration | (kg·kg−1) |
| xo | Maximum methanol concentration | (kg·kg−1) |
| x* | Equilibrium methanol concentration | (kg·kg−1) |
References
- Makahleh, F.; Amer, A.; Attar, H.; Badran, A. Modeling and simulation of a two stage adsorption chiller with heat recovery Part 1. Appl. Sci. 2022; Under review. [Google Scholar]
- Krzywanski, J.; Grabowska, K.; Sosnowski, M.; Żyłka, A.; Sztekler, K.; Kalawa, W.; Wójcik, T.; Nowak, W. Modeling of a re-heat two-stage adsorption chiller by AI approach. MATEC Web Conf. 2018, 240, 05014. [Google Scholar] [CrossRef]
- Benrajesh, P.; Rajan, A.J. Design and Analysis of a Two-Stage Adsorption Air Chiller. IOP Conf. Ser. Mater. Sci. Eng. 2017, 197, 012030. [Google Scholar] [CrossRef] [Green Version]
- Sosnowski, M.; Grabowska, K.; Krzywański, J.; Nowak, W.; Sztekler, K.; Kalawa, W. The effect of heat exchanger geometry on adsorption chiller performance. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1101, 012037. [Google Scholar] [CrossRef] [Green Version]
- Schwamberger, V.; Desai, A.; Schmidt, F.P. Novel Adsorption Cycle for High-Efficiency Adsorption Heat Pumps and Chillers: Modeling and Simulation Results. Energies 2020, 13, 19. [Google Scholar] [CrossRef] [Green Version]
- Jobard, X.; Padey, P.; Guillaume, M.; Duret, A.; Pahud, D. Development and Testing of Novel Applications for Adsorption Heat Pumps and Chillers. Energies 2020, 13, 615. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-G.; Bae, K.J.; Kwon, O.K. Performance Investigation of a Two-Bed Type Adsorption Chiller with Various Adsorbents. Energies 2020, 13, 2553. [Google Scholar] [CrossRef]
- Rouf, R.A.; Jahan, N.; Alam, K.C.A.; Sultan, A.A.; Saha, B.B.; Saha, S.C. Improved cooling capacity of a solar heat driven adsorption chiller. Case Stud. Therm. Eng. 2020, 13, 1–19. [Google Scholar] [CrossRef]
- Al Asfar, J.; Ayadi, O.; Al Salaymeh, A. Design and Performance Assessment of a Parabolic Trough Collector. JJMIE 2014, 8, 1–5. [Google Scholar]
- Abd-Elhady, M.M.; Hamed, A.M. Effect of fin design parameters on the performance of a two-bed adsorption chiller. Int. J. Refrig. 2020, 113, 164–173. [Google Scholar] [CrossRef]
- Basdanis, T.; Tsimpoukis, A.; Valougeorgis, D. Performance optimization of a solar adsorption chiller by dynamically adjusting the half-cycle time. Renew. Energy 2021, 164, 362–374. [Google Scholar] [CrossRef]
- Zhai, Q.; Wang, R.Z.; Wu, J.Y.; Dai, Y.J.; Ma, Q. Design and performance of a solar-powered air-conditioning system in a green building. Appl. Energy 2008, 4, 267. [Google Scholar]
- Sakoda, A.; Suzuki, M. Fundamental Study on Solar Powered Adsorption Cooling System. Chem. Eng. Jpn. 1984, 17, 52–57. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.Z.I.; Alam, K.C.A.; Saha, B.B.; Hamamoto, T.; Akisaw, A.; Kashiwagi, T. Parametric Study of A Two Stage Adsorption Chiller Using Reheat:The Effect of the Overall Thermal Conductance and Adsorbent Mass on System Performance. Int. J. Therm. Sci. 2006, 45, 511–519. [Google Scholar] [CrossRef]
- Alam, K.C.A.; Saha, B.B.; Hamamoto, T.; Akisaw, A.; Kashiwagi, T. Influence of Design and Operating Conditions on The Performance of A Two-Stage Adsorption Chiller. Chem. Eng. Commun. 2006, 91, 981–997. [Google Scholar] [CrossRef]
- Stefański, S.; Mika, L.; Sztekler, K.; Kalawa, W.; Lis, L.; Nowak, W. Adsorption bed configure rations for adsorption cooling application. E3S Web Conf. 2019, 108, 01010. [Google Scholar] [CrossRef]
- Hassan, H.Z.; Ahmad, A.A.; Al-Ansary, H.A.A. Development of a continuously operating solar-driven adsorption cooling system: Thermodynamic analysis and parametric study. Appl. Therm. Eng. 2012, 48, 332–341. [Google Scholar] [CrossRef]
- Ahmed, R.M.; Rezk, R.; Al-Dadah, K. Physical and Operating Conditions Effect on Silica gel/water Adsorption Chiller Performance. Appl. Energy 2012, 89, 142–149. [Google Scholar]
- Alam, K.C.A.; Saha, B.B.; Akisawa, A.; Kashiwagi, T. A Novel Parametric Analysis of a Conventional Silica-Gel Water Adsorption Chiller. ASHRAE Trans. 2011, 17, 323–332. [Google Scholar]
- Papoutsis, E.G.; Koronaki, I.P.; Papaefthimiou, V.D. Parametric Study of a Single-Stage Two-Bed Adsorption Chiller. J. Energy Eng. 2017, 143, 04016068. [Google Scholar] [CrossRef]
- Angrouza, Y.; Bouhal, T.; Alluhi, A.A.; Kouskou, T.; Zeraouli, J.Y. Energy and parametric analysis of solar absorption cooling systems in various Moroccan climates. Case Stud. Therm. Eng. 2017, 9, 28–39. [Google Scholar]
- Mohammed, R.H.; Mesalhy, O.; Elsayed, M.L.; Chow, L.C. Compact bed design for adsorption cooling systems: Parametric numerical study Conception. Int. J. Refrig. 2012, 80, 238–251. [Google Scholar] [CrossRef]
- PapoutsisI, E.G.; Koronaki, P.; Papaefthimiou, V.D. Numerical simulation and parametric study of different types of solar cooling systems under Mediterranean climatic conditions. Energy Build. 2017, 138, 601–611. [Google Scholar] [CrossRef]
- Al-Rbaiha, R.; Sakhrieh, A.; Al-Asfar, J.; Alahmer, A.; Ayadi, O.; Al-Salaymeh, A.; Al_hamamre, Z.; Al-bawwab, A.; Hamdan, M. Performance Assessment and Theoretical Simulation of Adsorption refrigeration System Driven by Flat Plate Solar Collector. JJMIE 2017, 11, 1–11. [Google Scholar]
- Shaban, N.A.; Al-Salaymeh, A.; Maaitah, A. Performance and Evaluation of Adsorption Chillers Powered by Solar Energy by means of PTC’s in Jordan. In Proceedings of the JIIRCRAC’ 15, Aqaba, Jordan, 8–10 March 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).