Abstract
Many investigations use a linearization method, and others use a structural properties method to determine the controllability and observability of robots. In this study, we propose a transformed structural properties method to determine the controllability and observability of robots, which is the combination of the linearization and the structural properties methods. The proposed method uses a transformation in the robot model to obtain a linear robot model with the gravity terms and uses the linearization of the gravity terms to obtain the linear robot model; this linear robot model is used to determine controllability and observability. The described combination evades the structural conditions requirement and decreases the approximation error. The proposed method is better than previous methods because the proposed method can obtain more precise controllability and observability results. The modified structural properties method is compared with the linearization method to determine the controllability and observability of three robots.
1. Introduction
The concept of controllability denotes the ability to move a robot around in its entire configuration space using only certain admissible manipulations. The exact definition varies slightly within the framework or the kind of applied robots. Controllability and observability are dual aspects of the same problem.
Many authors have proposed interesting controllers or observers such as [1,2,3,4,5,6,7,8,9]; however, in most of the studies, the robot models are assumed to be controllable or observable without any proof. A method to determine the controllability of a robot model is important because a robot model that is assured to be controllable can guarantee the existence of a controller to reach one of the objectives such as regulation, tracking, disturbance rejection, etc. A method to determine the observability of a robot model is important because a robot model that is assured to be observable can guarantee the existence of an observer to reach one of the objectives such as states estimation, disturbance estimation, etc. Hence, it would be interesting to study when the controllability and observability of robots is not assumed.
There are some studies about controllability and observability. In [10,11,12,13], the authors are focused on the local, linear, global, and exact controllability and observability. In [14,15,16], the authors discuss the controllability and observability of linear time-varying systems. In [17,18,19,20], the authors use algorithms to determine controllability and observability. In [21,22,23], the authors use the geometric method to determine controllability and observability. In [24,25,26], the authors consider the fact that robot models are changed from being linearly uncontrollable to linearly controllable when the equilibrium point is moved from the origin to a different one. In [27,28,29], the authors propose feedback for the linearization of robot models to determine controllability. In [30,31,32], the authors present a controllability analysis proving that some robots are not controllable. In [33,34,35], the authors extract properties of the mechanical parameters to demonstrate that some robots are controllable and observable. In [36,37,38], the authors design elastic, flexible, or micro-robots, which, since their design, are controllable. In [39,40], authors find a transformation to determine which states have the greatest contribution in controllability and observability.
From the aforementioned studies, some authors use a linearization method [24,25,26,27,28,29,30,31,32], and the other use a structural properties method [33,34,35,36,37,38,39,40] to determine the controllability and observability of robots. The linearization method is an approximation of the robot model around the origin, and the structural properties method is a different representation of the nonlinear model based on transformations. The linearization method has the problem that could produce erroneous results because of the approximation nature, and the structural properties method has the problem that the robot model requires to satisfy structural conditions. It would be interesting to propose a method to determine the controllability and observability of robots that evade the problems presented in the mentioned methods.
In this study, we propose a transformed structural properties method to determine the controllability and observability of robots that is the combination of the linearization method [24,25,26,27,28,29,30,31,32] and the structural properties method [33,34,35,36,37,38,39,40]. The proposed method uses a transformation in the robot model to obtain a linear robot model with the gravity terms and uses the linearization of the gravity terms to obtain a linear robot model; this linear robot model is used to determine controllability and observability. The combination of the linearization and structural properties methods contributes to evade the problems of both methods by evading the structural conditions requirement and decreasing the approximation error.
The proposed transformed structural properties method is better than previous methods because the proposed method could satisfy the following gravity terms condition used to obtain more precise controllability and observability results: if the gravity terms of the robot model contain constant or cosine functions, then the linearization is evaded, and a linear robot model is obtained; this linear robot model is used to determine the controllability and observability.
Finally, the transformed structural properties method is compared with the linearization method to determine the controllability and observability of the scara, two links, and cylindrical robots. The scara, two links, and cylindrical robots are selected because they satisfy the gravity terms condition and could be applied in pick and place, screwed, printed circuit boards, packaging, labeling, etc.
This paper is organized as follows. In Section 2, the linearization and the transformed structural properties methods are detailed. In Section 3, the linearization and the transformed structural properties methods are applied to determine the controllability and observability of the scara robot. In Section 4, the linearization and the transformed structural properties methods are applied to determine the controllability and observability of the two links robot. In Section 5, the linearization and the transformed structural properties methods are applied to determine the controllability and observability of the cylindrical robot. In Section 6, the conclusion and the forthcoming work are detailed.
2. Two Methods to Determine the Controllability and Observability of Robots
A method to determine the controllability of a robot model is important because a robot model which is assured to be controllable can guarantee the existence of a controller to reach one of the objectives such as regulation, tracking, disturbance rejection, etc. A method to determine the observability of a robot model is important because a robot model which is assured to be observable can guarantee the existence of an observer to reach one of the objectives such as states estimation, disturbance estimation, etc.
The main concern of this section is to present two methods to determine the controllability and observability of robots. First, the linearization method, which is known in the literature, will be presented. Second, the transformed structural properties method, which is the main contribution of this study, will be presented.
2.1. Linearization Method to Determine the Controllability and Observability of Robots
The robot model considered is detailed. The robot model is important because it is the starting point in determining the controllability and observability of robots with this method.
For the robots with degrees of freedom, considering the contact force and constraints, the robot model is:
is the identity matrix, is the joint angle or link displacement of the robot, is the velocity of the robot, is the state, is a matrix with the inertia terms, which is symmetric and positive definite, is a matrix with the centripetal and Coriolis terms, is a vector with the gravity terms, is the input, is a nonlinear function vector containing all the robot terms, , and is the output.
Now, the linearization method of [24,25,26,27,28,29,30,31,32] is presented. The linear robot model is important because it is required in determining the controllability and observability of robots. The linearization method is an approximation of the robot model around the origin.
The robot model (1) is linearized around the origin by the linearization method to obtain the following linear robot model:
, Since the linear robot model has been obtained in (2), now the known methods for linear systems [31,32] are used to determine the controllability and observability of robots.
Using the linear robot model (2) of the linearization method, the controllability matrix is:
If the rank of the controllability matrix is equal to , the robot model of the linearization method is controllable around the origin.
Using the linear robot model (2) of the linearization method, the observability matrix is:
If the rank of the observability matrix O is equal to , the robot model of the linearization method is observable around the origin.
2.2. Transformed Structural Properties Method to Determine the Controllability and Observability of Robots
The linear robot model with gravity terms considered is detailed. The linear robot model with gravity terms is important because it is the starting point in determining the controllability and observability of robots with this method.
By using the fact that the inverse of the robot inertia matrix is well defined, (1) is represented as the following linear robot model with gravity terms:
is the identity matrix, is the joint angle or link displacement of the robot, is the velocityof the robot, is the state, is a matrix with the inertia terms, which is symmetric and positive definite, is a matrix with the centripetal and Coriolis terms, is a vector with the gravity terms, is the input, is a nonlinear function vector containing only the gravity terms of , and is the output. , , .
Now the transformed structural method of this study is presented to determine the controllability and observability of robots, which is the combination of the linearization method of [24,25,26,27,28,29,30,31,32] and the structural properties method of [33,34,35,36,37,38,39,40]. The linearization method is an approximation of the robot model around the origin, and the structural properties method is a different representation of the nonlinear model based on transformations. The combination of the linearization and structural properties methods contributes to evade the problems of both methods by evading the structural conditions requirement and decreasing the approximation error.
The robot model (1) was transformed to obtain a linear robot model with the gravity terms (5), and the gravity terms are linearized around the origin by the linearization method to obtain the following linear robot model:
is the identity matrix and , , , and are described in (5), , .
Since the linear robot model has been obtained in (6), now the known methods for linear systems [31,32] are used to determine the controllability and observability of robots.
Using the linear robot model (6) of the transformed structural properties method, the controllability matrix is:
If the rank of the controllability matrix is equal to , the robot model of the transformed structural properties method is controllable around the origin.
Using the linear robot model (6) of the transformed structural properties method, the observability matrix is:
If the rank of the observability matrix is equal to , the robot model of the transformed structural properties method is observable around the origin.
Remark 1.
The linearization method uses the linearization in the robot model , being an approximation that could produce erroneous results, while the transformed structural properties method uses a transformation in one part of the robot model , evading the requirement to satisfy some structural conditions, and uses the linearization in the other part of the robot model , evading erroneous results because of the approximation nature.
Remark 2.
The proposed transformed structural properties method is better than previous methods because the proposed method could satisfy the following gravity terms condition used to obtain more precise controllability and observability results: if the gravity terms of the robot model (5) contain constant or cosine functions, then the linearization is evaded with , of (6) equal to zero, and a linear robot model is obtained with , of (6); this linear robot model (6) is used to determine the controllability and observability.
Remark 3.
We describe two methods, both methods are based on two stages, the second stage of both methods described by Equations (3), (7), (4) and (8) is equal, but the first stage of both methods described by Equations (1), (2), (5) and (6) is completely different. Thus, the difference of the first stage produces different results in both methods.
The examples of the following two sections satisfy the gravity terms condition.
3. Scara Robot
In this section, we compare the two methods to determine the controllability and observability of the scara robot.
The scara robot has three degrees of freedom. It has two rotary joints and two links configured in a horizontal position, it has one linear joint and one link configured in a vertical position. We express the scara robot of Figure 1, where , , are the angles of the joints one, two in rad and is the length of the link three, in m.
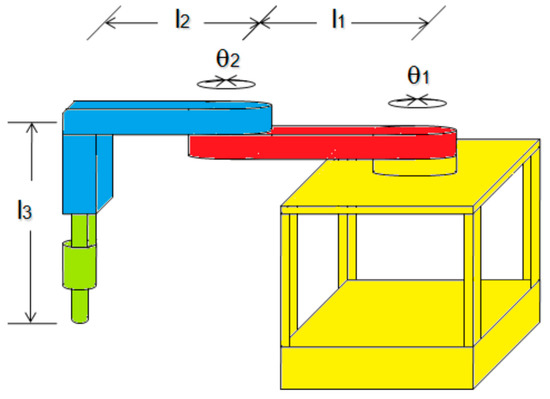
Figure 1.
Scara robot.
3.1. Linearization Method
Now, the linearization method of [24,25,26,27,28,29,30,31,32] is applied to the scara robot.
We write the scara robot as (1), and we detail it as:
where is a nonlinear function vector containing all the robot terms , which are described as follows:
, , are the masses of the links one, two, three, , , are the angles of the joints one, two in rad, is the length of the link three, in m, and is the acceleration gravity constant. m, , , kg, , kgm2, kgm2, m/s2.
By using the linearization method described in (2), the linear model is:
By using the linearization method described in (3), the controllability matrix is:
, , . Since the rank of the controllability matrix is 6, the scara robot is controllable.
By using the linearization method described in (4), the observability matrix is:
Since the rank of the observability matrix is 6, the scara robot is observable.
3.2. Transformed Structural Properties Method
Now, the transformed structural properties method of this study is applied to the scara robot.
We write the scara robot as (5), and we detail it as:
where is a matrix with the inertia terms , is a matrix with the centripetal and Coriolis terms , and is a vector with the gravity terms , which are described as follows:
the other terms of , , , are zero. , , are the masses of the links one, two, three, , , are the angles of the joints one, two in rad, is the length of the link three, in m, and is the acceleration gravity constant. m, , , kg, , kgm2, kgm2, m/s2.
By using the transformed structural properties method described in (6), the linear model is:
By using the transformed structural properties method described in (7), the controllability matrix is:
, , , . Since the rank of the controllability matrix is 6, the scara robot is controllable.
By using the transformed structural properties method described in (8), the observability matrix is:
Since the rank of the observability matrix is 6, the scara robot is observable.
3.3. Comparison of Results
In the proposed transformed structural properties method, the gravity terms of the scara robot model (14) and (15) contain constant functions, the linearization is evaded with , of (16) are equal to zero, and a linear robot model is obtained with , of (16). Thus, the transformed structural properties method satisfies the gravity terms condition of Remark 2. Furthermore, the linear model (16) of the transformed structural properties method is more approximated to the robot model than the linear model (11) of the linearization method, and the controllability and observability results of the transformed structural properties method (17) and (18) are more precise than the controllability and observability results of the linearization method (12) and (13).
4. Two-Link Robot
In this section, we compare the two methods to determine the controllability and observability in the two-link robot.
The two-link robot has two degrees of freedom. It has two rotary joints and two links configured in a vertical position. We express the two-link robot of Figure 2, where , are the angles of the joints one, two in rad.
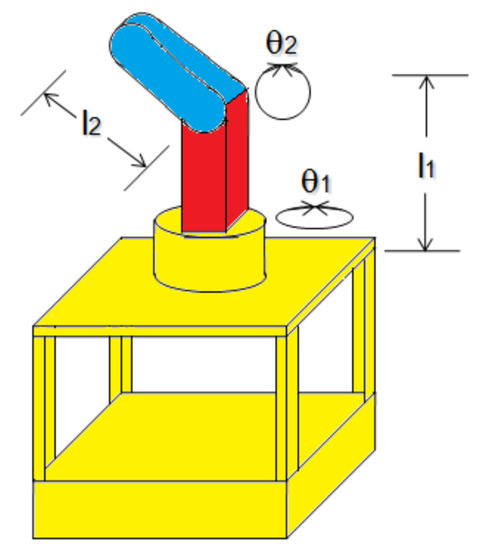
Figure 2.
Two-link robot.
4.1. Linearization Method
Now, the linearization method of [24,25,26,27,28,29,30,31,32] is applied to the two-link robot.
We write the two-link robot as (1), and we detail it as:
where is a nonlinear function vector containing all the robot terms , which are described as follows:
is the mass of the link two in kg, , are the angles of the joints one, two in rad, is the acceleration gravity constant, and and are the inertias in kgm2, , . kg, m, , , kgm2, kgm2, and m/s2.
By using the linearization method described in (2), the linear model is:
By using the linearization method described in (3), the controllability matrix is:
Since the rank of the controllability matrix is 4, the two-link robot is controllable.
By using the linearization method described in (4), the observability matrix is:
Since the rank of the observability matrix is 4, the two-link robot is observable.
4.2. Transformed Structural Properties Method
Now, the transformed structural properties method of this study is applied to the two-link robot.
We write the two links robot as (5), and we detail it as:
where is a matrix with the inertia terms , is a matrix with the centripetal and Coriolis terms , and is a vector with the gravity terms , which are described as follows:
is the mass of the link two in kg, , are the angles of the joints one, two in rad, is the acceleration gravity constant, and and are the inertias in kgm2, , . kg, m, , , kgm2, kgm2, and m/s2.
By using the transformed structural properties method described in (6), the linear model is:
By using the transformed structural properties method described in (7), the controllability matrix is:
Since the rank of the controllability matrix is 4, the two-link robot is controllable.
By using the transformed structural properties method described in (8), the observability matrix is:
Since the rank of the observability matrix is 4, the two-link robot is observable.
4.3. Comparison of Results
In the proposed transformed structural properties method, the gravity terms of the two-link robot model (24) and (25) contain cosine functions, the linearization is evaded with , of (26) are equal to zero, and a linear robot model is obtained with , of (26). Thus, the transformed structural properties method satisfies the gravity terms condition of Remark 2. Furthermore, the linear model (26) of the transformed structural properties method is more approximated to the robot model than the linear model (21) of the linearization method, and the controllability and observability results of the transformed structural properties method (27) and (28) are more precise than the controllability and observability results of the linearization method (22) and (23).
5. Cylindrical Robot
In this section, we compare the two methods to determine the controllability and observability ofthe cylindrical robot.
The cylindrical robot has three degrees of freedom. It has one rotary joint and one link configured in a horizontal position, and it has two linear joints and two links configured in a vertical position. We express the cylindrical robot of Figure 3, where is the angle of the joint one in rad, and , are the lengths of the links two, three, in m.
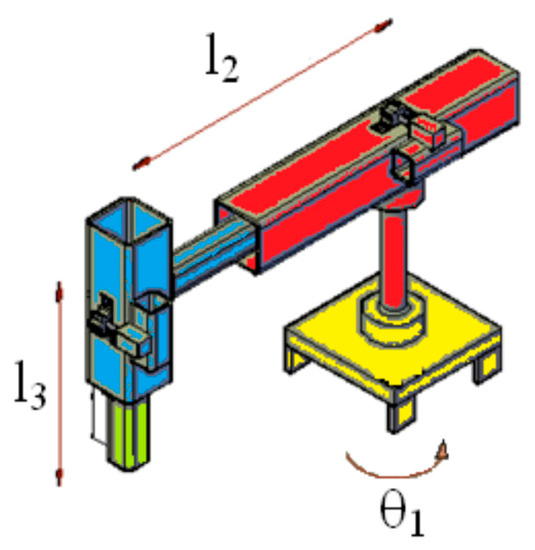
Figure 3.
Cylindrical robot.
5.1. Linearization Method
Now, the linearization method of [24,25,26,27,28,29,30,31,32] is applied to the cylindrical robot.
We write the cylindrical robot as (1), and we detail it as:
where is a nonlinear function vector containing all the robot terms , which are described as follows:
, , are the masses of the links one, two, three, is the angle of the joint one in rad, , are the lengths of the links two, three, in m, and is the acceleration gravity constant, , . m, m, , , , kg, kg, kg, kgm2, kgm2, kgm2, and m/s2.
By using the linearization method described in (2), the linear model is:
By using the linearization method described in (3), the controllability matrix is:
, , . Since the rank of the controllability matrix is 6, the cylindrical robot is controllable.
By using the linearization method described in (4), the observability matrix is:
Since the rank of the observability matrix is 6, the cylindrical robot is observable.
5.2. Transformed Structural Properties Method
Now, the transformed structural properties method of this study is applied to the cylindrical robot.
We write the cylindrical robot as (5), and we detail it as:
where is a matrix with the inertia terms , is a matrix with the centripetal and Coriolis terms , and is a vector with the gravity terms , which are described as follows:
, , are the masses of the links one, two, three, is the angle of the joint one in rad, , are the lengths of the links two, three in m, and is the acceleration gravity constant, , . m, m, , , , kg, kg, kg, kgm2, kgm2, kgm2, and m/s2.
By using the transformed structural properties method described in (6), the linear model is:
By using the transformed structural properties method described in (7), the controllability matrix is:
, , . Since the rank of the controllability matrix is 6, the cylindrical robot is controllable.
By using the transformed structural properties method described in (8), the observability matrix is:
Since the rank of the observability matrix is 6, the cylindrical robot is observable.
5.3. Comparison of Results
In the proposed transformed structural properties method, the gravity terms of the cylindrical robot model (34) and (35) contain constant functions, the linearization is evaded with , of (36) are equal to zero, and a linear robot model is obtained with , of (36). Thus, the transformed structural properties method satisfies the gravity terms condition of Remark 2. Furthermore, the linear model (36) of the transformed structural properties method is more approximated to the robot model than the linear model (31) of the linearization method, and the controllability and observability results of the transformed structural properties method (37) and (38) are more precise than the controllability and observability results of the linearization method (32) and (33).
6. Conclusions
In this study, we proposed the transformed structural properties method to determine the controllability and observability of robots. Some authors proposed a linearization method, and others proposed a structural properties method, while this study considered a method as the combination of the other two methods. The numerical results showed that the transformed structural properties method obtained a more approximated robot model and obtained more precise controllability and observability results. The proposed method could be used for any of the conventional structures of robots. In the forthcoming work, the proposed method will be used not only to determine the controllability and observability but the proposed method will also be used to obtain a controller and an observer.
Author Contributions
Investigation and formal analysis D.I.M., J.d.J.R., V.G., and T.M.V.; software and validation, M.A.I., J.P., and G.J.G.; writing—original draft, review—editing J.A.M.-C., D.M.-V., and C.A.-I. All authors have read and agreed to the published version of the manuscript.
Funding
This article received no external funding.
Acknowledgments
Authors are grateful tothe guest editors and reviewers for their valuable comments and insightful suggestions, which can help to improve this article significantly. Authors thank the Instituto Politécnico Nacional, Secretaría de Investigación y Posgrado, Comisión de Operación y Fomento de Actividades Académicas, and Consejo Nacional de Ciencia y Tecnología for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aguiar, M.; de Sousa, J.B.; Dias, J.M.; da Silva, J.E.; Mendes, R.; Ribeiro, A.S. Optimizing autonomous underwater vehicle routes with the aid of high resolution ocean models. In Proceedings of the MTS/IEEE Seatle Oceans, Singapore, 27–31 October 2019. [Google Scholar]
- Aguiar, M.; da Silva, J.E.; de Sousa, J.B. Minimal time delivery of multiple robots. In Proceedings of the 59th IEEE Conference on Decision and Control (CDC), Jeju Island, Korea, 14–18 December 2020. [Google Scholar]
- Aguiar, M.; de Sousa, J.B.; Dias, J.M.; da Silva, J.E.; Mendes, R.; Ribeiro, A.S. Trajectory Optimization for Underwater Vehicles in Time-Varying Ocean Flows. In Proceedings of the IEEE/OES Autonomous Underwater Vehicle Workshop (AUV), Porto, Portugal, 6–9 November 2018. [Google Scholar]
- Chen, P.-T.; Shen, D.-J.; Yang, C.-J.; Huang, K.D. Development of a Hybrid Electric Motorcycle that Accords Energy Efficiency and Controllability via an Inverse Differential Gear and Power Mode Switching Control. Appl. Sci. 2019, 9, 1787. [Google Scholar] [CrossRef]
- Kozlowski, K. Special Issue: Robot Motion and Control. J. Intell. Robot. Syst. 2019, 93, 617–619. [Google Scholar] [CrossRef]
- Pazderski, D.; Patelski, R.; Krysiak, B.; Kozlowski, K. Analysis of an Impact of Inertia Parameter in Active Disturbance Rejection Control Structures. Electronics 2020, 9, 1801. [Google Scholar] [CrossRef]
- Piasek, J.; Patelski, R.; Pazderski, D.; Kozlowski, K. Identification of a dynamic friction model and its application in a precise tracking control. Acta Polytech. Hung. 2019, 16, 83–99. [Google Scholar] [CrossRef]
- Xue, J.; Xu, M.; Huang, W.; Zhang, Z.; Wu, W.; Jin, L. Stability and Heat Input Controllability of Two Different Modulations for Double-Pulse MIGWelding. Appl. Sci. 2019, 9, 127. [Google Scholar] [CrossRef]
- Zhang, L.; Neusypin, K.A.; Selezneva, M.S. A New Method for Determining the Degree of Controllability of State Variables for the LQR Problem Using the Duality Theorem. Appl. Sci. 2020, 10, 5234. [Google Scholar] [CrossRef]
- Elamvazhuthi, K.; Kuiper, H.; Kawski, M.; Berman, S. Bilinear Controllability of a Class of Advection-Diffusion-Reaction Systems. IEEE Trans. Autom. Control 2019, 64, 2282–2297. [Google Scholar] [CrossRef]
- Moreau, C. Local Controllability of a Magnetized Purcell’s Swimmer. IEEE Control Syst. Lett. 2019, 3, 637–642. [Google Scholar] [CrossRef]
- Sun, Y. Linear Controllability versus Global Controllability. IEEE Trans. Autom. Control 2009, 54, 1693–1697. [Google Scholar]
- Zaytsev, P.; Wolfslag, W.; Ruina, A. The Boundaries of Walking Stability: Viability and Controllability of Simple Models. IEEE Trans. Robot. 2018, 34, 336–352. [Google Scholar] [CrossRef]
- Ishihara, J.Y.; Terra, M.H. Impulse Controllability and Observability of Rectangular Descriptor Systems. IEEE Trans. Autom. Control 2001, 46, 991–994. [Google Scholar] [CrossRef]
- Yang, Y. Controllability of Spacecraft Using Only Magnetic Torques. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 954–961. [Google Scholar] [CrossRef]
- Yoon, K.-H.; Park, Y.-W. Controllability of Magnetic Force in Magnetic Wheels. IEEE Trans. Magn. 2012, 48, 4046–4049. [Google Scholar] [CrossRef]
- Briot, S.; Martinet, P.; Rosenzveig, V. The Hidden Robot: An Efficient Concept Contributing to the Analysis of the Controllability of Parallel Robots in Advanced Visual Servoing Techniques. IEEE Trans. Robot. 2015, 31, 1337–1352. [Google Scholar] [CrossRef]
- Carrillo-Zapata, D.; Sharpe, J.; Winfield, A.F.T.; Giuggioli, L.; Hauert, S. Toward Controllable Morphogenesis in Large Robot Swarms. IEEE Robot. Autom. Lett. 2019, 4, 3386–3393. [Google Scholar] [CrossRef]
- Kim, J.I.; Hong, M.; Lee, K.; Kim, D.-W.; Park, Y.-L.; Oh, S. Learning to Walk a Tripod Mobile Robot Using Nonlinear Soft Vibration Actuators With Entropy Adaptive Reinforcement Learning. IEEE Robot. Autom. Lett. 2020, 5, 2317–2324. [Google Scholar] [CrossRef]
- Martinelli, A.; Siegwart, R. Observability Analysis for Mobile Robot Localization. In Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems, Edmonton, AB, Canada, 2–6 August 2005. [Google Scholar]
- Lou, Y.; Ji, Z.; Qu, J. New Results of Multi-Agent Controllability under Equitable Partitions. IEEE Access 2020, 8, 73523–73535. [Google Scholar] [CrossRef]
- Muralidharan, V.; Mahindrakar, A.D. Geometric Controllability and Stabilization of Spherical Robot Dynamics. IEEE Trans. Autom. Control 2015, 60, 2762–2767. [Google Scholar] [CrossRef]
- Nasrallah, D.S.; Michalska, H.; Angeles, J. Controllability and Posture Control of a Wheeled Pendulum Moving on an Inclined Plane. IEEE Trans. Robot. 2007, 23, 564–577. [Google Scholar] [CrossRef]
- Bullo, F.; Zefran, M. Modeling and Controllability for a Class of Hybrid Mechanical Systems. IEEE Trans. Robot. Autom. 2002, 18, 563–573. [Google Scholar] [CrossRef]
- Kang, W.; Xiao, M.; Tall, I.A. Controllability and Local Accessibility-A Normal Form Approach. IEEE Trans. Autom. Control 2003, 48, 1724–1736. [Google Scholar] [CrossRef]
- Rouhollahi, K.; Andani, M.E.; Izadi, I.; Karbassi, S.M. Controllability and observability analysis of basal ganglia model and feedback linearisation control. IET Syst. Biol. 2017, 11, 144–154. [Google Scholar] [CrossRef]
- Fruchard, M.; Sadelli, L.; Ferreira, A. Local Controllability, Trajectory Planning, and Stabilization of a Two-Agent Underactuated Microrobotic System. IEEE Syst. J. 2020, 14, 2892–2900. [Google Scholar] [CrossRef]
- Ouyang, B.; Ye, Q.; Patil, S.; Wang, C.; Lu, L.; Yan, Z. The Relation between Communication Range and Controllability of Networked Multi-Agent Systems. IEEE Access 2018, 6, 35901–35907. [Google Scholar] [CrossRef]
- Yang, J.-H.; Xu, H.-K. Robust Controller Design for Non-Minimum Phase UAV System and System Analysis. IEEE Access 2018, 6, 70734–70769. [Google Scholar] [CrossRef]
- Liljeback, P.; Pettersen, K.Y.; Stavdahl, O.; Gravdahl, J.T. Controllability and Stability Analysis of Planar Snake Robot Locomotion. IEEE Trans. Autom. Control 2011, 56, 1365–1380. [Google Scholar] [CrossRef]
- Meda-Campaña, J.A. On the Estimation and Control of Nonlinear Systems with Parametric Uncertainties and Noisy Outputs. IEEE Access 2018, 6, 31968–31973. [Google Scholar] [CrossRef]
- Meda-Campaña, J.A.; Grande-Meza, A.; Rubio, J.J.; Tapia-Herrera, R.; Hernandez-Cortes, T.; Curtidor-Lopez, A.; Paramo-Carranza, L.A.; Cazares-Ramirez, I.O. Design of stabilizers and observers for a class of multivariable TS fuzzy models on the basis on new interpolation functions. IEEE Trans. Fuzzy Syst. 2018, 26, 2649–2662. [Google Scholar] [CrossRef]
- Hao, Y.; Duan, Z.; Wen, G. Controllability and observability of an n-link robot with multiple active links. Int. J. Robust Nonlinear Control 2017, 27, 4633–4647. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, X. Controllability and Observability of an n-Link Planar Robot with a Single Actuator Having Different Actuator-Sensor Configurations. IEEE Trans. Autom. Control 2016, 61, 1129–1134. [Google Scholar] [CrossRef]
- Xin, X. Necessary and sufficient conditions for linear strong structural controllability and observability of n-link underactuated planar robot with multiple active intermediate links. IET Control Theory Appl. 2017, 11, 1873–1883. [Google Scholar] [CrossRef]
- Calanca, A.; Dimo, E.; Vicario, R.; Fiorini, P.; Serpelloni, M.; Legnani, G. Introducing Series Elastic Links for Affordable Torque-Controlled Robots. IEEE Robot. Autom. Lett. 2019, 4, 137–144. [Google Scholar] [CrossRef]
- Legrand, J.; Ourak, M.; Javaux, A.; Gruijthuijsen, C.; Ahmad, M.A.; Cleynenbreugel, B.V.; Vercauteren, T.; Deprest, J.; Ourselin, S.; Poorten, E.V. From a Disposable Ureteroscope to an Active Lightweight Fetoscope-Characterization and Usability Evaluation. IEEE Robot. Autom. Lett. 2018, 3, 4359–4366. [Google Scholar] [CrossRef]
- Yang, X.; Chen, Y.; Chang, L.; Calderon, A.A.; Perez-Arancibia, N.O. Bee+: A 95-mg Four-Winged Insect-Scale Flying Robot Driven by Twinned Unimorph Actuators. IEEE Robot. Autom. Lett. 2019, 4, 4270–4277. [Google Scholar] [CrossRef]
- Qi, J.; Wang, J.; Liu, H.; Dimitrovski, A.D. Nonlinear Model Reduction in Power Systems by Balancing of Empirical Controllability and Observability Covariances. IEEE Trans. Power Syst. 2017, 32, 114–126. [Google Scholar] [CrossRef]
- Xu, F.-Y.; Jiang, F.-Y.; Jiang, Q.-S.; Lu, Y.-X. Soft Actuator Model for a Soft Robot WITH Variable Stiffness by Coupling Pneumatic Structure and Jamming Mechanism. IEEE Access 2020, 8, 26356–26371. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).