Abstract
While the dependence assumption among the components is naturally important in evaluating the reliability of a system, studies investigating the issues of aggregation errors in Bayesian reliability analyses have been focused mainly on systems with independent components. This study developed a copula-based Bayesian reliability model to formulate dependency between components of a parallel system and to estimate the failure rate of the system. In particular, we integrated Monte Carlo simulation and classification tree learning to identify key factors that affect the magnitude of errors in the estimation of posterior means of system reliability (for different Bayesian analysis approaches—aggregate analysis, disaggregate analysis, and simplified disaggregate analysis) to provide important guidelines for choosing the most appropriate approach for analyzing a model of products of a probability and a frequency for parallel systems with dependent components.
1. Introduction
Bayesian analyses, which consider probability to be a subjective belief about unknown parameters of interest and usually incorporate pertinent knowledge which is not contained in the sample data, have been widely used in estimating failure rates in reliability analyses (see, e.g., [,,,,,]). Provided that component and system level data in a given monitoring duration are available, different alternatives can be chosen for implementing a Bayesian reliability analysis of a system. Two extreme approaches are the aggregate and disaggregate analyses. Aggregate analysis (AA) refers to the approach that uses only system-level (aggregate) data, while disaggregate analysis (DA) is the approach that uses only component-level (disaggregate) data. It might also be possible for reliability engineering practitioners to carry out the Bayesian estimation procedure at intermediate levels of aggregation.
Since aggregate analysis can save the effort and cost of collecting a large amount of component data, it is usually less costly and more practical. However, it might provide an inaccurate estimate of the system reliability by ignoring important information available at the component level []. Conversely, disaggregate analysis makes use of all the available data and usually provides more accurate results, but it can be very expensive and impractical. In practical applications, the exact component failures may not be pinpointed due to the restricted resources, and thus only masking data are available. However, the preference to conducting one analysis over another is usually related to the significance of the analysis and the trade-off between costs and the accuracy of results.
The phenomenon when the results of aggregate and disaggregate analyses do not agree is known as the aggregation error and the absence of the aggregation error is known as perfect aggregation []. Aggregation error is not a phenomenon that is limited in the field of reliability analysis. Studies about the aggregation error are largely known in various fields including economics, social sciences, and geo-statistics [,,]. Numerous studies about aggregation error in Bayesian reliability analysis have been conducted since it was first introduced in the 1990s. While most of the early research focused on finding the conditions under which perfect aggregation can be obtained, especially in cases where failures of components are independent to each other [,], recent studies tried to identify the sources of the aggregation error [,,] (in similar independent cases). Philipson [,] used a different term “Bayesian anomaly” for the similar phenomenon (i.e., aggregation error) discussed in other papers, but took a more extreme view to argue that the aggregation error is a fundamental problem in a Bayesian reliability analysis and even suggested a basic restructuring of the Bayes procedure []. However, other researchers [,,] disagreed with such argument and suggested that the aggregation error should not be construed as the evidence of inadequacy of Bayesian methods.
When the failures of the components of a system are dependent, implementing disaggregate Bayesian analysis can be even more difficult because a joint prior distribution must be specified and then updated with component-level data. In the real-world situation, a simplified disaggregate analysis (hereafter, DAI) without considering the dependence structure of the components might be used instead of the true disaggregate analysis. Although the computation for this simplified analysis becomes more straightforward and simpler (because only marginal distribution for each component needs to be specified and updated), the accuracy of the analysis might be seriously affected due to the ignorance of the critical information of dependence between components.
While the studies conducted before have compared different analysis approaches and investigated the aggregation errors for cases where data are available at both the component and system levels, there is not yet a generalized study on the situation where the components are correlated (even though the dependence assumption among the components is naturally important in evaluating the reliability of a system). Furthermore, while some studies in reliability analysis have used copula theory to handle joint failure or inter-correlation of multiple components [,], few studies (see, e.g., [,]) have reported on the effects of component dependence on the accuracy of Bayesian reliability analyses. Thus, little guidance is available on how to proceed, and how to choose appropriate analysis approach under the practical situations.
This study aimed to compare three Bayesian analysis approaches that can be used for evaluating system reliability in parallel systems where failures of components are dependent: disaggregate analysis (DA), aggregate analysis (AA), and simplified disaggregate analysis (DAI). Specifically, a parallel two-component system where Component 1 fails according to a Poisson process and Component 2 fails according to a Bernoulli process was analyzed, compared to the parallel beta-binomial system investigated in []. It is expected that the outcome of this study will be practically useful to reliability engineering practitioners who encounter Poisson-distributed failures (which are popular in modern science and engineering).
Furthermore, since the component failure of the reliability system in this study are correlated, copulas were thus used to construct bivariate distribution functions with correlated marginal random variables. A Monte Carlo simulation approach, namely regional sensitivity analysis (RSA) [], was used to generate a large number of simulated cases to investigate how the variation in the estimated reliability of different analyses can be attributed to variations of their input factors (e.g., parameters in the prior distributions of the Bayesian reliability analysis). However, the use of RSA does not effectively deal with parameter interactions. Therefore, a classification tree data mining approach (Recursive Partitioning) was utilized to identify and locate the values of the key factors and conditions that lead to a great magnitude of error. (For a review on machine learning methods for constructing tree models from data, readers are referred to the work of [].) There are two main advantages of using the classification tree data mining approach. First, it allows for easy interpretability of results in that decision nodes carry conditions that are easy to understand. Second, the IF-THEN rules allow for knowledge extraction and also enable the reliability practitioner to verify the model learned from the data. Therefore, this analysis will provide a guideline for selecting appropriate Bayesian estimation approaches in evaluating the reliability of a system in which components are correlated.
The rest of this paper is structured as follows. In Section 2, the formulation of copula-based Bayesian reliability analysis for systems with dependent components is thoroughly delineated. The Monte Carlo based procedure for generating the pseudo input factors and the regionalized sensitivity analysis are presented in Section 3. The integrated Monte Carlo filtering and classification tree learning are given in Section 4. In Section 5, the conclusions and the managerial implications of this study are given.
2. Copula-Based Bayesian Reliability Models
2.1. Products of a Probability and a Frequency for the Two-Component Parallel System
A two-component parallel Poisson–Bernoulli system was considered for this study. In particular, if a failure of Component 1 is detected, then Component 2 (i.e., the standby component) will be switched on. It was assumed that the failure rate of Component 1 follows a Poisson process with rate , while that of Component 2 follows a Bernoulli process with conditional failure probability given a failure of Component 1.
The system is monitored for a total of t times unit, and data on the numbers of failures for the two components are collected and are depicted by and , respectively. For a simple parallel system with a backup components described here, there will be failures in time t. Readers are referred to the work of [] for a concise description of other simple two-component reliability models.
2.2. Characterizing the Component Dependence
In reliability engineering, the assumption of component dependence is more realistic and therefore important in practice. In simplified terms, the concept of stochastic dependence implies that the state of some units can influence the state of others. However, the state can be given by the age, failure rate, failure probability, state of failure, or other condition measures. Several categories of stochastic dependence exist in the reliability engineering literature for two-component systems (see, e.g., []). For example, one of the categories (i.e., the Type I failure interaction) has to do with failure interactions which imply that the failure of Component 1 may induce the failure of Component 2 with a given probability (constant or time dependent) and the other way round. On the other hand, the Type II failure interaction means that every failure of Component 1 acts as a shock to Component 2, without inducing an instantaneous failure, but affecting its failure rate.
The failure of the system considered in this study was formulated using a Poisson process with rate for Component 1 and a Bernoulli process for Component 2 with conditional probability given the failure of Component 1. It was assumed that and were distributed with probability distributions and , respectively. A joint probability prior distribution for the parameters (i.e., failure rate and failure probability) of the distributions (i.e., Poisson and binomial failure models) that describe the failure mechanism of the elements of the system mentioned above was constructed using the Bayesian reliability analysis approach. Subjective belief was applied for the value of these parameters to incorporate the uncertainty in the prior belief associated with the failure rate and the failure probability.
Here, it is important to note that two interpretations of the prior distributions are considered in Bayesian reliability analysis. When empirical data are well available, prior distribution may be motivated empirically on the basis of observed data. In this case, it might be easier to justify the equivalence of dependence between reliability characteristics to the existing dependence between subjective beliefs about the reliability characteristics. However, when facing the situation characterized by lack of data, subjective interpretation might need to be considered and the degree of belief might not be given a frequency interpretation. While this subjective interpretation might be more controversial among reliability analysts, exploiting all a priori insights might still be very useful when empirical data is lacking or when dealing with rare events.
2.3. Disaggregate and Aggregate Analyses
In a Bayesian analysis framework, the prior distribution describes the analyst’s state of knowledge about the parameter value to be specified. The use of such added resources (such as physical theories, past experiences with similar devices, or expert opinions) is critical in the Bayesian approach. This prior belief is usually formulated by using statistical distributions that are flexible enough to model different situations. In this study, we assume that the prior distributions for (the failure rate of Component 1) and (the failure probability of Component 2) follow gamma distribution with shape parameter a and scale parameter b and beta distribution with shape parameters c and d, respectively. Both gamma and beta distributions are very flexible for modeling prior distributions with different shapes. Furthermore, gamma and beta distributions are natural conjugate prior distributions (for Poisson and binomial likelihood functions) and enable us to analytically derive close-formed posterior distributions (when components are independent). It is also useful to think of the (hyper-)parameters of a conjugate prior distribution (i.e., a, b, c, and d in the above formulation) as corresponding to having observed a certain number of pseudo-observations. This interpretation also enables a reliability engineer or a risk analyst to choose or determine prior distributions with appropriate hyper-parameters.
The major differences among the three analysis approaches lie on the propagation procedure used to update the prior beliefs. Let be the joint prior distribution. In the DA approach, the joint prior distribution needs to be updated first with disaggregate (i.e., component-level) data to obtain the joint posterior distribution.
where and are the joint posterior distribution and the likelihood function, respectively.
Because , the number of failure of Component 1, and , the number of failure of Component 2 (given the failure of Component 1), follow the Poisson and Bernoulli processes, respectively, and because the parameters of these two processes (i.e., and ) are now specified by the joint prior distribution , the dependence between and will definitely induce dependence between and . However, the joint likelihood distribution can still be calculated or factorized from conditional probabilities using the chain rule
Furthermore, we can justify that is independent of , given that the values of and are known, and is independent of , given that the value of is known, based on the local Markov property or the concept of d-separation (see, e.g., []). This “conditional independence” property thus enables us to factorize the joint posterior distribution as follows.
where and are the binomial likelihood function and Poisson likelihood function, respectively.
The resulting joint posterior distribution will then be propagated to get the system posterior distribution (for the system failure rate )
The posterior mean obtained by using DA approach is thus
In the AA approach, copula-based joint prior probability function needs to be propagated first to get the system prior distribution , which can be obtained by using
The system prior distribution then can be updated with aggregate data to get the system posterior distribution using Bayesian rule
where is the likelihood of given by observing system failures in time t, which is formulated using a Poisson process. The resulting posterior mean for the AA approach is thus
For the simplified disaggregate analysis (DAI) with independent component assumption, if the prior distribution for the failure rate and failure probability of Components 1 and 2 are gamma and beta distributed with parameters and (which are natural conjugate distributions for Poisson and binomial sampling processes, respectively), then the posterior distributions are still gamma and beta distributed with parameters and . The posterior mean for the DAI analysis is thus simply
According to [], the necessary and sufficient conditions to have perfect aggregation for the product is that . In that case, it can be interpreted as the pseudo number of trials of Component 2 must be equal to the pseudo number of failures of Component 1.
2.4. Bivariate Copula
The copula models have become important tools in high-dimensional statistical applications for framing and studying the dependence structure of multivariate distributions or random vectors. They have been widely used in formulating and analyzing system reliability in various fields (see, e.g., [,]). Functions that tie multivariate distribution functions to their one-dimensional marginal distribution functions are known in the mathematics field as copulas. In other words, they are multivariate distribution functions whose one-dimensional margins are uniform on the interval [0,1] []. In the bivariate case, let be a joint cumulative distribution function (CDF) for two random variables X and Y with one-dimensional marginal CDFs and . Then, there exists a two-dimensional copula C such that
for all x and y.
Since the purpose of this study was to investigate the performances of the different Bayesian risk analysis approaches for evaluating the reliability of a system where the failures of components are correlated, copulas were thus used to construct bivariate distribution functions with correlated marginal random variables. A measure of the dependence between marginals needs to be specified, and Kendall’s , a rank correlation coefficient, was used to measure the degree of correlation reflected in joint distributions constructed using copulas. In this study, Kendall’s is used instead of the most widely used Pearson correlation coefficient because the measure of Kendall’s only depends on the unique copula used for constructing the joint distribution (i.e., it is independent of the marginal distributions of the correlated random variables, and is therefore a function of the copula alone). It also indicates that there is monotonic (but not necessarily linear) relationship between the variables unlike the Pearson correlation coefficient which measures linear association only. For a discussion on when and when not use the Kendall’s coefficient is preferable, readers are referred to [].
Because this correlation coefficient depends only on rank orders, it is independent of the marginal distributions of the correlated random variables, and is therefore a function of the copula alone. In particular, for a copula function C, if random variables X and Y are continuous (e.g., the gamma and beta random variables that are used for formulate the prior distributions of failure rate and failure probability in this study), then we have
Some parametric copula families have parameters that control the strength of dependence. Those copulas usually have relatively simple closed-form expressions for Kendall’s . Even when closed-form expressions are not available, Kendall’s can still be easily obtained via numerical integration. In this study, Frank copula was chosen because it not only can formulate both negative and positive dependency but also covers a wide range of dependence. Let denote the parameter of Frank copula, copula function of Frank copula C is specified as follows.
where the maximum range of dependence can be achieved when approaches to or ∞. The copula density function can be obtained as follows.
For the parallel system considered in this study, the joint prior distribution of system can thus be constructed by using
where , , , and are cumulative distribution functions and probability density functions of gamma distribution with parameters and beta distribution with parameters , respectively.
3. Regionalized Sensitivity Analysis
3.1. Monte Carlo Simulation
The features of the systems under investigation (i.e., the parameters of the copula-based Bayesian reliability model) may possibly affect the magnitude of relative errors in posterior means obtained by using different Bayesian analysis approaches. These critical factors or features may be identified by analyzing or mining a large number of cases (i.e., systems) generated by using different features (or parameters).
A large set of pseudo input factors (including pseudo data) was generated by using Monte Carlo simulation (MCS) approach. In this study, initial parameters in the copula model (e.g., shape and scale parameters of components’ failure rate and probability, test time units, components’ number of failures, and association measure of Kendall’s ) are considered as the input factors (please refer to Table 1). The distribution of these input factors was converted to a standard uniform distribution for ensuring its effectiveness of covering specific search space of a parameter []. These pseudo parameters can then be further analyzed by utilizing DA, AA, and DAI to produce a set of posterior means for each approach.

Table 1.
Statistical distributions of the pseudo parameters.
3.2. Monte Carlo Filtering and Regionalized Sensitivity Analysis
To identify the key factors most responsible for the output realization of interest, regional sensitivity analysis (RSA) can be utilized. RSA performs a multi-parameter Monte Carlo simulation by sampling parameters from statistical distribution functions. To be specific, the reliability analyst proceeds in two steps: (1) qualitatively defining the system behavior (i.e., setting a target threshold for the model); and (2) classifying the model outputs into a binary set (namely, behavioral and non-behavioral). A “behavioral set B” or is the classification set whereby the model’s output results lie within the target threshold (i.e., leading to a small magnitude of error or uncertainty) while a “non-behavioral set ” or is the classification set whereby the model’s output results do not lie within the target threshold (i.e., leading to a large magnitude of error or uncertainty).
The RSA procedure is a Monte Carlo filtering based procedure that was first developed and applied to identify key processes or parameters resulting in great uncertainties in environmental systems [,]. By identifying or even ranking the influential parameters which are critical for producing uncertainties, this analysis can help in prioritizing research effort to further understand the system and/or reduce uncertainties of the system. In our analysis, the importance of a model parameter is determined by its role (relative to other parameters) in causing the absolute relative error of a Bayesian reliability analysis approach to exceed some pre-specified threshold. Correspondingly, in this study, the relative error between AA and DA approaches () and the relative error between DAI and DA () can be computed by using the following expressions.
In a similar way to [], the RSA procedure in this paper is implemented as follows. We first define ranges for k input parameters () to represent the variation in the inputs to the model, and then classify the resulting relative error as either acceptable (i.e., in the behavioral set B) or unacceptable (i.e., in the non-behavioral set ∼B). In our analysis, an acceptable realization is obtained when the relative error falls below a target threshold of 10%. This enables us to establish two subsets for each : () of m elements and :() of n elements with equal to the sum of pseudo parameters generated. To assess the statistical difference between the sets of parameter values that lead to acceptable and unacceptable realizations, a Kolmogorov–Smirnov two-sample test can then be performed by testing the hypotheses specified as follows:
where and are the probability density functions defined on the two subsets determined by the threshold value. The test statistic of the Kolmogorov–Smirnov test is defined by
where and are the corresponding cumulative distribution functions. The implication of the KS test results is as follows. A small p-value of the Kolmogorov–Smirnov test (and a large ) implies that the parameter has a high level of importance in leading to a great magnitude of the relative error.
The results of the Kolmogorov–Smirnov tests for the paired comparison analysis at 10% boundary value are shown in Table 2 and Table 3, respectively.

Table 2.
RSA results for AA−DA comparison.

Table 3.
RSA results for DAI−DA comparison.
Although all parameters are used to compute the posterior means, it is not all initial parameters of the copula-based models that critically affect the magnitude of error between the results of AA and DA. Some factors were found to be more important than others. This can be noticed in Table 2. It is evident that the (shape and scale) parameters of prior probability distributions for failure rate (of Component 1) and the failure probability (of Component 2) are the most significant. Additionally, the number of failures of Component 2 (system failure) is also significant under 5% level of significance. Figure 1 graphically displays the observed distribution of each parameter and enables one to visually compare whether the observed distribution of each parameter from behavioral and non-behavioral sets are different. The aggregation errors tend to be unacceptable when parameters a and b of Component 1 are small. The implication of this result is that DA is preferable when scientific uncertainty about the failure rate of Component 1 is relatively large. It should also be noted that the results obtained by AA tend to be significantly inferior to those obtained by DA for small values of (i.e., low number of system failure). DA results are more preferable when there is insufficient evidence of system failures. On the other hand, it can be noticed that Kendall’s was not significant in the analysis. Since both approaches (DA and AA) consider component dependence, this finding intuitively makes sense.
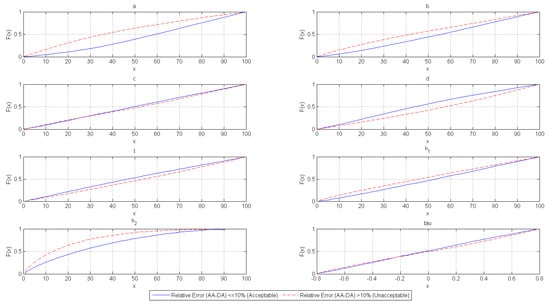
Figure 1.
Observed CDF of individual parameters in AA−DA analysis.
The same comparison can be drawn between DAI and DA. However, a difference in the results obtained can be observed in Table 3. For instance, Kendall’s was highly significant for the DAI–DA paired comparison, whereas it was the opposite case for AA−DA paired comparison. When is large (i.e., high correlation or high association), DAI tends to be unacceptable. Again, this intuitively makes sense since the component dependence is not taken into consideration in the DAI approach. Figure 2 graphically displays the cumulative distribution functions of each parameter and shows that when the numbers of failure of Components 1 and 2 are few, the results of DAI tends to be significantly inferior to those of DA. Particularly, when there is insufficient evidence of component failures available to the reliability analyst, results obtained by DA are much more accurate.
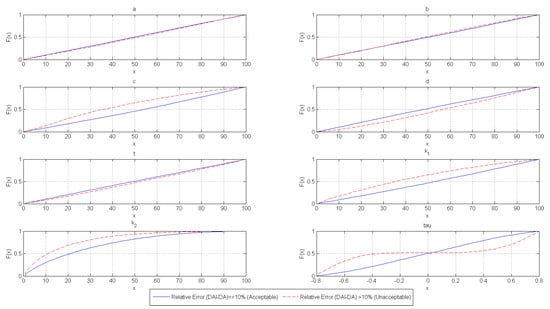
Figure 2.
Observed CDF of individual parameters in DAI−DA analysis.
As highlighted above in this section, MCF and RSA can be used to identify several key factors that are accountable for producing the output realization of interest which can fall either in a behavioral set or a non-behavioral set. However, it remains complicated to obtain the most appropriate approach for analysis since the relative importance of each input factor is only identified from a univariate analysis perspective mainly due to two reasons. First, the paired comparisons for AA and DAI approaches are carried out separately with the most accurate DA approach. Second, the Kolmogorov–Smirnov tests focus on testing the significance of each individual parameter separately. It is therefore essential to conduct a thorough analysis from a multivariate analysis approach in order to obtain a more complete insight for choosing the most suitable method. Some preliminary guidelines can be derived from the observed distribution functions depicted in Figure 2 and Figure 3. However, the actual range of values of the input factors which cause a great magnitude of error might still be unknown. Hence, to discover possible scenarios leading to a more certain analysis approach, we proceed in a similar way as [] and propose the classification tree learning.
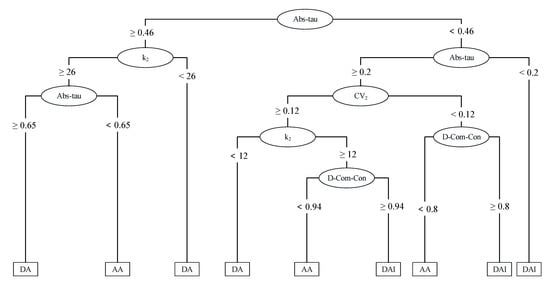
Figure 3.
Classification tree obtained from adjusted parameters.
4. Classification Tree Learning
To identify the interaction effects among the input factors (i.e., to identify the combination of conditions which lead to great magnitude of error in analyses), the classification tree learning is employed to further analyze the generated pseudo reliability data. Moreover, the original parameters are slightly modified so that any “qualitative” knowledge obtained from former studies or other resources can be incorporated as the input factors in the classification tree learning (see, e.g., [,,]).
A more integrated scheme to incorporate those three analysis approaches in one body is thus developed in this work. Rather than categorize the model outputs into binary classes (i.e., small and great magnitude of error) as done previously, the model outputs are classified into three categories, namely “DA”, “AA”, and “DAI”, which directly represent the most appropriate analysis approach. Therefore, a rule for determining the value of target variable (i.e., to categorize the model outputs into these three categories) needs to be established. For example, suppose that the threshold value of the relative error is set to 10%; then, the following cases can be classified as those shown in Table 4.

Table 4.
Rule for determining class label.
According to this labeling rule, when the resulting relative errors by utilizing AA or DAI approaches are smaller than the given threshold, we choose an analysis approach with a smaller error. However, if relative errors for both AA and DAI approaches are greater than 10%—the given threshold value—then the DA approach is chosen.
Classification Tree Model Based on Modified Parameters
To obtain a visualized representation of the rules that can be used to determine which approach should be employed under different values of parameters (i.e., different combinations), the Recursive Partitioning (rpart) package in R, which builds classification or regression models based on the concepts discussed in [], was implemented. Rpart builds classification models of a very general structure based on a double stage procedure. Initially, a single variable which best splits the data into two groups is found and the data is separated. This process is applied separately to each sub-group in a recursive manner until the sub-groups either reach a minimum size or until no improvement can be made. This results in an undoubtedly too complex model. Finally, cross-validation procedure is performed in order to trim back the full tree.
As mentioned above in this section, considering only the original parameters as the input factors (i.e., attributes) for the decision tree will not incorporate important qualitative knowledge into the model. In other words, we need modified parameters to build a more interpretable classification tree as well as to improve the prediction accuracy. Therefore, modified parameters for a model of products of a probability and a frequency for parallel systems are defined as input or attribute variables. Table 5 shows the list of the adjusted parameters and details. The classification tree can then be constructed by considering the adjusted parameters as input factors at 10% boundary value. Using 50,000 simulated cases, the tree that was constructed by utilizing rpart package in R is shown in Figure 3. In evaluating the performance of the classification tree model, we found the accuracy (61.4%) of the tree obtained utilizing the modified parameters as inputs to be higher than the accuracy (56.3%) of the classification tree obtained while using the initial input parameters. The classification tree model built by using modified parameters also performs significantly better than a random classifier (where a 1/3 accuracy is expected).

Table 5.
Adjusted parameters.
It can be deduced from the classification tree that four of the nine parameters can be regarded as key factors influencing the magnitude of errors: Abs-tau, D-Com-Con, , and (see Table 5 for description). It is possible to investigate the range and combination of these influencing variables and determine how they produce predictions (of the magnitude of errors) since classification tree learning is a white-box model. In that regard, the reliability analyst has the ability to identify the conditions where the most accurate but costly DA analysis should be used. The optimal analytical approach under different scenarios can be determined from the terminal nodes in Figure 3 to be one of AA, DA, or DAI.
A concise description of the extracted decision rules is provided in Table 6. Specifically, the left column contains the rule number, the middle column shows the pre-conditions of the rules, and the right column contains resulting optimal Bayesian analysis approach for that particular rule to be chosen.

Table 6.
Extracted decision rules.
The classification tree displayed in Figure 3 has two main branches. The right branch has a relatively lower absolute Kendall’s tau value () and encompasses Rules 1–6, whereas the left branch has a relatively higher absolute Kendall’s tau value () and encompasses Rules 7–9 (where the components are highly correlated). It can be observed that half of the right branch is dominated by the DAI class and two-thirds of the left branch is dominated by the AA class.
In what follows, we provide some discussion on some of the rules to assist in explaining the intuition behind the results obtained from the analysis (see Table 7 for some of the metrics used).

Table 7.
Parameter metrics for explaining the intuition behind results.
When the absolute Kendall’s tau value is relatively lower (i.e., ), we can derive Rules 1–6 from the right hand branch of the classification tree, and, when the absolute Kendall’s tau value is relatively higher (i.e., ), we can derive Rules 7–9 from the left hand branch. The different scenarios that can be observed are discussed below:
- (1)
- Rule 1: If the absolute Kendall’s tau value is low and strictly less than 0.2, then the optimal approach to use is DAI since this indicates a weak association between components. Therefore, the dependence information can safely be ignored. Additionally, only one variable is in this decision rule hence a higher predictive capacity can generally be implied.
- (2)
- Rules 2 and 3: When the absolute Kendall’s tau value is low such that it is not less than 0.2 but strictly less than 0.46 and is low, then DAI can be used provided that the overall component consistency is poor (i.e., there is high difference) since the dependence information can safely be ignored and the reliability analyst is certain about the failure probability of Component 2. However, when the overall component consistency is high (i.e., there is low difference), it is optimal to use the AA approach since the number of component failures for each individual component occurs as expected and the prior distribution is relatively informative.
- (3)
- Rule 4: If the absolute Kendall’s tau value is low such that it is not less than 0.2 but strictly less than 0.46, is high, and there is a low number of system failures, then the reliability analyst should consider utilizing the DA approach since there is considerable scientific uncertainty associated with the failure probability of Component 2 (thus, the prior distribution is uninformative). In this case, failure data for Component 2 is more substantial for Bayesian estimation. Therefore, AA should not be implemented since key evidence for Component 2 might be lost.
- (4)
- Rules 5 and 6: This involves cases whereby the absolute Kendall’s tau value is low such that it is not less than 0.2 but strictly less than 0.46. However, contrary to Scenario (3), the number of system failures is high. In this case, when the overall component consistency is high, the reliability analyst will do well to select the AA approach. Since the number of component failures for each individual component occurs as expected, little component-level information will be lost when AA is used. On the other hand, when the overall component consistency is poor, it would be optimal for the analyst to select the DAI approach since the components of the system can be assumed to be independent due to the low Kendall’s tau value.
- (5)
- Rules 7 and 8: If the absolute Kendall’s tau value is relatively high (i.e., ) and there is either a low or high number of system failures, then the reliability analyst should always select the DA approach since the components are highly dependent. As a result, DAI cannot be used and utilizing AA would result in losing relevant component-level data.
- (6)
- Rule 9: When the components of the system are moderately dependent (i.e., ) and there is a high number of system failures, the AA approach can be used to save effort and cost of collecting a large number of component data.
5. Conclusions
The guidance for choosing the most appropriate approach can be directly extracted from the classification tree, and, therefore, the findings in this work can be extremely helpful for the analysts in the reliability field. In addition, interactions among the input factors might also be revealed from the tree model so that the ranges of values of critical factors that affect the estimated error in reliability can be identified and located.
Moreover, other than providing the guidelines for choosing the most appropriate approach under certain conditions, reliability analysts can follow the steps of this work to build their own classification trees by using different threshold values, copula functions, modified parameter settings, and minimum number of terminal nodes based on their professional knowledge and various requirements in different problems in hand.
The results of previous research on a parallel beta-binomial system [] were compared to the Poisson–Bernoulli system analyzed in this study, and it was found that, in both cases, the Absolute Kendall’s value and the number of failures were key factors that influence the magnitude of error. However, difference of components’ and systems consistency (D-Com-Con and D-Sys-Con), the ratio of consistency, and coefficient of variation for both components (R-C1-Con, R-C2-Con, , and ) were key only in the beta-binomial system. In the Poisson–Bernoulli system, the key influencing factors were the number of failures of Component 2 () and the difference in components’ consistency (D-Com-Con). This information can be useful in deducing which type of data (aggregate or disaggregate) has more impact on either of the systems when evaluating their reliability.
It should be noted that this study focused more on the simulated cases in which realizations were obtained by drawing from all the possible situations. Therefore, the numerical value of Kendall’s tau was obtained arbitrarily from results of the simulation. While this study focused primarily on simulated cases, if one wants to apply the model to a real world problem, further investigation would need to be conducted in order to establish the connection between the copula-based joint prior and the empirical data or evidence available. Since the reliability engineering expert’s opinion would be sought on two or more variables which are dependent, there will also be a need for eliciting association between variables, a task that is much more complex than eliciting subjective distribution for a single variable of interest. Therefore, better performing elicitation methods (see, e.g., []) would need to be considered in order to obtain valid results.
It is worth noting that it is also theoretically possible to use certain parameters to explicitly formulate or describe the dependence between and (where they are both random variables with specific distributions) and then use Bayesian update to derive the posterior distributions of these parameters. Bayesian updates of the parameters (that used to formulate dependence structure) might not be analytically tractable but should be able to be dealt with using numerical methods. Additional research focusing on these aspects would be of great interest and value in further understanding the role of dependence and its influence on evaluating the reliability of a system.
Furthermore, although the results from this work are confined to the simple parallel system (and especially for the model of products of a probability and a frequency), the theoretical and practical scheme given in this work would still be very useful to be applied on more complex systems. The same process and method used in this work can also be applied to more complex systems such as systems with more than two components or systems combining both series and parallel sub-systems. Poisson-distributed failures are popular in modern science and engineering. For future studies, it would be interesting to explore real case studies by applying the methods outlined in this article.
Additionally, since (the possibly violated) assumption of independence is still used in most of the studies in application fields, the proposed concept, methods, and findings in the current research might also be useful in other fields also dealing with dependency.
Author Contributions
Conceptualization, S.-W.L.; methodology, S.-W.L.; software, S.-W.L.; validation, S.-W.L., T.B.M. and Y.-T.L.; formal analysis, S.-W.L. and Y.-T.L.; investigation, S.-W.L.; resources, S.-W.L.; data curation, Y.-T.L.; writing—original draft preparation, S.-W.L.; writing—review and editing, T.B.M. and S.-W.L.; visualization, S.-W.L., T.B.M. and Y.-T.L.; supervision, S.-W.L.; project administration, S.-W.L.; and funding acquisition, S.-W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was partially supported by the Ministry of Science and Technology of Taiwan under grant numbers 106-2410-H-011-004-MY3 and MOST MOST109-2410-H-011-014. Any opinions, findings, and conclusions or recommendations expressed herein are those of the authors and do not necessarily reflect the views of the sponsors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Only simulated data were created in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors thank the editors and two anonymous reviewers for their constructive and insightful comments that greatly improved the quality and presentation of this manuscript.
Conflicts of Interest
The authors declare that they have no conflicts of interest relevant to the manuscript submitted to Applied Sciences.
References
- Martz, H.F.; Waller, R.A. Bayesian Reliability Analysis; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Martz, H.F. Bayesian Reliability Analysis. In Encyclopedia of Statistics in Quality and Reliability; Wiley: New York, NY, USA, 2008; pp. 192–196. [Google Scholar]
- Liu, Y.; Abeyratne, A.I. Practical Applications of Bayesian Reliability; Wiley: New York, NY, USA, 2019. [Google Scholar]
- Guo, J.; Li, Z.; Jin, J. System reliability assessment with multilevel information using the Bayesian melding method. Reliab. Eng. Syst. Saf. 2018, 170, 146–158. [Google Scholar] [CrossRef]
- Syed, Z.; Shabarchin, O.; Lawryshyn, Y. A novel tool for Bayesian reliability analysis using AHP as a framework for prior elicitation. J. Loss Prev. Process. Ind. 2020, 64, 104024. [Google Scholar] [CrossRef]
- Zhang, C.W.; Pan, R.; Goh, T.N. Reliability assessment of high-Quality new products with data scarcity. Int. J. Prod. Res. 2020. in print. [Google Scholar] [CrossRef]
- Mosleh, A.; Bier, V.M. On Decomposition and Aggregation Error in Estimation: Some Basic Principles and Examples. Risk Anal. 1992, 12, 203–214. [Google Scholar] [CrossRef]
- Bier, V.M. On the concept of perfect aggregation in Bayesian estimation. Reliab. Eng. Syst. Saf. 1994, 46, 271–281. [Google Scholar] [CrossRef]
- Garrett, T.A. Aggregate versus disaggregated data in regression analysis: Implications for inference. Econ. Lett. 2003, 81, 61–65. [Google Scholar] [CrossRef]
- Denton, F.T.; Mountain, D.C. Exploring the effects of aggregation error in the estimation of consumer demand-elasticities. Econ. Model. 2011, 28, 1747–1755. [Google Scholar] [CrossRef][Green Version]
- Hagen-Zanker, A.; Jin, Y. Reducing aggregation error in spatial interaction models by location sampling. In Proceedings of the 11th International Conference on GeoComputation, University College, London, UK, 20–22 July 2011. [Google Scholar]
- Azaeiz, M.N.; Bier, V.M. Perfect aggregation for a class of general reliability models with Bayesian updating. Appl. Math. Comput. 1995, 73, 281–302. [Google Scholar]
- Guarro, S.; Yau, M. On the nature and practical handling of the bayesian aggregation anomaly. Reliab. Eng. Syst. Saf. 2009, 94, 1050–1056. [Google Scholar] [CrossRef]
- Johnson, V.E. Bayesian aggregation error? Int. J. Reliab. Saf. 2010, 4, 359–365. [Google Scholar] [CrossRef]
- Kim, K.O. Bayesian reliability when system and subsystem failure data are obtained in the same time period. J. Korean Stat. Soc. 2013, 42, 95–103. [Google Scholar] [CrossRef]
- Philipson, L.L. Anomalies in Bayesian launch range safety analysis. Reliab. Eng. Syst. Saf. 1995, 49, 355–357. [Google Scholar] [CrossRef]
- Philipson, L.L. The failure of Bayes system reliability inference based on data with multi-level applicability. IEEE Trans. Reliab. 1996, 45, 66–68. [Google Scholar] [CrossRef]
- Philipson, L.L. The Bayesian anomaly and its practical mitigation. IEEE Trans. Reliab. 2008, 57, 171–173. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Tan, G.; He, X. System Reliability Evaluation of a Bridge Structure Based on Multivariate Copulas and the AHP—EW Method That Considers Multiple Failure Criteria. Appl. Sci. 2020, 10, 1399. [Google Scholar] [CrossRef]
- Tan, G.; Kong, Q.; Wang, L.; Wang, X.; Liu, H. Reliability Evaluation of Hinged Slab Bridge Considering Hinge Joints Damage and Member Failure Credibility. Appl. Sci. 2020, 10, 4824. [Google Scholar] [CrossRef]
- Wong, T. Perfect Aggregation of Bayesian Analysis on Compositional Data. Stat. Pap. 2007, 48, 265–282. [Google Scholar] [CrossRef]
- Octavina. Bayesian Reliability Analysis of Series Systems with Dependent Components. Master’s Thesis, National Taiwan University of Science and Technology, Taipei, Taiwan, 2015. [Google Scholar]
- Lin, S.-W.; Liu, Y.-T.; Jerusalem, M.A. Bayesian reliability analysis of a products of probabilities model for parallel systems with dependent components. Int. J. Prod. Res. 2018, 56, 1521–1532. [Google Scholar] [CrossRef]
- Spear, R.C.; Cheng, Q.; Wu, S.L. An example of augmenting regional sensitivity analysis using machine learning software. Water Resour. Res. 2019, 56, 1–16. [Google Scholar] [CrossRef]
- Loh, W.-Y. Classification and regression trees. WIREs Data Min. Knowl. Discov. 2011, 1, 14–23. [Google Scholar] [CrossRef]
- Murthy, D.N.P.; Nguyen, D.G. Study of two-component system with failure interaction. Nav. Res. Logist. Q. 1985, 32, 239–247. [Google Scholar] [CrossRef]
- Korb, K.B.; Nicholson, A.E. Bayesian Artificial Intelligence; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 2006. [Google Scholar]
- Puth, M.-T.; Neuhauser, M.; Ruxton, G.D. Effective use of Spearman’s and Kendall’s correlation coefficients for association between two measured traits. Anim. Behav. 2015, 102, 77–84. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Spear, R.C.; Hornberger, G.M. Eutrophication in Peel Inlet–II: Identification of Critical Uncertainties via Generalized Sensitivity Analysis. Water Res. 1980, 14, 43–49. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; CRC Press: Boca Raton, FL, USA, 1984. [Google Scholar]
- O’Hagan, A.; Buck, C.E.; Daneshkhah, A.; Eiser, J.R.; Garthwaite, P.H.; Jenkinson, D.J.; Oakley, J.E.; Rakow, T. Uncertain Judgements: Eliciting Experts’ Probabilities; John Wiley & Sons, Ltd.: London, UK, 2006. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).