Abstract
The complex response characterizing elastomeric isolation bearings is reproduced by employing a novel uniaxial hysteretic model that has been recently formulated and successfully implemented in OpenSees. Such a novel OpenSees material model offers several advantages with respect to differential models typically available in commercial software products for structural analysis, such as 3D-BASIS and CSi programs. Firstly, it is based on a set of only five model parameters that have a clear mechanical significance; such a property not only allows one to drastically simplify the parameters identification process, but it also allows the model to be used in practice. In addition, the model does not require numerical methods for the evaluation of the restoring force since the latter is computed by solving an algebraic equation. To encourage researchers and designers to adopt the proposed model for research and practical purposes, we demonstrate its accuracy by performing some numerical tests in OpenSees. In particular, we first employ the recently implemented model to compute the nonlinear dynamic response of a seismically base-isolated structure with elastomeric bearings and, subsequently, we compare the results with those obtained by modeling the seismic isolators with the OpenSees BoucWen uniaxial material model, that is one of the most popular and accurate hysteretic models currently available in OpenSees.
1. Introduction
Seismic isolation represents one of the most efficient techniques currently available to protect structures from earthquake excitations [1,2,3,4]. Such a technique is based on the use of seismic isolation bearings which are special devices characterized by flexibility and energy dissipation capacity along their transverse directions and a large stiffness along the axial one [5].
Basically, elastomeric and sliding bearings are commonly used in seismic isolation. The first ones are constituted by alternating layers of rubber and thin reinforcing elements [6], whereas the second ones are made up of a metal slider that moves on a sliding metal surface [7].
Under the effect of a constant axial compressive load, deformation of both types of isolators, along their transverse directions, is characterized by a complex hysteretic behavior. Some examples of their typical restoring force-displacement hysteresis loops are described in [8,9,10,11].
Due to the hysteretic nature of the isolators’ behavior, a realistic prediction of the actual response of seismically base-isolated structures can only be achieved by performing nonlinear dynamic analyses. As shown by Vaiana et al. [12] and Greco et al. [13], the accuracy and computational efficiency of such sophisticated analyses are strongly related to a suitable combination of the time integration method, required to solve the nonlinear equilibrium equations, and the phenomenological models adopted to describe the hysteretic behavior of the seismic devices.
Among existing computer programs of structural analysis, 3D-BASIS, ETABS and SAP2000 are typically used in practice to perform nonlinear time history analyses of base-isolated structures. On the contrary, other commercially available computer programs, such as ANSYS and ABAQUS, that are also capable of modeling the behavior of seismic isolators, are rarely used for this purpose since they are not suitable for building analysis.
In 3D-BASIS, the nonlinear equilibrium equations are numerically solved by using the Newmark’s constant average acceleration method adopted in conjunction with the pseudo-force iterative procedure [14]. As regards the available hysteretic models, such a computer program offers the possibility of using accurate differential models that have been derived by modifying the celebrated Bouc–Wen model [15,16] to allow for the simulation of the complex response characterizing elastomeric and sliding bearings [9,14].
In CSi programs, namely ETABS and SAP2000, the nonlinear equilibrium equations can be solved by employing the computationally efficient Fast Nonlinear Analysis method [17], in which stiffness and mass orthogonal load dependent Ritz vectors of the linear elastic base-isolated structure are used to reduce the size of the nonlinear system to be solved. As for 3D-BASIS, in CSi programs the behavior of elastomeric and sliding bearings can be simulated by adopting accurate differential models that represent modified versions of the Bouc–Wen model [15,16].
The hysteretic models implemented in the above-described computer programs, though capable of accurately simulating the response of seismic isolation devices, are based on parameters lacking a clear mechanical significance, so that their calibration and use in practical applications is troublesome. In addition, sophisticated numerical techniques, such as multi-steps [18] or Runge–Kutta methods [19], are exploited to solve, at each time step of a nonlinear time history analysis, the differential equation defining such models.
To overcome such limitations, a class of uniaxial phenomenological models has been formulated in [20,21]; subsequently, it has been specialized to derive two models which are respectively suitable for elastomeric and sliding bearings [22,23]. In particular, the one developed for elastomeric bearings, that is of particular interest in this work, exploits just five parameters, directly derivable from the experimental hysteresis loop, and requires a straightforward computer implementation. Such a model has been denominated Algebraic Model since the output variable, namely the bearing restoring force, is computed by solving an algebraic equation in closed form.
To allow designers and researchers to adopt the Algebraic Model and fully exploit its appealing features, we have recently developed a computationally efficient identification algorithm capable of calibrating the five model parameters from experimental or numerical tests [24]. In addition, such a model has been implemented in the Open System for Earthquake Engineering Simulation (OpenSees), that is a powerful object-oriented, open source software currently adopted by many researchers in the field of structural engineering [25].
In this work, we employ, for the first time, a novel OpenSees material object, called HystereticPoly material model, to perform some nonlinear time history analyses on a seismically base-isolated structure with elastomeric bearings. In particular, the numerical accuracy of the proposed hysteretic material model is verified by comparing the results of several nonlinear analyses with the ones obtained by modeling each elastomeric bearing by means of the OpenSees Bouc–Wen material model.
The present paper is organized into three parts. The typical transverse hysteretic behavior displayed by elastomeric and sliding bearings, under an axial compressive load, is illustrated in the first part (Section 2).
In the second part (Section 3), the formulation of the Algebraic Model is summarized and the related OpenSees hysteretic material object is illustrated.
Finally, in the third part (Section 4), the accuracy of the HystereticPoly material model is validated by means of numerical simulations.
2. Seismically Base-Isolated Structures
A typical seismically base-isolated structure is composed by two substructures, as shown in Figure 1: the superstructure, that is designed by assuming a linear elastic behavior, and the base isolation system, that is designed in order to allow the superstructure to deform within its linear elastic range.
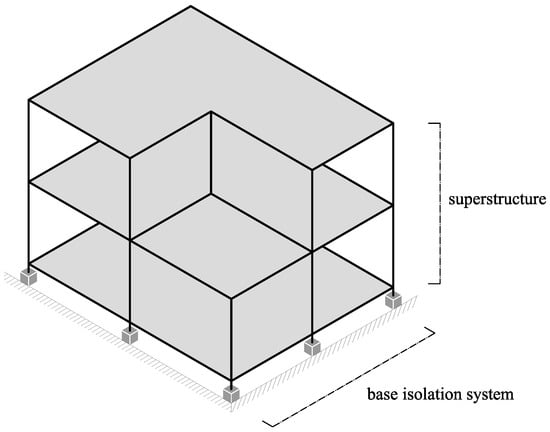
Figure 1.
A typical seismically base-isolated structure.
The base isolation system consists of special devices, called seismic isolators, and a full diaphragm, above the seismic isolation bearings, which is generally introduced to distribute the transverse loads uniformly among them [26].
There exist two main types of seismic isolation devices: elastomeric and sliding bearings. Both of them are characterized by a complex hysteretic behavior which allows the designers to employ one of the two existing seismic isolation strategies, denominated period elongation strategy and force limitation strategy, respectively.
In the former, the isolation bearings are employed to increase the fundamental period of the structure thus making its value conveniently different from the dominant period of the earthquake excitation; conversely, in the latter, the seismic isolators are adopted to control the maximum value of the transverse force acting at the base of each superstructure column.
In the next two subsections, we briefly describe the above-mentioned types of seismic isolators and we illustrate the typical force-displacement hysteresis loops characterizing their transverse response.
2.1. Elastomeric Bearings
Elastomeric bearings are designed as a stacking sequence of rubber sheets and thin reinforcing layers. The former guarantee flexibility and energy dissipation along the transverse directions, whereas the latter comply with two basic technical requirements. First, they prevent transverse bulging of the elastomer when axial compressive loads are applied on the bearing; second, reinforcing elements supply an axial stiffness by far greater, say at least several hundred times, than the transverse one.
Typically, reinforcing elements are made of thin steel plates [6] in the case of Steel Reinforced Elastomeric Bearings (SREBs) and thin layers of fiber fabric to produce Fiber Reinforced Elastomeric Bearings (FREBs) [27,28,29].
Figure 2a,b shows the sectional view of a typical SREB (FREB) in a deformed configuration and the shape of the related restoring force-displacement hysteresis loop.
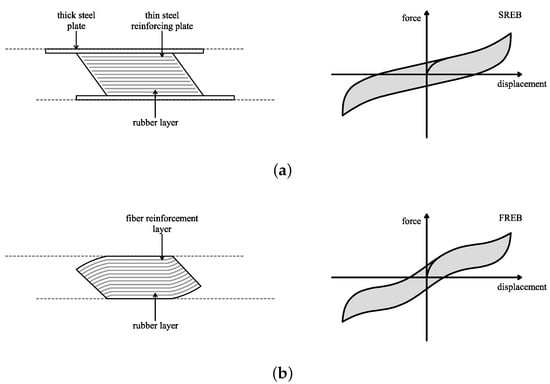
Figure 2.
Typical SREB (a) and FREB (b): sectional view in deformed configuration (left) and hysteresis loop shape (right).
2.2. Sliding Bearings
Sliding bearings are made of a slider that moves on a sliding surface. Such devices, having an axial stiffness that is very much greater than the transverse one, display an energy dissipation capacity due to the friction damping occurring at the sliding interface [5].
According to the type of sliding surface, sliding bearings can be classified into two main categories, namely Flat Surface Sliding Bearings (FSSBs) and Curved Surface Sliding Bearings (CSSBs) [7].
Figure 3a,b illustrates the sectional view of a typical FSSB (CSSB) in a deformed configuration together with the shape of the related restoring force-displacement hysteresis loop.
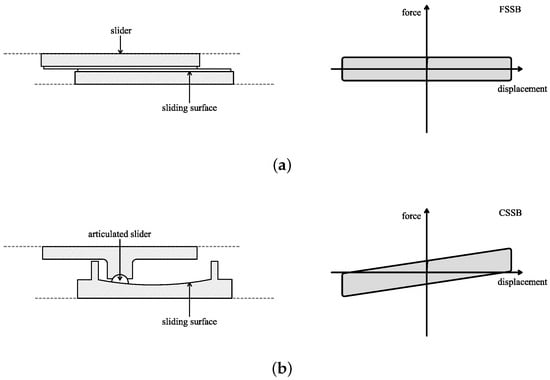
Figure 3.
Typical FSSB (a) and CSSB (b): sectional view in deformed configuration (left) and hysteresis loop shape (right).
3. Modeling of Elastomeric Bearings
Several uniaxial phenomenological models have been developed by researchers to reproduce the complex transverse hysteretic behavior of isolation bearings under the effect of a constant axial compressive load [9,14,30].
In this section, we focus on the modeling of elastomeric bearings, whereas the aspects related to the modeling of sliding bearings will be the objective of future papers. In particular, we first summarize the formulation of a hysteretic model recently developed by Vaiana et al. [22] and, subsequently, we illustrate the related material object that has been implemented in OpenSees [25].
The above-mentioned model, denominated Algebraic Model (AM) since the output variable is evaluated by solving an algebraic equation, is capable of simulating the typical hysteresis loops of both SREBs and FREBs by using a set of only 5 parameters (, , , , ) having a clear mechanical meaning.
3.1. Algebraic Model Formulation
In the Algebraic Model, u (f) represents the bearing transverse displacement (restoring force) whereas is the bearing transverse velocity.
The typical restoring force-displacement hysteresis loop characterizing such a model may be limited by two parallel straight lines (curves), as shown in Figure 5a,b of Ref. [22]. In particular, the restoring force, during the generic loading case (), is evaluated as:
whereas, during the generic unloading case (), it is computed as:
In Equations (1) and (2), and represent, respectively, the generic loading and unloading curves:
whereas and are, respectively, the upper and lower limiting curves:
The internal variable (), representing the displacement where the generic loading (unloading) curve intersects the upper (lower) limiting curve, is given by:
in which and are the coordinates of a generic point P belonging to or , as shown in Figure 7 of Ref. [22] for a typical hysteresis loop limited by two parallel curves.
Finally, the internal parameters and , representing, respectively, the half of the force difference between the upper and lower limiting curves, and the half of the displacement difference between the starting and ending points of a generic loading or unloading curve, are evaluated as:
where is a numerical parameter set equal to , whereas , , and , together with and , represent the five model parameters to be calibrated from experimental or numerical data [24]. Specifically, , , , , whereas and are reals.
3.2. OpenSees Uniaxial Model
The Algebraic Model described in Section 3.1 has been implemented in OpenSees v. 3.0, an open source, object-oriented framework for finite element analysis [25] whose core has been developed at the Pacific Earthquake Engineering Research Center headquartered at the University of California at Berkeley.
A version of such a framework with the implemented hysteretic material can be freely downloaded at the following link [31].
The command line of the model, belonging to the subclass uniaxialMaterial, is:
where $matTag is the progressive tag of the uniaxial material object, $ka,$kb,$a,$b1,$b2 represent, respectively, the five model parameters , , , , , whereas $tol is the model numerical parameter which can be set equal to [22].
uniaxialMaterial HystereticPoly $matTag $ka $kb $a $b1 $b2 $tol
As already explained in Section 3.1, the uniaxial material parameters need to satisfy the following conditions: , , , , whereas and are reals.
Figure 4 shows the four types of hysteresis loop shapes obtained for a sinusoidal transverse displacement when:
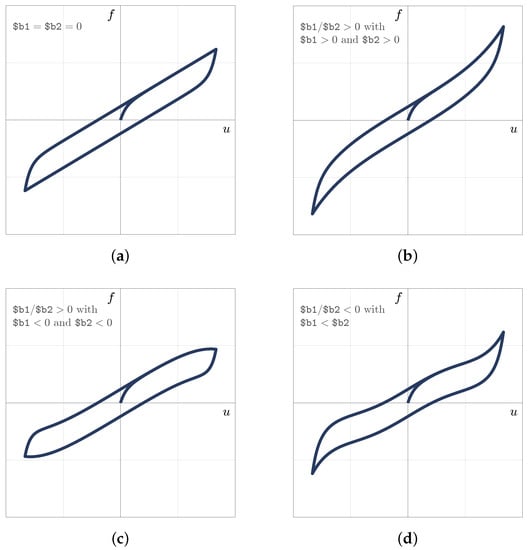
Figure 4.
Types of hysteresis loop shapes that can be simulated with the OpenSees uniaxial HystereticPoly material model.
- (a)
- ;
- (b)
- with and ;
- (c)
- with and ;
- (d)
- with .
We note that the hysteresis loop of Figure 4a,c is the typical restoring force-displacement hysteresis loop displayed by a SREB (FREB) at relatively large ( 100–150%) shear strains, whereas the one illustrated in Figure 4b,d represents the typical hysteresis loop of a SREB (FREB) at large ( > 100–150%) shear strains.
4. Nonlinear Time History Analyses in OpenSees
In this section, we present the results of several Nonlinear Time History Analyses (NLTHAs) carried out on a seismically base-isolated structure, subjected to bidirectional earthquake excitation, in order to investigate the accuracy of the novel OpenSees uniaxial material object described in Section 3.2.
In particular, such a model is employed to reproduce the decoupled biaxial hysteretic behavior of each elastomeric bearing adopted in the base isolation system of the analyzed structure. Due to its uniaxial nature, this model is not able to take into account the bidirectional interaction typically displayed by the restoring force components of each bearing along two generic orthogonal transverse directions. The implementation of a biaxial version of such a model, already formulated by Vaiana et al. [32], will be the objective of future works.
In order to demonstrate the accuracy properties of the proposed uniaxial material, the NLTHAs results are compared with those obtained by employing the OpenSees BoucWen material object. Such a model, originally formulated by Bouc and Wen [15,16], has been subsequently proposed by Nagarajaiah et al. [14] to simulate the complex response of elastomeric bearings.
In this work, the Newmark’s constant average acceleration method is adopted to numerically solve the nonlinear equilibrium equations of the analyzed structure since such a numerical time integration method is both accurate and unconditionally stable [33,34].
4.1. Base-Isolated Structure Properties
Figure 5a presents the three-dimensional (3D) structural model of the analyzed seismically base-isolated structure whose geometry is defined in a global, right-handed Cartesian coordinate system (O, X, Y, Z). In addition, Figure 5b shows the related extruded view to better illustrate the properties of beams and columns.
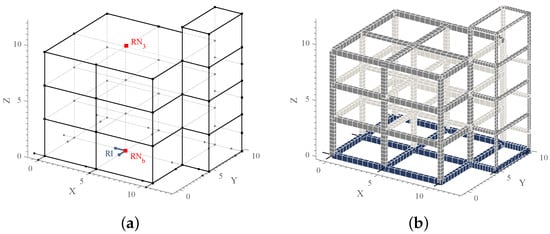
Figure 5.
3D structural model (a) of the analyzed base-isolated structure and related extruded view (b).
The superstructure is a three-story reinforced concrete structure with both horizontal and vertical geometric irregularities. The superstructure beams and columns have a linear elastic behavior and the floor diaphragms are rigid. The total mass of the superstructure is , the first three natural periods are s, s, and s, respectively, whereas the damping ratio of such three fundamental modes is equal to 5%.
Eleven lead rubber bearings, respectively placed under each column of the superstructure, and a rigid diaphragm above the base floor beams, these last ones assumed to have a linear elastic behavior, represent the main elements of the base isolation system, whose total mass is equal to . It has been designed in order to provide an effective isolation period s and an effective viscous damping ratio at the design displacement m. The design details are here omitted for brevity.
4.2. Applied Bidirectional Earthquake Excitation
The NLTHAs are carried out by imposing, along the X-axis (Y-axis), the component SN (SP) of the 1994 Northridge motion, illustrated in Figure 6a,b, and by adopting a ground acceleration record time step of s.
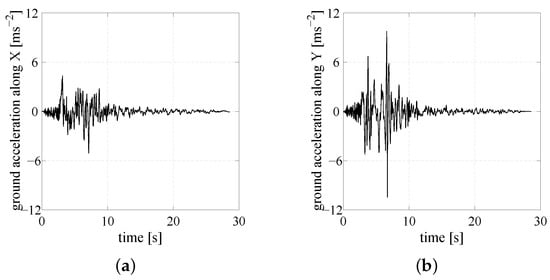
Figure 6.
SN (a) and SP (b) components of the ground acceleration recorded at the Jensen Filter Plant station during the Northridge earthquake of 17 January 1994.
4.3. Hysteretic Material Models Parameters
The adopted lead rubber bearings exhibit the restoring force-displacement hysteresis loop of Figure 7a when subjected to a sinusoidal transverse displacement having amplitude m and unit frequency, as the one illustrated in Figure 7b. Such a hysteresis loop is characterized by an effective (or secant) stiffness and an equivalent viscous damping ratio that allow the analyzed base-isolated structure to have a s and a at m.
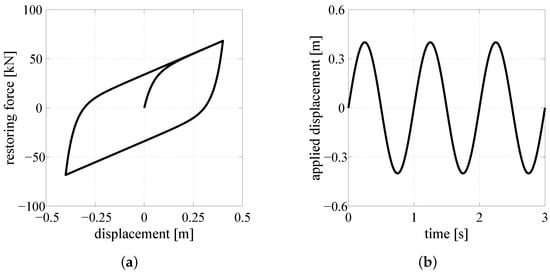
Figure 7.
Restoring force-displacement hysteresis loop (a) obtained by applying a harmonic transverse displacement (b) to each lead rubber bearing.
To perform the NLTHAs in OpenSees, each elastomeric bearing is modeled by inserting, under each superstructure column, two truss elements parallel to the X and Y axes, respectively. In particular, the axial hysteretic behavior of such elements is simulated by using both the HystereticPoly material model, presented in Section 3, and the widely used OpenSees BoucWen material model whose command line is:
where $matTag is the progressive tag of the uniaxial material object, whereas $alpha, $ko, $n, $gamma, $beta, $Ao, $deltaA, $deltaNu, $deltaEta represent the model parameters [35].
uniaxialMaterial BoucWen $matTag $alpha $ko $n $gamma $beta $Ao $deltaA $deltaNu $deltaEta
Specifically, the parameters adopted in the Algebraic Model (AM) and in the Bouc–Wen Model (BWM), selected to reproduce the hysteresis loop illustrated in Figure 7a, are listed in Table 1.

Table 1.
Parameters of the OpenSees hysteretic material models.
We note that the AM parameters have a clear mechanical significance which may allow such a model to be easily employed in actual applications. Indeed, when , $ka ($kb) represents the value of the tangent stiffness at the beginning (end) of the generic loading or unloading curve, whereas $a defines the rate of variation of the tangent stiffness from $ka to $kb. Conversely, the interpretation of the BWM parameters is not straightforward.
The current OpenSees library offers other four material objects suitable for the simulation of the uniaxial transverse response of elastomeric bearings: (1) Hysteretic material, (2) MultiLinear material, (3) KikuchiAikenHDR material, and (4) KikuchiAikenLRB material.
The first two models are characterized by a lower level of accuracy compared to the Bouc–Wen one since, differently from the latter, they are not smooth models and, for such a reason, their typical hysteresis loops are made of a series of straight lines instead of continuous curves. In addition, since the first derivative of their output variable is a noncontinuous function, the convergence of the nonlinear dynamic analyses may be drastically compromised [35].
The last two models are as accurate as the Bouc–Wen one but require more parameters which can be calibrated only by performing complicated and expensive experimental tests, as explained in [36].
For all those reasons, the numerical accuracy of the proposed OpenSees material object is demonstrated by comparing the results with those obtained by employing the Bouc–Wen material.
4.4. Numerical Results
The results of the analyses carried out on the 3D structural model of Figure 5 are shown in Table 2. Such results refer to two reference nodes, that is, the base isolation system reference node () and the superstructure third story reference node (), both highlight in red in Figure 5a.

Table 2.
Nonlinear time history analyses results.
Looking at Table 2, we may observe that the accuracy of the HystereticPoly material model is very satisfactory since the maximum and minimum values of the displacement along the X (Y) direction, namely (), as well as the ones of the total acceleration along the X (Y) direction, namely (), are numerically quite close to those predicted by using the celebrated Bouc–Wen material model.
Figure 8a,b and Figure 9a,b show, respectively, the time histories of the displacement and total acceleration along the X (Y) direction, whereas Figure 10a,b illustrates the restoring force-displacement hysteresis loops, displayed along the X (Y) direction, by the reference isolator () highlight in blue in Figure 5a. Generally speaking, the comparison between the responses of the analyzed structure obtained with the AM and the BWM shows a very good agreement.
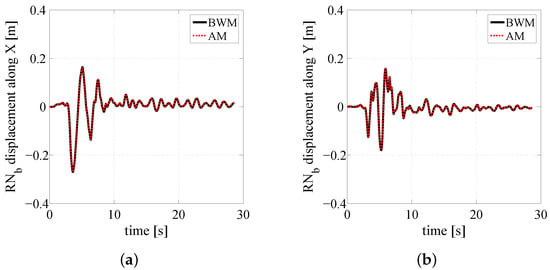
Figure 8.
Time histories of the displacement along the X (a) and Y (b) directions.
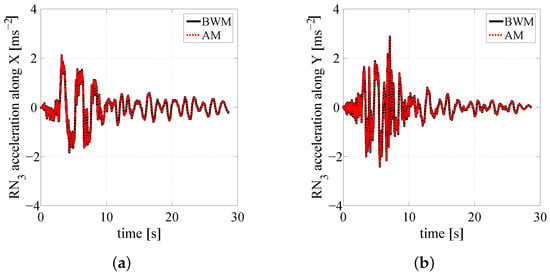
Figure 9.
Time histories of the total acceleration along the X (a) and Y (b) directions.
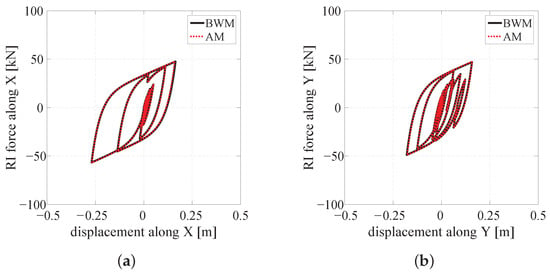
Figure 10.
Restoring force-displacement hysteresis loops of the along the X (a) and Y (b) directions.
5. Conclusions
The uniaxial hysteretic model formulated in [22] has been implemented in the OpenSees HystereticPoly material model and employed, for the first time, to simulate the behavior of elastomeric bearings typically adopted for the seismic protection of buildings and bridges.
The novel hysteretic material object requires the calibration of only five parameters that have a clear mechanical meaning, as shown in Section 3.2; for this reason, it can be easily calibrated and used for practical applications. In addition, this material model allows for the evaluation of the bearing restoring force by solving an algebraic equation thus avoiding convergence problems typical of differential hysteretic models.
In order to verify the numerical accuracy of the proposed material object, it has been used to analyze a base-isolated structure subjected to bidirectional earthquake excitation; subsequently, the results of the nonlinear time history analysis have been compared with those obtained by modeling the seismic isolators with the OpenSees Bouc–Wen uniaxial material. Such a comparison has shown a very good match between the results computed with the two different models thus demonstrating the numerical accuracy of the proposed one.
A comparative study among the proposed hysteretic material model and the other ones available in OpenSees, such as MultiLinear and KikuchiAiken materials, will be the topic of a future paper.
Author Contributions
Conceptualization, N.V.; Data curation, R.C.; Funding acquisition, L.R.; Methodology, N.V.; Project administration, L.R.; Software, R.C., S.S. and F.M.; Supervision, S.S., F.M. and L.R.; Validation, N.V.; Writing—original draft, N.V.; Writing—review and editing, N.V., S.S., F.M. and L.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Losanno, D.; Spizzuoco, M.; Serino, G. Optimal design of the seismic protection system for isolated bridges. Earthq. Struct. 2014, 7, 969–999. [Google Scholar] [CrossRef]
- Hadad, H.A.; Calabrese, A.; Strano, S.; Serino, G. A base isolation system for developing countries using discarded tyres filled with elastomeric recycled materials. J. Earthq. Eng. 2017, 21, 246–266. [Google Scholar] [CrossRef]
- Losanno, D.; Hadad, H.A.; Serino, G. Seismic behavior of isolated bridges with additional damping under far-field and near fault ground motion. Earthq. Struct. 2017, 13, 119–130. [Google Scholar]
- Madera Sierra, I.E.; Losanno, D.; Strano, S.; Marulanda, J.; Thomson, P. Development and experimental behavior of HDR seismic isolators for low-rise residential buildings. Eng. Struct. 2019, 183, 894–906. [Google Scholar] [CrossRef]
- Naeim, F.; Kelly, J.M. Design of Seismic Isolated Structures: From Theory to Practice; John Wiley and Sons Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Abe, M.; Yoshida, J.; Fujino, Y. Multiaxial behaviors of laminated rubber bearings and their modeling. I: Experimental study. J. Struct. Eng. 2004, 130, 1119–1132. [Google Scholar] [CrossRef]
- Constantinou, M.C.; Whittaker, A.S.; Kalpakidis, Y.; Fenz, D.M.; Warn, G.P. Performance of Seismic Isolation Hardware Under Service And Seismic Loading; Report No. MCEER-07-0012; State University of New York: Buffalo, NY, USA, 2007. [Google Scholar]
- Mokha, A.; Constantinou, M.C.; Reinhorn, A.M. Teflon bearings in base isolation. I: Testing. J. Struct. Eng. 1990, 116, 438–454. [Google Scholar] [CrossRef]
- Mokha, A.; Constantinou, M.C.; Reinhorn, A.M.; Zayas, V.A. Experimental study of friction-pendulum isolation system. J. Struct. Eng. 1991, 117, 1201–1217. [Google Scholar] [CrossRef]
- Kelly, J.M.; Takhirov, S.M. Analytical and Experimental Study of Fiber-Reinforced Elastomeric Isolators; PEER Report 2001/11; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2001. [Google Scholar]
- Tsai, C.S.; Chiang, T.-C.; Chen, B.-J.; Lin, S.-B. An advanced analytical model for high damping rubber bearings. Earthq. Eng. Struct. Dyn. 2003, 32, 1373–1387. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Paradiso, M.; Marmo, F.; Rosati, L. An efficient computational strategy for nonlinear time history analysis of seismically base-isolated structures. In Proceedings of the AIMETA 2019-XXIV Congresso dell’Associazione Italiana di Meccanica Teorica e Applicata, Rome, Italy, 15–19 September 2019. [Google Scholar] [CrossRef]
- Greco, F.; Luciano, R.; Serino, G.; Vaiana, N. A mixed explicit-implicit time integration approach for nonlinear analysis of base-isolated structures. Ann. Solid Struct. Mech. 2018, 10, 17–29. [Google Scholar] [CrossRef]
- Nagarajaiah, S.; Reinhorn, A.M.; Constantinou, M.C. Nonlinear dynamic analysis of 3-D base-isolated structures. J. Struct. Eng. 1991, 117, 2035–2054. [Google Scholar] [CrossRef]
- Bouc, R. Modèle mathématique d’hystérésis. Acustica 1971, 24, 16–25. [Google Scholar]
- Wen, Y.-K. Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 1976, 102, 249–263. [Google Scholar]
- Wilson, E.L. Three-Dimensional Static and Dynamic Analysis of Structures, 3rd ed.; Computers and Structures Inc.: Berkeley, CA, USA, 2002. [Google Scholar]
- Quarteroni, A.; Sacco, R.; Saleri, F. Numerical Mathematics; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Rosenbrock, H.H. Some general implicit processes for the numerical solution of differential equations. Comput. J. 1963, 5, 329–330. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. A class of uniaxial phenomenological models for simulating hysteretic phenomena in rate-independent mechanical systems and materials. Nonlinear Dyn. 2018, 93, 1647–1669. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Rosati, L. A generalized class of uniaxial rate-independent models for simulating asymmetric mechanical hysteresis phenomena. Mech. Syst. Signal Process. 2021, 146, 106984. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Marmo, F.; Rosati, L. An accurate and computationally efficient uniaxial phenomenological model for steel and fiber reinforced elastomeric bearings. Compos. Struct. 2019, 211, 196–212. [Google Scholar] [CrossRef]
- Vaiana, N.; Sessa, S.; Paradiso, M.; Rosati, L. Accurate and efficient modeling of the hysteretic behavior of sliding bearings. In Proceedings of the COMPDYN 2019-7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019. [Google Scholar] [CrossRef]
- Sessa, S.; Vaiana, N.; Paradiso, M.; Rosati, L. An inverse identification strategy for the mechanical parameters of a phenomenological hysteretic constitutive model. Mech. Syst. Signal Process. 2020, 139, 106622. [Google Scholar] [CrossRef]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2006. [Google Scholar]
- Naeim, F. The Seismic Design Handbook, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Al-Anany, Y.M.; Tait, M.J. Fiber reinforced elastomeric isolators for the seismic isolation of bridges. Compos. Struct. 2017, 160, 300–311. [Google Scholar] [CrossRef]
- Losanno, D.; Spizzuoco, M.; Calabrese, A. Bidirectional shaking-table tests of unbonded recycled-rubber fiber-reinforced bearings (RR-FRBs). Struct. Control Health Monit. 2019, 26, e2386. [Google Scholar] [CrossRef]
- Losanno, D.; Sierra, I.E.M.; Spizzuoco, M.; Marulanda, J.; Thomson, P. Experimental performance of unbonded polyester and carbon fiber reinforced elastomeric isolators under bidirectional seismic excitation. Eng. Struct. 2020, 209, 110003. [Google Scholar] [CrossRef]
- Manzoori, A.; Toopchi-Nezhad, H. Application of an extended Bouc-Wen model in seismic response prediction of unbonded fiber-reinforced isolators. J. Earthq. Eng. 2017, 21, 87–104. [Google Scholar] [CrossRef]
- Sessa, S. Modified OpenSees; vol 3.0.3 executable; University of California: Oakland, CA, USA, 2019. [Google Scholar]
- Vaiana, N.; Losanno, D.; Ravichandran, N. A novel family of multiple springs models suitable for biaxial rate-independent hysteretic behavior. Comput. Struct. 2021, 244, 106403. [Google Scholar] [CrossRef]
- Newmark, N.M. A method of computation for structural dynamics. J. Eng. Mech. Div. 1959, 85, 67–94. [Google Scholar]
- Paz, M.; Kim, Y.H. Nonlinear structural response. In Structural Dynamics; Springer: Cham, Swizterland, 2019. [Google Scholar] [CrossRef]
- Haukaas, T.; Kiureghian, A.D. Finite Element Reliability and Sensitivity Methods for Performance-Based Earthquake Engineering; PEER Report 2003/14; Pacific Earthquake Engineering Research Center, University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Kikuchi, M.; Aiken, I.D. An analytical hysteresis model for elastomeric seismic isolation bearings. Earthq. Eng. Struct. Dyn. 1997, 26, 215–231. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).