Abstract
With advancements in photoelectric technology and computer image processing technology, the visual measurement method based on point clouds is gradually being applied to the 3D measurement of large workpieces. Point cloud registration is a key step in 3D measurement, and its registration accuracy directly affects the accuracy of 3D measurements. In this study, we designed a novel MPCR-Net for multiple partial point cloud registration networks. First, an ideal point cloud was extracted from the CAD model of the workpiece and used as the global template. Next, a deep neural network was used to search for the corresponding point groups between each partial point cloud and the global template point cloud. Then, the rigid body transformation matrix was learned according to these correspondence point groups to realize the registration of each partial point cloud. Finally, the iterative closest point algorithm was used to optimize the registration results to obtain the final point cloud model of the workpiece. We conducted point cloud registration experiments on untrained models and actual workpieces, and by comparing them with existing point cloud registration methods, we verified that the MPCR-Net could improve the accuracy and robustness of the 3D point cloud registration.
1. Introduction
Technical advances and market competition have pushed manufacturing companies to offer larger and more precise machine parts. This trend calls for 3D measurement systems with higher measuring efficiency and accuracy [1,2]. The visual measurement method based on point cloud data has the advantages of possessing high measurement speed and accuracy, and no contact with the workpiece; thus, it has gradually been applied to the 3D measurement of large workpieces.
3D point cloud reconstruction involves obtaining a series of partial point clouds of a workpiece under multiple poses using a 3D measuring device and then fusing these point clouds to generate a complete 3D point cloud of the workpiece [3,4]. The accuracy and reliability of 3D reconstruction directly affect the accuracy of the measurement.
A key step in point cloud 3D reconstruction is establishing a partial or global reconstruction model of the workpiece through a series of processing steps such as point cloud denoising, point cloud registration, and surface reconstruction. The purpose of point cloud registration is to move point clouds with different poses to the same posture through rigid body transformation to eliminate the misalignment between pairwise point clouds [5].
In the field of 3D reconstruction, the vast majority of point cloud registration methods concern multiple partial point cloud registration [6], the basic principle of which is to reduce or eliminate the cumulative error of the 3D reconstruction by minimizing the registration error between partial point clouds under multiple poses, thereby improving the reconstruction accuracy. However, traditional point cloud registration methods, such as the turntable method [7] and the labeling method [8], are handcrafted methods with disadvantages such as low efficiency, high requirements for equipment accuracy, and missing point clouds in labeled areas.
With the development of deep learning technology and a greater number of publicly available datasets for point cloud models, many scholars have attempted to use deep learning methods to achieve point cloud registration and verify its effectiveness through experiments. However, to reduce computational complexity and improve the efficiency of 3D reconstruction, the existing deep learning-based point cloud registration methods often degenerate the multiple partial point cloud registration problem into a pairwise registration problem [9]. Then, by optimizing the relative spatial pose between the pairwise partial point clouds, the final reconstruction model of the workpiece is constructed based on the pairwise registration results.
However, due to the camera pose and environmental limitations, it is often impossible to ensure a sufficient overlap area between the pairwise point clouds. If the relationship between the partial point clouds and the overall structure of the workpiece is ignored, only the registration of partial point clouds is performed. This will increase the difficulty of point cloud registration, reduce the registration accuracy, and increase the final 3D reconstruction error.
The following are the remaining gaps in point cloud registration algorithms that need to be addressed:
- Some algorithms require the structures of pairwise point clouds to be the same. If the geometric structures of the pairwise point clouds are quite different, the registration accuracy will decrease;
- Some algorithms can complete the registration of two partially overlapping point clouds through partial-to-partial point-cloud registration methods. However, these methods rely on the individual training of specific partial data of the point cloud to establish the correspondence point relationship between the pairwise point clouds. Moreover, the registration accuracy is very sensitive to changes in the points.
From the above analysis, it can be concluded that existing deep learning-based point cloud registration methods can only be used for scene reconstruction and other occasions with low accuracy requirements. They are not suitable for the 3D reconstruction of large workpieces with high accuracy requirements. To solve this problem, we propose a multiple partial point cloud registration network using a global template named MPCR-Net.
MPCR-Net was inspired by PointNet [10]. It uses deep neural networks to extract and fuse the learnable features of partial point clouds and the global template point cloud. It then trains the rigid body transformation matrix for partial point clouds to register the correspondence partial point cloud to the global template point cloud and finally forms a complete point cloud of the workpiece. In MPCR-Net, the partial point cloud has the characteristics of a local geometric structure of the workpiece and is sampled by the measuring device; the global template point cloud has the complete geometric structure of the workpiece and is converted from the CAD model of the workpiece.
The key contributions of our work are listed as follows:
- A multiple partial point cloud registration method based on a global template is proposed. Each partial point cloud is gradually registered to the global template in patches, which can effectively improve the accuracy of the point cloud registration.
- A clipping network for the global template point cloud, TPCC-Net (clipping network for template point cloud), was designed. In TPCC-Net, the features of partial point clouds and the global template point cloud are extracted and fused through a neural network, and the correspondence points of each partial point cloud are cut out from the global template point cloud. Compared to the existing registration algorithm based on deep learning, this method can reduce the correspondence point estimation error and improve registration efficiency.
- A parameter estimation network for rigid body transformation, TMPE-Net (parameter estimating network for transformation matrix), was designed. The learnable features of a partial point cloud and its correspondence points generated through the TPCC-NET were extracted through a neural network, and the parameters of the rigid body transformation matrix were estimated to minimize the learnable feature gap between the partial point cloud and the global template point cloud.
2. Related Work
2.1. Classic Registration Algorithms
Classic registration algorithms for point clouds mainly include the iterative closest point (ICP) algorithm [11,12], variants of ICP [13,14,15,16,17,18,19], and geometry-based registration algorithms [20,21,22,23,24].
The ICP algorithm [11,12] represents a major milestone in point cloud registration and is extensively applied in various ways. The essence of ICP is to minimize the sum of the distances between correspondence points of pairwise point clouds using iterative calculations, thereby optimizing the relative pose of the pairwise point clouds. When the relative pose deviation of the pairwise point clouds is small, the algorithm is guaranteed convergence and can obtain an excellent registration result. Scholars have made various improvements to the ICP algorithm to enhance registration efficiency [16] and accuracy [17,18,19]. However, all ICP-style algorithms still rely on the direct calculation of the closest point correspondences; moreover, they cannot dynamically adjust according to the number of points and easily fall into local minima.
The workflow of geometry-based registration algorithms is as follows: calculate the geometric feature descriptors between pairwise point clouds [25], determine the correspondence relationship of the pairwise point clouds according to the similarity of the descriptors, and calculate the optimal matrix for rigid body transformation between the pairwise point clouds. Random-sample-consistency-based registration algorithms [20], such as the sample consensus initial alignment (SAC-IA) [24], are the most widely used geometry-based registration algorithms. In SAC-IA, the correspondence points are established by calculating the local fast point feature histograms (FPFH) of the pairwise point clouds, and registration is subsequently accomplished by minimizing the distance between correspondence points. The algorithm can achieve invariance to the initial pose, and a satisfactory registration result can still be obtained when the overlap in the pairwise point clouds is low.
Unfortunately, the registration results of the geometry-based registration algorithms mainly depend on the calculation accuracy of the geometric feature descriptors between pairwise point clouds. It is necessary to manually adjust the calculation parameters involved in the geometric feature descriptor, such as the neighborhood radius of the FPFH descriptor, to minimize calculation errors and improve registration accuracy. This method consumes a significant amount of time, and it is not easy to determine its optimal parameters.
2.2. Deep Learning-Based Registration Algorithms
Recent studies have shown that point cloud registration algorithms based on deep learning have higher registration accuracy than classic point cloud registration algorithms [26,27,28,29,30].
Charles et al. [10] proposed an end-to-end deep neural network (PointNet) that could directly take point clouds as a network input. PointNet overcomes the shortcomings of general deep learning methods that cannot effectively extract features from unstructured point clouds, and it establishes a learnable structured representation method for unstructured point clouds. PointNet and its variants have been successfully applied in point cloud classification, object detection [31], and point cloud completion tasks [32].
In point cloud registration tasks, some deep learning algorithms use the PointNet architecture to obtain the learnable structural features of the unstructured point clouds, train rigid body transformation matrices for point cloud registration based on these features, and obtain satisfactory point cloud registration results.
PointNetLK [33] is the first deep learning-based algorithm to use a learnable structured representation method for point cloud registration. PointNetLK modifies the classical Lucas and Kanade (LK) algorithm [34] to circumvent the inherent inability of the PointNet representation to accommodate gradient estimates through convolution. This modified LK framework is then unrolled as a recurrent neural network in which PointNet is integrated to construct the PointNetLK architecture. However, PointNetLK and similar algorithms, such as the DCP [35], DeepGMR [36], and PCRNet [37], work on the assumption that all the points in the point clouds are inliers by default. Naturally, they perform poorly when one of the point clouds has missing points, as in the case of partial point clouds.
Unfortunately, in actual point cloud 3D reconstruction tasks, it is rare for the geometric structures of pairwise point clouds to be the same, especially for large workpieces. Each raw point cloud collected by the measuring device can only map the local structure of the workpiece.
A class of point cloud registration algorithms, PRNet [38] and RPM-Net [39], which also contain the PointNet architecture, can handle partial-to-partial point cloud registration. Their application range is wider than that of PointNetLK and other algorithms that can only perform global point cloud registration. Unfortunately, these algorithms do not scale well when the number of points increases. If the number of points of the pairwise point clouds differs significantly, the estimation result of the rigid body transformation matrix will fluctuate with the number of points, resulting in a decrease in registration accuracy.
Other deep learning-based algorithms, such as the DGR [40] and multi-view registration network [41], can use neural networks to filter out some outliers from the correspondence points of pairwise point clouds, but these algorithms require a clear correspondence between the pairwise point clouds.
3. MPCR-Net
3.1. Overview
Most existing deep learning-based partial-to-partial point cloud registration algorithms iteratively perform registration between partial point clouds to realize the registration between multiple partial point clouds, before finally building a complete reconstruction model of the workpiece. However, when the overlapping area between the pairwise partial point clouds is small, the registration accuracy cannot be guaranteed, and a large 3D reconstruction error accumulates after the iterative registration of multiple partial point clouds.
We propose MPCR-Net, a multiple partial point cloud registration network, which uses a global template to improve the registration accuracy of a large workpiece. In this network, the template point cloud extracted from a CAD model is used as the global registration template, and multiple partial point clouds are gradually pasted onto the global template; the relative poses of partial point clouds and the template point clouds are subsequently optimized to obtain a fully registered point cloud of all the partial point clouds. Compared with existing registration algorithms, the MPCR-Net can guarantee the overlap rate between the pairwise point clouds (the partial point cloud can be approximately regarded as a subset of the template point cloud), thus reducing the registration difficulty and error.
MPCR-Net mainly comprises TPCC-Net and TMPE-Net. TPCC-Net uses a deep neural network to extract and merge the features of a partial point cloud and the global template point cloud; it then “cuts out” a correspondence partial template point cloud in the global template point cloud. TMPE-Net merges the features of partial point clouds and the correspondence partial template point clouds, then iteratively learns the optimal rigid body transformation matrix.
As shown in Figure 1, the overall workflow of the MPCR-Net is as follows:
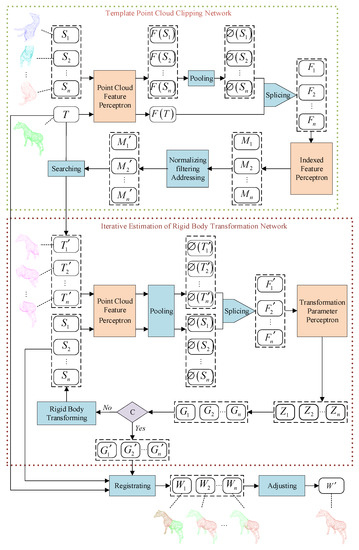
Figure 1.
The network architecture of the MPCR-Net.
- Suppose there are n partial point clouds and a global template point cloud , and are used as the inputs of TPCC-Net. In the TPCC-Net, the feature matrices of and of are obtained through the point cloud feature perceptron, respectively;
- Global feature vectors are obtained by pooling , then the fusion features are obtained by splicing and [42];
- Index features of are obtained through the index feature perceptron, and the indexes are obtained by normalizing, filtering, and addressing . According to , partial template clouds corresponding to respectively are cut out from ;
- Partial template clouds and partial point clouds are input into the TMPE-Net in the form of correspondence point groups . In the TMPE -Net, the global feature vector of is obtained from the point cloud feature perceptron and the pooling layer, and each group of global feature vectors is spliced to obtain the global fusion feature ;
- The dimension of is reduced through the transformation parameter perceptron and output the transformation parameter vectors , and the rigid body transformation matrixes are constructed according to ;
- Rigid body transformations are performed on according to transformation matrices , and the above steps are repeated iteratively to calculate until meet the stop condition C; then, all the iteration results are combined to construct the optimal rigid body transformation matrix ;
- is used to register to , and the ICP algorithm optimizes the registration results to obtain point clouds . are adjusted to the same coordinate system and obtain a fully registered point cloud spliced by . Subsequent 3D reconstruction tasks, such as surface reconstruction, can be performed based on .
3.2. TPCC-Net
3.2.1. Mathematical Formulation
Suppose that the index of a partial template point cloud corresponding to the partial point cloud in the global template point cloud is ; then
where the operator is used to represent the process of estimating in .
The symbol represents the extraction operation of the global features of a point cloud. For example, means to transform point cloud into a K-dimensional global feature vector.
Assuming that can be registered to completely, then and have similar global features of the point cloud, that is:
In Equation (2), and are the rotation and translation matrices used in the registration, respectively. The pose relationship between and is uncertain before registration, that is, the values of and are unknown; therefore, we temporarily ignore the influence of and and use Equation (3) to establish a weaker condition to relate to :
that is,
Equation (4) indicates that the point clouds and input to the TPCC-Net are linked together through the index , and all correspondence points that are similar to the features of can be determined from . We assume that can be calculated by operation ; then:
The search for correspondence points is to learn the index by training the TPCC-Net and then cutting out the correspondence point set of from the global template point cloud according to . We consider estimating by fusing the point cloud features of and .
3.2.2. Network Architecture
TPCC-Net mainly includes a point cloud feature perceptron, pooling layer, and index feature perceptron. The architecture of TPCC-Net is shown in Figure 2.
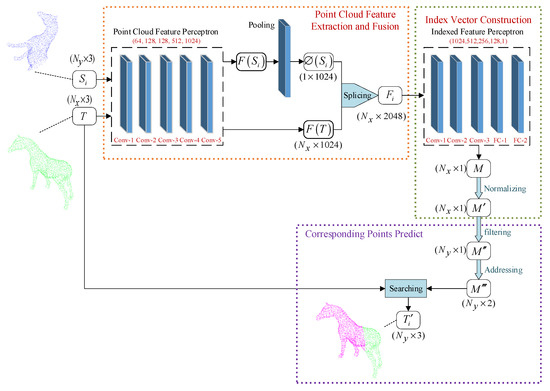
Figure 2.
The network architecture of the TPCC-Net.
The point cloud feature perceptron comprises of five convolutional layers of sizes 3–64, 64–128, 128–128, 128–512, and 512–1024. The main purpose of the point cloud feature perceptron and pooling layer is to generate the feature matrix and global feature vector of two input point clouds. The index feature perceptron consists of three convolutional layers of sizes 2048–1024, 1024–512, and 512–256 and two fully connected layers of sizes 256–128 and 128–1. Its main purpose is to estimate the index vector for correspondence point searching through dimensional transformation.
3.2.3. Working Process
TPCC-Net is divided into three main functional blocks. Taking the correspondence point estimation process of as an example, the working process of TPCC-Net is as follows.
- Extract and fuse point cloud features
- Suppose point clouds and contain and data points, respectively, and . Input and to the point cloud feature perceptron; it consists of five multi-layered perceptrons (MLPs), similar to PointNet. The dimensions of and are both increased to 1024 after the convolution processing of the point cloud feature perceptron. Afterward, generate the feature matrices and of and . Weights are shared between the MLPs used for and .
- Use the max-pooling function to downsample to generate a global feature vector corresponding to .
- Join and to build a point cloud fusion feature .
- Construct the index vector
- Input to the indexed feature perceptron; the dimension of is reduced to one, and the index feature is then output.
- Use the Tanh activation function to normalize to construct the index vector .
- Predict the correspondence points
- Encode all data points in to construct the index .
- Filter out the first elements close to zero from the index vector to form the index element vector .
- Find the address of the above elements in to construct the index .
- , according to each index in ; the elements corresponding to the index in are extracted from the global template point cloud , and all the extracted elements in are combined to construct the estimated correspondence point set of in . The correspondence point estimation process is shown in Figure 3, where the purple part is the correspondence point set .
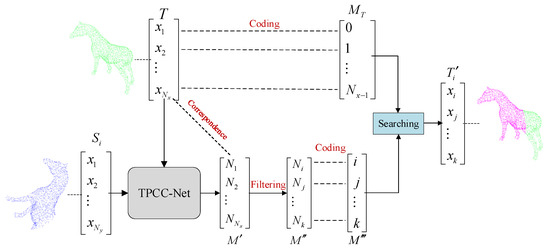 Figure 3. The estimating process of the correspondence points.
Figure 3. The estimating process of the correspondence points.
3.3. TMPE-Net
3.3.1. Mathematical Formulation
Suppose that can be fully registered to through a rigid body transformation; then the global features of the point clouds of and are similar, where is the corresponding point set of that is generated through TPCC-Net. Assuming that the rotation matrix and the translation vector used in the rigid body transformation are and , respectively, then:
Assuming that and can be calculated by operation , then
Similar to PointNetLK [33], in the TMPE-Net, we directly estimate and by fusing the point cloud features of and , and further optimize and by iteration .
3.3.2. Network Architecture
As shown in Figure 4, TMPE-Net mainly includes a point cloud feature perceptron, pooling layer, and transformation parameter perceptron. The architecture of the point cloud feature perceptron is the same as that of TPCC-Net. The architecture of transformation parameter perceptron is also similar to that of TPCC-Net, which consists of three convolutional layers of sizes 2048–1024, 1024–512, and 512–256, and two fully connected layers of sizes 256–128 and 128–7. Its main function is to estimate and .
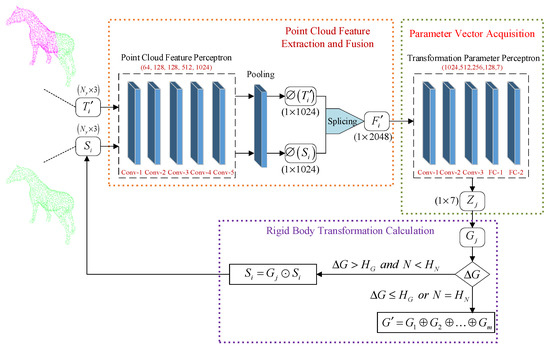
Figure 4.
The network architecture of the TMPE-Net.
3.3.3. Working Process
Taking the rigid body transformation of as an example, TPCC-Net works as follows:
- Extract and fuse the global feature vector of point clouds
- Input and its corresponding point set into point cloud feature perceptron; then, the dimensions of and are both increased to 1024, and the feature matrices and of and are generated. The weights of all convolutional layers in the point cloud feature perceptron are shared for and .
- Use the max-pooling function to downsample and to construct the global feature vectors and that correspond to and , respectively.
- Join and to build a global fusion feature of the point clouds.
- Construct the parameter vector
Input to the transformation parameter perceptron and the dimension of is reduced to seven; then, output the transformation parameter vector .
- 3.
- Estimate the rigid body transformation
In TMPE-Net, we estimate the rigid body transformation matrix through iterative training, and the process is as follows:
Suppose that the rigid body transformation matrix has been iteratively calculated times, and parameter vector can be obtained in the j-th () iteration. Assuming that , we use the first four elements () in to construct the rotation matrix [43]:
We then use the last three elements () in to construct the translation vector :
The rigid body transformation matrix estimated in one iteration is .
Suppose that the input partial point cloud of the j-th iteration is , and is the corresponding estimated rigid body transformation matrix for . Use to perform a rigid body transformation on to form a new partial point cloud , and use to represent the rigid body transformation operation.
Input to TMPE-Net for the (j + 1)-th iteration and output the rigid body transformation matrix . Then, the difference between the results of two consecutive iterations is calculated.
In Equation (11), and are the exponential mapping of and respectively, which refer to the rigid body transformation matrix of two consecutive iterations. represents the sum of squares of all elements of the matrix.
Set the minimum rigid body transformation threshold and the maximum number of iterations , and terminate the iterative training when or the current iteration number . We assume that TMPE-Net performs iteration calculations according to these conditions. Combine the rigid body transformation matrices from each iteration to obtain the final trained rigid body transformation matrix .
If the total number of iterations is , the final estimate can be computed during the iterative loop:
In Equation (12), represents the combined operation of all the iterated rigid body transformation matrices. The iterative estimation process of the rigid body transformation matrix is shown in Figure 5.
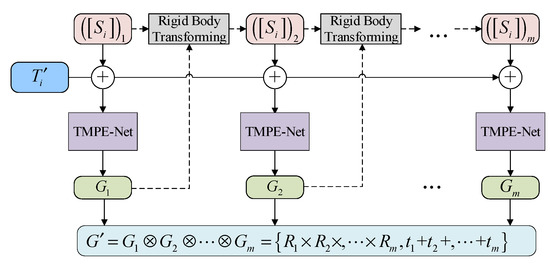
Figure 5.
The iterative estimation of rigid body transformation.
3.4. Loss Function
TPCC-Net uses the loss function to maximize the registration performance (i.e., the total number of correspondence points between the partial point clouds in the global template point cloud). In TMPE-Net, the loss function is the summation of two terms and . The objective of is to minimize the difference between the real rigid body transformation matrix and the estimated rigid body transformation matrix between the partial point clouds and corresponding partial template point clouds. The target of is to minimize the difference between the global feature vectors of the partial template point clouds and partial point clouds .
The mean square error (MSE) [44] is used to express the above loss function as follows:
where represents the MSE between the internal elements calculated; and represent the global feature vectors of the point cloud and , respectively; is the number of correspondence points correctly estimated by the TPCC-Net in the global template point cloud, and is the number of points in the partial point cloud.
3.5. Training
3.5.1. Preprocessing of Training Data
The original data used for training was the ModelNet40 [45] dataset, which contains 12468 CAD models in 40 categories. We randomly designated 20 categories of models as the training set and the other 20 categories of models as the test set. The creation process of a global template point cloud and a partial point cloud is illustrated in Figure 6.
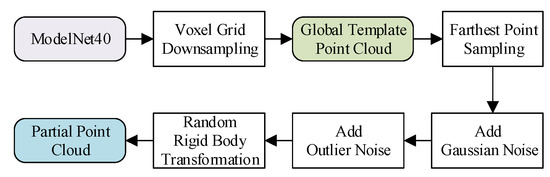
Figure 6.
The creation process of a template point cloud and a partial point cloud.
For each original point cloud in ModelNet40, the global template point cloud was obtained through voxel grid downsampling [46,47], consisting of 1024 data points.
The process of creating a partial point cloud was as follows:
- Each initial partial point cloud contained 568 data points, which were “cut” from a global template point cloud using the farthest point sampling (FPS) [42] algorithm.
- Gaussian noise of 0.0075 level to the initial partial point cloud was added to simulate the deviation of the coordinate value between the scanned data point and the data point in the global template point cloud under noisy conditions.
- 284 outlier noise points were randomly added to the initial partial point cloud to simulate the disturbance of the scanned point cloud structure by environmental noise and sensor error. This increased the structural difference between the initial partial point cloud and the template point cloud.
- A random rigid body transformation matrix was created, through which the initial partial point cloud was subjected to random rotation transformation (±45° around each Cartesian coordinate axis) around the origin of the coordinate and a random translation transformation (±0.5 unit along each Cartesian coordinate axis) to obtain the partial point cloud.
3.5.2. Training Method
TPCC-Net and TMPE-Net were trained using transfer learning [43]. First, TPCC-Net was trained separately to obtain the optimal network model parameter , which means that TPCC-Net using parameter would perform the best on the test set. Then, using the model parameter as the pre-training model of TMPE-Net, the rigid body transformation matrix between the correspondence point set and the partial point cloud was iteratively trained and evaluated in the test set. Finally, the optimal network model parameter of TMPE-Net was obtained.
4. Experiments
4.1. Experimental Environment
The software and hardware specifications used in the experiment are shown in Table 1.

Table 1.
Experimental environment.
4.2. Experiments Based on Untrained Models
We used untrained models in ModelNet40 to carry out correspondence point estimation and registration experiments, and explored the influence of correspondence points estimation accuracy, point cloud registration accuracy, and registration efficiency.
4.2.1. Evaluation Criteria for Experiments
- 1.
- Estimation accuracy
The estimation accuracy of correspondence points refers to the proportion of correspondence points correctly estimated by the algorithm during the experiment to the actual number of correspondence points. Taking MPCR-Net as an example, the estimation process of TPCC-Net is as follows:
Suppose the point clouds input into the network are partial point cloud A and global template point cloud B, and the point number of B is . Encode data points in B and extract the index addresses of all correspondence points of A and B. Input A and B to TPCC-Net to estimate the index address . Count the number of elements that are the same in and , and denote it as . The actual number of correspondence points is equal to ; thus, the estimation accuracy of correspondence points of TPCC-Net is:
- 2.
- Registration error
Rigid body transformation is composed of translation and rotation transformations. The registration error is subdivided into rotation and translation transformation errors. The registration error is calculated as follows:
Suppose the actual rotation angle of the partial point cloud relative to the template point cloud in the three Cartesian coordinate axis directions is , and the actual translation distance is . Input the global template point cloud and the corresponding point set of the partial point cloud in the global template point cloud into TMPE-Net and estimate the parameter vector .
Elements in represent the four parameters for the quaternion rotation matrix. The rotation Euler angles in the three directions corresponding to the parameter vector can be obtained according to the relationship between the quaternion rotation matrix and the Euler angle rotation matrix:
Calculate the mean absolute error between and :
is the rotation transformation error of TMPE-Net.
Elements in represents the translation distance of the partial point cloud relative to the template point cloud in the three directions estimated by TMPE-Net, and the average absolute difference between and is calculated as follows:
is the translation transformation error of TMPE-Net.
- 3.
- Evaluation of work efficiency
We consider the correspondence point search between partial point clouds and the template point cloud as the preparation stage for the point cloud registration, and the total time of the correspondence point estimation and rigid body transformation matrix calculation (registration) is used to measure the efficiency of the point cloud registration.
4.2.2. Correspondence Point Estimation
We used deep learning-based algorithms such as MPCR-Net, PRNet, and RPM-Net, which have correspondence point estimation and point cloud local registration functions, to carry out the correspondence point estimation experiments.
In the experiment, each global template point cloud contained 1024 data points and was sampled from each original point cloud model in the ModelNet40 dataset through the voxel grid downsampling [44,45,46] algorithm. The process of creating a partial point cloud was as follows:
- Using the FPS algorithm, the initial partial point cloud was sampled from the global template point cloud according to a sampling ratio of 0.05 to 0.95; the sampling ratio refers to the ratio of the data volume of the initial partial point cloud to the global template point cloud.
- The initial local point cloud was rotated by 20° around the three Cartesian coordinate axes with the coordinate origin as the center and translated 0.5 units along the three coordinate axes to obtain the local point cloud.
Taking the chair model in the ModelNet40 dataset as an example, its creation process of the global template point cloud, the initial partial point cloud, and the partial point cloud is shown in Figure 7, where the correspondence point estimation experiment was carried out under the condition that the proportion of correspondence points was 0.5. The green part is a global template point cloud that contained 1024 data points, the orange part is the initial partial point cloud that contained 512 data points sampled from the template point cloud at a sampling ratio of 0.5, and the blue part is the partial point cloud obtained after the initial partial point cloud was rotated and translated.
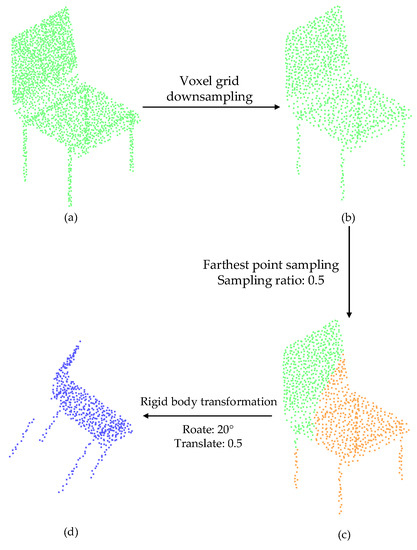
Figure 7.
The creation process of a global template point cloud, initial partial point cloud, and partial point cloud: (a) Chair model in ModelNet40; (b) Global template point cloud; (c) Initial partial point cloud; (d) Partial point cloud.
Taking the chair model as an example, when the proportion of correspondence points was 0.5, the accuracy of estimation of MPCR-Net, PRNet, and RPM-Net algorithms are shown in Figure 8, where green parts are the global template point clouds, and purple parts are the correspondence points estimated by three algorithms, respectively.
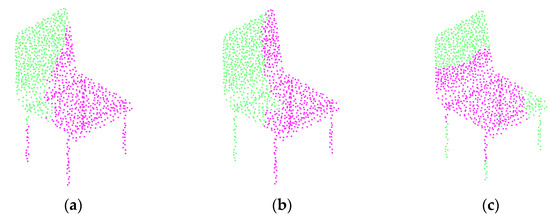
Figure 8.
Accuracy of correspondence point estimation: (a) TPCC-Net, p = 0.90; (b) PRNet, p = 0.51; (c) RPM-Net, p = 0.25.
The distribution of these estimated correspondence points and the initial partial point cloud (Figure 8c) in the global template point cloud were compared. The closer two distributions are, the more correspondence points are correctly estimated, and the higher the estimation accuracy p of the correspondence point estimation.
Under the condition that the proportion of correspondence points was 0.05 to 0.95, estimation experiments were performed on all models in the test set. Then, the average estimation accuracy of the correspondence point of the three algorithms was calculated.
As shown in Figure 9, the average estimation accuracy of the corresponding points of the three algorithms increased as the proportion of correspondence points increased. However, as the proportion of correspondence points decreased, the accuracy gap between PRNet, RPM-Net, and MPCR-Net gradually widened. When the proportion of correspondence points was 0.95, the estimation accuracies of the correspondence points of the PRNet and RPM-Net were 26.0% and 8.0% lower than that of MPCR-Net, respectively, and when the proportion of correspondence points was 0.05, the estimation accuracies of correspondence points of PRNet and RPM-Net were 86.9% and 91.2% lower than that of MPCR-Net, respectively. This indicates that compared to the PRNet and RPM-Net algorithms, the MPCR-Net algorithm proposed in this paper can effectively improve the estimation accuracy of the correspondence point, especially when the proportion of correspondence points is low.
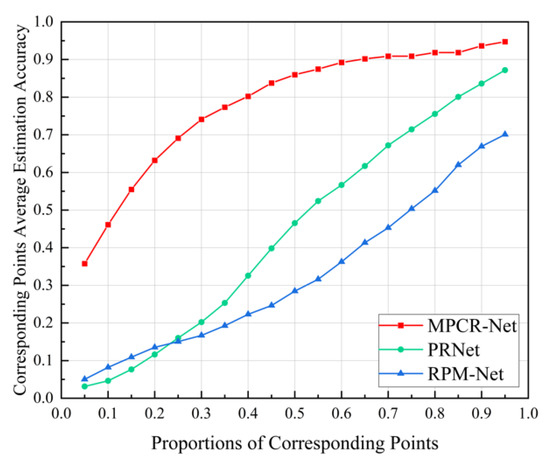
Figure 9.
Average estimation accuracy of correspondence points with different proportions of correspondence points.
4.2.3. Point Cloud Registration
To explore the influence of the proportion of correspondence points on the accuracy of point cloud registration, we used the MPCR-Net, PRNet, and RPM-Net algorithms to perform point cloud registration experiments.
The point cloud registration results of three algorithms on the chair model in the ModelNet40 dataset when the proportion of correspondence points is 0.5 are shown in Figure 10. The green parts are the template point cloud, and the red parts are the positions of the partial point cloud after registration by the three algorithms. and represent the calculation error of the rotation angle and the translation distance of each algorithm, respectively; the smaller the values of and are, the higher is the accuracy of point cloud registration.
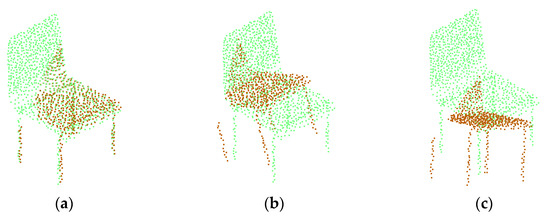
Figure 10.
Effect of registration: (a) TMPE-Net ΔR = 3.7°, Δt = 0.029; (b) PRNet ΔR = 17.5°, Δt = 0.269; (c) RPM-Net ΔR = 21.7°, Δt = 0.328.
Under the condition that the proportion of correspondence points was 0.05 to 0.95, the registration experiment was performed on all models in the test set, and the average registration errors of the three algorithms were calculated. Figure 11a, b show the average calculation error of the rotation angle, and the average calculation error of the translation distance, respectively. The average calculation error of the rotation angle of the MPCR-Net is 23.8–72.8% smaller than that of the PRNet and 27.1–77.6% smaller than that of the RPM-Net. The average calculation error of the translation distance of the MPCR-Net is 27.0–90.9% smaller than that of the PRNet and 30.2–94.3% smaller than that of the RPM-Net. This indicates that the registration accuracy of the MPCR-Net is higher than that of the other two algorithms, especially when the proportion of correspondence points is low.
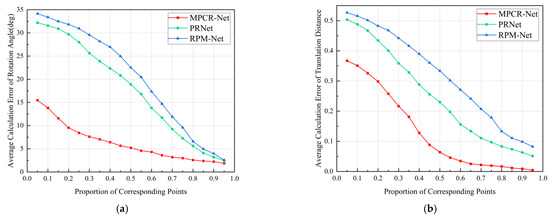
Figure 11.
Average registration error with different proportions of correspondence points: (a) Average calculation error of rotation angle; (b) Average calculation error of translation distance.
Figure 11 shows that average calculation errors of the rotation angle and the translation distance are negatively correlated with the proportion of correspondence points, indicating that the point cloud registration accuracy decreases as the proportion of correspondence points decreases. This is because the coordinate information of the correspondence points directly participates in the calculation of the rigid body transformation matrix in the point cloud registration. Since the average estimation accuracy of the correspondence points of PRNet and RPM-Net is significantly lower than that of MPCR-Net, the average registration accuracy is also lower than that of MPCR-Net.
When the proportion of correspondence points changes from 0.95 to 0.05, the average calculation errors of the rotation angle of the MPCR-Net increase by 13.6°, whereas the calculation errors of PRNet and RPM-Net increase by 29.7° and 31.6°, respectively. Simultaneously, the average calculation error of the translation distance also changes similarly. This indicates that, compared to the PRNet and RPM-Net algorithms, the MPCR-Net algorithm is more robust to changes in the number of correspondence points. When the correspondence point is low, the MPCR-Net algorithm can still maintain a high registration accuracy and effectively register two point clouds with a large difference in the amount of data.
4.2.4. Work Efficiency
As shown in Figure 12, under the condition that the proportion of correspondence points was 0.05 to 0.95, the average values of the total time for estimating the correspondence points and calculating the rigid body transformation matrix using the three algorithms for all models in the test set was recorded. Then, the values were used to measure the efficiency of the point cloud registration of the three algorithms.
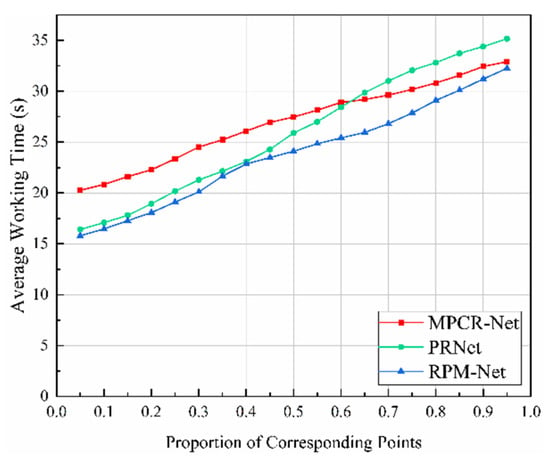
Figure 12.
Average time of MPCR-Net, PRNet, and RPM-Net under different proportions of correspondence points.
Figure 12 shows that as the proportion of correspondence points increases, the average time of each algorithm rises; this is because the number of point cloud data to be processed increases. Furthermore, as the proportion of correspondence points increases, the time-consuming growth rate of the MPCR-Net is slightly lower than that of the PRNet and RPM-Net. This is because the MPCR-Net dynamically adjusts the iterations based on the rigid body transformation matrix difference calculated by two consecutive iterations. As the proportion of correspondence points increases, the iterations required to obtain the optimal rigid body transformation matrix gradually decrease, thereby reducing the time consumption.
4.3. Experiments with Actual Workpieces
We used the MPCR-Net to perform a point cloud registration experiment on actual workpieces and then generated the surface reconstruction models. Then, we evaluated the point cloud registration accuracy by detecting the deviations between surface reconstruction models and actual digital models. Finally, we compared with other point cloud registration algorithms, such as PR-Net and RPM-Net, to verify the effectiveness and advancement of MPCR-Net.
4.3.1. Data Sampling and Processing
Actual workpieces used in the reconstruction experiment were the egg-shaped pressure hulls [47], which were tailor-welded using multiple stainless steel plates with a thickness of 2 mm. All the egg-shaped pressure hulls were numbered a–i sequentially, as shown in Figure 13. The overall dimensions of the egg-shaped pressure hull ‘a’ are: long-axis L = 256 mm and short-axis B = 180 mm; the egg-shaped coefficient S = 0.69. The CAD model and the global template point cloud of the shell ‘a’ are shown in Figure 14.

Figure 13.
Photo of egg-shaped pressure hulls.

Figure 14.
CAD model and global template point cloud of the hull ‘a’: (a) CAD model; (b) Global template point cloud.
As shown in Figure 15, the process of obtaining partial point clouds of the hull ‘a’ is as follows:

Figure 15.
Scanning scene photo of the hull ‘a’ to obtain partial point clouds.
- Paint the surface of the hull; place the painted hull on the rotating table and ensure that the 3D scanner is aligned with the geometric center of the hull.
- Control the rotating table to rotate the hull to a certain angle.
- Use the 3D scanner to scan the hull and obtain its partial point cloud under the initial angle.
- Repeat steps b and c to obtain partial point clouds of the hull at certain angles. The partial point clouds obtained are shown in Figure 16.
 Figure 16. Partial point clouds of the hull ‘a’ at different scanning angles.
Figure 16. Partial point clouds of the hull ‘a’ at different scanning angles.
Compared to the CAD model, the actual digital model includes machining errors. The generation process of the actual digital model of the hull ‘a’ is shown in Figure 17, and the details are as follows:

Figure 17.
Scanning scene photo of the hull ‘a’ and generate the actual digital model: (a) Scanning scene; (b) Actual digital model.
- Paste labels on the surface of the painted hull ‘a’.
- Using scan steps similar to the process of obtaining partial point clouds of the egg-shaped pressure hull, obtain partial point clouds of the hull at angles , respectively.
- In the measurement software Optical RevEng 2.4, which is provided by the 3D scanner manufacturer, use the turntable method and the label method to register point clouds , and use the ICP algorithm to fine-register the registration point clouds.
- Continuously adjust the fine registration point clouds manually according to the measurement results to make the registration point clouds closer to the hull.
- Perform surface reconstruction on the manually adjusted point clouds to obtain the actual digital model (Figure 17b) of hull ‘a’.
4.3.2. Analysis of Registration Accuracy of Multiple Partial Point Clouds
Taking the egg-shaped pressure hull ‘a’ as an example, use MPCR-Net to register all the partial point clouds to the global template point cloud and the ICP algorithm to optimize the registration results. Then generate the full registered point cloud. Figure 18 shows the full registration point cloud (Figure 18a) and its surface reconstruction model (Figure 18b) of hull ‘a’.

Figure 18.
The final 3D reconstruction results: (a) Full registered point cloud; (b) Surface reconscheme 19. Cloud maps of contour deviation of hulls a–i calculated by MPCR-Net.
The above method is used to generate surface reconstruction models of all egg-shaped pressure hulls a–i, and the registration accuracies can be indicated by detecting the surface contour deviation between surface reconstruction models and actual digital models. The contour deviation cloud maps of hulls a–i are shown in Figure 19; the smaller the deviation, the higher the registration accuracy.
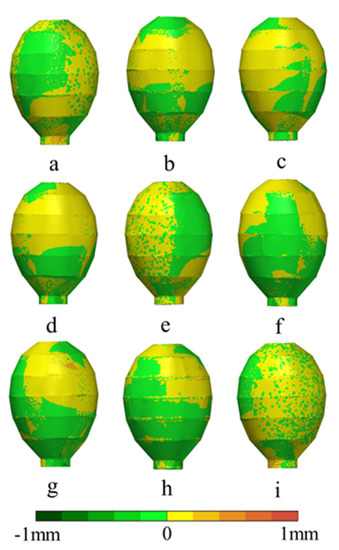
Figure 19.
Cloud maps of contour deviation of hulls a–i calculated by MPCR-Net.
The maximum positive deviation, maximum negative deviation, and the area ratio exceeding the distance tolerance of the surface contour between the surface reconstruction model and the actual digital model are denoted as indicators A, B, and C, respectively.
MPCR-Net, PRNet, and RPM-Net algorithms were used to perform surface reconstruction experiments on all egg-shaped pressure hulls a–i, and indicators A, B, and C were used to evaluate the reconstruction accuracy of three algorithms. The results are presented in Figure 20.
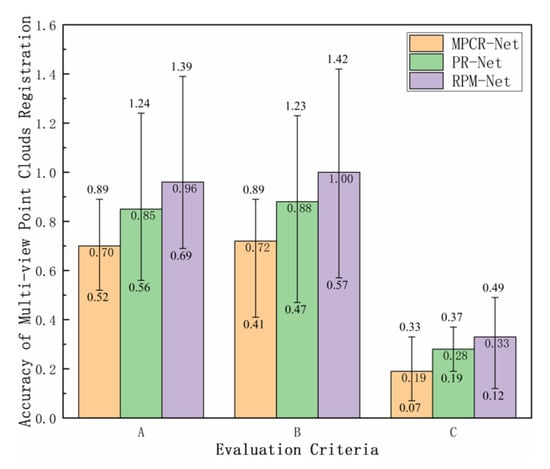
Figure 20.
Registration accuracy of MPCR-Net, PRNet, and RPM-Net on hulls a–i.
As shown in Figure 20, the smaller the values corresponding to indicators A, B, and C are, the higher the registration accuracy is. Each bar represents the average registration accuracy of each algorithm under different indicators for hulls a–i, and each error bar indicates the distribution range of the indicator on hulls a–i.
For indicator A, the average maximum positive deviation of the MPCR-Net was 17.6% smaller than that of PRNet and 27.1% smaller than that of RPM-Net. For indicator B, the average maximum negative deviation of MPCR-Net is 18.2% smaller than that of PRNet and 28.0% smaller than that of RPM-Net. For indicator C, the area ratio exceeding the distance tolerance of MPCR-Net is 32.1% lower than that of PRNet and 42.4% lower than that of RPM-Net. In summary, the performance of MPCR-Net for the accuracy indicators A, B, and C is better than that of PRNet and RPM-Net, indicating that MPCR-Net can provide higher registration accuracy for actual workpieces.
5. Conclusions
We designed a multiple partial point cloud registration network based on deep learning, called the MPCR-Net. MPCR-Net uses the global template point cloud converted from the CAD model of the workpiece to guide the registration of partial point clouds. All partial point clouds are registered to the global template point cloud through TPCC-Net and TMPE-Net in MPCR-Net, forming a fully registered point cloud of a workpiece. This can effectively reduce errors in multiple partial point cloud reconstruction.
Experiment results demonstrated that MPCR-Net has the following advantages:
- Using a global-template-based multiple partial point cloud registration method can fully guarantee the overlap rate between each partial point cloud and its corresponding partial template point cloud, thereby reducing the registration error and improving the point cloud reconstruction accuracy.
- Searching for correspondence points between partial point clouds and the global template point cloud through TPCC-Net does not require separate training for specific local data of point clouds, thereby effectively reducing the correspondence point estimation error.
- The rigid body transformation matrix parameters in the registration are estimated through TMPE-Net, and estimation results are robust to changes in data points. It eliminates the shortcomings of other algorithms that cannot effectively register two point clouds with significant differences in the amount of data.
Author Contributions
Conceptualization, S.S. and H.Y.; Formal analysis, C.W.; Funding acquisition, J.Z.; Investigation, C.W.; Methodology, S.S.; Resources, C.W. and K.C.; Software, C.W.; Supervision, J.Z.; Validation, S.S.; Visualization, K.C.; Writing—original draft, S.S.; Writing—review & editing, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Excellent Youth Foundation of Jiangsu Scientific Committee of China (Grant No. BK20190103) and Jiangsu Government Scholarship for Overseas Studies (Grant No. JS-2018-258).
Data Availability Statement
The study data can be obtained by email request to the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhong, K.; Li, Z.; Zhou, X.; Li, Y.; Shi, Y.; Wang, C. Enhanced phase measurement profilometry for industrial 3D inspection automation. Int. J. Adv. Manuf. Technol. 2015, 76, 1563–1574. [Google Scholar] [CrossRef]
- Han, L.; Cheng, X.; Li, Z.; Zhong, K.; Shi, Y.; Jiang, H. A Robot-Driven 3D Shape Measurement System for Automatic Quality Inspection of Thermal Objects on a Forging Production Line. Sensors 2018, 18, 4368. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, D.; Chen, X.; Yang, Y.-H. Frequency-Based 3D Reconstruction of Transparent and Specular Objects. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 660–667. [Google Scholar]
- Yang, H.; Liu, R.; Kumara, S. Self-organizing network modelling of 3D objects. CIRP Ann. 2020, 69, 409–412. [Google Scholar] [CrossRef]
- Cheng, X.; Li, Z.; Zhong, K.; Shi, Y. An automatic and robust point cloud registration framework based on view-invariant local feature descriptors and transformation consistency verification. Opt. Lasers Eng. 2017, 98, 37–45. [Google Scholar] [CrossRef]
- Pulli, K. Multiview registration for large data sets. In Proceedings of the Second International Conference on 3-D Digital Imaging and Modeling (Cat. no. pr00062), Ottawa, ON, Canada, 8 October 1999; pp. 160–168. [Google Scholar]
- Verdie, Y.; Yi, K.M.; Fua, P.; Lepetit, V. TILDE: A Temporally Invariant Learned DEtector. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Ouellet, J.-N.; Hébert, P. Precise ellipse estimation without contour point extraction. Mach. Vis. Appl. 2008, 21, 59–67. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, Y.; Sun, J. Deep learning based point cloud registration: An overview. Virtual Real. Intell. Hardw. 2020, 2, 222–246. [Google Scholar] [CrossRef]
- Charles, R.Q.; Su, H.; Kaichun, M.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 77–85. [Google Scholar]
- Besl, P.; McKay, N.D. A method for registration of 3-D shapes, Pattern Analysis and Machine Intelligence. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239. [Google Scholar] [CrossRef]
- Chen, Y.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput. 1992, 10, 145–155. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Rusinkiewicz, S. A symmetric objective function for ICP. ACM Trans. Graph. 2019, 38, 1–7. [Google Scholar] [CrossRef]
- Kamencay, P.; Sinko, M.; Hudec, R.; Benco, M.; Radil, R. Improved feature point algorithm for 3D point cloud registration. In Proceedings of the 2019 42nd International Conference on Telecommunications and Signal Processing (TSP), Budapest, Hungary, 1–3 July 2019; pp. 517–520. [Google Scholar]
- Yang, J.; Li, H.; Campbell, D.; Jia, Y. Go-ICP: A Globally Optimal Solution to 3D ICP Point-Set Registration. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2241–2254. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Srivatsan Rangaprasad, A.; Xu, M.; Zevallos-Roberts, N.; Choset, H. Bingham Distribution-Based Linear Filter for Online Pose Estimation. In Proceedings of the Robotics: Science and Systems XIII, Cambridge, MA, USA, 12–16 July 2017. [Google Scholar]
- Eckart, B.; Kim, K.; Kautz, J. Fast and Accurate Point Cloud Registration using Trees of Gaussian Mixtures. arXiv 2018, arXiv:1807.02587. [Google Scholar]
- Jost, T.; Hugli, H. A multi-resolution scheme ICP algorithm for fast shape registration. In Proceedings of the First International Symposium on 3D Data Processing Visualization and Transmission, Padua, Italy, 19–21 June 2002; pp. 540–543. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Chen, C.-S.; Hung, Y.-P.; Cheng, J.-B. A fast automatic method for registration of partially-overlapping range images. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No. 98CH36271), Bombay, India, 7 January 1998; pp. 242–248. [Google Scholar]
- Aiger, D.; Mitra, N.J.; Cohen-Or, D. 4-points congruent sets for robust pairwise surface registration. In ACM SIGGRAPH 2008 Papers, Proceedings of the SIGGRAPH ’08: Special Interest Group on Computer Graphics and Interactive Techniques Conference, Los Angeles, CA, USA, 11–16 August 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 1–10. [Google Scholar]
- Mellado, N.; Aiger, D.; Mitra, N.J. Super 4pcs fast global pointcloud registration via smart indexing. In Computer Graphics Forum; Wiley Online Library: Strasbourg, France, 2014; pp. 205–215. [Google Scholar]
- Rusu, R.B.; Blodow, N.; Beetz, M. Fast point feature histograms (FPFH) for 3D registration. In Proceedings of the 2009 IEEE International Conference on Robotics and Automation, Kobe, Japan, 12–17 May 2009; pp. 3212–3217. [Google Scholar]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing objects in range data using regional point descriptors. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 224–237. [Google Scholar]
- Kurobe, A.; Sekikawa, Y.; Ishikawa, K.; Saito, H. Corsnet: 3d point cloud registration by deep neural network. IEEE Robot. Autom. Lett. 2020, 5, 3960–3966. [Google Scholar] [CrossRef]
- Zeng, A.; Song, S.; Niessner, M.; Fisher, M.; Xiao, J.; Funkhouser, T. 3DMatch: Learning Local Geometric Descriptors from RGB-D Reconstructions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 199–208. [Google Scholar]
- Pais, G.D.; Ramalingam, S.; Govindu, V.M.; Nascimento, J.C.; Chellappa, R.; Miraldo, P. 3DRegNet: A Deep Neural Network for 3D Point Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 7191–7201. [Google Scholar]
- Lu, W.; Wan, G.; Zhou, Y.; Fu, X.; Yuan, P.; Song, S. DeepVCP: An End-to-End Deep Neural Network for Point Cloud Registration. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October 27–2 November 2019; pp. 12–21. [Google Scholar]
- Li, J.; Zhang, C.; Xu, Z.; Zhou, H.; Zhang, C. Iterative distance-aware similarity matrix convolution with mutual-supervised point elimination for efficient point cloud registration. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXIV 16, 2020. pp. 378–394. [Google Scholar]
- Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum PointNets for 3D Object Detection from RGB-D Data. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 918–927. [Google Scholar]
- Yuan, W.; Khot, T.; Held, D.; Mertz, C.; Hebert, M. PCN: Point Completion Network. In Proceedings of the 2018 International Conference on 3D Vision (3DV), Verona, Italy, 5–8 September 2018; pp. 728–737. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & Efficient Point Cloud Registration Using PointNet. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 7156–7165. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, Vancouver, BC, Canada, 24–28 August 1981; pp. 121–130. [Google Scholar]
- Wang, Y.; Solomon, J.M. Deep closest point: Learning representations for point cloud registration. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 3523–3532. [Google Scholar]
- Yuan, W.; Eckart, B.; Kim, K.; Jampani, V.; Fox, D.; Kautz, J. Deepgmr: Learning latent gaussian mixture models for registration. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; pp. 733–750. [Google Scholar]
- Sarode, V.; Li, X.; Goforth, H.; Aoki, Y.; Srivatsan, R.A.; Lucey, S.; Choset, H. PCRNet: Point Cloud Registration Network using PointNet Encoding. arXiv 2019, arXiv:1908.07906. [Google Scholar]
- Wang, Y.; Solomon, J.M. PRNet: Self-Supervised Learning for Partial-to-Partial Registration. arXiv 2019, arXiv:1910.12240. [Google Scholar]
- Yew, Z.J.; Lee, G.H. RPM-Net: Robust Point Matching Using Learned Features. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 11821–11830. [Google Scholar]
- Choy, C.; Dong, W.; Koltun, V. Deep Global Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 14–19 June 2020; pp. 2511–2520. [Google Scholar]
- Gojcic, Z.; Zhou, C.; Wegner, J.D.; Guibas, L.J.; Birdal, T. Learning Multiview 3D Point Cloud Registration. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1756–1766. [Google Scholar]
- Moenning, C.; Dodgson, N.A. Fast Marching Farthest Point Sampling; University of Cambridge, Computer Laboratory: Cambridge, UK, 2003. [Google Scholar]
- Olivas, E.S.; Guerrero, J.D.M.; Sober, M.M.; Benedito, J.R.M.; Lopez, A.J.S. Handbook Of Research On Machine Learning Applications and Trends: Algorithms, Methods and Techniques-2 Volumes; IGI Global: Hershey, PA, USA, 2009. [Google Scholar]
- Orts-Escolano, S.; Morell, V.; Garcia-Rodriguez, J.; Cazorla, M. Point cloud data filtering and downsampling using growing neural gas. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013. [Google Scholar]
- Sanyuan, Z.; Fengxia, L.; Yongmei, L.; Yonghui, R. A New Method for Cloud Data Reduction Using Uniform Grids; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Benhabiles, H.; Aubreton, O.; Barki, H. Fast simplification with sharp feature preserving for 3D point clouds. In Proceedings of the 11th International Symposium on Programming and Systems (ISPS), Algiers, Algeria, 22–24 April 2013. [Google Scholar]
- Zhang, J.; Wang, M.; Wang, W.; Tang, W.; Zhu, Y. Investigation on egg-shaped pressure hulls. Mar. Struct. 2017, 52, 50–66. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).