Abstract
The present paper places emphasis on the most widely used Computational Fluid Dynamics (CFD) approaches, namely the Eulerian and Lagrangian methods each of which is characterized by specific advantages and disadvantages. In particular, a weakly compressible smoothed particle (WCSPH) model, coupled with a sub-particle scale (SPS) approach for turbulent stresses and a new depth-integrated non-hydrostatic finite element model were employed for the simulation of regular breaking waves on a plane slope and solitary waves transformation, breaking and run-up. The validation of the numerical schemes was performed through the comparison between numerical and experimental data. The aim of this study is to compare the two modeling methods with an emphasis on their performance in the simulation of hydraulic engineering problems.
1. Introduction
Nowadays, numerical methods are becoming the main tool used by scientists and researchers to study fluid dynamics problems. Even if experimental investigations provide a lot of reliable data useful to calibrate numerical models, experimentation requires a lot of time to be planned and executed, usually at a high economical cost. Moreover, the results of experimental tests are limited to just a fixed number of points, while computational methods can provide the desired quantities in any point of the computational domain, allowing a better understanding of the physical phenomena under investigation.
The numerical models for the study of a fluid motion could be based on two different approaches, the Eulerian or the Lagrangian method. The main difference between the two methodologies is that while a Eulerian method discretizes space into a fixed grid and finds the unknown variables at the nodal points, the latter discretizes the continuum into a certain number of moving nodes. Moreover, while in a Lagrangian approach the properties of the single fluid particle are studied in accordance with the initial spatial and temporal position, the Eulerian approach represents the distribution of these properties in a domain without referring to the history of the particle’s trajectories. For example, from the experimental point of view, the PIV (Particle Image Velocimetry) technique allows reconstruction of the velocity vectors that occupy an instantaneous velocity field, based on the average particle motion in space [1,2,3]. Instead, from a Lagrangian viewpoint, PTV (Particle Tracking Velocimetry) traces the pathway of an individual particle from a sequence of images in a system. This method is better than PIV for handling non-stationary flow [4].
Eulerian approaches or grid-based methods such as the finite element method (FEM), finite difference method (FDM) and finite volume method (FVM) have been applied to a wide range of engineering applications such as breaking waves [5,6,7], eddies [8], hydraulic jumps [9,10,11,12], sediment transport [13] and current and oil drift modeling [14,15,16,17].
Despite their great success, grid-based methods suffer from some difficulties, in particular for those cases that present discontinuities or whose mesh needs to be modified during run time according to topological changes.
For these reasons, during the last few years, research has been focused on the development of Lagrangian and meshless techniques, such as the discrete element method (DEM) [18], immersed particle method (IPM) [19], smoothed particle hydrodynamics (SPH) [20] and finite volume particle method (FVPM) [21].
Lagrangian methods have been successfully applied in different fields of fluid dynamics, such as free surface flows [22], the breaking and impact of waves [23,24,25,26,27], multiphase flows [28,29], sediment transport [30,31,32], fluid-structure interaction problems [33,34,35], oscillating jets that induce breaking waves [36,37,38,39] and hydraulic jumps [40,41,42,43,44,45,46].
New research challenges in Computational Fluid Dynamics (CFD) are currently evolving; in particular, recently, research has been focused on coupling the Eulerian– Lagrangian techniques to combine the advantages of the individual models in a single model, thus increasing the accuracy, efficiency and regime of validity. For example, the SPH code is also being coupled with the discrete element Method [47] or with the distributed contact discrete element method (DCDEM) [48] for fluid–solid modeling.
The flow is described by the Navier-Stokes Equations and can be solved by using the two main classes of methods: finite element methods and meshfree methods. Both methodologies discretize a partial differential system into a set of algebraic equations that can be easily solved by computer implementation.
To simulate a turbulent flow, the RANS( Reynolds-Averaged Navier–Stokes) modeling approach has been widely employed leading to the Reynolds-averaged N-S, where the instantaneous values of velocity and pressure are defined as the sum of a mean and fluctuating component [49]. The simplest RANS models are the eddy viscosity models (based on the Boussinesq hypothesis) where the Reynolds stresses are modeled using an eddy (or turbulent) viscosity νt. The eddy viscosity can be determined from a turbulent time-scale (or velocity scale) and a turbulent length-scale using the turbulent kinetic energy (k) and the turbulence dissipation rate (ε).
The most commonly-applied turbulence model for its reasonable accuracy to estimate νt for a wide range of flows, is the two-equation k-ε model [50]. The two-equation k-ε model has been utilized in Shao [51,52] and De Padova et al. [53], showing a good comparison between the numerical and experimental turbulent quantities.
Another more recent approach is the Large Eddy Simulation (LES). The main difference between the RANS and LES approaches is that the N-S Equations are, in the former, time-averaged and, in the latter, space filtered.
Within Eulerian methods, the RANS approach is the most widely used, followed by LES due to its lower computational cost. Recently, hybrid RANS-LES methods, such as detached eddy simulation (DES), are growing in popularity [54].
The purpose of this paper is to show the versatility of a grid-based and meshless method to simulate free surface hydrodynamic problems. In Section 2, focus is put on giving the basic concepts of both numerical formulations; in Section 3, as an application, both a weakly compressible smoothed particle (WCSPH) model, coupled with a sub-particle scale (SPS) turbulence model and a non-hydrostatic discontinuous/continuous Galerkin model (non-hydrostatic D/C Galerkin) are used to study the physics of regular and solitary waves propagation, breaking and run-up.
2. Lagrangian and Eulerian Methods
2.1. SPH Formulation
SPH is a Lagrangian meshfree particle method developed by Lucy [55] and Gingold and Monaghan [56]; the reader is referred to [57,58,59,60] for a general description of SPH.
In the present paper, a WCSPH model, coupled with a sub-particle scale (SPS) approach to modeling turbulence [61] has been used. Description of the WCSPH can be found in Monaghan [62] and Gomez-Gasteira et al. [63]. WCSPH has been widely used for many applications such as wave breaking [23,25], dam break flows [64,65], wave generation and absorption [66], hydraulics jumps [42] and the interaction between jets and waves [38]. The alternative approach, developed by Lo and Shao [67,68], is defined as incompressible SPH. The reader can find a comparison between the two algorithms in [69,70,71]. The main difference between the two approaches exists in the way the pressures are calculated: the former explicitly uses an equation of state [23,62], while the latter solves a Poisson pressure equation with a source term as a function of velocity divergence or time variation density.
The motion is represented by the Navier-Stokes Equations for a weakly compressible SPH semi-discrete form:
where is the density, v is the velocity vector, P is the pressure, Γ denotes the dissipation terms and f represents accelerations due to external forces, such as gravity. In the SPH formalism, the discrete form of the continuity equation at a point i can be written as follows [72]:
The summations are extended to all of the particles j at a distance from i smaller than 2h (h defined as the smoothing length), i.e., lying within the circle where the adopted cubic-spline kernel function [60] is defined. The term represents a numerical diffusive term [73], which can be introduced in order to reduce density fluctuation. The general form of a density diffusion term is:
where is the Delta-SPH coefficient, which controls the magnitude of the diffusion term, ci is the numerical speed of sound, Vj is the associated volume of the j-th particle and is the artificial dissipation term; in the present paper, the artificial dissipation term proposed by Molteni and Colagrossi [74] was chosen.
The discrete form of the momentum equation, written in an SPH formalism, can be written as it follows [71]:
The momentum dissipation term Γi is obtained coupling the viscous dissipation in the laminar regime, as approximated by Lo and Shao [68], with a sub-particle scale (SPS) model [71]. The former can be expressed with the following formula:
where 𝜐0 is the kinematic viscosity and is a parameter that guarantees a non-singular operator. In the DualSPHysics solver, is equal to 0.001h2, with .
The SPS contribution to the momentum dissipation can be expressed as follows [71]:
where τ* is the sub-particle scale stress tensor, which can be modelled by an eddy viscosity closure as:
where , = 0.12 is the Smagorinsky constant, = 0.00066, is the initial particle spacing and is the local strain rate. A more detailed description of the LES-SPS model using Favre averaging in a weakly compressible approach can be found in [23].
2.2. Non-Hydrostatic Discontinuous/Continuous Galerkin Model
The Eulerian grid-based method used in this paper is the non-hydrostatic D/C Galerkin, presented in Calvo et. al [7]. The model is a two-dimensional depth-integrated non-hydrostatic model with the capacity of simulating wave propagation, breaking and run-up in a finite element framework.
Eulerian grid-based depth-integrated models using the Boussinesq-type Equations (BTEs) have been traditionally utilized to simulate wave propagation, but the high order partial derivative terms included in BTEs cause numerical instabilities The shallow water models with non-hydrostatic pressure distribution have shown their capacity for accurate modeling of nonlinear and dispersive waves since their introduction by Casulli and Stelling [75] and Stansby and Zhou [76]. The vertical momentum is considered in these models by the introduction of a non-hydrostatic pressure term into the Reynolds-averaged Navier-Stokes Equations. The non-hydrostatic models for water waves are classified as either single-layer models (two-dimensional depth-integrated non-hydrostatic) or multilayer models (three-dimensional non-hydrostatic), depending on the number of layers in the vertical discretization. The capabilities of the non-hydrostatic models for water waves with single or multiple layers in the vertical direction has been researched by Stelling and Zijlema [77]; Zijlema et al. [78]; Zijlema and Stelling [79] and Zijlema et al. [80], among others.
The non-hydrostatic D/C Galerkin model is constructed using a combination of discontinuous and continuous Galerkin methods, where the depth-integrated non-hydrostatic Equations are separated into hydrostatic and non-hydrostatic parts. The hydrostatic part corresponds to the depth-integrated shallow water
Equations and is solved with a discontinuous Galerkin FEM for the simulation of discontinuous flows, wave breaking and run-up. The non-hydrostatic part results in a Poisson-type equation where the non-hydrostatic pressure is resolved by a continuous Galerkin finite element method for the modeling of wave propagation and transformation. The model utilizes linear quadrilateral finite elements for horizontal velocities, water surface elevations and non-hydrostatic pressures that permit local refinement and complex boundaries.
The governing Equations in the conservation form for depth-integrated, non-hydrostatic flow in the Cartesian coordinates system (x, y and z) are:
where , and are the depth-averaged velocity components in the , and z directions; is the water density; is Manning’s roughness coefficient; is the gravitational acceleration. The flow depth is , where is the surface elevation measured from the still water level and is the water depth measured from the still water level. A linear distribution is assumed in the vertical direction for both the non-hydrostatic pressures and for the vertical velocities. The non-hydrostatic pressure on the free surface is assumed as zero and, in the bottom, as . The effects of the turbulence, Coriolis force, atmospheric pressure and baroclinic pressure gradient, are traditionally ignored in the study of non-hydrostatic wave propagation. However, simulation with these effects is possible; see, e.g., Stelling and Busnelli [81]. The average vertical velocity, , is , where is the vertical velocity at the surface and is the vertical velocity at the bottom. The kinematic boundary conditions of the free surface and the bottom are:
with being the components in x and y of the velocities next to the free surface and the bottom, respectively. Due to the linearization of the vertical momentum equation, it is well recognized that the depth-integrated non-hydrostatic models are only appropriate for weakly nonlinear cases [82].
The solution begins by solving the horizontal momentum Equations (8) and (9), without the non-hydrostatic pressure terms, by means of a discontinuous Galerkin method. These horizontal momentum Equations, coupled with the mass conservation Equation (10), can be written in the conservative form of Equation (14).
The vectors of conserved variables , source vector , and flux vectors are given in Equations (15) to (18).
In these Equations, and are discharges per unit width in the and directions and are equal to and , respectively.
The discontinuous Galerkin formulation of the governing Equation (14) is obtained by multiplying it with a shape function and integrate over an element, . The flux term is integrated using Gauss theorem, resulting in Equation (19). In this equation, is the outward unit normal vector at an element boundary .
In the discontinuous Galerkin method, the variable vector is approximated over a quadrilateral element by:
where are nodal values of the variables and are the bilinear approximation functions of the solution variables or shape functions. Since in a discontinuous Galerkin context the discontinuities of variables at the element boundaries are allowed, the intercell flux is taken as being dependent on the values in each of the two adjacent elements. Thus, the normal flux is not exclusively defined and is substituted by a numerical flux where and are the variables at the left (internal) and right (external) sides of the element boundary in the counterclockwise direction, respectively. Consequently, the second integral in Equation (19) is expressed as:
In this analysis, is chosen to be the common Harten-Lax-van Leer (HLL) numerical flux [83]. The first step of the solution process ends with the intermediate estimation of the conserved variables and from Equation (17): .
In the second step of the solution, a Poisson equation is constructed that is then solved by a continuous Galerkin method to obtain the non-hydrostatic pressures . A time approximation of the vertical moment Equation in (11) is:
The vertical velocity at the bottom is valued from the kinematic boundary condition (16), estimated as:
From the remaining part of the horizontal momentum, Equations (8) and (9) including the non-hydrostatic pressure terms:
The final horizontal velocities, influenced by the non-hydrostatic pressure, can be time approximated as
In the continuous Galerkin solution of the non-hydrostatic pressures, the continuous horizontal velocities and , continuous water level and flow depth , vertical velocities and and non-hydrostatic pressures are approximated with nodal variables, which have the same value in all the adjoining elements. The continuous intermediate velocities and are obtained from the intermediate evaluation of the discontinuous discharges integrating over the entire domain .
where the discontinuous intermediate velocities and are approximated in an element using the values of and , respectively, evaluated at the nodes. Similarly, the continuous water level elevations are obtained from:
where . Finally, the continuous flow depth, , is . To obtain a correct solution between the velocity field and the non-hydrostatic pressures, the continuity equation is applied directly to the water column
Substituting Equations (22), (23) and (25) in Equation (28), applying Gauss’s theorem in some terms, and neglecting others, a Poisson equation is established from which the hydrostatic pressure in the bottom, , is obtained.
A continuous Galerkin finite element model to solve the Poisson equation on an element is
After all of the variables in Equation (29) have been approximated, as in Equation (20), and all of the elements of the domain have been assembled, the resulting linear system is solved to obtain the non-hydrostatic pressures, .
In the last step of the solution, once the non-hydrostatic pressures are known, the Equations (27) are solved on an element to obtain the final solutions for the discharges and . A Galerkin finite element model to solve Equation (24) on an element is:
Finally, with the discharges , , , and the flow depth known, the unknown flow depth is determined from the continuity Equation (13) using the discontinuous Galerkin formulation in Equation (19). Details of the entire solution process can be found in Calvo et. al [7]. After each of the three solution steps, a special slope limiter for quadrilateral elements is applied. Details of the developed slope limiter for quadrilateral elements can also be found in Calvo et. al. [7].
3. Applications
A total number of four cases of breaking waves have been simulated in the present study, named T1, T2, T3 and T4, respectively. Among these, there is one case of spilling/plunging breaker (T1), one case of plunging breaker (T2), one case of a solitary wave propagation over a fringing reef (T3) and one case of a solitary wave run-up on a beach of constant slope (T4).
The validity of the numerical schemes described above, has been checked against the experimental observations. In particular, the first two data sets (T1 and T2) were based on experiments by De Serio and Mossa [84]; the third data set was chosen out of the experiments by Roeber [85] and Roeber et al. [86]; the last data set (T4) was chosen out of the experiments by Titov and Synolakis [87].
3.1. Experimental Set Up
3.1.1. Regular Breaking Waves on a Plane Beach
The experiments by De Serio and Mossa [84] were carried out in a wave flume 45 m long and 1 m wide, located at the Department of Civil, Environmental, Land, Building Engineering and Chemistry of the Polytechnic University of Bari, Italy (Figure 1). The flume has an initial flat bottom of 12 m extending from the wave paddle to section 73, while from section 73 up to the shoreline the bottom has a 1/20 slope, obtained with a wooden panel. The wavemaker is a piston-type, whose paddles produce the desired wave by moving the water mass according to a proper input signal. The wave elevations were measured with a resistance probe, while the instantaneous Eulerian velocities were acquired by a backscatter, two-component, four beam Laser Doppler Anemometer (LDA) system and a signal processor (Figure 1).

Figure 1.
Experimental apparatus: (a) a part of the wave channel and (b) the LDA probe.
Table 1 shows the main parameters of the two examined waves, in particular, the offshore wave height H0, the wave period T, the offshore wavelength L0, the Irribarren number ξ0, which has been estimated in section 76, located where the bottom is flat with water depth d equal to 0.70 m. Based on the Irribarren number ξ0, the two regular tested waves were characterized by a spilling/plunging and plunging breakers, respectively.

Table 1.
Experimental parameters of the analysed regular waves.
The sketch of Figure 2 shows the different sections named 76, 55, 49, 48, 47, 45, which have been used to make the comparisons between the simulated and measured free surface elevations.
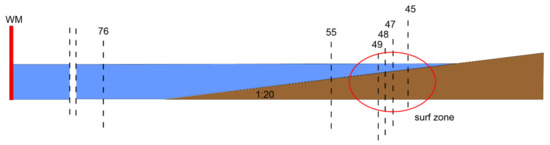
Figure 2.
Sketch of the channel with indications of the investigated sections used to calibrate the numerical model.
3.1.2. Solitary Waves
The experiment by Roeber [85] and Roeber et al. [86] was performed in a wave channel 48.8 m long and 2.16 m wide, equipped with a piston-type wavemaker for solitary wave generation. The test involves a steep solitary wave with a height A = 0.5 m and a water depth of h = 1 m, resulting in A/h = 0.5. The wave was transformed over a fringing reef with a 1:5 slope onto a dry reef flat. Further details on this experimental test can be found in Roeber [85] and Roeber et al. [86].
The experimental study by Titov and Synolakis [87], reproduced a solitary wave run-up with wave height A/h = 0.3 (where A is the solitary wave height and h is the still water depth) on a plane beach with a slope of 1:19.85. The solitary wave had a height A = 1 m with a water depth of 3.33 m, resulting in A/h = 0.3.
3.2. Numerical Parameters
In this section, the parameters used for all four tests (T1-T4) in both numerical approaches have been described.
3.2.1. SPH Parameters
The SPH results discussed here were obtained using the hardware accelerated DualSPHysics code [88]. Since the first release back in 2011, DualSPHysics has been shown to be robust and accurate for simulating free surface flows yet requiring high computational cost.
Therefore, recently, the high-performance computing of SPH has mainly focused on Graphical Processing Units (GPUs) [89], which are superior in terms of price and energy consumption compared to traditional CPUs. On DualSPHysics, the C++ programming language is used to code the SPH formulation for CPU execution, while GPU executions are based on NVIDIA’s CUDA architecture [72]. The specific features of the open-source code are detailed in [72,89].
For the first two tests (T1–T2), following the experimental setting [84], the numerical wave tank was 22.5 m long and 0.97 m high, while the initial water depth was equal to 0.70 m. In De Padova et al., [27] the convergence analysis for T1 showed that only d/Δx ≥ 35 (Δx≤ 0.02 m) guaranteed the independence of the SPH result from the resolution and yielded a result in accordance with the experiments. However, in this study, simulations were performed by choosing a higher resolution than shown by De Padova et al. [25,27], in order to show the efficient and reliable use of DualSPHysics code executed on a GPU architecture also with a large number of particles. In particular, the 2D flow (T1 and T2) was simulated by discretizing the computational domain through a particle distribution with initial particle distance Δx =Δz varying from to 0.02 to 0.003 m. Figure 3 shows that d/Δx ≥ 35 (Δx≤ 0.02 m) guaranteed the independence of the SPH result from the resolution. This again confirms the results by [27]. Following, the results and performance analysis for T1 and T2 were carried out considering an initial particle distance Δx = Δz = 0.01 m.
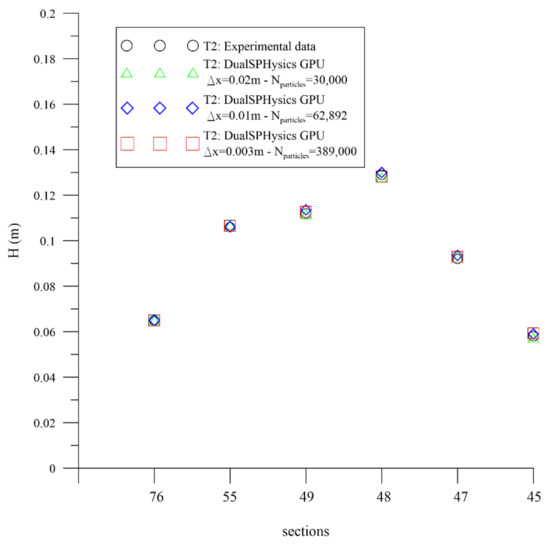
Figure 3.
Effect of the initial particle resolution Σ on the SPH numerical simulation of test T2.
In all four tests T1-T4, the solid boundary conditions needed for idealizing the seabed, are discretized by a set of boundary particles that differ from the fluid particles. When a fluid particle approaches the boundary, the density, and hence the pressure exerted by the boundary particles, increase. This generates the necessary repulsive force on the water particles.
Instead, the offshore boundary condition is treated as a dynamic boundary condition [90], i.e., the numerical wave paddle is composed of wall particles whose density is computed with the continuity equation and pressure obtained from the equation of state [72]. For both of the regular waves’ tests, the first order numerical wavemaker is located at a distance of 0.5 m offshore on the side of section 76.
For the third test (T3), following the experimental setting by (Roeber [85] and Roeber et al. [86]), the numerical flume was 45 m long, with an initial water depth of 1 m. The fringing reef, whose slope was 1/5, was 5.1 m long and its toe was at a distance of 17 m from the numerical wavemaker. The latter generated the solitary wave according to the Rayleigh solitary wave generation theory; in this case, an initial particle distance of Δx = Δz = 0.02 m with a total number of particles equal to 50,242.
In the last test (T4), following the experimental setting by Titov and Synolakis [87], the numerical wave tank was 154.83 m long, with an initial water depth of 3.33 m. The toe of the inclined beach was at 34.83 m from the piston, which was of the same type as that described for the third case. The initial particle distance was Δx = Δz = 0.025 m, resulting in a total number of 369,885 particles.
For all of the cases, the initial conditions are described by setting the velocities of all the particles of the computational domain u = 0 at time t = 0. Moreover, the pressure distribution is assumed to be hydrostatic at the beginning of the computation. In the SPH computations, the free surface is easily and accurately tracked by the particles. To simplify, a pressure equal to zero is given to each of the surface particles.
According to De Padova et al. [25], the ratio of the smoothing length h to the initial particle spacing Δx was maintained to a constant value of h/Δx = 1.5 for all four simulations (T1-T4). Table 2 shows the main characteristics of the SPH simulations.

Table 2.
Main characteristics of the SPH simulations.
3.2.2. Eulerian Model Parameters
Among the most important parameters in the simulation of wave propagation, breaking and run-up using the non-hydrostatic D/C Galerkin model are the breaking waves parameters. Wave overturning and small-scale processes related to wave breaking cannot be reproduced in depth-averaged models, consequently some kind of closure is required. Usually, this closure involves two steps. The first is a trigger mechanism to locate in space and time the limits of breaking. The second is a mechanism that generates the dissipation of energy in the model.
The dissipation of energy is accomplished by shifting locally to the depth-integrated hydrostatic shallow water Equations, modeling breaking wave fronts as shocks. This procedure was firstly presented by Smit et al. [91] as the hydrostatic front approximation (HFA) method for the modeling of wave breaking.
For the trigger mechanism of wave breaking, two different criteria are used. The first criterion is used for solitary waves and establish that wave breaking occurs when [92,93,94]. This criterion is referred to as the local criterion in Bacigaluppi et al. [95]. All of the elements containing a node with the wave breaking condition are shifted to the hydrostatic mode by making , and = = in the element.
The second criterion is used for regular waves and was first introduced by Kazolea et al. (2014) [96] as the surface variation criterion. A node is flagged if , with ∈ [0.3, 0.65] depending on the type of breaker. Flagged nodes are clustered to form a breaking region. All of the elements containing a flagged node are shifted in the element to hydrostatic mode by making , and = = . More details regarding the implementation of this detection criterion can be found in Bacigaluppi et al. (2019) [95].
The boundaries conditions in all tests are: at wall boundaries the gradients of water elevations and the velocities normal to the boundary are set to zero; at open boundaries, the water elevations are determined by a Sommerfeld radiation condition; at wave inflow boundaries, the water elevations and velocities are calculated with the corresponding inflow wave analytical formula; no boundary conditions are required for the non-hydrostatic pressure.
In the simulation of tests T1 and T2, the experiments of De Serio and Mossa [84] were replicated with a numerical domain of 32 m long and 0.24 m wide and the initial water depth was 0.70 m. Square elements with sizes Δx = Δy = 0.04 m were considered, resulting in 5607 nodes. The surface variation criterion was used as the trigger mechanism of wave breaking. The parameter Ɣ was chosen to replicate the waves before and after the breaking zone (consequently trying to match the total energy dissipation of wave breaking with the HFA method).
In test T3, we analyzed the tests of Roeber [85] and Roeber et al. [86] with a numerical domain of 45 m long and 0.2 m wide and a water depth of 1 m. Square elements with ∆x = ∆y = 0.05 m were used, leading to 4505 nodes. A Manning coefficient of n = 0.01 was established to represent the finished concrete surface of the reef model. The local criterion was utilized as the trigger mechanism of wave breaking.
Finally, in test T4, the experimental setting of Titov and Synolakis [87] was reproduced in a numerical domain of 220 m long and 2.4 m wide and a water depth of 3.33 m. Square elements with sizes Δx = Δy = 0.4 m were considered, resulting in 3857 nodes. A Manning coefficient n = 0.01 was used to define the bed surface roughness. The local criterion was used to activate wave breaking. Table 3 shows the main characteristics of the non-hydrostatic D/C Galerkin simulations.

Table 3.
Main characteristics of the non-hydrostatic D/C Galerkin simulations.
4. Results and Performance Analysis
The efficiency and performance of both numerical approaches have been analysed in this section. The numerical results have been compared with laboratory experiments by De Serio and Mossa [84] in T1 and T2, by Roeber [85] and Roeber et al. [86] in T3 and Titov and Synolakis [87] in T4.
4.1. Spilling/Plunging and Plunging Breaking Waves on a Plane Beach
Both numerical approaches reproduce the breaking waves quantitatively well in both tests (T1 and T2). In fact, in the horizontal direction of the surf zone, the following zones can be distinguished [97]. Initial wave deformation occurs in what has been termed the shoaling zone (section 76–49), where wave profile is characterized by a rapid change in shape. Subsequently, the wave reaches the breaking point in the outer zone (section 48–47) originating an overturning jet whose strength depends on the type of breaker. In the inner surf zone (section 45), the wave undergoes a gradual transformation into a turbulent bore, until reaching the swash zone. Figure 4a,b show the snapshot of the free surface for both the cases of a spilling/plunging (T1) and a plunging breaking wave (T2).
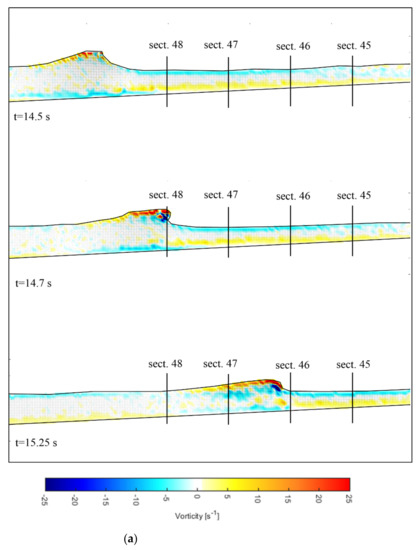
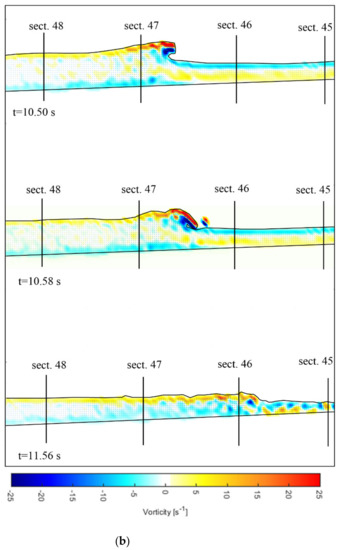
Figure 4.
DualSPHysics model: Snapshots of free surface and vorticity field for (a) spilling/plunging breaking wave (T1) and (b) plunging breaking wave (T2).
As an example, in Figure 5a,b, both laboratory and numerical wave surface elevations, at vertical sections 49, 48 and 45, have been plotted for T1 and T2.
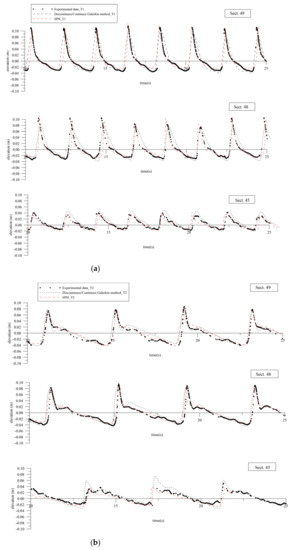
Figure 5.
Computed and measured surface elevation for (a) spilling/plunging breaking wave (T1) and (b) plunging breaking wave (T2).
Table 4 shows the statistical analysis of the comparison between the two numerical models with the experimental results in terms of the index proposed by Wilmott [98].
where Xc and Xm are the modeled and measured values, respectively, while the bar denotes the average of the modeled and measured values. It takes into account the relative error among experimental and output values, and it will exhibit values closer to one for higher levels of accordance.

Table 4.
Statistical analysis of the comparison of the free surface for T1 and T2.
Both codes have been shown to be robust, efficient and reliable and a good agreement has been observed for all sections for the wave elevations. However, in the shallow waters (sections 49–48), the computed Galerkin method results appear to slightly underpredict the wave crest and slightly overestimate the experimental values in the trough. After the breaking wave (section 45), a slight overestimate of the crest data is observed for the Galerkin method in T1 and T2. The statistical parameter in Table 4 confirms these conclusions.
Furthermore, skewness [99], a measure of crest-trough shape, has been computed and shown in Figure 6a,b for both tests (T1–T2). The trend of wave skewness increases as the wave shoals and breaks (sections 48–49) and decreases near the shoreline (sections 47–45). Indeed, for both experimental and computed data, the trend generally becomes more pronounced as the water depth decreases, with higher crests and shallower troughs evident. However, the SPH model shows better results than the Galerkin model in terms of the wave shape. The reason for the underestimation of the breaking waves in the Galerkin model is that the HFA method requires high vertical resolution for capturing the hydrostatic shock of the series of regular breaking waves; high vertical resolution that is obviously not present in depth-averaged models. Smit et al. [91] indicated that a multilayer version of a non-hydrostatic shallow water model would require at least 20 layers to obtain a correct solution of wave height using the HFA method. Similar underestimations are observed in other works using the HFA method in depth-averaged models for the simulation of a breaking wave series [79,95,100,101].
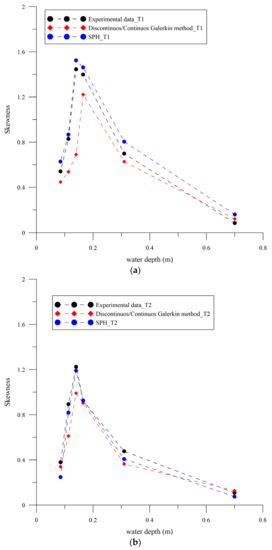
Figure 6.
Comparison of experimental and numerical skewness of surface wave elevation for: (a) spilling/plunging breaking wave (T1) and (b) plunging breaking wave (T2).
4.2. Solitary Waves Propagation
Both numerical approaches reproduce the principal processes well in both two tests (T3 and T4); in fact, in test T3, as shown by Roeber (2010) [85] and Roeber et al. (2010) [86], the wave evolves from subcritical flow to supercritical flow over the reef edge at x = 22 m, collapses at x = 23 m, and, subsequently, rushes over the initially dry reef flat (Figure 7).
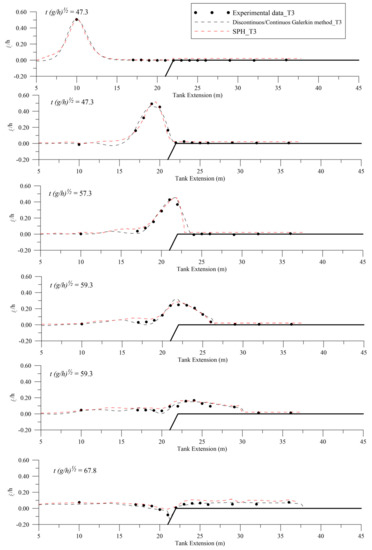
Figure 7.
Comparison of experimental and numerical surface profiles of a solitary wave over a fringing reef (T3).
Additionally, in T4, both of the numerical approaches reproduce the wave breaking and run-up processes well. In fact, both of the numerical results confirm the experimental findings by Titov and Synolakis [87]; in fact, the breaking of waves occurs between t(g/h)½ = 20 and 25 and the maximum run-up was observed at t(g/h)½ = 45 (Figure 8).
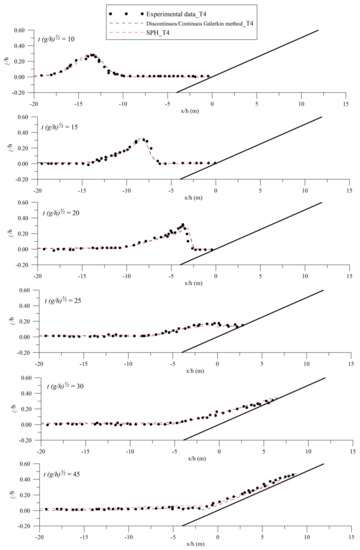
Figure 8.
Comparison of experimental and numerical surface profiles of a solitary wave run-up on a plane beach (T4).
4.3. Performance Analysis
Both codes have been shown to be robust, efficient and reliable in simulating the analysed phenomena. However, in terms of computing cost, the Eulerian method was faster than the Lagrangian method. In fact, tracking sufficient number of particles and analyzing them in the Lagrangian approach required more time than the Eulerian iterations.
With the large numbers of neighboring particle interactions and the time step restricted by the Courant condition for weakly compressible flow, SPH is computationally demanding.
However, in this work the power computing of GPUs was used to accelerate DualSPHysics when compared with the performance achieved using a classic version of SPHysics code [25].
This important acceleration of the code using the new GPU technology can be observed in Figure 9 where the runtime of the hardware accelerated DualSPHysics code is shown by comparing its performance against the classic version of SPHysics code using a single core. In particular, in De Padova et al. [25], the open-source code SPHysics [23], was executed up to t=25s from the beginning for test T1 and T2 and it cost about 40 h of CPU time using a personal computer (CPU 2.66 GHz and RAM 4.0 GMB PC). An initial particle distance of Δx = Δz 0.022 m was chosen for these two tests, resulting in a total number of 30,000 particles.
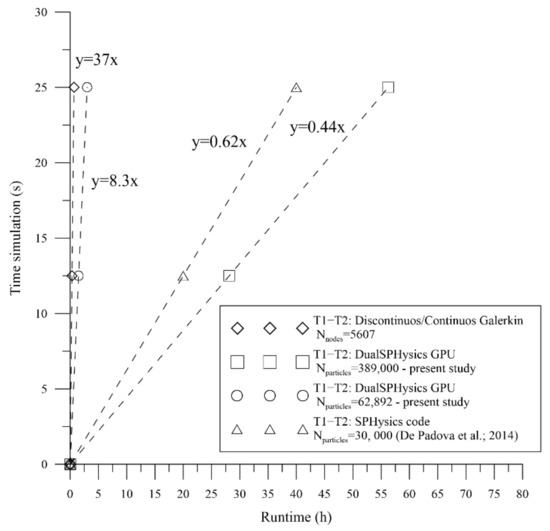
Figure 9.
Comparison of runtime in T1 and T2.
In this study, with an initial particle distance of Δx = Δz = 0.01 m and a total number of 62,892 particles, the hardware accelerated smoothed particle hydrodynamics code DualSPHysics was executed up to t = 100 s from the beginning and cost about 12 h of CPU time using a personal computer (CPU 2.70 GHz and RAM 384 GB PC, equipped with a NVIDIA Quadro K2000 GPU). Furthermore, with an initial particle distance of Δx = Δz 0.003 m and a total number of 389,000 particles, the hardware accelerated smoothed particle hydrodynamics code DualSPHysics was executed up to t = 100 s from the beginning and cost about 225 h of CPU time using a personal computer (CPU 2.70 GHz and RAM 384 GB PC, equipped with a NVIDIA Quadro K2000 GPU).
Instead, the discontinuous Galerkin FEM was executed up to t = 100 s from the beginning and cost about 9.75 h of CPU time using a personal computer (CPU 2.66 GHz and RAM 4.0 GMB PC). Square elements with sizes Δx = Δy = 0.04 m were chosen for these two tests, resulting in a total number of 5607 nodes.
5. Conclusions
The most widely used CFD approaches, namely the Eulerian and Lagrangian methods, are characterized by specific advantages and disadvantages. The most relevant advantages of Lagrangian approaches over Eulerian methods are the exact conservation of mass and momentum and the meshless properties. Moreover, the Lagrangian method gives detailed information of individual particles that can be crucial in many applications. In terms of computing cost, the Eulerian method was faster than the Lagrangian method. In fact, tracking a sufficient number of particles and analyzing them in the Lagrangian approach required more time than the Eulerian iterations.
New research challenges on Computational Fluid Dynamics (CFD) are constantly on-going; in particular, recently, research has focused on coupling the Eulerian–Lagrangian techniques to combine the advantages of the individual models in a single model, thus increasing the accuracy, efficiency and regime of validity.
The present study dealt with the comparison of the Lagrangian and Eulerian approaches in the simulation of regular breaking waves on a plane slope and solitary waves transformation, breaking and run-up. The performance of the numerical models was evaluated in accordance with experimental data.
Both Eulerian and Lagrangian approaches were capable of simulating the analysed phenomena. However, the Lagrangian method showed more accuracy to reproduce the wave shape, both in deep waters and shoaling zones right up to the breaking region. Eulerian models cannot reproduce wave overturning exactly (e.g., only one water surface elevation value is permitted). Additionally, when using the HFA method in the case of regular waves, a high vertical resolution multilayer model is required to capture the hydrostatic shock of a breaking wave [91].
For the tests T3–T4, the numerical results demonstrated that the Eulerian and Lagrangian methods have similar accuracy on predicting the solitary wave transformation, breaking and run-up processes.
In this study, the hardware accelerated DualSPHysics code on a GPU was used; the new DualSPHysics code is a user-friendly platform designed to encourage researchers to use the SPH technique to investigate novel and real CFD problems that are beyond the scope of classical models. In recent years, DualSPHysics code has been shown to be accurate for simulating coastal engineering problems, with a continuous improvement in efficiency thanks to the exploitation of hardware such as GPUs for scientific computing.
In this study, this important acceleration of the code using the new GPU technology has been observed by comparing its performance against the classic version of SPHysics code using a single core.
Author Contributions
D.D.P., L.C., P.M.C. performed the numerical modeling and analysed the results; M.M. conceived and coordinated the experiments; D.D.P. wrote the manuscript; L.C., P.M.C., M.M. and D.M. discussed and revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
Lucas Calvo participated in this research thanks to the support of the Sistema Nacional de Investigación (SNI), of Secretaría Nacional de Ciencia, Tecnología e Innovación (SENACYT), Panamá.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no competing interests.
References
- Chang, K.A.; Liu, P.L.F. Measurement of Breaking Waves Using Particle Image Velocimetry. In Proceedings of the Coastal Engineering 1996, Orlando, FL, USA, 2–6 September 1996; American Society of Civil Engineers: Orlando, FL, USA, 5 August 1997; pp. 527–536. [Google Scholar]
- Umeyama, M. Eulerian–Lagrangian Analysis for Particle Velocities and Trajectories in a Pure Wave Motion Using Particle Image Velocimetry. Philos. Trans. R. Soc. A. 2012, 370, 1687–1702. [Google Scholar] [CrossRef]
- Maraglino, D.; Ben Meftah, M.; De Serio, F.; Mossa, M. Field Measurements in a Flow around a Hydrofoil: Some Preliminary Results. In Proceedings of the 2019 IMEKO TC19 International Workshop on Metrology for the Sea, Genova, Italy, 3–5 October 2019; pp. 270–275. [Google Scholar]
- Umeyama, M. Coupled PIV and PTV Measurements of Particle Velocities and Trajectories for Surface Waves Following a Steady Current. J. Waterw. Port Coast. Ocean Eng. 2011, 137, 85–94. [Google Scholar] [CrossRef]
- Lemos, C.M. Wave Breaking: A Numerical Study; Lecture Notes in Engineering; Springer: Berlin, Germany; New York, NY, USA, 1992; ISBN 9783540549420. [Google Scholar]
- Lin, P.; Liu, P.L.-F. A Numerical Study of Breaking Waves in the Surf Zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Calvo, L.; De Padova, D.; Mossa, M.; Rosman, P. Non-Hydrostatic Discontinuous/Continuous Galerkin Model for Wave Propagation, Breaking and Runup. Computation 2021, 9, 47. [Google Scholar] [CrossRef]
- Danilov, S.; Wang, Q. Resolving Eddies by Local Mesh Refinement. Ocean Model. 2015, 93, 75–83. [Google Scholar] [CrossRef] [Green Version]
- Viti, N.; Valero, D.; Gualtieri, C. Numerical Simulation of Hydraulic Jumps. Part 2: Recent Results and Future Outlook. Water 2018, 11, 28. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Oberai, A.A.; Lahey, R.T.; Drew, D.A. Modeling Air Entrainment and Transport in a Hydraulic Jump Using Two-Fluid RANS and DES Turbulence Models. Heat Mass Transf. 2011, 47, 911–919. [Google Scholar] [CrossRef]
- Witt, A.; Gulliver, J.; Shen, L. Simulating Air Entrainment and Vortex Dynamics in a Hydraulic Jump. Int. J. Multiph. Flow 2015, 72, 165–180. [Google Scholar] [CrossRef] [Green Version]
- Bayon, A.; Valero, D.; García-Bartual, R.; Vallés-Morán, F.J.; López-Jiménez, P.A. Performance Assessment of OpenFOAM and FLOW-3D in the Numerical Modeling of a Low Reynolds Number Hydraulic Jump. Environ. Model. Softw. 2016, 80, 322–335. [Google Scholar] [CrossRef]
- De Padova, D.; Ben Meftah, M.; De Serio, F.; Mossa, M. Management of Dredging Activities in a Highly Vulnerable Site: Simulation Modelling and Monitoring Activity. JMSE 2020, 8, 1020. [Google Scholar] [CrossRef]
- De Padova, D.; De Serio, F.; Mossa, M.; Armenio, E. Investigation of the current circulation offshore Taranto by using field measurements and numerical model. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference, 1–5 (IEEE, 2017), Torino, Italy, 22–25 May 2017. [Google Scholar] [CrossRef]
- Kostianoy, A.G.; Bulycheva, E.V. Numerical Simulation of Risks of Oil Pollution in the Southeastern Baltic Sea and in the Gulf of Finland. Mod. Probl. Remote Sens. Earth Space 2014, 11, 56–75. [Google Scholar]
- De Padova, D.; Mossa, M.; Adamo, M.; De Carolis, G.; Pasquariello, G. Synergistic Use of an Oil Drift Model and Remote Sensing Observations for Oil Spill Monitoring. Environ. Sci. Pollut. Res. 2017, 24, 5530–5543. [Google Scholar] [CrossRef]
- Armenio, E.; Meftah, M.B.; De Padova, D.D.; Serio, F.D.; Mossa, M. Monitoring Systems and Numerical Models to Study Coastal Sites. Sensors 2019, 19, 1552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fleissner, F.; Gaugele, T.; Eberhard, P. Applications of the Discrete Element Method in Mechanical Engineering. Multibody Syst. Dyn. 2007, 18, 81–94. [Google Scholar] [CrossRef]
- Rabczuk, T.; Gracie, R.; Song, J.-H.; Belytschko, T. Immersed Particle Method for Fluid-Structure Interaction: Particle method for fluid-structure interaction. Int. J. Numer. Meth. Eng. 2010, 81, 48–71. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed Particle Hydrodynamics (SPH): An Overview and Recent Developments. Arch. Comput. Methods Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef] [Green Version]
- Aubry, R.; Idelsohn, S.R.; Oñate, E. Particle Finite Element Method in Fluid-Mechanics Including Thermal Convection-Diffusion. Comput. Struct. 2005, 83, 1459–1475. [Google Scholar] [CrossRef]
- Oñate, E.; Idelsohn, S.R.; Celigueta, M.A.; Rossi, R. Advances in the Particle Finite Element Method for the Analysis of Fluid–Multibody Interaction and Bed Erosion in Free Surface Flows. Comput. Methods Appl. Mech. Eng. 2008, 197, 1777–1800. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Rogers, B.D. Numerical Modeling of Water Waves with the SPH Method. Coast. Eng. 2006, 53, 141–147. [Google Scholar] [CrossRef]
- Makris, C.V.; Memos, C.D.; Krestenitis, Y.N. Numerical Modeling of Surf Zone Dynamics under Weakly Plunging Breakers with SPH Method. Ocean Model. 2016, 98, 12–35. [Google Scholar] [CrossRef]
- De Padova, D.; Dalrymple, R.A.; Mossa, M. Analysis of the Artificial Viscosity in the Smoothed Particle Hydrodynamics Modelling of Regular Waves. J. Hydraul. Res. 2014, 52, 836–848. [Google Scholar] [CrossRef]
- De Padova, D.; Brocchini, M.; Buriani, F.; Corvaro, S.; De Serio, F.; Mossa, M.; Sibilla, S. Experimental and Numerical Investigation of Pre-Breaking and Breaking Vorticity within a Plunging Breaker. Water 2018, 10, 387. [Google Scholar] [CrossRef] [Green Version]
- Canelas, R.; Ferreira, R.M.L.; Domínguez, J.M.; Crespo, A.J.C. Modelling of Wave Impacts on 886 Harbour Structures and Objects with SPH and DEM. In Proceedings of the 9th SPHERIC 887 International Workshop, CNAM, Paris, France, 3–5 June 2014. [Google Scholar]
- Mokos, A.; Rogers, B.D.; Stansby, P.K.; Domínguez, J.M. Multi-Phase SPH Modelling of Violent Hydrodynamics on GPUs. Comput. Phys. Commun. 2015, 196, 304–316. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M. Multi-Phase Simulation of Infected Respiratory Cloud Transmission in Air. AIP Adv. 2021, 11, 035035. [Google Scholar] [CrossRef]
- Manenti, S.; Sibilla, S.; Gallati, M.; Agate, G.; Guandalini, R. SPH Simulation of Sediment Flushing Induced by a Rapid Water Flow. J. Hydraul. Eng. 2012, 138, 272–284. [Google Scholar] [CrossRef]
- Ulrich, C.; Leonardi, M.; Rung, T. Multi-Physics SPH Simulation of Complex Marine-Engineering Hydrodynamic Problems. Ocean Eng. 2013, 64, 109–121. [Google Scholar] [CrossRef]
- Fourtakas, G.; Rogers, B.D. Modelling Multi-Phase Liquid-Sediment Scour and Resuspension Induced by Rapid Flows Using Smoothed Particle Hydrodynamics (SPH) Accelerated with a Graphics Processing Unit (GPU). Adv. Water Resour. 2016, 92, 186–199. [Google Scholar] [CrossRef]
- Hwang, S.-C.; Khayyer, A.; Gotoh, H.; Park, J.-C. Development of a Fully Lagrangian MPS-Based Coupled Method for Simulation of Fluid–Structure Interaction Problems. J. Fluids Struct. 2014, 50, 497–511. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH Numerical Investigation of the Velocity Field and Vorticity Generation within a Hydrofoil-Induced Spilling Breaker. Environ. Fluid Mech. 2016, 16, 267–287. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M. Modelling Fluid–Structure Interactions: A Survey of Methods and Experimental Verification. Proc. Inst. Civ. Eng.-Eng. Comput. Mech. 2020, 173, 159–172. [Google Scholar] [CrossRef]
- Espa, P.; Sibilla, S.; Gallati, M. SPH Simulations of a Vertical 2-D Liquid Jet Introduced from the Bottom of a Free Surface Rectangular Tank. Adv. Appl. Fluid Mech. 2008. undefined. [Google Scholar]
- De Padova, D.; Mossa, M.; Sibilla, S. Characteristics of Nonbuoyant Jets in a Wave Environment Investigated Numerically by SPH. Environ. Fluid Mech. 2020, 20, 189–202. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. Numerical Investigation of the Behaviour of Jets in a Wave Environment. J. Hydraul. Res. 2020, 58, 618–627. [Google Scholar] [CrossRef]
- Barile, S.; De Padova, D.; Mossa, M.; Sibilla, S. Theoretical Analysis and Numerical Simulations of Turbulent Jets in a Wave Environment. Phys. Fluids 2020, 32, 035105. [Google Scholar] [CrossRef]
- López, D.; Marivela, R.; Garrote, L. Smoothed Particle Hydrodynamics Model Applied to Hydraulic Structures: A Hydraulic Jump Test Case. J. Hydraul. Res. 2010, 48, 142–158. [Google Scholar] [CrossRef]
- Federico, I.; Marrone, S.; Colagrossi, A.; Aristodemo, F.; Antuono, M. Simulating 2D Open-Channel Flows through an SPH Model. Eur. J. Mech.-B/Fluids 2012, 34, 35–46. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S.; Torti, E. 3D SPH Modelling of Hydraulic Jump in a Very Large Channel. J. Hydraul. Res. 2013, 51, 158–173. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH Modelling of Hydraulic Jump Oscillations at an Abrupt Drop. Water 2017, 9, 790. [Google Scholar] [CrossRef] [Green Version]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH Numerical Investigation of the Characteristics of an Oscillating Hydraulic Jump at an Abrupt Drop. J. Hydrodyn. 2018, 30, 106–113. [Google Scholar] [CrossRef]
- De Padova, D.; Mossa, M.; Sibilla, S. SPH Numerical Investigation of Characteristics of Hydraulic Jumps. Environ. Fluid Mech. 2018, 18, 849–870. [Google Scholar] [CrossRef]
- Jonsson, P.; Andreasson, P.; Hellström, J.G.I.; Jonsén, P.; Staffan Lundström, T. Smoothed Particle Hydrodynamic Simulation of Hydraulic Jump Using Periodic Open Boundaries. Appl. Math. Model. 2016, 40, 8391–8405. [Google Scholar] [CrossRef]
- Canelas, R.B.; Crespo, A.J.C.; Domínguez, J.M.; Ferreira, R.M.L.; Gómez-Gesteira, M. SPH–DCDEM Model for Arbitrary Geometries in Free Surface Solid–Fluid Flows. Comput. Phys. Commun. 2016, 202, 131–140. [Google Scholar] [CrossRef]
- Verbrugghe, T.; Stratigaki, V.; Altomare, C.; Domínguez, J.; Troch, P.; Kortenhaus, A. Implementation of Open Boundaries within a Two-Way Coupled SPH Model to Simulate Nonlinear Wave–Structure Interactions. Energies 2019, 12, 697. [Google Scholar] [CrossRef] [Green Version]
- Rodi, W. Turbulence Models and Their Application in Hydraulics: A State-of-the-Art Review, 3rd ed.; IAHR Monograph Series; Balkema: Rotterdam, The Netherland, 1993; ISBN 9789054101505. [Google Scholar]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Shao, S. Incompressible SPH Simulation of Wave Breaking and Overtopping with Turbulence Modelling. Int. J. Numer. Meth. Fluids 2006, 50, 597–621. [Google Scholar] [CrossRef]
- Shao, S. Simulation of Breaking Wave by SPH Method Coupled with k-∈ Model. J. Hydraul. Res. 2006, 44, 338–349. [Google Scholar] [CrossRef]
- De Padova, D.; Ben Meftah, M.; De Serio, F.; Mossa, M.; Sibilla, S. Characteristics of Breaking Vorticity in Spilling and Plunging Waves Investigated Numerically by SPH. Environ. Fluid Mech. 2020, 20, 233–260. [Google Scholar] [CrossRef]
- Moin, P.; Mahesh, K. Direct numerical simulation: A Tool in Turbulence Research. Annu. Rev. Fluid Mech. 1998, 30, 539–578. [Google Scholar] [CrossRef] [Green Version]
- Lucy, L.B. A Numerical Approach to the Testing of the Fission Hypothesis. Astron. J. 1977, 82, 1013. [Google Scholar] [CrossRef]
- Gingold, R.A.; Monaghan, J.J. Smoothed Particle Hydrodynamics: Theory and Application to Non-Spherical Stars. Mon. Not. R. Astron. Soc. 1977, 181, 375–389. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed Particle Hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Liu, G.-R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method; World Scientific: Singapore, 2003; ISBN 9789812564405. [Google Scholar]
- Liu, G.R. Mesh Free Methods: Moving beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2003; ISBN 9780849312380. [Google Scholar]
- Monaghan, J.J.; Lattanzio, J.C. A Refined Particle Method for Astrophysical Problems. Astron. Astrophys. 1985, 149, 135–143. [Google Scholar]
- Gotoh, H.; Shibahara, T.; Sakai, T. Sub-Particle-Scale Turbulence Model for the MPS Method—Lagrangian Flow Model for Hydraulic Engineering. Adv. Methods Comput. Fluid Dyn. 2001, 9, 339–347. [Google Scholar]
- Monaghan, J.J. Simulating Free Surface Flows with SPH. J. Comput. Phys. 1994, 110, 399–406. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J.C. State-of-the-Art of Classical SPH for Free-Surface Flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- Crespo, A.J.; Gómez-Gesteira, M.; Dalrymple, R.A. Modeling Dam Break Behavior over a Wet Bed by a SPH Technique. J. Waterw. Port Coast. Ocean Eng. 2008, 134, 313–320. [Google Scholar] [CrossRef]
- Khayyer, A.; Gotoh, H. On Particle-Based Simulation of a Dam Break over a Wet Bed. J. Hydraul. Res. 2010, 48, 238–249. [Google Scholar] [CrossRef]
- Altomare, C.; Domínguez, J.M.; Crespo, A.J.C.; González-Cao, J.; Suzuki, T.; Gómez-Gesteira, M.; Troch, P. Long-Crested Wave Generation and Absorption for SPH-Based DualSPHysics Model. Coast. Eng. 2017, 127, 37–54. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S. Simulation of Near-Shore Solitary Wave Mechanics by an Incompressible SPH Method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar] [CrossRef]
- Shao, S.; Lo, E.Y.M. Incompressible SPH Method for Simulating Newtonian and Non-Newtonian Flows with a Free Surface. Adv. Water Resour. 2003, 26, 787–800. [Google Scholar] [CrossRef]
- Shipilova, O.; Bockmann, A.; Skeie, G.; Bergan, P. Assessment of Incompressible and Weakly Compressible SPH for Marine Applications. In Proceedings of the International Conference 4th Spheric Workshop, Nantes, France, 27–29 May 2009; pp. 273–277. [Google Scholar]
- Lee, E.-S.; Moulinec, C.; Xu, R.; Violeau, D.; Laurence, D.; Stansby, P. Comparisons of Weakly Compressible and Truly Incompressible Algorithms for the SPH Mesh Free Particle Method. J. Comput. Phys. 2008, 227, 8417–8436. [Google Scholar] [CrossRef]
- Fulk, D.A.; Quinn, D.W. An Analysis of 1-D Smoothed Particle Hydrodynamics Kernels. J. Comput. Phys. 1996, 126, 165–180. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Fourtakas, G.; Altomare, C.; Canelas, R.B.; Tafuni, A.; García-Feal, O.; Martínez-Estévez, I.; Mokos, A.; Vacondio, R.; Crespo, A.J.C.; et al. DualSPHysics: From Fluid Dynamics to Multiphysics Problems. Comp. Part. Mech. 2021. [Google Scholar] [CrossRef]
- Antuono, M.; Colagrossi, A.; Marrone, S. Numerical Diffusive Terms in Weakly-Compressible SPH Schemes. Comput. Phys. Commun. 2012, 183, 2570–2580. [Google Scholar] [CrossRef]
- Molteni, D.; Colagrossi, A. A Simple Procedure to Improve the Pressure Evaluation in Hydrodynamic Context Using the SPH. Comput. Phys. Commun. 2009, 180, 861–872. [Google Scholar] [CrossRef]
- Casulli, V.; Stelling, G.S. Numerical Simulation of 3D Quasi-Hydrostatic, Free-Surface Flows. J. Hydraul. Eng. 1998, 124, 678–686. [Google Scholar] [CrossRef]
- Stansby, P.K.; Zhou, J.G. Shallow-Water Flow Solver with Non-Hydrostatic Pressure: 2D Vertical Plane Problems. Int. J. Numer. Methods Fluids 1998, 28, 541–563. [Google Scholar] [CrossRef]
- Stelling, G.; Zijlema, M. An Accurate and Efficient Finite-Difference Algorithm for Non-Hydrostatic Free-Surface Flow with Application to Wave Propagation. Int. J. Numer. Meth. Fluids 2003, 43, 1–23. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Further Experiences with Computing Non-Hydrostatic Free-Surface Flows Involving Water Waves. Int. J. Numer. Meth. Fluids 2005, 48, 169–197. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.S. Efficient Computation of Surf Zone Waves Using the Nonlinear Shallow Water Equations with Non-Hydrostatic Pressure. Coast. Eng. 2008, 55, 780–790. [Google Scholar] [CrossRef]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An Operational Public Domain Code for Simulating Wave Fields and Rapidly Varied Flows in Coastal Waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Stelling, G.S.; Busnelli, M.M. Numerical Simulation of the Vertical Structure of Discontinuous Flows. Int. J. Numer. Meth. Fluids 2001, 37, 23–43. [Google Scholar] [CrossRef]
- Bai, Y.; Cheung, K.F. Dispersion and Nonlinearity of Multi-Layer Non-Hydrostatic Free-Surface Flow. J. Fluid Mech. 2013, 726, 226–260. [Google Scholar] [CrossRef]
- Harten, A.; Lax, P.D.; van Leer, B. On Upstream Differencing and Godunov-Type Schemes for Hyperbolic Conservation Laws. SIAM Rev. 1983, 25, 35–61. [Google Scholar] [CrossRef]
- De Serio, F.; Mossa, M. Experimental Study on the Hydrodynamics of Regular Breaking Waves. Coast. Eng. 2006, 53, 99–113. [Google Scholar] [CrossRef]
- Roeber, V. Boussinesq-Type Model for Nearshore Wave Processes in Fringing Reef Environment. Ph.D. Thesis, University of Hawaii at Manoa, Honolulu, HI, USA, 2010. [Google Scholar]
- Roeber, V.; Cheung, K.F.; Kobayashi, M.H. Shock-Capturing Boussinesq-Type Model for Nearshore Wave Processes. Coast. Eng. 2010, 57, 407–423. [Google Scholar] [CrossRef]
- Titov, V.V.; Synolakis, C.E. Modeling of Breaking and Nonbreaking Long-Wave Evolution and Runup Using VTCS-2. J. Waterw. Port Coast. Ocean Eng. 1995, 121, 308–316. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.C.; Gómez-Gesteira, M. Optimization Strategies for CPU and GPU Implementations of a Smoothed Particle Hydrodynamics Method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-Source Parallel CFD Solver Based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. 3D SPH Simulation of Large Waves Mitigation with a Dike. J. Hydraul. Res. 2007, 45, 631–642. [Google Scholar] [CrossRef]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-Induced Wave Breaking in a Non-Hydrostatic, near-Shore Wave Model. Coast. Eng. 2013, 76, 1–16. [Google Scholar] [CrossRef]
- Fang, K.; Zou, Z.; Dong, P.; Liu, Z.; Gui, Q.; Yin, J. An Efficient Shock Capturing Algorithm to the Extended Boussinesq Wave Equations. Appl. Ocean Res. 2013, 43, 11–20. [Google Scholar] [CrossRef]
- Shi, F.; Kirby, J.T.; Harris, J.C.; Geiman, J.D.; Grilli, S.T. A High-Order Adaptive Time-Stepping TVD Solver for Boussinesq Modeling of Breaking Waves and Coastal Inundation. Ocean Model. 2012, 43–44, 36–51. [Google Scholar] [CrossRef]
- Tonelli, M.; Petti, M. Hybrid Finite Volume—Finite Difference Scheme for 2DH Improved Boussinesq Equations. Coast. Eng. 2009, 56, 609–620. [Google Scholar] [CrossRef]
- Bacigaluppi, P.; Ricchiuto, M.; Bonneton, P. Implementation and Evaluation of Breaking Detection Criteria for a Hybrid Boussinesq Model. Water Waves 2019, 2(2), 207–241. [Google Scholar] [CrossRef] [Green Version]
- Kazolea, M.; Delis, A.I.; Synolakis, C.E. Numerical Treatment of Wave Breaking on Unstructured Finite Volume Approximations for Extended Boussinesq-Type Equations. J. Comput. Phys. 2014, 271, 281–305. [Google Scholar] [CrossRef]
- Christensen, E.D.; Walstra, D.-J.; Emerat, N. Vertical Variation of the Flow across the Surf Zone. Coast. Eng. 2002, 45, 169–198. [Google Scholar] [CrossRef]
- Wilmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Kennedy, A.B.; Chen, Q.; Kirby, J.T.; Dalrymple, R.A. Boussinesq Modeling of Wave Transformation, Breaking, and Runup. I: 1D. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 39–47. [Google Scholar] [CrossRef] [Green Version]
- Tissier, M.; Bonneton, P.; Marche, F.; Chazel, F.; Lannes, D. A New Approach to Handle Wave Breaking in Fully Non-Linear Boussinesq Models. Coast. Eng. 2012, 67, 54–66. [Google Scholar] [CrossRef]
- Kazolea, M.; Ricchiuto, M. On Wave Breaking for Boussinesq-Type Models. Ocean Model. 2018, 123, 16–39. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).