Time-Division Color Holographic Projection in Large Size Using a Digital Micromirror Device ^†

Abstract

Holographic projection is a simple projection as it enlarges or reduces reconstructed images without using a zoom lens. However, one major problem associated with this projection is the deterioration of image quality as the reconstructed image enlarges. In this paper, we propose a time-division holographic projection, in which the original image is divided into blocks and the holograms of each block are calculated. Using a digital micromirror device (DMD), the holograms were projected at high speed to obtain the entire reconstructed image. However, the holograms on the DMD need to be binarized, thereby causing uneven brightness between the divided blocks. We correct this by controlling the displaying time of each hologram. Additionally, combining both the proposed and noise reduction methods, the image quality of the reconstructed image was improved. Results from the simulation and optical reconstructions show we obtained a full-color reconstruction image with reduced noise and uneven brightness.

1. Introduction

Computer-generated holograms (CGHs) [1] are widely used in optical fields such as holographic displays [2] and wavefront control [3] as they can control light waves. Holographic projections [4,5], a type of holographic display, employ holographic features to enable special projections (e.g., multi-projection [5,6]) that are difficult to achieve using conventional projections. Additionally, holographic projections do not require zoom lenses as the enlargement and reduction in the reconstructed image can be done computationally [7]. Therefore, in principle, it is a simple projector, consisting only of a light source and a spatial light modulator (SLM) [5,6,7,8,9]. One critical challenge for the practical realization of holographic projection is the degradation of image quality due to noise superimposed on the reconstructed image. Multiple factors can cause noise, including the random phase added to the original image and the expansion of the pixel pitch when enlarging the reconstructed image. Several studies have proposed methods for reducing noise. The multi-random phase method [10] averages out the noise by reconstructing CGHs with different random phases in a time-division manner at high speed. Each reconstructed point of the CGH image has side lobes due to diffraction effects, which cause noise due to random interference between these side lobes. In the pixel separation method [11], several images with separated pixels are prepared from an original image, and the CGHs of these pixel-separated images are calculated. Using time-division reconstruction of CGHs at high speed opens the possibility of a reconstructed image with reduced noise. The down-sampling method [12] reduces noise in the reconstructed image by obtaining a down-sampled CGH from the original image. The random phase-free method [13] adds a virtual convergence light to the original image, resulting in a good reconstructed image without a random phase. However, this method works well for amplitude holograms, but needs improvements for phase-only and binary holograms [14,15]. Optimization of CGH using the Gerchberg–Saxton algorithm [16,17] and the gradient descent method [18] obtains a reconstructed image with good image quality, however, it is computationally expensive due to iterative calculations.

This paper proposes a time-division holographic projection projected on a large screen. The proposed method divides an original image into blocks, and the CGHs of each block generated is calculated. Then, a digital micromirror device (DMD) is used to project the CGHs at high speed to obtain the entire reconstructed image. The CGH to be displayed on the DMD needs to be binarized. However, the binarized CGHs lose the brightness information of the divided original image, causing uneven brightness in the reconstructed image. To solve this problem, the proposed method changed the display time of the CGHs proportional to the average brightness value of the divided original image. Additionally, combining our method with the multi-random phase [10] and pixel separation methods [11], we improved the image quality of the reconstructed image. From the simulation and optical reconstructions, we obtain a large-color reconstructed image with reduced noise and color unevenness. The rest of the paper is organized as follows: Section 2 describes each aforementioned corrective method. Section 3 presents the simulation and optical results. Section 4 holds the conclusion.

2. Methods

In a holographic projection, a random phase is added to the original image to diffuse the object light widely. Then, the CGH is generated using propagation calculation. Given the complex amplitude of the original image $u_o\left(x_i,y_i\right)$, the random phase $u_i\left(x_i,y_i\right)$, the complex amplitude of the CGH $u_h\left(x_h,y_h\right)$, the propagation distance $z$, and the light propagation operator ${\mathrm{Prop}}_z\left[·\right]$, the CGH calculation is expressed by

$$u_h\left(x_h,y_h\right)={\mathrm{Prop}}_z\left[u_o\left(x_i,y_i\right)u_i\left(x_i,y_i\right)\right].$$

(1)

As a DMD is used in this study, only the real part of Equation (1) is extracted and binarized to generate binary CGH. In the binarization, we use one if the real part is positive, and zero otherwise.

Figure 1 shows the simulated results of the reconstructed image when the size of the original image is twice larger than the CGH. Table 1 shows the simulation condition. We used only the red wavelength in this simulation. Figure 1a shows the original image. Without the random phase, only the part with the same size as the CGH is reconstructed, as shown in Figure 1b. However, by adding a random phase, the entire original image is reconstructed as shown in Figure 1c. This causes speckle noise in the reconstructed image. There are methods to reduce these speckle noises, such as the multi-random phase and pixel separation methods.

Figure 1. Original and simulated reconstructed images: (a) original image, (b) reconstructed image without random phase, (c) reconstructed image with random phase.

Table 1. Calculation parameters.

Parameters	Values
CGH resolution	1920 × 1080 pixels
CGH pixel pitch	7.56 µm
Wavelength of RGB lasers	Red: 632 nm, Green: 520 nm, Blue: 450 nm
Projection distance	3.0 m

In the following subsections, we explain the multi-random phase and pixel separation methods. Further, the proposed methods, a combination of multi-random and pixel separation methods, and the correction method for color unevenness are explained.

2.1. Multi-Random Phase Method

The multi-random phase method [10] averages out the noise in the reconstructed image using rapidly switching multiple CGHs generated by adding different random phases to the original image. When the number of CGHs is $N$, the mean square error of the reconstructed image decreases by $\sqrt{\mathrm{N}}$.

2.2. Pixel Separation Method

The pixel separation method [11] is a method for preparing multiple images such that the pixels of the original image are separated at certain intervals, and superimposing the reconstructed images by rapidly switching the CGHs of each separated image. Separating the pixels reduces undesired interference between side robes of adjacent reconstructed pixels.

Figure 2 shows how the pixels of an original image are separated. We group $n\times m$ pixels and then generate the $n\times m$ separated images. Figure 2a shows a case where a single group consists of 6 pixels ($2\times 3$). Figure 2b shows the separated image of pixels assigned “1” in Figure 2a. We generate six pixel-separated images as shown in Figure 2b–g, and calculate the CGHs for each image.

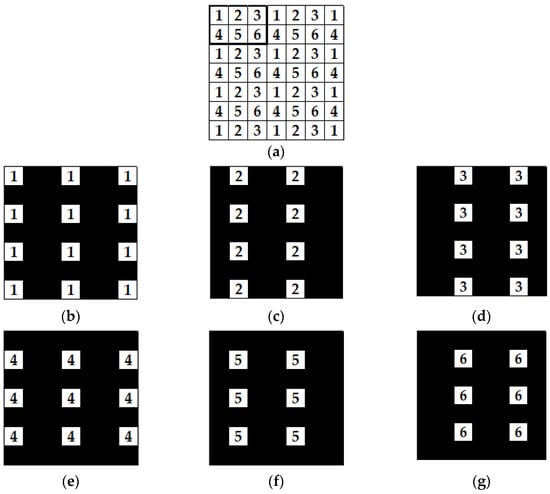
Figure 2. Original and pixel-separated images: (a) original image, (b) separated image of number 1, (c) separated image of number 2, (d) separated image of number 3, (e) separated image of number 4, (f) separated image of number 5, and (g) separated image of number 6.

2.3. Proposed Method: Time-Division Reconstruction Method

In a holographic projection [7], the reconstructed image is enlarged by setting the pixel pitch of the original image larger than that of the CGH. Thus, we obtain a large reconstructed image without a zoom lens. However, with increased pixel pitch and a fixed number of pixels, the image quality deteriorates.

A time-division reconstruction method that divides the original image into blocks after up-sampling without changing the pixel pitch is proposed, and projects the CGHs of the divided blocks by switching them rapidly. As the pixel pitch is not manipulated, projecting a large-screen reconstruction image with higher quality than the method for changing the pixel pitch is possible [7].

Figure 3 shows an example of calculating CGH when the original image is divided into four after adding a random phase. As the centers of each divided block have an offset from the center of the CGH, it is necessary to use off-axis diffraction to calculate the propagation from divided blocks of CGH. Several off-axis calculations have been proposed [19,20], but this study used that proposed in [20]. Figure 4 shows the reconstruction process. High-speed DMD was used and, by switching the CGHs at high speed, we obtained the entire reconstructed image.

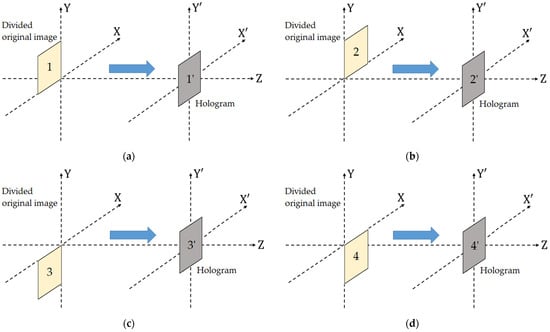
Figure 3. Recording of CGH using time-division reconstruction method: (a) recording of divided original image 1, (b) recording of divided original image 2, (c) recording of divided original image 3, and (d) recording of divided original image 4.

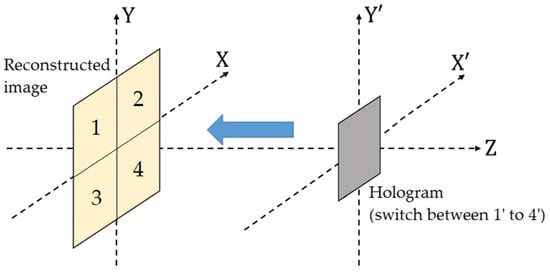
Figure 4. Reconstruction of CGH using the time-division reconstruction method.

Figure 5 shows our optical system. For color reconstruction, a time-division color reconstruction method was used [21]. RGB semiconductor lasers were used as light sources and switched the RGB lasers using the synchronizing signals outputted from the DMD. A 4f optical system and a spatial filter were placed between the DMD and the screen to eliminate direct light.

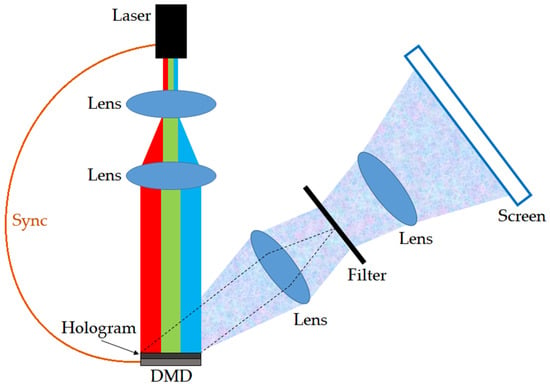
Figure 5. Optical system using a DMD.

2.4. Uneven Color Correction

CGHs generated using the method outlined in Figure 3 should be binarized before displayed on DMD. However, this study binarized CGHs after the original image was divided, so the relative brightness information between each CGH is lost. Thus, uneven colors occurred in the reconstructed image. Figure 6 displays the reconstructed image using the optical system in Figure 5. Figure 6a,b show the original color image and the optical reconstruction image with color unevenness, respectively.

Figure 6. Color original image (a) and optically reconstructed image with color unevenness (b).

To correct the color unevenness of each divided block closer to its original brightness, we increase the projection time when the divided block is darkened. Conversely, if the divided brock is brighter, the projection time is shortened to eliminate color unevenness. Therefore, the projection time of each divided block is adjusted to perform time-division reconstruction. The projection time used is determined from the average brightness value of the original blocked images. The method is shown in Figure 7 and consists of three steps.

Figure 7. Calculation of projection time: (a) calculate the average brightness value, (b) calculate the ratio of the average values relative to the reference, and (c) calculate the projection times for each division block. The blue rectangle indicates the reference block.

In Figure 7a, the average brightness values of each divided block of the original image are calculated. In Figure 7b, an arbitrarily divided block is defined as a reference (the blue rectangular indicates the reference block), and the ratio of the average value per divided block to the reference block is calculated. In Figure 7c, multiplying the ratio by the hologram display time of the reference block, the projection times of each divided block can be determined and set in the DMD. The reference block should be set so that the projection time of each block does not exceed the performance of the DMD. The calibration of the projection times is required for each new image projection. However, the calibration is not complex and time-consuming.

Figure 8 shows the optical reconstruction image after adjusting the projection time and correcting the color unevenness. Compared to Figure 6b, the color unevenness was eliminated and confirmed the effectiveness of this method.

Figure 8. Optical reconstruction image with color unevenness corrected. The brightness and contrast were adjusted to make the reconstructed image clearer.

3. Results

This chapter presents the results of simulations and optical experiments using each method described in Section 2. Table 1 shows the parameters for calculating CGHs. The resolution and pixel pitch of the CGHs was determined using DMD. We used DLP LightCrafter 6500 made by TEXAS INSTRUMENTS, which has a refresh rate of 9523 Hz and displays binary CGHs. Table 2 summarizes the proposed and comparative methods.

Table 2. Summary of methods.

		Methods	Summary
Comparison Methods	(a)	Pixel pitch expansion	Used the method of in [7]. The pixel pitch of the original image is four times (30.24 µm) to enlarge the reconstructed image. The pixel pitch should not exceed the Nyquist frequency.
	(b)	Pixel pitch expansion + Multi-random phase	This combines (a) above with the multi-random phase method [10]. Six CGHs with different random phases are projected.
	(c)	Pixel pitch expansion + Pixel separation	This combines method (a) with the pixel separation method [11] and projects six CGHs with different separation images.
Proposed Methods	(d)	Time-division reconstruction + Uneven color correction	A method that combines time-division reconstruction method with uneven color correction. Up-samples the original image to four times its resolution (7680 × 4320 pixels). Divide the original image horizontally and vertically into 4 × 4 blocks.
	(e)	Time-division reconstruction + Uneven color correction + Multi-random phase	This combines method (d) with the multi-random phase method [10]. Six CGHs with different random phases were projected onto each block.
	(f)	Time-division reconstruction + Uneven color correction + Pixel separation	This combines method (d) with the pixel separation method [11] and projects six CGHs with different separation images.

3.1. Simulation Results

Figure 9 shows the reconstruction results from the simulation. The size of all reconstructed images is approximately 11.3 cm × 6.5 cm. The methods used in Figure 9a–f correspond to methods (a)–(f) in Table 2.

Figure 9. Reconstruction images by simulation: the methods used in (a–f) correspond to Table 2.

Table 3 shows the image quality evaluation using mean squared error (MSE). The MSE evaluates the average error per pixel between the original and reconstructed images. The smaller the MSE, the closer the reconstructed image is to the original image. The MSE is expressed by

$$\text{MSE}=\frac{1}{XY}{{\displaystyle \sum }}_{x=1}^X{{\displaystyle \sum }}_{y=1}^Y{\left\{I_o\left(x,y\right)-I_R\left(x,y\right)\right\}}^2$$

(2)

where we denote the original image as $I_o\left(x,y\right)$, the reconstruction intensity of the reconstructed image as $I_R\left(x,y\right)$, and the size of the original and reconstructed images is $X\times Y$.

Table 3. Image quality evaluation of simulation results.

		Methods	MSE
Comparison Method	(a)	Pixel pitch expansion	9648.8
	(b)	Pixel pitch expansion + Multi-random phase	4509.9
	(c)	Pixel pitch expansion + Pixel separation	4316.4
Proposed Method	(d)	Time-division reconstruction + Uneven color correction	9640.3
	(e)	Time-division reconstruction + Uneven color correction + Multi-random phase	4107.0
	(f)	Time-division reconstruction + Uneven color correction + Pixel separation	4085.6

Comparing Figure 9a,d, Figure 9d has higher contrast. However, comparing methods (a) and (d) in Table 3, there is no significant difference in MSE. This is due to the time-division reconstruction method, which creates boundaries between the divided blocks, hindering the decrease in the MSE.

Compared to Figure 9a, applying the multi-random phase method or pixel separation methods reduces the speckle noise, improving the image quality in each reconstructed image. Subjectively, no significant difference in the quality of the reconstructed image between the multi-random phase and pixel separation methods exists. Table 3 also shows that the MSEs are reduced by applying either the multi-random phase or pixel separation methods. Quantitatively, no significant difference between the MSEs of the multi-random phase and pixel separation method exists. Figure 9e,f of the proposed methods are subjectively superior to other methods. In particular, Figure 9f has the best MSE.

3.2. Optical Reconstruction Results

Figure 10 shows the results of an optical experiment with a single color. Each method in Figure 10a–f corresponds to methods (a)–(f) in Table 2. Figure 10d has a higher contrast than Figure 10a. Compared to Figure 10a, applying the multi-random phase or pixel separation methods reduces speckle noise and improves the image quality in each reconstructed image. Subjectively, there is no significant difference in the quality of the reconstructed image using the multi-random phase method and the pixel separation method.

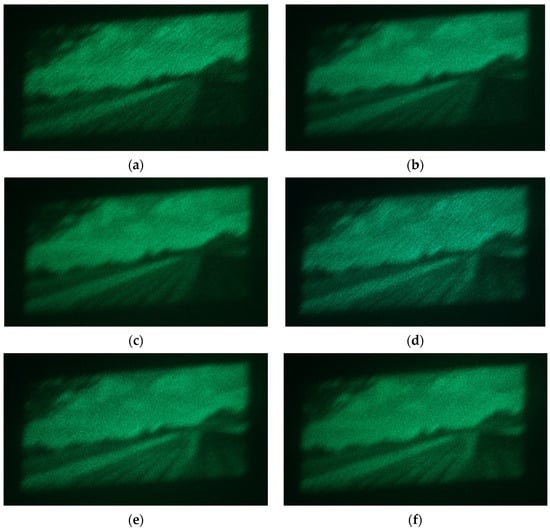
Figure 10. Optical reconstruction results: the methods used in (a–f) correspond to Table 2. The brightness and contrast were adjusted to make the reconstructed image clearer.

In Figure 10d, obtained using the proposed time-division method by averaging six reconstructed images, the projection time per one reconstructed image was about 5.3 ms. Thus, the projection time per average reconstruction was 31.8 ms in Figure 10e,f as six images were projected in each division block. The image quality of the reconstructed image can be improved by increasing the number of projections for each divided block. However, due to the upper limit used in the frame rate of DMD, it is necessary to determine the number of projections for each divided block so that flicker does not occur in the reconstructed image.

3.3. Full-Color Reconstruction Results

The optical system shown in Figure 5 was used for the full-color reconstruction. We used a method of time-division switching for RGB light sources [21]. Only the proposed method (d) in Table 2 (Time-division reconstruction + Uneven color correction) was validated, as it requires three times the binary CGHs than the proposed method.

Figure 11 shows the results of the full-color reconstruction. The brightness and contrast were adjusted to make the reconstructed image clearer. As the number of divided blocks is 4 × 4, 48 binary CGHs are required to obtain the full-color reconstruction image. The overall size of the reconstructed image was 6.5 cm and 11.6 cm in height and width, respectively. The multi-random phase and pixel separation methods could not be applied as the number of projections increased.

Figure 11. Colored original image (a) and full-color reconstruction (b).

To confirm the effectiveness of the proposed method, Figure 12 shows the reconstructed image using another original image. As in Figure 11, we obtained a full-color reconstruction image with both reduced noise and color unevenness. Figure 13 shows a reconstructed video “Vegetables” using the proposed method in the Supplementary Section (Video S1) to confirm the effectiveness of the proposed method. All the calculations were performed by our wave optics library [22].

Figure 12. Another colored original image (a) and full-color reconstruction (b).

Figure 13. Screenshot of Video “Vegetables.” This video is provided in the Supplementary Materials.

4. Conclusions

To improve the image quality of the reconstructed image in large-screen holographic projection using binary CGHs, we proposed a time-division method and a method to reduce color unevenness. The average values of the division blocks were used to adjust the display times of the binary CGHs and reduce the color unevenness. Furthermore, the multi-random phase and pixel separation methods combined with the proposed were used to reduce the speckle noise. The effectiveness of the proposed method was confirmed by simulation and optical reconstructions. Additionally, synchronizing the DMD with the RGB light sources showed that the proposed method was capable of full-color reconstruction.