Featured Application
The multicriteria methodology for the scheduling of a hybrid EV charging station could be applied to any commercial EV charging station. The driver’s preferences about the amount of renewable energy share can be easily implemented in a charging software application.
Abstract
The increasing electric vehicle fleet requires an upgrade and expansion of the available charging infrastructure. The uncontrolled charging cycles greatly affect the electric grid, and for this reason, renewable energy sources and battery storage are getting incorporated into a hybrid charging station solution. Adding a renewable source and a battery to the charging station can help to “buffer” the power required from the grid, thus avoiding peaks and related grid constraints. To date, the origin of the energy coming from the battery has not been traced. In this paper, a solution of the hybrid electric vehicle charging station coupled with the small-scale photovoltaic system and battery energy storage is proposed to eliminate the adverse effects of uncontrolled electric vehicle charging, with the exact calculation of renewable energy share coming from energy stored in the battery. The methodology for the multicriteria optimization of the charging/discharging schedule of a battery and electric vehicle charging level is based on multi-attribute utility theory. The optimization criteria include the minimization of charging costs, maximization of renewable energy (from both the solar plant and the battery), and the minimization of battery degradation. The problem is solved using a genetic algorithm optimization procedure adapted to the multicriteria optimization function. The methodology is tested on an illustrative example, and it is proven that the decision-maker’s preferences greatly affects the choice of the optimal strategy and the optimal battery capacity.
1. Introduction
Environmental pollution, climate change, and global energy policy lead to the accelerating growth of electric vehicles (EV) [1,2,3]. According to numerous studies related to the EV charging technologies [4], the increased level of EV chargers and the lack of coordination in charging schemes could lead to:
- (a)
- Voltage dips during periods of EV charging (particularly for fast chargers);
- (b)
- Reduction in power quality (both slow and fast charging stations are sources of harmonic distortion);
- (c)
- EV battery deterioration and capacity decrease (due to the battery’s voltage level or temperature increase);
- (d)
- Overloading of distribution network transformers;
- (e)
- Increased energy losses (especially with larger direct current (DC) fast charging station penetration)
Because they are clean and naturally abundant, renewable energy resources such as solar are an important component to provide the energy for the EV charging [5,6]. Photo-voltaic (PV) generation is often integrated into EV charging stations to lower the cost and reduce the carbon footprint as well, and different control strategies are used for the integration of small EVs [7]. Strategies are including a grid-connected residential photovoltaic system with plug-in hybrid electric vehicle (PHEV) [8,9] and solar-charged electric and fuel cell vehicles [10]. A comprehensive review of the current status and latest technologies for the integration of EV with the PV array and wind generator is given in [11].
A major disadvantage of charging EV from PV is the variability in PV production. To address the random nature of renewable energy, battery energy storage is often utilized. The combination of EV charger and the battery energy system (BES) can help to reduce adverse effects on the grid (reduce the peak load demand from the EVs, reduce grid losses and contribute to the grid regulation and reinforcement) [12].
The energy storage is charged when there is excess in the wind or solar energy. When this generation is insufficient, storage is used to charge the EV. In [13], three different algorithms for charging and discharging the local storage in the presence of EV chargers are compared. The first strategy is to discharge the battery at a constant rate during specific times of the day, and the second is based on available solar energy and the number of connected EVs. It was shown that a third strategy—a discharging based on the sigmoid function of connected EVs is the best strategy, compensating 71% of EV energy requirements from the gird. However, the amount of renewable energy coming from the battery is not calculated. In [14], a 10 kWh Li-ion battery bank is integrated into the EV–PV charger. It was proven that small-sized storage in the order of 10 kWh could help to alleviate the daily solar variations and reduce the grid energy by 25%. The paper [15] focused on the control and operation of a fast-charging station for EVs within a microgrid consisted of a PV system, a Li-ion BES and fast charging units. It is shown that with the proper control algorithm, the fast charging station requires the minimum amount of energy from the grid. The analysis was focused on fast chargers only, with a 120 A charging current. The battery-buffered EV charger can help to increase the distribution network flexibility as well. It can provide ancillary services for supporting the power grid, such as primary and secondary frequency and voltage control. Different smart charging schemes provide the flexibility of EV charging to closely match the PV production. A multiobjective decision-making methodology for the daily scheduling of EV fleet is proposed in [16,17], including the minimization of the service waiting time, the maximization of ancillary service revenue, and the minimization of costs incurred by vehicle charging. The number of client requests and service waiting times are modeled by the queuing theory.
To determine the optimal size and control scheme of an EV charger supported by BES, different optimization or control algorithms are proposed with various criteria and constraints. An optimization model for deploying the energy storage system for minimizing the load variance from the grid point of view and cost reduction from the customer’s perspective is given in [18]. The minimization of the operating cost using real-time electricity price is developed in [19]. The financial model was also used as the objective in [20], using a particle swarm optimization (PSO)-based optimization model to size the PV and BES in a grid-connected PV/BES combination. EV charging cost represented as a convex function of load demand is minimized in [21].
In [22,23], a genetic algorithm was employed to solve the optimization model for the design of an EV fast-charging station, optimizing the number of chargers, installed power of renewable energies and storage, and minimizing the imported power from the grid. The uncertainty of the EV power demand is simulated by the Erlang B queuing model. The isolation niche immune genetic algorithm (INIGA) and price-incentive model is applied in [24] for the scheduling of generators, intelligent management of energy storage units and optimization of operating efficiency of the network, and the ordinal optimization theory into the microgrid operation, considering the wind power uncertainty is used in [25].
The additional criteria, as the minimization of the lifecycle cost, taking into account environmental emissions, is presented in [26], and different energy sources such as renewable energy technology-based and diesel generators are considered. The number of chargers and capacity of PV and BES using an operator to maximize the net present value are determined in [27], while [28] developed an energy management system to optimize the energy flow among PV, BES, and the grid. A mixed-integer linear programming (MILP) model to coordinate the charging/discharging pattern of EVs with a BES is used in [29], and an optimization model to determine the optimal sizes of PV and BES in a grid-connected photovoltaic/battery energy storage/electric vehicle charging station and investigate the optimal energy management and the interaction with the utility grid is solved by the MAPSO method in [30]. In [31], a 15 kW PV-grid system connected with a 40 kWh Li-ion battery is tested for different load scenarios for minimizing the energy imported from the utility, using the simulation results without any optimization algorithm. The smart charging scheme for individual homes with EV chargers and PV installation is presented in [32], but only on user’s preferences, not taking the grid connection into account.
The majority of the already mentioned research is dealing with the day-ahead scheduling of battery operation. In [33], real-time control is introduced besides the hour ahead optimization. A four-stage optimization and control algorithm is proposed to minimize total operating cost for a charging station integrated with PV, fixed battery storage and a commercial building. Total operation costs consist of the cost of power from the distribution grid, BES and PV operating costs, cost of unsupplied demand, cost of discharging EVs, and profits from charging EVs and selling the excess power to the grid. Chance-constrained optimization is used to cope with the optimization parameter uncertainties. Although the model offers higher tolerability for uncertain parameters, the origin of the energy that is charging and discharging the battery is not taken into account.
Besides various criteria used in current optimization methodologies, the exact amount of renewable energy in the EV charging process has not been taken into account in all of the previous research. Another disadvantage of the current research methodologies is the single-criterion optimization instead of the multicriteria approach. Different factors, such as operational cost, customer satisfaction, load loss, and profit for charging station owners, are considered only in the objective function.
In this paper, the novel charging system is proposed to eliminate the adverse effects of uncontrolled EV charging and to track the origin of the energy for the charging of EV. The methodology for the multicriteria optimization of the charging/discharging schedule of a battery and EV charging level is based on multi-attribute utility theory. The optimization criteria include the minimization of charging costs, maximization of renewable energy share, and the minimization of battery degradation. The contribution of this paper can be stated as:
- the simultaneous optimization of charging/discharging BES and EV charging power;
- the implementation of energy tracking methodology that monitors the origin of energy from and to the battery;
- the multiobjective optimization of different conflicting criteria.
This problem is solved using the genetic algorithm optimization procedure adapted to the multicriteria optimization function. After the introduction and the literature review, the tracking of the energy origin while charging and discharging the battery is explained in Section 2. The optimization model with objective function and constraints is presented in Section 3, and the illustrative example for the optimization procedure is given in Section 4. After the discussion of results in Section 5, a conclusion and further research directions are given at the end.
2. Energy Tracking Methodology
An individual charging system for EVs connected to a public distribution network consisting of a solar power plant and an energy storage system will be analyzed. Through the low voltage AC lines, the vehicle is charged in the following ways: (a) only from the network if there is no production from PV panels, (b) only from PV panels if the production is large enough to cover the load of the individual system and vehicle charging, (c) from the battery if the battery is not charging and is in discharge mode, (d) in parallel from the PV power plant, network, and battery. The principle connection scheme is given in Figure 1. Arrows are indicating the possible power direction.
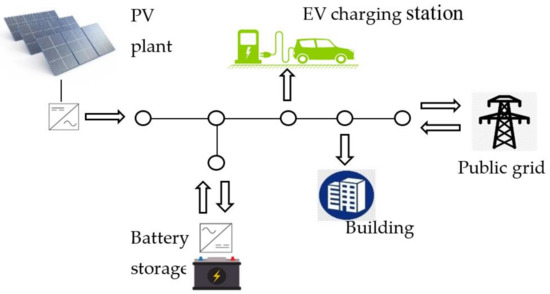
Figure 1.
Connection scheme of Photo-voltaic (PV)/battery energy system (BES)/electric vehicles (EV) charging system.
As one of the desired criteria is the maximization of energy from renewable sources (i.e., the solar power plant), it is necessary to develop a methodology for monitoring the origin of energy. This methodology will be explained in the sequel.
2.1. Energy Tracking during Battery Charge/Discharge
The energy used to charge the battery comes from the public grid and the PV power plant. As stated in the introduction, the possibility of monitoring and managing the origin of the energy to charge the EV has not been considered so far. The reason for this is the lack of the methodology of registering the origin of the energy coming out of the battery. Therefore, it is necessary to create a system that can monitor how much energy from renewable sources entered the battery, how much came out and finally, how much energy is charged to the car from renewable sources or the network.
Figure 2 shows the principle of energy tracking and registration of energy origin. Blue circles indicate the energy of unknown origin (from the distribution network), and green indicates energy from renewable sources. When charging the battery (Figure 2a), the amounts of energy entering the battery are determined by the state of the network and the instantaneous power of both sources. It can be easily determined by solving power flows equations in the network. The maximal energy to which the battery can be charged is limited by the battery capacity.
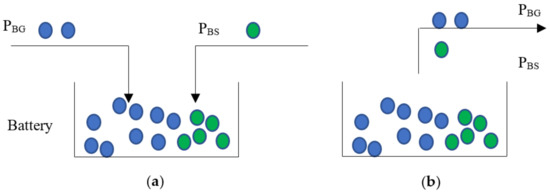
Figure 2.
Battery charging/discharging from different sources (a) battery charging; (b) battery discharging.
When discharging the battery, the situation is different (Figure 2b). The amount of energy emitted from a battery is determined by the relative ratio of available energy coming from different sources.
Let us indicate the state of charge of the battery with SOC, the amount of accumulated energy from renewable sources (solar) with SOCS, and the accumulated energy from the grid with SOCG. The battery power PB, the share of battery power from solar energy PBS and the share of battery power from the grid PBG will be positive if the battery is charging and negative if it is discharging. The charge and discharge behavior of the battery during the time step Δt can be generically modeled as follows:
In Equations (1)–(3), the charging/discharging efficiency factor kc/d equals ηc when charging and 1/ηd when discharging the battery. If the total power that discharges the battery is PB, then the power from renewable sources (PBS) and the grid (PBG) are given by Equations (5) and (6), respectively:
2.2. Energy Tracking during EV Charging
Figure 3 shows the charging process of an electric vehicle. The power is now coming from three different sources (PV, public grid, and battery). Because the battery power can be divided into different sources, EV power contains four components (Equation (7)): power from the PV panel (PS), power from the public grid (PG), battery power originating from the PV panel (PBS), and battery power originating from the grid (PBG).
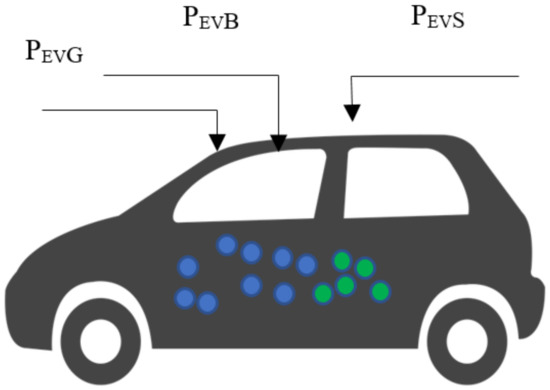
Figure 3.
EV charging.
The same logic is valid for any other load in the network: battery during the charging process and other loads. The power flow equations are solved, and voltages and powers in individual nodes are determined. The power flow equations in the presence of PVs, BES, EVs, and public grid are presented in Equations (8) to (11), where they express the active power balance, (8), reactive power balance, (9), active and reactive power flow of lines, (10) and (11). Equations (8)–(11) represents the general case with more power sources in different nodes.
2.3. Battery Degradation Model
The degradation model of energy storage batteries is based on Li-ion batteries, as the most used resource in medium-size energy storage systems. Li-ion batteries are losing storage capacity with calendar aging and cycling. The methodology is not taking into account the calendar aging, which will not affect the short-term planning horizon. Cycle life loss is related to temperature, charge and discharge rate and energy throughput [34]. The effects of discharge rates and capacity loss of a battery cell induced by cycling can be captured by an exponential function (12).
Qloss is the percentage of capacity loss induced by cycling. Both factors B1 and B2, are functions of temperature. Irate is the charge/discharge rate expressed as a C-rate. Ah is the total Ah-throughput for a given period. Coefficient values and units are given in [34].
After the determination of all necessary components, the multi-attribute objective function can be composed.
3. Optimization Problem
The goal of the optimization problem is to optimize the hourly scheduling of battery charge/discharge and to optimize the power and time required to charge the EV. The problem is treated as a multicriterial because three criteria will be simultaneously taken into account. The optimization is based on the minimization of supply costs, maximization of renewable energy for the EV charging and the minimization of the battery wear. The scheduling is optimized using 24 h-ahead forecasts of PV plant production, load demand of other consumers, and expected arrivals of EVs.
The first criterion is the maximization of renewable (solar) energy charging the EV.
The second criterion is the minimization of battery installation and operation and energy supply costs. Assuming that the energy is traded at the spot market with hourly prices ct, the criterion can be mathematically represented in (14). cB represents the levelized daily costs of battery installation and operation (€/kWh·day).
The third criterion refers to the aging of the batteries (15).
Optimization process constraints are related to the active and reactive power balance in the network Equations (7)–(11), minimal and maximal battery state of charge (16), minimal and maximal allowed charge/discharge rate (17) maximal rated power of EV charger (18) and capacity of the grid connection supply feeder (19).
Multi-attribute utility theory (MAUT) defines the utilities of multiple-attribute outcomes as a function of the utilities of each attribute taken individually. The theory specifies several possible functions and the conditions to be met under which each of these functions (multiplicative, additive and multilinear) would be appropriate. The multi-attribute utility function is of the following form if mutual utility independence exists (20).
- ui(xi) = the single-attribute utility value for attribute i with value xi (ranges from 0 to 1);
- ki = a parameter from the tradeoffs for component i;
- K = a normalization constant.
The utility function (20) reflects different types of interactions between individual criteria. In the compensatory case, the performance of one criterion compensates for the lack of performance by the other one (21). In the additive case, the performance of one criterion does not interact with the value of the other ones (22). In the complementary case, the balanced performance of all criteria is more important than the individual criteria fulfillment (23).
If additive independence exists, the multi-attribute utility function is also additive (24):
The multicriteria optimization used in this paper is based on the methodology applied for the EV charging fleet schedule presented in [17]. In this methodology, the first step in scheduling optimization is the single objective optimization of all of the previously explained objectives (13)–(15). The outputs of this optimization are utility functions based on maximal renewable energy (Ures), minimal battery and energy costs (Utc), and minimal battery degradation (Ubd). In the second step, the multiobjective optimization is performed applying MAUT for the utility aggregation (20). Individual utilities for renewable energy, costs and battery degradation are represented in Equations (25)–(27), respectively.
Finally, the optimization problem can be reduced to the maximization of the aggregated utilities (28).
The methodology will be illustrated on a case study of a hybrid PV/BES/EV charger for three cases: single-criterion optimization, multicriteria optimization with equal criteria weights, and multicriteria optimization for the complementary case. The optimization problem is solved using the continuous variable constrained genetic algorithm solver. The genome consists of 48 variables (two vectors of 24 battery powers PB,t and 24 EV charging powers PEV,t). The fitness function is given with the Equation (22), obtained after the calculation of (13)–(15) and (20)–(25). Equality constraints are given in Equations (1)–(4) and (7)–(11). Inequality constraints relating to the maximal and minimal charging/discharging powers and battery state of charge are given in Equations (16)–(19). The Matlab GA solver was used with the size of the initial population of 200.
4. Results
The method is illustrated by the example of the hybrid system shown in Figure 1. The system consists of a solar power plant with a rated power of P = 100 kW, one EV charger with a rated power of 22 kW, and a battery with a capacity of C = 30 kWh. The expected EV charging is 60 kWh from 6–12 h and 60 kWh from 16–22 h. Other input values are presented in Table 1.

Table 1.
Input values for the optimization.
The energy price for the 24 h period is presented in Figure 4.
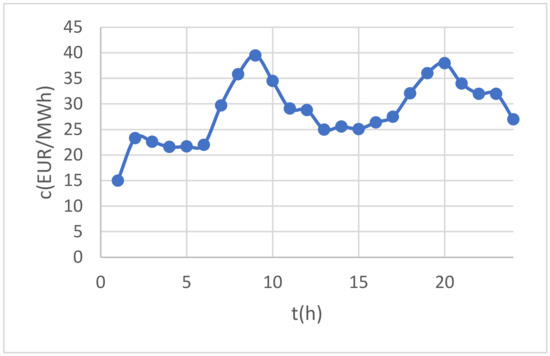
Figure 4.
Energy prices for the next 24 h period.
For the sake of simplification, all of the inverters are working in unity power factor mode, without the reactive power generation. The optimization is performed in two steps: in the first step, utility functions for each criterion are determined. In the second step, a multi-attribute approach is used for the battery and EV charging schedules. Because the battery capacity is not changing during the first simulation, battery costs are not taken into account.
Single-criterion optimizations were performed for all three criteria: minimum procurement costs, minimum battery aging, and maximization of car charging from solar energy by the Equations (13)–(15). The optimization problem is solved with the genetic algorithm in MATLAB (The MathWorks, Inc., Natic, MA, USA). The maximal generation number for the GA algorithm is 100, with the population size set to the array length of 200. Optimization is performed on Intel(R)Xeon(R) CPU E5-26670@ 2.90 GHz processor (Intel, Santa Clara, CA, USA) with 32 GB RAM. The total time of optimization is 47 s.
The results are shown in Table 2.

Table 2.
Single-criterion optimization results.
Results of the maximization of the solar energy share in the EV charging process are presented in Figure 5. Figure 5a presents, besides the forecasted values for the PV production (PS) and load demand (PL)—the power from the grid (Pg), battery power (Pbat), and the optimized EV charging power (Pev). Figure 5b represents the state of charge (SOC) of two virtual “battery compartments”—for renewable solar energy (SOCS) and energy from the grid (SOCg). Figure 5c gives the EV solar (Pevs) power component and grid component (Pevg), while Figure 5d represents the share of battery power from renewables (Pbs) and battery power coming from the stored grid energy (Pbg) in the optimized charge and discharge battery schedule.
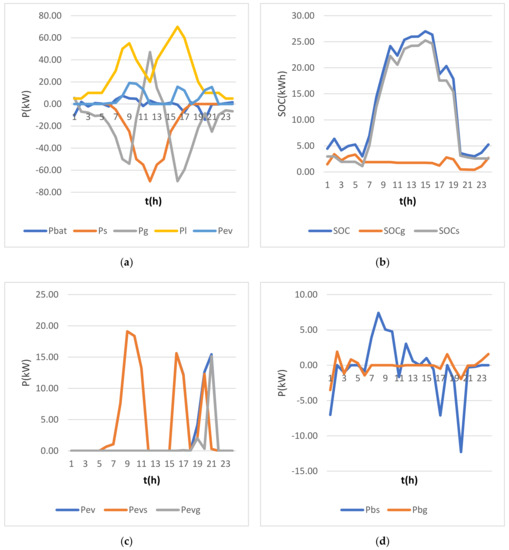
Figure 5.
Single-criterion optimization results for the maximal solar energy criteria (a) power flows, (b) state of charge (SOC) of battery, (c) EV charging power, (d) battery charge/discharge schedule.
The weighting factors for each criteria are the same: k1 = k2 = k3 = 0.33. Results are presented in Figure 6.
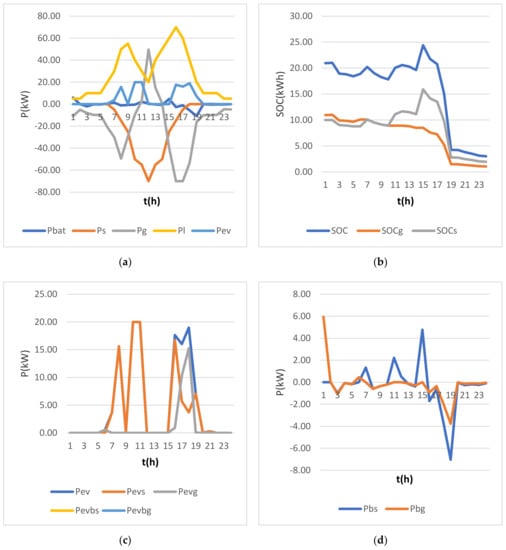
Figure 6.
Multicriteria optimization results (a) power flows, (b) SOC of battery, (c) EV charging power, (d) battery charge/discharge schedule.
The absolute and relative values of individual criteria are presented in Table 3. Relative values Ui for single criteria are obtained using the scalarization expressions (24)–(26). Optimization results for the complementary multi-attribute case are presented in Figure 7.

Table 3.
Multicriteria optimization results.
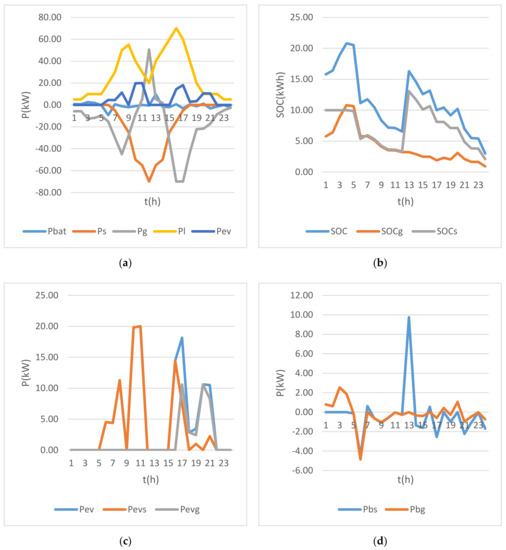
Figure 7.
Multicriteria optimization results for the complementary case (a) power flows, (b) SOC of battery, (c) EV charging power, (d) battery charge/discharge schedule.
Using the optimization model, the analysis of the optimal battery capacity for different weighting coefficients in the optimization function was performed. Two cases were compared: (a) greater importance is given to one of the criteria, and (b) a balanced distribution of criteria values (complementary case). Figure 8 shows the optimization results using an additive model (24), where preference is given to a higher share of renewable energy when charging an electric car. The coefficients in this case are: k1 = 0.6, k2 = 0.3 and k3 = 0.1. The graph represents the values of the individual utility function and the total utility function for different system configurations, starting from the case when the battery is not installed at all (C = 0) to the maximum capacity of 70 kWh. The calculation for all configurations was done with the same relative parameters: the initial state of charge of the battery is equal to one half of the battery capacity (SOC0 = 0.5 C), where the initial shares of energy from the network and solar panels are equally distributed (SOCBS,0 = SOCBG,0 = 0.5 SOC0).
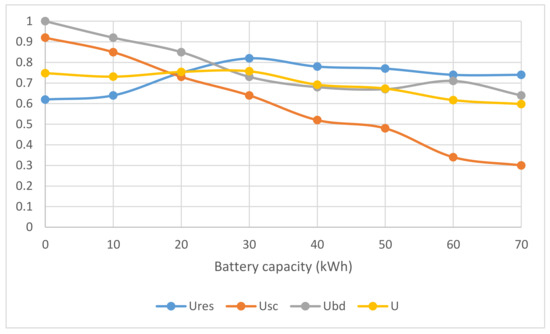
Figure 8.
Utility function dependence on battery capacity for the additive case.
In the second case, the analysis of the change of utility function depending on the battery capacity was performed for the complementary case (20), with the coefficients: k1 = 0.2, k2 = k3 = 0.3; K = 0.3. The results are shown in Figure 9.
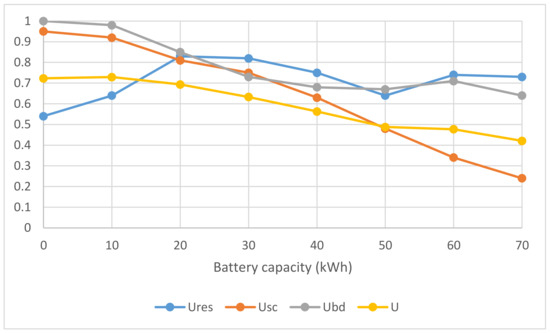
Figure 9.
Utility function dependence on battery capacity for the complementary case.
5. Discussion
The analysis of different cases shows significant differences between charging schemes with single-criterion and multicriteria optimization. Differences are also noticeable in the case of different preferences of decision-makers. In the case where battery management is optimized only by maximizing the EV charging energy originating from renewable sources, 103.91 kWh (86.7% of required energy) comes from the solar power plant. Most of this energy comes directly from the power plant, at the time when the greatest sunshine and the arrival of the vehicle coincide (Figure 5c). The battery is charging and discharging more intensively but does not exceed the battery capacity.
In the case of multicriteria optimization, the battery degradation criterion is influencing the charging/discharging process, and the amount of renewable energy in the charging process is reduced to 67.2 kWh (56%). The charging of the vehicle itself is now more balanced and does not reach the maximum allowable value.
Finally, in the complementary attribute case, the amount of renewable energy in the charging process is increased in comparison with the previous case to 87.7 kW (73%). The energy supply costs are higher, but the final solution demonstrates the balanced performance of all criteria.
The methodology proved that the energy stored in the battery greatly depends on the load of other consumers in the station because the amount of solar energy is proportional to the ratio of individual load (battery, EV, consumers) and the total load of the network. In the complementary case, the balanced performance across renewable energy amount, total costs and battery degradation are prevalent. In the additive case, the performance of one criterion does not interact with the value of the other ones, but two criteria are worse than in the other two scenarios. The integral optimization of the battery size and schedule, as well as the EV charging optimization, will be the focus of our future research.
In the case of an additive model, it can be seen that the maximum utility function is achieved at a battery capacity of 30 kWh. In case there is no battery installed, there is no battery wear (Ubd = 1), the total costs are also close to the minimum values (Usc = 0.9), but the share of energy from renewable sources is the lowest (Ures = 0.62). As the capacity increases, the value of this function increases to a maximum of (Ures = 0.85). This value also determines the total maximum of the system. As battery capacity continues to grow, the share of renewables is not increased due to constrained battery charging and discharging power.
In the complementary model, the emphasis is on the balanced values of all individual criteria. It can be seen that preference is given to lower values of battery capacity since then system costs and battery degradation are as important as the share of renewable sources. The optimal value of battery capacity is achieved with C = 10 kWh.
6. Conclusions
This paper is presenting the novel multicriteria optimization methodology for the day—ahead charging/discharging scheduling of hybrid PV/EV/BES system. Introducing the new concept of renewable energy monitoring and tracking, it is possible to maximize the exact renewable energy share when charging an EV. Other criteria that are simultaneously optimized are the total costs of the system (consisting of battery installation and operation costs, and costs of importing the energy from the grid) and battery degradation rate.
Simulations on the example of a hybrid system have shown that it is possible to quantify the influence of different criteria on the optimal solution of the problem. In the case of maximizing only the EV charging energy originating from renewable sources, 86.7% of the required energy comes from the solar power plant. In the case of multicriteria optimization, the criteria for battery degradation is influencing the charging/discharging process, and the amount of renewable energy in the charging process is reduced to 56%.
In addition, the influence of different decision-maker’s preferences was quantified. In the complementary attribute case, the amount of renewable energy in the charging process is increased in comparison to the additive attribute aggregation to 73%.
Finally, the battery capacity was optimized. In the case of an additive model, the maximum utility function is achieved at a battery capacity of 30 kWh. In the complementary model, the emphasis is on the balanced values of all individual criteria, and the preference is given to lower values of battery capacity since then system costs and battery degradation are as important as the share of renewable sources. The optimal value of battery capacity is achieved with C = 10 kWh.
Author Contributions
Authors worked jointly on this paper. Conceptualization, A.P. and A.J.; methodology, A.P. and A.J.; software, A.P.; validation, A.J.; formal analysis, A.P. and A.J.; investigation, A.P. and A.J.; resources, A.P. and A.J.; data curation, A.P.; writing—original draft preparation, A.P.; writing—review and editing, A.J.; visualization, A.P.; supervision, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Serbian Ministry of Education, Science and Technological Development through the Mathematical Institute of the Serbian Academy of Sciences and Arts.
Data Availability Statement
Please refer to suggested Data Availability Statements in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| SOCt | Battery state of charge at time t |
| SOCS,t | Solar energy share state of charge at time t |
| SOCG,t | Public grid energy share state of charge at time t |
| C | Battery capacity (kWh) |
| kc/d | Charging/discharging efficiency |
| PB,t | Battery power at time t (kW) |
| PBS, | Battery power originating from solar energy at time t (kW) |
| PBG,t | Battery power originating from the public grid at time t (kW) |
| PEV,t | Electric vehicle charging power at time t (kW) |
| PEVS,t | Electric vehicle charging power originating from solar energy at time t (kW) |
| PEVG,t | Electric vehicle charging power originating from the public grid at time t (kW) |
| PEVBS,t | Electric vehicle charging power originating from the solar battery share at time t (kW) |
| PEVBG,t | Electric vehicle charging power originating from the grid battery share at time t (kW) |
| PS,i,t; QS,i,t | Solar PV plant power at node i, at time t (kW) |
| PB,i,t; QB,i,t | Battery power at node i, at time t (kW) |
| PL,i,t; QL,i,t | Load demand at node i, at time t (kW) |
| PG,i,t; QG,i,t | Public grid power at node i, at time t (kW) |
| PEV,i,t; QEV,i,t | EV charging power at node i, at time t (kW) |
| Pbi,j; Qbi,j | Power flow in branch b from node i to j |
| Vi, θi | Voltage magnitude and angle at the node i |
| Gij, Bij | Branch conductance and susceptance from node i to j |
| φb | Total set of branches |
| Ah | Energy flow in ampere-hours |
| Qloss | Battery degradation (%) |
| Irate | Battery charge/discharge rate expressed in capacity ratio C |
| ct | Spot energy price at time t (€/kWh) |
| cB | Levelized daily battery installation and operation costs (€/kWh∙day) |
| Ures | Renewable energy share utility function |
| Utc | Total costs utility function |
| Ubd | Battery degradation utility function |
References
- Larminie, J.; Lowry, J. Electric Vehicle Technology Explained; Wiley: New York, NY, USA, 2003. [Google Scholar]
- Ehsani, M.; Gao, Y.; Gay, S.E.; Emadi, A. Modern Electric, Hybrid Electric and Fuel Cell Vehicles; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Wirasingha, S.G.; Pihef, A.E. Plug-in hybrid electric factor. IEEE Trans. Veh. Technol. 2011, 60, 1279–1284. [Google Scholar] [CrossRef]
- Nichoals, M.; Hall, D. Lessons Learned on Early Electric Vehicle Fast-charging Deployments, White Paper for the International Council on Clean Transportation. 2018. Available online: https://www.theicct.org/sites/default/files/publications/ZEV_fast_charging_white_paper_final.pdf (accessed on 29 March 2020).
- Bhatti, A.R.; Salam, Z.; Aziz, M.J.B.A.; Yee, K.P.; Ashique, R.H. Electric vehicles charging using photovoltaic: Status and technological review. Renew. Sustain. Energy Rev. 2016, 54, 34–47. [Google Scholar] [CrossRef]
- Kawamura, N.; Muta, M. Development of solar charging system for plug-in hybrid electric vehicles and electric vehicles. In Proceedings of the 2012 International Conference on Renewable Energy Research and Applications (ICRERA), Nagasaki, Japan, 11–14 November 2012; IEEE: Nagasaki, Japan, 2012; pp. 1–5. [Google Scholar]
- Mesentean, S.; Feucht, W.; Kula, H.-G.; Frank, H. Smart charging of electric scooters for home to work and home to education transports from grid connected photovoltaic-systems. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; IEEE: Manama, Bahrain, 2010; pp. 73–78. [Google Scholar]
- Gurkaynak, Y.; Khaligh, A. Control and Power Management of a Grid Connected Residential Photovoltaic System with Plug-in Hybrid Electric Vehicle (PHEV) Load. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; IEEE: Washington, DC, USA, 2009; pp. 2086–2091. [Google Scholar]
- Gurkaynak, Y.; Li, Z.; Khaligh, A. A novel grid-tied, solar powered residential home with plug-in hybrid electric vehicle (PHEV) loads. In Proceedings of the 2009 IEEE Vehicle Power and Propulsion Conference, Dearborn, MI, USA, 7–11 September 2009; IEEE: Dearborn, MI, USA, 2009; pp. 813–816. [Google Scholar]
- Robalino, D.M.; Kumar, G.; Uzoechi, L.O.; Chukwu, U.C.; Mahajan, S.M. Design of a docking station for solar charged electric and fuel cell vehicles. In Proceedings of the 2009 International Conference on Clean Electrical Power, Capri, Italy, 9–11 June 2009; IEEE: Capri, Italy, 2009; pp. 655–660. [Google Scholar]
- Sujitha, N.; Krithiga, S. RES based EV battery charging system: A review. Renew. Sustain. Energy Rev. 2017, 75, 978–988. [Google Scholar] [CrossRef]
- Tesfaye, M.; Castello, C.C. Minimization of impact from electric vehicle supply equipment to the electric grid using a dynamically controlled battery bank for peak load shaving. In Proceedings of the 2013 IEEE PES Innovative Smart Grid Technologies Conference (ISGT), Washington, DC, USA, 24–27 February 2013; IEEE: Washington, DC, USA, 2013; pp. 1–6. [Google Scholar]
- Castello, C.C.; LaClair, T.J.; Maxey, L.C. Control strategies for electric vehicle (EV) charging using renewables and local storage. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; IEEE: Dearborn, MI, USA, 2014; pp. 1–7. [Google Scholar]
- Mouli, G.C.; Bauer, P.; Zeman, M. System design for a solar powered electric vehicle charging station for workplaces. Appl. Energy 2016, 168, 434–443. [Google Scholar] [CrossRef]
- García-Triviño, P.; Torreglosa, J.P.; Fernández-Ramírez, L.M.; Jurado, F. Control and operation of power sources in a medium-voltage direct-current microgrid for an electric vehicle fast charging station with a photovoltaic and a battery energy storage system. Energy 2016, 115, 38–48. [Google Scholar] [CrossRef]
- Janjic, A.; Velimirovic, L. Optimal Scheduling of Utility Electric Vehicle Fleet Offering Ancillary Services. ETRI J. 2015, 37, 273–282. [Google Scholar] [CrossRef]
- Janjic, A.; Velimirovic, L.; Stankovic, M.; Petrusic, L. Commercial electric vehicle fleet scheduling for secondary frequency control. Electr. Power Syst. Res. 2017, 147, 31–41. [Google Scholar] [CrossRef]
- Mossoba, J.; Kromer, M.; Faill, P.; Katz, S.; Borowy, B.; Nichols, S.; Casey, L.; Maksimovic, D.; Traube, J.; Lu, F. Analysis of solar irradiance intermittency mitigation using constant DC voltage PV and EV battery storage. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 18–20 June 2012; IEEE: Dearborn, MI, USA, 2012; pp. 1–6. [Google Scholar]
- Chaudhari, K.; Ukil, A.; Kumar, K.N.; Manandhar, U.; Kollimalla, S.K. Hybrid Optimization for Economic Deployment of ESS in PV-Integrated EV Charging Stations. IEEE Trans. Ind. Inform. 2018, 14, 106–116. [Google Scholar] [CrossRef]
- Bhatti, A.R.; Salam, Z.; Sultana, B.; Rasheed, N.; Awan, A.B.; Sultana, U.; Younas, M. Optimized sizing of photovoltaic grid-connected electric vehicle charging system using particle swarm optimization. Int. J. Energy Res. 2019, 43, 500–522. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, Y.J.A. A Model Predictive Control Approach for Low-Complexity Electric Vehicle Charging Scheduling: Optimality and Scalability. IEEE Trans. Power Syst. 2017, 32, 1050–1063. [Google Scholar] [CrossRef]
- Domínguez-Navarro, J.A.; Dufo-López, R.; Yusta, J.; Artal-Sevil, J.; Bernal-Agustín, J.L. Design of an electric vehicle fast-charging station with integration of renewable energy and storage systems. Int. J. Electr. Power Energy Syst. 2019, 105, 46–58. [Google Scholar] [CrossRef]
- Badea, G.; Felseghi, R.; Varlam, M.; Filote, C.; Culcer, M.; Iliescu, M.; Raboaca, M.S. Design and Simulation of Romanian Solar Energy Charging Station for Electric Vehicles. Energies 2018, 12, 74. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, J. The Energy Management and Optimized Operation of Electric Vehicles Based on Microgrid. IEEE Trans. Power Deliv. 2014, 29, 1427–1435. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, N.; Kang, C.; Wang, R.; Wang, J.; Cui, Z.; Yang, Z. Day-ahead battery scheduling in microgrid considering wind power uncertainty using ordinal optimization. In Proceedings of the 2014 North American Power Symposium (NAPS), Pullman, WA, USA, 7−9 September 2014; pp. 1–6. [Google Scholar]
- Hafez, O.; Bhattacharya, K. Optimal design of electric vehicle charging stations considering various energy resources. Renew. Energy 2017, 107, 576–589. [Google Scholar] [CrossRef]
- Baik, S.H.; Jin, Y.G.; Yoon, Y.T. Determining Equipment Capacity of Electric Vehicle Charging Station Operator for Profit Maximization. Energies 2018, 11, 2301. [Google Scholar] [CrossRef]
- Torreglosa, J.P.; García-Triviño, P.; Fernández-Ramirez, L.M.; Jurado, F. Decentralized energy management strategy based on predictive controllers for a medium voltage direct current photovoltaic electric vehicle charging station. Energy Convers. Manag. 2016, 108, 1–13. [Google Scholar] [CrossRef]
- Yao, L.; Damiran, Z.; Lim, W.H. Optimal Charging and Discharging Scheduling for Electric Vehicles in a Parking Station with Photovoltaic System and Energy Storage System. Energies 2017, 10, 550. [Google Scholar] [CrossRef]
- Dai, Q.; Liu, J.; Wei, Q. Optimal Photovoltaic/Battery Energy Storage/Electric Vehicle Charging Station Design Based on Multi-Agent Particle Swarm Optimization Algorithm. Sustainability 2019, 11, 1973. [Google Scholar] [CrossRef]
- Hassoune, A.; Khafallah, M.; Mesbahi, A.; Bouragba, T. Power Management Strategies of Electric Vehicle Charging Station Based Grid Tied PV-Battery System. Int. J. Renew. Energy Res. 2018, 8, 1–10. [Google Scholar]
- Wi, Y.-M.; Lee, J.-U.; Joo, S.-K. Electric vehicle charging method for smart homes/buildings with a photovoltaic system. IEEE Trans.Consum. Electron. 2013, 59, 323–328. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized Operational Cost Reduction for an EV Charging Station Integrated With Battery Energy Storage and PV Generation. IEEE Trans. Smart Grid 2019, 10, 2096–2106. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel–cobalt–manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).