Type Synthesis of Variable Compression Ratio Engine Mechanisms

Abstract

Type synthesis of two-degrees-of-freedom (DOF) planar mechanisms has been carried out using graph theory to determine the possible kinematic structures of variable compression ratio (VCR) engine mechanisms with two to three independent loops, and has resulted in the structures of 87 mechanisms satisfying search specification. By applying evaluation criteria to the enumerated mechanisms, the kinematic structures of three mechanisms are selected as suitable VCR engine mechanisms and verified by analysis results. In this research, VCR engine mechanisms with revolute joints and only one prismatic joint are enumerated, and the basic method to determine the VCR engine mechanisms with higher pairs is discussed. The procedure used in this research can be utilized to determine the kinematic structures of desired mechanisms and the results can be used as an atlas of two-DOF adjustable slider-crank mechanisms.

1. Introduction

The automobile market of today is built around a common goal of creating environmentally friendly vehicles, such as electric and fuel cell electric vehicles. However, most vehicles sold on the market are still powered by internal combustion (IC) engines, and in order to keep pace with this global trend, technologies for ecofriendly and high-efficiency IC engines are constantly being developed, with variable compression ratio (VCR) engines being a classic example. The VCR engine operates at high or low compression ratios to maximize the efficiency or to avoid knock depending on the operating conditions, and numerous studies have proved that the technology can improve fuel efficiency and performance [1,2,3,4,5].

Among the literature on the kinematic structures of VCR engines [6,7,8,9,10,11,12,13,14,15,16,17,18], Freudenstein and Maki [6] applied a systematic search procedure for the type synthesis of one-degree-of-freedom (DOF) variable-stroke IC engine mechanisms and enumerated 39 kinematic structures with six and eight links, and then determined three potentially acceptable mechanisms by evaluating the enumerated structures. H. N. Pouliot et al. [7] developed a nine-link variable-displacement engine and obtained data on power, fuel consumption, and emission with engine dynamometer tests. A VCR system with a multi-link mechanism was presented by Moteki et al. [8]. Tanik and Söylemez [9] proposed a compliant variable-stroke mechanism. Mendler and Gravel [10] introduced the two-cylinder ENVERA VCR engine; Rabhi et al. [11] studied the gear design and dimensioning for the MCE-5 VCR engine. A variable displacement engine with the capability to vary stroke length and compression ratio independent of one another was designed and analyzed by Rosso et al. [12]. Cassiani et al. [13] analyzed the kinematic and dynamic model of the Saab Variable Compression (SVC) engine mechanism. Kwak et al. [14] proposed a kinematic conceptual design procedure for in-line four-cylinder VCR engine mechanisms considering vertical second harmonic acceleration.

The compression ratio of the VCR engine can be modified by moving or tilting the cylinder head, moving the crankshaft axis, varying the piston deck height or the combustion chamber volume, moving the crankpin, or modifying the connecting rod geometry using a control linkage system [1,15,16]. Mo et al. [17] classified various VCR engine mechanisms according to their kinematic graphs. Hoeltgebaum et al. [18] classified VCR engines based on a patent survey to investigate the topological and structural characteristics, and suggested that there are still possibilities for the development of new VCR engine mechanisms.

The type synthesis of mechanisms refers to the determination of possible kinematic structures to perform a given task. The aim of this paper is to find all possible two-DOF VCR engine mechanisms with two to three independent loops and with up to nine links by a systematic type synthesis procedure. For this, graph theory is applied to enumerate unlabeled graphs that represent the possible kinematic chains of VCR engines. By labeling the enumerated graphs according to a practical specification for the kinematic structure of the VCR engine, 87 mechanisms are enumerated from 17 graphs. Applying strict evaluation criteria to the enumerated kinematic structures, three of them are selected as appropriate VCR engine mechanisms, and their variable compression ratio capability is verified by the results of kinematic analysis.

2. Kinematic Chains, Graphs, and Graph Enumeration

2.1. Kinematic Chains, Mechanisms, and Graphs

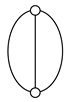
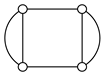
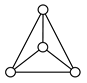
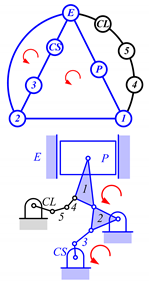
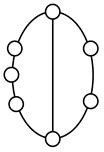
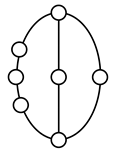
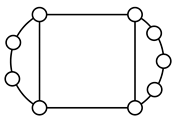
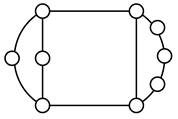
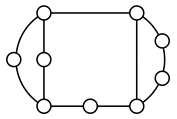
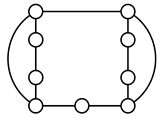
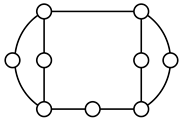
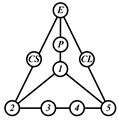
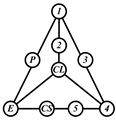
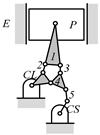
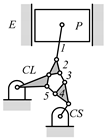
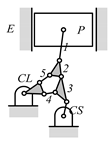
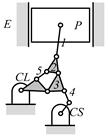
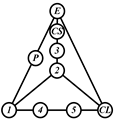
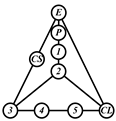
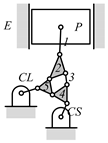
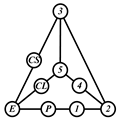
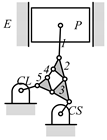
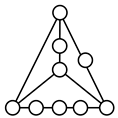
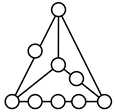
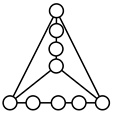
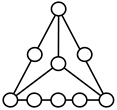
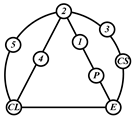
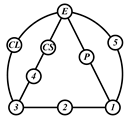
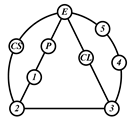
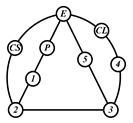
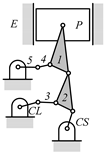
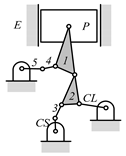
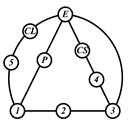
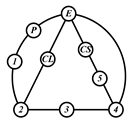
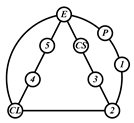
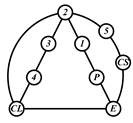
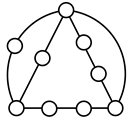
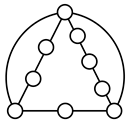
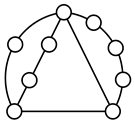
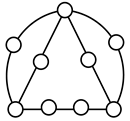
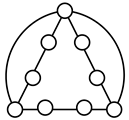
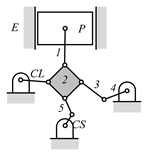
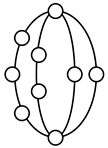
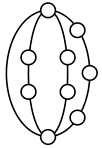
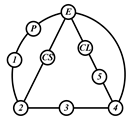
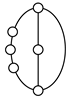
A kinematic chain is defined as a set of links connected by joints. If one of the links in a kinematic chain is fixed and relative motion between all links is possible, it is called a mechanism. A graph is defined as a set of vertices connected by edges, and the kinematic structure of a kinematic chain with l links and j joints can be represented by a unique graph in which the links are represented by l vertices and the joints by j edges. For example, the Watt chain with six links and seven joints shown in Figure 1a is represented by the conventional graph with six vertices and seven edges shown in Figure 1c.

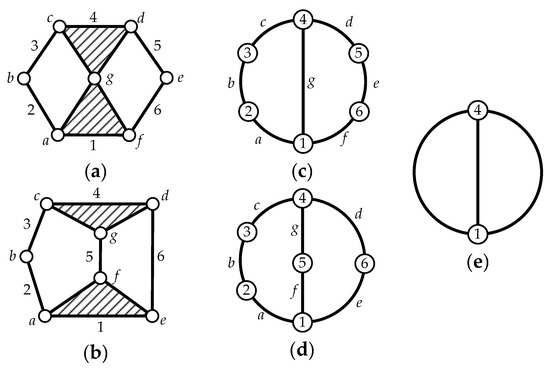
Figure 1. Kinematic chains and their graphs: (a) Watt chain; (b) Stephenson chain; (c) conventional graph of (a); (d) conventional graph of (b); and (e) contracted graph of (c) and (d).

A link in a kinematic chain is referred to as a binary, ternary, or quaternary link if it has two, three, or four joints. Equivalently, a vertex in a graph is called a binary, ternary, or quaternary vertex, or vertex of degree two, three, or four if it is connected by two, three, or four edges.

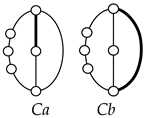
Binary links connected in series by joints between nonbinary links form a binary link chain in a kinematic chain, and binary vertices connected in series by edges between nonbinary vertices form a binary string in its conventional graph. A contracted graph can be obtained by replacing every binary string in a conventional graph with a single edge, and this process is called a contraction. Figure 1e shows the contracted graph of the conventional graph depicted in Figure 1c.

Conversely, if a contracted graph of kinematic chains to be synthesized is determined, it can be expanded by replacing the edges in the contracted graph by binary strings to obtain conventional graphs, and each graph can be translated into the corresponding kinematic chain. For example, if the contracted graph shown in Figure 1e is determined for the synthesis of one-DOF planar six-link kinematic chains, it can be expanded to the two conventional graphs in Figure 1c,d, and then each graph can be translated into the kinematic chain shown in Figure 1a,b, respectively. In this paper, the above procedure is used for the enumeration and type synthesis of VCR engine mechanisms that can be outlined as follows [19].

2.2. Number Synthesis of Kinematic Chains

For the enumeration of kinematic chains, the number of links and the number of joints need to be determined. For this, the general DOF equation for a mechanism and Euler’s formula for the number of independent loops in a connected graph can be used. The DOF of a mechanism, F, can be obtained by:

$$F=\lambda \left(l-j-1\right)+{{\displaystyle \sum }}_{i=1}^j{f}_i,$$

(1)

where λ is the DOF of the space within which a mechanism operates, l is the number of links, j is the number of joints, and f_i is the degrees of relative motion permitted by joint i.

The number of independent loops, L_ind, in a connected graph, hence in the corresponding kinematic chain can be determined by Euler’s formula which can be written as:

$$L_{ind}=j-l+1.$$

(2)

Note that the total number of loops in a graph is L_ind + 1 because there is always a peripheral or external loop. Substituting Equation (2) into Equation (1) gives:

$$F=-\lambda L_{ind}+{{\displaystyle \sum }}_{i=1}^j{f}_i.$$

(3)

In order to find the number of links and the number of joints in kinematic chains to be synthesized for a prescribed number of DOF and number of independent loops, the joints that will be used in the kinematic chains need be classified according to the DOFs permitted by the joints. For example, a revolute joint permits two paired links to rotate, with respect to each other, about the rotation axis. Hence, the revolute joint is a one-DOF joint. The prismatic and helical joints are also one-DOF joints. The joints that permit two-DOF are the cylindrical, cam, and gear joints; the planar and spherical joints are three-DOF joints. Let j_i denote the number of joints that permits i-DOF. Then, the total number of joints is:

$$j=j_1+j_2+j_3,$$

(4)

and ${{\displaystyle \sum }}_{i=1}^j{f}_i$ in Equation (3) can be written as:

$${{\displaystyle \sum }}_{i=1}^j{f}_i=j_1+2j_2+3j_3=j+j_2+2j_3.$$

(5)

For example, the kinematic chains shown in Figure 1 have six links and seven revolute joints. Hence, Equation (4) becomes j = j₁ = 7; Equation (5) gives ${{\displaystyle \sum }}_{i=1}^j{f}_i=j_1=7;$ since the kinematic chain is planar, $\lambda =3$ and Equation (1) yields F =1; Equation (2) gives $L_{ind}=2.$ Substituting Equation (5) into Equation (3) yields the number of joints in a kinematic chain or edges in a graph as:

$$j=F+\lambda L_{ind}-j_2-2j_3,$$

(6)

and substituting Equation (6) into Equation (2) gives the number of links or vertices as:

$$l=F+\left(\lambda -1\right)L_{ind}-j_2-2j_3+1.$$

(7)

For the enumeration of graphs, vertices need to be classified according to its degree. The degree of a vertex is defined as the number of edges connected to the vertex. Let l_i denote the number of vertices of degree i. Then, for a connected graph, since every vertex is connected to at least two other vertices, the minimum degree of a vertex is two, and the total number of vertices in a graph is:

$$l=l_2+l_3+\cdots +l_m,$$

(8)

where m is the maximum degree of a vertex that can be found by the fact that the total number of loops of which a vertex is a part is equal to its degree. Hence it can be written that:

$$2\le m\le L_{ind}+1.$$

(9)

Since each of the l_i vertices is connected by i edges and each edge connects two vertices, it follows that:

$$2j=2l_2+3l_3+\cdots +m{l}_m.$$

(10)

Subtracting Equation (8) from Equation (10) yields:

$$l_2=2j-l-\left\{2l_3+3l_4+\cdots \left(m-1\right)l_m\right\},$$

(11)

and subtracting Equation (10) from three times Equation (8) gives:

$$l_2=3l-2j+\left\{l_4+2l_5+\cdots \left(m-3\right)l_m\right\}.$$

(12)

Since the values in the parentheses in Equations (11) and (12) are equal to or greater than zero, it follows that:

$$3l-2j\le l_2\le 2j-l.$$

(13)

By solving Equations (8) and (10) simultaneously with Equations (9) and (13), all possible combinations of non-negative integer values of l_i can be determined.

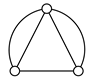
As shown in Figure 1c,e, since all of the binary vertices in a conventional graph are removed in its contracted graph, the number of vertices in the contracted graph, l^c, can be determined by:

$$l^c=l-l_2,$$

(14)

and since the number of removed edges from a conventional graph to form its contracted graph is equal to the number of binary vertices, the number of edges in the contracted graph, j^c, is:

$$j^c=j-l_2.$$

(15)

After enumerating contracted graphs with l^c vertices and j^c edges given by Equations (14) and (15), the edges in the contracted graphs need to be replaced by binary strings to determine conventional graphs. Let a binary string of length i in a conventional graph be defined as a string of i vertices of degree two connected in series by i + 1 edges between nonbinary vertices. For example, the string g in Figure 1c is a binary string of length 0; the string d-6-e in Figure 1d is a binary string of length 1, and the strings a-2-b-3-c in Figure 1c,d are binary strings of length 2. Let b_i denote the number of binary strings of length i, then the number of binary vertices in a conventional graph equals:

$$l_2=b_1+2b_2+\cdots +q{b}_q,$$

(16)

where q is the longest binary string in a conventional graph, which can be determined by the fact that the DOF of a binary string in the graph of a mechanism must be less than that of the mechanism as a whole. Hence from Equation (3), it can be written that:

$$q\le F+\lambda -2.$$

(17)

Likewise, since the number of binary strings in a conventional graph is equal to the number of edges in its contracted graph, it follows that:

$$j^c=b_0+b_1+b_2+\cdots +b_q=j-l_2.$$

(18)

By solving Equations (16) and (18) simultaneously with Equation (17), all possible combinations of non-negative integer values of b_i can be determined. Then, permute the edges of each contracted graph with each combination of binary strings obtained to enumerate conventional graphs.

2.3. Number Synthesis of Planar Two-DOF VCR Engine Kinematic Chains with One-DOF Joints

The number of links, l, and the number of joints, j, according to the number of independent loops, L_ind, for planar two-DOF VCR engine mechanisms with only one-DOF joints that obey the general DOF equation given by Equation (1), can be obtained by inserting F = 2, λ= 3, j₂ = j₃ = 0 into Equations (6) and (7); the numbers of l_i, b_i, l^c, and j^c can be determined using Equations (8)–(18).

In this research, the search of possible VCR engine mechanisms is limited to the kinematic chains with two to three independent loops to find linkages having a moderate number of links. The results of the number synthesis are shown in Table 1.

Table 1. Number synthesis solutions for possible two-degrees-of-freedom (DOF) variable compression ratio (VCR) engine mechanisms with only one-DOF joints and with up to three independent loops and nine links.

Lind	l	j	l2	l3	l4	lc	jc	b0	b1	b2	b3
1	5	5	5	0	0	-	-	-	-	-	-
2	7	8	5	2	0	2	3	0	1	2	0
								0	2	0	1
								1	0	1	1
3	9	11	5	4	0	4	6	1	5	0	0
								2	3	1	0
								3	1	2	0
								3	2	0	1
								4	0	1	1
			6	2	1	3	5	0	4	1	0
								1	2	2	0
								1	3	0	1
								2	0	3	0
								2	1	1	1
								3	0	0	2
			7	0	2	2	4	0	1	3	0
								0	2	1	1
								1	0	2	1
								1	1	0	2

2.4. Graph Enumeration

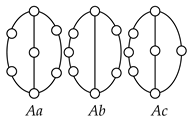
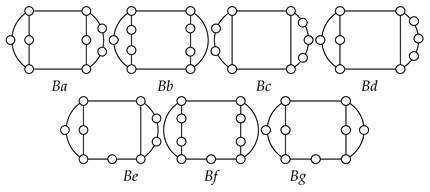
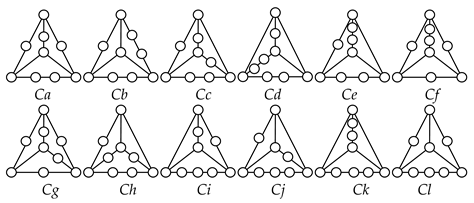
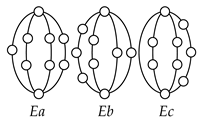
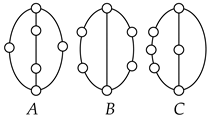
Table 2 shows five contracted graphs and 38 conventional graphs that are enumerated according to the numbers and types of vertices and binary strings given in Table 1, except for the five-link kinematic chain with one independent loop. The five-link kinematic chain with one independent loop cannot be represented by a contracted graph because it does not have ternary or higher links.

Table 2. Graphs of planar two-DOF kinematic chains enumerated according to Table 1.

Lind	Contracted Graph	Conventional Graphs
2	A
3	B
	C
	D
	E

In general, a variable mechanism requires at least two independent loops [6]: a driving loop and a control loop, hence the kinematic chains with one independent loop are excluded from the type synthesis in this study.

3. Search Specification for the Kinematic Structures of VCR Engine Mechanisms

For the type synthesis of possible VCR engine mechanisms, the links required in the engine, such as the engine block, control link, crankshaft, and piston, need to be assigned to the vertices and revolute and prismatic joints to the edges in the conventional graphs shown in Table 2. For this, the search specifications for the kinematic structures of two-DOF VCR engine mechanisms sought in this research are listed in Table 3.

Table 3. Search specification of VCR engine mechanisms.

	Search Specification
1	The search is limited to two-DOF planar mechanisms having two to three independent loops that can be represented by the conventional graphs shown in Table 2.
2	The engine (cylinder) block is the ground link that is considered fixed.
3	The engine block is a ternary or higher link [6,18]: the piston is connected to the engine block by a prismatic joint; the crankshaft and control link are connected to the engine block by a respective revolute joint, hence a control via a floating-link connection is excluded.
4	Mechanisms with revolute joints and only one prismatic joint are enumerated: any revolute joint can be replaced by a prismatic joint after the enumeration, except for the joints connecting 1) the engine block and crankshaft, and 2) the piston and connecting rod (For examples, see Table 6b,c; Table 6d,e). This joint substitution simplifies the enumeration.
5	The crankshaft and piston are binary links [6,18].
6	The crankshaft, control link, and piston are not connected directly to each other.

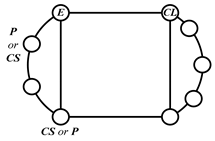
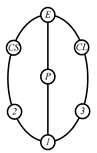
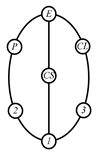
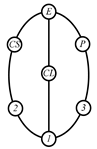
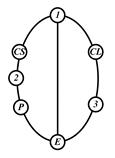
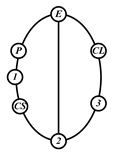
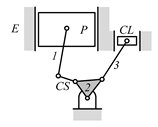
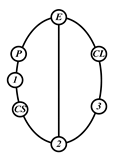
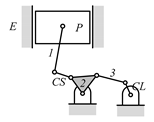
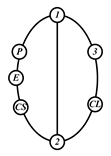
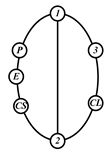
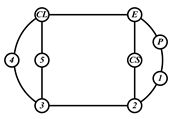
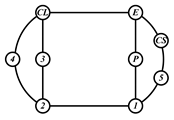
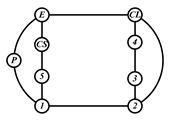
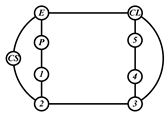
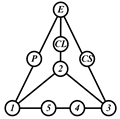
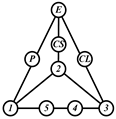
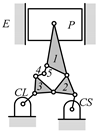
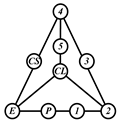
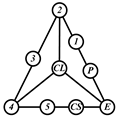
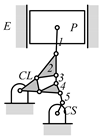
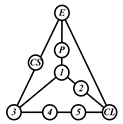
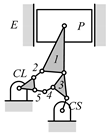
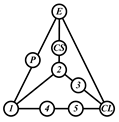
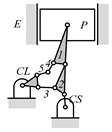
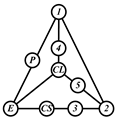
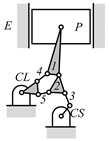
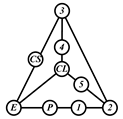
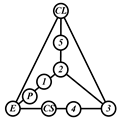
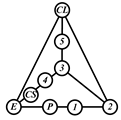
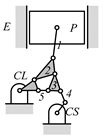
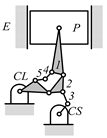
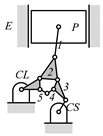
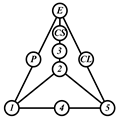
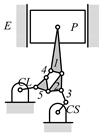
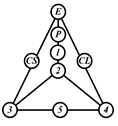
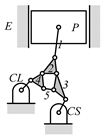
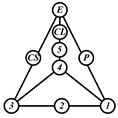
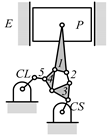
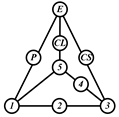
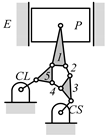
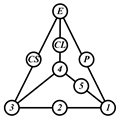
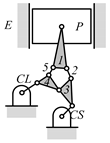
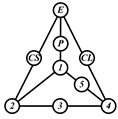
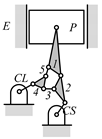
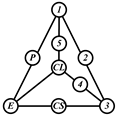
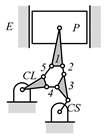
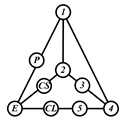
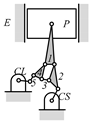
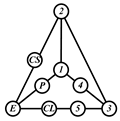
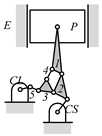
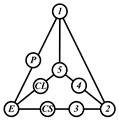
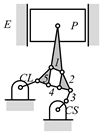
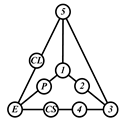
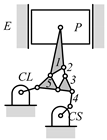
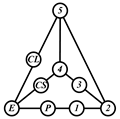
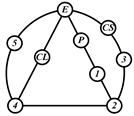
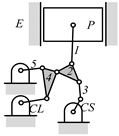
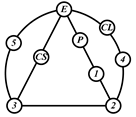
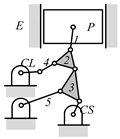
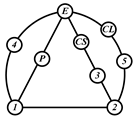
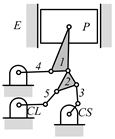
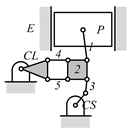
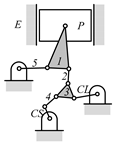
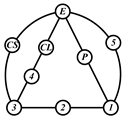
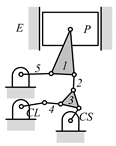
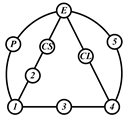
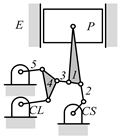
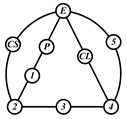
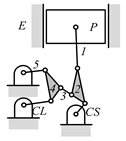
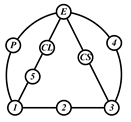
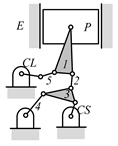
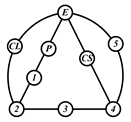
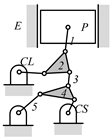
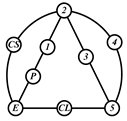
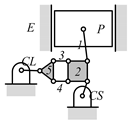
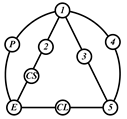
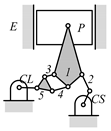
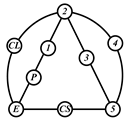
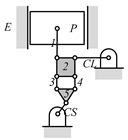
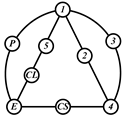
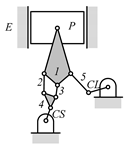
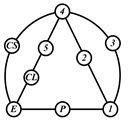
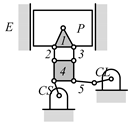
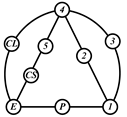
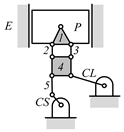
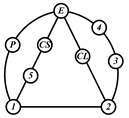
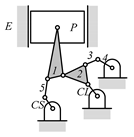
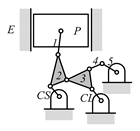
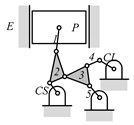
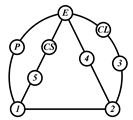
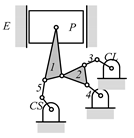
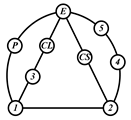
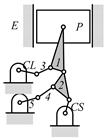
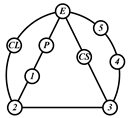
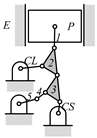
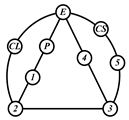
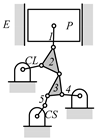
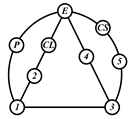
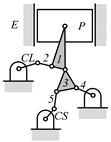
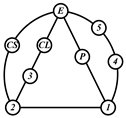
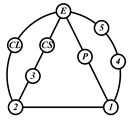
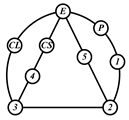
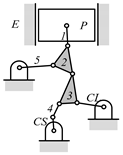
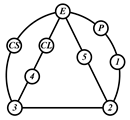
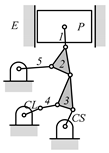
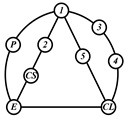
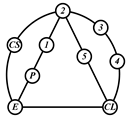
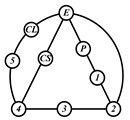
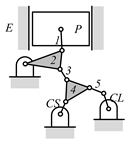
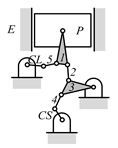
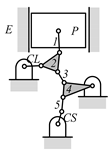
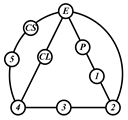
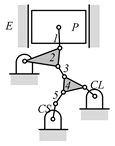
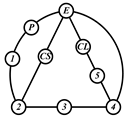
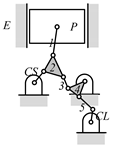
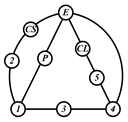
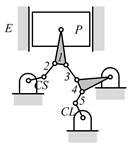
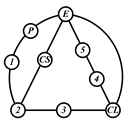
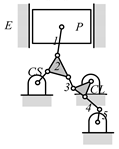
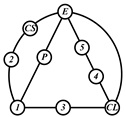
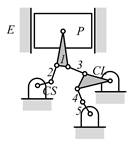
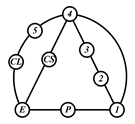
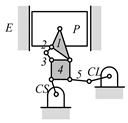
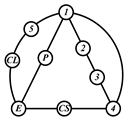
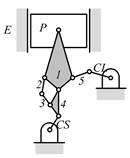
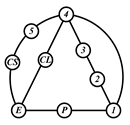
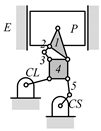
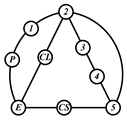
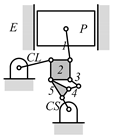
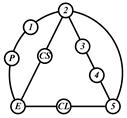
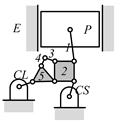
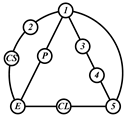
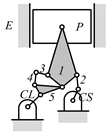
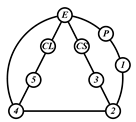
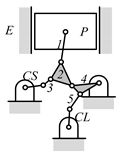
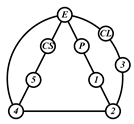
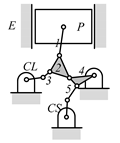
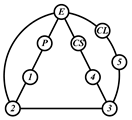
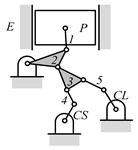
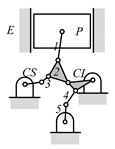
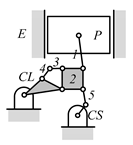
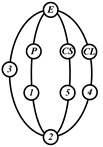
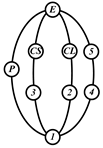
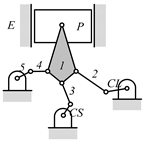
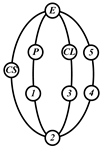
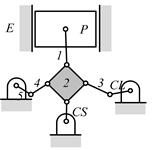
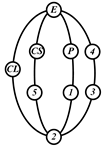
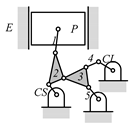
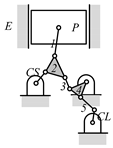
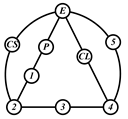
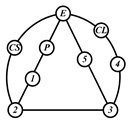
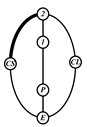
By search specification 3 in Table 3, the engine block (E), crankshaft (CS), control link (CL), and piston (P) are assigned to the vertices in the conventional graphs as shown in Figure 2. Some of the VCR engine mechanisms that do not satisfy search specification 2 or 3 in Table 3 are discussed in Section 4.2.

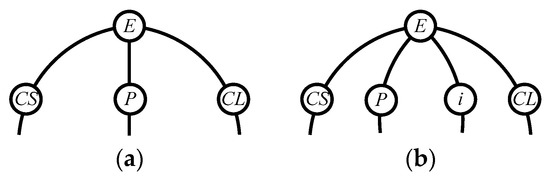
Figure 2. Assignment of engine block (E), crankshaft (CS), piston (P), and control link (CL): (a) When E is a ternary link and (b) When E is a quaternary link where i represents link i.

When assigning the links to the vertices in the graphs in Table 2, there are cases that would result in mechanisms that cannot be used as VCR engine mechanisms. These cases are listed in Table 4 and excluded from the enumeration.

Table 4. Excluded cases from the enumeration.

Case	Labeled Graph and Mechanism	Comment
I		Partially locked mechanism: The DOF associated with any loop in a mechanism must be at least equal to one [19]. A four-link loop consisting of the engine block, crankshaft, control link, and a floating link shown left becomes a structure when the control link is fixed in a position.
II	Four-link slider-crank mechanism Six-link slider-crank mechanism	No stroke variation: The stroke cannot be varied when the engine block, crankshaft, connecting rod, and piston are assigned to a one-DOF loop or a one-DOF multi-loop. If these links are in a one-DOF loop, they form a four-link slider-crank mechanism which is the kinematic structure of the fixed-stroke engine and the stroke does not change. If these links are assigned to a one-DOF multi-loop, they form a one-DOF six-link slider-crank mechanism and the stroke does not change.
III		Links cannot be assigned according to the search specification: No matter where the engine block is assigned, either the piston or the crankshaft would be assigned to a ternary link. This violates search specification 5 in Table 3.

4. Type Synthesis of VCR Engine Mechanisms with One-DOF Joints

In this section, links are assigned to the vertices in the 38 unlabeled conventional graphs in Table 2 to find the possible VCR engine mechanisms. By labeling the graphs according to the search specifications given in Table 3 and the excluded cases given in Table 4, the kinematic structures of three seven-link and 84 nine-link VCR engine mechanisms are determined as follows.

4.1. VCR Engine Mechanisms with Seven Links and Eight Joints

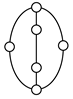
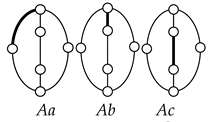
As shown in Table 2, there are three unlabeled graphs of two-DOF kinematic chains with seven links and eight joints expanded from contracted graph A. The labeled graphs determined by assigning the engine block, piston, crankshaft, control link, and other links to the vertices in the unlabeled graphs according to the search specification are shown in Table 5 along with the corresponding schematic diagram and the lists of patents or the excluded cases from the enumeration given in Table 4. As shown, three possible kinematic structures are found from the graph Aa in Table 2, and no feasible VCR engine mechanisms are determined from graphs Ab and Ac due to the search specifications and excluded cases.

Table 5. VCR engine mechanisms with seven links and eight joints expanded from the contracted graph A in Table 2.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
02Aa01	Ford—US7191756 [20] FEV—US5595146 [21]	02Aa02	Daimler—US6772717B2 [22] Nissan—US7669559B2 [23] Honda—US7905210B2 [24] Pattakon—US8267055B2 [25] Mayflower—US6009845 [26]
02Aa03		02Ab00	Case I (See Table 6)
02Ac00	Cases I and II

Note that the first and second digits of the graph identification number shown under the labeled graph in Table 5 denote the number of two-DOF joints and the number of independent loops in the corresponding graph, respectively, and the following two alphabet letters identify the conventional graph in Table 2.

4.2. Seven-Link and Eight-Joint VCR Engine Mechanisms Not Satisfying the Search Specification

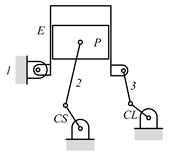
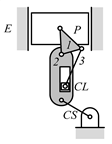
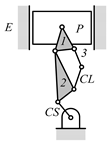
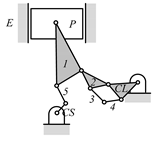
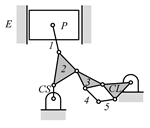
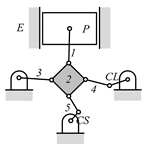
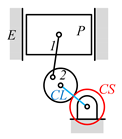
Some patented VCR engine mechanisms derived from the graph 02Ab00 in Table 5 are shown in Table 6, which are not enumerated in this paper because they do not satisfy the search specifications given in Table 3. Table 6a shows the labeled graph and schematic diagram of the VCR engine introduced by SAAB [27]. The compression ratio is varied by tilting the engine (cylinder) block. In this case, since the engine block is not the ground link, it does not satisfy search specification 2 and is excluded from the enumeration. The examples of the VCR engine that varies the compression ratio by moving the crankshaft axis are shown in Table 6b,c, each of which is patented by Caterpillar [28] and Hyundai [29]. As their crankshafts are not directly connected to the engine block, they do not satisfy search specification 3. The VCR engines developed by FEV [30] shown in Table 6d and by Daimler [31] shown in Table 6e use a floating control link to rotate the eccentric piston pin to vary the compression ratio. Both are excluded from enumeration in this study, since they do not fit search specification 3.

Table 6. VCR engine mechanisms enumerated from the graph 02Ab00 in Table 5: (a) SAAB; (b) Caterpillar; (c) Hyundai; (d) FEV; and (e) Daimler.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
	SAAB—EP0560825B1 [27]		Caterpillar—US7370613B2 [28]
(a)		(b)
	Hyundai—US20100326404A1 [29]		FEV—DE102012014917A1 [30]
(c)		(d)
	Daimler—DE3148193 A1 [31]
(e)

4.3. Enumeration by Joint Substitution

As mentioned in search specification 4 in Table 3, any revolute joint can be replaced by a prismatic joint, except for the joints connecting the engine block and the crankshaft, and the piston and the connecting rod. The examples are shown in Table 6: the revolute joint connecting the engine block and the control link shown in Table 6c is replaced by the prismatic joint in Table 6b; the revolute joint joining the connecting rod (link 2) and the control link in Table 6e is substituted by the prismatic joint in Table 6d. The substitution of revolute joints by prismatic joints can be applied to the mechanisms enumerated in this research to find more diverse kinematic structures and makes the mechanism enumeration simple.

4.4. VCR Engine Mechanisms with Nine Links and Eleven Joints

According to the search specifications given in Table 3, links are assigned to the vertices in the unlabeled graphs of two-DOF kinematic chains with nine links and eleven joints shown in Table 2. As a result, 84 labeled graphs and the corresponding VCR engine mechanisms are determined as shown in Table 7, Table 8, Table 9 and Table 10. The patented nine-link VCR engine mechanisms [32,33,34,35,36] are also listed in the tables along with the corresponding schematic diagrams.

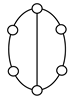
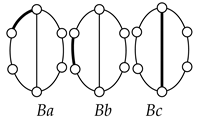
Table 7. VCR engine mechanisms with nine links and 11 joints expanded from the contracted graph B in Table 2.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
03Ba01	Hyundai US 20100000497A1 [32]	03Ba02
03Bb01		03Bb02
03Bc00	Case III	03Bd00	Case II
03Be00	Cases I and II	03Bf00	Case I
03Bg00	Cases I and II

Table 8. VCR engine mechanisms with nine links and 11 joints expanded from the contracted graph C.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
03Ca01		03Ca02
03Ca03		03Ca04
03Ca05		03Cb01
03Cc01		03Cc02
03Cc03		03Cc04
03Cd01		03Cd02
03Ce01		03Ce02
03Cf01		03Cf02
03Cf03		03Cg01
03Cg02		03Cg03
03Cg04		03Ch01	Hyundai US 7966980B2 [33]
03Ch02		03Ch03
03Ch04		03Ch05
03Ch06		03Ci00	Case I
03Cj00	Case I	03Ck00	Case III
03Cl00	Case I

Table 9. VCR engine mechanisms with nine links and 11 joints expanded from the contracted graph D.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
03Da01		03Da02
03Da03		03Da04
03Db01		03Db02
03Db03		03Db04
03Db05		03Db06
03Db07		03Db08
03Db09		03Db10
03Db11		03Db12
03Dc01		03Dc02
03Dc03		03Dc04
03Dc05		03Dc06
03Dc07		03Dc08
03Dc09		03Dc10
03Dc11		03Dc12
03Dc13		03Dc14
03Dd01		03Dd02
03Dd03	General Motors US 4270495 [34]	03Dd04
03Dd05	Nissan US 20130327302A1 [35]	03Dd06
03Dd07		03Dd08
03Dd09		03Dd10
03Dd11		03Dd12
03Dd13		03Dd14
03De01		03De02	Ford US 5136987 [36]
03De03		03De04
03De05		03Df00	Cases I and II
03Dg00	Cases I and II	03Dh00	Cases I and II
03Di00	Cases I and II	03Dj00	Case I
03Dk00	Cases I and II	03Dl00	Cases I and II
03Dm00	Case I

Table 10. VCR engine mechanisms with nine links and 11 joints expanded from the contracted graph E.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
03Ea01		03Ea02
03Ea03		03Ea04
03Eb00	Case I and II	03Ec00	Case I and II

A mechanism with multiple joints that connects more than three links cannot be represented by a graph. For graph representation, a multiple joint can be reconfigured by coaxial binary joints in different ways without affecting the functionality of the mechanism. Even though the graphs of the reconfigured mechanisms are nonisomorphic, they are kinematically equivalent. These equivalent mechanisms are called pseudoisomorphic mechanisms [19]. The mechanism patent by Hyundai [32] in Table 7 originally has a multiple joint and it is reconfigured and classified as 03Ba01 [17] in this research, while the same mechanism is classified as 03Dc03 in Hoeltgebaum et al. [18].

5. Selection of Suitable VCR Engine Mechanisms

The detailed evaluation of the mechanisms enumerated in Section 4 is quite difficult since the relationship between the stroke variation and the kinematic structure of each mechanism cannot be foreseen before the dimensional synthesis and analysis are carried out. Besides the difficulties in the dimensional synthesis of 2-DOF mechanisms, the same kinematic structure may have completely different kinematic and dynamic characteristics depending on the dimensions and pivot positions of implemented mechanisms. For example, Kwak et al. [14] showed that by adjusting the link lengths and pivot position of an initially designed Stephenson III VCR engine mechanism within prescribed tolerances, the maximum of the vertical second harmonic acceleration sum at the joints was decreased by 58.333% without sacrificing a desired stroke. Another example is that the kinematic chain 02Aa02 shown in Table 5 was patented by five automotive companies and implemented differently. For these reasons, the following four practical evaluation criteria that consider kinematic structure, force transmissibility, side thrust, and reliability are applied in this research to determine appropriate candidate VCR engine mechanisms by excluding inadequate kinematic structures.

The first criterion used to exclude unsuitable mechanisms is the presence of an unnecessary loop. Among the 87 enumerated mechanisms in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10, some nine-link linkages contain an unnecessary loop such that removing two links in that loop does not affect the function of the VCR engine. For example, the mechanism 03Bb01 in Table 7 has four-link loop with links 2-3-4-CL, but removing links 3 and 4 does not affect the relative motion between the remaining links. There are 30 mechanisms corresponding to this case and they are listed in Table 11. In fact, removing two links from the listed mechanisms results in one of the seven-link VCR engine mechanisms shown in Table 5. For example, 03Bb01 in Table 7 becomes 02Aa01 in Table 5 when links 3 and 4 are removed, and 03Bb02 in Table 7 becomes 02Aa02 in Table 5 when links 4 and 5 are removed.

Table 11. List of excluded mechanisms by the evaluation criteria.

Criterion	Excluded Mechanisms in Table 5, Table 6, Table 7, Table 8, Table 9 and Table 10
Presence of an unnecessary loop	03Bb01, 03Bb02, 03Ca01, 03Ca02, 03Ca03, 03Cc01, 03Cc02, 03Ce01, 03Ce02, 03Dc01, 03Dc02, 03Dc05, 03Dc06, 03Dc09, 03Dc10, 03Dc13, 03Dc14, 03Dd07, 03Dd08, 03Dd09, 03Dd10, 03Dd11, 03Dd12, 03Dd13, 03Dd14, 03De04, 03De05, 03Ea02, 03Ea03, 03Ea04
Three or more links are used to connect the piston and crankshaft	02Aa03, 03Ca04, 03Ca05, 03Cb01, 03Cc03, 03Cc04, 03Cd01, 03Cd02, 03Cf01, 03Cf02, 03Cf03, 03Cg01, 03Cg02, 03Cg04, 03Ch03, 03Ch04, 03Ch05, 03Ch06, 03Da01, 03Da02, 03Da03, 03Da04, 03Db01, 03Db02, 03Db05, 03Db06, 03Db09, 03Db10, 03Db11, 03Db12, 03Dc07, 03Dc08, 03Dc11, 03Dc12, 03Dd01, 03Dd02, 03Dd03, 03Dd04, 03De01, 03De02, 03De03, 03Ea01
Piston is not connected with binary link	02Aa01, 03Ba02, 03Cg03, 03Ch01, 03Ch02, 03Db03, 03Db08, 03Dc04, 03Dd06
Engine block is not a quaternary link	02Aa02, 03Ba01, 03Db07

Considering the force transmissibility and power loss from the piston to the crankshaft, the second evaluation criterion used in this research is the number of links connecting the piston and the crankshaft. The mechanisms having three or more links between the piston and the crankshaft are classified as unsuitable mechanisms. There are 42 mechanisms corresponding to this case as listed in Table 11.

The third criterion selected in this research is that the piston must be connected to a binary connecting rod to avoid excessive side thrust and piston friction [6]. There are nine mechanisms that have ternary or higher connecting rod as listed in Table 11 and they are excluded from the suitable VCR engine mechanisms.

Lastly, the fourth criterion is chosen to consider the reliability and efficiency in varying the compression ratio. If the links connected to the engine block by joints are only the piston, crankshaft, and control link, the force exerted by the piston would be imparted not only to the crankshaft, but a large portion of the piston force would also be transferred to the control link. This may require a large force or torque to vary and maintain the compression ratio. Consequently, it would be necessary to use a powerful actuator, and could even cause failure of the actuator. In order to reduce the force transmitted to the control link and force/torque required to alter and maintain the compression ratio, the ground connected control link can be installed in an independent loop in which neither the piston nor the crankshaft is included. By examining Figure 2, it can be concluded that the control link must be in an independent loop with another ground connected link other than the piston or crankshaft, and hence the engine block must be a quaternary link. The example can be found in the evolution of the Nissan VC-T engine which was initially designed with the mechanism [23] represented by the graph 02Aa02 shown in Table 5, then modified and produced in the form of the kinematic structure [35] with the graph 03Dd05 shown in Table 9. Applying the fourth criterion to the remaining six kinematic structures, three mechanisms are excluded as listed in Table 11.

Excluding the aforementioned 84 cases, the remaining three mechanisms shown in Table 12 are selected as suitable VCR engine mechanisms in this research, only one of which has been patented.

Table 12. Suitable VCR engine mechanisms.

Schematic diagram
Labeled graph	03Db04	03Dc03	03Dd05

Underlined graph identification numbers denote patented VCR engine kinematic chains.

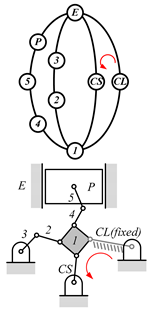
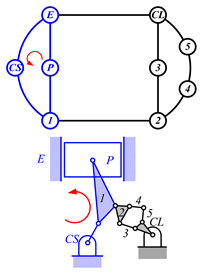
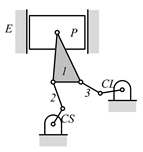
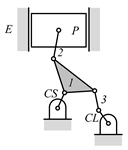
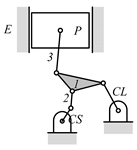
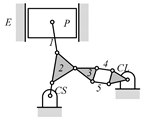
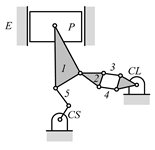
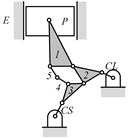
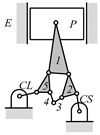
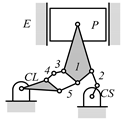
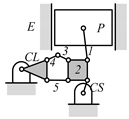
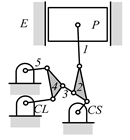
Examining the kinematic structures of the selected mechanisms in Table 12, each has an identical driving loop consisting of the engine block (E)—piston (P)—link 1—link 2—crankshaft (CS), but their control loops are different. In order to observe the variation principle of each mechanism, consider the case when the control link, CL, of each mechanism is actuated and positioned for a specific compression ratio. In the cases of the two mechanisms derived from graphs 03Db04 and 03Dd05, the four-link control loop (E-CL-4-5 or E-CL-5-4) in each mechanism becomes a structure, namely the engine block, and the two VCR engine mechanisms become Stephenson III six-bar slider-crank linkages. Hence, the piston displacement of each mechanism depends on the position of the revolute joint connecting link 3 and link 4. In the case of the kinematic structure derived from graph 03Dc03, when the control link is fixed in a position, the five-link control loop (E-CL-4-3-5) becomes a four-bar linkage and the piston displacement is determined by the moving path of the joint connecting link 2 and link 3.

In order to verify the compression ratio variability of the selected VCR engine mechanisms, kinematic analysis is carried out to find the piston displacement, cylinder volume, piston velocity, and piston acceleration of each mechanism at high and low compression ratio (C.R.) and compared with those of a 0.5 L conventional fixed-compression ratio single-cylinder engine mechanism with a crank length of 43 mm, connecting rod length of 140 mm, and piston offset of 0 mm. As mentioned above, the mechanisms in Table 12 have identical driving loops. For a fair comparison, the same dimensions are used for the links (1, 2, CS, and a piston offset of 0 mm) in the driving loop. In addition, since the mechanisms derived from 03Db04 and 03Dd05 are identical except their control loops, if the dimensions of links in the driving loop, link 3, and the position of the joint connecting link 3 and link 4 are the same, then the two mechanisms have the same piston motion. Hence, they are analyzed identically.

Note that the following results are based on the dimensions of each mechanism determined empirically or from a previous study [14]. For detailed analysis, the dimensional synthesis and dynamic analysis must be followed to identify the pros and cons of each mechanism. The analysis results of the piston displacement, cylinder volume, piston velocity, and piston acceleration at high and low compression ratio are shown in Figure 3 and Figure 4 for each mechanism along with those of the conventional engine mechanism. The high and low compression ratio, top dead center (TDC) position, bottom dead center (BDC) position, and stroke obtained by each mechanism are shown in Table 13. The dimensions of the analyzed mechanisms are listed in Table 14 in which the control link angle is measured from the positive x-axis, and the mechanisms drawn in scale are shown in Figure 5.

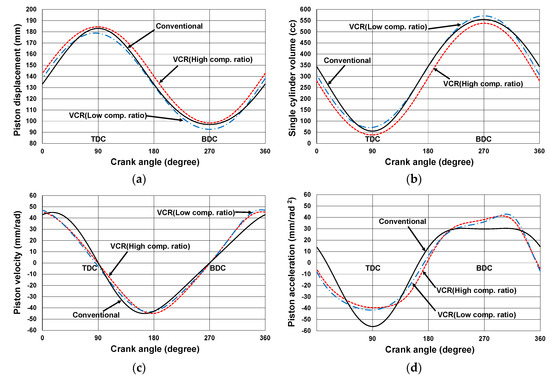
Figure 3. Analysis results of mechanisms derived from graphs 03Db04 and 03Dd05: (a) piston displacement; (b) single-cylinder volume; (c) piston velocity; (d) piston acceleration.

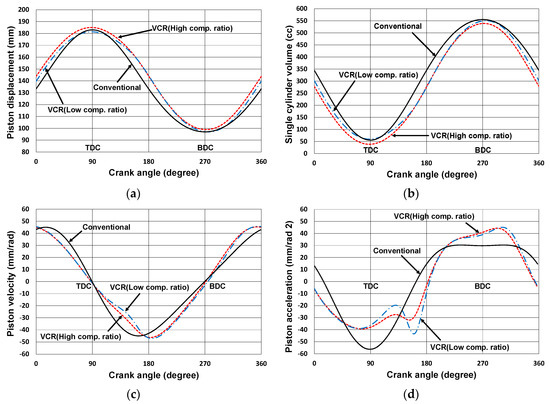
Figure 4. Analysis results of mechanism derived from graph 03Dc03: (a) piston displacement; (b) single-cylinder volume; (c) piston velocity; (d) piston acceleration.

Table 13. Analysis results of VCR engine mechanisms in Table 12 with the dimension in Table 14.

	03Db04 and 03Dd05		03Dc03		Slider-Crank
	High C.R.	Low C.R.	High C.R.	Low C.R.	-
Compression ratio (C.R)	14.000	8.028	14.016	9.233	10.000
TDC (mm)	184.422	178.791	185.008	181.370	183.000
BDC (mm)	98.419	92.726	98.908	96.964	97.000
Stroke (mm)	86.003	86.065	86.100	84.406	86.000

Table 14. Dimensions of mechanisms in Figure 3 and Table 12.

		03Db04	03Dd05	03Dc03	Slider-Crank
Bore diameter (mm)	86.00
Piston offset (mm)	0
Combustion chamber volume (cc)		38.43			55.51
Link length (mm)	rCS	25.00	25.00	25.00	43.00
	r1	140.00	140.00	140.00	140.00
	r2a	56.00	56.00	56.00	-
	r2b	42.00	42.00	42.00	-
	r2c	95.50	95.50	95.50	-
	r3	73.50	73.50	-	-
	r3a	-	-	140.00	-
	r3b	-	-	145.00	-
	r3c	-	-	65.00	-
	r4	-	-	95.00	-
	r4a	14.14	20.55	-	-
	r4b	14.14	9.42	-	-
	r4c	20.00	20.55	-	-
	r5	11.05	20.00	65.00	-
	rCL	11.05	20.00	20.00	-
Pivot positions (mm)	rax	53.19	61.15	114.84	-
	ray	−60.32	−66.37	−212.50	-
	rbx	69.11	75.00	210.00	-
	rby	−72.42	−75.00	−110.00	-
Control link angle (°)	High C.R.	27.5	356.5	187.2	-
	Low C.R.	78.0	27.7	172.8	-

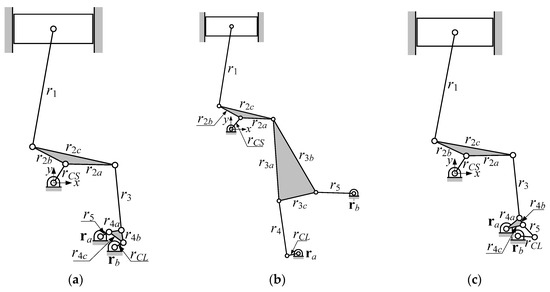
Figure 5. Analyzed VCR engine mechanism derived from graph: (a) 03Db04; (b) 03Dc03; (c) 03Dd05.

It is known that increasing the compression ratio of an engine from 8 to 14 produces a thermal efficiency gain from 50 to 65 percent [16]. From this viewpoint, as shown in Figure 3 and Figure 4, and Table 13, the selected mechanisms are capable of being used as VCR engine mechanisms. In the case of the two mechanisms from 03Db04 and 03Dd05, the compression ratio is varied from 8 to 14, whereas for the mechanism from 03Dc03, the compression ratio is varied from 9.2 to 14.

6. Discussion

In this research, two-DOF planar VCR engine mechanisms with only one-DOF joints are enumerated. As can be seen from Equations (6) and (7), for given numbers of F and L_ind, the numbers of links and joints required in a mechanism decrease by the number of two-DOF joints, j₂. Hence, as a future work, it would be worth challenging the type synthesis of feasible two-DOF variable mechanisms with higher pairs, such as gear joints that allow two-DOF.

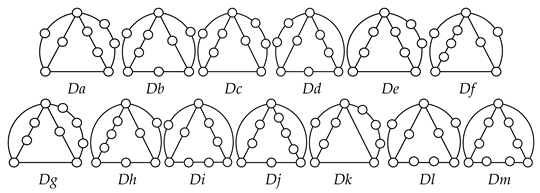
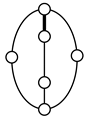
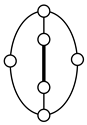
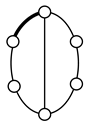
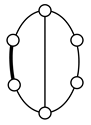
Using the equations in Section 2.2, mechanisms with higher pairs can also be enumerated. The numbers of links and joints for planar two-DOF mechanisms according to the numbers of L_ind and j₂ can be determined by inserting F = 2, λ = 3, and j₂ into Equations (6) and (7); the numbers of l_i, b_i, l^c and j^c by Equations (8)-(18). For example, for L_ind = 2 and j₂ =1, the result of the number synthesis is shown in Table 15. Unlike the conventional graph with only one-DOF joints, a three-link loop is permitted in a graph if the loop contains a two-DOF joint as an edge. The contracted and conventional graphs enumerated according to Table 15 are shown in Table 16. Now, a two-DOF joint must be assigned to an edge in the conventional graphs in Table 16. By permuting the edges of each conventional graph with a two-DOF joint, the graphs shown in Table 17 are obtained, in which the thick edges denote two-DOF joints.

Table 15. Numbers of links and joints for possible two-DOF, two-independent loop VCR engine mechanisms with one-DOF joints and a two-DOF joint.

j2	Lind	l	j	l2	l3	l4	lc	jc	b0	b1	b2	b3
1	2	6	7	4	2	0	2	3	0	2	1	0
									1	0	2	0
									1	1	0	1

Table 16. Graphs of two-DOF kinematic chains enumerated according to Table 15.

j2	Lind	Contracted Graph	Conventional Graph
1	2

Table 17. Graphs enumerated by assigning a two-DOF joint to an edge in the conventional graphs in Table 16.

Contracted Graph	Conventional Graph	Assign a Two-DOF Joint
	A
	B
	C

Table 18 shows the results of type synthesis obtained by labeling the links to the eight unlabeled graphs in Table 17 according to the search specifications and excluded cases given in Table 3 and Table 4. As shown in Table 18, only one graph, 12Aa01 yields a possible VCR engine mechanism with one gear joint. A similar approach can be applied to find feasible mechanisms with more independent loops and higher pairs.

Table 18. Type synthesis of VCR engine mechanisms with one two-DOF joint, six links, and seven joints.

Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram	Labeled Graph	Schematic Diagram
12Aa01		12Ab00	Cases I and II	12Ac00	Cases I and II
12Ba00	Case I	12Bb00	Case I	12Bc00	Case III
12Ca00	Case III	12Cb00	Case III

7. Conclusions

The type synthesis of mechanisms that determines the possible kinematic structures of a desired mechanism is quite a challenging problem. In this study, a systematic procedure for the type synthesis of mechanisms using graph theory is carried out to find the all possible two-DOF planar VCR engine mechanisms with two to three independent loops and with only one-DOF joints.

In order to find the corresponding graphs, the numbers of links and joints according to the number of independent loops are determined, and 38 unlabeled graphs of two-DOF kinematic chains shown in Table 2 are enumerated. The search specification that VCR engine mechanisms must satisfy and the excluded cases from the enumeration are identified, and they are used to assign the links to the vertices in the enumerated unlabeled graphs. As a result, the kinematic structures of three seven-link and 84 nine-link VCR engine mechanisms are determined. Applying the four practical evaluation criteria to the 87 synthesized mechanisms, three kinematic structures are selected as the suitable VCR engine mechanism. For verification, the selected mechanisms are analyzed with the dimensions determined empirically. The results show that the selected mechanisms are capable of being used as VCR engine mechanisms.

In addition, the basic method to determine the kinematic structures of VCR engine mechanisms with higher pairs is discussed. The results of this study can serve as an atlas of adjustable linkages and be useful in the design of various two-DOF mechanisms. Even though the mechanisms are enumerated for the use in the VCR engine in this research, the proposed procedure can be used for the type synthesis to find the kinematic structures of other mechanisms.