Identification and Model Update of the Dynamic Properties of the San Silvestro Belfry in L’Aquila and Estimation of Bell’s Dynamic Actions

Abstract

The authors investigated the dynamic behaviour of the San Silvestro belfry in L’Aquila (Italy). The 2009 earthquake in L’Aquila caused severe damages to the entire masonry complex. Extensive rehabilitation works, ended in 2019, repaired the structure and enhanced its seismic safety. In this paper, the authors discuss three aspects typical of masonry towers by interpreting the outcomes of Operational Modal Analysis carried out on December 2019: the interactions between the tower and the masonry complex, the dynamic effects of the bell, and the seismic reliability assessment of the tower. Specifically, the experimental mode shapes drive the estimation of an equivalent cross-section, whose principal axes of inertia match with the directions of oscillation of the mode shapes, and the parameters of an equivalent cantilevered beam roughly representative of the tower dynamics. In a second step, a two-degrees-of-freedom analytical model simulates the dynamic coupling between the tower and the more massive bell. The response of the system to a set of seven strong-motion earthquakes yields the assessment of the bell effects over the seismic performance of the masonry tower.

1. Introduction

The study of masonry towers attracts numerous scholars. Many research on their seismic performance, which can be quite diverse depending on the dynamic features of the tower. Specifically, in some cases, masonry towers are the first structures to suffer damages or collapse, see Figure 1a and Figure 2, while in some instances they are the sole to endure, see Figure 1b.

Figure 1. Pictures of damaged masonry towers during seismic sequences, taken by Italian Fire Department: (a) an almost collapsed masonry tower struck by the 1997 earthquake in Umbria (Italy), (b) the masonry tower in Amatrice (Italy), which did not collapse despite the neighbouring masonry structures were all raised to the ground by the 2016 earthquake.

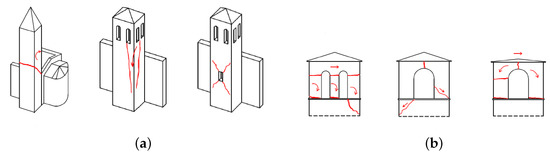
Figure 2. (a) collapse mechanisms of the stem; (b) collapse mechanisms of the bell-cell.

For these reasons, the assessment of the dynamic response of masonry towers is essential before any retrofitting intervention. However, practitioners are still not acquainted with dynamic identification, which can provide useful information, especially in the case of slender structures, like belfries.

Besides, dozens of papers present the dynamic response of masonry towers to ambient excitation. Most of the researchers discuss the results of Operational Modal Analysis (OMA) by tuning finite element models to the observed dynamics [1,2,3,4]. A few researchers show the outcomes of continuous dynamic monitoring and the impact of ambient parameters over the modal parameters [5]. Further, some papers present the coupling between the towers and the ringing bells and assess the effects of the bells on the seismic performance [6,7].

Despite the numerous researchers on masonry belfries, each belfry is a stand-alone case and, still, may add pieces of information on the understanding of the dynamics of slender masonry structures.

A few papers present in-depth investigations on the dynamics of masonry towers via rigorous experimental, analytical and numerical approaches.

Among them, Bennati et al. [7] endeavoured to determine an accurate analytical description of both the bells’ motion and their actions using experimental measurements and a rough mechanical model. They [7] concluded that the dynamic effects of the bells over the considered belfry (Tower of Matilde) could be described analytically with surprising accuracy by merely representing the motion of every single bell as an equivalent pendulum.

The authors of the current paper, clinging to this evidence, attempted to interpret the dynamics of the San Silvestro bell tower in L’Aquila, by modelling the more massive bell with an equivalent pendulum and the tower with a single degree-of-freedom (DOF) oscillator.

The bells’ swinging can seriously affect the seismic performance of masonry towers. Although a considerable distance between the resonance frequency of the tower and the frequency of oscillation of the bell can prevent unfortunate consequences, the seismic performance mostly depends on the frequency features of the earthquake.

The paper presents the case study of the San Silvestro belfry, discussed via experimental tests and analytical modelling. The first two sections describe the case study and the outcomes of OMA. In the following part, a two-DOF dynamic systems tuned to the experimental eigenfrequencies give information on the expected coupling between the structure and the more massive bell under earthquake.

2. San Silvestro Belfry

S.Silvestro Church is a medieval building, built between the XIII and XIV century and located in the centre of L’Aquila.

The S.Silvestro complex comprises the church, the belfry tower, the canonical house and the chapel, which used to be a tower of the city wall, see Figure 3 and Figure 4.

Figure 3. (a) View of the S.Silvestro Church in 1906; (b) View of the facade after the last restoration.

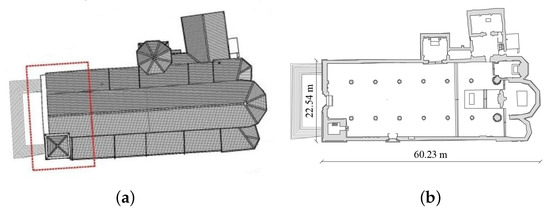
Figure 4. (a) The S.Silvestro Complex; (b) Plan of the church.

From its construction, the church experienced numerous earthquakes, and multiple restorations, in particular the one in 1461. Historical maps proved the unchanged external configuration of the complex, see Figure 5.

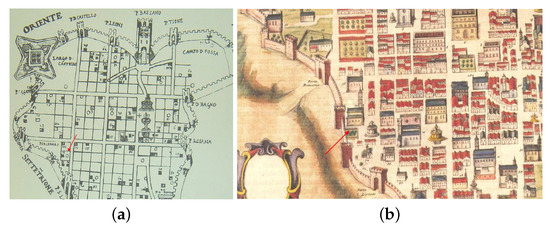
Figure 5. (a) Historical Map by Fonticulano (1575); (b) Historical Map by Antonelli (1622).

The 1969 restoration uncovered the church from the baroque additions and returned to light the ancient medieval structure. The 2009 earthquake in L’Aquila [8,9,10,11] caused the last rehabilitation works.

2.1. Description

Three naves divide the interior; the length of the central nave is two times the length of the lateral ones, Figure 4b. Ogival arches separate the naves and support a masonry wall with an 0.80 m thickness and a 5 m height. The facade has a large gothic window. The belfry stands at the right side of the façade, and its length equals that of the lateral nave. It has a rectangular plan 5.5 times, 6.9 m with a 33 m height.

A steel staircase reaches the bell cell, distinguished by slender masonry piers and large windows.

The thickness of the masonry decreases along with the height with the following discretization: 1.05, 1.20, 1.40 and 1.60 m. The belfry was built in local masonry [12,13], Figure 6a, with irregular units arranged in irregular texture and embedded in lime mortar, the so-called the “Apparecchio Aquilano” [14] in Figure 6b.

Figure 6. Texture of the masonry, before the restoration (a); the apparecchio Aquilano (b).

2.2. Observed Damage and Restoration

The 2009 earthquake caused many damages to the S.Silvestro church, see Figure 7: the facade and the bell-tower were the more damaged parts. The failures originated from the asymmetrical structural configuration, due to the presence of the belfry on the right side of the church.

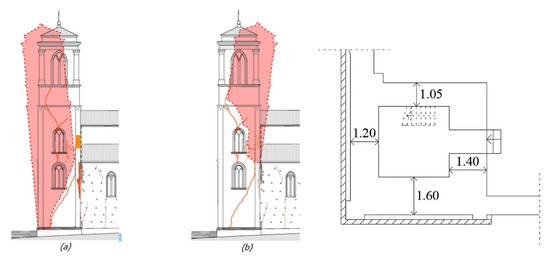
Figure 7. (a) Observed collapse mechanisms of the San Silvestro bell tower; (b) Cross-section of the masonry tower.

The gable exhibited incipient overturning in the unrestrained front, Figure 8 and Figure 9. Nonetheless, the steel rods prevented the collapse of the facade.

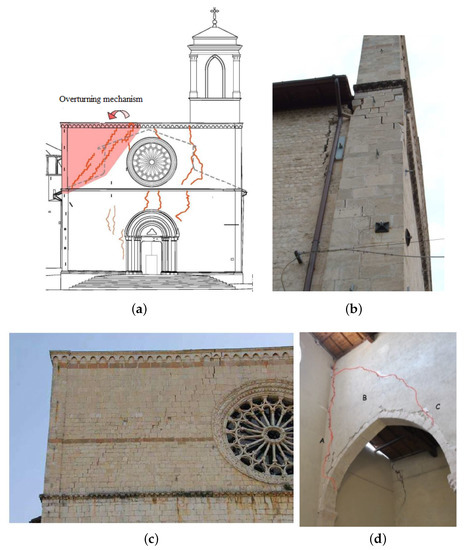
Figure 8. (a) Observed collapse mechanisms of the San Silvestro facade; (b,c) External views of the cracks; (d) Internal view of the cracks.

Figure 9. (a–d) View of the San Silvestro belfry after the 2009 earthquake.

The bell tower had extended cracks due to diverse overturning mechanisms, identified by the damage pattern marked in red in Figure 9 The first mechanism affected the entire tower as an overturning about a cylindrical hinge located by the basement.

The second mechanism involved the upper part of the belfry as an overturning about a cylindrical hinge located by the gutter of the nave walls (10.20 m). The two mechanisms, depicted in Figure 9, generated diagonal cracks which evidenced the local response of the belfry. The restoration of the tower mainly focused on the repair of damages, closing the cracks using diatons and grout injections. The interventions likely achieved box-like structural behaviour using steel rods. The position of the steel rods is close to the location of the previous ones. Further, the grout injections affected all the walls, aiming at improving the mechanical property of the masonry.

The structural interventions after the 2009 earthquake focused on the repair of damages by mainly closing the cracks using horizontal stone connections (diatons) and improving the mechanical properties of masonry using grout injections. Steel rods were installed to enhance the united behavior of the structural members. The experimental tests reported in this paper were carried out after the repair interventions.

3. Dynamic Identification: Results and Discussion

On December 2 2019, the authors measured the response of the masonry tower to ambient excitation. The covariance-driven Stochastic Subspace Identification (SSI) method yield the estimate of the experimental modal parameters [15,16,17]. The authors used a set of 10 Force-Balance monoaxial accelerometers (SARA Instruments SA10). They have a dynamic range higher than 165 dB in the frequency interval 0.1–20 Hz and a 5 V/g sensitivity. The acquisition system consists of two measurements chains, each one driven by a master recorder unit, synchronized by a GPS sensor. In the current application, two accelerometers provided the reference location in two orthogonal directions [18], while the other eight were placed in the lower levels in several measurement points, see Figure 10. The data were sampled at a rate of 200 Hz. The cut-off frequency of the anti-aliasing filter was set to 20 Hz. The number of samples was set to N = 720,000, which resulted in a measurement time of 1 h. Since two accelerometers were fixed, the remaining eight were each one rotated and placed in two different locations, resulting in four measurement setups, which increased the mode shape resolution. Data from multi-setup measurements (4 setups) were then merged following the approach recalled in [19,20]. The identification was carried out under environmental conditions; additionally, the authors recorded the response of the three top accelerometers to the ringing bells to derive an elementary analytical model of the coupled bell-tower dynamics.

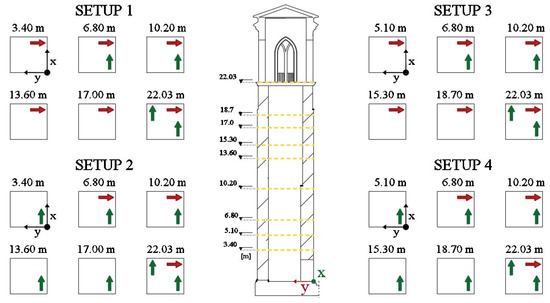
Figure 10. Experimental setup with the different configurations and the two measuring directions.

Two modes arise from the stabilization diagram, see Figure 11a and Table 1.

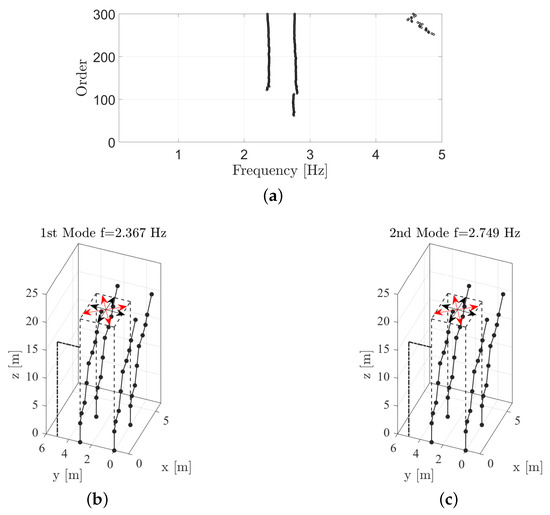
Figure 11. (a) Stabilization diagram; (b,c) View of the first two experimental mode shapes. The black double arrows indicate the two inertia principal axis of the tower cross-section, while the red ones the directions of the mode shapes.

Table 1. Results of Operational Modal Analysis (OMA).

Mode	Frequency [Hz]	Damping [%]
1st	2.367	3.727
2nd	2.749	1.957

Unfortunately, the ambient excitation did not sufficiently excite the upper modes. The root-mean-square of the recorded acceleration signals is very low, approximately equals to $2\times {10}^{-4}$ g. Both modes are translational in two orthogonal directions and resemble the first mode of a plane cantilevered beam. The two directions of the identified modes likely indicate the two inertia principal axis of the tower cross-section.

However, the principal axis of inertia of the belfry cross-section do not match with the directions of the two translational modes. The constraint provided by the facade and the nave walls likely determine the observed axis rotation. Hence, the authors attempted to assess the degree of restraint offered by the neighbouring structures, by estimating an equivalent cross-section comprehensive of parts of the facade and the nave wall, which yield the observed translational directions. The two directions uncouple the belfry dynamics, which oscillates like two plane clamped-free planar beams along the two principal axes of inertia of the tower.

The mode shapes further provide information on the constraint exhibited by the neighbouring facade and nave walls along with the height. The mode shape can be possibly divided into three sections, see Figure 12: AB almost moves with the ground; BC involves the dynamics of the tower interacting with the facade and the nave wall; CD represents the dynamics of the tower with the facade. Nevertheless, as a whole, the mode shapes resemble the ones of a cantilevered beam, as evidenced in the next section. The estimated damping ratios range between 2% and 4%; The values are consistent with the damping of masonry. However, a reliable estimate of damping requires further investigations.

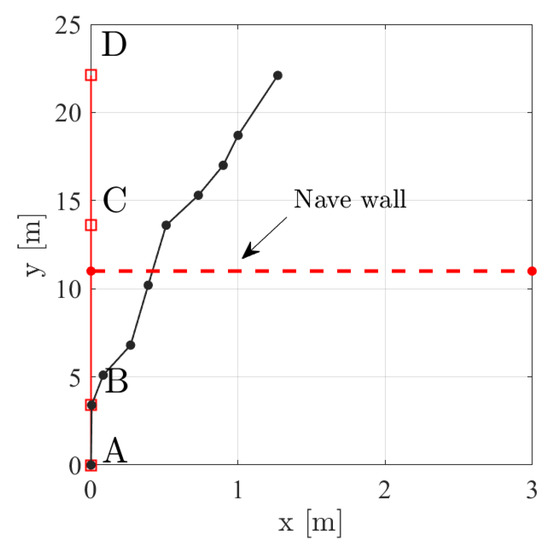
Figure 12. A: Detail of the lateral displacement of the belfry. Two discontinuity points likely emerge: B and C. The distance AC approximates the distance of the lateral nave rooftop to the ground.

4. Estimate of the Equivalent Cross-Section

The directions of oscillation of the identified bending modes are orthogonal between each other. The Cartesian axis $(x^{\prime },y^{\prime })$ in Figure 13a indicate the mentioned directions of oscillation. The inertia axes of the equivalent cross-section, obtained from the weighted average of the wall thickness along with the belfry height, are indicated by the (x,y) axes in Figure 13a: these axes do not agree with the experimental axes of inertia. Given the structural bond between the belfry and the adjacent masonries, it is likely that parts of the facade and nave wall join the belfry dynamics and may aggregate to form an equivalent cross-section, whose principal axes of inertia match with the experimental ones. The length of facade $L_f$ and nave wall $L_n$, which minimize the squared difference between the experimental axes and those of the equivalent cross-section are chosen as optimum parameters. The two portions of facade and nave walls add to the averaged cross-section, returning a sort of elastic continuum comprehensive of the nearby masonry contributions. The contributing facade and nave wall measure 0.43 and 0.52 respectively.

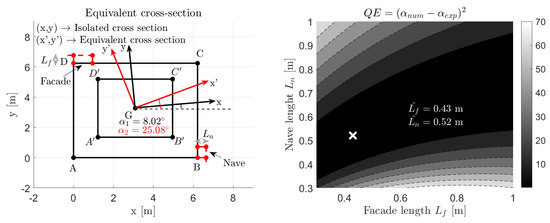
Figure 13. (a) Equivalent cross-section of the San Silvestro belfry; (b) Contour plot of the optimization function.

Table 2 reports the moment of inertia of the isolated and equivalent cross-sections, which are needed in the analytical model updating shown in the next paragraph.

Table 2. Inertia of the isolated and equivalent cross-section.

Cross-Section	Ix [m${}^4$]	Iy [m${}^4$]
Isolated	107.78	107.86
Equivalent	120.22	115.07

5. Analytical Model Updating

The tuning of analytical or numerical models to the experimental modal parameters requires a proper selection of a set of parameters to optimize. The detected modes resemble the first mode of a clamped-free Euler Bernoulli beam [21]. Hence, the authors attempted to estimate the equivalent length L and the elastic modulus E of a cantilevered beam, by assuming the equivalent cross-section in Figure 13a. The following function is the chosen measure of the distance between the estimated modal parameters and the numerical ones [22]

$$C=su{m}_{i=1}^n{g}_i{\left(\frac{f_i^m-f_i^c}{f_i^m}\right)}^2+bsu{m}_{i=1}^n\left(1-diag\left(MAC(M_i^m,M_i^c)\right)\right),$$

(1)

the apex ${(\ast )}^m$ indicates a measured variable, where the apex ${(\ast )}^c$ a calculated variable, $M_i$ is the mode shape vector, n is the number of modes, MAC is the modal assurance criterion [23], while $g_i$ and b are weighting factors. The weighting factors are set equal to one. The parameters $\{\widehat{E},L\}$, which minimize the objective function in Equation (1), are assumed as optimum, see Figure 13b.

Figure 14 shows the contour plot of the objective function, obtained by choosing a proper discretization of the two parameters’ domains $dE=0.1$ MPa and $dL=0.1$ m. The white mark in Figure 14 indicates the pair of optimum: $\widehat{E}=991.3$ MPa and $\widehat{L}=12.3$ m. The two values return modal parameters of the cantilevered beam, which coarsely agree with the experimental ones, Table 3.

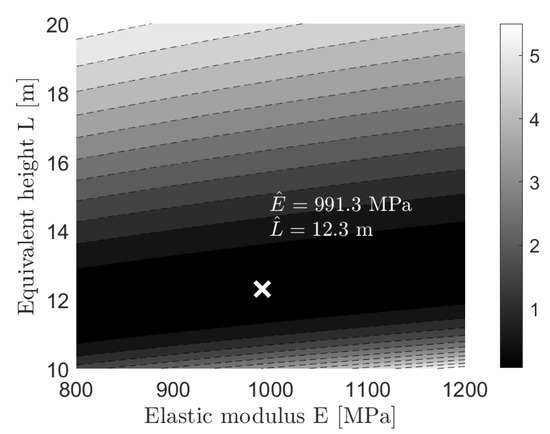
Figure 14. Contour plot of the optimization function: the cross indicates the minimum point.

Table 3. Comparison between analytical and experimental modal parameters.

Analytical Model f[Hz]	OMA f[Hz]	Error [%]	MAC
2.163	2.367	−9.43%	0.88
2.901	2.749	5.24%	0.86

Finite element models or more accurate analytical modelling [24,25,26,27] may give a closer matching; Still, a simple mechanical system represents the dynamic of the masonry tower satisfactorily in the first linear range of response. The elastic modulus lies in the range of values typical of masonry [28]. The equivalent length is almost $12.3/26=47\%$ of the maximum height of the tower. The constraint given by the neighbouring structures and the tapering of the walls likely reduces the equivalent slenderness of the tower significantly.

6. Discussion: Response to Ringing Bell

The experimental modes match with the modes of a clamped-free Euler Bernoulli beam. The authors estimated the effect of the bells on the tower dynamics by adopting a two-degrees-of-freedom mechanical system, depicted in Figure 15. The lower substructure represents the tower, while the upper substructure the more massive bell. Concerning Figure 15, Newton’s equations of motion for the two-degrees-of-freedom model can be directly written and expressed in the following matrix form

$$\left[\begin{array}{cc}{m}_1& 0\\ 0& m_2\end{array}\right]\left\{\begin{array}{c}{\ddot{x}}_1\left(t\right)\\ {\ddot{x}}_2\left(t\right)\end{array}\right\}+\left[\begin{array}{cc}{c}_1+c_2& -c_2\\ -c_2& c_2\end{array}\right]\left\{\begin{array}{c}{\dot{x}}_1\left(t\right)\\ {\dot{x}}_2\left(t\right)\end{array}\right\}+\left[\begin{array}{cc}{k}_1+k_2& -k_2\\ -k_2& k_2\end{array}\right]\left\{\begin{array}{c}{x}_1\left(t\right)\\ x_2\left(t\right)\end{array}\right\}=-\left\{\begin{array}{c}{m}_1\\ m_2\end{array}\right\}{\ddot{x}}_g\left(t\right),$$

(2)

where $k_1$ and $m_1$ are the stiffness and mass values of the lower substructure, $k_2$ and $m_2$ are the stiffness and mass values of the upper substructure, $c_1$ and $c_2$ are the damping coefficient, $x_g\left(t\right)$ is the base excitation. $c1$ and $c_2$ are expressed in terms of modal damping $c_1=2x{i}_{1}omeg{a}_1$ and $c_2=2x{i}_{2}omeg{a}_2$, where $x{i}_1$ and $x{i}_2$ are the modal damping.

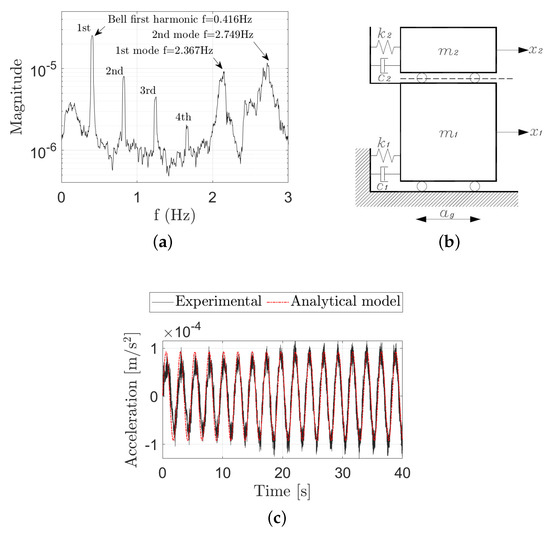
Figure 15. (a) FFT of a top accelerometer response to the bell swinging (b) Main 2-DOF archetype system; (c) Superposition of the experimental and analytical response to ringing bells.

Two mechanical systems approximately reproduce the tower dynamics, tuned to the first and second natural frequencies respectively. The estimate of the mass matrix derives, as follows, from the first natural frequency of the tower and the bell, by assuming the uncoupling of the bell-tower dynamics. Specifically, Equation (3) yields the mass and the elastic constant of the spring from the natural frequency of a cantilevered Euler-Bernoulli beam,

$$omeg{a}_1^2=\frac{k_1}{m_1}=\frac{{\left(betah\right)}^4}{h^4}\frac{EI}{roA}\to k_1=\frac{{\left(betah\right)}^{4}EI}{h^3},m_1=roAh,$$

(3)

where $omega1$ is the natural pulsation of the substructure. The first solution of the eigenvalue problem of a clamped-free beam is $betah=1.875$. Equation (4) returns the mass and the elastic constant of the spring from the natural frequency of a physical pendulum, representative of the more massive bell. If the amplitude is limited to small swings, the pulsation is [29]

$$omeg{a}_2^2=\frac{k_2}{m_2}=\frac{Mgd}{I_p}\to k_2=\frac{I_p}{gd},m_2=M,$$

(4)

where $omega2$ is the natural pulsation of the substructure, $k_2$ and $m_2$ the stiffness and mass values of an equivalent SDOF oscillator, $I_p$ is the moment of inertia of the pendulum about the pivot point, M is the mass of the pendulum, d is the distance between the pivot point and the centre of mass and g is the gravity acceleration. The modal viscous dampings of the substructure and the bell are set equal to 3.7% (see Table 1) and 1% respectively. Table 4 lists the parameters adopted in the mechanical model.

Table 4. Parameters of the model in Equation (2).

Parameter	Value
A [${\mathrm{m}}^2$]	25.16
$I_I$ [${\mathrm{m}}^4$]	120.22
$I_{II}$ [${\mathrm{m}}^4$]	115.07
h [m]	12.3
$ro$ [${\mathrm{kg}/\mathrm{m}}^3$]	1800
E [MPa]	991.3
M [Kg]	≈1000
$I_p/gd$ [N/m]	6825.2
$x{i}_1$ [%]	3.7
$x{i}_2$ [%]	1

The experimental response of the masonry tower to the swinging of the more massive bell agrees with the response of the mechanical system in Equation (2) to the oscillation of the upper substructure, Figure 15b. As noticed by Bennati et al. [7], this evidence further confirms that a simple pendulum reproduces the effect of swinging bells over the towers adequately.

The FFT of the acceleration time-history of a top accelerometer, reported in Figure 15a, clearly present the peaks corresponding to the oscillation frequency of the bell at $f=0.416$ Hz and the natural frequencies of the tower at $f=2.367$ Hz and $f=2.749$ Hz. Nevertheless, there are three additional peaks at $0.828$ Hz, $1.282$ Hz and $1.652$ Hz. These peaks are equidistant and decreasing in the same proportion as if they were higher harmonics of the ringing bell. This aspect is quite peculiar: [6,7] did not observe the repetition of resonance peaks from the FFT of the experimental responses. Regrettably, the authors had not the chance to further examine this aspect via experimental testing.

Figure 16 presents the frequency response functions of the mechanical system in Equation (2), tuned to the two detected experimental frequencies, respectively. In each plot, two FRFs show the effects of the bell: the FRFs of the system without the bell coincide with the same system with the mass $m_2$ for frequency values higher than $0.8$ Hz; The mass $m_2$ determines an additional peak by the resonance frequency of the bell.

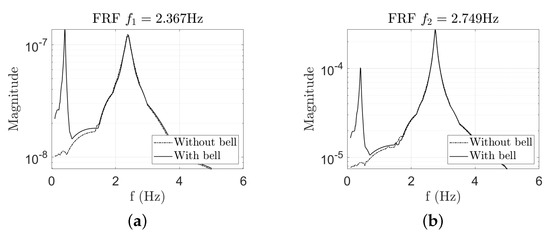
Figure 16. Estimate of the Frequency Response Function (FRF) of the mechanical system in Figure 15 without and with the contribution of the $m_2$ mass. The lower substructure is tuned to the first (a) and second natural frequency (b) respectively.

The ratio between the two masses is approximately $m_2/m_1\approx 0.2\%$: it is expectable that the bell does not influence the seismic performance of the tower. However, the effect of the more massive bell over the seismic performance requires further investigations, despite the frequency content of earthquakes generally exceeds 0.4 Hz. The authors chose a set of seven ground motion earthquakes in Table 5, currently used in seismic analysis, to numerically assess the effect of the more massive bell over the maximum displacement of the lower substructure [30,31].

Table 5. List of the earthquakes adopted in the analysis.

	Name	Areas Affected	Year	Mw	PGA [${\mathbf{m}/\mathbf{s}}^2$]
1	El Centro	United States, Mexico	1940	6.9	3.50
2	Erzican	Erzincan Province, Turkey	1939	7.8	5.03
3	Kobe	Japan	1995	6.9	6.76
4	L’Aquila	Italy	2009	6.3	6.63
5	Northridge	Southern California, United States	1994	6.7	5.51
6	Loma Prieta	San Francisco, United States	1989	6.9	6.55
7	Parkfield	California, United States	2004	6.0	4.96

The bar plot in Figure 17 shows the results of the time-history analysis: the maximum displacements of the lower substructure coincide in both the considered cases, without and with the mass $m_2$ contribution.

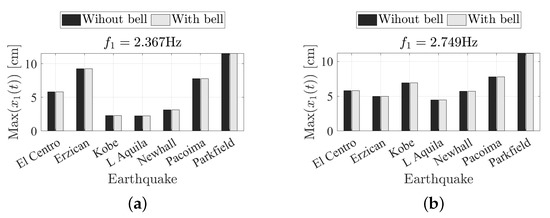
Figure 17. Maximum displacement of the substructure with mass $m_1$ tuned to the first (a) and second (b) bending mode respectively.

This aspect proves that the more massive bell of the San Silvestro belfry can be left free to swing and does not need to be constrained: its oscillation does not affect the seismic performance of the masonry tower.

It is worth to notice that a cantilevered beam with a free length equals to the maximum height of the belfry (≈25 m) would have a natural frequency approximately equals to $0.5$ Hz: The lack of connections to the facade and the nave walls would have lowered the natural frequency of the tower to values similar to the oscillation frequency of the bell, with likely unfortunate consequences.

7. Conclusions

The dynamic identification of the San Silvestro belfry evidenced two cantilevered-like stable modes. The directions of oscillation do not coincide with the principal axis of inertia of the tower cross-section. In essence, the authors assessed the portions of facade and nave walls which, added to the cross-section of the tower, yield an equivalent cross-section with the principal axis of inertia coincident with the directions of the experimental modes.

Additionally, the authors determined the elastic modulus and the equivalent length of a clamped-free Euler Bernoulli beam, representative of the tower’s dynamics in the first linear range of response. The obtained elastic modulus $E=991.3$ MPa lies in the range of values typical of historical masonries. The equivalent length is almost the $50\%$ of the maximum height of the tower: the walls’ tapering and the connections to the facade and the nave walls reduce the equivalent slenderness significantly.

A simple two-degrees-of-freedom mechanical system accurately reproduces the response of the masonry tower to the swinging of the more massive bell. The response of the mechanical system to a set of seven strong-motion earthquakes proves that the bell does not affect the seismic performance of the masonry tower. There are two evident causes: (1) the frequency of oscillation of the bell is distant from the natural frequencies of the tower, (2) the mass of the bell is less than 0.2% of the mass of the tower. The authors will aim at developing a refined FEM model to counterbalance the results from the presented rough analytical modeling and thoroughly understand the limits of the current analysis.