Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation
Abstract
Featured Application
Abstract
1. Introduction
2. Theoretical Background and Numerical Simulation
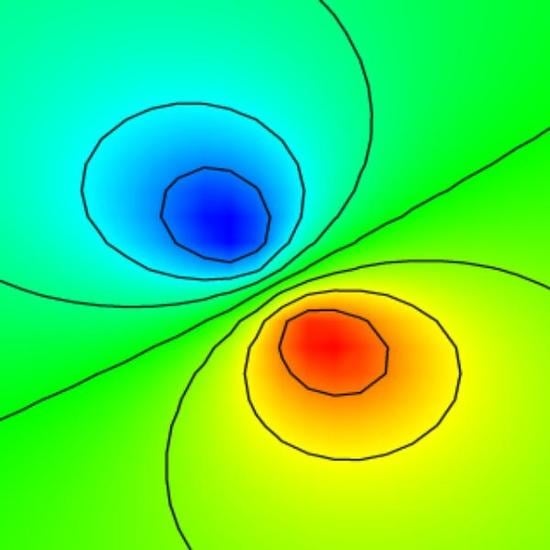
2.1. Spectral Gouy Rotation of Bessel–Gauss Beams
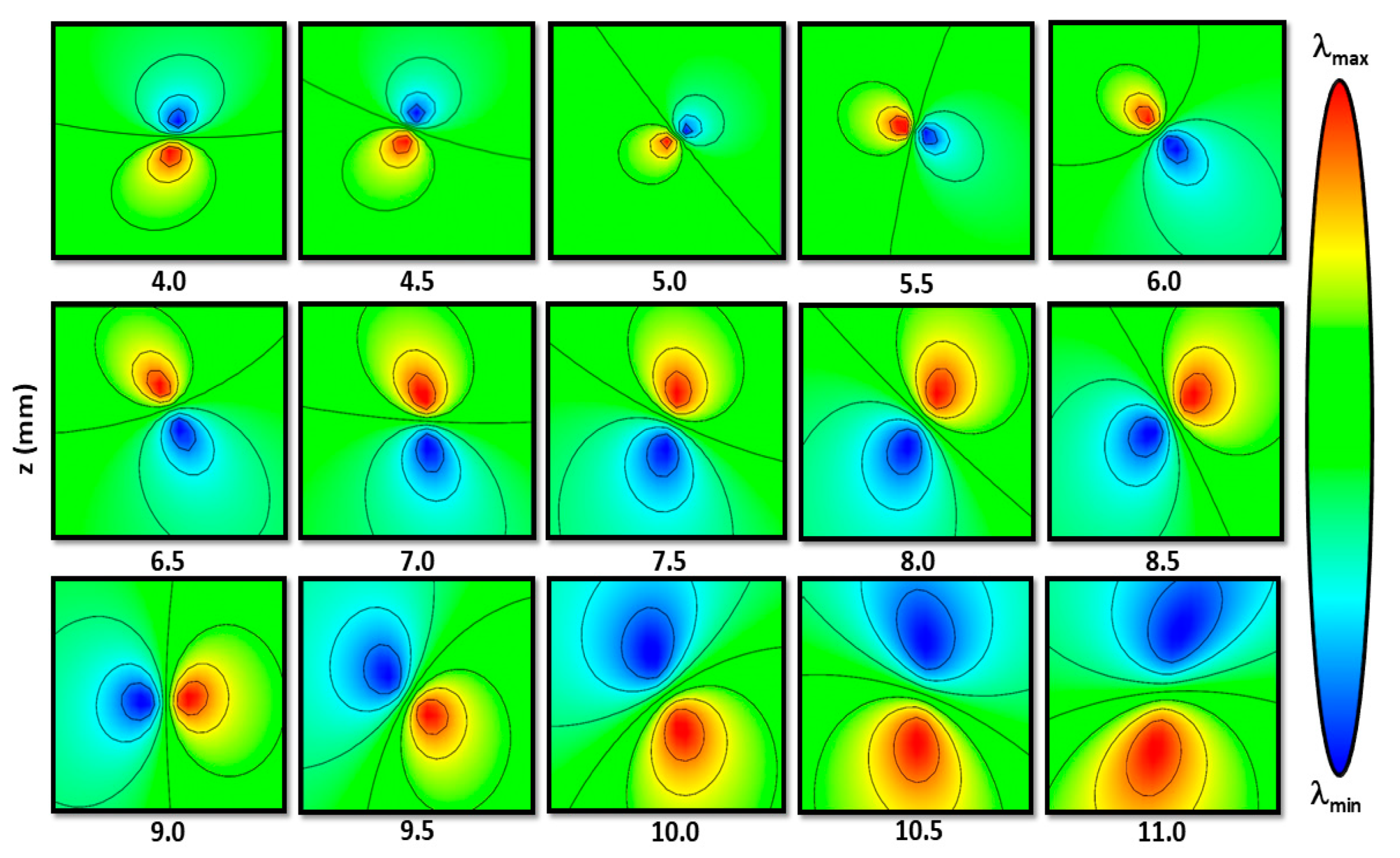
2.2. Numerical Simulation
3. Experimental Techniques and Mathematical Tools
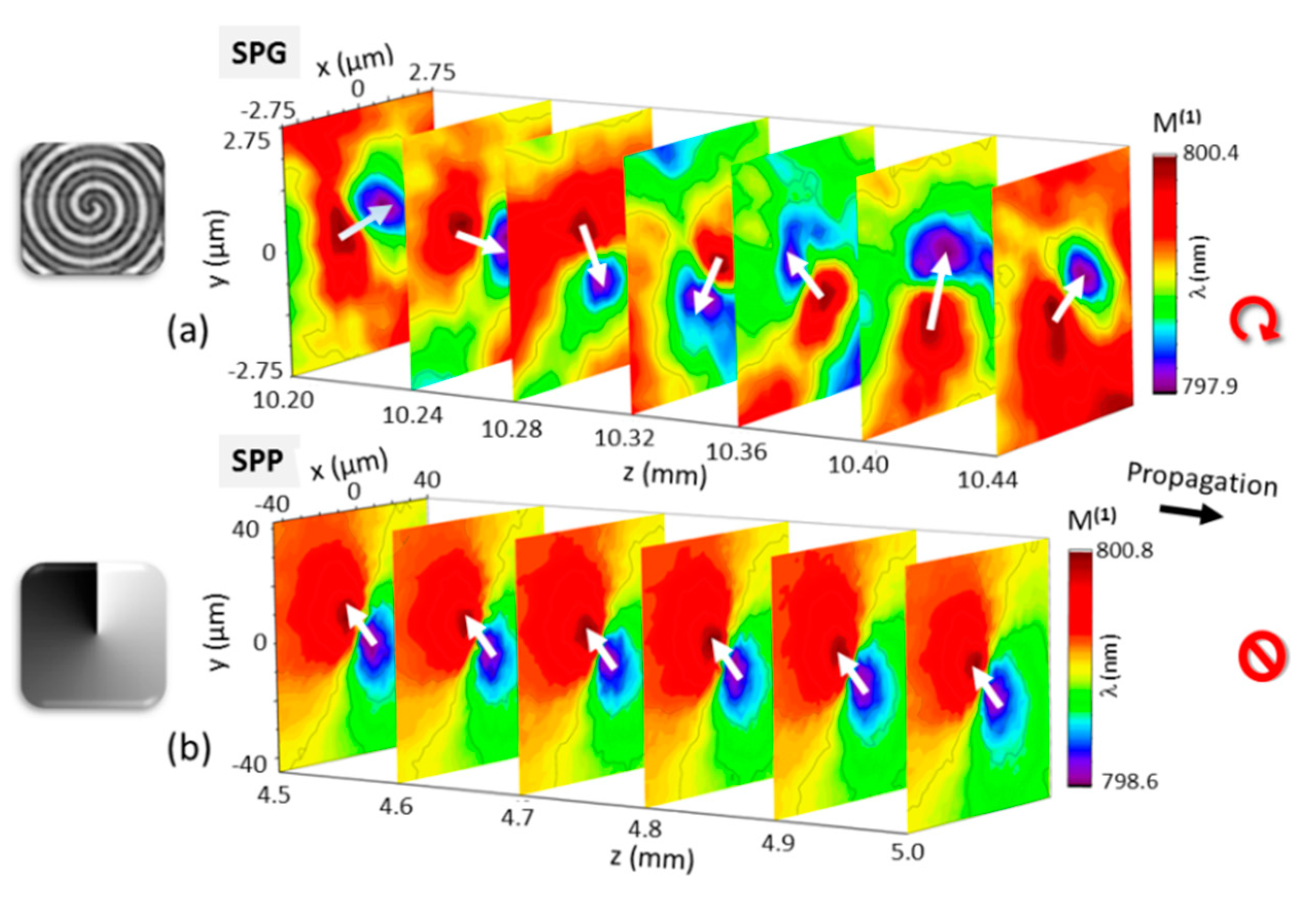
3.1. Shaping of Femtosecond Vortex Pulses with Stationary and Adaptive Components
3.2. Vortex Analysis with Spectral Statistical Moments
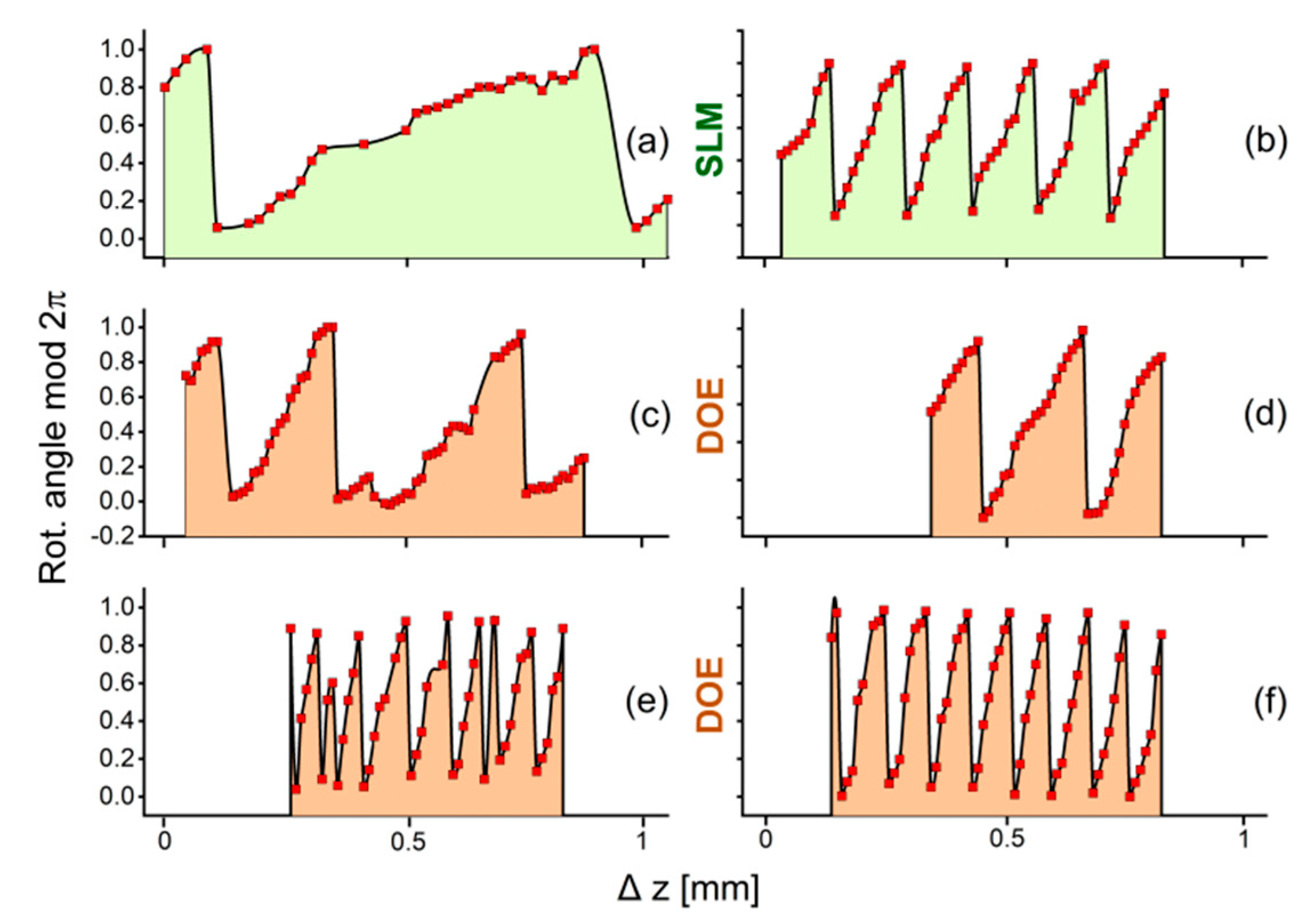
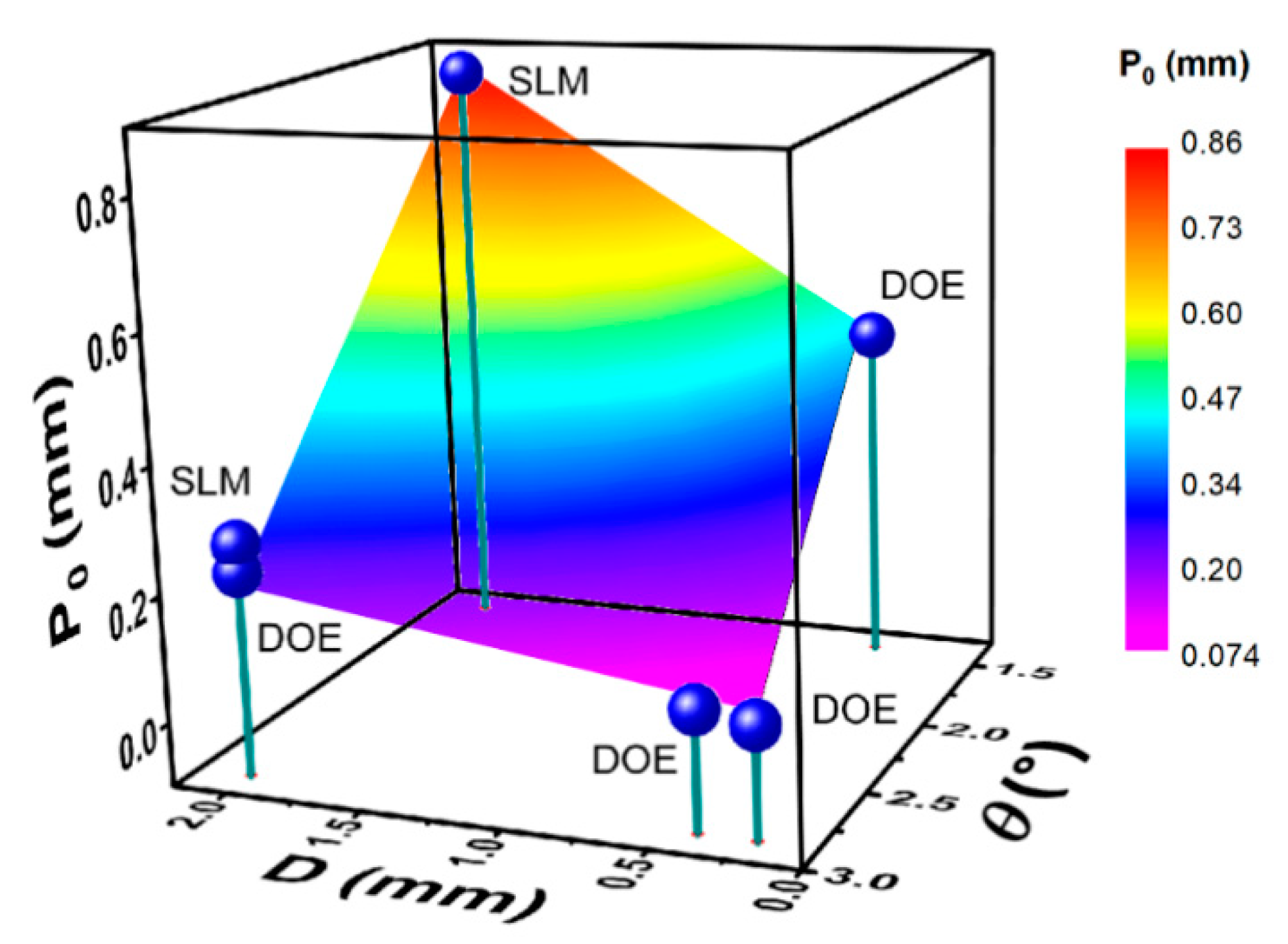
3.3. Rotation Control and Relevant Parameters
4. Experimental Results and Discussion
4.1. Parameters of Applied Spiral Phase Shapers
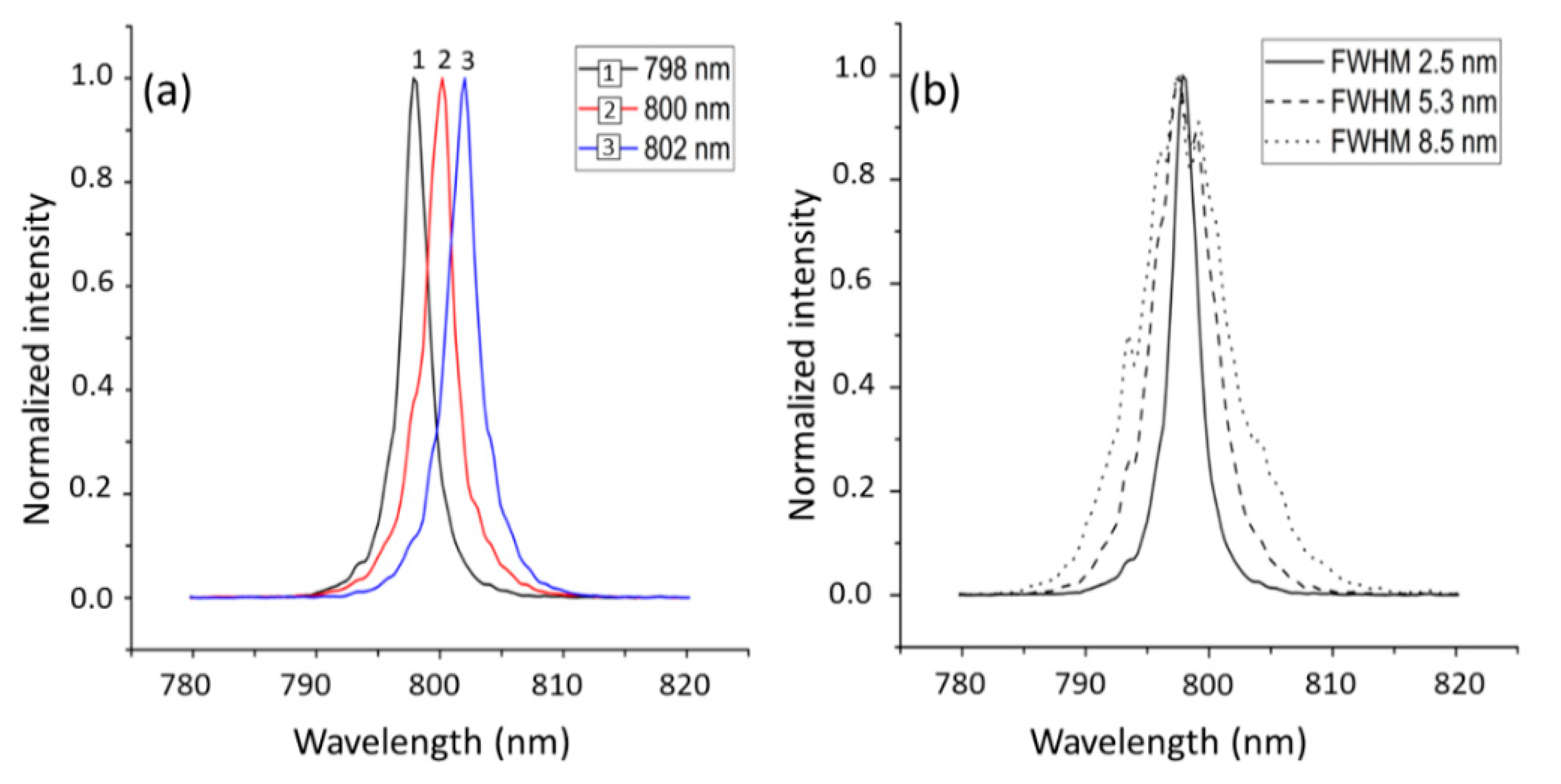
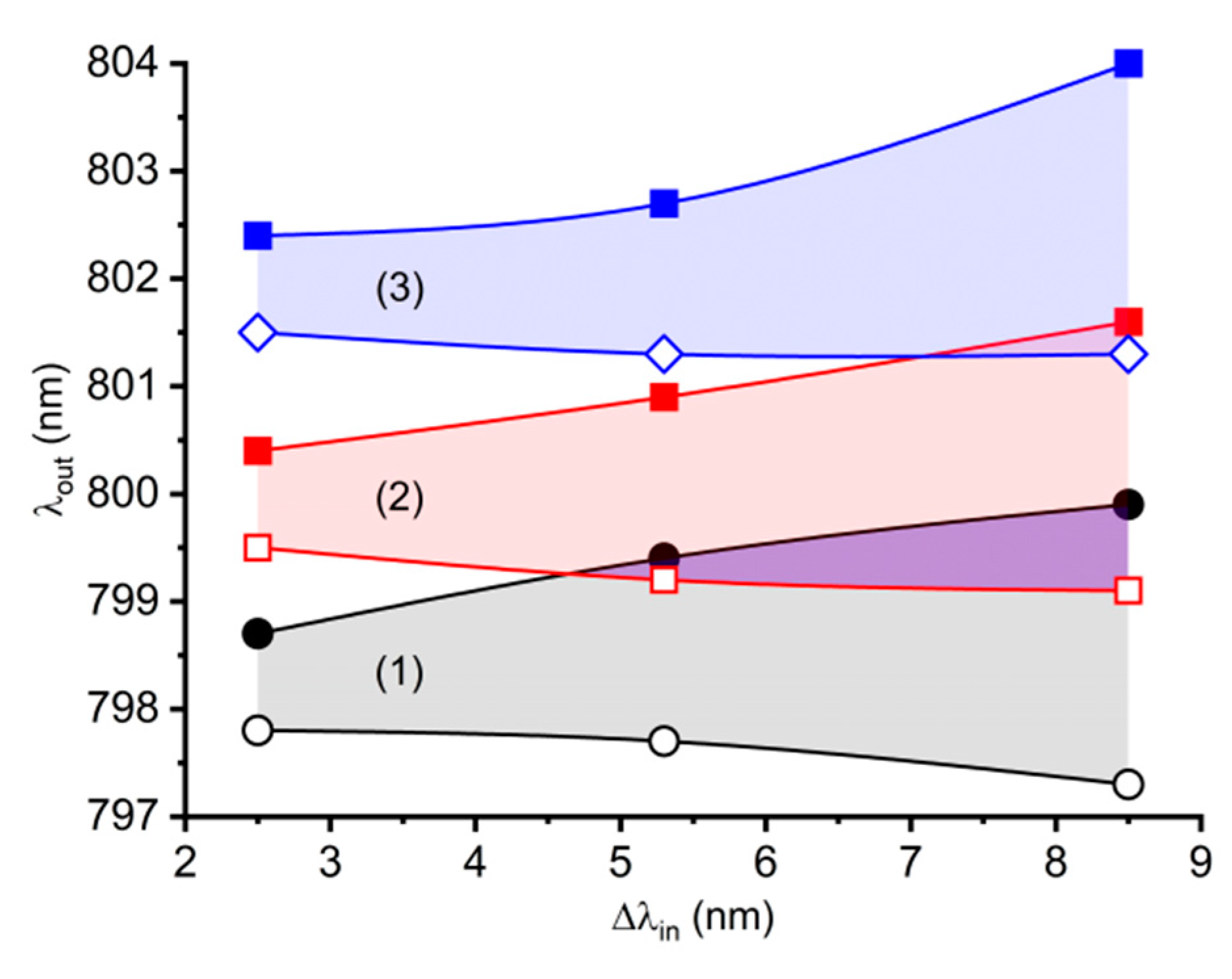
4.2. Spectral Control by Tuning Center Wavelength and Bandwidth
4.3. Variation of Grating Parameters
4.4. Rotation Control by Chirped Spirals and Multibeam Superposition
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bazhenov, V.Y.; Soskin, M.S.; Vasnetsov, M.V. Screw dislocations in light wavefronts. J. Mod. Opt. 1992, 39, 985–990. [Google Scholar] [CrossRef]
- Allen, L.; Barnett, S.M.; Padgett, M.J. Optical Angular Momentum; CRC Press: Bristol, UK, 2003. [Google Scholar]
- Leach, J.; Keen, S.; Padgett, M.J.; Saunter, C.; Love, G.D. Direct measurement of the skew angle of the Poynting vector in a helically phased beam. Opt. Express 2006, 14, 11919–11924. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.; Babiker, M. (Eds.) The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Mann, A. ‘Twisted’ light beams promise an optical revolution. PNAS 2018, 115, 5621–5623. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct observation of transfer of angular-momentum to absorptive particles from a laser-beam with a phase singularity. Phys. Rev. Lett. 1995, 75, 826–829. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; Volke-Sepulveda, K.; Chávez-Cerda, S.; Sibbett, W.; Dholakia, K. Transfer of orbital angular momentum to an optically trapped low-index particle. Phys. Rev. A 2002, 66, 063402. [Google Scholar]
- Shvedov, V.G.; Desyatnikov, A.S.; Rode, A.V.; Izdebskaya, Y.V.; Krolikowski, W.Z.; Kivshar, Y.S. Optical vortex beams for trapping and transport of particles in air. Appl. Phys. A 2010, 100, 327–331. [Google Scholar] [CrossRef]
- Babiker, M.; Bennett, C.R.; Andrews, D.L.; Dávila Romero, L.C. Orbital angular momentum exchange in the interaction of twisted light with molecules. Phys. Rev. Lett. 2002, 89, 143601. [Google Scholar] [CrossRef]
- Picón, A.; Mompart, J.; Vázquez de Aldana, J.R.; Plaja, L.; Calvo, G.F.; Roso, L. Photoionization with orbital angular momentum beams. Opt. Express 2010, 18, 3660–3671. [Google Scholar] [CrossRef]
- Hnatovsky, C.; Shvedov, V.G.; Krolikowski, W.; Rode, A.V. Materials processing with a tightly focused femtosecond laser vortex pulse. Opt. Lett. 2010, 35, 3417–3419. [Google Scholar] [CrossRef]
- Hamazaki, J.; Morita, R.; Chujo, K.; Kobayashi, Y.; Tanda, S.; Omatsu, T. Optical-vortex laser ablation. Opt. Express 2010, 18, 2144–2151. [Google Scholar] [CrossRef]
- Ni, J.; Wang, C.; Zhang, C.; Hu, Y.; Yang, L.; Lao, Z.; Xu, B.; Li, J.; Wu, D.; Chu, J. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material. Light Sci. Appl. 2017, 6, e17011. [Google Scholar] [CrossRef] [PubMed]
- Omatsu, T.; Miyamoto, K.; Toyoda, K.; Morita, R.; Arita, Y.; Dholakia, K. A New Twist for Materials Science: The formation of chiral structures using the angular momentum of light. Adv. Opt. Mat. 2019, 7, 1801672. [Google Scholar] [CrossRef]
- Tamburini, F.; Anzolin, G.; Umbriaco, G.; Bianchini, A.; Barbieri, C. Overcoming the Rayleigh criterion limit with optical vortices. Phys. Rev. Lett. 2006, 97, 163903. [Google Scholar] [CrossRef]
- Crabtree, K.; Davis, J.A.; Moreno, I. Optical processing with vortex-producing lenses. Appl. Opt. 2004, 43, 11360–11367. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.J.; Tur, M.; Ramachandran, S.; Molisch, A.F.; Ashrafi, N.; Ashrafi, S. Optical communications using orbital angular momentum beams. Adv. Opt. Phot. 2015, 7, 66–106. [Google Scholar]
- Cozzolino, D.; Bacco, D.; Da Lio, B.; Ingerslev, K.; Ding, Y.; Dalgaard, K.; Kristensen, P.; Galili, M.; Rottwitt, K.; Ramachandran, S.; et al. Orbital angular momentum states enabling fiber-based high-dimensional quantum communication. Phys. Rev. Appl. 2019, 11, 064058. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photon. 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Wang, X.; Nie, Z.; Liang, Y.; Wang, J.; Li, T.; Jia, B. Recent advances on optical vortex generation. Nanophotonics 2018, 7, 1533–1556. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation, from topological charge to multiple singularities. Light Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Dorrah, A.H.; Rosales-Guzmán, C.; Forbes, A.; Mojahedi, M. Evolution of orbital angular momentum in three-dimensional structured light. Phys. Rev. A 2018, 98, 043846. [Google Scholar] [CrossRef]
- Yang, Y.; Zhu, X.; Zeng, J.; Lu, X.; Zhao, C.; Cai, Y. Anomalous Bessel vortex beam: Modulating orbital angular momentum with propagation. Nanophotonics 2018, 7, 677–682. [Google Scholar] [CrossRef]
- Rozas, D.; Law, C.T.; Swartzlander, G.A. Propagation dynamics of optical vortices. J. Opt. Soc. Am. B 1997, 14, 3054–3065. [Google Scholar] [CrossRef]
- Porras, M.A. Upper bound to the orbital angular momentum carried by an ultrashort pulse. Phys. Rev. Lett. 2019, 122, 123904. [Google Scholar] [CrossRef] [PubMed]
- Gbur, G.; Visser, T.D.; Wolf, E. Anomalous behavior of spectra near phase singularities of focused waves. Phys. Rev. Lett. 2002, 88, 01390. [Google Scholar] [CrossRef]
- Berry, M.V. Coloured phase singularities. New J. Phys. 2002, 4, 66–73. [Google Scholar] [CrossRef]
- Berry, M.V. Exploring the colours of dark light. New J. Phys. 2002, 4, 74–80. [Google Scholar] [CrossRef]
- Popescu, G.; Dogariu, A. Spectral anomalies at wave-front dislocations. Phys. Rev. Lett. 2002, 88, 183902. [Google Scholar] [CrossRef]
- Leach, J.; Padgett, M.J. Observation of chromatic effects near a white-light vortex. New J. Phys. 2003, 5, 154. [Google Scholar] [CrossRef]
- Angelsky, O.V.; Hanson, S.G.; Maksimyak, A.P.; Maksimyak, P.P. Feasibilities of interferometric and chromascopic techniques in study of phase singularities. Appl. Opt. 2005, 44, 5091–5100. [Google Scholar] [CrossRef]
- Zapata-Rodríguez, C.J. Analytical characterization of spectral anomalies in polychromatic aperture beams. Opt. Commun. 2006, 257, 9–15. [Google Scholar] [CrossRef]
- Ding, C.; Pan, L.; Lü, B. Phase singularities and spectral changes of spectrally partially coherent higher-order Bessel-Gauss pulsed beams. J. Opt. Soc. Am. A 2009, 26, 2654–2661. [Google Scholar] [CrossRef] [PubMed]
- Bock, M.; Grunwald, R. Mapping the spectral twist of few cycle vortex pulses. Proc. SPIE 2016, 9764, 97640O. [Google Scholar]
- Bock, M.; Liebmann, M.; Elsaesser, T.; Grunwald, R. Gouy Phase Rotation in Spectral Maps of Ultrashort Vortex Pulses; Digest Paper EE-1.4; CLEO/Europe-EQEC: Munich, Germany, 2017. [Google Scholar]
- Liebmann, M.; Treffer, A.; Bock, M.; Elsaesser, T.; Grunwald, R. Spectral anomalies and Gouy rotation around the singularity of ultrashort vortex pulses. Opt. Express 2017, 25, 26076–26088. [Google Scholar] [CrossRef]
- Baumann, S.M.; Kalb, D.M.; MacMillan, L.H.; Galvez, E.J. Propagation dynamics of optical vortices due to Gouy phase. Opt. Express 2009, 17, 9818–9827. [Google Scholar] [CrossRef] [PubMed]
- Hamazaki, J.; Mineta, Y.; Oka, K.; Morita, R. Direct observation of Gouy phase shift in a propagating optical vortex. Opt. Express 2006, 14, 8382–8392. [Google Scholar] [CrossRef]
- Miyahara, H.; Qi, Y.; Kurihara, T.; Ando, S. Rotation of multi-zeros optical beam during propagation and its application to distance measurement. In Proceedings of the SICE Annual Conference 2011, Tokyo, Japan, 13–18 September 2011. FrC03-06. [Google Scholar]
- Schulze, C.; Roux, F.S.; Dudley, A.; Rop, R.; Duparré, M.; Forbes, A. Accelerated rotation with orbital angular momentum modes. Phys. Rev. A 2015, 91, 043821. [Google Scholar] [CrossRef]
- Yamane, K.; Sakamoto, M.; Murakami, N.; Morita, R.; Oka, K. Picosecond rotation of a ring-shaped optical lattice by using a chirped vortex-pulse pair. Opt. Lett. 2016, 41, 4597–4600. [Google Scholar] [CrossRef]
- Rego, L.; Dorney, K.M.; Brooks, N.J.; Nguyen, Q.L.; Liao, C.-T.; Román, J.S.; Couch, D.E.; Liu, A.; Pisanty, E.; Lewenstein, M.; et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 2019, 364, eaaw9486. [Google Scholar] [CrossRef]
- Liebmann, M.; Treffer, A.; Bock, M.; Wallrabe, U.; Grunwald, R. Controlling the spectral rotation of ultrashort vortex pulses. Proc. SPIE 2020, 11297, 112970W. [Google Scholar]
- Gouy, L.G. Sur une propriete nouvelle des ondes lumineuses. C. R. Acad. Sci. Paris 1890, 110, 1251–1253. [Google Scholar]
- Gouy, L.G. Sur la propagation anomale des ondes. Compt. Rendue Acad. Sci. Paris 1890, 111, 33–35. [Google Scholar]
- Rubinowicz, A. On the anomalous propagation of phase in the focus. Phys. Rev. 1938, 54, 931–936. [Google Scholar] [CrossRef]
- Boyd, R.W. Intuitive explanation of the phase anomaly of focused light beams. J. Opt. Soc. Am. 1980, 70, 877–880. [Google Scholar] [CrossRef]
- Kim, M.-S.; Scharf, T.; da Costa Assafrao, A.; Rockstuhl, C.; Pereira, S.F.; Urbach, H.P.; Herzig, H.P. Phase anomalies in Bessel-Gauss beams. Opt. Express 2012, 20, 28929–28940. [Google Scholar] [CrossRef] [PubMed]
- Martelli, P.; Tacca, M.; Gatto, A.; Moneta, G.; Martinelli, M. Gouy phase shift in nondiffracting Bessel beams. Opt. Express 2010, 18, 7108–7120. [Google Scholar] [CrossRef]
- Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Spectral self-imaging and Gouy rotation echos of propagating vortex pulse arrays. Proc. SPIE 2019, 10935, 109350T. [Google Scholar]
- Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Self-imaging of tailored vortex pulse arrays and spectral Gouy rotation echoes. Opt. Lett. 2019, 44, 1047–1050. [Google Scholar] [CrossRef]
- Musigmann, M.; Jahns, J.; Bock, M.; Grunwald, R. Refractive-diffractive dispersion compensation for optical vortex beams with ultrashort pulse durations. Appl. Opt. 2014, 53, 7304–7311. [Google Scholar] [CrossRef]
- Bock, M.; Brunne, J.; Treffer, A.; König, S.; Wallrabe, U.; Grunwald, R. Sub-3-cycle vortex pulses of tunable topological charge. Opt. Lett. 2013, 38, 3642–3645. [Google Scholar] [CrossRef]
- Liebmann, M.; Treffer, A.; Bock, M.; Seiler, T.; Jahns, J.; Elsaesser, T.; Grunwald, R. Spectral meta- moments reveal hidden signatures of vortex pulses. In Proceedings of the EPJ Web of Conferences, Beijing, China, 19–24 May 2019; Volume 205, p. 01005. [Google Scholar]
- Yadav, B.K.; Kandpal, H.C. Spectral anomalies of polychromatic DHGB and its applications in FSOJ. Lightwave Technol. 2011, 29, 960–966. [Google Scholar] [CrossRef]
- Pu, J.; Cai, C.; Nemoto, S. Spectral anomalies in Young’s double-slit interference experiment. Opt. Express 2004, 12, 5131–5139. [Google Scholar] [CrossRef] [PubMed]
- Ghebjagh, S.G.; Sinzinger, S. Composite spiral multi-value zone plates. Appl. Opt. 2020, 15, 4618–4623. [Google Scholar] [CrossRef] [PubMed]

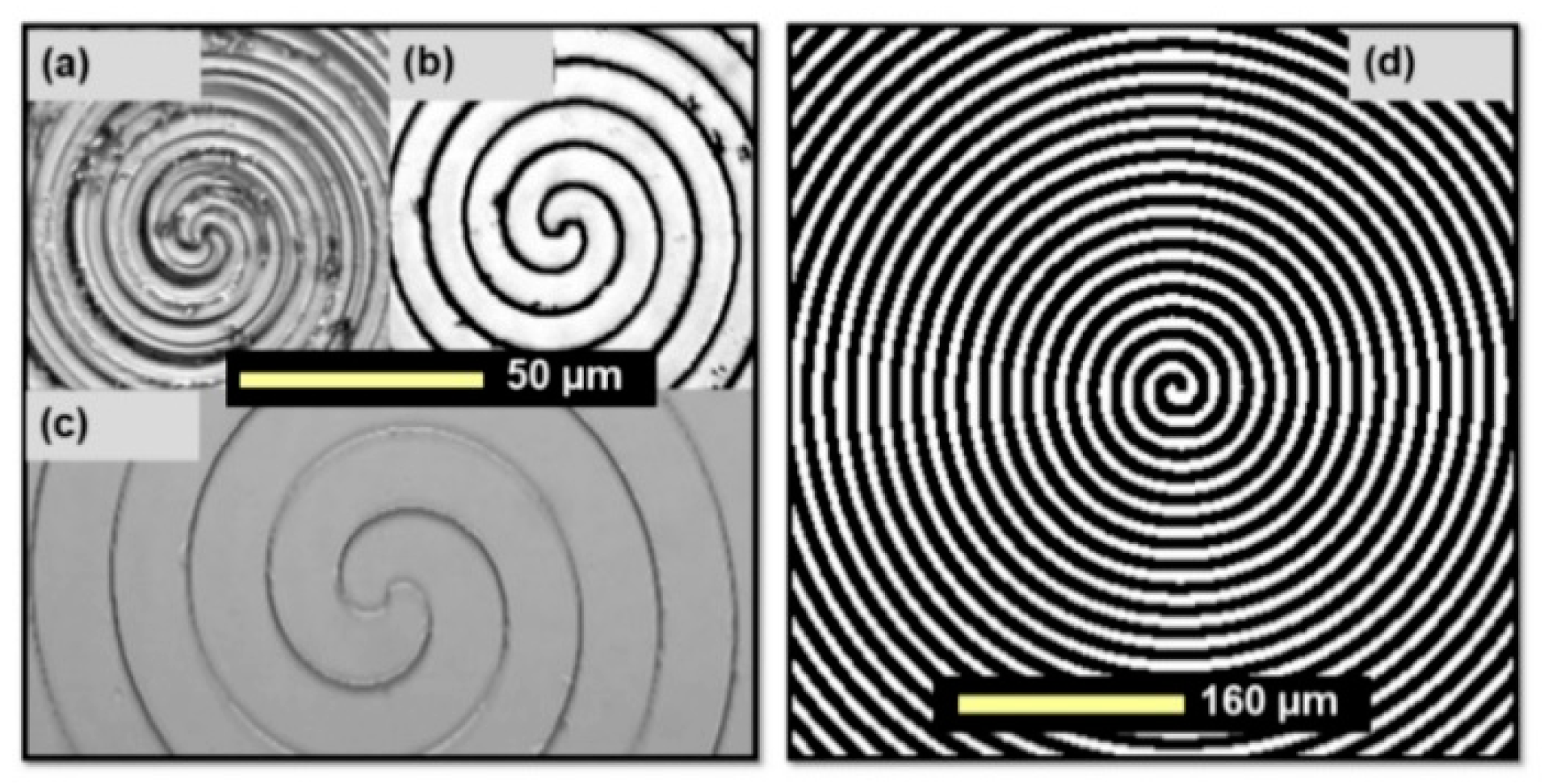
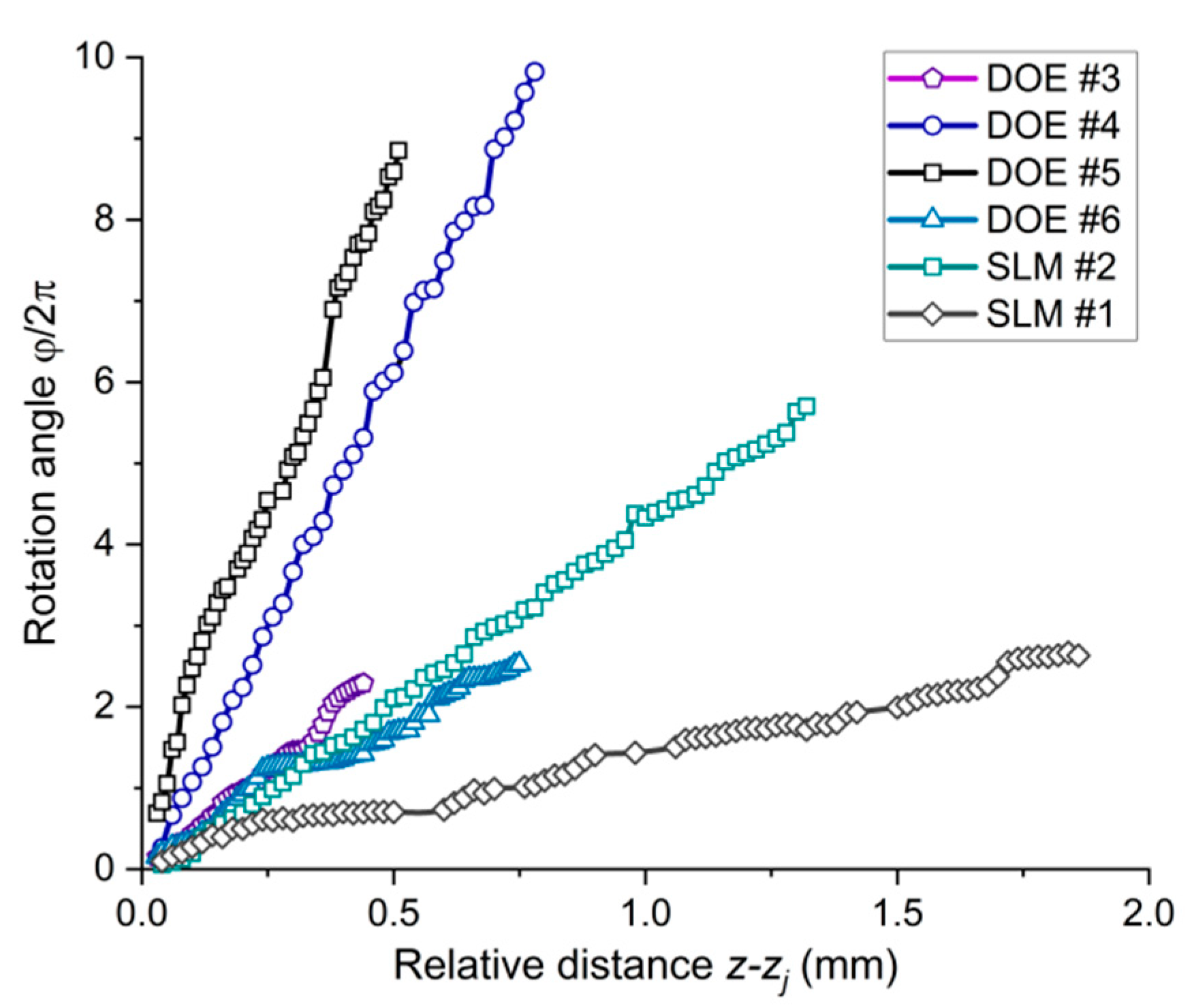
| Spiral Phase Gratings (SPG) Con-Figuration | Type of Orbital Angular Momentum (OAM) Shaper | Grating Period (µm) | Aperture Diameter (mm) | Depth of Focal Zone (mm) | Fresnel Number (Aperture)1 | 1st Order Diffraction Angle (°) |
|---|---|---|---|---|---|---|
| 1 | SLM_32 | 32 | 2 | 40 | 250 | 1.43 |
| 2 | SLM_16 | 16 | 2 | 20 | 500 | 2.87 |
| 3 | DOE 4-step | 16 | 2 | 20 | 500 | 2.87 |
| 4 | DOE 2-step | 16 | 0.4 | 4 | 100 | 2.87 |
| 5 | DOE 2-step | 16 | 0.2 | 2 | 50 | 2.87 |
| 6 | DOE 2-step | 32 | 0.4 | 8 | 50 | 1.43 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liebmann, M.; Treffer, A.; Bock, M.; Wallrabe, U.; Grunwald, R. Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation. Appl. Sci. 2020, 10, 4288. https://doi.org/10.3390/app10124288
Liebmann M, Treffer A, Bock M, Wallrabe U, Grunwald R. Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation. Applied Sciences. 2020; 10(12):4288. https://doi.org/10.3390/app10124288
Chicago/Turabian StyleLiebmann, Max, Alexander Treffer, Martin Bock, Ulrike Wallrabe, and Ruediger Grunwald. 2020. "Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation" Applied Sciences 10, no. 12: 4288. https://doi.org/10.3390/app10124288
APA StyleLiebmann, M., Treffer, A., Bock, M., Wallrabe, U., & Grunwald, R. (2020). Ultrashort Vortex Pulses with Controlled Spectral Gouy Rotation. Applied Sciences, 10(12), 4288. https://doi.org/10.3390/app10124288