DEUFRABASE: A Simple Tool for the Evaluation of the Noise Impact of Pavements in Typical Road Geometries
Abstract
1. Introduction
2. Principle of the Method
- , which is the A-weighted equivalent sound pressure level based on the 1 hour-traffic of passenger cars (PC) and heavy trucks (HT),
- , which is the A-weighted equivalent sound pressure level based on the traffic distribution of PC and HT over the 24 h of a day,
- , which is the day–evening–night A-weighted equivalent sound pressure level, calculated from the .
- the hourly-traffic distribution during the three periods of a full day: [6:00–18:00] for the daytime period, [18:00–22:00] for the evening period and [22:00–6:00] for the night period. In the present approach, to be as close as possible to real configurations, two main vehicle classes are considered; the passenger cars (PC) and the heavy trucks (HT), defined by their traffic distribution and , respectively,
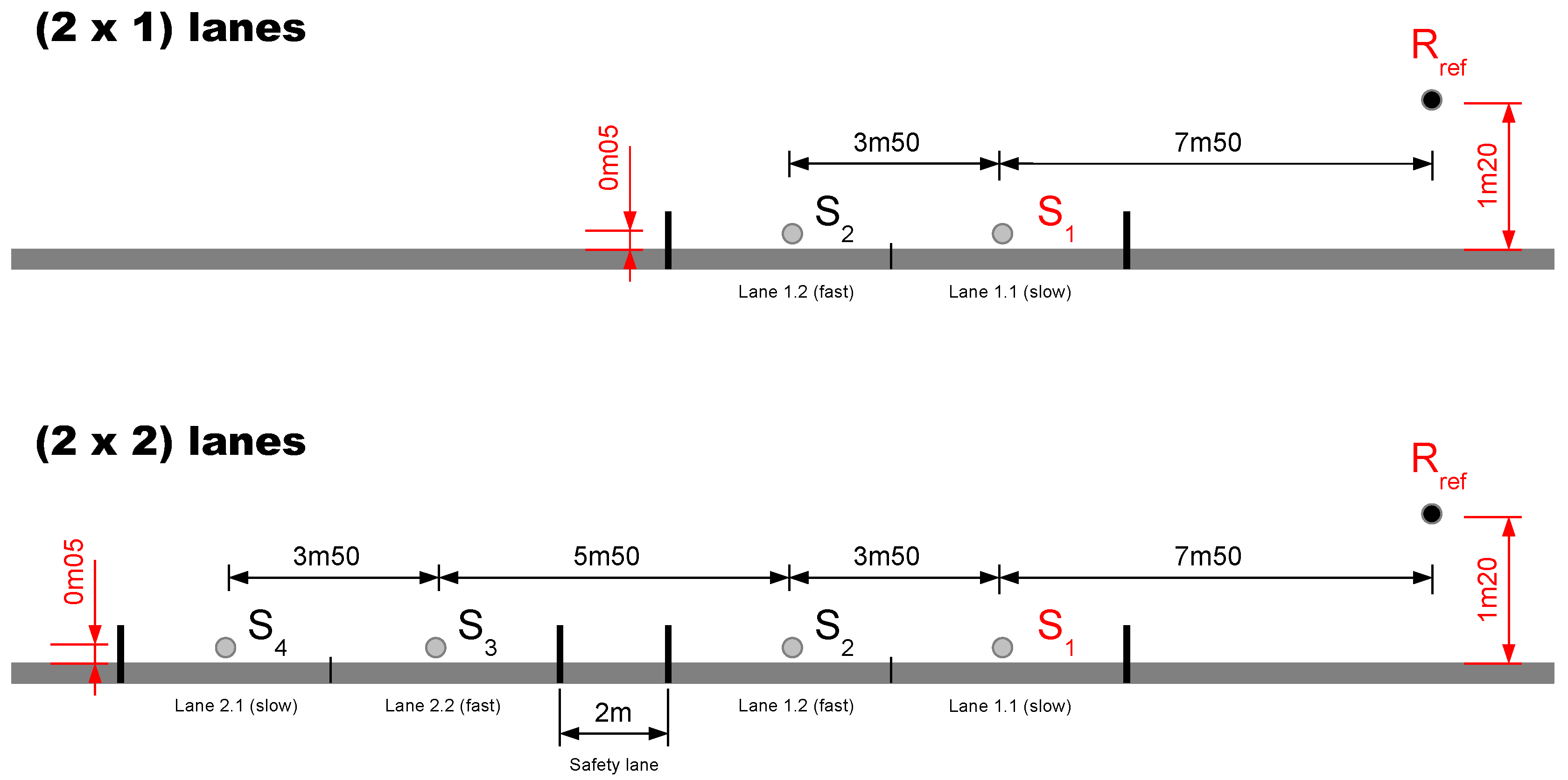
- the number and the width of traffic lanes,
- the reference speed of each vehicle class (90 or 110 km/h for PC and 80 km/h for HT),
- the A-weighted pass-by maximum sound pressure level for PC and HT vehicles (in global and third octave values) measured at a reference microphone, according to the International Organization for Standardization (ISO) statistical pass-by (SPB) method [7] (7.50 m from the right lane axis and 1.20 m above the ground),
- typical road geometries with different ground parameters,
- different meteorological conditions.
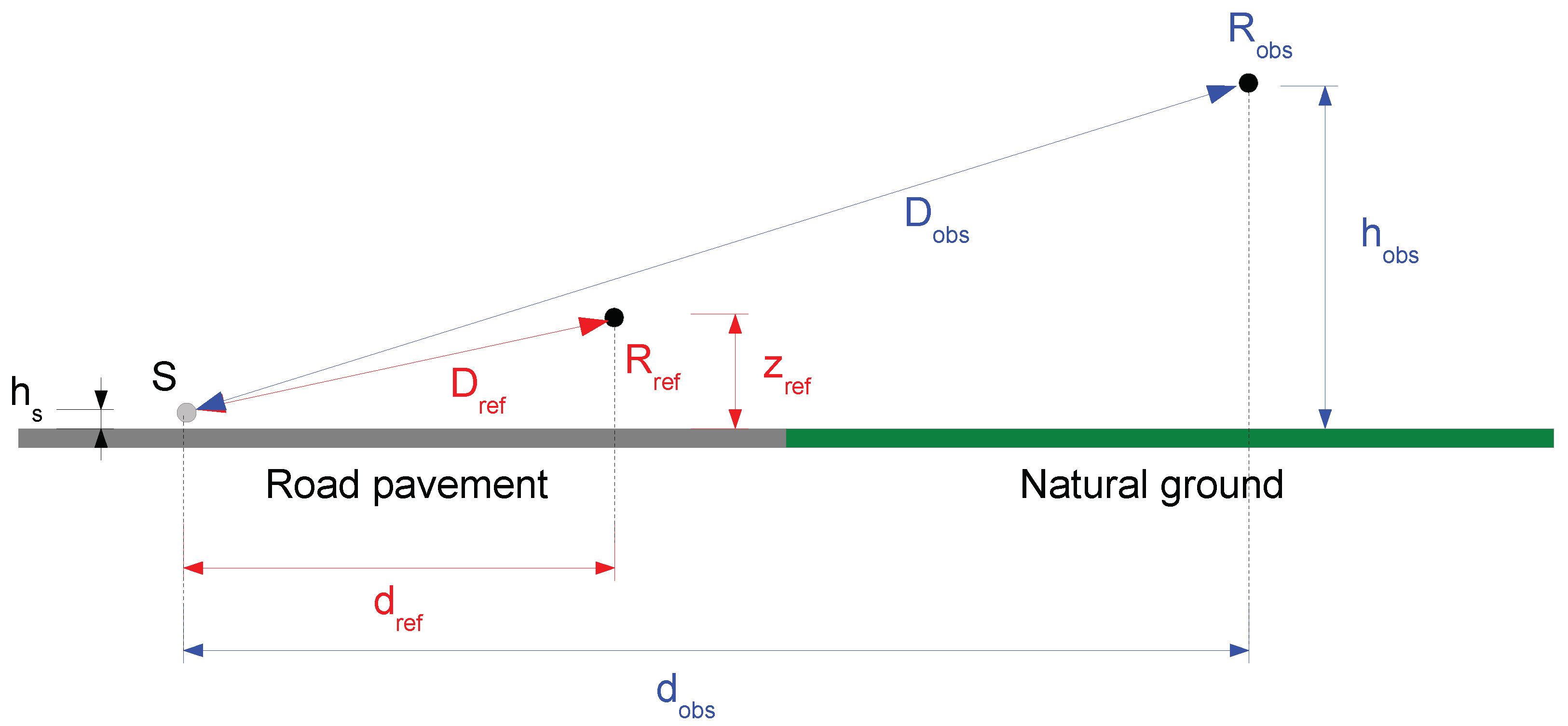
2.1. Sound Pressure Level Calculation
2.2. Input Parameters
2.2.1. Road Configurations
- for grassy soils (): kNsm−4,
- for porous asphalts (): kNsm−4, %, ,
- for dense pavements, the impedance Z is considered as infinite ().
2.2.2. Pavement Data
2.2.3. Traffic Data
3. Implementation of the Method
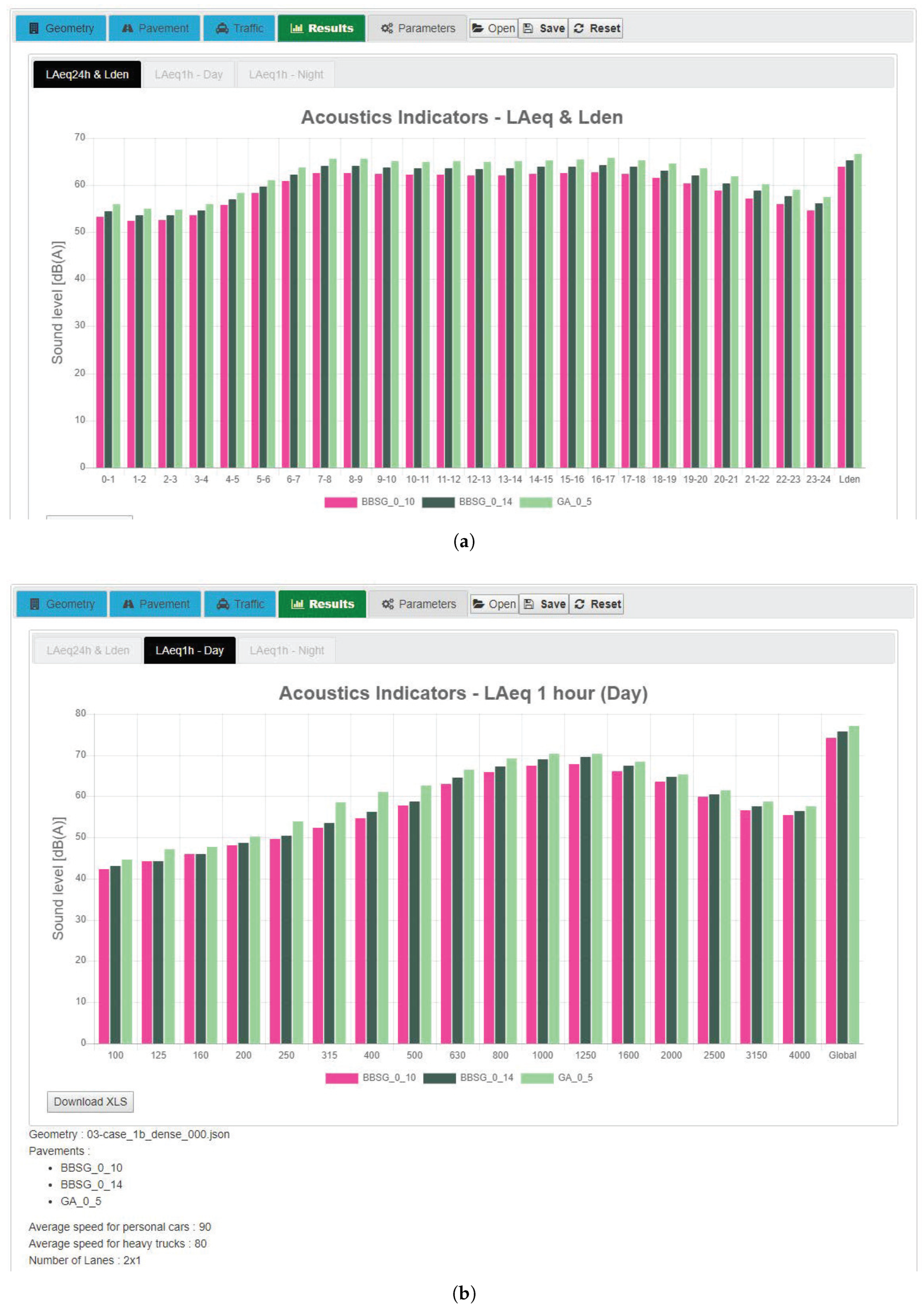
3.1. Calculation Tool
- select a road configuration in a list (‘Geometry’ tab of the web tool), as defined in Table 1;
- select one or more road pavements in a list (‘Pavement’ tab). The pavement list displayed depended on the selected road configuration at the first step (i.e., dense or porous road surface). At this step, the user had the possibility to consider his own noise emission data, at the condition that it respects the proposed JSON file format and the measurement conditions (CPB method). Note that the user can also consider emission data that would have been measured at other traffic speeds, by ‘bypassing’ the expected data in the file for each reference speed (for example, by associating the expected values at 90 km/h for a PC, with data measured at another speed);
- define the traffic flow and composition, as well as the number of lanes (‘Traffic’ tab). Depending the noise indicator to be calculated ( or /), the user had to provide the traffic distribution of a given hour or for each of the 24 h periods. At this step, the user also had the possibility to use the proposed average daily traffic distribution or his own data.
3.2. General Considerations
- the calculation of the ‘attenuation’ term in Equation (5) between the reference receiver and the receiver located far away were always carried out with respect to the median axis of the right traffic lane,
- because the traffic is distributed among the different lanes (two or four depending on the road configuration), a set of excess attenuation relative to free field and geometrical attenuation should have been estimated for all the respective traffic lanes, which was not the case in the present version of the DEUFRABASE. This assumption induced a small over-estimation of the resulting or . Moreover, considering the accuracy of the average values for each pavement with respect to the measured distribution (±3 dB), the uncertainties on the or estimations were inside the range of variation. Thus, this small over-estimation was acceptable and can be credited to the local residents, which consequently will be more protected when better effective means of traffic noise reduction will be installed, such as noise barriers or more efficient low noise pavements.
- For an observation point that is very close to a reflecting façade, the reflection effect ( dB) should be introduced ‘manually’ by the user at the very end of the calculation (the DEUFRABASE tool does not consider this reflection effect).
3.3. Additional Calculations
3.3.1. Calculations
3.3.2. Speed Correction
- changing the PC speed to , without changing the HT speed (80 km/h),
- changing both the PC and HT speeds, to and to respectively.
Changing the PC Speed
- firstly to compute the alone, for the whole PC traffic flow, at the reference speed (i.e., without considering the HT contribution), using the DEUFRABASE,
- secondly, to compute the whole including both PC and HT contributions at the reference speeds, using the DEUFRABASE,
- lastly, to calculate the final according to Equation (19).
Changing Both the PC and HT Speeds
- firstly, to compute the alone, for the whole PC traffic flow, at the reference speed, i.e., without considering the HT contribution, using the DEUFRABASE,
- secondly, to compute the alone, for the whole HT traffic flow, at the reference speed, without considering the PC contribution (i.e., percentage of HT = 100%), using the DEUFRABASE,
- thirdly, to compute the whole including both PC and HT contributions at the reference speeds, using the DEUFRABASE,
- lastly, to calculate the final according to Equation (20).
3.4. Example of DEUFRABASE Calculation
- in the ‘Geometry’ tab, the configuration ‘1b, dense discontinuity, short’ is considered (see Table 1),
- in the ‘Pavement’ tab, the ‘BBSG 0/14’ pavement is selected in the database (i.e., the French name ’Béton Bitumineux Semi-Grenu (BBSG)’ of the DAC 0/14 pavement),
- in the ‘Traffic’ tab, the road traffic is distributed on both lanes, for PC and HT vehicles separately (by checking ’Your Own Traffic Data’ instead of using pre-defined data), with the reference speeds of 90 km/h and 80 km/h for the PC and HT respectively.
4. Validation
- the exact number of PC and HT in each direction,
- the impedance characteristics of the different surfaces (road and close environment),
- the atmospheric conditions (temperature, wind direction and velocity),
- the vertical sound speed gradient .
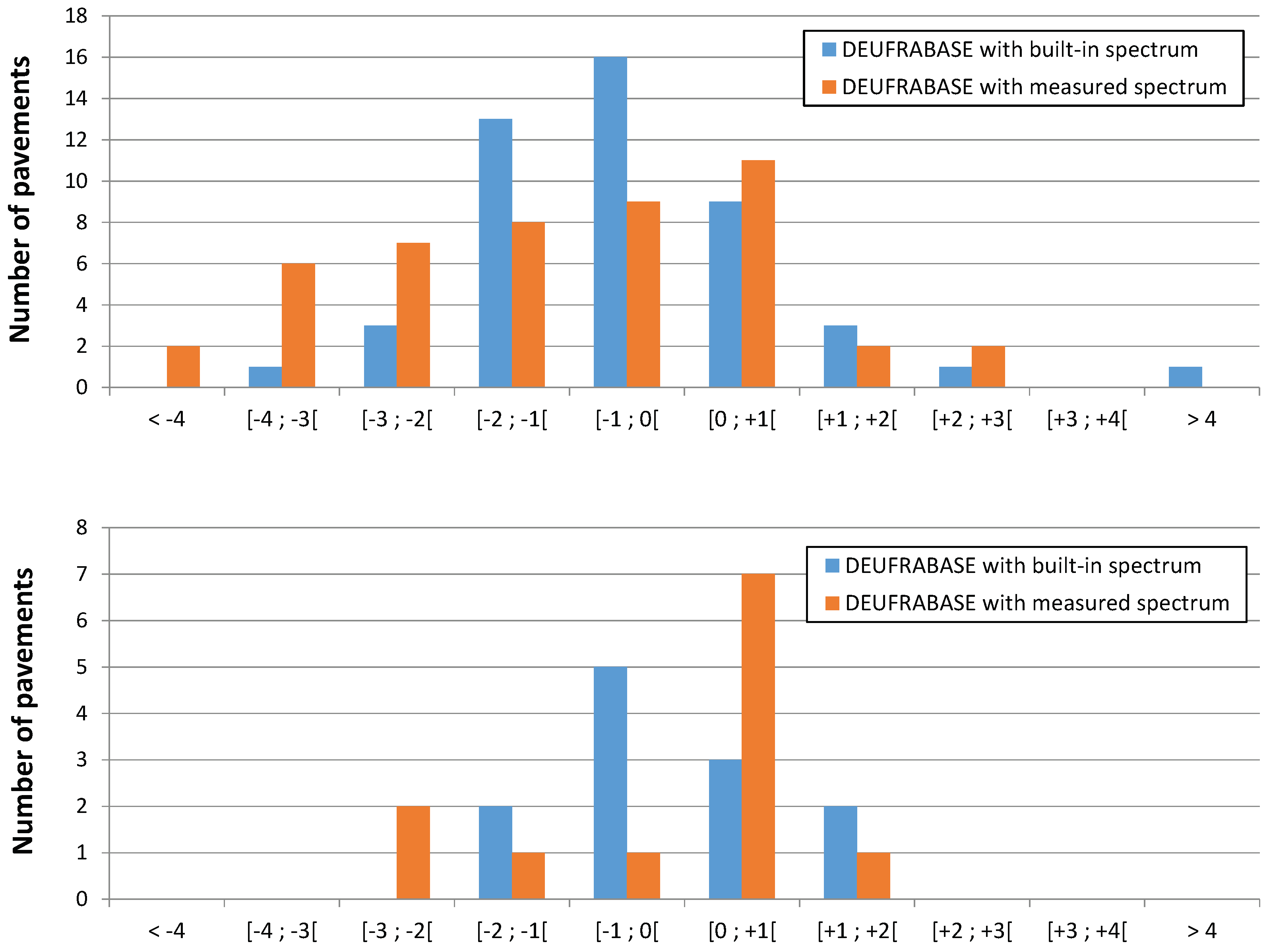
- The a priori ‘worst’ prediction considered the real traffic data only, while the other parameters (emission spectra and impedance characteristics) can be selected in the database. In this case, all the 47 road pavements can lead to a comparison between measurements and DEUFRABASE predictions.
- The a priori ‘best’ prediction considered all real input parameters (traffic data, emission spectra and impedance characteristics). Thus, for this comparison, one must extract from the 47 road configurations, those whose impedance characteristics are ‘similar’ to the one in the DEUFRABASE. In this case, only 12 road configurations representative of the three main pavement classes (three with low noise, four with intermediate, and five noisy) can be retained. One can also consider the emission spectra given by the DEUFRABASE instead of the measured one, leading to a priori results that are a little less precise (‘upper-intermediate’).
- An ‘intermediate’ prediction was also possible, considering the real traffic data and the measured emission spectra, but using the impedance characteristics available in the DEUFRABASE. In this case, all the 47 road configurations can be considered for comparison.
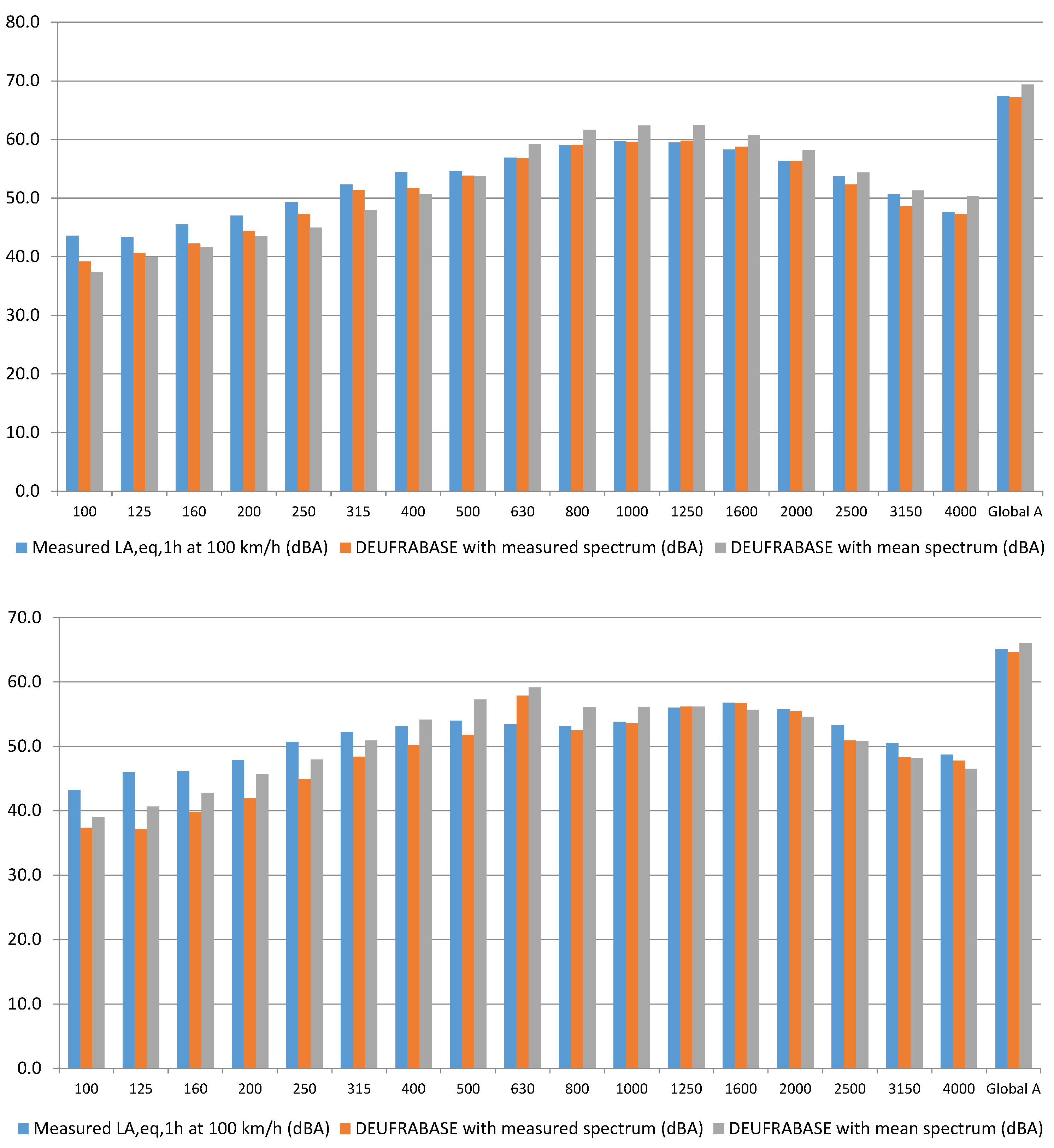
4.1. Spectral Validation
- in global value, a very good agreement can be observed. The deviation being closed to one or two decibels;
- for each 1/3 octave band, one can note a rather good agreement between calculations and measurements above 500 Hz and particularly when considering the real measured 1/3 octave emission spectrum (red bars, ‘intermediate’ prediction) in the computation. When using an average pavement spectrum estimated from a rather large number of pavement samples for each family (gray bars, ‘worst’ prediction), which can be partially different of one particular measured pavement, the deviation is a little bit larger (around 2 dB(A)) but still acceptable. Below 500 Hz, more important differences occurred, especially for the porous asphalt. They can be explained for a small part by this difference between measured and averaged emission spectra and for a larger part by the fact that impedance values of surfaces located each side of the discontinuity, estimated from the input parameters detailed in Section 2.2.1, may slightly differ from the in situ values.
4.2. Validation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Environmental Noise Guidelines for the European Region; World Health Organization: Copenhagen, Denmark, 2018. [Google Scholar]
- Ögren, M.; Molnár, P.; Barregard, L. Road traffic noise abatement scenarios in Gothenburg 2015–2035. Environ. Res. 2018, 164, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Directive 2002/49/EC of the European Parliament and of the Council of 25 June 2002 Relating to the Assessment and Management of Environmental Noise—Declaration by the Commission in the Conciliation Committee on the Directive Relating to the Assessment and Management of Environmental Noise. 2002. Available online: http://data.europa.eu/eli/dir/2002/49/oj/eng (accessed on 21 February 2019).
- Kephalopoulos, S.; Paviotti, M.; Anfosso-Lédée, F. Common Noise Assessment Methods in Europe (CNOSSOS-EU); Publications Office of the European Union: Luxembourg, 2012. [Google Scholar] [CrossRef]
- Berengier, M.; Droste, B.; Gauvreau, B.; Duhamel, D.; Auerbach, M. DEUFRABASE: A German-French acoustic database on road pavements. J. Acoust. Soc. Am. 2008, 123, 3391. [Google Scholar] [CrossRef]
- Bérengier, M.; Pichaud, Y.; Le Fur, J.F. Effect of low noise pavements on traffic noise propagation over large distances: Influence of ground and atmospheric conditions. In Proceedings of the 29th International Congress on Noise Control Engineering, Nice, France, 27–31 August 2000. [Google Scholar]
- International Organization for Standardization. Acoustics—Measurement of the Influence of Road Surfaces on Traffic Noise—Part 1: Statistical Pass-By Method; ISO 11819-1:1997; International Organization for Standardization: Geneva, Switzerland, 1997. [Google Scholar]
- Bérengier, M.; Gauvreau, B.; Blanc-Benon, P.; Juvé, D. Outdoor Sound Propagation: A Short Review on Analytical and Numerical Approaches. Acta Acust. United Acust. 2003, 89, 980–991. [Google Scholar]
- Bérengier, M.; Duhamel, D.; Gauvreau, B.; Droste, B.; Auerbach, M. A Benchmark on analytical and numerical models for road traffic noise propagation. In Proceedings of the 19th International Congress on Acoustics, Madrid, Spain, 2–7 September 2007. [Google Scholar]
- Rasmussen, K.B. A note on the calculation of sound propagation over impedance jumps and screens. J. Sound Vib. 1982, 84, 598–602. [Google Scholar] [CrossRef]
- Bonnet, M. Boundary Integral Equation Methods for Solids and Fluids; John Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Anfosso-Lédée, F.; Dangla, P.; Bérengier, M. Sound propagation above a porous road surface with extended reaction by boundary element method. J. Acoust. Soc. Am. 2007, 122, 731–736. [Google Scholar] [CrossRef] [PubMed]
- Lihoreau, B.; Gauvreau, B.; Bérengier, M.; Blanc-Benon, P.; Calmet, I. Outdoor sound propagation modeling in realistic environments: Application of coupled parabolic and atmospheric models. J. Acoust. Soc. Am. 2006, 120, 110–119. [Google Scholar] [CrossRef]
- International Organization for Standardization. Acoustics—Attenuation of Sound during Propagation Outdoors—Part 1: Calculation of the Absorption of Sound by the Atmosphere; ISO 9613-1:1993; International Organization for Standardization: Geneva, Switzerland, 1993. [Google Scholar]
- Bérengier, M.; Hamet, J. Acoustic classification of road pavements: Ranking differences due to distance from the road. Int. J. Heavy Veh. Syst. 1999, 6, 13. [Google Scholar] [CrossRef]
- Delany, M.E.; Bazley, E.N. Acoustical properties of fibrous absorbent materials. Appl. Acoust. 1970, 3, 105–116. [Google Scholar] [CrossRef]
- Bérengier, M.C.; Stinson, M.R.; Daigle, G.A.; Hamet, J.F. Porous road pavements: Acoustical characterization and propagation effects. J. Acoust. Soc. Am. 1997, 101, 155–162. [Google Scholar] [CrossRef]
- Hamet, J.F.; Pallas, M.A.; Gaulin, D.; Bérengier, M. Acoustic modelling of road vehicles for traffic noise prediction: Determination of the sources heights. J. Acoust. Soc. Am. 1998, 103, 2919–2920. [Google Scholar] [CrossRef]
- DEUFRABASE: A French-German Database for Road Noise Evaluation. Available online: http://deufrabase.ifsttar.fr/ (accessed on 21 February 2019).
- Besnard, F.; Hamet, J.F.; Lelong, J.; Le Duc, E.; Guizard, V.; Fürst, N.; Doisy, S.; Dutilleux, G. Road Noise Prediction: 1-Calculating Sound Emission from Road Traffic; Sétra, Service d’études sur les transports, les routes et leurs aménagements: Bagneux, France, 2011. [Google Scholar]
- Noise-Environment—European Commission. Available online: http://ec.europa.eu/environment/noise/europe_en.htm (accessed on 21 February 2019).
- Skarabis, J.; Stöckert, U. Noise emission of concrete pavement surfaces produced by diamond grinding. J. Traffic Transp. Eng. (Engl. Ed.) 2015, 2, 81–92. [Google Scholar] [CrossRef]
- Vaitkus, A.; Andriejauskas, T.; Vorobjovas, V.; Jagniatinskis, A.; Fiks, B.; Zofka, E. Asphalt wearing course optimization for road traffic noise reduction. Constr. Build. Mater. 2017, 152, 345–356. [Google Scholar] [CrossRef]
- International Organization for Standardization. Acoustics—Measurement of the Influence of Road Surfaces on Traffic Noise—Part 2: The Close-Proximity Method; ISO 11819-2:2017; International Organization for Standardization: Geneva, Switzerland, 2017. [Google Scholar]
- Pallas, M.A.; Bérengier, M.; Chatagnon, R.; Czuka, M.; Conter, M.; Muirhead, M. Towards a model for electric vehicle noise emission in the European prediction method CNOSSOS-EU. Appl. Acoust. 2016, 113, 89–101. [Google Scholar] [CrossRef]
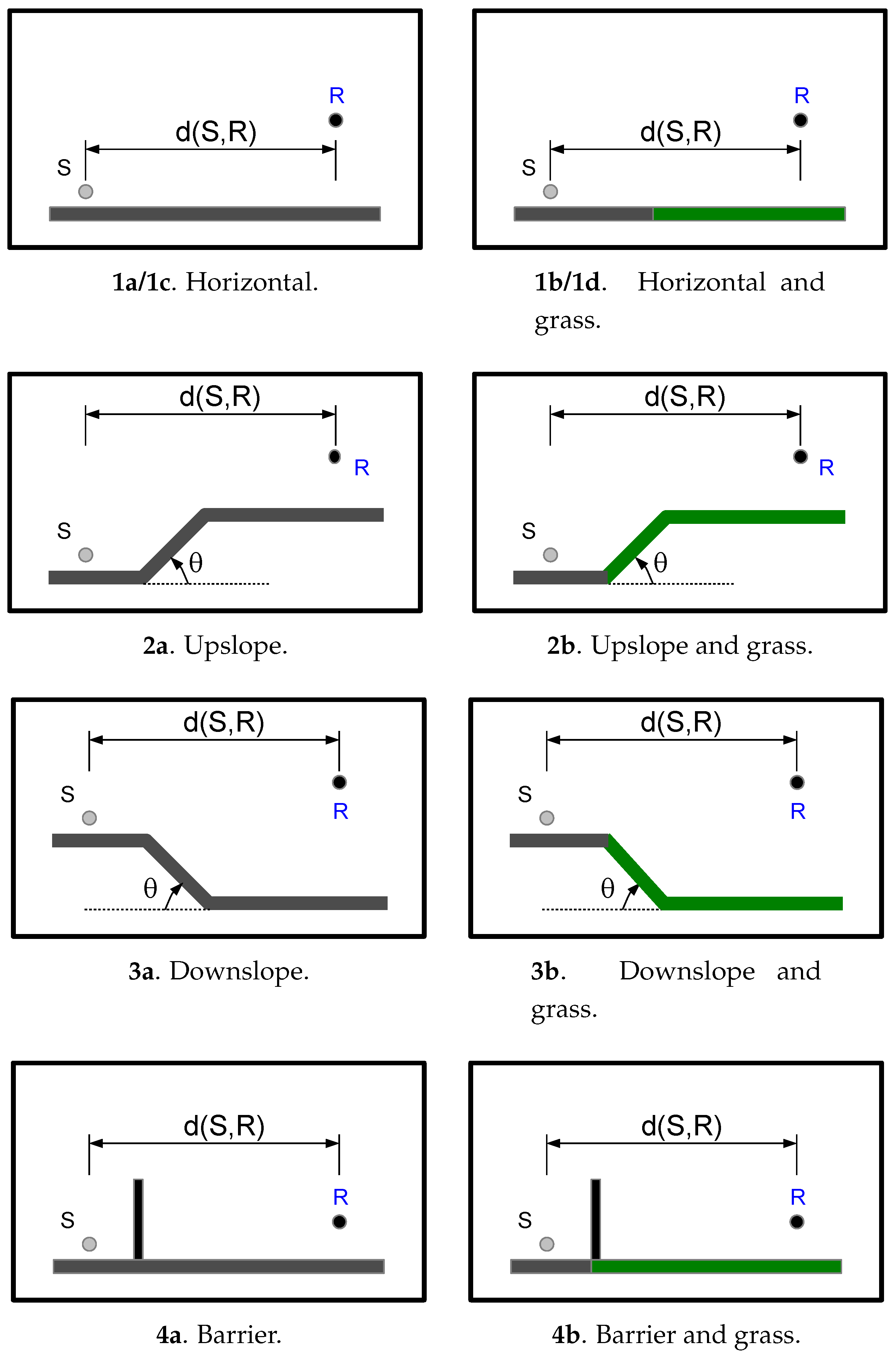
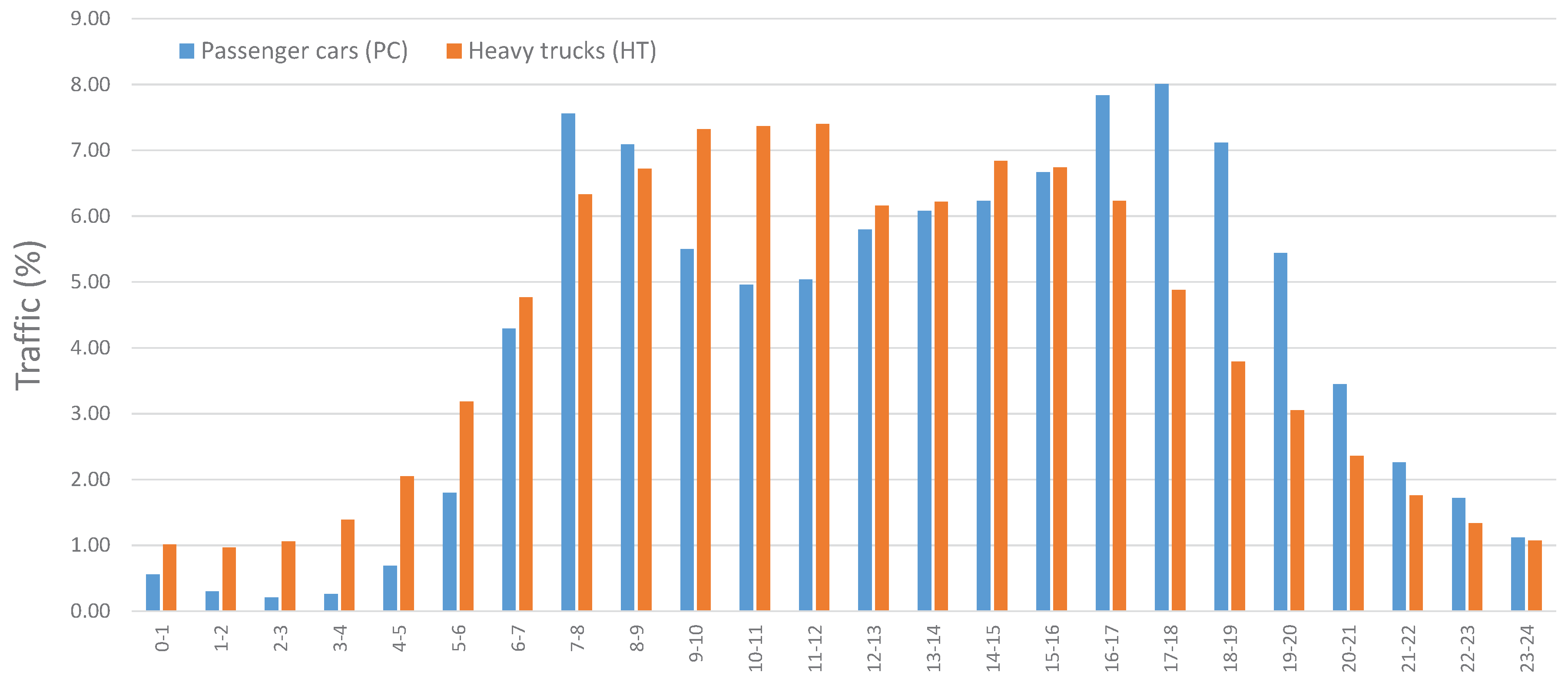
| Geometry | (deg) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1a (dense, short) | 0 | 1.20 | 7.50 | - | - | - | - | - | - | - | - | |
| 1a (porous, short) | 0 | 1.20 | 7.50 | - | - | - | - | - | - | - | - | |
| 1b (dense, discontinuity, short) | 0 | 1.20 | 7.50 | 4 | - | - | - | - | - | - | ||
| 1b (porous, discontinuity, short) | 0 | 1.20 | 7.50 | 4 | - | - | - | - | - | - | ||
| 1c (dense, long) | 0 | 2 | 200 | - | 4 | - | - | - | - | - | - | |
| 1c (dense, long, gradient) | 0.25 | 2 | 200 | - | 4 | - | - | - | - | - | - | |
| 1c (porous, long) | 0 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 1c (porous, long, gradient) | 0.25 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 1d (dense, discontinuity, long) | 0 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 1d (dense, discontinuity, long, gradient) | 0.25 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 1d (porous, discontinuity, long) | 0 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 1d (porous, discontinuity, long, gradient) | 0.25 | 2 | 200 | 4 | - | - | - | - | - | - | ||
| 2a (dense, upslope, short) | 0 | 2 | 50 | - | - | - | - | - | - | - | - | |
| 2a (dense, upslope, long, gradient) | 0.25 | 2 | 100 | - | - | - | - | - | - | - | - | |
| 2b (dense, discontinuity, upslope, short) | 0 | 2 | 50 | 4 | 4 | +1.5 | 8 | - | - | - | ||
| 2b (dense, discontinuity, upslope, long, gradient) | 0.25 | 2 | 100 | 4 | 4 | +1.5 | 8 | - | - | - | ||
| 2b (porous, discontinuity, upslope, short) | 0 | 2 | 50 | 4 | 4 | +1.5 | 8 | - | - | - | ||
| 2b (porous, discontinuity, upslope, long, gradient) | 0.25 | 2 | 100 | 4 | 4 | +1.5 | 8 | - | - | - | ||
| 3a (dense, downslope, short) | 0 | 2 | 50 | - | - | 4 | -1.5 | 8 | - | - | - | |
| 3a (dense, downslope, long, gradient) | 0.25 | 2 | 100 | - | - | 4 | -1.5 | 8 | - | - | - | |
| 3b (dense, downslope, discontinuity, short) | 0 | 2 | 50 | 4 | 4 | -1.5 | 8 | - | - | - | ||
| 3b (dense, downslope, discontinuity, long, gradient) | 0.25 | 2 | 100 | 4 | 4 | -1.5 | 8 | - | - | - | ||
| 3b (porous, downslope, discontinuity, short) | 0 | 2 | 50 | 4 | 4 | -1.5 | 8 | - | - | - | ||
| 3b (porous, downslope, discontinuity, long, gradient) | 0.25 | 2 | 100 | 4 | 4 | -1.5 | 8 | - | - | - | ||
| 4a (dense, barrier) | 0 | 3 | 40 | - | - | - | - | - | 4 | 36 | 2 | |
| 4b (dense, barrier, discontinuity) | 0 | 3 | 40 | 4 | - | - | - | 4 | 36 | 2 | ||
| 4b (porous, barrier, discontinuity) | 0 | 3 | 40 | 4 | - | - | - | 4 | 36 | 2 |
| Country | Description | Name | PC 90 km/h | PC 110 km/h | HT 80 km/h |
|---|---|---|---|---|---|
| FR | PA 0/6 | Porous asphalt 0/6 | 72.8 | 75.4 | 80.3 |
| GE | PA 0/8 | Porous asphalt 0/8 | 79.0 | 81.0 | 85.3 |
| GE | TLPA 0/8 | Twin layer porous asphalt 0/8 | 75.9 | 77.4 | 81.7 |
| FR | PA 0/10 | Porous asphalt 0/10 | 74.2 | 76.8 | 82.0 |
| FR | PA 0/14 | Porous asphalt 0/14 | 76.1 | 78.7 | 83.9 |
| FR | VTAC 0/6 – Type 1 | Very thin asphalt concrete 0/6—Type 1 | 74.9 | 77.5 | 82.8 |
| FR | VTAC 0/6 – Type 2 | Very thin asphalt concrete 0/6—Type 2 | 73.4 | 76.0 | 81.4 |
| FR | UTAC 0/6 | Ultra thin asphalt concrete 0/6 | 74.1 | 76.7 | 83.5 |
| FR | VTAC 0/8 – Type 1 | Very thin asphalt concrete 0/8—Type 1 | 76.2 | 78.8 | 82.6 |
| FR | TAC 0/10 | Thin asphalt concrete 0/10 | 77.6 | 80.2 | 85.6 |
| FR | VTAC 0/10 – Type 1 | Very thin asphalt concrete 0/10—Type 1 | 79.0 | 81.6 | 85.2 |
| FR | VTAC 0/10 – Type 2 | Very thin asphalt concrete 0/10—Type 2 | 75.3 | 77.9 | 82.6 |
| FR | UTAC 0/10 | Ultra thin asphalt concrete 0/10 | 78.3 | 81.0 | 84.4 |
| FR | VTAC 0/14 | Very thin asphalt concrete 0/14 | 80.4 | 83.0 | 86.2 |
| FR | DAC 0/10 (Ref) | Dense asphalt concrete 0/10 | 78.0 | 80.6 | 85.4 |
| FR | DAC 0/14 | Dense asphalt concrete 0/14 | 80.0 | 82.7 | 86.2 |
| FR | SMA 0/5 ln | Low noise stone mastic asphalt 0/5 | 78.7 | 80.9 | 88.7 |
| FR | SMA 0/8 ln | Low noise stone mastic asphalt 0/8 | 78.7 | 80.5 | 87.1 |
| FR | SMA 0/8 S | Special stone mastic asphalt 0/8 | 80.1 | 81.9 | 85.9 |
| GE | SMA 0/11 | Stone mastic asphalt 0/11 | 81.8 | 83.9 | 88.3 |
| GE | SMA 0/11 S | Special stone mastic asphalt 0/11 | 81.4 | 83.4 | 87.5 |
| FR | CASS | Cold applied slurry surfacing | 78.6 | 81.2 | 85.3 |
| FR | SD 6/10 | Surface dressing 6/10 | 80.0 | 82.6 | 85.9 |
| FR | SD 10/14 | Surface dressing 10/14 | 82.1 | 84.7 | 86.4 |
| GE | GA 0/5 | Mastic asphalt 0/5 | 81.8 | 83.1 | 88.6 |
| GE | GA 0/5 ln | Low noise mastic asphalt 0/5 | 81.7 | 82.6 | 87.0 |
| GE | CC | Cement concrete | 81.2 | 83.8 | 87.5 |
| GE | CC | Cement concrete | 83.0 | 84.4 | 90.9 |
| GE | CC 0/16 Kamm | Cement concrete treated with jute-cloth | 80.9 | 82.7 | 87.9 |
| GE | EAC 0/5 | Exposed aggregate concrete 0/5 | 82.1 | 83.6 | 90.4 |
| GE | EAC 0/8 | Exposed aggregate concrete 0/8 | 82.6 | 84.9 | 88.7 |
| GE | CCST 0/16 | Cement concrete treated with synthetic turf | 81.6 | 83.6 | 89.7 |
| Number of Vehicles per Lane | Percentage of HT | Distribution of Vehicles | Global Traffic () | Global Traffic () |
|---|---|---|---|---|
| 20,000 | 10% | PC: 18,000 HT: 2000 | 40,000 | 80,000 |
| 20,000 | 15% | PC: 17,000 HT: 3000 | 40,000 | 80,000 |
| 10,000 | 10% | PC: 9000 HT: 1000 | 20,000 | 40,000 |
| 10,000 | 15% | PC: 8500 HT: 1500 | 20,000 | 40,000 |
| Number of Lanes | PC Distribution per Lane | HT Distribution per Lane |
|---|---|---|
| () | 100% | 100% |
| () | Slow lane: 50% – Fast lane: 50% | Slow lane: 90% – Fast lane: 10% |
| Hourly Period | PC (in %) | HT (in %) |
|---|---|---|
| 0–1 | 0.56 | 1.01 |
| 1–2 | 0.30 | 0.97 |
| 2–3 | 0.21 | 1.06 |
| 3–4 | 0.26 | 1.39 |
| 4–5 | 0.69 | 2.05 |
| 5–6 | 1.80 | 3.18 |
| 6–7 | 4.29 | 4.77 |
| 7–8 | 7.56 | 6.33 |
| 8–9 | 7.09 | 6.72 |
| 9–10 | 5.50 | 7.32 |
| 10–11 | 4.96 | 7.37 |
| 11–12 | 5.04 | 7.40 |
| 12–13 | 5.80 | 6.16 |
| 13–14 | 6.08 | 6.22 |
| 14–15 | 6.23 | 6.84 |
| 15–16 | 6.67 | 6.74 |
| 16–17 | 7.84 | 6.23 |
| 17–18 | 8.01 | 4.88 |
| 18–19 | 7.12 | 3.79 |
| 19–20 | 5.44 | 3.05 |
| 20–21 | 3.45 | 2.36 |
| 21–22 | 2.26 | 1.76 |
| 22–23 | 1.72 | 1.34 |
| 23–24 | 1.12 | 1.07 |
| Total | 100 | 100 |
| Measurement ( = 100 km/h) | DEUFRABASE Results | ||
|---|---|---|---|
| 1/3 Octave Bands (Hz) | dB(A) | dB(A) | dB(A) |
| 100 | 48.4 | 43.1 | 43.4 |
| 125 | 51.5 | 44.2 | 44.4 |
| 160 | 52.0 | 46.0 | 46.2 |
| 200 | 53.8 | 48.6 | 48.8 |
| 250 | 57.8 | 50.5 | 50.7 |
| 315 | 62.4 | 53.5 | 53.6 |
| 400 | 62.1 | 56.2 | 56.3 |
| 500 | 63.2 | 58.8 | 58.9 |
| 630 | 67.4 | 64.6 | 64.7 |
| 800 | 68.3 | 67.2 | 67.3 |
| 1000 | 67.7 | 68.9 | 69.2 |
| 1250 | 68.1 | 69.5 | 69.8 |
| 1600 | 66.8 | 67.4 | 67.7 |
| 2000 | 64.7 | 64.7 | 65.0 |
| 2500 | 62.0 | 60.5 | 60.8 |
| 3150 | 60.0 | 57.5 | 57.8 |
| 4000 | 57.2 | 56.4 | 56.7 |
| Global | 76.2 | 75.7 | 75.9 |
| Configuration | Noise Level Results | Traffic Data | Emission Spectra | Impedance |
|---|---|---|---|---|
| Measurements | Measured | Measured | Measured | Measured |
| Prediction (worst) | DEUFRABASE | Measured | Database | Database |
| Prediction (intermediate) | DEUFRABASE | Measured | Measured | Database |
| Prediction (upper-intermediate) | DEUFRABASE | Measured | Database | Database (Similar) |
| Prediction (best) | DEUFRABASE | Measured | Measured | Database (Similar) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bérengier, M.; Picaut, J.; Pahl, B.; Duhamel, D.; Gauvreau, B.; Auerbach, M.; Gusia, P.; Fortin, N. DEUFRABASE: A Simple Tool for the Evaluation of the Noise Impact of Pavements in Typical Road Geometries. Environments 2019, 6, 27. https://doi.org/10.3390/environments6030027
Bérengier M, Picaut J, Pahl B, Duhamel D, Gauvreau B, Auerbach M, Gusia P, Fortin N. DEUFRABASE: A Simple Tool for the Evaluation of the Noise Impact of Pavements in Typical Road Geometries. Environments. 2019; 6(3):27. https://doi.org/10.3390/environments6030027
Chicago/Turabian StyleBérengier, Michel, Judicaël Picaut, Bettina Pahl, Denis Duhamel, Benoit Gauvreau, Markus Auerbach, Peter Gusia, and Nicolas Fortin. 2019. "DEUFRABASE: A Simple Tool for the Evaluation of the Noise Impact of Pavements in Typical Road Geometries" Environments 6, no. 3: 27. https://doi.org/10.3390/environments6030027
APA StyleBérengier, M., Picaut, J., Pahl, B., Duhamel, D., Gauvreau, B., Auerbach, M., Gusia, P., & Fortin, N. (2019). DEUFRABASE: A Simple Tool for the Evaluation of the Noise Impact of Pavements in Typical Road Geometries. Environments, 6(3), 27. https://doi.org/10.3390/environments6030027





