Abstract
Foreshocks, observed before some large earthquakes, remain debated in terms of their origins and predictive value. While aftershocks fit well within bottom-up triggering models like ETAS, foreshocks may arise from distinct preparatory processes. Observations suggest real seismic catalogs exhibit more foreshocks than ETAS predicts, and laboratory experiments show that fault heterogeneity enhances foreshock activity. Here, I use a numerical model that reproduces key statistical properties of seismicity to investigate the role of fault heterogeneity. My simulations confirm that increasing interface disorder promotes foreshocks, aligning with laboratory findings and suggesting that fault complexity influences seismic precursors.
1. Introduction
A pronounced increase in seismicity rate following large earthquakes is a well-established feature of instrumental catalogs and is commonly attributed to aftershocks [1]. In the bottom-up triggering framework [2], every event can give rise to its own descendants, whose occurrence probability depends on the time, space, and magnitude of the triggering event. The ETAS model [3,4] and variation (e.g. [5,6,7]) is a prime example: it assumes that the probability of an earthquake is the sum of all triggering probabilities from previous earthquakes, which decay with temporal and spatial distance from the triggering event and scale exponentially with its magnitude, plus a constant background rate.
Although aftershocks dominate seismic sequences worldwide, observations also show a modest increase in seismic activity prior to some large earthquakes [1,8,9,10]. These foreshocks typically occur close in space and time to the main shock epicenter. In a bottom-up view, foreshocks can be explained as rare instances where the triggered event happens to exceed the magnitude of its precursor. Consequently, foreshocks and main shocks would share the same physical origin as any standard parent-child pairing, thus offering little predictive value. By contrast, in what is often termed the nucleation model or top-down loading model [2,9], foreshocks are regarded as passive indicators of an ongoing tectonic preparatory process, such as the stress accumulation caused by aseismic slip preceding the main shock. Within this perspective, foreshocks might be generated by mechanisms distinct from ordinary triggering cascades (as in the cascade model), potentially carrying useful precursory information.
Because the ETAS model has become the standard baseline for assessing the significance of clustering hypotheses [3,4,11,12,13,14], many studies have tested whether foreshock properties in real catalogs differ from those in synthetic ETAS catalogs. Early results suggested that ETAS-type branching processes could largely capture the main statistical features of foreshocks [15,16,17,18]. Subsequent investigations [1,9,10,12,19,20,21,22] have noted that real main shocks tend to be preceded by more numerous and often more spatially distributed foreshocks than is predicted by ETAS. Although rigorous statistical testing of foreshock spatial patterns can be challenging, refs. [9,10] demonstrated, by comparing three ETAS variants, that real catalogs systematically show a statistically significant surplus of foreshocks. They argued that foreshocks arise from mechanisms beyond the normal branching processes driving ordinary seismicity.
Recent laboratory observations [23] highlight that fault-zone heterogeneity can play a crucial role in determining the presence and extent of foreshock sequences. In controlled stick–slip experiments on rough or damaged fault surfaces, researchers observe lengthy, intense foreshock activity. In contrast, smoothing the fault or increasing fluid pressure reduces geometric complexity and suppresses long foreshock chains. These findings suggest that local variations in stress concentration and fracture properties influence foreshock nucleation and may help reconcile disparate views on the robustness of foreshock activity.
In this paper, employing a numerical model that captures the main universal statistical properties of seismicity, including the Gutenberg–Richter distribution, Omori-like decay, Productivity Law and spatial clustering, I reproduce the observed foreshock excesses under certain heterogeneity conditions. My simulations show that increasing interface disorder promotes foreshocks in line with laboratory results.
2. The Model
I consider a D-dimensional lattice of blocks that mimic fault segments within a seismogenic zone. Each block i is characterized by its displacement , with the associated stress given by:
where the first term represents the driving force exerted by a slow tectonic loading, modeled as a spring of stiffness and velocity , which we assume to be infinitesimally small (). The second term accounts for elastic interactions between neighboring blocks, where represents the coupling strength. I consider short-range elasticity kernel, i.e., interactions are limited to nearest neighbors with for adjacent blocks and otherwise.
All physical quantities in the model are expressed in nondimensional units. The displacement is in arbitrary units of length, and both the stress and the threshold are in arbitrary units of force or stress. Similarly, the loading velocity and time t are nondimensional, with the product representing loading in model units. This nondimensional approach allows the model to capture the qualitative and statistical properties of seismicity independently of the specific physical scale. A block remains stationary until the local stress exceeds a random threshold , sampled from a Gaussian distribution with mean 1 and variance 5. This choice corresponds to a high coefficient of variation (), representing strong heterogeneity in local strength. Such broad disorder reflects the variability in fault strength observed in natural systems and promotes emergent critical behavior in the model. The block that first becomes unstable is identified as the one with the smallest stress gap , as this block is closest to failure. Since all blocks are loaded uniformly, the smallest determines the earliest instability time under increasing stress. In this context, is a measure of stability margin. This instability occurs at time , where for the block j with the minimum . The system-wide stress is increased by , applied equally to all blocks, triggering an avalanche.
Once a block becomes unstable, it moves to a new equilibrium position, drawing a new pinning threshold. It is important to note that in this model, each block represents a fault patch capable of sustaining repeated slip events. Therefore, we do not model the physical fracture or permanent damage of the block itself, but rather its transition between successive metastable states. This movement redistributes stress as follows:
The relaxation function is introduced phenomenologically to represent the progressive reduction in stress redistribution capacity following an avalanche, consistent with viscoelastic or frictional healing effects. This function is chosen to be monotonic and decreasing, ensuring that the system evolves toward a stable state after each avalanche, in agreement with the behavior observed in both laboratory and natural fault systems [24]. The avalanche propagates when redistributed stress causes additional instabilities, repeating the above process iteratively. The avalanche ceases when all blocks satisfy . This occurs instantaneously in the model’s timescale, with relaxation commencing afterward. Following an avalanche, decreases, causing gradual stress increments in previously slipping blocks. As a result, some blocks may become unstable at a later time , leading to a new instability event. Each new instability leads to another avalanche governed by Equation (3), with fixed throughout. This cycle continues until relaxation ceases (). A subsequent avalanche occurs at , where is the smallest remaining stress gap. At this point, , and relaxation resumes post-avalanche. The ratio ensures separation of timescales between relaxation and tectonic loading.
This model is fully determined by two parameters: , which controls the stress redistribution, and , the variance of the disorder distribution. Specifically, the disorder parameter represents the variability in local fault strength arising from factors such as fault roughness, lithological heterogeneity, damage distribution, and fluid pressure variations. A higher models a more heterogeneous fault, while a lower corresponds to a more homogeneous or mature fault interface. Conversely, scales the amplitude of stress transferred to neighboring blocks during an avalanche through the term . Physically, represents the degree of viscoelastic or time-dependent coupling in the system. Previous studies [25,26] have shown that strongly influences the temporal clustering of events and the emergence of realistic aftershock sequences. In this work, we adopt , which yields statistical properties in good agreement with empirical seismicity.
In [25], it was demonstrated that this model is capable of capturing all statistical properties of earthquakes, such as the Gutenberg-Richter law, Omori-Utsu law, productivity law, and spatial clustering. In particular, ref. [25] explored the emergence of realistic aftershock sequences and compared the model’s predictions to empirical seismic catalogs, highlighting the role of relaxation in reproducing Omori decay. The related studies [27,28] focused on a two-block model of a fault coupled to a creeping region, and showed analytically that aftershock rates are proportional to the afterslip rate, providing a physical interpretation of the Omori law as emerging from the logarithmic evolution of afterslip. For additional technical details and validation of the present model, we refer the reader to these works.
In this numerical model, the event magnitude is defined as , where S represents the size of the avalanche. This definition, commonly used in simulations of earthquake dynamics (e.g., [1]), allows a direct analog of the Gutenberg-Richter law to be established. Unlike empirical seismic catalogs, in this numerical model, I have perfect control over sequence identification (ideal declustering), and there are no issues related to Short-Term Aftershock Incompleteness (STAI) [29]. Consequently, all events are recorded in the numerical catalog, ensuring a complete representation of the dynamics.
While the present model assumes an idealized complete catalog to isolate the intrinsic effects of fault heterogeneity, extensions of the model to include observational incompleteness (such as STAI), for example via [30], and more complex tectonic forcings are possible and constitute an interesting direction for future work.
In this study, I do not model a specific real earthquake catalog. Rather, we employ a numerical model that captures the universal statistical properties of seismicity, allowing us to systematically explore the effect of fault heterogeneity under controlled conditions. The comparison with real seismicity and laboratory results is thus qualitative in nature.
3. Results
To investigate the relationship between fault heterogeneity and foreshock activity, I performed numerical simulations using a square fault of size with . Although [25] demonstrated that the model’s universality ensures that statistical law exponents remain unchanged under parameter variations, the parameter controls the degree of disorder, allowing a direct investigation of its impact on foreshocks.
The mainshock in each simulation is identified as the largest event in a given seismic sequence, with all preceding events classified as foreshocks and all subsequent events as aftershocks. Varying , I analyzed how increasing fault heterogeneity influences the frequency of foreshocks.
In Figure 1, I present two examples of disorder on the fault, illustrated through contour plots of . At first glance, the two distributions appear visually similar. However, a closer examination of the color bar values reveals that the variance in the left plot (a) is smaller than in the right plot (b), indicating a lower level of heterogeneity in the disorder. To further recognize these differences, the insets display the probability distributions of for both cases. The left inset corresponds to plot (a) and exhibits a narrower distribution, reinforcing the observation of lower variance. Conversely, the right inset, associated with plot (b), shows a broader distribution, confirming the greater variability in disorder.
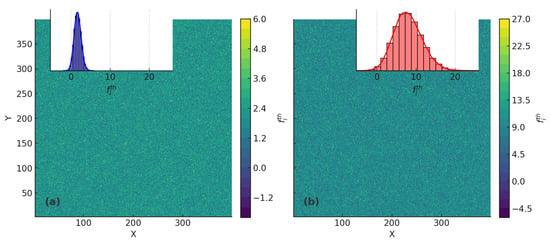
Figure 1.
Contour plots of illustrating two different disorder realizations on the fault. (a) corresponds to the case with lower variance, while (b) exhibits a broader distribution. The insets display the probability distributions of , providing a quantitative comparison of the disorder heterogeneity.
In Figure 2, I present the productivity law for foreshocks, given by:
where represents the binned magnitude of the mainshock and is the average number of foreshocks. We observe that the productivity exponent stabilizes around 1, in agreement with the numerical results reported in [25] and consistent with statistical analyses of real earthquake catalogs [19].
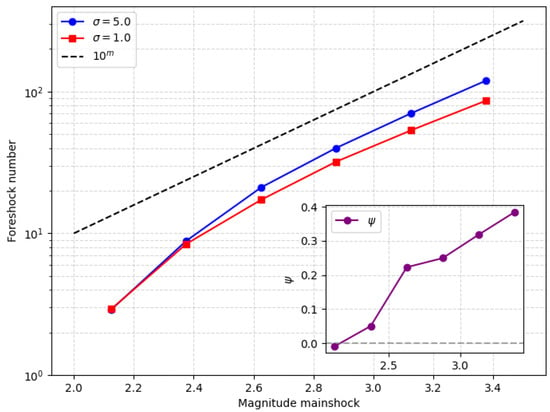
Figure 2.
(Main panel) The foreshock productivity law computed for the numerical catalog. Blue and red color represents and , respectively. The black dashed line represents the theoretical line , with , showing a good agreement with the experimental data. (Inset) The quantity calculated for the two curves of the main panel.
The two curves shown in Figure 2 correspond to productivity laws computed for systems with (red curve) and (blue curve). Strikingly, we note that , indicating that higher disorder leads to a systematically larger number of foreshocks. To quantify this effect, I define the parameter:
where and are the variances of the two considered datasets p and q. The parameter expresses, in percentage terms, how much the number of foreshocks in dataset q exceeds that in dataset p. From the inset of Figure 2, I observe that the relative increase in foreshock occurrence due to greater heterogeneity grows with increasing mainshock magnitude, exceeding the value of 0.3 for .
Interestingly, in Figure 3 I find different result in the aftershock productivity.
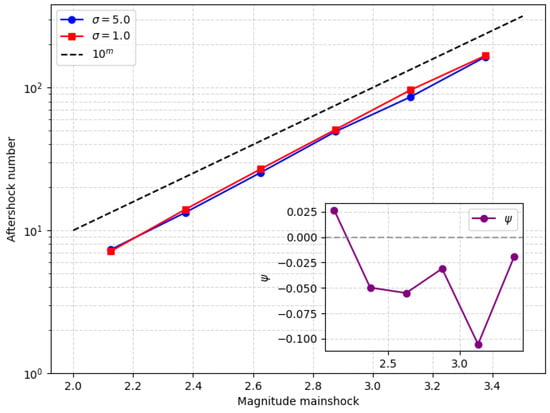
Figure 3.
(Main panel) The aftershock productivity law computed for the numerical catalog. Blue and red color represents and , respectively. The black dashed line represents the theoretical line , with , showing a good agreement with the experimental data. (Inset) The quantity calculated for the two curves of the main panel.
Indeed, the productivity law for aftershocks appears to be essentially universal with respect to the variance .
Since a crucial point in seismology is that some seismic sequences do not exhibit any foreshocks, in the Appendix A, I also show the number of seismic sequences that include at least one foreshock. In this case as well, we observe that the difference between the most heterogeneous case and the one with the smallest remains consistently positive for every mainshock magnitude.
The reason why the homogeneous case was not considered is that the system belong to a different universality class, distinct from the one that accurately describes seismic occurrence. Further details are provided in the Appendix A.
4. Discussion
My results demonstrate that increasing fault heterogeneity, quantified by the disorder parameter , systematically enhances foreshock activity. This conclusion aligns with laboratory observations [23], theoretical models [9,31], and statistical analyses of seismic catalogs [32,33]. Below, I discuss my findings in the context of these studies, emphasizing their implications for understanding foreshock dynamics and potential predictive value.
Laboratory experiments on rough and damaged fault surfaces have consistently shown that geometric complexity increases foreshock activity [23]. Goebel et al. (2024) [23] demonstrated that in laboratory stick-slip experiments, increased roughness prolongs the preparatory phase before failure, generating more foreshocks. Our numerical results confirm this trend: when fault heterogeneity is high , the number of foreshocks systematically exceeds that observed in more homogeneous cases . The productivity exponent obtained from our simulations suggests that foreshock sequences follow a scaling behavior similar to aftershock sequences but with a stronger dependence on heterogeneity with respect to aftershocks (Figure 3).
Further supporting this idea, McLaskey (2019) showed that heterogeneous stress distributions on laboratory faults promote localized slow-slip events that precede large dynamic ruptures. These events often manifest as small-scale foreshocks, highlighting the role of heterogeneous nucleation conditions. My results provide a numerical counterpart to this phenomenon, demonstrating that disorder in threshold stress values enhances foreshock occurrence in synthetic seismicity.
An alternative perspective on foreshocks suggests they emerge from progressive localization of seismicity, leading up to the mainshock [32]. Ben-Zion & Zaliapin (2020) [32] analyzed real seismic catalogs and found that foreshocks tend to cluster around the eventual mainshock epicenter, coalescing into high-density seismicity patches before failure. In my simulations, the increased number of foreshocks under high disorder conditions may reflect a similar localization effect. As shown in Figure A1 of the Appendix A, the fraction of sequences containing foreshocks increases with , implying that disorder enhances the spatial coalescence of seismicity before failure.
Recent case studies further support the relevance of these mechanisms in natural seismicity. For instance, ref. [34] analyzed the Mw6.8 2018 Zakynthos earthquake (Hellenic Subduction Zone) and demonstrated that a well-developed short-term foreshock sequence provided crucial information for the timing and rupture characteristics of the mainshock. This observation is fully consistent with the nucleation model and with the trends seen in our numerical simulations under increasing heterogeneity. Cattania (2021) [31] provided a theoretical framework for understanding foreshock clustering in rough fault models, demonstrating that localized stress interactions can create small precursory events that eventually cascade into a mainshock. In a related approach, recent numerical simulations by [35] demonstrated that cascading foreshocks and earthquake swarms can naturally emerge in discrete fault network models, reinforcing the view that fault heterogeneity and elastic interactions play a central role in foreshock dynamics. My model, which includes short-range elastic interactions between neighboring blocks, reproduces this cascading behavior, suggesting that foreshocks in our system are not purely random but instead result from stress redistribution processes influenced by fault roughness.
5. Conclusions
My numerical simulations provide strong evidence that increasing fault heterogeneity enhances foreshock activity, aligning with laboratory observations and real seismicity analyses. This result suggests that foreshocks are not merely statistical anomalies predicted by bottom-up ETAS-type models but instead emerge from fundamental physical processes tied to fault complexity.
A key implication of our findings is that fault disorder plays a critical role in the balance between bottom-up and top-down foreshock generation mechanisms. While classical ETAS models attribute foreshocks to random aftershock-like triggering, my results, along with laboratory studies and theoretical models, suggest that stress accumulation on small locked patches-consistent with McLaskey’s [33] cascade-up model-can significantly contribute to foreshock sequences. This highlights the importance of fault heterogeneity in controlling the nucleation of large earthquakes.
Furthermore, our model demonstrates that stress redistribution and relaxation processes modulate foreshock occurrence, reinforcing previous observations that stress relaxation can prolong the preparatory phase before failure. The fact that higher heterogeneity leads to an increased proportion of sequences with foreshocks suggests that spatial variations in fault roughness may be a key factor in determining the likelihood of precursory activity. However, as noted in previous studies, not all large earthquakes are preceded by foreshocks, and additional factors such as Seismic Network Density Incompleteness (SNDI) [36] may influence foreshock detectability.
From a forecasting perspective, my results indicate that heterogeneity-dependent foreshock activity could be leveraged as a diagnostic tool for seismic hazard assessment. However, distinguishing foreshock sequences from ordinary background seismicity remains a challenge.
Ultimately, my findings emphasize the fundamental role of disorder in seismic nucleation and foreshock dynamics, bridging the gap between laboratory experiments, numerical models, and natural earthquake observations. Future studies should explore whether the observed scaling laws hold across different tectonic settings, potentially improving our understanding of earthquake precursors and their predictive value. Finally, from an operational perspective, this modeling framework can contribute to seismic hazard assessment by highlighting the role of fault heterogeneity in modulating the probability of observable foreshock sequences. In practice, one could leverage independent geophysical proxies, such as variations in fault zone imaging, stress field heterogeneity, aftershock spatial patterns, or seismic velocity anomalies, to estimate the level of disorder () on different fault segments. The model then provides a controlled way to quantify how such heterogeneity influences the likelihood and characteristics of foreshock activity. Integrating this information with statistical forecasting models (e.g., ETAS-based approaches) could help refine probabilistic seismic hazard assessments, especially in regions where fault properties are heterogeneous. These are promising directions for future applied work.
Funding
This research received no external funding.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
I would like to acknowledge the Earth Observatory of Singapore (EOS), and the Singapore Ministry of Education Tier 3b project “Investigating Volcano and Earthquake Science and Technology (InVEST)”. I also thank Eugenio Lippiello and Alberto Rosso for useful discussions.
Conflicts of Interest
I declare no conflicts of interest.
Appendix A
Appendix A.1. Number of Sequences with Foreshocks
It is useful to show the proportion of sequences with and without foreshocks. Therefore, comparing the foreshock occurrence across different levels of heterogeneity helps to assess whether disorder influences the predictability of seismic events and whether foreshocks can be used as robust precursors. Figure A1 illustrates the percentage of seismic sequences that begin with at least 1 foreshock as a function of the mainshock magnitude for two different levels of disorder, characterized by and . The blue curve represents the case with higher heterogeneity (), while the red curve corresponds to the less heterogeneous case (). The results indicate the fraction of sequences containing foreshocks is systematically higher for , suggesting that greater heterogeneity in the system promotes foreshock activity. To quantify this effect, we introduce the relative increase , defined as:
where and are the average number of sequence for the datasets with variances and , respectively. In this case, and . The inset of Figure A1 displays as a function of the mainshock magnitude, confirming that the relative increase in foreshock occurrence due to higher heterogeneity grows with increasing . This trend suggests that the effect of disorder on foreshock activity becomes more pronounced for larger mainshocks, potentially indicating a mechanism where heterogeneity influences the precursory behavior leading up to significant events.
Also, in Figure A1, both curves display a slight decrease in the percentage of sequences with foreshocks at the highest mainshock magnitudes. This behavior is well understood and has two main origins. I attribute this behavior to the fact that very large events tend to involve a substantial portion of the system and may nucleate more abruptly, reducing the relative contribution of observable foreshocks. This effect, sometimes called “geometric saturation”.
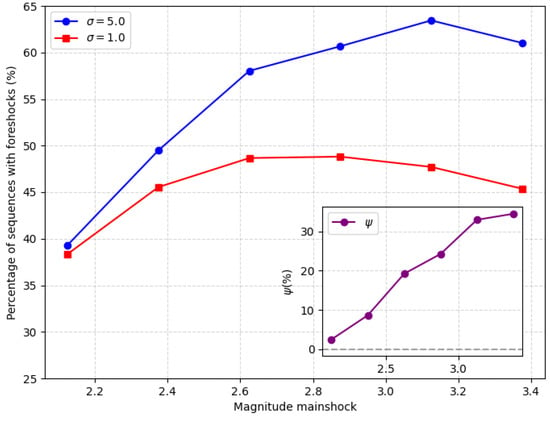
Figure A1.
Percentage of seismic sequences that begin with a foreshock as a function of the mainshock magnitude. The blue curve corresponds to the dataset with , while the red curve represents the dataset with . The main plot illustrates that the probability of having a foreshock is higher for the more heterogeneous case. The inset displays the relative difference between the two cases, showing that the increase in foreshock occurrence due to higher heterogeneity becomes more pronounced for larger mainshocks.
Appendix A.2. The Homogeneous Case σ = 0
In the homogeneous case, all thresholds are equal:
Thus, the distance to failure becomes
where is the nearly uniform stress level due to the slow loading. In this situation, if the stress increment delivered to a neighboring block j upon the failure of block i satisfies
then the triggering condition is either fully met or not met for all blocks in a uniform way. The process becomes deterministic; for instance, if each failure triggers exactly new failures, we have
and the probability generating function (PGF) of the number of triggered failures is
The avalanche size generating function then satisfies
Since is analytic at , we can expand near as
for some constant . By standard Tauberian theorems (see, e.g., [37]), this analytic behavior implies that the avalanche size distribution decays exponentially or is narrowly peaked around a characteristic avalanche size .
When , even though the stresses remain nearly uniform under slow loading, the distances to failure
now exhibit significant variability due to the randomness. When block i fails and redistributes a stress increment to a neighboring block j, the probability that block j is triggered to fail is given by
If the probability density of is smooth near , then for small we have
with being the density at . Consequently, the mean number of triggered failures (the branching ratio) is
At criticality, we impose . In the critical regime, the avalanche size generating function exhibits a non-analytic behavior near of the form
with typically emerging in such SOC systems [38]. The non-analytic term leads, via Tauberian theorems, to a power-law tail in the avalanche size distribution:
which is exactly the prediction of depinning avalanches in mean field. This scale-free behavior is a hallmark of self-organized criticality and is driven by the stochastic triggering due to threshold heterogeneity.
Even if the stresses may exhibit small variations due to previous avalanche history, in the homogeneous case these variations remain negligible. This is because (i) the tectonic loading is imposed uniformly through the driving term , and (ii) in the absence of threshold disorder, the stress redistribution dynamics become quasi-regular, leading to statistical self-averaging of block displacements. As a result, the stress levels remain nearly uniform across the system, consistent with the separation of timescales imposed by the slow driving . Only when heterogeneity in the thresholds (quantified by ) is introduced does the triggering process become stochastic, leading to a non-analytic generating function and a power-law distribution of avalanche.
It is important to clarify that in the homogeneous case (), the triggering process is deterministic and the corresponding PGF is , which is a simple polynomial, not a power-law. Therefore, the avalanche process in this case is not scale-free. The emergence of a power-law distribution of avalanche sizes arises only when disorder is introduced (), making the triggering probabilistic and the PGF non-analytic near . This distinction explains why the scale-free, fractal behavior is not a feature of the deterministic homogeneous case, but rather a consequence of threshold heterogeneity.
Appendix A.3. Universality of the Exponent τ = 3/2
In our model (as in many spring-block or interface-depinning models with quenched disorder and infinite time-scale separation), the avalanche-size distribution
arises as a universal feature of a SOC state. We summarize here why is both physically sensible and empirically observed in seismicity.
- Separation of timescales enforces marginal stability. The tectonic loading is infinitely slow compared to both coseismic slip and viscoelastic relaxation. This hierarchy of timescales forces the system to hover at a marginally stable point: between one avalanche and the next, the stress accumulates until exactly one block reaches its failure threshold. This enforces a branching ratio equal to unity, the hallmark of a critical branching process [37]
- Mapping to a critical branching process or depinning interface. In a critical branching process, each “parent” failure triggers, on average, one “daughter” failure, leading to . Similarly, in elastic interface depinning models with quenched disorder, the avalanche-size distribution near the depinning transition also scales as in any dimension [39].
- Why does not lead to unphysical divergences. A pure power-law with would imply a divergent mean if extended to . However, in any real fault (and in our finite lattice), a natural cutoff limits the maximum avalanche size. Once a slipping region spans the entire lattice, it cannot grow larger. This finite-size cutoff ensures a well-behaved .
In summary, reflects the fact that the model self-organizes into a critical state where each slipped block triggers on average one further slip. The finite fault size imposes a natural cutoff, ensuring physical consistency. This scaling is both theoretically expected and quantitatively consistent with observed earthquake statistics.
Appendix A.4. Algorithmic Description of the Model
We provide here a step-by-step outline of the numerical procedure used to simulate the model:
- 1.
- Initialization. The blocks are initialized with displacements . The failure thresholds are drawn from a Gaussian distribution with mean 1 and variance . The initial stresses are set according to Equation (1).
- 2.
- Driving. The tectonic loading is increased until the most unstable block reaches its threshold, i.e., . The corresponding time increment is .
- 3.
- Avalanche. The block j that reaches the threshold fails, triggering an avalanche:
- The stress is redistributed to neighboring blocks according to Equation (3).
- The block j is assigned a new random threshold .
- If any neighboring block now satisfies , it also fails and the process repeats recursively.
The avalanche continues until all blocks satisfy . - 4.
- Relaxation. After the avalanche, the relaxation function decreases according to a prescribed relaxation law.
- 5.
- Repeat. The system returns to Step 2. The driving continues, and the process repeats to generate the synthetic catalog.
The synthetic catalog consists of a list of avalanches with their corresponding sizes S, location and occurrence times t, from which magnitudes and sequence patterns (foreshocks, mainshocks, aftershocks) are extracted.
References
- de Arcangelis, L.; Godano, C.; Grasso, J.R.; Lippiello, E. Statistical physics approach to earthquake occurrence and forecasting. Phys. Rep. 2016, 628, 1–91. [Google Scholar] [CrossRef]
- Mignan, A. The debate on the prognostic value of earthquake foreshocks: A meta-analysis. Sci. Rep. 2014, 4, 4099. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical model for standard seismicity and detection of anomalies by residual analysis. Tectonophysics 1989, 169, 159–174. [Google Scholar] [CrossRef]
- Petrillo, G.; Zhuang, J. Bayesian earthquake forecasting approach based on the epidemic type aftershock sequence model. Earth Planets Space 2024, 76, 78. [Google Scholar] [CrossRef]
- Petrillo, G.; Lippiello, E.; Zhuang, J. Including stress relaxation in point-process model for seismic occurrence. Geophys. J. Int. 2024, 236, 1332–1341. [Google Scholar] [CrossRef]
- Petrillo, G.; Kumazawa, T.; Napolitano, F.; Capuano, P.; Zhuang, J. Fluids-triggered swarm sequence supported by a nonstationary epidemic-like description of seismicity. Seismol. Res. Lett. 2024, 95, 3207–3220. [Google Scholar] [CrossRef]
- Brodsky, E.E.; Lay, T. Recognizing foreshocks from the 1 April 2014 Chile earthquake. Science 2014, 344, 700–702. [Google Scholar] [CrossRef]
- Petrillo, G.; Lippiello, E. Testing of the foreshock hypothesis within an epidemic like description of seismicity. Geophys. J. Int. 2021, 225, 1236–1257. [Google Scholar] [CrossRef]
- Petrillo, G.; Lippiello, E. Incorporating Foreshocks in an Epidemic-like Description of Seismic Occurrence in Italy. Appl. Sci. 2023, 13, 4891. [Google Scholar] [CrossRef]
- Ogata, Y. Space-Time Point Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Comparing foreshock characteristics and foreshock forecasting in observed and simulated earthquake catalogs. J. Geophys. Res. Solid Earth 2014, 119, 8457–8477. [Google Scholar] [CrossRef]
- Zhuang, J.; Ogata, Y.; Vere-Jones, D. Analyzing earthquake clustering features by using stochastic reconstruction. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Liu, Y.; Zhuang, J.; Guo, Y.; Jiang, C.; Tian, Q.; Zhang, Y.; Long, F. Background and clustering characteristics of recent seismicity in Southwestern China. Geophys. J. Int. 2024, 238, 1291–1313. [Google Scholar] [CrossRef]
- Helmstetter, A.; Sornette, D. Foreshocks explained by cascades of triggered seismicity. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Felzer, K.; Abercrombie, R.; Ekstrom, G. A Common Origin for Aftershocks, Foreshocks, and Multiplets. Bull. Seismol. Soc. Am. 2004, 94, 88–98. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Felzer, K.R.; Michael, A.J. Improved tests reveal that the accelerating moment release hypothesis is statistically insignificant. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef]
- Marzocchi, W.; Zhuang, J. Statistics between mainshocks and foreshocks in Italy and Southern California. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Spatial organization of foreshocks as a tool to forecast large earthquakes. Sci. Rep. 2012, 2, 846.
- Shearer, P.M. Self-similar earthquake triggering, Båth’s law, and foreshock/aftershock magnitudes: Simulations, theory, and results for southern California. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Seif, S.; Zechar, J.D.; Mignan, A.; Nandan, S.; Wiemer, S. Foreshocks and their potential deviation from general seismicity. Bull. Seismol. Soc. Am. 2019, 109, 1–18. [Google Scholar] [CrossRef]
- Trugman, D.T.; Ross, Z.E. Pervasive foreshock activity across southern California. Geophys. Res. Lett. 2019, 46, 8772–8781. [Google Scholar] [CrossRef]
- Goebel, T.H.; Schuster, V.; Kwiatek, G.; Pandey, K.; Dresen, G. A laboratory perspective on accelerating preparatory processes before earthquakes and implications for foreshock detectability. Nat. Commun. 2024, 15, 5588. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. Solid Earth 2004, 109. [Google Scholar] [CrossRef]
- Petrillo, G.; Lippiello, E.; Landes, F.P.; Rosso, A. The influence of the brittle-ductile transition zone on aftershock and foreshock occurrence. Nat. Commun. 2020, 11, 3010. [Google Scholar] [CrossRef] [PubMed]
- Petrillo, G.; Rosso, A.; Lippiello, E. Testing of the Seismic Gap Hypothesis in a Model With Realistic Earthquake Statistics. J. Geophys. Res. Solid Earth 2022, 127, e2021JB023542. [Google Scholar] [CrossRef]
- Lippiello, E.; Petrillo, G.; Landes, F.; Rosso, A. Fault heterogeneity and the connection between aftershocks and afterslip. Bull. Seismol. Soc. Am. 2019, 109, 1156–1163. [Google Scholar] [CrossRef]
- Lippiello, E.; Petrillo, G.; Landes, F.; Rosso, A. The genesis of aftershocks in spring slider models. Stat. Methods Model. Seism. 2021, 1, 131–151. [Google Scholar]
- Godano, C.; Petrillo, G.; Lippiello, E. Evaluating the incompleteness magnitude using an unbiased estimate of the b value. Geophys. J. Int. 2024, 236, 994–1001. [Google Scholar] [CrossRef]
- Hainzl, S. Rate-dependent incompleteness of earthquake catalogs. Seismol. Res. Lett. 2016, 87, 337–344. [Google Scholar] [CrossRef]
- Cattania, C.; Segall, P. Precursory Slow Slip and Foreshocks on Rough Faults. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020430. [Google Scholar] [CrossRef]
- Ben-Zion, Y.; Zaliapin, I. Localization and coalescence of seismicity before large earthquakes. Geophys. J. Int. 2020, 223, 561–583. [Google Scholar] [CrossRef]
- McLaskey, G.C. Earthquake Initiation From Laboratory Observations and Implications for Foreshocks. J. Geophys. Res. Solid Earth 2019, 124, 12882–12904. [Google Scholar] [CrossRef]
- Papadopoulos, G.; Agalos, A.; Minadakis, G.; Triantafyllou, I.; Krassakis, P. Short-Term Foreshocks as Key Information for Mainshock Timing and Rupture: The Mw6.8 25 October 2018 Zakynthos Earthquake, Hellenic Subduction Zone. Sensors 2020, 20, 5681. [Google Scholar] [CrossRef]
- Im, K.; Avouac, J.P. Cascading foreshocks, aftershocks, and earthquake swarms in a discrete fault network. Geophys. J. Int. 2023, 235, 831–852. [Google Scholar] [CrossRef]
- Lippiello, E.; Petrillo, G. b-more-incomplete and b-more-positive: Insights on a robust estimator of magnitude distribution. J. Geophys. Res. Solid Earth 2024, 129, e2023JB027849. [Google Scholar] [CrossRef]
- Harris, T.E. The Theory of Branching Processes; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar]
- Bak, P.; Tang, C.; Wiesenfeld, K. Self-organized criticality: An explanation of 1/f noise. Phys. Rev. Lett. 1987, 59, 381–384. [Google Scholar] [CrossRef]
- Jagla, E.A.; Landes, F.P.; Rosso, A. Viscoelastic effects in avalanche dynamics: A key to earthquake statistics. Phys. Rev. Lett. 2014, 112, 174301. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).