Abstract
To estimate the expected damage due to rockfalls and debris flows for buildings and people, it is essential to assess the response of brick walls to boulder impacts. There are scarce physical tests of the impact of boulders on brick walls, which are typical of residential buildings. A simple and low-cost experimental setup for investigating the damage of unreinforced brick walls that are subjected to a boulder’s impact is presented. The setup consists of a ramp that is adjusted with a light steel structure. Seven pilot tests for five single-leaf brick walls of a 1000 × 1000 mm2 area, hit by a 72.925 kg granite boulder, and from five release heights (0.25 m, 0.50, 1.00 m, 2.50 m, and 3.00 m) are performed. The observed damage indicates that wall breakthrough occurs for translational kinetic energies as low as 500 J. The prevalent failure mechanism is local shear damage. Additionally, a numerical model to simulate the physical tests was developed using the FEM. Using the same properties as in the physical testing, the numerical model is found to realistically reproduce the displacement of a node at the centre of the impact, as well as the translational impact velocity and energy, for the same five boulder release heights.
1. Introduction
Impact-based modelling for natural hazards has gained ground over hazard assessment for providing essential information on the expected loss to assist disaster risk reduction. Understanding and predicting the damage to buildings caused by mass gravitational movements such as rockfalls and debris slides has a twofold aim: (i) preventing the physical loss of structures and (ii) protecting the population in peril inside buildings. Probabilistic and Bayesian-based quantitative risk assessment approaches [1,2,3,4] require the definition of damage scenarios and the establishment of thresholds for the hazard intensities that are sufficient to cause a certain level of damage.
Load-bearing brick or stone masonries have long been ubiquitous structures in mountainous areas, where an important fraction of landslides occur. Similarly, for wooden or reinforced concrete frame structures, sediment transport, involving coarse material in the case of rockfalls or finer material for debris flows and slides, breaks through the infill walls of residential buildings, putting people in jeopardy and leading to physical damage, injuries, and fatalities [5]. Understanding the masonry’s response and failure due to boulder hits is essential to determine the stability of a structure or to assess the damage due to material breakthrough into the building.
Experimental and numerical methods, including the finite element method [6], the discrete element method [7] and the PFEM [8,9], have been proven powerful in assessing the impact response of structural elements that are subjected to boulder and other mass impacts corresponding to rockfalls and debris flows. Machine learning techniques have been applied by [9] for the prediction of the damage to brick walls based on numerical analysis results [10]. The literature on the response of protection elements such as flexible [11,12] and rigid obstacles to boulders, i.e., embankments and gallery slabs [13], is rich [14,15,16,17]. Protection structures are designed to resist impact energies of hundreds or thousands of kJ. Albeit, in some cases, net failure has also been observed for lower energies of some tens of kJ [18] due to the so-called ‘‘bullet effect,’’ which refers to the perforation of a rockfall protection mesh by the impact of a small block which has a kinetic energy lower than the design value, where the design value is determined through tests with relatively large blocks [19].
The capacity of structural elements, which are typical of residential buildings, to sustain damage due to boulder hits is substantially lower. In real-life events, impact energies of a few tens of kJ and pressures of few tens of kPa have been reported to cause the collapse of reinforced concrete (RC) frames, brick masonry, and timber walls [20,21]. This has also been confirmed by analytical–numerical methods [22,23] and laboratory testing [24]. Ref. [25] reported thresholds for the failure of RC frame structures of 5 or 10 kPa for frames without or with seismic design, accordingly, and [26] reported a threshold of 14 kJ for single column failures. For damage to brick walls, their impact energy thresholds have been reported to be up to 5.5 kJ for no damage [10,27], from 4.2 to 16.9 kJ for substantial cracks [23,24], and greater than 4.4 kJ for wall breach or collapse [23]. Nevertheless, the damage states for the energy ranges that are reported in these studies overlap, and the damage thresholds remain vaguely defined for energies below 4 kJ.
Masonry, as a composite material consisting of inhomogeneous, anisotropic, and non-standardized materials, presents large variability in its mechanical properties [28]. Out-of-plane failure depends strongly on the mortar, the block–mortar bond, and its tensile and shear strengths [29,30]. For those reasons, the dynamic limit conditions demonstrate large variability [31]. Experimental testing for in-plane [32] and out-of-plane [33,34] impact loading for masonry structures has mostly been developed for earthquake action. A substantial contribution to the impact response of walls also comes from the study of vehicle impacts [35]; however, given the high deformability of vehicles compared to rock masses, these results are not transferable to rock impacts.
For landslide-related risks, the damage thresholds established by means of back analysis [27] involve a large amount of uncertainty, despite being based on real data. These are related to the assumptions made for hazard characterization (boulder size, shape, velocity, …) and the transfer of contact forces or energy during the boulder–structure interaction. Aleatory uncertainties concerning the location of the impact also introduce variability into the wall response [36]. These uncertainties can be reduced with experimental testing conducted in a controlled environment.
There are limited studies on rockfall and debris impact physical testing for walls, which are characteristic of buildings, whether infill or structural walls. The reasons are the rather costly experimental settings, the long time it takes to cure the materials, and the respective safety issues for the laboratory testing. The existing studies have mostly set out to investigate impact forces and wall stiffness [37,38]. Ref. [24] performed a series of tests to assess the damage to a 240 × 2700 × 3000 mm3 wall where the hit was induced using an iron sphere attached to a pendulum. Varying impact locations, falling heights, and weights of the sphere were investigated. The damage included extensive cracking, caused by an approximately 86 kg sphere with a maximum falling height of 5 m; full collapse was not reached.
Experimental results for rockfall damage of brick walls are necessary for the calibration and development of numerical models that permit us to investigate the behaviour of buildings in different scenarios. Given the scarcity of these tests in the literature, the work presented here aims to address this gap.
It includes the design of a simple and low-cost experimental setup, consisting of a ramp adjusted on a light steel structure. The aim is to investigate the response of unreinforced brick walls that are impacted by boulders. In this work, the results from a first series of impact tests for five identical single-leaf brick walls of a 1000 × 1000 mm2 area are analysed. The boulder release height on the ramp varied to generate different impact energies. The objectives were (a) the definition of damage thresholds and the investigation of failure mechanisms and (b) the provision of quantitative data to calibrate numerical models of walls hit by rockfalls. To verify that calibration is possible and to assess the numerical modelling parameters, numerical simulation of the tests is performed using the finite element method. The reference parameters for comparison between the physical testing and the numerical modelling are the impact energy dissipation and the resultant damage.
The tests presented here served as pilot tests for a longer series of ongoing tests, where the impact characteristics, wall parameters, and boundary conditions will vary.
2. The Medium-Scale Experimental Setting
The experiments were conducted using a 11.0 m long and 1.1 m wide rolling ramp (Figure 1). A spherical granite boulder of a 37.5 cm diameter (d) and a 72.925 kg weight (w) was released from different heights, with different levels of initial potential energy. The rolling ramp formed an angle of 21° from the horizontal. A narrower 40 cm wide channel was designed on the ramp to constrain the block trajectory. In this way, the energy is not lost due to lateral impacts, and a central hit on the wall is achieved. The brick walls were placed at the lower end of the channel, orthogonally to the ramp. The ramp intersected the walls at a height of 250 mm, which was also designed in order to achieve a central hit on the wall.
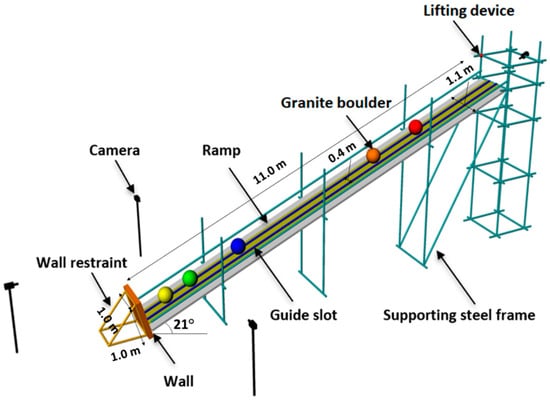
Figure 1.
Experimental setting for the impact test: The boulder is released from different heights on the ramp. The wall sample is placed at the bottom of the ramp. The impact is registered by 4 video cameras, placed laterally and orthogonally to the ramp.
The experimental setting was developed to be time- and cost-effective. The ramp, which consists of four steel frames, was constructed in less than seven days. The steel frames were made of 50 mm diameter circular pipes, which were anchored in and attached by fasteners to the ramp. Four cameras were placed around the ramp to record the tests, including one frontal camera that was placed on the scaffold and one rear-view camera. Out of these, one lateral camera and the rear-view cameras were smartphone cameras. A high-speed and high-resolution camera was placed on the left side of the ramp instead, orthogonally to it. Slow-motion videos were recorded to measure the displacement and velocity of the boulder from image sequences.
The smartphones were used due to being low-cost, easy to obtain, and easy to use. Their precision for these experiments was checked. The minimum required image resolution was 1080 p at 120 fps. In order to measure the speed of the boulder, slow-motion videos of 1080 p at 240 fps were processed to extract the data. The images were obtained with a 12-megapixel lens smartphone camera with a 26 mm (wide) focal length. The (diagonal) screen size was 5.8″ (147.3 mm). The screen resolution was 1920 × 1080 px at 380 ppi. The camera was placed at a distance of 1 m from the ramp. The real width of the frame was 2290 mm, and the image resolution was 0.84 pixels per mm, which provided a position error σx = ±1.68 mm. One limitation of the method is that the image resolution variations due to lens distortion, and the respective errors were not taken into consideration, as distortion data for the smartphone lens were not available. Concerning the time resolution, for 240 fps, the average time interval between frames was Δt = 4.16 × 10−3 s. The camera was not frame rate-guaranteed; however, given that the frame was still and that the light level was constant, deviation from the average time interval was not expected to be substantial. Assuming negligible error in time, the error in speed depends on the error in the position of the sphere.
The impact energy was controlled by releasing the boulder from a given height of the ramp using a hoist. The rolling boulder loses energy due to friction; hence, the impact velocity cannot be determined by the energy balance equation. It was not feasible to place sensors on the wall in order to measure the force at the point of application of the boulder to the wall, as the walls were expected to be destroyed.
The upper and two lateral boundaries of the wall were supported by a steel base which was fixed on the ground and restrained the out-of-plane deformation of the wall borders. The lowest part of the wall was fixed. The effects and limitations of these boundary conditions are discussed in the Conclusions section.
3. Wall Specifications
In [24], it has been indicated that 240 mm thick walls may not reach full collapse for energies below 4 kJ. Hence, as a baseline, we designed 120 mm thick single-leaf walls.
The walls were constructed according to the specifications of the Chinese Brick and Concrete Structural Design code [39]. Considering the required time for the curation of the mortar, the testing took place 14 days after the construction of the walls.
For experimental characterization of the mechanical strength of the wall, six normal compression tests for cubic brick samples with an edge of 50 mm and four tests for cubic mortar samples with an edge of 50 mm were performed. Table 1 summarizes the results. The compressive strength of the mortar after 28 days of curing (full curing) and of the bricks varied between 9.15 and 11.60 MPa and 15.83 and 23.62 MPa, respectively. The strength of the mortar at the age of 14 days was obtained by reducing the aforementioned value by 23% according to Equation (1), which was adapted from [40]. The obtained material strengths are compatible with the mortar type M7.5 and the brick type MU20 [39].
where

Table 1.
Average axial compressive strength of mortar and bricks after laboratory testing.
: Mortar strength at age t;
: Mortar strength at 28 days;
: Age (days).
4. Experimental Tests and Results
Seven impact tests were performed using the experimental setup. An additional objective of these pilot tests was to check practical issues involving the stability and resistance of the ramp, as well as the efficiency of the data acquisition equipment.
For the first three out of seven tests, the same wall was used, and the release height (H) was 0.25 m. The test was repeated until the wall was substantially damaged. For the rest of the tests, a different wall was used each time, and the release heights were 0.5, 1, 2.5, and 3 m, respectively. The release height was the unique variable.
The speed vector in the direction of movement on the ramp (vi) and the translational kinetic energy (Ei) were calculated as derivatives of the boulder displacement. The latter was measured using images that were extracted from the slow-motion videos (Table 2). The speed is the rate of displacement between one frame before the impact and the frame corresponding to the moment of the impact. The impact’s translational kinetic energy in the direction of the path of the sphere was calculated as a function of the speed.

Table 2.
Observed translational and angular impact velocity, translational and rotational kinetic energy, and errors of the translational impact velocity and energy for the seven tests.
When the translational speed is calculated using two sequential frames, the displacement error is equal to 2σx. Then, the absolute speed error is given by Equation (2), and it is equal to σvi = ±0.808 m/s. The relative percentage error of the translational speed (σrvi) for each test was calculated according to Equation (3), and it is also given in Table 2.
σvi = 2σx/Δt,
σrvi = 100% σvi/vi,
Accordingly, the absolute translational kinetic energy error (σEi) is given by Equation (4), and it is 23.79 J. The respective relative percentage error (σrEi) for each test, as calculated by Equation (5), is given in Table 2 too.
σEi = 1/2m σvi2,
σrEi = 100% σEi/Ei,
The angular impact velocity (ωi) was calculated as a function of the translational velocity (vi) using Equation (6). The rotational impact energy (Eωi) was given by Equation (7) as a function of the moment of inertia of the sphere (I) about the center of mass (m). The moment of inertia (I) is given by Equation (8), and it is 1.03 kg∙m2.
ωi = 2vi/d,
Eωi = Iωi2/2,
These calculations provide a conservative upper limit for the energy that is transmitted from one hard body (sphere) to another (wall), which in reality is smaller due to the elastic–plastic indentation, where a fraction of the prior to the intersection energy is dissipated [41].
For the H = 3 m release height, a rebound of approximately 10 cm above the ramp was observed before the impact on the wall, resulting in a smaller impact velocity than that for H = 2.5 m. Right after the wall breaching, the sphere continued to roll in the same direction.
5. Damage Analysis and Failure Mechanisms
The damage and the cracks on the walls were inventoried after each test. The residual out-of-plane deflection di on the damaged walls was measured. The final damage state at the end of each test is presented in Figure 2 for tests 1a, 1b, and 1c and in Figure 3 for tests 2, 3, 4, and 5. A description of the damage and the failure mechanisms is provided in the following paragraphs and summarized in Table 3. Based on the observations, three damage classes were established: minor, for cracks up to a 20 mm width not affecting the stability of the wall; moderate, for cracks of more than a 100 mm width affecting the stability of the wall; and high, for full collapse.

Figure 2.
Wall damage for tests 1a, 1b, and 1c. The direct impact area is on the lower half of the wall. The purple lines indicate open cracks with a width smaller than 10 mm, and the yellow lines indicate cracks with a width from 10 to 20 mm. The damage occurs mainly due to the failure of the brick–mortar bond. For test 1b, the vertical crack is additionally formed through brick failure. The deflection of the wall for the 3 tests is shown in green. The upper half of the wall does not have visible damage.

Figure 3.
Wall damage for tests 2, 3, 4, and 5. For test 2, a flexural mechanism of failure around the vertical axis is observed with a deflection of 200 mm, leading to the opening of a crack of 120 mm, which crosses the bricks and mortar. For tests 3, 4, and 5, full collapse is reached, and the boulders traverse the wall through a local breach which is formed by shear failure.

Table 3.
Wall damage description and failure mechanisms.
Test 1a: A horizontal, continuous, and stepped shear crack with a 6 mm opening was caused at the height of the impact location. No vertical cracks developed. The failure mechanism was shear. The boulder did not penetrate the wall, no breach was observed, and the stability of the wall was not affected. The damage was classified as minor.
Test 1b: The cumulative damage due to a similar impact as for the 1a test consisted of the further opening of the horizontal crack up to 13 mm, the creation of a new horizontal crack at the height of the intersection of the boulder’s lowest point with the wall, and a vertical crack of 8 mm on the lower part of the wall. The horizontal cracks resulted from the brick–mortar bond failure, while the vertical crack transversed the bricks and reached the centre of the wall. The upper part of the wall that did not suffer a direct impact remained intact. A double flexural mechanism was observed on the lower part of the wall, in combination with the out-of-plane shear failure of a zone whose limits were marked by the upper and lower bounds of the boulder. The boulder did not penetrate the wall, no breach was observed, and the stability of the wall was slightly affected. The damage was classified as minor.
Test 1c: The cumulative damage resulted in further opening of the existing cracks up to 20 mm. The out-of-plane displacement due to the shear deformation of the lower zone in the direct area of the impact was highly visible. The upper part of the wall remained intact. As in the case of test 1b, a double flexural mechanism was observed on the lower part of the wall in combination with the out-of-plane shear failure of a zone that was delimited by the upper and lower bounds of the boulder. The boulder did not penetrate the wall, and a minor breach was formed. The stability of the wall was highly affected. The damage was classified as moderate.
Test 2: A prevalent flexural mechanism of failure was observed around the vertical axis, with a deflection of 200 mm, leading to the opening of a crack of 120 mm that crossed the bricks and the mortar (Figure 3). Shear failure and further shear cracks along the brick-wall bonds were also observed at the level of the lower bound of the boulder. The boulder did not penetrate the wall; however, a breach was formed, and the stability of the wall was highly affected. The damage was classified as moderate.
Test 3: The wall broke into fragments due to a prevalent shear failure mechanism. Flexure around the vertical axis also occurred. The largest prisms belonged to the upper part of the wall, which was not directly hit. The upper part was broken in two through a vertical crack, right above the impact area. The boulder penetrated the wall, which collapsed. The collapse was generalized and complete. In the directly impacted area, the failure occurred mainly through the bonds, and few bricks were broken. The damage was classified as high.
Test 4: The mode of failure was similar to that in test 3. The damage was classified as high.
Test 5: The boulder rebounded to a height of 10 cm due to its increased velocity and it landed on the ramp before hitting the wall, which resulted in a lower impact velocity than for the test 4. The mode of failure was similar to that in tests 3 and 4.
The relation between the observed translational velocity and the translational energy with the wall damage is depicted in Figure 4. The indicated values are low compared to the energy thresholds reported by [20] and [24]. One reason is that those studies did not address the response of single-leaf brick walls as we did here. Moreover, these damage thresholds are affected by the partial development of the strength of the mortar due to its incomplete curing. Scale effects are another possible explanation, which requires further investigation.
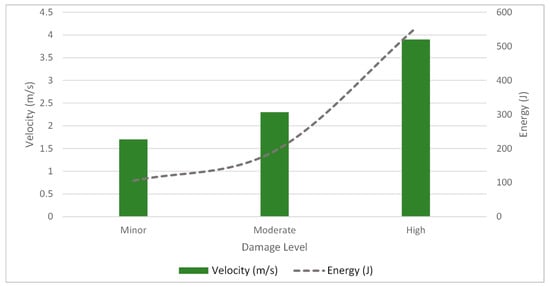
Figure 4.
Relation of boulder impact velocity and translational energy to wall damage.
The boulder run-off after traversing the wall was additionally measured in situ. For tests 3, 4, and 5, the run-off distance was 0.5, 1.9, and 1.3 m, respectively. In [20], a power-law relation between the kinetic energy and the run-off distance was indicated, and the power-law exponent was 0.72. For the tests performed here, the exponent is 1.6 (r2 = 0.99).
6. Numerical Simulation of the Impact Tests
The second objective of these pilot tests was to obtain quantitative data for the calibration of numerical models that simulate rock boulder impacts on walls in order to assess at a later stage, which is out of the scope of this paper, the expected damage to entire buildings. To this end, a numerical model was developed.
In particular, the model was developed using the finite element method, FEM, and the software LS-DYNA R11.1.0, combined with a contact modelling algorithm, in order to reproduce the failure of the wall. As observed from the tests, the brick–mortar bond is critical for the impact resistance of the masonry. The mortar was modelled by an in-between brick contact surface, defined as “CONTACT_AUTOMATIC_SURFACE_TO_SURFACE_ TIEBREAK”, which offered a tension- and shear stress-based failure criterion which allowed the release of the two bodies. The contact surface model employs the penalty function method, which can directly extract the response of the element boundaries and simulate the mortar brick bonding [42]. This assumption cannot describe the failure within the mortar body. Nonetheless, the brick–mortar bond is expected to have a lower flexural and shear strength than the mortar itself and thus to fail first, so this simplification does not alter the wall failure results. The brick material was simulated using the model “MAT_WINFRITH_CONCRETE”. The boulder was modelled as a non-deformable rigid body using the “MAT_RIGID” material.
The parameters for the numerical simulation of the brick and of the mortar correspond to the standardized materials that were used for the experiments (see Section 3): M7.5 for the mortar and MU20 for the bricks (Table 4). The masonry wall’s tensile and shear strengths were derived by the Chinese Brick and Concrete Structural Design Specifications [39] for these materials, and both are 0.23 MPa. A dynamic friction coefficient of 0.70 was adopted according to the friction coefficient value for masonry units sliding on each other when the contact interface is dry, as specified in [39]. The slightly higher value of 0.71 was selected for the static friction coefficient, as a larger value than that of the dynamic friction coefficient is required in order for the program LS-DYNA to differentiate between static and dynamic friction.

Table 4.
Parameters used in the masonry wall FEM.
Five numerical simulations were performed to reproduce the physical testing for the five release heights (H), 0.25, 0.50, 1, 2.5, and 3 m (considering undamaged walls), and to calculate the impact velocities and energies. The final damage state as calculated by the numerical tests is presented in Figure 5. For H = 0.25 m, horizontal cracks are formed, as in test 1a. For H = 0.50 m, as in test 2, a flexural mechanism of failure deforms the wall in the directly impacted area; in this case, the numerical model realistically reproduces the failure of the brick–wall bond; however, it does not reproduce the failure of the bricks as in the experiment. For H = 1.0 m, H = 2.5 m, and H = 3.0 m, collapse takes place similarly to in tests 3, 4, and 5, and it occurs due to the same local shear failure mechanism.
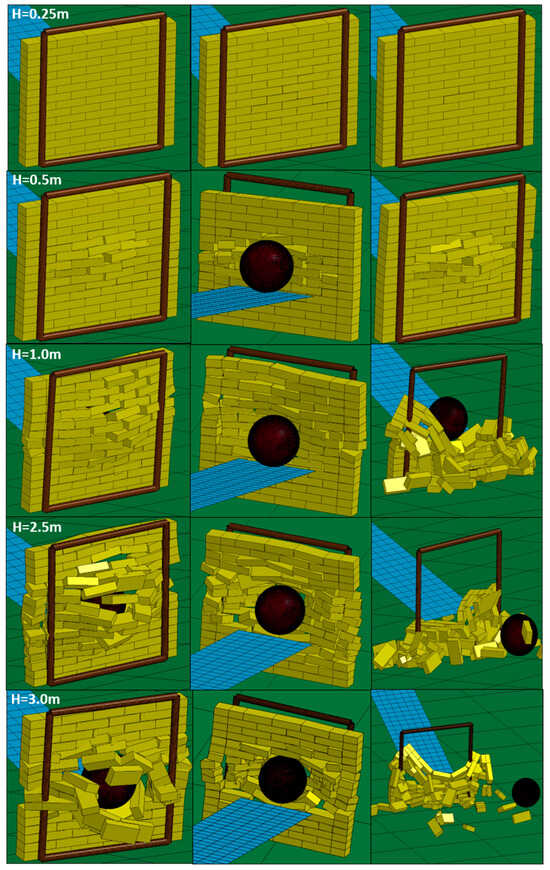
Figure 5.
Wall damage results for the simulation of the experiments using the FEM.
Figure 6 presents the displacement of a node in the centre of the boulder–wall interaction area for H = 0.25 m and H = 0.5 m. For H = 0.25 m, the peak wall displacement is elastic (t = 0.6 s). For H = 0.5 m, after t = 1.1 s, the displacement becomes plastic, with subsequent dissipation of energy up to the formation and extended opening of cracks. The transition from an elastic to a plastic response is indicated in the numerical model by the failure of the brick–mortar bond. The calculated nodal displacements for H = 0.25 m and H = 0.5 m are 5.0 mm and 129 mm, which are consistent with the values of 6.0 mm and 120 mm that were observed in tests 1a and 2, accordingly.
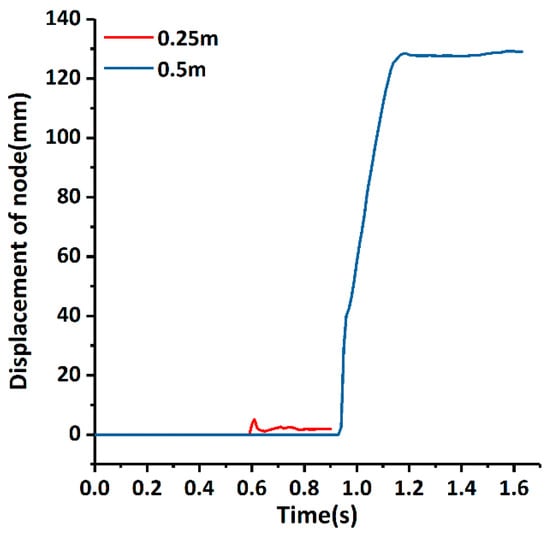
Figure 6.
Time evolution of the displacement of a node in the centre of the boulder–wall interaction area indicating elastic and plastic response of the wall for H = 0.25 m and H = 0.5 m.
The boulder velocity and translational kinetic energy are plotted in Figure 7. The velocity differences between the numerical and experimental modelling were −4%, 8%, −5%, +4%, and +22%, accordingly, with reference to the observed test velocities. In the latter case, the large difference is ought to the observed rebound that the numerical modelling did not reproduce.
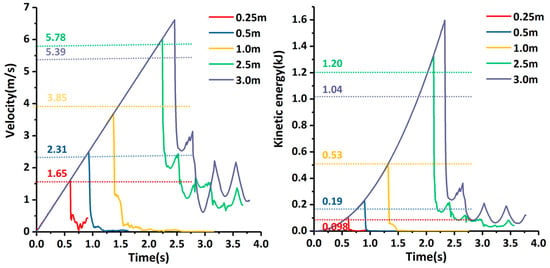
Figure 7.
Time evolution of the velocity and kinetic energy considering different boulder release heights. The continuous lines indicate the numerical modelling results and the dotted lines the experimental testing results.
The total energy dissipated by the impact was calculated from the chart as the difference between the peak value minus the maximum kinetic energy after the steep drop. For H = 0.25 and H = 0.5 m, the boulder’s energy, which was 107 J and 250 J, respectively, was fully dissipated, and the block did not transverse the wall. Instead, for the release heights of H = 1, H = 2.5, and H = 3 m, the boulder’s kinetic energy dropped by 49 J, 117 J, and 135 J, accordingly, which represented 99%, 89%, and 84% of the impact energy.
The comparison between the numerical modelling and physical testing indicated that the developed FEM, using the selected materials and parameters, can realistically simulate the damage observed in the experimental tests and thus can be used for damage analysis of further structures with the same material properties.
7. Conclusions
This paper summarizes the results of seven pilot tests of the impacts of a spherical granite boulder on a 1 × 1 m2 single-leaf brick wall. Emphasis was placed on the design of a flexible and cost-efficient experimental setting. The presented experimental setting was prepared within seven days and performed well during the tests. Smartphone cameras recording slow-motion videos with a resolution of 1080 p at 240 fps proved adequate for the calculation of the impact velocity for boulder speeds up to 6 m/s.
The results of the presented experimental setting indicated that for the tested single-leaf walls, the boulder transverses the wall for translational energies higher than 500 J. The principal mechanism of failure is shear. For tests 1a, 1b, and 1c with a lower velocity, shear failure occurred along the height of the boulder for the entire width of the wall. Instead, for higher velocities, a local effect in the direct impact area was observed, and a square breach was formed with an edge equal to the diameter of the boulder. This supports that for fragmental rockfalls, the structural failure is usually local, as pointed out in [10].
For velocities greater than 2.31 m/s, flexural rotation around the vertical axis is observed, which mainly owes to the lack of fixed support at the vertical boundaries of the wall during the test. For larger walls with respect to the size of the boulder, the collapse of the entire wall is not certain. As the impact stresses are propagated from the centre of the impact to the entire wall, for larger walls, the stress propagation zone is expected to be restricted; thus, full collapse may be avoided [5]. The aforementioned points underline the need for further tests with a larger ratio between the wall and boulder dimensions, as well as improved boundary conditions.
Another restriction of the presented experimental setting is the lack of a vertical compression load (weight) on the walls that increases their shear resistance, as occurs for real structural walls. Taking into consideration the additional weight on the walls may lead to substantially increased damage energy thresholds. Moreover, the inclined wall that was used in this experimental setting resulted in a reduction in the wall’s self-weight, which also provided more conservative results compared to a strictly vertical wall.
The incidence angle (the angle between the rock boulder and the wall) also plays an important role in the transmission of the impact energy. In reality, it may take different values. For the experiments performed, the angle between the ramp and the wall was orthogonal; however, this does not necessarily result in an orthogonal incidence angle given that slight bouncing can cause the latter to vary to some degree. The effect of the variability of the incidence angle has not been studied in detail in this work. Further limitations concern the shape of the boulder. In reality, for collisions between hard bodies with nonconforming surfaces, the contact area is small, and the deformations are concentrated around the point of contact. Also, for polyhedral rock blocks, a rebound is observed during the first impact, which often leads to the blocks bouncing back and stopping. For this experimental setting, this phenomenon, which has an important effect on the penetration and propagation of the boulders into buildings and subsequently on the damage caused, was not taken into consideration. Future tests are foreseen in order to lift the aforementioned restrictions.
The results of the experiments presented cannot be used directly for damage assessment of wall–boulder systems at a real scale. Nevertheless, the comparison between numerical modelling and the experimental testing indicates that the developed FEM, using the selected materials and parameters, can realistically simulate the damage observed. Thus, the same FEM model properties can be used for damage analysis of further structures, as, for example, the same material properties and constitutive laws can be used for numerical analysis of thicker walls built with the same materials.
Finally, if such numerical simulations are to be used for further structural elements and buildings, the experimentally estimated dynamic and static friction coefficients have to be verified.
Author Contributions
O.M.: Conceptualization, methodology, formal analysis, writing—original draft preparation, visualization. X.F.: Conceptualization, methodology, resources, supervision, project administration, funding acquisition. Z.L.: Methodology, software, validation, formal analysis, investigation, visualization, writing—original draft. D.W.: Conceptualization, methodology. Q.X.: Conceptualization, methodology. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the State Key Laboratory of Geohazard Prevention and Geoenvironment, Chengdu, China, and the Open Fund Mission Statement for the project SKLGP2018K004 “Vulnerability of buildings to rockfall impacts”.
Data Availability Statement
The data is included within the article.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Corominas, J.; Mavrouli, O. Rockfall quantitative risk assessment. In Rockfall Engineering; Lambert, S., Ed.; Irstea Wiley: Dordrecht, The Netherlands, 2011; pp. 255–301. [Google Scholar]
- De Biagi, V.; Parisi, F.; Asprone, D.; Chiaia, B.; Manfredi, G. Collapse resistance assessment through the implementation of progressive damage in finite element codes. Eng. Struct. 2017, 136, 523–534. [Google Scholar] [CrossRef]
- Cui, P.; Zou, Q.; Xiang, L.Z.; Zeng, C. Risk assessment of simultaneous debris flows in mountain townships. Prog. Phys. Geog. 2013, 37, 516–542. [Google Scholar] [CrossRef]
- Kaynia, A.M.; Papathoma-Köhle, M.; Neuhäuser, B.; Ratzinger, K.; Wenzel, H.; Medina-Cetina, Z. Probabilistic assessment of vulnerability to landslide: Application to the village of Lichtenstein, Baden-Württemberg, Germany. Eng. Geol. 2008, 101, 33–48. [Google Scholar] [CrossRef]
- Liu, W.; Yan, S.; He, S. Landslide damage incurred to buildings: A case study of Shenzhen landslide. Eng. Geol. 2018, 247, 69–83. [Google Scholar] [CrossRef]
- Luo, H.Y.; Fan, R.L.; Wang, H.J.; Zhang, L.M. Physics of building vulnerability to debris flows, floods and earth flows. Eng. Geol. 2020, 271, 105611. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Oñate, E.; Idelsohn, S.R.; Del Pin, F.; Aubry, R. The Particle Finite Element Method—An Overview. Int. J. Comput. Methods 2004, 01, 267–307. [Google Scholar] [CrossRef]
- Mavrouli, O.; Skentou, A.; Carbonell, J.M.; Tsoukalas, M.; Núñez-Andrés, A.; Asteris, P. Deep Neural Networks for the Estimation of Masonry Structures Failures under Rockfalls. Geosciences 2023, 13, 156. [Google Scholar] [CrossRef]
- Mavrouli, O.; Giannopoulos, P.G.; Carbonell, J.M.; Syrmakezis, C. Damage analysis of masonry structures subjected to rockfalls. Landslides 2017, 14, 891–904. [Google Scholar] [CrossRef]
- Volkwein, A.; Roth, A.; Gerber, W.; Vogel, A. Flexible rockfall barriers subjected to extreme loads. Struct. Eng. Int. 2009, 19, 327–332. [Google Scholar] [CrossRef]
- Volkwein, A.; Schellenberg, K.; Labiouse, V.; Agliardi, F.; Berger, F.; Bourrier, F.; Dorren, L.K.; Gerber, W.; Jaboyedoff, M. Rockfall characterisation and structural protection-a review. Nat. Hazards Earth Syst. 2011, 11, 2617–2651. [Google Scholar] [CrossRef]
- Schellenberg, K.; Volkwein, A.; Roth, A.; Vogel, T. Rockfall–Falling weight tests on galleries with special cushion layers. In Proceedings of the 3rd International Conference on Protection of Structures Against Hazards, Venice, Italy, 28–29 September 2006; pp. 28–29. [Google Scholar]
- De Miranda, S.; Gentilini, C.; Gottardi, G.; Govoni, L.; Mentani, A.; Ubertini, F. Virtual testing of existing semi-rigid rockfall protection barriers. Eng. Struct. 2015, 85, 83–94. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, Z.X.; Liu, Y.P.; He, J.W.; Chan, S.L.; Zhao, S.C. Numerical simulation of responses of flexible rockfall barriers under impact loading at different positions. J. Constr. Steel Res. 2020, 167, 105953. [Google Scholar] [CrossRef]
- Lambert, S.; Bourrier, F.; Gotteland, P.; Nicot, F. An experimental investigation of the response of slender protective structures to rockfall impacts. Can. Geotech. J. 2020, 57, 1215–1231. [Google Scholar] [CrossRef]
- Qi, X.; Zhao, L.; Hao, C.R.; Yu, Z.X.; Zhao, S.C. Numerical simulation of dynamic responses of semi-rigid rockfall protection barriers subjected to impact loading at different positions. Bull. Eng. Geol. Environ. 2022, 81, 367. [Google Scholar] [CrossRef]
- Buzzi, O.; Spadari, M.; Giacomini, A.; Fityus, S.; Sloan, S.W. Experimental testing of rockfall barriers designed for the low range of impact energy. Rock Mech. Rock. Eng. 2013, 46, 701–712. [Google Scholar] [CrossRef]
- Spadari, M.; Giacomini, A.; Buzzi, O.; Hambleton, J.P. Prediction of the bullet effect for rockfall barriers: A scaling approach. Rock. Mech. Rock. Eng. 2012, 45, 131–144. [Google Scholar] [CrossRef]
- Grant, A.; Wartman, J.; Massey, C.; Olsen, M.J.; O’Banion, M.; Motley, M. The impact of rockfalls on dwellings during the 2011 Christchurch, New Zealand, earthquakes. Landslides 2018, 15, 31–42. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, Y.T. The physical vulnerability of different types of building structure to debris flow events. Nat. Hazards 2016, 80, 1475–1493. [Google Scholar] [CrossRef]
- Li, P.; Li, T.; Lu, Z.; Li, J. Parametric Study on Dynamic Response of FRP Masonry Structures under the Impacts of Debris Flow. Shock. Vib. 2018, 2018, 4527571. [Google Scholar] [CrossRef]
- Liu, S.G.; Li, Z.J.; Zhang, H.; Wu, W.; Zhong, G.H.; Lou, S. A 3-D DDA damage analysis of brick masonry buildings under the impact of boulders in mountainous areas. J. Mt. Sci. 2018, 15, 657–671. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.X.; Wang, D.; Qian, H. The quantitative estimation of the vulnerability of brick and concrete wall impacted by an experimental boulder. Nat. Hazards Earth Syst. Sci. 2016, 16, 299–309. [Google Scholar] [CrossRef]
- Petrazzuoli, S.M.; Zuccaro, G. Structural resistance of reinforced concrete buildings under pyroclastic flows: A study of the Vesuvian area. J. Volcanol. Geotherm. Res. 2004, 133, 353–367. [Google Scholar] [CrossRef]
- Mavrouli, O.; Corominas, J. Rockfall vulnerability assessment for reinforced concrete buildings. Nat. Hazards Earth Syst. Sci. 2010, 10, 2055–2066. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B.; Frattini, P. Integrating rockfall risk assessment and countermeasure design by 3D modelling techniques. Nat. Hazards Earth Syst. Sci. 2009, 9, 059. [Google Scholar] [CrossRef]
- Mavrouli, O.A.; Syrmakezis, C.A. Investigation of masonry elasticity and shear moduli using finite element micro-models. Smart Struct. Syst. 2008, 4, 171–182. [Google Scholar] [CrossRef]
- Rafsanjani, S.H.; Lourenço, P.B.; Peixinho, N. Analysis of masonry walls subjected to high strain rate out-of-plane loads with a rate dependent interface model. In Proceedings of the 9th International Masonry Conference, Guimarães, Portugal, 7–9 July 2014; pp. 1–11. [Google Scholar]
- Beattie, G.; Molyneaux, T.C.; Gilbert, M.; Burnett, S. Masonry shear strength under impact loading. In Proceedings of the 9th Canadian Masonry Symposium, Fredericton, NB, Canada, 4 June 2001. [Google Scholar]
- Lourenço, P.B.; Hunegn, T.; Medeiros, P.; Peixinho, N. Testing and analysis of masonry arches subjected to impact loads. In Proceedings of the Sixth International Conference on Arch Bridges, Fuzhou, China, 11–13 October 2010; pp. 603–610. [Google Scholar]
- Van Vliet, M.R. Shear Tests on Masonry Panels; Literature Survey and Proposal for Experiments; TNO Building and Construction Research Report; TNO: Delft, The Netherlands, 2004. [Google Scholar]
- Derakhshan, H.L.; Ingham, J.M. Out-of-Plane testing of an unreinforced masonry wall subjected to one-way bending. In Proceedings of the Australian Earthquake Engineering Conference, AEES, Ballarat, Victoria, Australia, 24–28 November 2008. [Google Scholar]
- Pourfalah, S.; Cotsovos, D.M.; Suryanto, B.; Moatamedi, M. Out-of-plane behaviour of masonry specimens strengthened with ECC under impact loading. Eng. Struct. 2018, 173, 1002–1018. [Google Scholar] [CrossRef]
- Beattie, G.; Molyneaux, T.C.; Gilbert, M.; Hobbs, B.; Burnett, S.; Newton, P.; Gration, D.A. Improving the impact resistance of masonry parapets. In Proceedings of the LS-DYNA Users Conference, LSTC, Paris, France, 18–19 June 2001. [Google Scholar]
- Mavrouli, O.; Corominas, J. Vulnerability of simple reinforced concrete buildings to damage by rockfalls. Landslides. 2010, 7, 169–180. [Google Scholar] [CrossRef]
- Meguid, M.A.; Gao, G.; Abouelkair, M.M.; Abdelrahman, M.Z. Modelling the impact of particle flow on rigid structures: Experimental and numerical investigations. In Proceedings of the 3rd International Symposium on Mine Safety Science and Engineering, Montreal, QC, Canada, 13–19 August 2016; pp. 140–144. [Google Scholar]
- Gao, G.; Meguid, M.A. Modeling the impact of a falling rock cluster on rigid structures. Int. J. Geomech. 2017, 18, 04017141. [Google Scholar] [CrossRef]
- GB 50003-2011; Specification of the design of masonry structures. Construction Industry of China: Beijing, China, 2011.
- Yongzhi, L. Hardening strength of masonry mortar at different ages. Archit. Technol. 1983, 7, 51. [Google Scholar]
- Lim, C.T.; Stronge, W.J. Normal elastic-plastic impact in plane strain. Math. Comput. Model. 1998, 28, 323–340. [Google Scholar] [CrossRef]
- LS-DYNA R12 Keyword Manual Vol. 1. Available online: https://lsdyna.ansys.com/manuals/ (accessed on 16 August 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).