Abstract
Shear wave velocity is an important parameter for estimating soil properties used in analyzing the dynamic response of soil to seismic loading. This paper focuses on developing a model for predicting shear wave velocity in unsaturated soils. The model was developed primarily for the interpretation of seismic cone penetration tests (SCPTs) in unsaturated soil to account for seasonal variations in moisture conditions. In practice, SCPTs typically occur over a period of days without the option of choosing a wet or dry period. The question becomes, if tests are conducted during a dry period, how can shear wave velocity corresponding to a wetter period be predicted, or vice versa? Answering this question was the primary motivation of this work. The work involved field testing with the seismic cone penetrometer during wet and dry periods and a focused study at three sites involving comparison between field and laboratory testing for shear wave velocity. The model presented in this paper is built upon the significant work of many other researchers with reference to new experimental data obtained by the authors. It is demonstrated that a stress-based model incorporating matric suction can provide reasonable predictions of shear wave velocity and provides a method to interpret the impact of changing moisture content on shear wave velocities determined with SCPTs.
1. Introduction
Shear wave velocity is an important parameter for estimating soil properties used in analyzing the dynamic response of soil to seismic loading. There is a vast number of publications addressing shear wave velocity measurement, interpretation, and modeling in soil. However, this paper focuses on developing a model for predicting shear wave velocity in unsaturated soils. This model was developed primarily for the interpretation of seismic cone penetration tests (SCPTs) in unsaturated soil to account for seasonal variations in moisture conditions. In practice, SCPTs typically occur over a period of days without the option of choosing a wet or dry period. The question becomes, if tests are conducted during a dry period, how can shear wave velocity corresponding to a wetter period be predicted, or vice versa? Answering this question was the primary motivation of this work.
The model presented in this paper to address this question was built upon the significant work of many other researchers with reference to new experimental data obtained by the authors. Specifically, mathematical models representing the relationships between net normal stress, matric suction and shear wave velocity were investigated. The experimental work involved conducting SCPTs at several different test sites at different times of the year, representing wet and dry soil conditions. Each time SCPTs were conducted at a test site, companion samples were obtained for laboratory testing to determine basic soil properties, water content, and suction. At three test sites, the testing program involved SCPTs and companion sampling to obtain thin-walled tube samples. For these three sites, additional laboratory testing included shear wave velocity measurements using bender elements on samples at the field moisture contents. In addition, the tube samples were subjected to wetting and drying, and additional shear wave velocity measurements were obtained with the corresponding determinations of moisture content and suction. Based on the field and laboratory testing data, it was demonstrated that a stress-based model incorporating matric suction can provide reasonable predictions of shear wave velocity and provides a method to interpret the impact of changing moisture content on shear wave velocities determined with SCPTs.
2. Background
2.1. Shear Wave Velocity in Soil
Derivation of the three-dimensional equations of motion for an isotropic linear elastic material can be used to develop the governing equations for irrotational or dilational waves, and distortional waves of rotation with respect to the three principal directional axes. The former represents a primary or p-wave, while the latter, which is the focus of this paper, represents a shear or s-wave. Equation (1) represents the wave equation with respect to rotation about one axis; similar equations can be developed for the other two principal directions [1].
Ωx represents the rotation about the x-axis, and t is time. The ratio of shear modulus G to density ρ has units of velocity squared, and shear wave velocity, Vs, is defined by Equation (2):
Shear wave velocity, Vs, represents a fundamental material property that describes the speed at which a wave travels in a medium. It can be measured using various techniques in the lab and field and such measurements are used to determine the shear modulus, G. Since the strains induced during the wave propagation are very small, G determined from shear wave velocity measurements is referred to as the small strain shear modulus, Gmax. Gmax is an important parameter used in ground response analysis.
According to Equation (2), shear wave velocity increases as shear modulus increases and density decreases. In soil, the density and shear modulus are related since the shear modulus represents the shear stiffness of the soil skeleton. For the same soil and given effective stress, an increase in density would increase the shear modulus. Thus, to some degree, the decrease in vs. due to increasing density is offset by an increase in shear modulus that results from increasing density. However, typically, for a given effective stress, changes in shear modulus due to changes in density are not proportional, and hence, shear wave velocity tends to increase with increasing density. The interdependency of Gmax and ρ in Equation (2) can be investigated using Equation (3), which is an empirical equation applicable to a broad range of soil types [2].
In Equation (3), Gmax is in MPa, A and n are material parameters depending on soil type, e is void ratio, and σ’ is effective confining stress in kPa. Equation (4) represents Equation (3), except with dry density, ρd, replacing void ratio as the variable of interest.
In Equation (4), additional parameters include Gs, the specific gravity of soil solids, and ρw, density of water. Substituting Equation (4) into Equation (2), one can estimate shear wave velocity and the influence of ρd and Gmax using Equation (5). Note that for dry sand, ρ = ρd.
Using values typical for clays and sands [2] for A (30) and n (0.5), and a range of dry density representing loose (soft) to dense (stiff) soils, values of vs. in Figure 1 were determined. It was assumed that ρ = ρd in the calculations, which would be appropriate for dry sand. The baselines in Figure 1 represent vs. for ρd = 1400 kg/m3, Gs = 2.65, and σ’ = 10 and 1000 kPa. Equation (4) gives Gmax = 14 MPa and Gmax = 140 MPa for σ’ = 10 kPa and σ’ = 1000 kPa, respectively, for the baseline conditions. The bold solid line shows the combined effect of increasing ρd and corresponding increasing Gmax, based on Equation (5). The other two lines show the influence of only increasing ρd with Gmax constant at the baseline value or increasing Gmax with ρd constant at the baseline value. As indicated, at constant confining stress, the change in shear modulus due to increasing density has a dominant influence on shear wave velocity, resulting in a significant net increase in vs. with increasing density. Increasing the effective confining stress significantly increases the baseline Vs, but the influence of density and shear modulus relative to the baseline remains the same, as shown in Figure 1. The effect of confining stress is more clearly seen in Figure 2 for different dry densities and the corresponding shear modulus. As expected, based on Equation (5), there is a nonlinear relationship between vs. and confining stress.

Figure 1.
Shear wave velocity versus dry density for a typical soil calculated using the empirical relationship in Equation (5) based on the work of Bui et al. [2].

Figure 2.
Shear wave velocity versus effective confining stress for a typical soil calculated using the empirical relationship in Equation (5) based on the work of Bui et al. [2]. The curves in the figure represent different densities between 1400 and 2000 kg/m3.
In recent decades, researchers have focused on understanding the behavior of unsaturated soils and effects of varying saturation on soil properties. In the field, unsaturated soils can make up a substantial part of the upper layers of the soil profile, which are affected by seasonal weather and climate changes that cause wetting and drying. Understanding the behavior of shear wave velocity in unsaturated soils is particularly important because of its use in determining seismic site class and Gmax for earthquake ground response analysis [1]. While some published research has greatly improved our understanding of the influence of variable saturation on shear wave velocity, the authors have been systematically investigating this topic with the aim of providing a deeper understanding of seasonal effects on shear wave velocity measurements obtained with a seismic cone penetration test (SCPT). Through this research, and building on the work of others, a preliminary framework for predicting changes in shear wave velocity, determined with the SCPT, due to seasonal variations in moisture content was developed. This methodology is built around a stress-based model for unsaturated soils.
2.2. Previous Studies of vs. and Gmax in Unsaturated Soils
As soil changes from a saturated or dry condition to an unsaturated condition, the interparticle stresses change. As the water content of the soil decreases, the capillary pressure or matric suction in the soil increases, resulting in changes in stiffness and shear strength of the soil. The variation of the soil water content with respect to suction is presented graphically as the soil water characteristic curve (SWCC). The SWCC is not a unique relationship between soil suction and water content, as it is different for drying and wetting paths, and the path depends on the initial state of the soil prior to drying or wetting. The path dependency of the SWCC for wetting and drying is an example of hysteretic behavior [3].
Some studies have examined the effect of changing the soil moisture content on shear wave velocity (e.g., [4,5,6,7,8]). The results of this work have shown that as soil saturation increases, shear wave velocity decreases, with the highest shear wave velocity near the dry condition and the lowest near the saturated condition. Other researchers have examined the effect of hysteresis on shear wave velocity (e.g., [8,9,10]). Measurements of shear wave velocity were taken along the wetting and drying path for various soil types, and the results showed that shear wave velocity is higher along the drying path when compared to that along the wetting path.
The effects of suction and confining stress on shear wave velocity have been investigated (e.g., [5,11,12,13]) using suction-controlled testing. The tests were done by saturating the soil specimens and controlling the matric suction to measure the shear wave velocity along the drying paths. Additionally, the shear wave velocity was measured at various confining stresses during testing. The results have shown that shear wave velocity was directly proportional to suction; as suction increased, shear wave velocity increased. Additionally, the results have shown that an increase in the confining stress leads to an increase in shear wave velocity.
Some researchers have examined the influence of hysteresis on the small strain shear modulus, Gmax (e.g., [8,9]), which is directly related to shear wave velocity, as shown in Equation (2). Khosravi and McCartney [9] investigated the effect of hysteresis on low-plasticity soils. The results have shown that along the wetting and drying paths, the shear modulus varies due to hysteresis. Dong and Lu [8] examined the effect of varying saturation on the shear modulus and found that there is a strong relationship between the shear modulus and suction stress.
The work described in this paper builds on the significant body of literature described above. This paper describes a part of a comprehensive study aimed at developing a rational approach to interpreting shear wave velocity measurements from seismic cone penetration tests (SCPTs) conducted in unsaturated soils prone to seasonally variable moisture conditions. The study involved conducting SCPTs at several sites during wet and dry periods with companion test borings to determine corresponding moisture content and suction profiles. In addition, laboratory testing of natural clayey soils from three sites was conducted to compare shear wave velocity determined with SCPTs and in the lab with bender elements. The results from the field and laboratory work are presented in this paper to demonstrate the use of a stress-based model for interpretation of shear wave velocity in unsaturated soil obtained with SCPTs.
3. Experimental Methodology
3.1. SCPTs in Unsaturated Soil
Seismic cone testing was conducted at nine different sites at two different times representing wet and dry weather periods. During each visit, a minimum of three SCPT soundings were conducted, from which average cone parameters were determined. The cone was equipped with two dual-axis geophones for detecting shear waves generated at the ground surface. The arrival time for reference waves and distance of wave travel at each test depth were used to determine the average shear wave velocity for layers between the test depths in general accordance with ASTM Standard D7400/D7400M-19 Standard Test Methods for Downhole Seismic Testing [14]. Soil profiles and average shear wave velocity determinations from SCPTs at three of the test sites are summarized in Figure 3. Of the nine sites, these three demonstrated the greatest impact of varying moisture content on shear wave velocity. As shown in the figures, gravimetric water content (wn), total suction (ψ) measured with a chilled mirror hygrometer, and shear wave velocity (Vs) were strongly correlated, with vs. increasing as the soil dried and suction increased.

Figure 3.
Soil profiles and shear wave velocities determined from the SCPT at three test sites in Oklahoma during wet (first visit) and dry (second visit) periods. From top to bottom the sites are: (a) Wa, (b) We, and (c) F. Unless noted otherwise, solid symbols indicate data from the first visit and open symbols indicate data from the second visit.
As mentioned previously, the question to answer is: if tests are conducted during a dry period, how can shear wave velocity corresponding to a wetter period be predicted, or vice versa? To begin, simple empirical correlations between water content or suction and shear wave velocity seemed like a reasonable first step. For example, in Figure 4, the data from the three sites shown in Figure 3 are summarized, with only results from cohesive soil shown.

Figure 4.
Shear wave velocity from the SCPT plotted against (a) water content and (b) total suction for cohesive soils at three test sites in Oklahoma during wet and dry periods.
There is considerable scatter in the data shown in Figure 4, which is typical for field testing in variable soil profiles. The trends in the water content–shear wave velocity data are relatively stronger than shown for the suction–shear wave velocity data. Ideally, vs. would be plotted against matric suction since it is the component of total suction that influences mechanical behavior the most. Total suction measurements are significantly influenced by soil type and chemistry of the pore water, which likely explains the lack of stronger trends in this plot. It is known that salt contents in natural soils can significantly influence the total suction measurement, and therefore total suction is not always a good surrogate for matric suction when salt is present (e.g., [15]). In spite of the scatter, trends in Figure 4 show the strong dependence of shear wave velocity on water content at each site.
Because of the inherent variability in field measurements, a systematic laboratory study was conducted to study the relationship between shear wave velocity, moisture content, and suction, as well as other parameters of interest.
3.2. SCPT and Laboratory Testing of Shear Wave Velocity in Unsaturated Soil
To better understand the variation in shear wave velocity with changing moisture conditions, an in-depth study was conducted at three test sites, different from those presented previously, and designated Site 10, 11, and 12. At each site, shear wave velocity measurements were obtained from the SCPT in the unsaturated profile, and Shelby tube samples were obtained from discrete depths in this zone on the same day. Shelby tube samples were subjected to shear wave velocity measurements in the laboratory at the natural water content under confining stresses simulating the in situ condition. Additionally, these samples were wetted and dried, and additional shear wave velocity measurements were obtained for wet and dry conditions.
In the laboratory, controlled wetting/drying was conducted in a vapor equilibrium chamber by placing the samples on a porous plate above a saltwater solution. Two different chambers were used, one containing a salt solution corresponding to high suction (6.6 MPa) for drying, and one corresponding to low suction (0.23 MPa) for wetting. After drying or wetting, the samples were removed, weighed, and subjected to shear wave velocity measurements using bender elements. Small specimens were extracted to make water content and total suction measurements corresponding to each shear wave velocity test. Total suction measurements were made using a chilled mirror hygrometer.
For shear wave velocity testing, test specimens were enclosed in a rubber membrane sealed to the bottom and top platens containing the bender elements within a triaxial testing chamber. The specimens were subjected to confining air pressure equal to the estimated in situ vertical total stress. Bender element testing was conducted using a function generator to produce a sine wave pulse. Based on previous studies [16,17,18], the frequency and amplitude of the generated signal were set at 4 kHz and 20 Vpp, respectively. A four-channel oscilloscope and analog to digital reader with a maximum sampling rate of 1 GSa/s was used to display and collect the shear wave signals from the bender element pairs. The start-to-start time domain interpretation mentioned in ASTM D8295 Standard Test Method for Determination of Shear Wave Velocity and Initial Shear Modulus in Soil Specimens using Bender Elements [14] was used to determine shear wave velocity [16,19].
The results of field and lab testing at the natural water content are shown in Figure 5 for each test site, along with basic index properties and USCS group symbols. As shown in each graph, with one exception, the shear wave velocities determined by SCPT were practically the same as those determined using bender element testing on discrete specimens. This indicates that vs. determinations were robust and reliable from both the lab and the field methods used. Based on this observation, it stands to reason that changing the specimen water contents under laboratory conditions and measuring vs. should provide a reasonable surrogate for SCPT-determined values of vs. under similar water contents. As mentioned above, the one exception where field and lab vs. measurements differed significantly was at a depth of 1 m (Figure 5b). This difference is attributed to the fact that lab measurements represent discrete layers having a thickness equal to that of the test sample, whereas the SCPT determinations involve averaging over larger layer thicknesses. If soil conditions vary considerably between SCPT depths, then lack of agreement between lab and field vs. values can occur since the lab measurement represents a sublayer from the larger layer over which the SCPT vs. value is determined. Furthermore, SCPT measurements are more susceptible to the influence of varying moisture contents in the near surface soils, which can be large in the upper 1 m.
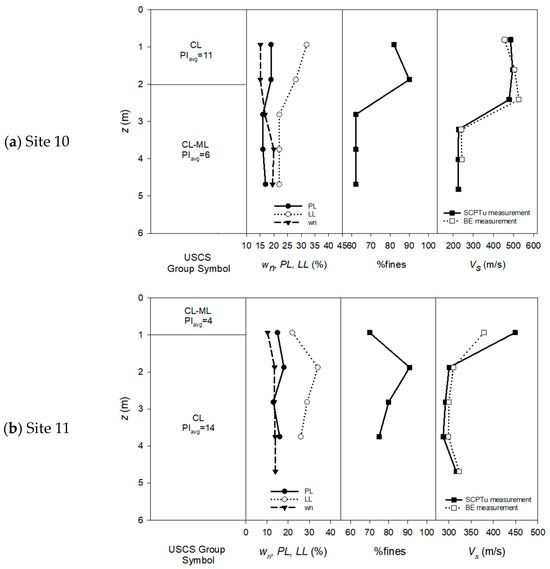

Figure 5.
Soil properties and shear wave velocities determined in the field using SCPT and in the lab using bender elements on specimens under confining stresses simulating in situ conditions. From top to bottom, test sites are designated: (a) 10, (b) 11, and (c) 12.
In Figure 6, vs. values under dry and wet conditions determined in the laboratory are presented for each test site. As shown in Figure 6, there are substantial differences in vs. for dry and wet conditions, and it is noted that at the time of the SCPT, the in situ condition was closer to the wet condition. The challenge in using vs. values from the SCPT is estimating how the vs. will change as moisture conditions change in the unsaturated soil. This is particularly important for determining seismic site class when dryer conditions prevail at the time of SCPTs. Additionally, for modeling ground motion and response of overlying structures to earthquakes, both dry and wet conditions may be of interest depending on the natural frequency of the overlying structures.

Figure 6.
Water content, total suction, and shear wave velocities determined in the lab using bender elements on specimens at in situ, wet, and dry conditions. From top to bottom, tests sites are designated: (a) 10, (b) 11 and (c) 12.
3.3. Stress-Based Model for Shear Wave Velocity
As a first step in developing a stress-based model for interpreting vs. measurements from the SCPT, the data presented in Figure 6 for the three test sites were summarized in graphs depicting shear wave velocity in relationship to natural water content and measured total suction in Figure 7. Figure 7a depicts the data from all depths, while Figure 7b,c show the data separated based on the predominant soil types at these sites: lean clay (CL) and silty lean clay (CL-ML).

Figure 7.
Water content and total suction versus shear wave velocities determined in the lab using bender elements on specimens at in situ, wet, and dry conditions. (a) All soils, (b) CL soils, (c) CL-ML soils.
As expected, the relationships shown in Figure 7 are similar to those for other test sites shown in Figure 4, except the relationships were statistically stronger, owing to the much more controlled nature of the testing during wetting and drying in the laboratory. Coefficients of determination for the trend lines in Figure 7 show strong correlations between Vs, w, and ψ. When separated by soil type, the correlations got stronger for the CL soils and slightly weaker for the CL-ML soils. These empirical relationships can be useful for predicting changes in shear wave velocity due to changes in moisture content. However, they also demonstrate the importance of the stress state, since matric suction is a significant component of effective stress in unsaturated soil, particularly in the upper soil profile where net normal stresses are lower.
As shown in Figure 7, Sites 11 and 12 exhibited similar relationships between w, ψ, and Vs, while Site 10 exhibited significantly higher vs. for a given w and ψ, except at lower values of suction; around 200 kPa, the three trend lines converge. As total suction got closer to 200 kPa, matric suction was likely approaching zero, and total suction equaled the osmotic suction. Since matric suction largely controls mechanical behavior, this would explain why vs. was similar for all soils as total suction approached 200 kPa. The SWCC for these sites helps explain this behavior. Figure 8 shows the measured water contents versus total suction and estimated matric suction for each site, for all soils (Figure 8a) and separated by soil type (Figure 8b,c). Figure 8 indicates that Sites 11 and 12 had similar soil–water characteristic behavior, while Site 10 was substantially different. For a given water content, Site 10 had higher matric suction compared to that of Sites 11 and 12, except at higher water contents where matric suction approached zero. This helps explain the higher shear wave velocities observed at Site 10 for total suctions greater than 200 kPa.

Figure 8.
Water content versus total suction (left) and estimated matric suction (right) from specimens at in situ, wet, and dry conditions. (a) All soils, (b) CL soils, (c) CL-ML soils.
Previous researchers have proposed models for saturated and unsaturated soil relating shear wave velocity to effective stress. A general power relationship between shear wave velocity and effective stress was proposed by Santamarina et al. [20], shown in Equation (6).
where A and β are experimentally determined fitting parameters. This form is similar to that in Equation (5), and thus parameters A and β would encompass the influence of density and other material properties.
Extending this model to unsaturated soils, Sawangsuriya et al. [21] proposed Equation (7), which includes the Bishop effective stress defined by Equation (8).
where A and β are fitting parameters, and χ is the effective stress parameter.
Bishop’s [22] proposed parameter χ could be equal to the degree of saturation S. Although this assumption is acceptable in some cases, it does not accurately describe the soil behavior near dry conditions and for fine-grained soils [23]. The challenge of defining the effective stress parameter χ has been addressed by many researchers. Multiple definitions have been proposed for the effective stress parameter χ [23,24,25,26,27,28,29].
The suction stress (σs) concept was proposed by Lu and Likos [23] to describe the contributions of various interparticle forces to effective stress, as given by Equation (9). Lu et al. [6,28] and Oh et al. [29,30] have demonstrated the implementation of this concept through their studies. Lu et al. [28] have demonstrated that suction stress can be defined as the product of effective degree of saturation, θe, and matric suction (Equation (10)). Thus, effective stress takes the form of Equation (11). This essentially results in an equation of similar form to Bishop’s equation, with χ = θe, and the resulting expression for shear wave velocity is given by Equation (12).
For unsaturated soil, the relationship between shear wave velocity and stress state can thus be represented by an equation of form similar to those shown in Equations (6), (7), and (12). The difficulty in using Equations (7) and (12) for interpreting SCPT-determined values of vs. lies in the determination of the degree of saturation or effective degree of saturation. This would require at a minimum, thin-walled tube sampling in layers of interest. Even with companion samples corresponding to one water content profile, it is difficult to determine changes in degree of saturation because of volume changes that accompany the drying or wetting of clayey soils. Another approach would be to treat the net normal stress and matric suction independently, such as in Equation (13), where A1, A2, β1, and β2 represent fitting parameters associated with net normal stress and matric suction.
In this study, however, the variation in net normal stress over the depths of interest was relatively small and did not have an appreciable influence on Vs, as indicated in Figure 9 for the CL soils. The CL-ML soils showed similar behavior. Net normal stress was simply estimated as the total vertical stress at the test depths, assuming that pore air pressure was zero.

Figure 9.
Net normal stress versus shear wave velocity for CL soils at test sites (a) 10, (b) 11, and (c) 12.
Given the strong relationship between suction and shear wave velocity, for this paper, a simplified expression was adopted, as given by Equation (14). This essentially equals Equations (7) or (12) with χ or θe, respectively, equal to one.
Intuitively, compared to Equation (14), Equations (7) or (12) seem more correct in that, through the degree of saturation, they can capture the nonlinearity associated with the variation in the solid–water interfacial area caused by changing water content. However, parameters A and β can accommodate this nonlinearity. Further, from a practical perspective, as discussed previously, Equation (14) is more easily applied to the interpretation of SCPT vs. measurements, where information to accurately predict existing or future degrees of saturation is lacking. As discussed below, to utilize Equation (14), one would need to estimate the matric suction for the soil and moisture conditions of interest.
Equation (14) is represented by the power relationship parameters shown in Figure 10 for CL and CL-ML soils. As indicated by coefficients of determination in Figure 10, the power relationship is a reasonable model for the relationship between shear wave velocity and stress state variables. It is important to note that in the preceding analysis, it was assumed that the soils representing CL and CL-ML were the same at each test depth. While the soils are geologically similar, they do vary with respect to their index properties. In spite of the natural variations with depth at each test site, the observed relationships were relatively strong. In a similar manner, Equation (14) was applied to the SCPT vs. results shown in Figure 4. Figure 11 indicates that incorporating net normal stress resulted in a slight improvement in statistical strength of the fitted power curves as compared to that with suction alone. The results of this analysis suggest that the use of Equation (14) provided a reasonable means of predicting the influence of changing moisture conditions on vs. determined with the SCPT.

Figure 10.
Net normal stress plus matric suction versus shear wave velocity for (a) CL soils and (b) CL-ML soils.

Figure 11.
(a) Total suction and (b) net normal stress plus total suction (right) versus shear wave velocity for results from SCPTs shown in Figure 4.
4. Discussion
From a practical perspective, applying the model represented by Equation (14) requires, at a minimum, companion sampling from which soil type, water content, and soil suction can be determined or estimated. There are various levels of sophistication that can be used to determine matric suction, from use of simple empirical correlations for the SWCC (e.g., [31]) to indirect and direct methods of measurement of total, matric, and osmotic suction. Once the water contents and associated matric suctions of interest are determined, the estimates of the A and β parameters are needed to predict how vs. will vary with changing suction. It is possible that in a natural soil profile, the water content will vary with depth on a given testing date. If the soil profile is geologically similar with depth, then in such cases, site-specific plots, such as those in Figure 10 and Figure 11, may provide a means to estimate A and β. This would be ideal, since such an approach provides site-specific values of A and β. Alternatively, A and β may be estimated using empirical correlations based on physical and index properties for different soil types. For example, Table 1 presents the soil classification, plasticity index (PI), percent of fines (f), and A and β for the sites and soil types included in this paper. While the data are relatively limited, there does appear to be a relationship between the index properties and parameters A and β for the CL soils as shown in Figure 12. In Figure 12, the product of PI and f is used to represent the index properties of the soil. This parameter was found by Zapata et al. [31] to work well for correlations to determine fitting parameters for the SWCC.

Table 1.
Index properties and parameters A and β for test soils.

Figure 12.
(a) Parameter A and (b) parameter β versus the product of percent of fines (f) and plasticity index (PI) for CL soils listed in Table 1.
As more field data, such as that presented in this paper, are accumulated, it will be possible to provide typical ranges of A and β for various soil types having various physical and index properties. However, it is expected that datasets used for such correlations will exhibit considerable scatter because shear wave velocity depends on other factors such as void ratio, structure, and stress history, whose influence is not captured by index properties obtained from disturbed samples.
The method presented above based on Equation (14) provides a rational way of predicting how shear wave velocity will change with changes in suction due to changing moisture content. However, there are limitations to the proposed approach as discussed. Natural site variability can cause large scatter in site-specific relationships between shear wave velocity and stress state parameters of interest. Furthermore, attempts to develop correlations between the power model parameters and index properties is expected to exhibit considerable scatter because of natural soil variations and dependence of shear wave velocity on other factors such as void ratio, soil structure, and stress history, for example. What is needed to further this work is additional laboratory and field studies on multiple soil types in which all important parameters of interest are carefully controlled or measured. In the meantime, caution should be exercised in using the method outlined in this paper and site-specific data should be used to the extent possible in determining the model parameters.
5. Conclusions
In this study, shear wave velocity was determined in the field with SCPTs and in the laboratory using the bender element method under wetting and drying conditions on Shelby tube samples obtained from SCPT sites. The following conclusions are based on the analysis of the test results:
- Shear wave velocity (Vs) determined with the SCPT was strongly dependent on the moisture content and suction in the soil at the time of testing.
- At three test sites, shear wave velocities determined with the SCPTs were nearly identical to values determined in the laboratory with bender elements under similar stress conditions on thin-walled tube samples obtained on the same day as SCPTs. This suggests that shear wave velocity measurements in the field and laboratory are robust and reliable.
- Soil water content and suction are strongly correlated with Vs. These relationships can be used to predict changes in vs. resulting from seasonal changes in moisture conditions.
- A stress-based power model incorporating net normal stress and suction provides a reasonable framework for estimating how shear wave velocity determined with SCPTs may change due to changing moisture conditions. This is important when considering that moisture conditions at the time of SCPTs may not represent future conditions of interest.
Author Contributions
Conceptualization, G.A.M. and T.A.; methodology, T.A., G.A.M. and K.K.M.; software, T.A. and G.A.M.; validation, T.A. and G.A.M.; formal analysis, T.A. and G.A.M.; investigation, T.A.; resources, T.A. and G.A.M.; data curation, T.A. and G.A.M.; writing—original draft preparation, T.A. and G.A.M.; writing— T.A., G.A.M. and K.K.M.; visualization, T.A. and G.A.M.; supervision, G.A.M. and K.K.M.; project administration, G.A.M. and T.A.; funding acquisition, G.A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Oklahoma Department of Transportation (ODOT) via the Federal Highway Administration (FHWA) grant number ODOT SPR Item Number 2308.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kramer, S.L. Geotechnical Earthquake Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1996; 653p. [Google Scholar]
- Bui, M.T.; Clayton, C.R.I.; Priest, J.A. The universal void ratio function for small strain shear modulus. Int. Conf. Recent Adv. Geotech. Earthq. Eng. Soil Dyn. 2010, 29. Available online: https://scholarsmine.mst.edu/icrageesd/05icrageesd/session01/29 (accessed on 17 August 2024).
- Miller, G.A.; Khoury, C.N.; Muraleetharan, K.K.; Liu, C.; Kibbey, T.C.G. Effects of soil skeleton deformations on hysteretic soil water characteristic curves: Experiments and simulations. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Cho, G.C.; Santamarina, J.C. Unsaturated particulate materials—Particle-level studies. J. Geotech. Geoenviron. Eng. 2001, 127, 84–96. [Google Scholar] [CrossRef]
- Yang, S.R.; Lin, H.D.; Kung JH, S.; Liao, J.Y. Shear wave velocity and suction of unsaturated soil using bender element and filter paper method. J. GeoEngineering 2008, 3, 67–74. [Google Scholar]
- Lu, Z.; Sabatier, J.M. Effects of soil water potential and moisture content on sound speed. Soil Sci. Soc. Am. J. 2009, 73, 1614–1625. [Google Scholar] [CrossRef]
- Asslan, M.; Wuttke, F. Wave velocity change and small-strain stiffness in unsaturated soils: Experimental investigation. In Unsaturated Soils: Research and Applications; Springer: Berlin/Heidelberg, Germany, 2012; pp. 355–362. [Google Scholar]
- Dong, Y.; Lu, N. Dependencies of shear wave velocity and shear modulus of soil on saturation. J. Eng. Mech. 2016, 142, 04016083. [Google Scholar] [CrossRef]
- Khosravi, A.; McCartney, J.S. Impact of hydraulic hysteresis on the small-strain shear modulus of low plasticity soils. J. Geotech. Geoenviron. Eng. 2012, 138, 1326–1333. [Google Scholar] [CrossRef]
- Khosravi, A.; Shahbazan, P.; Pak, A. Impact of hydraulic hysteresis on the small strain shear modulus of unsaturated sand. Soils Found. 2018, 58, 344–354. [Google Scholar] [CrossRef]
- Sawangsuriya, A.; Edil, T.B.; Bosscher, P.J. Modulus−suction−moisture relationship for compacted soils. Can. Geotech. J. 2008, 45, 973–983. [Google Scholar] [CrossRef]
- Sawangsuriya, A.; Edil, T.B.; Bosscher, P.J. Modulus-suction moisture relationship for compacted soils in post compaction state. J. Geotech. Geoenviron. Eng. 2009, 135, 1390–1403. [Google Scholar] [CrossRef]
- Whalley, W.; Jenkins, M.; Attenborough, K. The velocity of shear waves in unsaturated soil. Soil Tillage Res. 2012, 125, 30–37. [Google Scholar] [CrossRef]
- ASTM. Annual Book of ASTM Standard; American Society for Testing and Materials, ASTM International: West Conshohocken, PA, USA, 2019; Volume 4.08. [Google Scholar]
- Wei, Y.; Miller, G.A. Determining Osmotic Suction Using a Chilled Mirror Device. Geotech. Test. J. 2019, 42, 1457–1474. [Google Scholar] [CrossRef]
- Viggiani, G.; Atkinson, J.H. Interpretation of bender element tests. Geotechnique 1995, 45, 149–154. [Google Scholar] [CrossRef]
- Leong, E.C.; Cahyadi, J.; Rahardjo, H. Measuring shear and compression wave velocities of soil using bend-er-extender elements. Can. Geotech. J. 2009, 46, 792–812. [Google Scholar] [CrossRef]
- Lings, M.L.; Greening, P.D. A novel bender/extender element for soil testing. Géotechnique 2001, 51, 713–717. [Google Scholar] [CrossRef]
- Lee, J.-S.; Santamarina, J.C. Bender elements: Performance and signal interpretation. J. Geotech. Geoenviron. Eng. 2005, 131, 1063–1070. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Klein, A.; Fam, M.A. Soils and Waves, Particulate Materials Behavior, Characterization and Process Monitoring; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Sawangsuriya, A.; Edil, T.B.; Bosscher, P.J.; Wang, X. Small-strain stiffness behavior of unsaturated compacted subgrade. In Unsaturated Soils 2006; American Society of Civil Engineers: Reston, VA, USA, 2006; pp. 1121–1132. [Google Scholar]
- Bishop, A.W. The principle of effective stress. Teknisk Ukeblad Samarbeide Med. Teknikk. 1959, 106, 859–863. [Google Scholar]
- Lu, N.; Likos, W.J. Suction stress characteristic curve for unsaturated soils. J. Geotech. Geoenviron. Eng. 2006, 132, 131–142. [Google Scholar] [CrossRef]
- Vanapalli, S.K.; Fredlund, D.G.; Pufahl, D.E.; Clifton, A.W. Model for the prediction of shear strength with respect to soil suction. Can. Geotech. J. 1996, 33, 379–392. [Google Scholar] [CrossRef]
- Öberg, A.L.; Sällfors, G. Determination of shear strength parameters of unsaturated silts and sands based on the water retention curve. Geotech. Test. J. 1997, 20, 40–48. [Google Scholar] [CrossRef]
- Khalili, N.; Khabbaz, M.H. A unique relationship for χ for the determination of the shear strength of unsaturated soils. Geotechnique 1998, 48, 681–687. [Google Scholar] [CrossRef]
- Likos, W.J.; Lu, N. Hysteresis of capillary stress in unsaturated granular soil. J. Eng. Mech. 2004, 130, 646–655. [Google Scholar] [CrossRef]
- Lu, N.; Godt, J.W.; Wu, D.T. A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 2010, 46, 1–14. [Google Scholar] [CrossRef]
- Oh, S.; Lu, N.; Kim, Y.K.; Lee, S.J.; Lee, S.R. Relationship between the soil-water characteristic curve and the suction stress characteristic curve: Experimental evidence from residual soils. J. Geotech. Geoenviron. Eng. 2012, 138, 47–57. [Google Scholar] [CrossRef]
- Oh, W.T.; Vanapalli, S.K. Semi-empirical model for estimating the small-strain shear modulus of unsaturated non-plastic sandy soils. Geotech. Geol. Eng. 2014, 32, 259–271. [Google Scholar] [CrossRef]
- Zapata, C.E.; Houston, W.N.; Houston, S.L.; Walsh, K.D. Soil–water characteristic curve variability. In Advances in Unsaturated Geotechnics; American Society of Civil Engineers: Reston, VA, USA, 2000; pp. 84–124. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).