Abstract
Thermally induced moisture flow in unsaturated soils involves complex coupled thermal–hydro processes with the moisture flow in both the vapor and liquid phases. The accurate measurement of the moisture flow in unsaturated sands remains a challenging task due to low moisture migration, the temperature effect on moisture sensors, and the gravity effect on moisture flow. This study aims to accurately measure transient moisture flow, heat transfer, and thermal conductivity in a silty sand with 35% non-plastic fines in a closed heat cell with a controlled 1-D temperature gradient. The heat cell consists of two temperature-controlled heat exchanger plates, heat flux sensors, moisture sensors, thermocouples, and thermal conductivity sensors. The soil moisture sensors were calibrated in the test soil at room temperature and then at elevated incremental temperatures. Soil samples compacted at various initial moisture contents were tested under a constant 1-D temperature gradient of 4 °C/cm. Soil moisture redistribution, temperature, and thermal conductivity profiles were determined from the test results. Transient temperature responses indicated that a lower initial moisture content led to a higher temperature drop after reaching the peak, or a more concaved temperature profile in a steady state due to enhanced moisture migration driven by the temperature gradients. Dry soils exhibited uniform thermal properties, while moist soils showed varying thermal conductivity profiles. A critical moisture content was identified when the maximum moisture migration occurred. Thermal conductivity in soils increased with the distance from the heat source due to thermally induced moisture migration. These findings provide valuable insights into coupled moisture–heat flow dynamics in unsaturated sands.
1. Introduction
Water in soils moves and redistributes under the influence of the temperature gradient [,,,]. The water redistribution in the soil induces the associated heat transfer and changes in soil thermal properties. Therefore, moisture flow in unsaturated soils under non-isothermal conditions is highly coupled with the heat transfer process. Coupled heat transfer and moisture flow in unsaturated soils are critical to the understanding of many thermal geotechnical structures, such as buried electrical cables [,,], ground heat exchangers [], energy piles [], thermally active embankments [], and heat storage in soils []. For example, buried electrical transmission cables generate heat, causing a rising temperature in the cable sheath, which leads to the migration of moisture away from the cable under the thermal gradient. The soil surrounding the cable dries out, and its thermal conductivity decreases remarkably. As a result, the cable temperature continues to rise, which may lead to cable failure and the thermal instability of the soil surrounding the cable [,]. In an energy pile, the moisture moves away from the pile during the heating operation and moves toward the pile during the cooling operation. The moisture flow causes thermal and mechanical changes in the soil near the pile and thus can affect the thermal performance of the energy pile, as well as its bearing capacity [,]. The study of thermally induced moisture movement is crucial for effectively addressing these thermal geotechnical problems. This understanding can improve the design of more resilient infrastructures and energy systems that can better adapt to environmental thermal changes.
Thermally induced soil water movement in unsaturated soils is a complex process involving various components in both the vapor and liquid phases governed by different physical laws [,]. Soil vapor pressure increases with the increase in temperature. Water molecules in the vapor diffuse from a warmer region towards a lower temperature region in the direction of the decreasing temperature gradient. This vapor diffusion process is generally governed by Fick’s first law of diffusion [,,]. The vapor condenses to liquid water in the cooler temperature region and creates an additional difference in the soil moisture potential, contributing to the liquid moisture flow. The liquid moisture flow caused by the temperature gradient is more complex and is governed by several physical phenomena, such as thermo-self-diffusion, thermos-osmotic flow in fine-textured soil, and thermocapillary film flow []. The net liquid moisture flow is a combination of all the above liquid flow phenomena. The most dominant liquid moisture flow is the viscous capillary flow caused by a net differential in soil suction. The dynamic balance of the vapor and liquid water flow determines the net moisture movement in the soil, or whether it becomes dry or wet [,,].
Thermally induced moisture migration in unsaturated soil is a complex process influenced by several factors, including temperature gradient, soil type, moisture content, and gravitational effects [,,,,,]. Bouyoucos [] used a closed soil column to measure both heat flux and moisture for several soils at different moisture contents and temperature gradients. The researcher concluded that the thermally induced moisture flux was influenced by the laws of surface tension and the viscosity of water in the soil and were maximized at an optimum moisture content. This optimum moisture content was defined as at the point at which water transfer from warmer to colder parts is most efficient under a constant thermal gradient [,]. The findings are corroborated by various subsequent researchers [,,,,,]. They determined that the quantity of water migrating from warm to cool regions was mainly influenced by the initial moisture content and magnitude of the temperature gradients. Wang and Su [] tested thermally induced moisture flow in loess soils and found that a higher gradient and a lower soil density cause more pronounced moisture migration. When the initial moisture content is close to dry or near saturation, the thermally induced moisture increase is small. However, maximum thermally induced moisture flow was observed in soils with a moderate initial moisture content. Hedayati-Dezfooli [] also determined that the temperature gradient is the primary factor causing moisture migration. It was found that a significant moisture migration was observed at a temperature difference of roughly 65 °C between the top and bottom plates. Dang [] observed that coarser soils could not hold pore water, and they experienced more significant moisture movements than did fine and medium soils. Faizal et al. [] remarked that changes in volumetric water content continued to fluctuate in a time-dependent, nonlinear, and slower manner after the fluctuations in soil temperature had settled, and soil temperatures and volumetric water content increased the most in the areas closest to the heat source. Recently, Kaneza et al. [] determined that unsaturated sand with a high moisture content achieved thermal equilibrium faster than samples with a lower moisture content. The researchers also noticed that gravity has an impact on the moisture movement in the soil, depending on the direction of the temperature gradient: when the bottom of the soil was heated, and the top cooled, less pore water moved away from the heated end, and the increased thermal conductivity affected the temperature near that end, resulting in a higher steady-state temperature.
Although many studies have been conducted analyzing thermally induced moisture flow, it is still challenging to accurately measure and predict the coupled moisture–heat flow process in unsaturated soils, particularly sandy soils, due to low moisture migration and temperature effects on soil moisture measurement. In this study, a silty sand at various initial moisture contents was tested in a heat cell at a constant temperature gradient. The heat cell was equipped with heat flux, thermocouples, thermal conductivity, and moisture sensors to monitor the thermal and moisture properties under a controlled 1-D temperature gradient. The moisture sensors were calibrated for moisture measurement with the test soil at room temperature; the temperature effect on the soil moisture sensor was also evaluated with the developed heat cell. This research brings new insight to the analysis of unsaturated soil behavior.
2. Materials and Methods
2.1. Soil Heating Test Cell
A fabricated soil heating test cell, originally developed by Kaneza et al. [], was modified with additional sensors for conducting heating test on the soil. The modified heating cell, which consists of two concentric acrylic cylinders with a height of 10.16 cm and a wall thickness of 0.635 cm, with inside diameters of 8.89 cm and 20.96 cm, respectively, is shown in Figure 1 and Figure 2. Two heat exchanger systems, consisting of copper plates and supporting rings, are placed at the top and bottom of the heating cell. The heat exchanger plates are 29.21 cm in diameter and 2.54 cm thick, with an inside spiral channel of 0.65 cm × 0.65 cm, extending up to a radius of 22.23 cm. The inner and outer diameters of the support rings are 22.23 cm and 29.21 cm, respectively, while the copper plates have a diameter of 29.21 cm and a thickness of 0.24 cm. Two O-rings were used to seal the outer column to the heat exchanger plates, and threaded rods were used to ensure a fixed soil heating system. The tubes, heat exchangers, and rings are made of clear cast acrylic. An illustration of the modified soil cell is provided in Figure 1. Via the inlet and outlet in the heat exchanger plates, warm and cold water is circulated from and to the temperature-controlled water bath (SD07R-20-A11B from PolyScience, Niles, IL, USA) to the heat exchangers. The features of the heat exchanger, including the water bath circulator and the engraved spiral channels with cross sections, are shown in Figure 3. To facilitate effective and uniform heat transfer from both the hot and cold ends, two copper plates are placed between the heat exchanger and the soil sample.
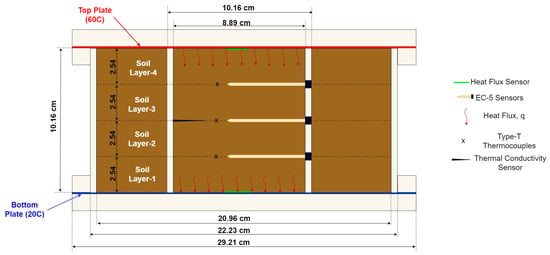
Figure 1.
Schematics of the soil heating cell setup.

Figure 2.
Photos of the heating cell during soil compaction placement.

Figure 3.
Heat exchanger plate with spiral channels (Left) and water circulator (Right).
The weight of the moist soil, based on the targeted density and the volume of the apparatus for each soil-layer, was obtained and equally distributed over the whole area of the testing apparatus, followed by the application of gentle compaction. The soil samples at different moisture contents were compacted on four layers of equal thickness for ease of compaction and sensor installation. The heat flux sensors were closely placed at the middle of the top and bottom copper plates and fixed at these position with the aid of tape at four corners of the heat flux sensors. The soil was compacted and slightly raised in the middle section to ensure proper contact of the heat flux sensor with the soil and the top copper plate. The remainder of the sensors were directly embedded in the soil sample; thus, had proper contact with the soil particles.
2.2. Test Sand
The test sand was collected from the riverbank of a bridge construction site in Benbrook, Texas, USA. A series of geotechnical tests were performed on the Benbrook sand, namely the wet sieve analysis [], dry sieve analysis [], hydrometer analysis [], the Atterberg limits tests (liquid limit, LL, and plastic limit, PL [,], and the specific gravity (Gs) test []. The sieve analyses and hydrometer analyses established the particle size curves of the soil. The resulting soil index properties, including the percentage of particle sizes and specific gravity, are summarized in Table 1. The Benbrook sand is classified as silty sand (SM), with 35% non-plastic fine particles. The maximum dry density was determined to be 18.3 kN/m3 (1.865 g/cm3) at an optimum moisture of 12.3% (w/w) using the Standard Proctor Test.

Table 1.
Particle size analysis and soil properties.
The pressure plate and filter paper methods were adopted to measure low and high suction, respectively, to obtain the SWCC curve, followed by the determination of the best curve fitting to find the parameters for the van Genuchten model. The silty sand was compacted at 95% of the maximum dry density () and the optimum moisture content () determined from the standard proctor test to prepare the soil specimen for the proposed lab testing. The particle size distribution and standard proctor compaction curve are presented in Figure 4 and Figure 5 respectively. The best-fit SWCC curve is illustrated in Figure 6. Ultimately, the residual and saturated volumetric moisture content ( were estimated, and the van Genuchten’s empirical parameters were determined. The residual and saturated volumetric moisture content (θr and θs) of 0.024 and 0.300 m3/m3 were estimated, and the van Genuchten empirical parameters of α = 4.527 m−1, n = 1.246, and m = 0.197 were determined.
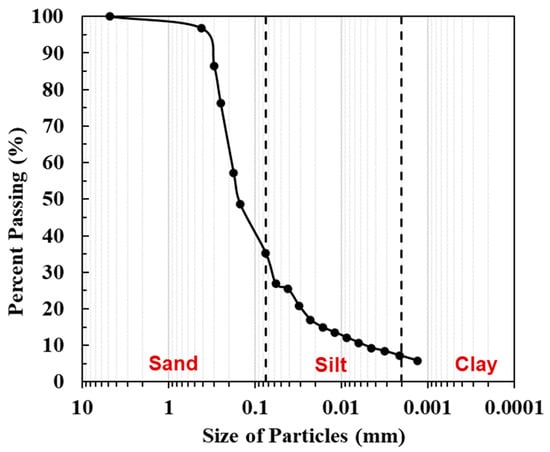
Figure 4.
Soil particle size distribution curves of the silty sand.
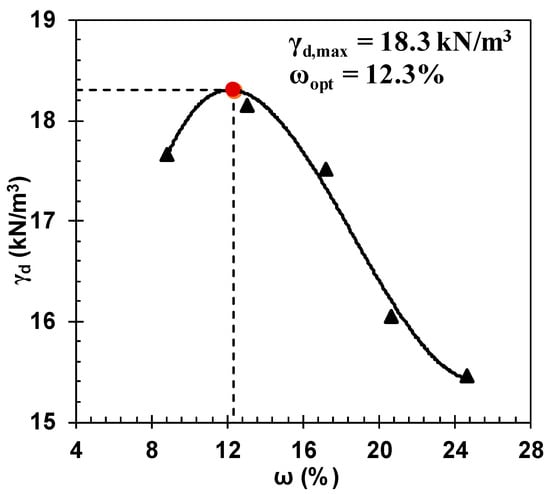
Figure 5.
Soil compaction curve.
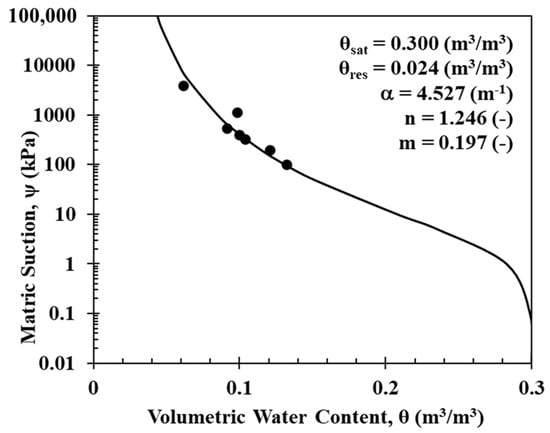
Figure 6.
Soil water retention characteristics of the silty sand.
2.3. Sensors and Calibration
Temperature, moisture content, thermal conductivity, and heat flux measurements were obtained during the heating cell test using T-type thermocouples from Omega Engineering Inc., Norwalk, CT, USA, ECH2O EC-5 from Meter Group, Washington, DC, USA, KD2 Pro (KS-1) from Meter Group, Washington, USA, TEMPOS SH-3 Sensor from Meter Group, and HFS-5 from Omega Engineering Inc., Connecticut, USA, respectively. Two Omega HFS heat flux sensors, 34 mm 27 mm 0.36 mm, were attached to the top and bottom copper plates, respectively, to measure the temperature of the respective plates and the heat flux. A KD-2 Pro KS-1 single probe sensor, 60 mm in length and 1.27 mm in diameter, was installed at the middle height of the soil, and the thermocouples and moisture sensors were installed at 2.5 cm, 5.0 cm, and 7.5 cm from the bottom heat exchanger plate. The arrangement of the sensors is presented in the schematics and lab-test configuration in Figure 1 and Figure 2, respectively.
The EC-5 sensors, with an overall dimension of 89 mm length, 18 mm wide, and 7 mm thick and a probe length of 50 mm, measure the soil dielectric permittivity of the soil, which is affected by mineralogy, texture, density, salinity, moisture content, and soil temperature [,]. Sensor-specific calibration must be performed to obtain the accurate soil moisture for sandy soil, since the effect of soil properties on EC-5 sensor readings is more pronounced []. The guidelines provided by Meter Group Inc., Washington, DC, USA have been followed for calibration tests to increase the accuracy of the EC-5 sensors to the ±1–2% range. Three EC-5 sensors were calibrated to the measure volumetric moisture content at room temperature. Soil samples were prepared at the same target gravimetric water content and dry density to calibrate the EC-5 moisture sensor, which was later used in the heating cell test. The VWC readings from the EC-5 sensor were recorded over a 1 h period at the mean room temperature of 21.69 °C, and the average readings were captured for calibration with the configuration as shown in Figure 7. Figure 8 presents the EC-5 sensor average readings vs. the oven-drying moisture content, and Table 2 explains the linear fitting equations for the EC-5 VWC correction at room temperature. The developed calibration equations show a close match between the EC-5 VWC and the correct VWC based on oven drying.
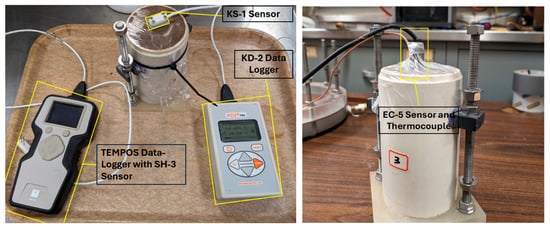
Figure 7.
Setup for thermal conductivity (Left) and EC-5 VWC (Right) measurement at room temperature.
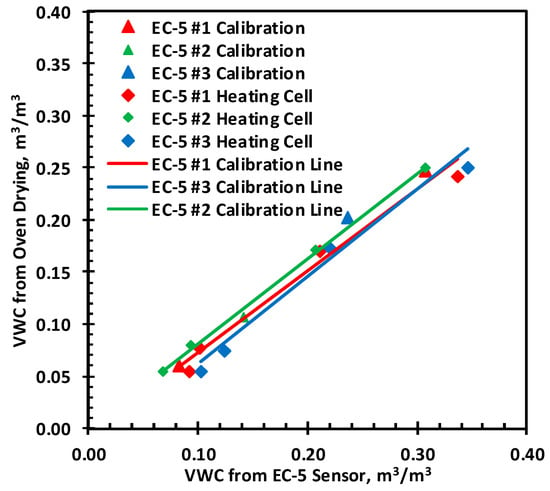
Figure 8.
VWC readings for EC-5 sensor.

Table 2.
VWC calibration for sensors.
The moisture measurement obtained using the EC-5 capacitance sensor is affected by temperature, as the dielectric permittivity of the soil is also affected by temperature [,]. Therefore, the temperature effect on EC-5 was also calibrated using the heat cell. Two heating cell tests were performed to evaluate the effect of temperature on EC-5. In the first heating cell test, the soil was prepared at a VMC of =0.077 m3/m3, and three EC-5 sensors were used to capture its moisture readings, as shown in Figure 1. Two thermocouples were placed in the middle of the soil layers to record the soil temperature. The top and bottom heating plates were supplied with hot water of the same temperature and maintained for at least 6 h until a steady-state temperature was reached. The temperature was increased from 20 °C to 55 °C at an increment of 5 °C. The average temperature and VWC reading over an hour during the steady state were used for the calibration. The first temperature calibration test is shown in Figure 9, exhibiting no significant sensor dependency. Therefore, in the second heating cell test, three soil layers with different target moisture contents (0.055 m3/m3, 0.172 m3/m3, and 0.249 m3/m3) were prepared and separated with a plastic sheet between each layer to calibrate the three sensors simultaneously at different moisture contents.
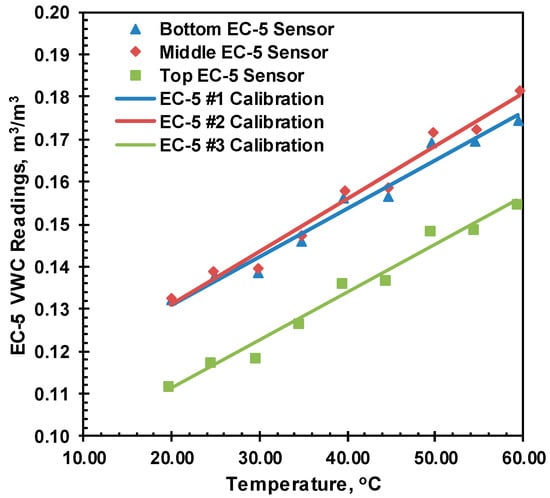
Figure 9.
Temperature correction for EC-5 sensor for VWC = 0.077 m3/m3, dry density.
Individual temperature corrections for each sensor at each moisture content were proposed; however, the correction slopes for all EC-5 sensors were very close to each other, and single correction slopes were used for all sensors at a specific moisture content. The temperature calibration chart and the table for the same moisture content from different sensors are presented in Figure 9. The calibration results for the remaining volumetric moisture contents are presented in Figure 10, along with the calibration chart in Table 3.
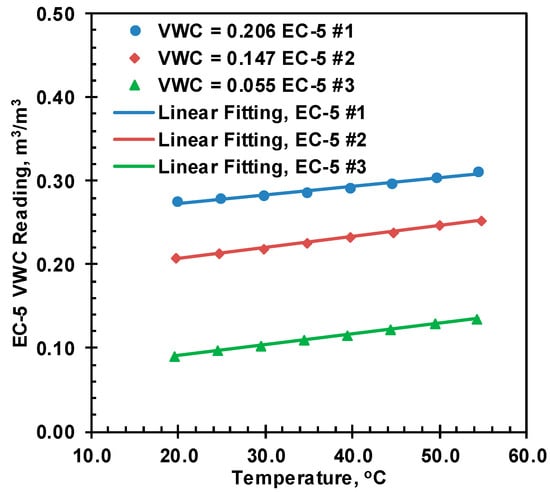
Figure 10.
Temperature correction for VWC 0.055, 0.147, and 0.206.

Table 3.
Temperature dependency of sensors.
2.4. Thermal Conductivity of Compacted Soil Samples
In this study, two thermal conductivity probes, KD-2 Pro (KS-1) and TEMPOS SH-3, were used for thermal conductivity measurement. KS-1 is a single needle sensor with a mean read time of one minute; and SH-3 is a dual-probe sensor, 30 mm in length, with 6 mm spacing, and a 1.3 mm diameter, with a mean read time of two minutes; however, both sensors have the same thermal conductivity measurement range up to 2.0 W/(m·K). The initial thermal conductivity of the soil was measured with a TEMPOS SH-3 sensor. The KS-1 was used to monitor the thermal conductivity in the heating cell. TEMPOS SH-3 was used for the initial thermal conductivity reading of the heating cell soil before the heating test. A noticeable difference was observed between the SH-3 and KS-1 sensors. Therefore, the thermal conductivity of the compacted soil at different moisture contents was measured with both sensors for comparison.
The thermal conductivity of the soil changes with moisture content []. A KD-2 Pro (KS-1) was utilized to monitor the thermal conductivity of the compacted soil samples at room temperature, with varying moisture contents and relatively constant dry density. The compacted soil samples were placed in the moisture equilibrium room for more than 12 h to facilitate further moisture equilibrium before measuring the thermal properties. Figure 11 and Figure 12 represents the variation in thermal conductivity measured for the same soil using the KD-2 Pro and TEMPOS sensors, and the 1:1 line in Figure 12 represents the line of perfect agreement for both sensors.
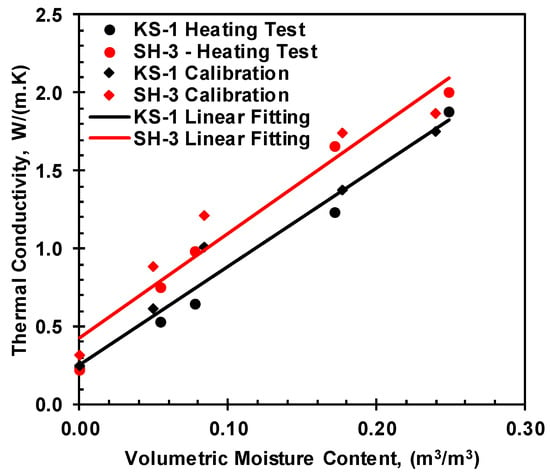
Figure 11.
Comparison of the two thermal conductivity sensors.
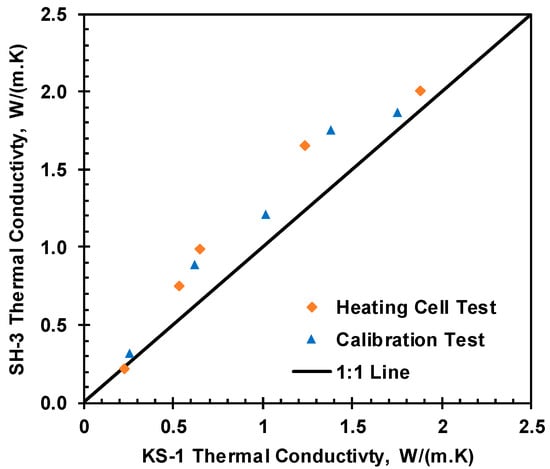
Figure 12.
Thermal conductivity comparison of KS-1 and SH-3 sensors.
2.5. Soil Heating Tests
A series of soil heating tests were performed in the heating cell, where the soil was tested under different initial moisture contents at the same temperature gradient to measure the change in soil moisture content, temperature profile, and thermal conductivity of the soil. The test chamber’s dual cell design and insulation with fiberglass ensure the 1-D heat transfer of the tested soil specimen in the inner soil column []. Three EC-5 sensors and three thermocouples (TCs) were used to measure water content and temperature variations during the heating process. The testing device, its dimensions, and all its main features are detailed in the work of [], and the measuring devices are illustrated in Figure 1.
Moist soil samples with various target moisture contents and a constant target dry density were prepared and placed in a moisture room for 24 h to achieve moisture equilibrium. A constant target dry density of 1.6 g/cm was selected to represent about 86% of compaction, which can be achieved at all selected moisture content levels. The prepared moist soil sample was compacted in four layers, with each layer thickness measuring 2.54 cm, for sensor installation and uniform compaction. Proper care was taken to compact the soil around the sensors to achieve uniform compaction without damaging the sensors. Five soil samples, including dry soil with a consistent dry density, were prepared, whose geotechnical and thermal properties are presented in Table 4. The compacted soil sample in the heating cell setup was maintained at room temperature for 24 h to facilitate further moisture equilibrium. The temperature-controlled water baths were then initiated, with the temperature of the top and bottom heating plates set to 60 °C and 20 °C, respectively. The volumetric moisture, temperature, thermal conductivity, and heat flux readings were recorded during the heating test until moisture equilibrium was reached. Two steady-state types were encountered during the heating test: temperature equilibrium and moisture equilibrium. The temperature and moisture equilibrium reached the steady state during the heating cell test when the thermocouple and ECH2O EC-5 sensor’s respective readings, temperature, and VWC, did not differ by more than 0.1 °C and 0.001 m3/m3 at an hourly interval. The test was terminated when the soil sample reached moisture equilibrium during the heating cell test. Table 5 indicates the time required for the test to attain a steady state, the moisture loss at the top, and the initial and steady-state thermal conductivity. Also, the onset of the steady state for the temperature and moisture plots is marked with arrows in the respective plots. The recorded soil heating test data can be found can be found in the Supplementary Materials.

Table 4.
1-D Heating test regarding the silty sand in the heating cell.

Table 5.
Heating cell regarding the test steady-state time and the changed soil parameter.
3. Results and Discussions
3.1. Temperature Response
The recorded temperature variations for specimens of different moisture contents are shown in Figure 13a–e represent the soil with initial volumetric moistures of 0.000, 0.055, 0.078, 0.172, and 0.249 m3/m3, respectively. The temperature at the hot end is slightly less than 60 °C, and that of the cold plate is slightly higher than 20 °C, which can be attributed to the temperature loss from the top and bottom copper plates, as well as imperfect contact between the copper plates and the soil column. For all moisture contents, the temperature reached equilibrium after 2000 min. The temperature readings of 0.055 m3/m3 and 0.078 m3/m3 showed a higher peak, which slowly decreased before reaching thermal equilibrium. The decrease in temperature after the peak is caused by moisture migration induced by the temperature gradient for all moisture soils. However, for the initial volumetric moisture of 0.172 m3/m3 and 0.249 m3/m3, no significant peak was observed during the heating test, which can be correlated to lower moisture migration. Figure 14 presents the temperature profile at different time steps, including the steady state. The steady-state temperature profile of the dry soil is almost linear, indicating a 1-D temperature gradient, whereas the soil samples with moisture content show concavity in the temperature profile. A linear temperature profile at a 1-D heat transfer indicates the uniform thermal properties of the dry soil. On the contrary, a concaved temperature profile indicates variations in thermal conductivity along the temperature gradient as the result of moisture migration.
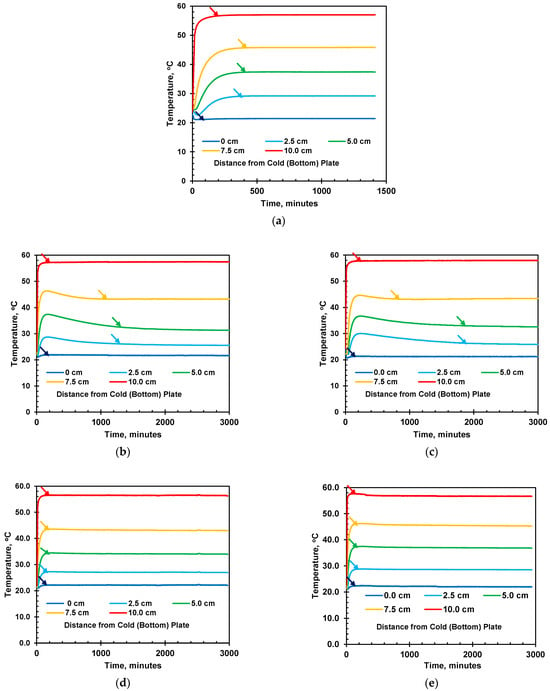
Figure 13.
Temperature variations with time for (a) VWC = 0.000, (b) VWC = 0.055, (c) VWC = 0.078, (d) VWC = 0.172, and (e) VWC = 0.249 m3/m3.
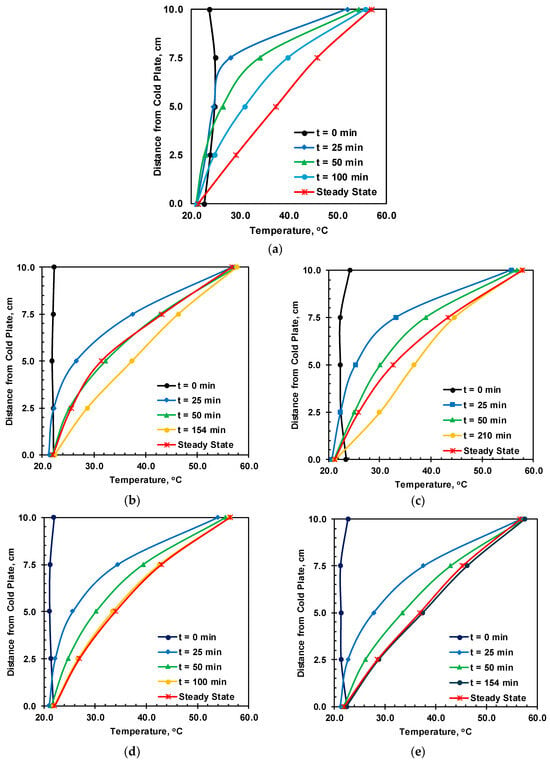
Figure 14.
Temperature profile during different stages of the heating test for (a) 0.000, (b) 0.055, (c) 0.078, (d) 0.172, and (e) 0.249 m3/m3.
3.2. Moisture Movement
The raw EC-5 moisture reading in the heating cell test for the initial moisture content of 0.078 m3/m3 is presented in Figure 15 as an example representing all the tested specimens. The initial and final moisture contents at different cross-sections of the soil column represent the equivalent volumetric moisture content measured by the oven-drying method. The EC-5 sensor determines the volumetric water content by measuring the dielectric constant of the soil using capacitance and frequency domain technology at a 70-MHz frequency to minimize salinity and textural effects. The sensor can only determine the liquid unbound water in the soil. The moisture vapor in the pore air has no noticeable impact on the dielectric constant of air (approximately 1) and is, therefore, negligible. The temperature impact on the EC-5 sensor, as shown in Figure 9 and Figure 10, is attributed to the release of bound water from the fine soil particle surfaces [].
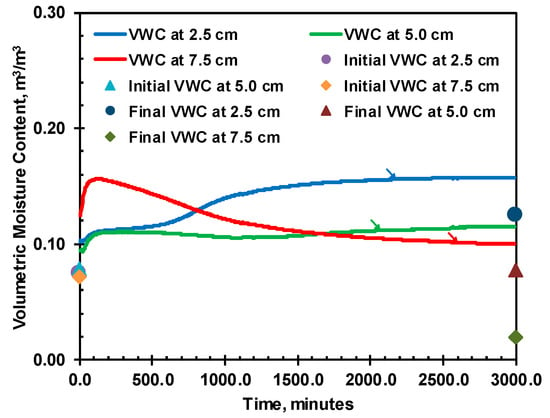
Figure 15.
Raw EC-5 VWC data for initial VWC of 0.078 m3/m3.
The first sharp rise in EC-5 VWC readings at the initial stage, as shown in Figure 15, directly corresponds to the thermal effect on the EC-5 moisture readings. Thus, the VWC readings were first corrected for temperature based on the raw reading and temperature measured by the thermocouple using Equation (5) for 0.078 m3/m3. After the temperature correction, the moisture increase before the peak was close to zero, indicating that the temperature effect was correct, with nearly no moisture movement during this initial heating stage. Secondly, the temperature-corrected moisture content was corrected for the oven-drying moisture content measured before and after the heating cell tests, using correction Equations (1)–(3), depending on the sensor identification. The corrected VWC during the heating cell test is shown in Figure 16b, where the corrected VWC closely matches the final moisture obtained from oven drying. Similar moisture correction steps were applied to the moisture content data for soils of other moisture contents, and the corrected readings, along with initial and final oven drying VWC, are presented in Figure 16.
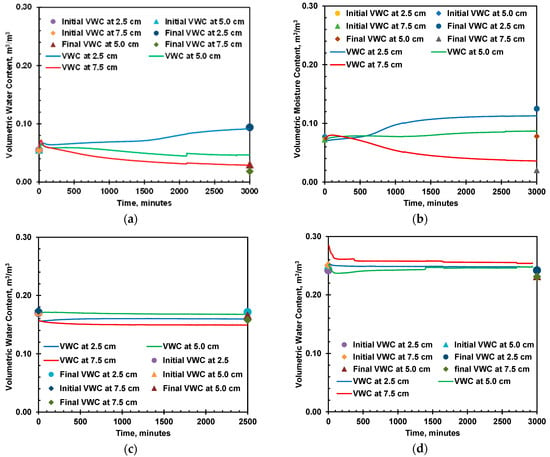
Figure 16.
Soil moisture variation with time for initial VWC of (a) 0.055, (b) 0.078, (c) 0.172, and (d) 0.249 m3/m3.
The moisture variations in the soil column during the heating cell test for all the tested specimens are shown in Figure 16, which portrays the moisture migration during the heating cell test for initial volumetric moisture contents of 0.055, 0.078, 0.172, and 0.249 m3/m3 in (a), (b), (c), and (d), respectively. The graph represents migration of the pore water from hot region to the colder region, i.e., from the top (hot) plate toward the bottom (colder) plate. The initial and final volumetric moisture contents in different layers, based on the oven-drying method, are also presented in the graph. The corrected volumetric moisture content closely matches the volumetric moisture reading from the EC-5 sensor. The soil heating test reached the steady state at 2100, 2600, 1000, and 750 min for 0.055, 0.078, 0.172, and 0.249 m3/m3, respectively. Figure 17 shows the moisture profile of the soil column at different depths during steady state. A very large moisture migration has occurred for the initial moisture contents of 0.055 m3/m3 and 0.078 m3/m3. However, a very small moisture movement has occurred for an initial moisture content of 0.172 m3/m3 and 0.249 m3/m3. The interaction between temperature and suction gradients can explain the variations in moisture transport. Temperature gradients primarily induce moisture movement through the vapor phase, whereas suction gradients govern liquid-phase flow. Higher soil suction levels intensify the effects of temperature on capillary action, thereby increasing moisture flux. According to Taylor and Cavazza [], under non-isothermal conditions, moisture predominantly migrates in the vapor phase. Figure 6 depicts the soil–water characteristic curve, illustrating suction levels of 19,000 kPa and 2100 kPa for initial moisture contents of 0.055 m3/m3 and 0.078 m3/m3, respectively. Conversely, moisture contents of 0.172 m3/m3 and 0.249 m3/m3 exhibit significantly lower suction levels at 28 kPa and 3 kPa, respectively. This observation shows the dominance of vapor-phase movement in unsaturated soils, where higher initial moisture content correlates with a reduced vapor phase. Consequently, moisture migration is less pronounced under high initial moisture conditions.
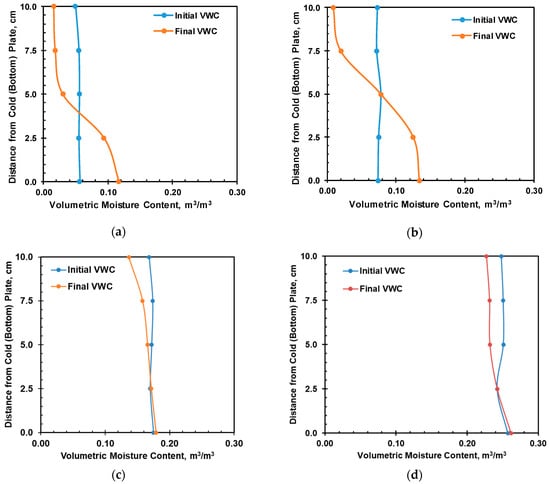
Figure 17.
Initial and steady-state moisture profile from oven drying for initial moisture content of (a) 0.055, (b) 0.078, (c) 0.172, and (d) 0.249 m3/m3.
3.3. Thermal Critical Moisture Content
The maximum reduction or increase in the volumetric moisture in each tested soil specimen occurred at the top and bottom of the soil column after the moisture equilibrium was reached during the heating test. Figure 18a,b represent the volumetric moisture loss and gain at the hot and cold end of the soil columns at the conclusion of the heating test for each tested initial moisture content. Among all the tested soil specimens, the maximum moisture migration of 0.067 m3/m3 and 0.064 m3/m3, which occurred at the hot and cold end of the soil column, are observed in the soil specimen with the initial moisture content of 0.078 m3/m3, which is the thermal critical moisture content for this sandy soil.
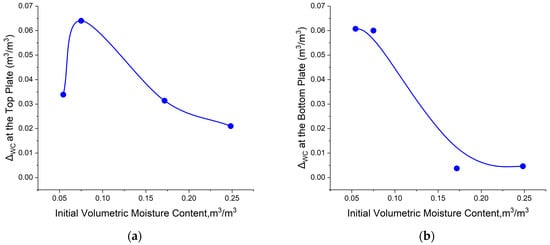
Figure 18.
Moisture change at (a) 10.0 cm and (b) 0.0 cm.
The critical moisture content studied here is the moisture content that marks a decline in the drying or diffusion rate in unsaturated soil. When the initial moisture content is below this critical value, the moisture migration increases with the initial moisture content but then starts to decrease beyond this point. Typically, water retention of soil decreases with rising temperature due to the reduced adhesion of pore water to the soil solid particles, allowing heat-induced pore water movement from the heated source to a cooler region. This soil behavior is due to a decline in the surface tension and viscosity of pore water as the temperature increases. However, once the critical moisture content is surpassed, the behavior of the soil deviates from the conventional patterns. This could be attributed to the transition from partial to full saturation, where capillary forces that are responsible for significant water displacement start to dissipate, restricting moisture movement in saturated soil. This contrast arises because unsaturated soils contain a vapor phase that allows for moisture migration through the temperature gradients, whereas in saturated soils, water is tightly bound to soil particles, limiting its movement. Sandy soils are more sensitive to the critical moisture content due to their water retention limitations and narrow ranges. This explains the notable decrease in the difference in VWC compared to the initial VWC observed at both the top and bottom regions of the soil specimen. It should be noted that a critical moisture content of 0.078 was observed, based on the limited data points presented in Figure 18. Additional tests on soil samples with a gravimetric moisture content between 0.035 and 0.1 can provide a more accurate critical moisture content value.
3.4. Thermal Conductivity and Heat Flux
The soil column is depicted in 1D, as shown in Figure 19. Heat transfer only occurs in the vertical direction, as described in the previous section. Temperature measurements were captured at each layer boundary (T1, T2, …, T5), and heat flux was measured at the top and bottom surfaces.
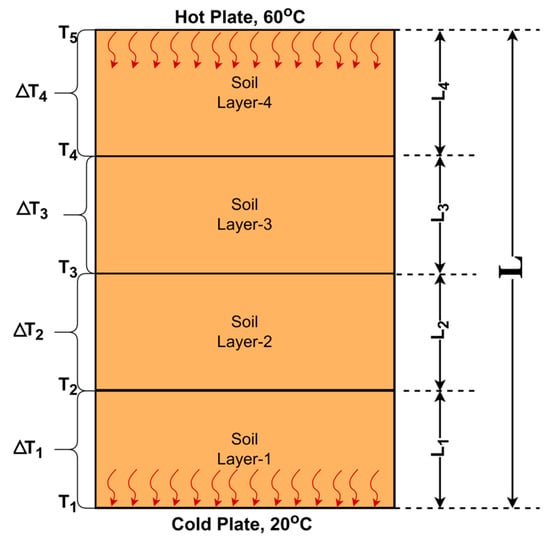
Figure 19.
Schematics for the thermal conductivity analyses.
Thermal conductivity (k) for the soil sample with heat flux a thickness of layer , represented by L1, L2, L3, and L4, and a temperature difference of is obtained by the following equation:
The negative sign represents the heat flux from the higher temperature to the lower temperature zone. The soil column is treated as four layered soils during the heating cell test to calculate the thermal conductivity of the soil layers, and the equivalent thermal conductivity of the entire soil column can be calculated based on the thermal resistance relationship for series connection, which can be given as follows:
where, and represents the length ratio ( and thermal conductivity of the soil layer, respectively.
The thermal conductivity of each soil layer and the equivalent thermal conductivity of the soil column were determined using Equations (8) and (9), as shown in Figure 20. The graph shows the thermal conductivity measured by the KS-1 sensor at the middle height of the soil column. At the steady state, thermal conductivity increases from top to bottom. Thermal conductivity profiles at the steady state for all soil specimens are plotted in Figure 21. The thermal conductivity measured by the KD-2 (KS-1) sensor, located at the interface of the second and third layers, is also presented in Figure 20. Thermal conductivity revealed by KS-1 first increases to a peak at about 200 min and decreases until reaching a steady state, reflecting the temperature effect on the rise before the peak and moisture migration after the peak, as shown in Figure 13b and Figure 15.
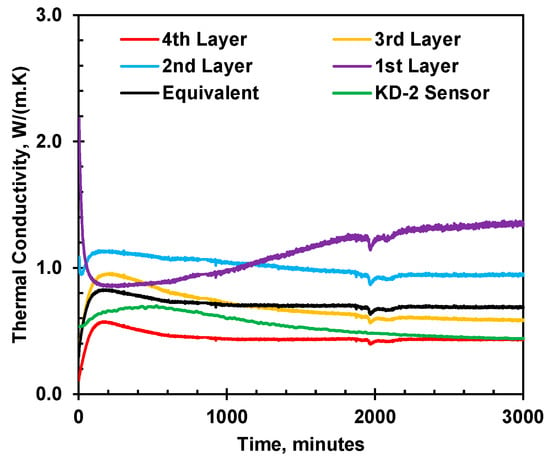
Figure 20.
Thermal conductivity at 0.055 m3/m3 moisture content during heating test.
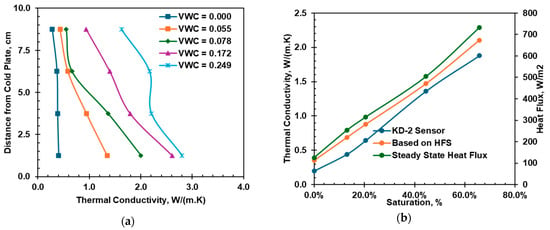
Figure 21.
(a) Thermal conductivity profile at steady state and (b) equivalent thermal conductivity and heat flux of the heating cell at steady state.
The thermal conductivity and heat flux of different initial moisture soil columns at a steady state during the heating cell test are shown in Figure 21. The thermal conductivity profile at equilibrium for different initial moisture contents is presented in Figure 21a, where the thermal conductivity increases with initial moisture content. Soil thermal conductivity increases with the increased distance to the heat source due to thermally induced moisture migration. Thermal conductivity increases with the increase in temperature for the silty sand at constant moisture; thermal conductivity decreases slightly with the increase in temperature for the dry silty sand. The variation in thermal conductivity along the height of the soil column is due to the combined effect of temperature and moisture content. Figure 21b contrasts the measured thermal conductivity from KS-1 sensor with the soil column’s equivalent thermal conductivity calculated based on steady state heat flux and thermocouple readings during heating test for varying initial saturation of the soil sample. The equivalent thermal conductivity generally shows a close relationship with the thermal conductivity measured by the KS-1 sensor. The measured heat flux increases with the increase in the initial degree of saturation.
4. Conclusions
This study investigated the dynamic interactions between temperature, moisture content, and thermal conductivity in an unsaturated silty sand under a constant thermal gradient of 400 °C/m. Using a comprehensive array of sensors—three EC-5 moisture sensors, two heat flux sensors, three thermocouples, and a KS-1 sensor—the experiment continuously monitored key parameters across various sections of the soil column during controlled heating. In addition to real-time measurements during heating, thermal conductivity at room temperature was compared using different sensors to evaluate their reliability and accuracy under varying soil conditions.
The investigations showed significant temperature sensitivity of the EC-5 moisture sensors within the tested range of 20 °C to 60 °C. Therefore, correction of the temperature effects is essential for accurately measuring thermally induced moisture migration during transient states. Moreover, steady-state vertical temperature profiles within moist specimens exhibited concave shapes, indicating variations in thermal conductivity attributed to thermally induced moisture flow dynamics. Specimens with low initial moisture content exhibited notable thermally induced moisture flow due to high suction levels. A critical thermal moisture content of 0.078 m3/m3 was identified, marking the point at which a maximum moisture loss of 0.067 m3/m3 occurred. Increased suction levels amplified the effect of temperature on moisture migration, leading to more significant vapor-phase movement in soils with lower initial moisture contents. However, beyond a critical moisture content, the soil behavior changed as capillary forces decreased, restricting moisture movement.
Furthermore, it was observed that thermal conductivity increased proportionally along with the distance from the heating source under steady-state conditions, illustrating the impact of moisture migration away from the heat source on soil thermal properties. Under a constant thermal gradient, both the equivalent thermal conductivity and the heat flux of the soil column increased with a higher initial moisture content. Discrepancies observed between equivalent thermal conductivity readings from heat flux measurements and those from the KD-2 Pro (KS-1) sensor suggest influences such as soil compaction heterogeneity, inadequate sensor–soil contact, and temperature-induced variations affecting measurement accuracy.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/geosciences14080207/s1.
Author Contributions
Conceptualization, X.Y., N.K.; methodology, N.K., X.Y., A.P.; validation, X.Y., N.K., A.P.; formal analysis, A.P., X.Y., N.K.; investigation, N.K., A.P., X.Y.; resources, X.Y., L.R.H.; data curation, A.P., X.Y., N.K.; writing—original draft preparation, N.K., X.Y., A.P.; writing—review and editing, X.Y., L.R.H.; visualization, A.P., X.Y., N.K.; supervision, L.R.H., X.Y.; project administration, X.Y., A.P.; funding acquisition, X.Y. All authors have read and agreed to the published version of the manuscript.
Funding
The funding support from the University of Texas at Arlington to the authors A., Pokhrel, and N.K. is acknowledged.
Data Availability Statement
Data in the text and in the Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Raudkivi, A.J.; van U’u, N. Soil Moisture Movement by Temperature Gradient. J. Geotech. Engrg. Div. 1976, 102, 1225–1244. [Google Scholar] [CrossRef]
- Oh, H. Thermal Resistivity Dry-Out Curves for Thirteen Sandy Soils. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2014. [Google Scholar]
- Oh, H.; Tinjum, J.M. Comparison of Two Laboratory Methods for Measuring Soil Critical Temperature. Geotech. Test. J. 2021, 44, 339–357. [Google Scholar] [CrossRef]
- Kaneza, N.; Wang, X.; Yu, X. Moisture Migration in Unsaturated Sands under Controlled Thsermal Gradient: A Heat Cell Study. Int. J. Geomech. 2024, 24, 04024060. [Google Scholar] [CrossRef]
- Abdel-Hadi, O.N.; Mitchell, J.K. Coupled Heat and Water Flows around Buried Cables. J. Geotech. Eng. Div. 1981, 107, 1461–1487. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Abdel-Hadi, O.N.; Chan, C.K.; Kao, T.C.; McMillan, J.C. Backfill Materials for Underground Power Cables. Phase II. Backfill Treatments, Heat and Moisture Flow Analyses, and Field Tests. Interim Report; No. EPRI-EL-1894; Department of Civil Engineering, California University: Berkeley, CA, USA, 1981. [Google Scholar]
- Verschaffel-Drefke, C.; Balzer, C.; Schedel, M.; Hinrichsen, V.; Sass, I. Experiment for validation of numerical models of coupled heat and mass transfer around energy cables. Vadose Zone J. 2022, 21, e20173. [Google Scholar] [CrossRef]
- Platts, A.B.; Cameron, D.A.; Ward, J. Improving the performance of Ground Coupled Heat Exchangers in unsaturated soils. Energy Build. 2015, 104, 323–335. [Google Scholar] [CrossRef]
- Akrouch, G.A.; Sánchez, M.; Briaud, J.-L. An experimental, analytical and numerical study on the thermal efficiency of energy piles in unsaturated soils. Comput. Geotech. 2016, 71, 207–220. [Google Scholar] [CrossRef]
- Lahoori, M.; Rosin-Paumier, S.; Jannot, Y.; Boukelia, A.; Masrouri, F. Thermal energy storage in embankments: Investigation of the thermal properties of an unsaturated compacted soil. E3S Web Conf. 2020, 205, 7011. [Google Scholar] [CrossRef]
- McCartney, J.S.; Jafari, N.H.; Hueckel, T.; Sánchez, M.; Vahedifard, F. Emerging Thermal Issues in Geotechnical Engineering. In Geotechnical Fundamentals for Addressing New World Challenges; Lu, N., Mitchell, J., Eds.; Springer Series in Geomechanics and Geoengineering; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Faizal, M.; Bouazza, A.; McCartney, J.S. Thermohydraulic Responses of Unsaturated Sand around a Model Energy Pile. J. Geotech. Geoenviron. Eng. 2021, 147, 04021105. [Google Scholar] [CrossRef]
- Pham, T.A.; Sutman, M. A Simplified Method for Bearing-Capacity Analysis of Energy Piles Integrating Temperature-Dependent Model of Soil–Water Characteristic Curve. J. Geotech. Geoenviron. Eng. 2023, 149, 04023080. [Google Scholar] [CrossRef]
- Başer, T.; McCartney, J.S.; Dong, Y.; Lu, N. Evaluation of Coupled Thermal and Hydraulic Relationships Used in Simulation of Thermally-Induced Water Flow in Unsaturated Soils. In PanAm Unsaturated Soils 2017; American Society of Civil Engineers: Reston, VA, USA, 2018. [Google Scholar] [CrossRef]
- Radhakrishna, H.S.; Lau, K.-C.; Crawford, A.M. Coupled Heat and Moisture Flow through Soils. J. Geotech. Engrg. 1984, 110, 1766–1784. [Google Scholar] [CrossRef]
- Bouyoucos, G.T. Effect of Temperature on the Movement of Water vapor and Capillary Moisture in Soils. J. Agric. Res. 1915, 5, 141–172. [Google Scholar]
- Crawford, C.B. Soil temperature and thermal properties of soils. Highw. Res. Board Spec. Rep. 1951, 2, 17–41. [Google Scholar]
- Gurr, C.G.; Marshall, T.J.; Hutton, J.T. Movement of Water in Soil due to a Temperature Gradient. Soil Sci. 1952, 74, 335–346. [Google Scholar] [CrossRef]
- Jackson, R.D.; Rose, D.A.; Penman, H.L. Circulation of Water in Soil under a Temperature Gradient. Nature 1965, 205, 314–316. [Google Scholar] [CrossRef]
- Kuzmak, J.M.; Sereda, P.J. The Mechanism by which Water Moves through a Porous Material Subjected to a Temperature Gradient, II: Salt Tracer and Streaming Potential to Defect Flow in the Liquid Phase. Soil Sci. 1957, 84, 419–422. [Google Scholar] [CrossRef]
- Kuzmak, J.M.; Sereda, P.J. The Mechanism by Which Water Moves through a Porous Material Subjected to a Temperature Gradient, I: Introduction of a Vapor Gap into a Saturated System. Soil Sci. 1957, 84, 291–299. [Google Scholar] [CrossRef]
- Maclean, D.J.; Gwatkin, P.M. Moisture Movements Occurring in Soil Due to the Existence of a Temperature Gradient; Road Research Laboratory: London, UK, 1953. [Google Scholar]
- Taylor, S.A.; Cavazza, L. The Movement of Soil Moisture in Response to Temperature Gradients. Soil Sci. Soc. Am. 1954, 18, 351–358. [Google Scholar] [CrossRef]
- Wang, T.-H.; Su, L.-J. Experimental Study on Moisture Migration in Unsaturated Loess under Effect of Temperature. J. Cold Reg. Eng. 2010, 24, 77–86. [Google Scholar] [CrossRef]
- Hedayati-Dezfooli, M. Development of an Experimental Apparatus for Studying High-Temperature Heat and Mass Transfer in Soils. Ph.D. Thesis, Toronto Metropolitan University, Toronto, ON, Canada, 2016. [Google Scholar]
- Dang, L. Experimental and Numerical Studies of Heat and Moisture Transfer in Soils at Various Conditions. Ph.D. Thesis, Toronto Metropolitan University, Toronto, ON, Canada, 2017. [Google Scholar]
- ASTM D1140-00; Standard Test Methods for Amount of Material in Soils Finer than the No. 200 (75-µm) Sieve. American Society for Testing and Materials: West Conshohocken, PA, USA, 2000.
- ASTM D6913M-17; Standard Test Methods for Particle-Size Distribution (Gradation) of Soils Using Sieve Analysis. American Society for Testing and Materials: West Conshohocken, PA, USA, 2017.
- ASTM D7928-21; Standard Test Method for Particle-Size Distribution (Gradation) of Fine-Grained Soils Using the Sedimentation (Hydrometer) Analysis 1. American Society for Testing and Materials: West Conshohocken, PA, USA, 2021.
- ASTM D4318-17e1; Standard Test Methods for Liquid Limit, Plastic Limit, and Plasticity Index of Soils 1. American Society for Testing and Materials: West Conshohocken, PA, USA, 2018. [CrossRef]
- Texas Department of Transportation. Test Procedure for Determining Plastic Limit of Soils; Texas Department of Transportation: Austin, TX, USA, 1999. [Google Scholar]
- ASTM D0854-14; Standard Test Methods for Specific Gravity of Soil Solids by Water Pycnometer 1. American Society for Testing and Materials: West Conshohocken, PA, USA, 2014. [CrossRef]
- Campbell, C.S. Response of the ECH2O Soil Moisture Probe to Variation in Water Content, Soil Type, and Solution Electrical Conductivity; Application note; Decagon Devices Inc.: Washington, DC, USA, 2001. [Google Scholar]
- Cobos, D.; Campbell, C. Correcting Temperature Sensitivity of ECH2O Soil Moisture Sensors: Application Note; Decagon Devices: Pullman, WA, USA, 2013. [Google Scholar]
- Or, D.; Wraith, J.M. Temperature effects on soil bulk dielectric permittivity measured by time domain reflectometry: A physical model. Water Resour. Res. 1999, 35, 371–383. [Google Scholar] [CrossRef]
- Abu-Hamdeh, N.H.; Reeder, R.C. Soil thermal conductivity effects of density, moisture, salt concentration, and organic matter. Soil Sci. Soc. Am. J. 2000, 64, 1285–1290. [Google Scholar] [CrossRef]
- Kaneza, N. An Experimental Study of Coupled Thermo-Hydro Behavior in Unsaturated Soil. Master’s Thesis, University of Texas at Arlington, Arlington, TX, USA, 2020. [Google Scholar]
- Wraith, J.M.; Or, D. Temperature effects on soil bulk dielectric permittivity measured by time domain reflectometry: Experimental evidence and hypothesis development. Water Resour. Res. 1999, 35, 361–369. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).