Comparison of K-Means and Hierarchical Clustering Methods for Buffalo Milk Production Data
Simple Summary
Abstract
1. Introduction
2. Materials and Methods
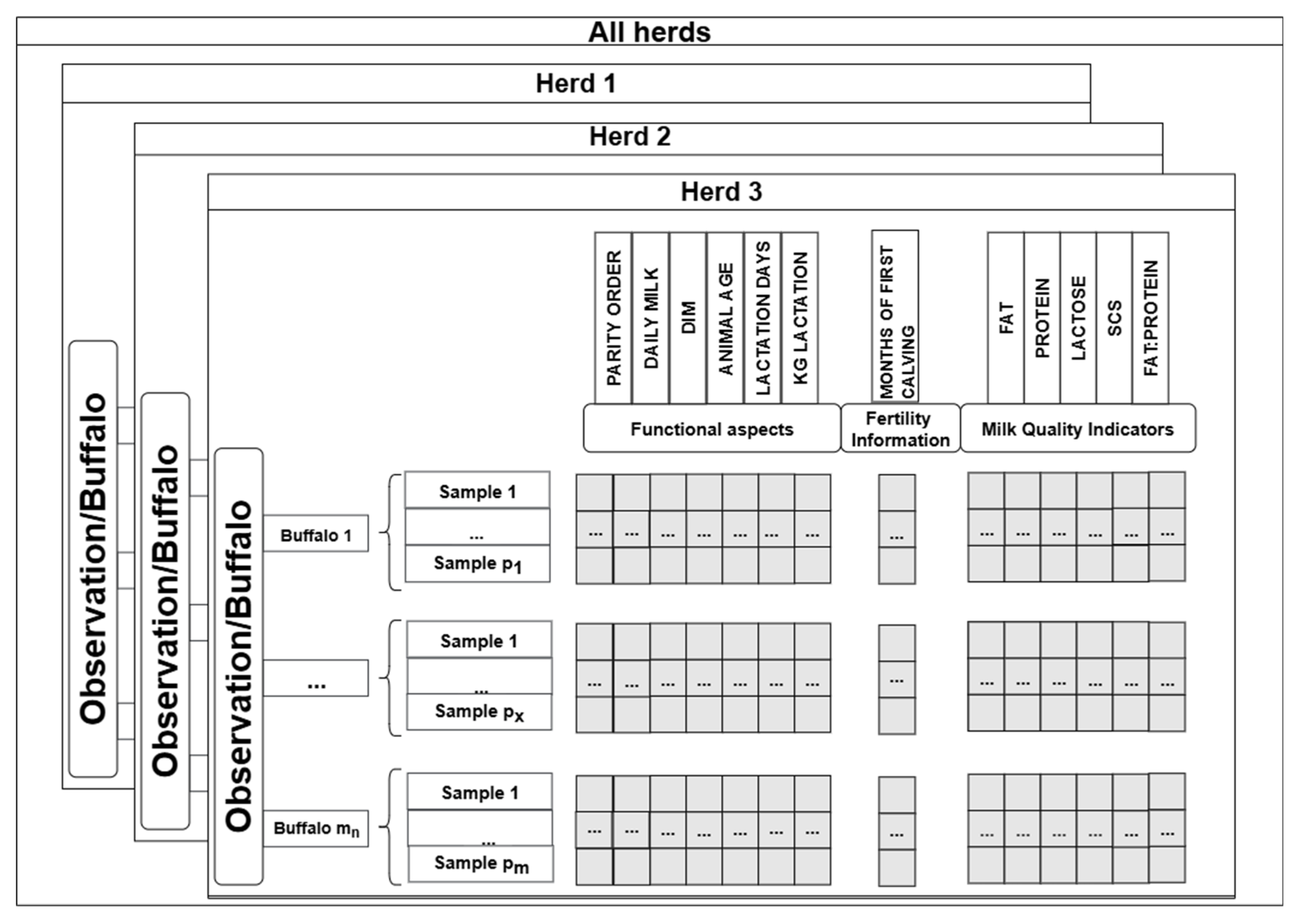
2.1. Data Description and Preprocessing
- Animal and milk yield characteristics: parity order, daily milk yield, days in milk (DIM), age, lactation length and total lactation milk yield;
- Reproduction information: age at first calving (month);
- Milk quality: fat, protein, lactose, SCS and the fat/protein ratio.
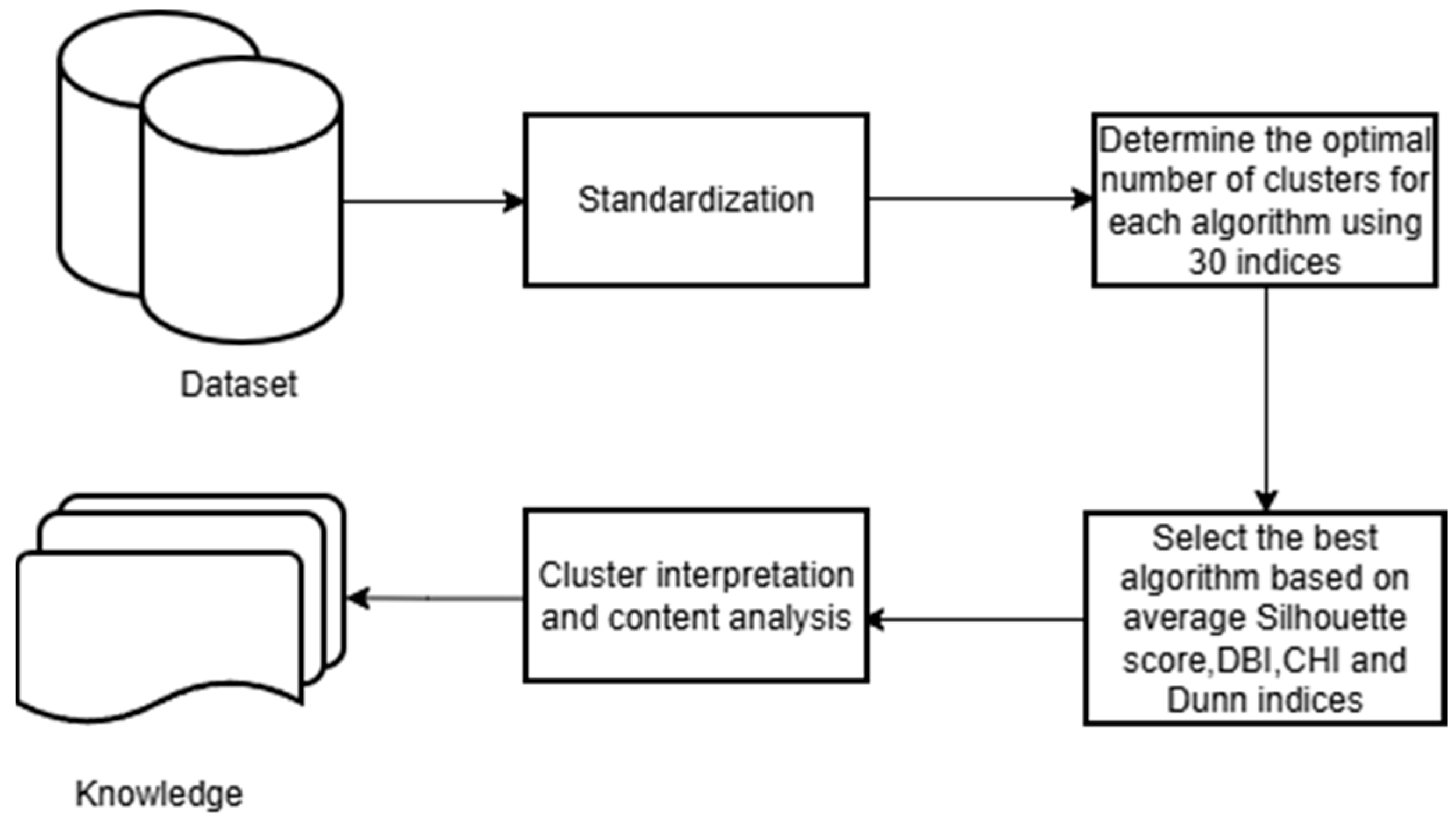
2.2. Cluster Analysis
2.3. Statistical Analysis and Cluster Exploration
3. Results
4. Discussion
4.1. Clustering Performance
4.2. Clustering Ability to Create Homogenous Groups
4.3. Practical Application
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gong, L.; Luo, L.; Gao, J.; Xiong, Y.; Chen, C.; Gan, H.; Song, H.; Morrone, S.; Dimauro, C.; Gambella, F.; et al. Industry 4.0 and Precision Livestock Farming (PLF): An up to Date Overview across Animal Productions. Sensors 2022, 22, 4319. [Google Scholar] [CrossRef]
- Peyraud, J.-L.; MacLeod, M. Future of EU Livestock: How to Contribute to a Sustainable Agricultural Sector? Final Report; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Trapanese, L.; Bifulco, G.; Calanni Macchio, A.; Aragona, F.; Purrone, S.; Campanile, G.; Salzano, A. Precision livestock farming applied to the dairy sector: 50 years of history with a text mining and topic analysis approach. Smart Agric. Technol. 2025, 10, 100827. [Google Scholar] [CrossRef]
- Pugliese, R.; Regondi, S.; Marini, R. Machine learning-based approach: Global trends, research directions, and regulatory standpoints. Data Sci. Manag. 2021, 4, 19–29. [Google Scholar] [CrossRef]
- Le Duc, T.; Leiva, R.G.; Casari, P.; Östberg, P.O. Machine learning methods for reliable resource provisioning in edge-cloud computing: A survey. ACM Comput. Surv. 2019, 52, 94. [Google Scholar] [CrossRef]
- Can Machine Learning Algorithms Perform Better than Multiple Linear Regression in Predicting Nitrogen Excretion from Lactating Dairy Cows|Scientific Reports. Available online: https://www.nature.com/articles/s41598-022-16490-y (accessed on 1 August 2025).
- Wang, J.; Bell, M.; Liu, X.; Liu, G. Machine-Learning Techniques Can Enhance Dairy Cow Estrus Detection Using Location and Acceleration Data. Animals 2020, 10, 1160. [Google Scholar] [CrossRef]
- Tremblay, M.; Kammer, M.; Lange, H.; Plattner, S.; Baumgartner, C.; Stegeman, J.A.; Duda, J.; Mansfeld, R.; Döpfer, D. Identifying poor metabolic adaptation during early lactation in dairy cows using cluster analysis. J. Dairy Sci. 2018, 101, 7311–7321. [Google Scholar] [CrossRef]
- Franceschini, S.; Grelet, C.; Leblois, J.; Gengler, N.; Soyeurt, H. Can unsupervised learning methods applied to milk recording big data provide new insights into dairy cow health? J. Dairy Sci. 2022, 105, 6760–6772. [Google Scholar] [CrossRef]
- Matera, R.; Pierro, F.; Santinello, M.; Iraci Fuintino, A.; Pacelli, G.; Norton, T.; Neglia, G. Precision livestock farming in buffalo species: A sustainable approach for the future. Smart Agric. Technol. 2025, 11, 101060. [Google Scholar] [CrossRef]
- Warner, D.; Vasseur, E.; Lefebvre, D.M.; Lacroix, R. A machine learning based decision aid for lameness in dairy herds using farm-based records. Comput. Electron. Agric. 2020, 169, 105193. [Google Scholar] [CrossRef]
- Costa, A.; Negrini, R.; De Marchi, M.; Campanile, G.; Neglia, G. Phenotypic Characterization of Milk Yield and Quality Traits in a Large Population of Water Buffaloes. Animals 2020, 10, 327. [Google Scholar] [CrossRef]
- Ali, A.K.A.; Shook, G.E. An Optimum Transformation for Somatic Cell Concentration in Milk1. J. Dairy Sci. 1980, 63, 487–490. [Google Scholar] [CrossRef]
- Brotzman, R.L.; Cook, N.B.; Nordlund, K.; Bennett, T.B.; Gomez Rivas, A.; Döpfer, D. Cluster analysis of Dairy Herd Improvement data to discover trends in performance characteristics in large Upper Midwest dairy herds. J. Dairy Sci. 2015, 98, 3059–3070. [Google Scholar] [CrossRef]
- Abreu, B.D.S.; Barbosa, S.B.P.; Silva, E.C.D.; Santoro, K.R.; Batista, Â.M.V.; Martinez, R.L.V. Principal component and cluster analyses to evaluate production and milk quality traits. Rev. Ciência Agronômica 2020, 51, e20196977. [Google Scholar] [CrossRef]
- Çelik, M.; Dadaşer-Çelik, F.; Dokuz, A.Ş. Anomaly detection in temperature data using DBSCAN algorithm. In Proceedings of the 2011 International Symposium on Innovations in Intelligent Systems and Applications, Istanbul, Turkey, 15–18 June 2011; pp. 91–95. [Google Scholar]
- Atif, M.; Farooq, M.; Abiad, M.; Shafiq, M. The least sample size essential for detecting changes in clustering solutions of streaming datasets. PLoS ONE 2024, 19, e0297355. [Google Scholar] [CrossRef]
- Charrad, M.; Ghazzali, N.; Boiteau, V.; Niknafs, A. NbClust: An R Package for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Wong, P.C. Unsupervised Machine Learning. In Computational Psychometrics: New Methodologies for a New Generation of Digital Learning and Assessment: With Examples in R and Python; von Davier, A.A., Mislevy, R.J., Hao, J., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 173–193. ISBN 978-3-030-74394-9. [Google Scholar]
- Lee, M.; Lee, S.; Park, J.; Seo, S. Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm. Animals 2020, 10, 1348. [Google Scholar] [CrossRef]
- Martin-Collado, D.; Byrne, T.J.; Amer, P.R.; Santos, B.F.S.; Axford, M.; Pryce, J.E. Analyzing the heterogeneity of farmers’ preferences for improvements in dairy cow traits using farmer typologies. J. Dairy Sci. 2015, 98, 4148–4161. [Google Scholar] [CrossRef]
- Khan, I.K.; Daud, H.B.; Zainuddin, N.B.; Sokkalingam, R.; Farooq, M.; Baig, M.E.; Ayub, G.; Zafar, M. Determining the optimal number of clusters by Enhanced Gap Statistic in K-mean algorithm. Egypt. Inform. J. 2024, 27, 100504. [Google Scholar] [CrossRef]
- Silvestre, A.M.; Martins, A.M.; Santos, V.A.; Ginja, M.M.; Colaço, J.A. Lactation curves for milk, fat and protein in dairy cows: A full approach. Livest. Sci. 2009, 122, 308–313. [Google Scholar] [CrossRef]
- Kirsanova, E.; Heringstad, B.; Lewandowska-Sabat, A.; Olsaker, I. Alternative subclinical mastitis traits for genetic evaluation in dairy cattle. J. Dairy Sci. 2019, 102, 5323–5329. [Google Scholar] [CrossRef]
- Luna-Palomera, C.; Domínguez-Viveros, J.; Aguilar-Palma, G.N.; Castillo-Rangel, F.; Sánchez-Dávila, F.; Macías-Cruz, U.; Luna-Palomera, C.; Domínguez-Viveros, J.; Aguilar-Palma, G.N.; Castillo-Rangel, F.; et al. Analysis of the Lactation Curve of Murrah Buffaloes with Mixed Non-Linear Models. Chil. J. Agric. Anim. Sci. 2021, 37, 200–208. [Google Scholar] [CrossRef]
- Gargiulo, J.I.; Garcia, S.C.; Hovey, R.C. Sources of variation underlying the production of lactose by dairy cows. J. Dairy Sci. 2025, 108, 4403–4421. [Google Scholar] [CrossRef]
- Alessio, D.; Velho, J.; Mcmanus, C.; Knob, D.; Vancin, F.; Antunes, G.; Busanello, M.; Carli, F.; Thaler-Neto, A. Lactose and its relationship with other milk constituents, somatic cell count, and total bacterial count. Livest. Sci. 2021, 252, 104678. [Google Scholar] [CrossRef]
- Cattaneo, L.; Piccioli-Cappelli, F.; Minuti, A.; Trevisi, E. Metabolic and physiological adaptations to first and second lactation in Holstein dairy cows. J. Dairy Sci. 2023, 106, 3559–3575. [Google Scholar] [CrossRef]
- Rebuli, K.B.; Ozella, L.; Vanneschi, L.; Giacobini, M. Multi-algorithm clustering analysis for characterizing cow productivity on automatic milking systems over lactation periods. Comput. Electron. Agric. 2023, 211, 108002. [Google Scholar] [CrossRef]
- Ghavi Hossein-Zadeh, N. Comparison of non-linear models to describe the lactation curves for milk yield and composition in buffaloes (Bubalus bubalis). Animal 2016, 10, 248–261. [Google Scholar] [CrossRef] [PubMed]
- Minervino, A.H.H.; Zava, M.; Vecchio, D.; Borghese, A. Bubalus bubalis: A Short Story. Front. Vet. Sci. 2020, 7, 570413. [Google Scholar] [CrossRef]
- Trapanese, L.; Bifulco, G.; Aragona, F.; GianMaria, P.; Pedota, G.; Pasquino, N.; Salzano, A. Explorative analysis of Saanen and Camosciata goats data through an unsupervised machine learning approach. In Proceedings of the 2024 International Workshop Measurements and Applications Inveterinary and Animal Sciences, Torino, Italy, 22–24 April 2024. [Google Scholar]
- Barrientos-Blanco, J.A.; White, H.; Shaver, R.D.; Cabrera, V.E. Graduate Student Literature Review: Considerations for nutritional grouping in dairy farms. J. Dairy Sci. 2022, 105, 2708–2717. [Google Scholar] [CrossRef]
- Kalantari, A.S.; Armentano, L.E.; Shaver, R.D.; Cabrera, V.E. Economic impact of nutritional grouping in dairy herds. J. Dairy Sci. 2016, 99, 1672–1692. [Google Scholar] [CrossRef]
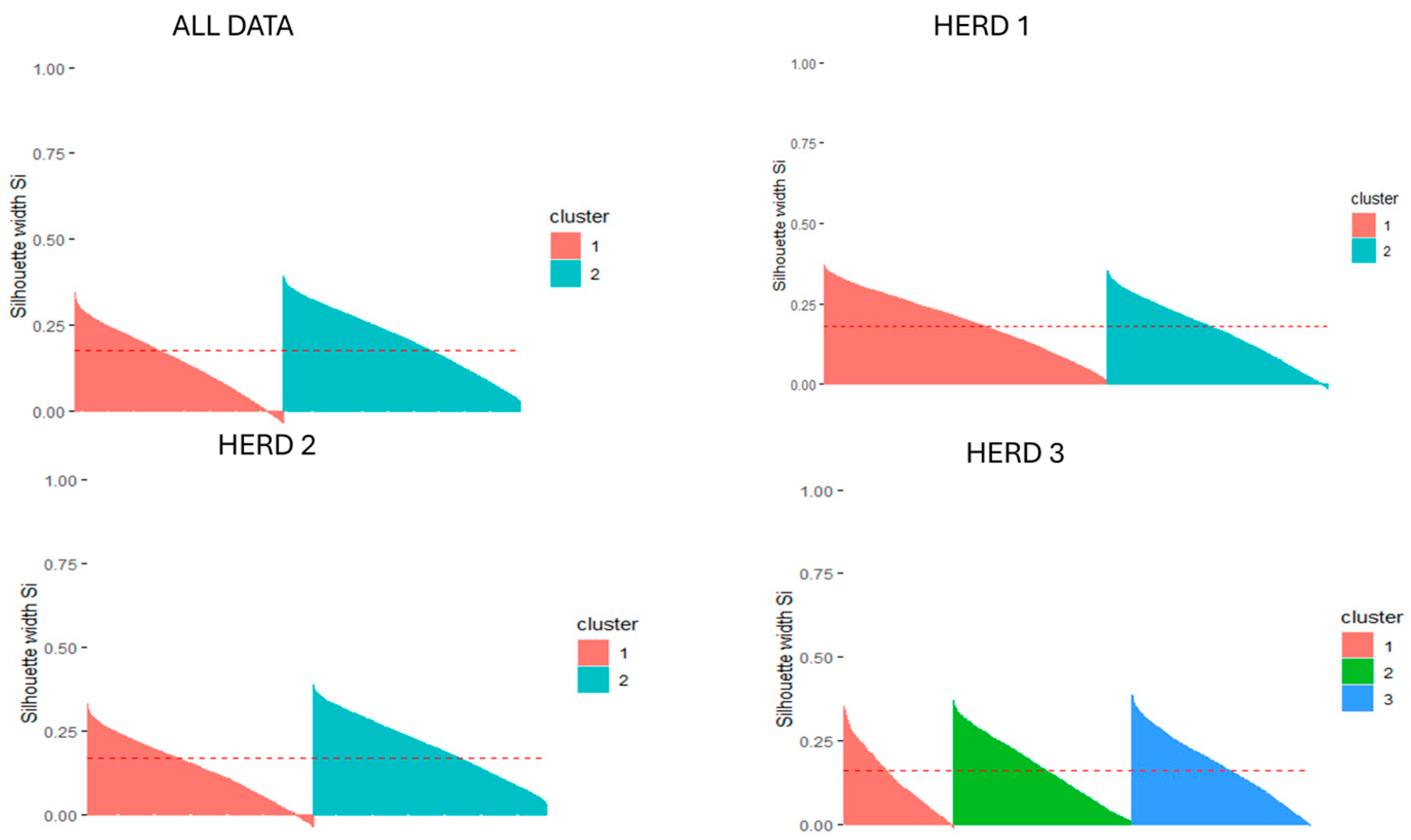
| Dataset | K-Means | Hierarchical | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| N of Clusters | Average Silhouette Score | DBI | CHI | Dunn | N of Clusters | Average Silhouette Score | DBI | CHI | Dunn | |
| Total dataset | 2 | 0.18 | 2.07 | 3877 | 0.0213 | 3 | 0.11 | 2.30 | 2109 | 0.0300 |
| Herd 1 | 2 | 0.18 | 2.08 | 1307 | 0.0272 | 3 | 0.11 | 2.50 | 992 | 0.0343 |
| Herd 2 | 2 | 0.17 | 2.16 | 1191 | 0.0298 | 3 | 0.10 | 2.29 | 729 | 0.0534 |
| Herd 3 | 3 | 0.18 | 2.05 | 1034 | 0.0241 | 3 | 0.12 | 2.11 | 951 | 0.0451 |
| Traits | Cluster 1 | Cluster 2 | p-Value |
|---|---|---|---|
| N. of samples | 7825 | 8877 | |
| Animal characteristics: | |||
| Parity order | 1.58 ± 0.77 | 1.68 ± 0.85 | <0.0001 |
| Primiparous (%) | 52.65 | 55.98 | |
| Days in milk (d) | 213 ± 70 | 89 ± 55 | <0.0001 |
| Lactation length (d) | 324 ± 75 | 293 ± 60 | <0.0001 |
| Age at first calving (mo) | 33 ± 5 | 34 ± 4 | NS |
| Age (y) | 4.18 ± 1.13 | 3.95 ± 1.17 | <0.0001 |
| Milk production and composition: | |||
| Lactation milk yield (kg) | 2476 ± 758 | 2638 ± 736 | <0.001 |
| Daily milk yield (kg/d) | 6.18 ± 2.40 | 10.89 ± 3.00 | <0.0001 |
| Fat (%) | 9.74 ± 1.18 | 7.47 ± 1.05 | <0.0001 |
| Protein (%) | 4.99 ± 0.36 | 4.53 ± 0.33 | <0.0001 |
| Fat: Protein | 1.96 ± 0.22 | 1.65 ± 0.23 | <0.0001 |
| Lactose (%) | 4.58 ± 0.37 | 4.86 ± 0.27 | <0.0001 |
| Somatic cell score | 4.16 ± 1.57 | 2.99 ± 1.54 | <0.0001 |
| Traits | Cluster 1 | Cluster 2 | p-Value |
|---|---|---|---|
| N. of samples | 2505 | 3223 | |
| Animal characteristics: | |||
| Parity order | 1.61 ± 0.77 | 1.59 ± 0.78 | NS |
| Primiparous (%) | 55.96 | 55.83 | |
| Days in milk (d) | 211.31 ± 61.57 | 86.94 ± 50.77 | <0.0001 |
| Lactation length (d) | 302.33 ± 59.42 | 283.57 ± 52.48 | <0.0001 |
| Age at first calving (mo) | 34.72 ± 2.91 | 34.67 ± 2.68 | NS |
| Age (y) | 4.20 ± 1.05 | 3.75 ± 0.96 | <0.0001 |
| Milk production and composition: | |||
| Lactation Milk yield (kg) | 3034 ± 692 | 3024 ± 655 | <0.001 |
| Daily milk yield (kg/d) | 8.19 ± 2.40 | 12.67 ± 2.75 | <0.0001 |
| Fat (%) | 9.44 ± 1.10 | 7.23 ± 1.03 | <0.0001 |
| Protein (%) | 4.90 ± 0.37 | 4.43 ± 0.32 | <0.0001 |
| Fat: Protein | 1.93 ± 0.20 | 1.64 ± 0.23 | <0.0001 |
| Lactose (%) | 4.64 ± 0.27 | 4.85 ± 0.27 | <0.0001 |
| Somatic cell score | 3.96 ± 1.33 | 3.08 ± 1.51 | <0.0001 |
| Traits | Cluster 1 | Cluster 2 | p-Value |
|---|---|---|---|
| Number of samples | 2741 | 2833 | |
| Animal characteristics: | |||
| Parity order | 1.55 ± 0.78 | 1.57 ± 0.80 | NS |
| Primiparous (%) | 57.03 | 56.49 | |
| Days in milk (d) | 229 ± 72 | 86.00 ± 54.63 | <0.0001 |
| Lactation length (d) | 352.90 ± 90.94 | 314.76 ± 83.22 | <0.0001 |
| Age at first calving (mo) | 32.10 ± 6.48 | 31.26 ± 4.83 | NS |
| Age (y) | 4.05 ± 1.22 | 3.60 ± 1.19 | <0.0001 |
| Milk production and composition: | |||
| Lactation Milk yield (kg) | 2214 ± 718 | 2107 ± 733 | <0.0001 |
| Daily milk yield (kg/d) | 4.78 ± 2.06 | 8.64 ± 2.80 | <0.0001 |
| Fat (%) | 10.08 ± 1.25 | 8.02 ± 1.10 | <0.0001 |
| Protein (%) | 5.02 ± 0.36 | 4.71 ± 0.31 | <0.0001 |
| Fat: Protein | 2.01 ± 0.23 | 1.71 ± 0.24 | <0.0001 |
| Lactose (%) | 4.49 ± 0.48 | 4.87 ± 0.27 | <0.0001 |
| Somatic cell score | 4.77 ± 1.62 | 3.51 ± 1.59 | <0.0001 |
| Traits | Cluster 1 | Cluster 2 | Cluster 3 | p-Value |
|---|---|---|---|---|
| Number of samples | 1270 | 2067 | 2063 | |
| Animal characteristics: | ||||
| Parity order | 2.89 ± 0.65 A | 1.31 ± 0.48 C | 1.45 ± 0.60 B | <0.0001 |
| Primiparous (%) | 0 | 60.56 | 56.74 | |
| Days in milk (d) | 122.37 ± 64.22 B | 84.04 ± 53.62 C | 219.95 ± 59.30 A | <0.001 |
| Lactation length (d) | 270.83 ± 37.84 C | 303.91 ± 48.30 B | 311.77 ± 49.80 A | <0.0001 |
| Age at first calving (mo) | 35.78 ± 3.39 | 37.17 ± 3.72 | 36.64 ± 3.57 | NS |
| Age (y) | 5.82 ± 0.82 A | 3.69 ± 0.73 C | 3.69 ± 0.73 B | <0.001 |
| Milk production and composition: | ||||
| Lactation Milk yield (kg) | 2556 ± 610 A | 2480 ± 539 B | 2441 ± 548 B | <0.0001 |
| Daily milk yield (kg/d) | 10.07 ± 3.06 A | 9.95 ± 2.44 A | 6.18 ± 1.97 B | <0.0001 |
| Fat (%) | 8.06 ± 1.15 B | 7.25 ± 1.01 C | 9.70 ± 1.16 A | <0.0001 |
| Protein (%) | 4.59 ± 0.35 B | 4.54 ± 0.33 C | 5.04 ± 0.34 A | <0.0001 |
| Fat/Protein | 1.76 ± 0.23 B | 1.60 ± 0.22 C | 1.93 ± 0.21 A | <0.0001 |
| Lactose (%) | 4.76 ± 0.31 B | 4.87 ± 0.26 A | 4.58 ± 0.28 C | <0.0001 |
| Somatic cell score | 3.18 ± 1.42 B | 2.36 ± 1.46 C | 3.55 ± 1.47 A | <0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trapanese, L.; Bifulco, G.; Santinello, M.; Pasquino, N.; Campanile, G.; Salzano, A. Comparison of K-Means and Hierarchical Clustering Methods for Buffalo Milk Production Data. Animals 2025, 15, 3246. https://doi.org/10.3390/ani15223246
Trapanese L, Bifulco G, Santinello M, Pasquino N, Campanile G, Salzano A. Comparison of K-Means and Hierarchical Clustering Methods for Buffalo Milk Production Data. Animals. 2025; 15(22):3246. https://doi.org/10.3390/ani15223246
Chicago/Turabian StyleTrapanese, Lucia, Giovanna Bifulco, Matteo Santinello, Nicola Pasquino, Giuseppe Campanile, and Angela Salzano. 2025. "Comparison of K-Means and Hierarchical Clustering Methods for Buffalo Milk Production Data" Animals 15, no. 22: 3246. https://doi.org/10.3390/ani15223246
APA StyleTrapanese, L., Bifulco, G., Santinello, M., Pasquino, N., Campanile, G., & Salzano, A. (2025). Comparison of K-Means and Hierarchical Clustering Methods for Buffalo Milk Production Data. Animals, 15(22), 3246. https://doi.org/10.3390/ani15223246







