Surface Electromyography-Based Wrist Angle Estimation and Robotic Arm Control with Echo State Networks

Abstract

Continuous estimation of joint angles based on surface electromyography (sEMG) signals is a promising method for naturally controlling prosthetic limbs and assistive devices. However, conventional methods based on neural networks have limitations such as long training times and calibration burdens. This study investigates the use of an echo state network (ESN), which enables fast training, to estimate wrist joint angles from sEMG. Five participants mimicked the motion of a 1-degree-of-freedom robotic arm by flexing and extending their wrist, while sEMG signals from the wrist flexor and extensor muscles and the robotic arm’s angle were recorded. The ESN was trained to take two sEMG channels as input and the robotic joint angle as output. High-accuracy estimation with a median coefficient of determination R² = 0.835 was achieved for representative ESN parameters. Additionally, the effects of the reservoir size, spectral radius, and time constant on estimation accuracy were evaluated using data from a single participant. Furthermore, online estimation of joint angles based on sEMG signals enabled successful control of the robotic arm. These results suggest that sEMG-based ESN estimation offers fast, accurate joint control and could be useful for prosthetics and fundamental studies on body perception.

1. Introduction

Continuous estimation of joint angles based on surface electromyography (sEMG) signals is a promising technique for enabling natural control of prosthetic hands and assistive suits. Conventional myoelectric prostheses commonly control joint rotation speed in proportion to muscle activation levels [1]. However, such systems require the user to learn the mapping between muscle activity and movement through training. Although many studies have investigated methods for classifying specific hand postures from muscle activity patterns [2,3,4,5,6], achieving smooth and goal-directed manipulation of objects using prosthetic or assistive devices requires technology that continuously adjusts joint angles according to the user’s intent. Such estimation techniques are also used in psychological or neuroscientific research on body perception involving artificial limbs; for example, in psychological experiments that evaluate the sense of body ownership and sense of agency during voluntary control of robotic arms [7,8].

The relationship between sEMG and joint angle is nonlinear and dynamic. Muscle activity, approximated by the envelope of the sEMG signal, scales the viscoelastic properties of muscles [9]. Joint motion is induced by torque generated from muscle tension, interacting with the dynamics of the limb, such as inertia [10]. This process involves factors like the nonlinear force–length relationship of muscles and posture-dependent variations in moment arms, requiring complex physical models to estimate movements from sEMG. Furthermore, muscle and limb parameters vary among individuals, necessitating parameter tuning when using physical models for prediction [11,12,13]. These complexities demand significant computational resources, which can be a bottleneck for use in portable systems such as prosthetic limbs.

To model the relationship between muscle activity and joint angles using sEMG, machine learning approaches have been widely adopted. Methods capable of reproducing dynamic responses, such as recurrent neural networks (RNNs), time delay neural networks (TDNNs), and convolutional neural networks (CNNs), have been extensively used [14,15,16,17,18]. These models are effective in capturing complex nonlinear relationships due to their strong function approximation capabilities. However, they require optimization of nonlinear cost functions using gradient-based methods, which cannot guarantee that a global optimum is reached and often involve long training times. Furthermore, calibration of machine learning models requires not only sEMG signals but also the corresponding joint angle data, which must be collected using posture sensors or motion capture markers attached to the user’s limb. This is not feasible for amputees, and the setup and measurement process are time-consuming, making it burdensome for daily use or for use during psychological experiments.

Recently, echo state networks (ESNs), a type of RNN capable of fast training, have drawn attention [19,20,21]. ESNs are characterized by having a randomly weighted and fixed internal network called a reservoir, with learning applied only to the output layer. This structure allows for much faster training compared to conventional RNNs and is well suited for applications requiring immediate use after training. To the best of the authors’ knowledge, although there have been studies attempting to estimate elbow joint angles from sEMG using ESNs [22], the parameter settings used in such models have not been thoroughly explored, and it remains unclear whether accurate estimation is possible without the use of posture sensors.

In this study, we focus on wrist joint motion with the goal of applying the method to sEMG-controlled robotic arms, such as prosthetic hands. We investigate whether joint angle estimation from sEMG using an ESN is feasible in able-bodied participants, with a view toward potential future applications in myoelectric prostheses. During calibration, we test whether it is possible to train the neural network without attaching posture sensors to the user by having the user imitate the movement of a robotic arm and using the arm’s joint angles as training signals. We also examine how key ESN parameters (the number of reservoir neurons, spectral radius, and time constant) affect estimation performance. Furthermore, we evaluate whether a trained ESN can be used for online control of a robotic arm using sEMG signals.

2. Materials and Methods

2.1. Data Acquisition

The experimental setup used in this study is shown in Figure 1. Surface EMG signals were recorded from two muscles involved in wrist flexion and extension: the flexor carpi radialis and the extensor carpi ulnaris. Bipolar dry electrodes (Oisaka Electronic Equipment, Fukuyama, Japan) were used for sEMG recording, amplified using a P-EMG plus amplifier (Oisaka Electronic Equipment) with a total gain of 10,000. The two electrodes were placed on the target muscles and fixed with a belt, along with a dry reference electrode. The experimenter identified the muscle locations based on the positions of the tendons and the ulna, and the electrodes were placed approximately one-third of the distance between the elbow and the wrist at sites where muscle activity during flexion and extension could be confirmed. The analog filters built into the amplifier were not used, and all noise processing was performed digitally on a PC (see Section 2.2). The amplified sEMG signals were sampled at 2000 Hz using a data acquisition (DAQ) device (NI USB-6212, National Instruments, Austin, TX, USA) with an input range of ±10 V and 16-bit quantization, and recorded on a PC.

Figure 1. Experimental setup for sEMG measurement and robotic arm motion.

The robotic arm consisted of a wooden hand model attached to an AC servo motor (FHA-11C, Harmonic Drive LLC, Beverly, MA, USA), which was driven in velocity control mode using a motor controller (HA-680, Harmonic Drive LLC). The control frequency was 100 Hz, and the PC sent velocity commands to the motor controller via the DAQ device. The joint angle of the robotic arm was recorded in synchrony with the sEMG signals by capturing the signal from the rotary encoder embedded in the motor through the digital input of the DAQ device.

In each trial, the robotic arm followed a 35 s trajectory defined by a sinusoidal waveform with a gradually increasing frequency (0.1–0.4 Hz) and an amplitude of 45°. During this motion, the PC simultaneously recorded sEMG signals and joint angles of the robotic arm while sending motor commands. The angle coordinate was defined such that the neutral wrist position was 0°, flexion was positive, and extension was negative. Data acquisition, digital filtering, and motor control were performed using MATLAB (R2024a, MathWorks, Natick, MA, USA).

The participants observed the motion of the robotic arm and imitated its movement with their own wrist while sEMG signals were recorded. They were instructed not to apply force with their fingers and to replicate the posture of the robotic hand as closely as possible. The participants could observe their real-time sEMG waveforms using an oscilloscope during the experiment.

2.2. sEMG Preprocessing

The sEMG preprocessing and angle estimation pipeline used in this study is illustrated in Figure 2. First, motion artifacts were removed from the raw sEMG signals using a second-order Butterworth high-pass filter with a cutoff frequency of 25 Hz, which is close to the frequency reported as optimal in previous research [23]. No notch filter for power line noise was applied to avoid potential loss of EMG components. The signals were then full-wave-rectified and smoothed using a low-pass filter with the following impulse response to convert them into muscle activation signals:

$$h\left(t\right)=6.44\times \left(e^{-10.80t}-e^{-16.52t}\right).$$

(1)

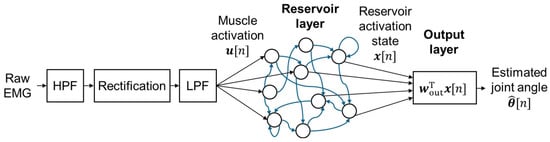
Figure 2. Overview of signal processing and ESN-based wrist angle estimation pipeline.

This filter was originally derived in neural network studies for estimating joint torque, and it approximates the delay between EMG and muscle tension [24]. The resulting muscle activation signals were resampled at 100 Hz, synchronized with the motor angle data, and used as input data for ESN training and performance evaluation.

2.3. Echo State Network

The echo state network (ESN) used in this study consists of a reservoir layer that changes its internal state in response to input signals, and an output layer that computes the estimated output from the reservoir state (Figure 2). We employed a leaky integrator ESN [25], implemented in the ESNToolbox provided by H. Jaeger [26].

Let time be denoted by $t$, the input be a $K$-dimensional vector $\mathit{u}\left(t\right)$, the number of reservoir neurons be $N$, and the reservoir state be an $N$-dimensional vector $\mathit{x}\left(t\right)$. The reservoir dynamics are governed by the following:

$$\dot{\mathit{x}}\left(t\right)={\displaystyle \frac{1}{c}}\left(-a\mathit{x}\left(t\right)+f\left({\mathit{W}}_{\mathrm{i}\mathrm{n}}\mathit{u}\left(t\right)+\mathit{W}\mathit{x}\left(t\right)\right)\right),$$

(2)

where $a$ is the leaking rate (fixed at 1 in this study), $c$ is the time constant, and $f$ is the activation function, set to tanh in this study. The equation was discretized using Euler’s method as follows:

$$\mathit{x}\left[n+1\right]=\left(1-a{\displaystyle \frac{\delta }{c}}\right)\mathit{x}\left[n\right]+{\displaystyle \frac{\delta }{c}}f\left({\mathit{W}}_{\mathrm{i}\mathrm{n}}\mathit{u}\left[n\right]+\mathit{W}\mathit{x}\left[n\right]\right),$$

(3)

where $n$ is the discrete time index and $\delta$ is the real time per discrete step (set to 0.01 s, matching the sampling interval of the muscle activation data). The input weights ${\mathit{W}}_{\mathrm{i}\mathrm{n}}$ were initialized with uniform random values in the range [−1,1]. The reservoir weight matrix $\mathit{W}$ had a sparse connection density of $\mathrm{m}\mathrm{i}\mathrm{n}(10/N,1)$, meaning that each neuron was connected to at most about 10 others [27]. The spectral radius of $\mathit{W}$ was adjusted to a predefined value (≤1).

The output of the ESN was computed as follows:

$$\widehat{\theta }\left[n\right]={\mathit{w}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{T}}\left[\begin{array}{c}\mathit{x}\left[n\right]\\ \mathit{u}\left[n\right]\end{array}\right],$$

(4)

where ${\mathit{w}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ is the output weight vector of dimension $N+K$. The weight ${\mathit{w}}_{\mathrm{o}\mathrm{u}\mathrm{t}}$ was optimized using ordinary least squares (OLS) to minimize the squared error between the predicted output and the training target values. Let the training input and output data be $\mathit{u}\left[1\right],\dots ,\mathit{u}\left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]$ and $\theta \left[1\right],\dots ,\theta \left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]$, and the corresponding reservoir states be $\mathit{x}\left[1\right],\dots ,\mathit{x}\left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]$.

The squared error to be minimized is as follows:

$$E=\sum _{n=1}^{N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}}{\left(\theta \left[n\right]-{\mathit{w}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{\mathrm{T}}\left[\begin{array}{c}\mathit{x}\left[n\right]\\ \mathit{u}\left[n\right]\end{array}\right]\right)}^2.$$

(5)

The optimal weights have the following analytical solution:

$${\mathit{w}}_{\mathrm{o}\mathrm{u}\mathrm{t}}={\left({\mathit{X}}^T\mathit{X}\right)}^{-1}{\mathit{X}}^{\mathrm{T}}\mathit{\theta }$$

(6)

where

$$\mathit{X}={\left[\begin{array}{ccc}\mathit{x}\left[1\right]& \dots & \mathit{x}\left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]\\ \mathit{u}\left[1\right]& \dots & \mathit{u}\left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]\end{array}\right]}^{\mathrm{T}},$$

(7)

and $\mathit{\theta }={\left[\theta \left[1\right],\dots ,\theta \left[N_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}\right]\right]}^{\mathrm{T}}$.

In this study, the ESN received two-dimensional muscle activation signals (unit: 10⁻⁴ V) as input and produced estimated joint angles (unit: rad) as output. The output weight vector was trained using the joint angles of the robotic arm, which were imitated by the participants.

2.4. ESN Evaluation Experiment

Five adult participants (S1–5, all male, 21–40 years old) took part in the experiment. The study was approved by the Institutional Review Board of Tokyo Denki University.

The participants wore a belt on their forearm, to which the sEMG electrodes and reference electrode were attached. The participants stood in a position where they could visually compare the angle of the robotic arm with their own wrist angle from above. Then, while observing the movement of the robotic arm (as described in Section 2.1), the participants performed wrist flexion and extension movements to imitate the arm’s motion. During this task, the participants were instructed to avoid applying force with their fingers and to match the hand posture to that of the robotic hand model as closely as possible. The experimenter visually monitored the participants throughout the trials to ensure that the imitation was performed with sufficient quality.

After several practice trials, each participant performed five repetitions of wrist motion. During these sessions, sEMG signals and the posture of the robotic arm were recorded and later used for evaluating the performance of the ESN.

2.5. Online Robotic Arm Control Experiment

We assessed online control of a robotic arm using sEMG-based wrist angle estimation via an ESN. The same robotic arm as that used in the ESN evaluation experiment was used in this experiment. A block diagram of the control system is shown in Figure 3a. The estimation and control cycle was set to 0.01 s, identical to that in the ESN evaluation experiment. From the deviation between the estimated angle and the robotic arm angle, ${\omega }_{\mathrm{P}}\left[n\right]$ was computed according to Equation (8), and then the smoothed angular velocity ${\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}\left[n\right]$ was obtained using Equation (9). This value was used as the target joint angular velocity of the robotic arm, and the motor was driven under velocity control.

$${\omega }_{\mathrm{P}}\left[n\right]=K_{\mathrm{P}}\left(\widehat{\theta }\left[n\right]-{\theta }_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\left[n\right]\right),$$

(8)

$${\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}\left[n\right]=r{\omega }_{\mathrm{r}\mathrm{e}\mathrm{f}}\left[n-1\right]+\left(1-r\right){\omega }_{\mathrm{P}}\left[n\right].$$

(9)

Here, $r$ is a constant that determines the smoothness of the filter output, for which a value of 0.3 was used in this experiment. $K_{\mathrm{P}}$ = 3.14 s^–1 was used as the proportional gain for angular velocity control. Assuming that the motor perfectly follows the velocity command, the Bode plot of the control system is illustrated in Figure 3b. The system behaves like a low-pass filter with a cutoff frequency of approximately 0.5 Hz.

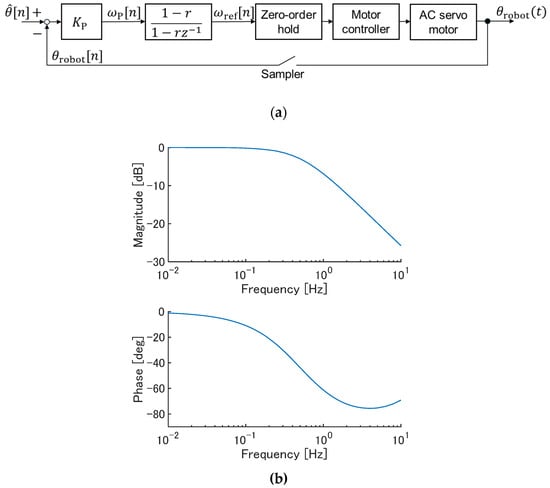
Figure 3. The robotic arm control system based on joint angles estimated from sEMG signals. (a) Block diagram. In the second block, $z$ denotes the variable in the z-transform. (b) A Bode plot (theoretical; discrete-time transfer function from $\widehat{\theta }\left[n\right]$ to ${\theta }_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\left[n\right]$).

All participants (S1–5) completed the experiment. The ESN, trained under the representative parameter settings described in Section 2.6.2 (10 reservoir neurons, spectral radius of 0.25, and time constant of 0.5 s), estimated joint angles from sEMG signals online, and these estimates were used as target angles for the robotic arm. For 36 s, each participant freely moved their wrist within the range of movement speeds used in the ESN evaluation experiment. Afterward, participants were asked whether they felt that the robotic arm moved as intended.

2.6. Evaluation

2.6.1. Evaluation of Estimation Accuracy

The coefficient of determination R² was used as the evaluation metric for estimation accuracy. It was calculated based on the joint angles of the robotic arm ${\theta }_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\left[n\right]$ and the estimated angles $\widehat{\theta }\left[n\right]$ obtained from sEMG signals during one movement trial (lasting 35 s and consisting of $N_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}$ = 3500 samples), using the following formula:

$${\mathrm{R}}^2=1-{\displaystyle \frac{{\sum }_{n=1}^{N_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}}{\left(\widehat{\theta }\left[n\right]-{\theta }_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\left[n\right]\right)}^2}{{\sum }_{n=1}^{N_{\mathrm{t}\mathrm{e}\mathrm{s}\mathrm{t}}}{\left({\theta }_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\left[n\right]-{\overline{\theta }}_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}\right)}^2}}$$

(10)

where ${\overline{\theta }}_{\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{o}\mathrm{t}}$ is the mean of the joint angles of the robotic arm. Note that R² can take negative values when the sum of squared prediction errors exceeds the variance of the reference data.

Initially, estimation accuracy was evaluated for all participants under the representative parameter settings (10 reservoir neurons, spectral radius of 0.25, and time constant of 0.5 s). The parameter was determined in a trial-and-error manner by identifying the minimum of the estimation error for participant S1 before the experiment. To compute this, one of the five recorded trials was used as training data and another as test data. All 20 combinations of training and test trials were evaluated. Since the reservoir weights in the ESN are randomly initialized, each combination was evaluated five times with different reservoir weight initializations, training, and error calculations. Thus, the evaluation was based on 100 total trials.

To examine the quality of the EMG signals underlying the estimation, we calculated the signal-to-noise ratio (SNR) for each participant. All five sessions of EMG recordings used for ESN evaluation were included, and the SNR was computed for each channel using the following formula:

$$\mathrm{S}\mathrm{N}\mathrm{R}={\left({\displaystyle \frac{A_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}+\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}}{A_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}}}\right)}^2,$$

(11)

where $A_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}+\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$ denotes the root-mean-square (RMS) amplitude of the EMG signal and $A_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$ corresponds to the RMS amplitude during periods without muscle activity [28]. In this study, these values were approximated using the rectified and low-pass-filtered EMG signals: the overall RMS amplitude was used as $A_{\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\mathrm{a}\mathrm{l}+\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$ and the 5th percentile amplitude was used as $A_{\mathrm{b}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}}$.

Furthermore, to evaluate the independence and redundancy of the multi-channel input signals, we calculated the correlation coefficients between the activation of the muscles of the two channels across the five sessions.

2.6.2. Evaluation of Parameter Effects

To investigate the effect of ESN parameters on wrist angle estimation, we evaluated estimation accuracy only for participant S1 while varying the number of reservoir neurons, the spectral radius, and the time constant. The baseline parameter setting was 10 reservoir neurons, a spectral radius of 0.25, and a time constant of 0.5 s, which we used for the robotic arm control experiment and the evaluation of estimation accuracy.

We varied each parameter independently as follows:

• Number of reservoir neurons: 2, 4, 6, ..., 30;
• Spectral radius: 0.001, 0.0025, 0.005, 0.01, 0.025, 0.05, 0.1, 0.25, 0.5, and 1;
• Time constant: 0.01 s, 0.025 s, 0.05 s, 0.1 s, 0.25 s, 0.5 s, 1 s, and 2.5 s.

Each condition was evaluated individually while keeping the other parameters fixed at their baseline values.

3. Results

3.1. Representative Results of Angle Estimation

Figure 4 shows the estimation results for participant S1 using test data under the condition where the number of reservoir neurons was 10, the spectral radius was 0.25, and the time constant was 0.5 s. In the upper graph, the blue line represents the measured joint angle of the robotic arm following the trajectory described in Section 2.1, while the red line indicates the joint angle estimated from sEMG during the mimicking task. In the latter part of the sequence, the estimated values are biased by approximately 15° towards the positive direction, but the overall movement pattern is well reproduced.

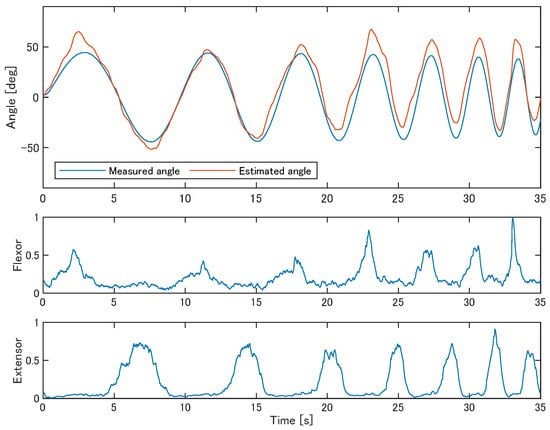
Figure 4. Examples of the estimated joint angles from sEMG compared to the measured robotic arm trajectory (participant S1). The lower two panels show the muscle activation derived from sEMG signals of the two muscles, which served as input to the ESN.

Figure 5a shows the estimation accuracy in terms of R² for the five participants (S1–S5). For each participant, 100 data points were used for the plot, corresponding to all 20 combinations of five training trials and four test trials, with five different sets of reservoir weights randomly initialized. Although the ESN occasionally yielded very low estimation accuracy, the median values indicate that in more than half of the cases, the coefficient of determination exceeded 0.7. Figure 5b presents examples of the estimation results for participants S2–S5. As illustrated in the case of S3, the estimated trajectory sometimes deviated substantially; however, for multiple participants, the estimation results closely followed the movements of the presented robotic arm.

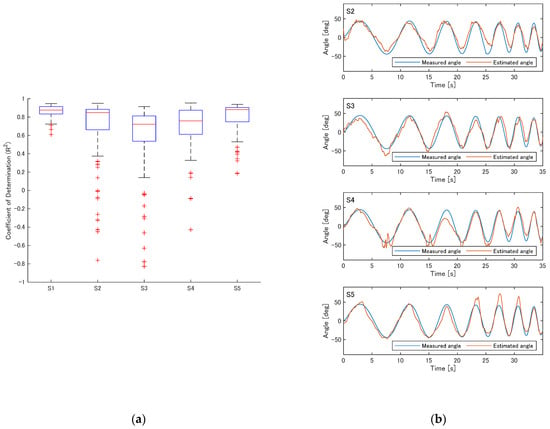
Figure 5. Estimation accuracy of the ESN under the representative parameter settings (10 reservoir neurons, spectral radius of 0.25, and time constant of 0.5 s). (a) R² values for participants S1–S5. (b) Examples of estimation results for participants S2–S5.

The estimation accuracy for all participants is summarized in Table 1. Although some participants exhibited mean coefficients of determination below 0.5, the median values exceeded 0.7 for all participants. Across all participants and trials, the mean coefficient of determination was 0.714 ± 0.34 (mean ± standard deviation), while the median value (interquartile range) was 0.835 (0.676–0.892).

Table 1. Estimation accuracy (R²) and sEMG signal quality for all participants (Q1: the 25th percentile; Q3: the 75th percentile).

Participant	R2 (Mean ± S.D.)	R2 (Median (Q1–Q3))	SNR of sEMG		Correlation of Flexor and Extensor
			Flexor	Extensor
S1	0.862 ± 0.07	0.876 (0.834–0.913)	1.7	9.5	−0.41
S2	0.754 ± 0.23	0.853 (0.662–0.884)	28.9	103.7	−0.44
S3	0.485 ± 0.68	0.719 (0.536–0.812)	5.4	6.2	−0.12
S4	0.660 ± 0.28	0.753 (0.611–0.874)	31.2	13.6	−0.28
S5	0.782 ± 0.21	0.876 (0.749–0.904)	7.9	17.1	−0.42
All	0.714 ± 0.34	0.835 (0.676–0.892)	15.0 ± 13.9	30.0 ± 41.4	−0.42 ± 0.14

Table 1 also includes information on the quality of the sEMG signals used. For every participant, at least one of the two channels showed an SNR comparable to or higher than the range reported in a previous study on sEMG (4.3–96.9 [28]). The correlation between the measured activation of the two muscles tended to be moderately negative, reflecting the fact that the two muscles are a flexor and an extensor. This also indicates that, as expected, their activities were not completely redundant, since there were instances where only one of the muscles was activated. This interpretation is consistent with the results of the ablation study (see Section 3.2). Taken together, these results suggest that the sEMG recordings in this study are of adequate quality to validate the joint angle estimation.

The time required to train a single ESN, including the computation of reservoir states based on the training data, was 0.044 ± 0.00 s on the laptop used in this study (CPU: Intel Core i7-1355U).

3.2. Effect of Number of Reservoir Neurons

Figure 6a shows the R² values for participant S1 when the number of reservoir neurons varied. As the number increased from 2 to around 10, R² improved. Beyond that, the median of R² remained largely unchanged, but cases of extremely low R² values became more frequent.

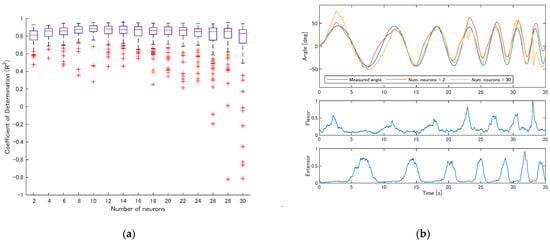
Figure 6. The effect of the number of reservoir neurons on estimation accuracy (participant S1). (a) R² values as the number of reservoir neurons varied from 2 to 30; (b) example estimation results with 2 and 30 reservoir neurons.

Figure 6b presents example estimation results when the number of reservoir neurons was 2 and 30. With a small number of neurons, although the estimated movements were attenuated during the fastest motion, the estimation accuracy remained reasonably acceptable. However, when the number of neurons was excessively large, the estimated angle occasionally deviated entirely from the actual measured joint angle, showing unstable behavior.

To examine whether the EMG signals used in this study were redundant, we conducted an ablation study in which the same analysis described in this section was performed using only the flexor or only the extensor EMG as input. The ESN settings were identical to those of the two-channel condition except for the number of input channels. In both the flexor-only and extensor-only case, the coefficient of determination did not reach the best median value obtained when both muscles were used (10 reservoir neurons, R² = 0.876) for any number of reservoir neurons or in any of the repeated trials. These results suggest that the flexor and extensor EMG signals provide non-redundant information for joint angle estimation.

3.3. Effect of Spectral Radius of Reservoir Weights

Figure 7a shows the R² values for participant S1 when the spectral radius of the reservoir weights varied. Overall, there were few differences across conditions, but when the spectral radius was below 0.01, extremely low R² values occasionally occurred. When the spectral radius was set to 1, relatively low R² values were slightly more frequent.

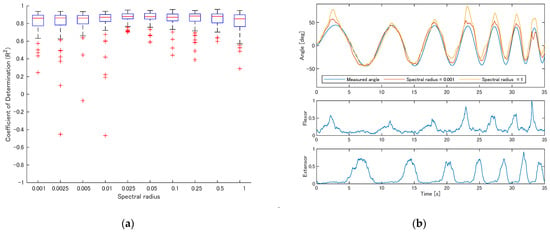
Figure 7. Effect of spectral radius on estimation performance (participant S1). (a) R² values across spectral radius ranging from 0.001 to 1; (b) example estimation results with spectral radius = 0.001 and 1.

Figure 7b shows example estimation results for spectral radii of 0.001 and 1. With a small spectral radius, the estimated trajectory exhibited small oscillations while, with a spectral radius of 1, the estimation error tended to be slightly larger.

3.4. Effect of Reservoir Time Constant

Figure 8a shows the R² values for participant S1 when the time constant of the reservoir varied. As the time constant increased from 0.01 s, R² improved; however, beyond 0.5 s, the frequency of extremely low R² values increased.

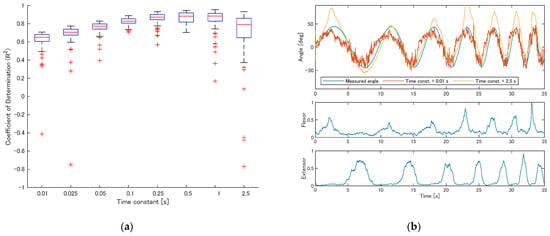
Figure 8. Effect of reservoir time constant on estimation accuracy (participant S1). (a) R² values across time constants ranging from 0.01 to 2.5 s; (b) example estimation results with time constants of 0.01 s and 2.5 s.

Figure 8b shows estimation examples for time constants of 0.01 s and 2.5 s. With a short time constant, the estimated values included many fluctuations. With a long time constant, the estimated values changed smoothly but the predictions frequently diverged from the true values, leading to a reduction in accuracy.

3.5. Online Robotic Arm Control with sEMG

Figure 9a and Video S1 in the Supplementary Materials show participant S1 controlling the robotic arm online. The robotic arm successfully followed the participant’s wrist motion. Due to the nature of the control strategy, the robot’s response was delayed by approximately 0.3 s relative to the estimated angle. This delay was consistent with the theoretical characteristics of the control system (Figure 3b), which predict a lag of 0.26–0.30 s for the frequency range of the target motions (0.1–0.4 Hz). Figure 9b presents the estimated joint angles and the robotic arm joint angles during online control for the other participants (S2–S5). For S1–S4, the robotic arm closely followed the estimated values, while for S5, who moved their wrist at a slightly faster pace (approximately 0.6 Hz), the movements were attenuated as predicted by the amplitude characteristics of the control system shown in Figure 3b. When asked whether they felt the robot move as intended, participants S1–S4 answered “Yes”, while participant S5 reported that the arm followed well during extension but did not fully bend during flexion.

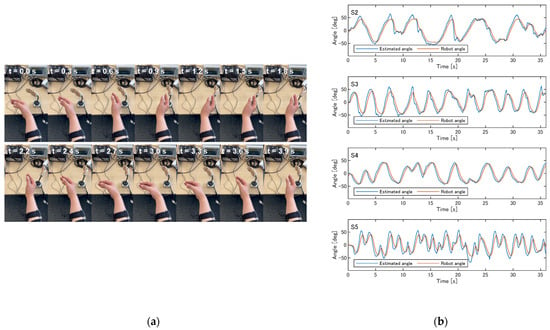
Figure 9. Online control of the robotic arm by participants. (a) An example of participant S1 controlling the robotic arm (see Video S1 in the Supplementary Materials). (b) The estimated joint angles and robotic arm joint angles during online control for participants S2–S5.

4. Discussion

4.1. Estimating Joint Angles from sEMG with ESN

In this study, we demonstrated that it is possible to estimate wrist joint angles using an echo state network (ESN), a type of neural network, based on sEMG signals from the wrist flexor and extensor muscles. Since the internal connections of the ESN are randomly fixed and only the output layer is trained, the weights of the output layer can be computed analytically using OLS. This allows for faster computation compared to other RNNs, TDNNs or CNNs. Although most studies on neural networks for motion estimation from sEMG do not report training times, one study using a CNN–LSTM to classify knee movements from four sEMG channels reported a training time of 34.48 s [29]. In contrast, in the MATLAB implementation in this study, the training process—including reservoir state computation—was completed in 0.044 ± 0.00 s, suggesting that training time would not be a bottleneck for practical applications such as prosthetics, assistive suits, or psychological experiments.

Under the representative parameter settings, the R² from only two muscle channels achieved 0.714 ± 0.34 (mean ± standard deviation) and a median of 0.835. As shown in Figure 5a, because the ESN employs randomly initialized reservoir weights, extremely low accuracy occasionally occurs, resulting in a lower mean compared to the median. However, since training is sufficiently fast, reinitializing the reservoir weights can readily yield results close to the median. We compared our results with those of Bao et al. [16], who used six sEMG channels and approximately three minutes of 0.1 Hz movements for training. For flexion–extension movements of six participants, the mean R² values were 0.57, 0.63, 0.61, 0.78, and 0.86 for support vector regression (SVR), random forests (RFs), CNN, LSTM, and CNN–LSTM, respectively. Despite its high-speed training, the results of the present study are comparable to these methods.

An ESN is a machine learning approach based on complex dynamics, known as reservoir computing [30]. Because only neuron state updates and ordinary least squares are required, specialized computing hardware such as GPUs is not necessary. For example, an ESN with more neurons than in the present study has been implemented on a microcontroller (Arduino Mega) [31]. Furthermore, physical reservoir computing could potentially reduce the computational burden even further. Recently, physical reservoir computing has attracted attention, in which the reservoir is implemented using hardware such as electronic circuits or soft materials [32]. The results of this study regarding the dynamics of the reservoir could be useful for designing physical reservoirs, enabling the development of low-power sEMG interfaces that minimize reliance on digital computation.

4.2. Effects of ESN Parameters

We examined the behavior of the ESN when varying the number of reservoir neurons, spectral radius, and time constant, starting from a set of parameters that yielded good accuracy in participant S1. When the number of neurons was too large, the estimated outputs occasionally exhibited high-frequency fluctuations that were entirely different from the target output (a phenomenon also reported by Day et al. [22]). This is likely to reflect overfitting of the output layer to the training data. To avoid this, it may be necessary to reduce the number of neurons or to regularize the output weights using ridge regression, a common practice in reservoir computing [27]. Although reducing the number of neurons decreases accuracy, extremely low estimation performance was rare (see Figure 6a). Therefore, when prioritizing stability over maximum accuracy, a smaller reservoir may be preferable.

The spectral radius is defined as the largest absolute eigenvalue of the weight matrix and reflects how much influence the reservoir state has on future states. When the spectral radius was very small, the smoothness of the estimated output decreased, likely because the influence of past states diminished. On the other hand, a larger spectral radius may lead to instability. In reservoir computing, it is often said that maximal computational power is achieved near the “edge of chaos” [33]. For leaky integrator ESNs, stability is guaranteed when the spectral radius does not exceed the leaking rate $a$ [25], which was 1 in this study. Therefore, setting the spectral radius as high as possible while staying below $a$ may enhance performance. However, Figure 7a suggests that the effect of spectral radius was limited in our conditions, possibly because the large leaking rate retained influence from past states even when the spectral radius was small.

The time constant determines the rate of change of the reservoir states and had a significant effect on the smoothness of the estimated output. As shown in Figure 8b, even when the output was not smooth with a short time constant, the estimation generally followed the target trajectory. When the time constant was large, the influence of erroneous reservoir activity persisted over time, resulting in large estimation errors. To achieve optimal performance, it may be necessary to balance the smoothness of wrist motion and the suppression of error persistence when selecting the time constant.

4.3. Effect of Using Robotic Arm Angles as Training Data

In this study, calibration was performed by having the participant mimic the movement of the robotic arm, allowing the robot’s joint angles to be used as training data without attaching any angle sensors to the participant. This means that ESN calibration could be performed with only the sEMG sensors necessary for control, without any additional sensors for joint angle measurement.

However, because the consistency between the robotic arm’s motion and wrist joint angles depends entirely on how the participant moves their hand, errors can be introduced into the training data, potentially reducing the accuracy of angle estimation. The estimation errors reported in this study may include such effects (e.g., the latter part of the sequence in Figure 4). Nonetheless, the estimated trajectories successfully reproduced the key characteristics of the original motion, and the robotic arm in the online control experiments followed the participants’ movements. These results suggest that a sufficient sense of agency—i.e., the feeling that the device is moving in accordance with the user’s intention—can be achieved without direct joint angle measurement.

It should also be noted that, in the present experiment, the accuracy of the imitation was verified only through visual inspection by the experimenter. The degree to which the imitation was performed accurately was not quantitatively measured, nor was the difference examined between using such imitation and using precise joint angle measurements for ESN training. Therefore, further studies with more precise measurements are needed to validate these aspects.

Furthermore, since this training method does not rely on direct measurement of human joint angles, it may be applicable to prosthesis users, including those without intact limbs. When applying machine learning-based myoelectric prostheses to amputees, training data are often obtained using a mirrored training paradigm, in which bilateral movements are performed and the motions of the intact contralateral hand are recorded [34,35]. This approach allows for the flexion–extension movements of the wrist to be reproduced even in amputees [35]. Although the present study did not employ mirrored movements directly, it shares the same principle of replacing direct measurement of target wrist motion with a similar motion measured elsewhere. Therefore, it is expected that the proposed method could also be trained by using mirrored movements in prosthesis users. However, this study only involved able-bodied participants, and it is still unclear whether similar results can be achieved with amputees. Future studies are needed to validate the method with actual amputee participants, particularly using a mirrored training paradigm.

4.4. Online Control of the Robotic Arm

As shown in Figure 9a and Supplementary Video S1, the robotic arm controlled by sEMG signals through the ESN was able to follow not only the periodic motions used for ESN evaluation but also free, non-periodic movements, although with a delay of approximately 0.3 s due to the characteristics of the control system. The additional degree of freedom provided by the wrist joint of a prosthetic arm is expected to improve dexterity during object manipulation and reduce compensatory movements involving the trunk or shoulder [36]. While further studies are required before application to amputees, robotic arm control using an ESN could contribute to enhancing the dexterity of myoelectric prostheses through short training sessions. Under the current settings, the tracking became insufficient as the motion speed increased, indicating that a practical system will require careful selection of the maximum speed of target movements and the corresponding design of the control system.

In this experiment, participants reported that they felt the robotic arm move as they intended when it successfully followed the estimated angles. This suggests that the estimation accuracy was sufficient to induce a sense of agency. Previous studies using virtual hands aligned with participants’ own hand movements have shown that a delay of around 0.3 s reduces this sense of agency, with an even stronger effect on the sense of ownership [37]. Since the delay observed in this study is consistent with the theoretical delay predicted from the control system, reducing this delay is important in enabling the robotic hand to be incorporated into the user’s body representation in a manner equivalent to their own hand.

5. Conclusions

In this study, we investigated whether it is possible to estimate wrist joint angles from surface electromyography (sEMG) signals using an echo state network (ESN), with the aim of enabling voluntary control of a robotic arm. The ESN architecture allows for rapid training by randomly fixing the reservoir weights and training only the output layer using ordinary least squares. Moreover, by having the user imitate the motion of a robotic arm during calibration, it becomes possible to use the robot’s joint angles as training data, thereby eliminating the need to attach joint angle sensors to the user.

In our experiments, we achieved a high estimation accuracy with a median coefficient of determination R² = 0.835 using sEMG signals from just two muscles. We also systematically investigated the effects of key ESN parameters, including the number of reservoir neurons, spectral radius, and time constant, on estimation accuracy and stability. Furthermore, we confirmed that a trained ESN could be used to control a robotic arm in real-time, with the robot successfully tracking the user’s wrist movement based on sEMG input with a delay of approximately 0.3 s.

This approach enables training without direct measurement of human joint angles, suggesting the potential for application in prosthetic control for individuals without physical joints. Future work will focus on extending this method to actual prosthesis users and exploring its use in fundamental studies on body perception.