Novel Design and Control of Ultrasonic Transducers for a Media-Free Contactless Micro-Positioning System
Abstract
1. Introduction
2. Novel Transducer Design
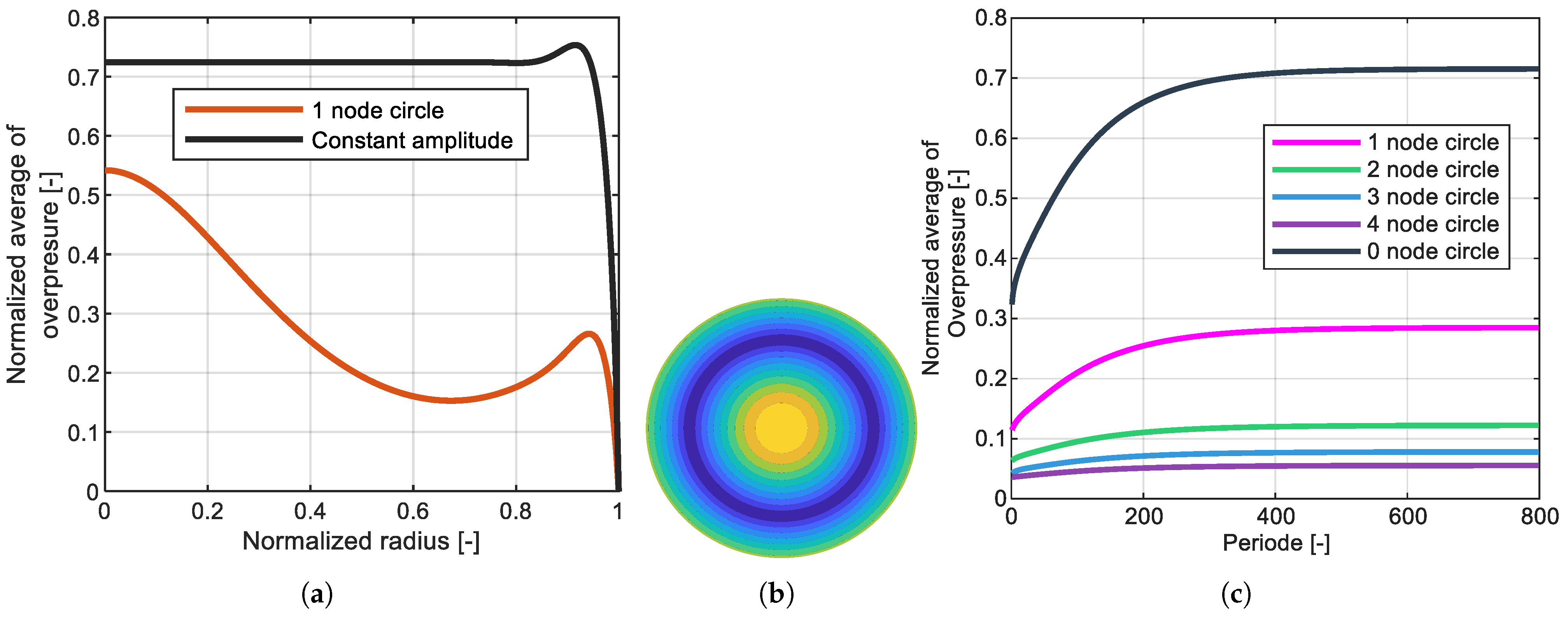
2.1. Squeeze-Film Levitation
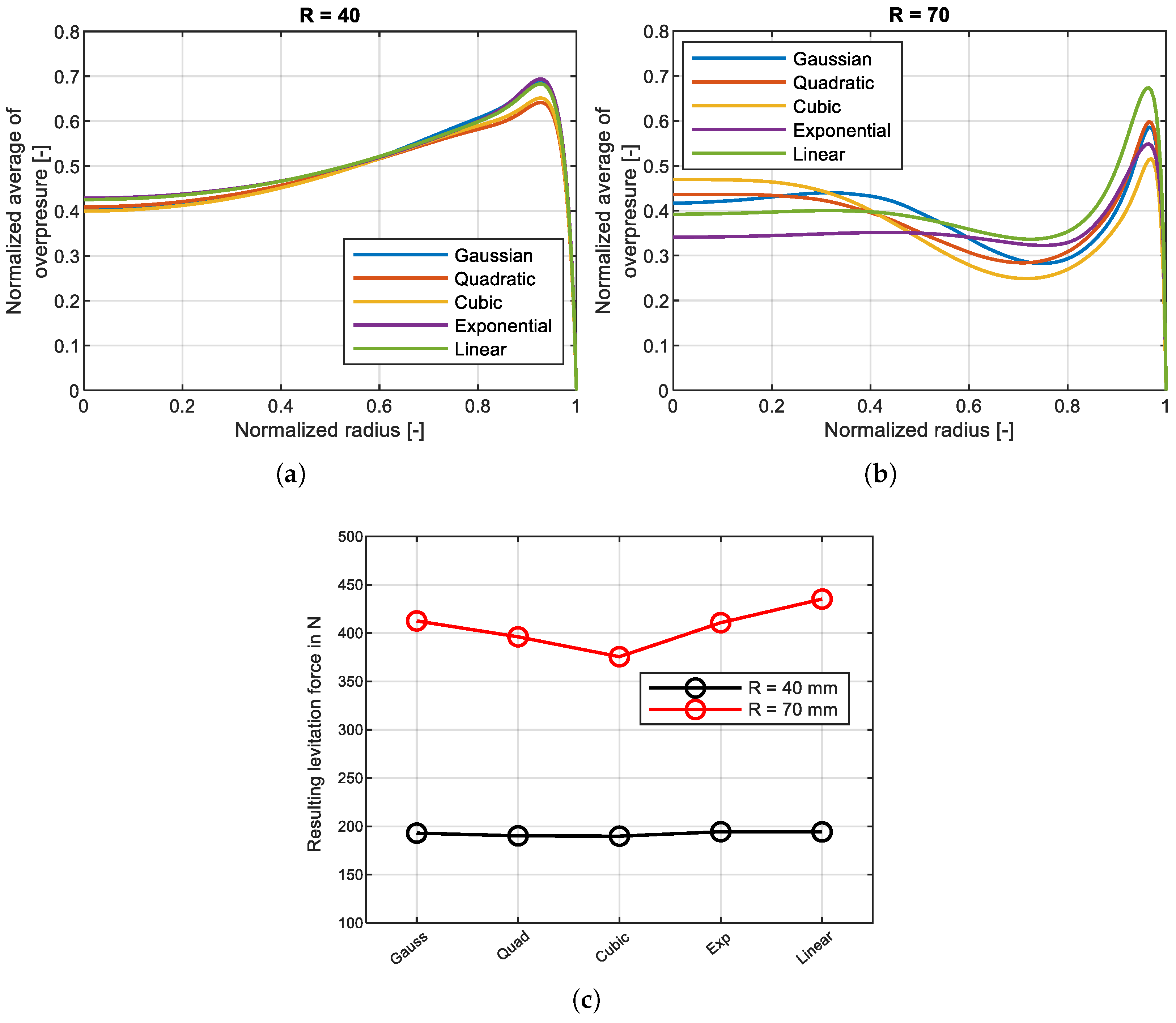
2.2. Geometry Optimization
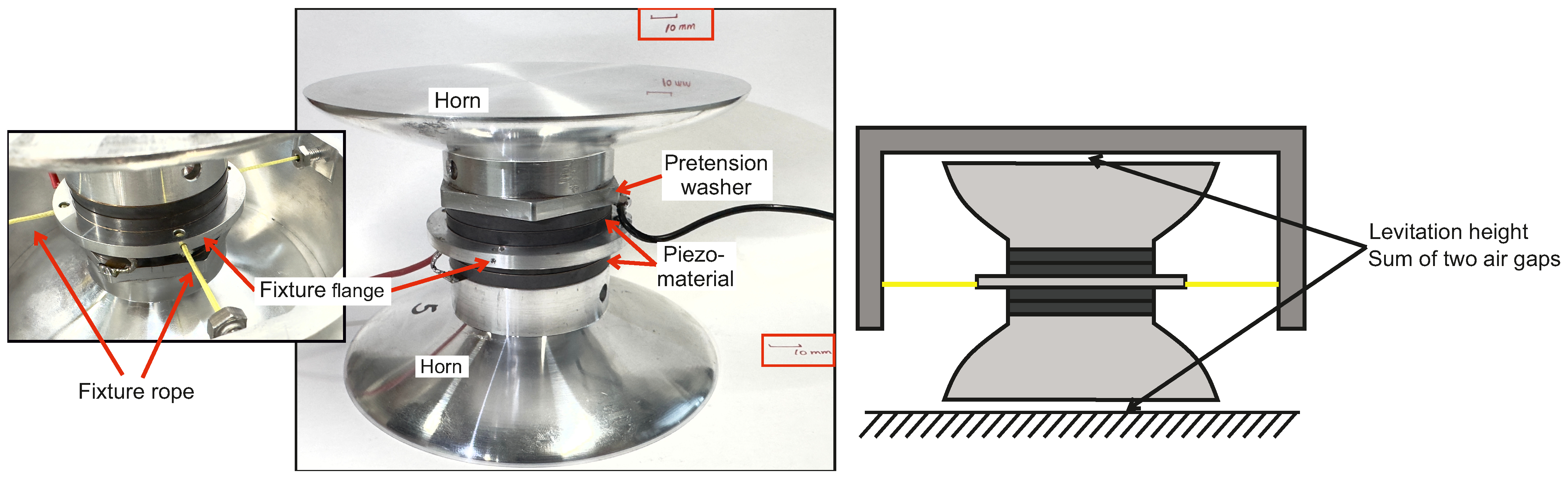
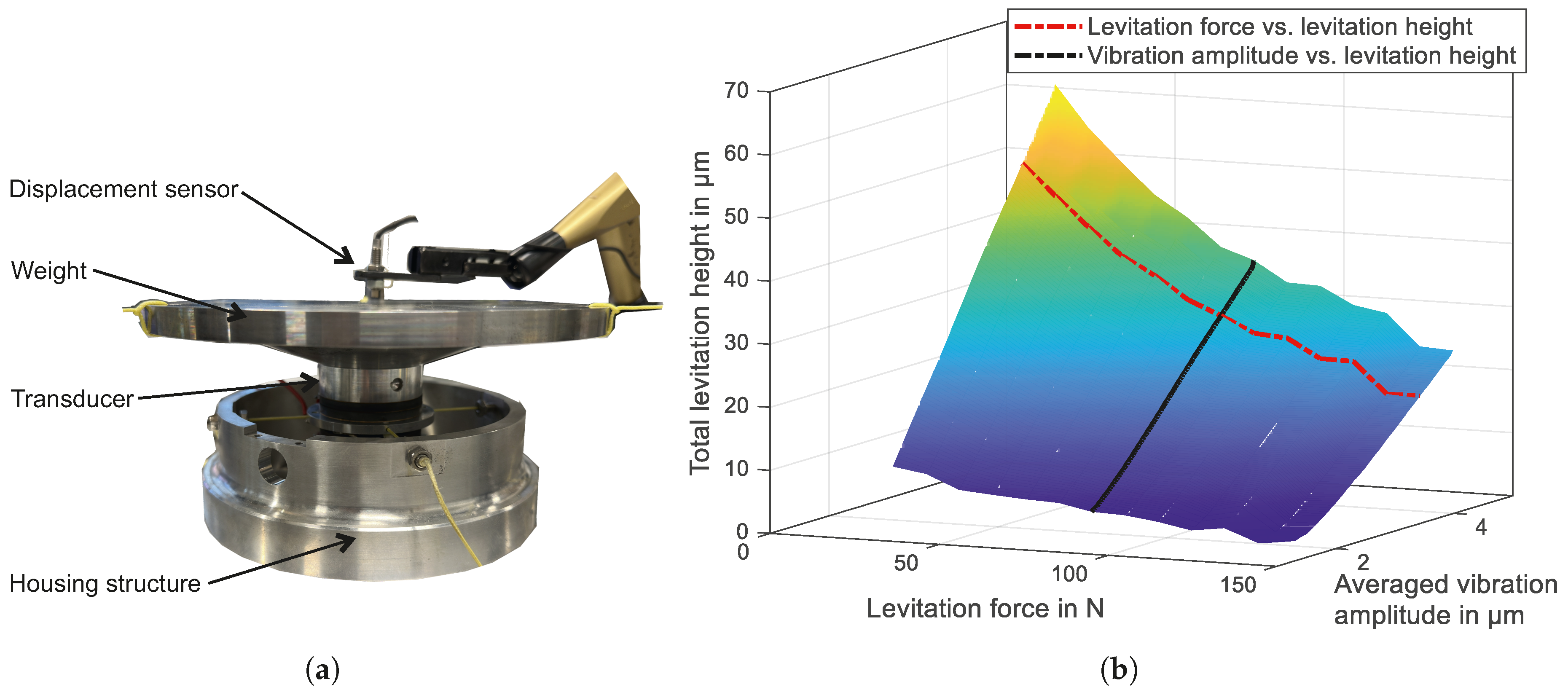
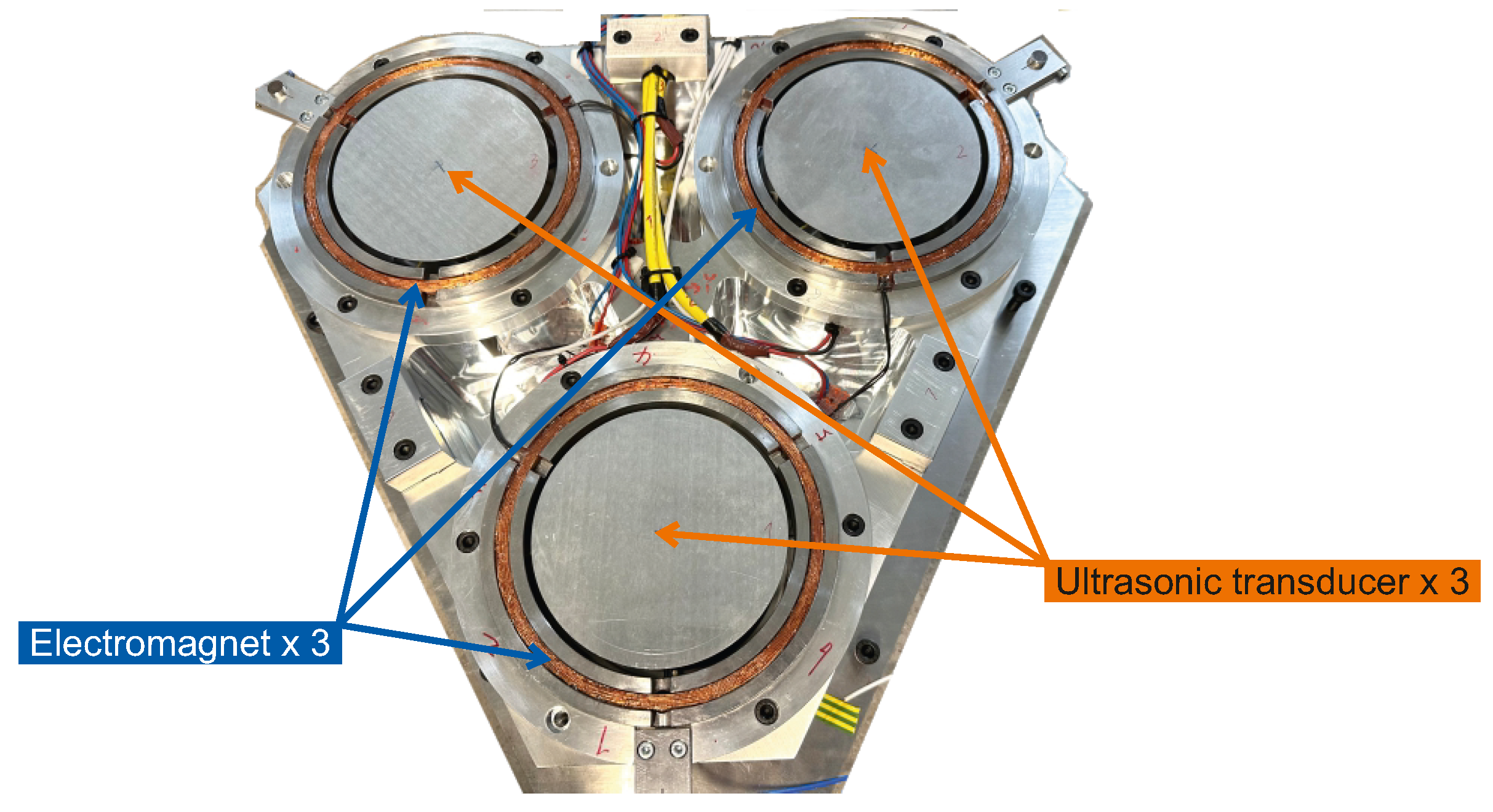
2.3. Transducer Assembly and Characterization
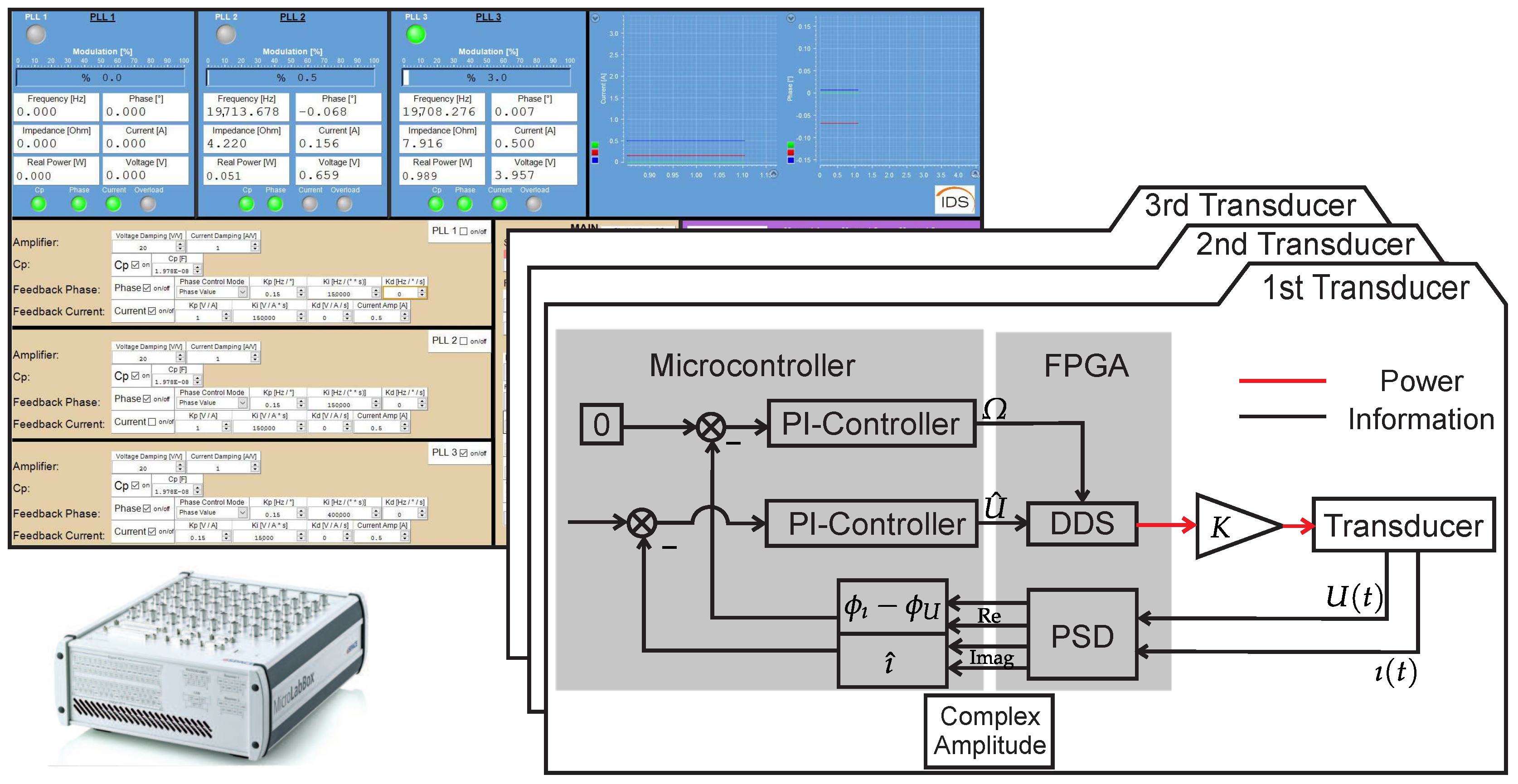
3. Transducer Control Strategy
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MEMS | Multidisciplinary Digital Publishing Institute; |
| PSD | Phase-sensitive demodulation; |
| RCP | Rapid Control Prototyping. |
References
- Zhu, J.; Liu, X.; Shi, Q.; He, T.; Sun, Z.; Guo, X.; Liu, W.; Sulaiman, O.B.; Dong, B.; Lee, C. Development Trends and Perspectives of Future Sensors and MEMS/NEMS. Micromachines 2020, 11, 7. [Google Scholar] [CrossRef]
- Huang, Y.; Sai Sarathi Vasan, A.; Doraiswami, R.; Osterman, M.; Pecht, M. MEMS Reliability Review. IEEE Trans. Device Mater. Reliab. 2012, 12, 482–493. [Google Scholar] [CrossRef]
- Denkena, B.; Dahlmann, D.; Krueger, R. Electromagnetic Levitation Guide for Use in Ultra-Precision Milling Centres. Procedia CIRP 2015, 37, 199–204. [Google Scholar] [CrossRef]
- Reiners, J.; Denkena, B.; Wallaschek, J. Kombinierte Ultraschall-Levitations-Magnetführung; Number Band 11/2022 in Berichte aus dem IFW; TEWISS Verlag: Garbsen, Germany, 2022. [Google Scholar]
- Amano, T.A.T.; Koike, Y.K.Y.; Nakamura, K.N.K.; Ueha, S.U.S.; Hashimoto, Y.H.Y. A Multi-Transducer Near Field Acoustic Levitation System for Noncontact Transportation of Large-Sized Planar Objects. Jpn. J. Appl. Phys. 2000, 39, 2982. [Google Scholar] [CrossRef]
- Chen, K.; Gao, S.; Pan, Y.; Guo, P. Self-Running and Self-Floating Two-Dimensional Actuator Using near-Field Acoustic Levitation. Appl. Phys. Lett. 2016, 109, 123503. [Google Scholar] [CrossRef]
- Li, W.; Zhu, Y.; Feng, K.; Zhang, K. Effect of Surface Grooves on the Characteristics of Noncontact Transportation Using Near-Field Acoustic Levitation. Tribol. Trans. 2018, 61, 960–971. [Google Scholar] [CrossRef]
- Hu, J.; Yang, Y.; Qiu, J.; Yu, W. Acoustic Levitation Characteristics of Hexagon Ultrasonic Arrays and Their Manipulate Methods. In Proceedings of the 2019 14th Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), Shijiazhuang, China, 1–4 November 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Li, W.; Zhang, P.; Yang, S.; Cai, S.; Feng, K. A Novel Two-Dimensional Non-Contact Platform Based on near-Field Acoustic Levitation. Int. J. Mech. Sci. 2024, 265, 108865. [Google Scholar] [CrossRef]
- Davis, S.; Gabai, R.; Bucher, I. Realization of an Automatic, Contactless, Acoustic Levitation Motor via Degenerate Mode Excitation and Autoresonance. Sens. Actuators A Phys. 2018, 276, 34–42. [Google Scholar] [CrossRef]
- Gabai, R.; Shaham, R.; Davis, S.; Cohen, N.; Bucher, I. A Contactless Stage Based on Near-Field Acoustic Levitation for Object Handling and Positioning—Concept, Design, Modeling, and Experiments. IEEE/ASME Trans. Mechatron. 2019, 24, 1954–1963. [Google Scholar] [CrossRef]
- Shi, M.; Liu, X.; Feng, K.; Zhang, K. Experimental and Numerical Investigation of a Self-Adapting Non-Contact Ultrasonic Motor. Tribol. Int. 2021, 153, 106624. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Ding, Z.; Zhang, R.; Chen, T.; Rong, X.; Song, R.; Li, Y. Development of a Compact and Contactless Stage Capable of Levitating\Rotating Wafer Functioning as an Ultrasonically Virtual Hand. IEEE Trans. Ind. Electron. 2024, 71, 14610–14619. [Google Scholar] [CrossRef]
- Li, H.; Cao, C.; Yang, S.; Song, Z.; Li, L.; Cui, S.; Bulading, A.; Zeng, Q. Levitation and Driving Performance of a Non-Contact Rotation Actuator Excited by near-Field Ultrasonic Energy. Phys. Fluids 2025, 37, 077114. [Google Scholar] [CrossRef]
- Foresti, D.; Nabavi, M.; Klingauf, M.; Ferrari, A.; Poulikakos, D. Acoustophoretic Contactless Transport and Handling of Matter in Air. Proc. Natl. Acad. Sci. USA 2013, 110, 12549–12554. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Twiefel, J.; Ma, Z.; Yu, T.; Wallaschek, J.; Fischer, P. Dynamic Acoustic Levitator Based On Subwavelength Aperture Control. Adv. Sci. 2021, 8, 2100888. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Wang, X.; You, F.; Xiao, H. Review of Ultrasonic Particle Manipulation Techniques: Applications and Research Advances. Micromachines 2023, 14, 1487. [Google Scholar] [CrossRef] [PubMed]
- Andrade, M.A.B.; Pérez, N.; Adamowski, J.C. Review of Progress in Acoustic Levitation. Braz. J. Phys. 2018, 48, 190–213. [Google Scholar] [CrossRef]
- Zhao, S.; Wallaschek, J. A Standing Wave Acoustic Levitation System for Large Planar Objects. Arch. Appl. Mech. 2011, 81, 123–139. [Google Scholar] [CrossRef]
- Andrade, M.A.B.; Okina, F.T.A.; Bernassau, A.L.; Adamowski, J.C. Acoustic Levitation of an Object Larger than the Acoustic Wavelength. J. Acoust. Soc. Am. 2017, 141, 4148–4154. [Google Scholar] [CrossRef]
- Zhao, S.; Mojrzisch, S.; Wallaschek, J. An Ultrasonic Levitation Journal Bearing Able to Control Spindle Center Position. Mech. Syst. Signal Process. 2013, 36, 168–181. [Google Scholar] [CrossRef]
- Salbu, E.O.J. Compressible Squeeze Films and Squeeze Bearings. J. Basic Eng. 1964, 86, 355–364. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape; Van Nostrand Reinhold Co.: New York, NY, USA, 1979. [Google Scholar]
- Mojrzisch, S.; Wallaschek, J. Transient Amplitude Behavior Analysis of Nonlinear Power Ultrasonic Transducers with Application to Ultrasonic Squeeze Film Levitation. J. Intell. Mater. Syst. Struct. 2013, 24, 745–752. [Google Scholar] [CrossRef]
- Ille, I.; Wallaschek, J.; Sextro, W. Modellbasierter, Resonanter Betrieb Schwach Gedämpfter Ultraschallsysteme; Number Band 03/2022 in Berichte aus dem IDS; TEWISS Verlag: Garbsen, Germany, 2022. [Google Scholar]
- Ille, I.; Twiefel, J. Model-Based Feedback Control of an Ultrasonic Transducer for Ultrasonic Assisted Turning Using a Novel Digital Controller. Phys. Procedia 2015, 70, 63–67. [Google Scholar] [CrossRef]
- Smith, R.W.M.; Freeston, I.L.; Brown, B.H.; Sinton, A.M. Design of a Phase-Sensitive Detector to Maximize Signal-to-Noise Ratio in the Presence of Gaussian Wideband Noise. Meas. Sci. Technol. 1992, 3, 1054. [Google Scholar] [CrossRef]
- Li, R.; Li, Y.; Sang, H.; Liu, Y.; Chen, S.; Zhao, S. Study on Near-Field Acoustic Levitation Characteristics in a Pressurized Environment. Appl. Phys. Lett. 2022, 120, 034103. [Google Scholar] [CrossRef]
- Denkena, B.; Wallaschek, J.; Buhl, H.; Twiefel, J.; Ding, C.; Chen, Z. Media-Free and Contactless Micro-Positioning System Using Ultrasonic Levitation and Magnetic Actuators. Actuators, 2025; submitted. [Google Scholar]



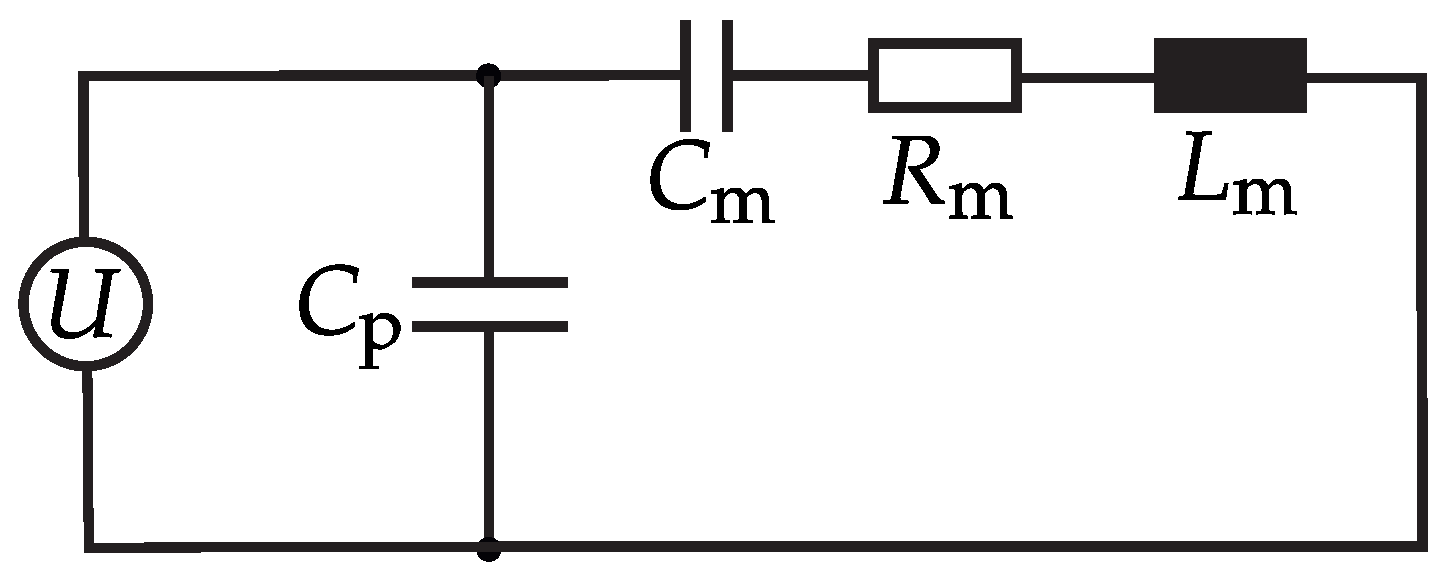
| Parameter | Value | Unit |
|---|---|---|
| 30.71 | mH | |
| 4.89 | Ohm | |
| 1.61 | nF | |
| 18.38 | nF | |
| 890.37 | - | |
| 171.81 1 | mm/As |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Twiefel, J.; Ding, C.; Buhl, H.; Denkena, B.; Wallaschek, J. Novel Design and Control of Ultrasonic Transducers for a Media-Free Contactless Micro-Positioning System. Actuators 2025, 14, 547. https://doi.org/10.3390/act14110547
Chen Z, Twiefel J, Ding C, Buhl H, Denkena B, Wallaschek J. Novel Design and Control of Ultrasonic Transducers for a Media-Free Contactless Micro-Positioning System. Actuators. 2025; 14(11):547. https://doi.org/10.3390/act14110547
Chicago/Turabian StyleChen, Zijian, Jens Twiefel, Chenglong Ding, Henning Buhl, Berend Denkena, and Jörg Wallaschek. 2025. "Novel Design and Control of Ultrasonic Transducers for a Media-Free Contactless Micro-Positioning System" Actuators 14, no. 11: 547. https://doi.org/10.3390/act14110547
APA StyleChen, Z., Twiefel, J., Ding, C., Buhl, H., Denkena, B., & Wallaschek, J. (2025). Novel Design and Control of Ultrasonic Transducers for a Media-Free Contactless Micro-Positioning System. Actuators, 14(11), 547. https://doi.org/10.3390/act14110547









