Abstract
This paper presents an innovative three-level direct yaw moment control strategy for distributed drive electric vehicles (DDEV) under emergency conditions. The phase plane analysis is used at the supervisory level to design the stability boundary function taking into account the impact of the road adhesion coefficient. To guarantee the performance of finite-time convergence and singularity-free methods, the adaptive nonsingular fast terminal sliding mode control (ANFTSMC) is developed at the decision level to determine the extra yaw moment for tracking the intended side slip angle and yaw rate. Among this, the unstable domain in the phase plane is further separated into moderately and severely unstable according to the degree of vehicle instability, which is defined by the distance between the state phase point and the stability boundary. Meanwhile, the adaptive weight between the handling and stability is obtained. At the executive level, the quadratic programming algorithm is adopted to allocate four-wheel torque with the objective of optimal tire utilization rate. Finally, the co-simulation test is executed in both closed-loop and open-loop circumstances; according to the simulation results, the presented ANFTSMC method outperforms the SMC, and it can decrease the tracking error and improve the handling and stability.
1. Introduction
Electric vehicles (EVs) stand out as a compelling remedy for energy scarcity and environmental pollution [1]. As a kind of EV, distributed drive electric vehicles (DDEV) exhibit distinct advantages over centralized configurations due to the four wheels can be controlled independently, accurately, and quickly [2]. Thus, the most effective platform for implementing advanced vehicle dynamics control is generally acknowledged to be the DDEV. In order to improve driving safety and reduce the number of traffic accidents, active safety control systems have been the subject of intensive research. Among these, active front wheel steering (AFS) and direct yaw moment control (DYC) are effective techniques to enhance lateral stability and handling. The difference is that AFS can change lateral tire force by producing an additional angle to the front wheel, but DYC can provide a corrective yaw moment created by longitudinal tire force [3]. It is noteworthy that DYC outperforms AFS, particularly in ensuring vehicle stability during emergency conditions including high speed, slippery pavement, and substantial steering wheel angles [4]. This is due to the fact that in the nonlinear work domain under emergency conditions, the control margin of longitudinal tire force surpasses that of lateral tire force [5]. Consequently, DYC exhibits superior performance across both linear and nonlinear work domains of DDEV.
Extensive research has been conducted on DYC. Typically, DYC comprises two parts: one is the extra yaw moment calculation, and another is the torque distribution. The two critical determinants impacting the handling and stability of DDEV are the yaw rate and side slip angle. Thus, the corrective yaw moment is generated to make the current yaw rate and side slip angle reach the desired values. Several control methodologies have been developed, encompassing diverse approaches such as model predictive control (MPC), sliding mode control (SMC), fuzzy control (FC), and others.
Zhang [6], Zhao [7], and Wang [8] proposed the fuzzy controller to determine the corrective yaw moment. Zhao designed the fuzzy rule base, the discrepancy between the actual and intended state is the input, and the additional yaw moment is the output. Wang established a fuzzy-based DYC strategy to respectively track the desired states, and the switching scheme is presented. Fuzzy control has a relatively low requirement for the precision of the vehicle dynamics model; however, the fuzzy rules are formulated based on empirical knowledge, resulting in a high level of complexity. Shen [9], Liang [10], and Zhu [11] presented the model predictive controller to track the driver’s intended command. To improve tracking precision and stability within the handling limit, Shen employed the MPC method to calculate the corrective yaw moment. Liang designed a dual linear time vary MPC structure considering energy saving and stability. The model predictive control can predict future situations with multi-objectives and actuator constraints, but it requires a significant amount of computation. Mok established a sliding mode controller that produces a corrective yaw moment to track the intended yaw rate [12]. Park presented a smooth sliding mode control approach to enhance the convergence speed and handling, incorporating a feed-forward term related to the desired yaw rate [13]. Chae developed a cascade structure controller, where the outer layer determines the intended yaw rate, and the inner layer creates the additional yaw moment [14]. To accommodate changes in road adhesion conditions, Zhai proposed a handling stability control scheme with an enhanced sliding mode control algorithm [15]. Ding presented a second-order sliding mode controller using a power integrator technique to improve vehicle stability and reduce system chattering [16]. Zhang integrated sliding mode control with a fuzzy algorithm to eliminate system chattering, and the continuous discrete symbolic function is generated using fuzzy rules. This approach can improve vehicle stability and control error convergence rate [17]. The remarkable advantage of sliding mode control is its robustness to parametric uncertainties, external disturbances, and unmodeled dynamics [18]. Therefore, for strongly nonlinear vehicle systems, it offers superior robustness to changes in vehicle state parameters such as velocity, road adhesion, and so on. However, one drawback is that it can take a long time for the system state tracking error to asymptotically converge to an equilibrium point.
The extra yaw moment is produced by adjusting the four-wheel torque, a technique known as torque allocation control. The torque allocation scheme varies due to the high redundancy with multiple actuators of DDEV. Generally, the torque allocation method mainly includes rules-based and optimization-based approaches. The rules-based method distributes the longitudinal tire force with a specific proportion, such as average allocation and axle load proportional allocation [19]. It has the advantage of simple computation but neglects the influence of road adhesion conditions, which determine the generated maximum tire forces in emergency conditions. The optimization-based method calculates the wheel torque based on the multiple objectives with constraints. Zhai proposed a torque optimal distribution strategy that considered the impact of wheel slip and variations in road adhesion [20]. Peng presented a torque coordination control strategy to balance vehicle stability and energy consumption [21]. Hu designed a two-level torque distribution formula: one is the allocation between both axles, with the allocation proportion calculated by the model predictive control method, and another is the distribution between four wheels to satisfy the extra yaw moment [22]. Guo presented a two-step approach based on the Karush–Kuhn–Tucker optimality criterion to distribute the four-wheel torque [23].
Several studies on direct yaw moment control have been carried out, but there are still some issues that need to be resolved, especially considering the characteristics of nonlinearity and over-actuation of DDEV under emergency conditions. The angle formed by the driving direction and longitudinal axis is called the side slip angle, which represents the traceability to the desired trajectory [24]. The yaw rate is the definition of the deflection angle rate around the vertical axis, and it represents vehicle steering and maneuverability performance [25]. In the previous studies, the major control variables of most DYC strategies are yaw rate and side slip angle, but the research on the coordination control between the two parameters is scarcer. It is imperative to point out that the control priority and weight between handling and stability should be adjusted with the change in vehicle state, and a clear quantitative indicator needs to be defined to describe the degree of vehicle instability.
This paper proposes a novel DYC methodology with a three-level framework to coordinate handling and stability for DDEV. The top level is contributed to resolve the reference value of key control parameters, and the impact of road adhesion conditions is taken into account. Furthermore, the stability boundary function is obtained by employing the phase plane analysis approach. In the middle level, to overcome the drawback that SMC cannot drive the state to asymptotically converge with the equilibrium point with finite time, and the singularity issue of terminal sliding mode control (TSMC), the adaptive nonsingular fast terminal sliding mode control (ANFTSMC) method is adopted to determine the extra yaw moment. Additionally, this method introduces a nonlinear sliding hyperplane instead of the conventional linear sliding hyperplane to improve the performance of fast finite-time convergence. Meanwhile, the concept of vehicle instability degree is introduced based on the distance between the state point and the stability boundary, and the unstable domain in the phase plane is further split into sections that are moderately and severely unstable. The vehicle instability degree provides the design basis for determining the control weight coefficient between the side slip angle and yaw rate. The lower level is implemented to allocate four-wheel torque with the objectives of minimizing allocation error and maximizing stability margin. Additionally, the limiting conditions of peak motor torque and friction ellipse are considered. Eventually, the simulation model of the presented DYC strategy is built on the co-simulation platform of Carsim and Simulink, and its effectiveness is confirmed under both closed-loop and open-loop driving conditions.
The remainder of the paper is structured as follows. The dynamics modeling of DDEV is described in Section 2. The stability boundary function is formulated, employing the phase plane analysis approach outlined in Section 3. The decision controller is designed in Section 4. The executive controller is introduced in Section 5. The simulation is validated in Section 6, and Section 7 is the conclusion.
2. Dynamics Modeling of DDEV
2.1. 7-DOF Model
The seven-degrees-of-freedom (7-DOF) vehicle dynamics model is adopted for subsequent phase plane analysis and control strategy design, as shown in Figure 1, which incorporates the longitudinal, lateral, yaw, and rotation of four wheels.
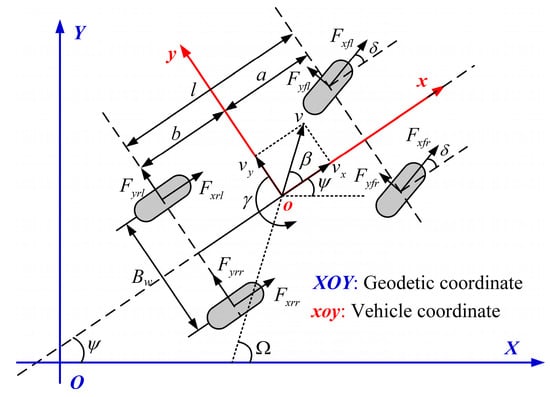
Figure 1.
7-DOF vehicle dynamics model.
The longitudinal and lateral motions are modeled as follows:
The resultant yaw moment includes two parts; Mzx is derived from the longitudinal tire forces, Mzy is derived from the lateral tire forces, and is described as follows:
The yaw moment derived from the left-front wheel can be indicated as follows:
Therefore, the yaw motion is described as follows:
where m is the vehicle mass. a and b correspond to the length between the vehicle’s gravity center and the front and rear axles. ax and ay correspond to the longitudinal and lateral acceleration. vx and vy correspond to the longitudinal and lateral speeds. δ is the steering angle of the front wheels, assuming the steering angles of the front left and right wheels are equal. γ is the yaw rate. ∑Mz is the resultant yaw moment. Iz is the inertia moment about the z-axis. Bw is the wheel track. Fyij is lateral tire force. Fxij is longitudinal tire force. The symbol ij (ij = fl, fr, rl, rr) denotes front left, front right, rear left, and rear right.
The β and γ satisfy the following relationship:
where Ω is the course angle, is the yaw angle.
Figure 2 shows the wheel rotational dynamics model. The longitudinal tire force of each wheel is calculated as follows:
where ωij is the wheel angular speed. Jωij is the wheel inertia moment. Re is the effective rolling radius. Tdij and Tbij are the motor driving and braking torque.
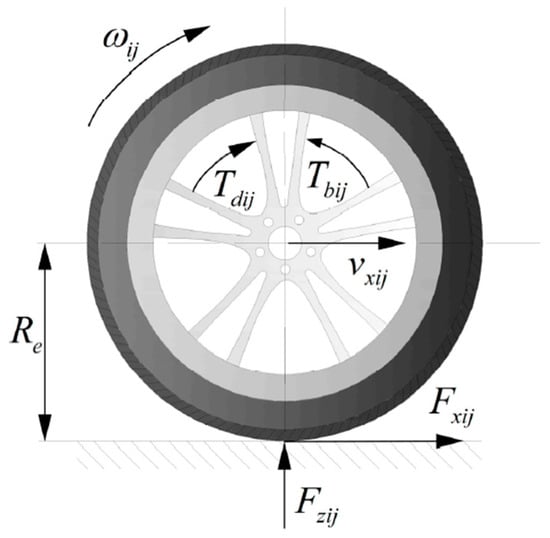
Figure 2.
Wheel rotational dynamics model.
2.2. Magic Formula Tire Model
Tires provide the vehicle’s interaction with the road, and thus the tire characteristics have a direct impact on the vehicle’s dynamic performance [26]. Tire forces and moments are related to a variety of factors, such as tire slip angle, slip ratio, vertical load, and road adhesion coefficient. The tire characteristics can be described by the appropriate model. In this study, the most famous Magic Formula is selected because of its high fitting precision and unified expression form. It can be expressed as follows:
where Y corresponds to the longitudinal tire force, lateral tire force, or aligning torque. Corresponding to Y, X indicates the longitudinal tire slip ratio or side angle. B, C, and D represent the stiffness, shape, and peak factor. E is the curvature factor. Sh and Sv are the shifts of horizontal and vertical.
The longitudinal tire force under the condition of pure longitudinal slip can be described as follows:
where the coefficients are defined as follows:
The lateral tire force in the case of pure side slip is formulated as follows:
where the coefficients are defined as follows:
where ai (i = 0, 1, …, 8) are the fitting parameters of lateral tire force, bi (i = 0, 1, …, 8) are the fitting parameters of longitudinal tire force, and they can be obtained by the tire force testing given in the following Table 1.

Table 1.
Fitting parameters of the Magic Formula.
The expression for tire slip angle is as follows:
The tire slip ratio can be calculated as follows:
where vwxij denotes the wheel center velocity, as shown in Equation (16):
The tire vertical load has an impact on the coefficients in Magic Formula, and, when the vehicle is turning, the tire vertical load is transformed and calculated as the following equation:
where Fzij is the vertical load, hg is the height of the gravity center, l is the wheelbase, and g is the gravity acceleration.
In practice, the longitudinal and lateral tire forces coexist and interact, and satisfy the following equation:
Based on the above analysis, the characteristic curves are drawn in Figure 3 under different conditions, including pure longitudinal slip, pure side slip, and combined condition.
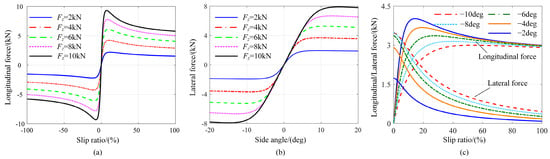
Figure 3.
The characteristic curve of tire forces: (a) the longitudinal tire force under different vertical forces; (b) the lateral tire force under different vertical forces; (c) the combined condition under different tire slip angles.
2.3. Reference Model
The handling and stability control is intended to address two critical issues of trajectory maintenance and driving stability, which are determined by the key control variables of the DYC system: the side slip angle and yaw rate. The steady-state steering characteristics of the vehicle and the driving intention can be described by the reference model. The 2-DOF model has less computation and parameters, and it includes two degrees of freedom in lateral and yaw. It is widely used as the control reference model [27]. Therefore, the 2-DOF model is employed to deduce the desired control value.
The motion equation in lateral and yaw is derived as follows:
where Fyf and Fyr are the lateral tire forces of the front and rear wheels, respectively.
Under the steady-state steering condition, vx is constant, δ is small, and the lateral tire force is a linear function of tire slip angle as follows:
where Cf is the cornering stiffness of the front wheel, and Cr is the cornering stiffness of the rear wheel. αf and αr are the slip angles of the front and rear wheels, respectively.
Meanwhile, Equation (14) can be rewritten as follows:
Thus, Equation (19) is rewritten as follows:
Under the steady-state steering conditions, , are established, and the intended value of yaw rate and side slip angle is deduced as:
where K is the insufficient steering coefficient, it is defined as follows:
In addition, the desired value is related to the road adhesion capacity and tire nonlinearity, and the limiting value is as follows [28]:
In summary, the desired value is reconstructed as follows:
3. Stability Boundary Function
The proposed DYC strategy with a hierarchical architecture is displayed in Figure 4, which includes supervisory, decision, and executive levels. At the supervisory level, the 2-DOF model is employed to calculate the control reference values of yaw rate and side slip angle, and the limited road adhesion capacity and tire nonlinearity are considered. Meanwhile, to guarantee the control strategy works timely and accurately, the concept of vehicle instability degree is proposed, and the phase plane is further partitioned into stable, moderately unstable, and severely unstable regions. The objective of the decision level is to generate extra yaw moment by adopting the ANFTSMC algorithm, and the coordination control weight between the side slip angle and yaw rate is designed based on the vehicle instability degree. Finally, the four-wheel torque is dynamically adjusted by the optimization distribution method at the executive level.
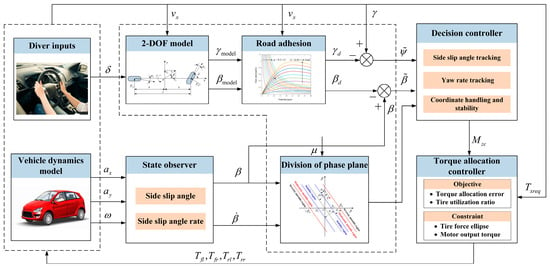
Figure 4.
The control strategy architecture.
It is essential to make sure that stability control intervenes promptly while avoiding interference with the driver’s operation. The phase plane is widely used to research the dynamic response characteristics of nonlinear systems [29]. The schematic of the phase plane is displayed in Figure 5. In order to streamline calculation, the boundary lines of the stability domain are set as AB and CD, and the stability boundary function can be formulated by the two-line method as follows:
where E1 and E2 are constant coefficients.
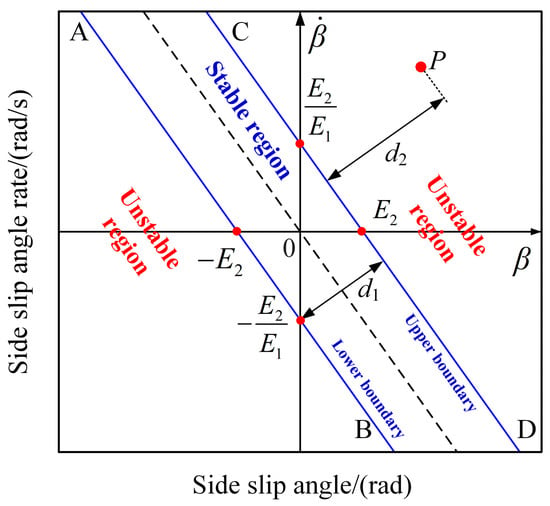
Figure 5.
The schematic of phase plane.
Therefore, when Equation (30) holds, starting from the arbitrary initial state in the stability domain, the phase trajectory can converge to the equilibrium point. On the contrary, the vehicle is unstable and needs to be applied to additional control quickly. The road adhesion coefficient μ, vehicle velocity vx, and front-wheel steering angle δ are the major factors that determine the boundary of the stability domain. This paper focuses on emergency conditions, so the effect of road adhesion coefficient on stability boundary is emphasized.
The nonlinear characteristic of the vehicle is mostly attributed to the tire. Based on the established tire model and 7-DOF vehicle model in Section 2, combining Equation (12) with Equations (2) and (3), the state equation is derived as below:
Based on the phase plane analysis theory, vx, μ, and δ are given, the initial vehicle state point is set, and the solution of this state equation is a phase trajectory curve. Set δ = 0, vx = 80 km/h, 0.1 ≤ μ ≤ 0.8, and the simulation is carried out under different road adhesion coefficients at 0.1 intervals. The phase trajectories can be drawn in Figure 6, and, based on the division principle of whether the phase trajectory curve converges to the equilibrium point, the phase plane is partitioned into two parts (stable and unstable domains). It is observed that when the road adhesion coefficient is less than 0.6, the stable region expands as the road adhesion coefficient increases, which means that the high road adhesion coefficient can provide a large stability margin. When the road adhesion coefficient is beyond 0.6, the stable region is almost invariable. Therefore, based on the two-line method, the boundary coefficients E1 and E2 under different road adhesion coefficients are obtained in Table 2.
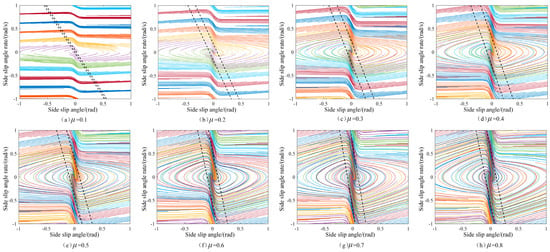
Figure 6.
The β− phase plane with different road adhesion coefficients.

Table 2.
The stable boundary with different tire-road adhesion coefficients.
4. Decision Controller
At the decision level, the extra yaw moment is obtained for tracking the intended side slip angle and yaw rate. The DDEV shows strong nonlinearity under extreme driving conditions, and the parameters of the vehicle and environment change with the driving state. The vehicle model is built with certain assumptions to simplify the calculation, which will cause inevitable errors. The SMC is one of the variable structure controls, and it can make the system state slide along a certain sliding hyperplane by changing the system structure when the state deviates from the expected trajectory. The advantages of SMC are robust to parametric uncertainties, external disturbances, and unmodeled dynamics. Thus, it is frequently employed in research on vehicle dynamics control [30].
Since it is hard to control lateral tire force directly, the decision controller is designed to determine the additional yaw moment Mzc, which is related to longitudinal tire forces. Based on Equation (5), Mzc is expressed as follows:
The basic equation of a second-order uncertain nonlinear system is as follows:
where x = [x1, x2]T is the system state vector. f(x) and g(x) are the nonlinear functions of x. u is the control input. d(x) represents the system uncertainties and external disturbances, D is the upper boundary, d(x) D and D > 0.
There are two key steps of the sliding mode controller design. The first is the sliding surface, where the system state points exhibit the desired dynamic characteristics. The second is the control law, which makes the state reach the sliding surface and keep on it. Nevertheless, the system state cannot asymptotically converge to the equilibrium point within a finite time. To overcome this shortcoming, the nonlinear function is used to design the sliding surface, which is terminal sliding mode control (TMSC) [31]. In addition, boundless control input exists when the control output is within the neighborhood of the origin. To avoid this control singularity problem, the nonsingular terminal sliding mode control (NTSMC) is further proposed, which not only has the advantage of SMC but also satisfies finite-time convergence and is singularity-free [32]. These merits ensure accurate tracking to the desired state [33]. Therefore, the NTSMC is implemented in this paper to design the decision controller for obtaining the additional yaw moment. The decision level includes two controllers, which make efforts to track the intended side slip angle and yaw rate. Meanwhile, to enhance the convergence speed of tracking error, an exponential term is introduced to establish the sliding mode switching function, and self-adaptation is used to predict the unknown upper boundary to enhance the controller performance.
4.1. Side Slip Angle Tracking Controller
According to Equation (2) of the 7-DOF vehicle model, the sliding mode equation of the side slip angle is derived as follows:
The time derivative of Equation (34) is given as follows:
Based on Equation (33), set x1 = β and x2 = , and the control system model is described as follows:
where dβ(x,t) is the system uncertainties and external disturbances, satisfying |dβ(x,t)| ≤ Dβ and Dβ > 0, Dβ is the upper boundary.
The error between the actual and desired value is expressed as follows:
The time derivative of Equation (37) is given as follows:
To enhance the convergence speed, the exponential term is introduced in the sliding mode switching function of NTSMC, which is defined as follows:
where , are constant and satisfy , .
To avoid the complex item in Equation (40) when and , Equation (40) is rewritten as follows:
where , are constant, satisfying , ,.
The derivative of Equation (41) yields:
To improve the dynamic quality in the reaching phase, the trajectory of the system state point approach to the sliding mode surface is specified as the following reaching law:
where , . This reaching law includes two parts: the constant reaching law and the index reaching law . The approaching speed is determined by when the state point is far from the sliding mode surface and depends on when the state point is in proximity to the sliding mode surface. These two reaching laws can guarantee the state point fast traverse forward sliding mode surface while also reducing the chattering.
Substituting Equation (43) into (42) yields:
Then, the control law of NFTSMC is obtained as follows:
where , ; thus, there is no negative exponential term in this control law, which effectively overcomes the singularity problem of the conventional TSMC.
To further alleviate the chattering caused by the inappropriate setting of the unknown upper boundary of system uncertainties and external disturbances, self-adaptation is employed to estimate the unknown upper boundary. The estimation error is defined as follows:
The self-adaptation law is set as follows:
where is the adaptive gain .
The derivation of Equation (46) as follows:
Finally, the control law of NFTSMC with self-adaptation can be obtained as follows:
4.2. Yaw Rate Tracking Controller
Based on Equation (5) of the 7-DOF vehicle model, the sliding mode equation of the yaw rate is formulated as follows:
Set , , and the control system model of the yaw rate is given as follows:
where dγ(x,t) is the system uncertainties and external disturbances, and satisfying |dγ(x,t)| ≤ Dγ and Dγ > 0, Dγ is the upper boundary.
The error between the actual and desired value is formulated as follows:
The first and second derivates of Equation (52) are as follows:
The sliding mode switching function is designed as follows:
where , , , are constant, , , , .
The derivate of Equation (55) is as follows:
The reaching law is selected as follows:
where , .
Substituting Equation (57) into (56), the control law can be obtained as follows:
Similar to the side slip angle tracking controller, the adaptation law is designed for the estimation of unknown upper boundaries for system uncertainties and external disturbances, and the estimation error is expressed as follows:
The definition of adaptation law is as follows:
where is adaptation gain, .
The derivation of Equation (59) is as follows:
The control law of ANFTSMC for the yaw rate is further deduced as follows:
4.3. Proof of the Stability and Finite-Time Convergence
First, the stability of the side slip angle control system is verified. The following Lyapunov function is constructed:
Substituting the control law (49) into Equation (42) yields the following:
Substituting the Equations (64), (47) and (46), the time derivative of V1 can be obtained as follows:
Since , then:
Therefore, based on the Lyapunov stability criterion, the existence and reachability of sliding mode motion are proved, and the side slip angle control system is asymptotically stable. In addition, V1, s, are bounded and set at , .
Then, prove that the tracking error of the side slip angle can converge with finite time and consider the Lemma 1 as follows:
Lemma 1.
Considering the nonlinear system , if the Lyapunov function V(x) satisfies [34]
where V(x) is a continuous differentiable positive function. , , are constant, , , . The initial state at to time is . Then, it is considered that the system can converge to the equilibrium pointwithin a finite time T:
where is the starting value.
Reconstruct the Lyapunov function as follows:
Substituting the control law (49) into (69), since , , the derivative of Equation (69) is as follows:
where
Thus, for the case of , then , if , are chosen such that , the and are established, is validated. Therefore, based on Lemma 1, within finite time tr in Equation (73), the tracking error can converge to the equilibrium point:
where is the starting value of .
For the case , the system state point in the reaching phase (), substituting the control law (49) into (39) as follows:
Since , , , when , then , will decrease quickly. When , then , will increase quickly. Therefore, the phase trajectory as shown in Figure 7, for the case , starting from the arbitrary initial state in the phase plane, the tracking error can converge to the equilibrium point.
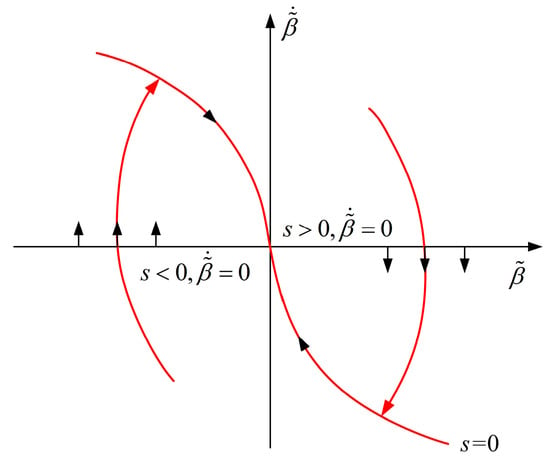
Figure 7.
Phase trajectory.
When s = 0, then
The tracking error becomes with a finite time ts given as follows [35]:
where represents the Gauss hypergeometric function.
In conclusion, the control system stability of side slip is proved both when and . The system state can reach the sliding mode surface and the tracking error can converge to the equilibrium point with finite time. Similar to the above analysis, the stability and finite-time convergence of the yaw rate control system can be proved.
In addition, there are inevitably chattering phenomena when the system state points near the sliding mode surface. At this moment, the state points back and forth across the sliding mode surface [36]. This is due to the discontinuity characteristic of the sign function in reaching law. In order to attenuate chattering, the sign function is substituted as the saturation function around the switching surface.
where is the width of the boundary layer.
4.4. Adaptive Weight between the Handling and Stability
The decision level comprises two controllers, and the control weight should be adapted in real time when the vehicle motion state changes. In the previous research, the phase plane is simply separated by stable and unstable regions, and the research on weight allocation is lacking. In this paper, the concept of vehicle instability degree is proposed. It is the foundation for the distribution of control weight and is defined by the distance between the state point and stability boundary. According to the vehicle instability degree, the phase plane is further separated into three domains, including stable, moderately unstable, and severely unstable. This method can realize stability control while guaranteeing the handling.
As shown in Figure 5, set point P as the arbitrary point in the instability region, and then
where d1 is the width of the stability region, d2 is the distance between point P and the stability boundary, and |PO| is the distance between point P and the centerline of the stability region.
Based on the distance between point P and the stability boundary, the degree of vehicle instability can be defined as follows:
where represents the degree of vehicle instability. The distance between point P and the stability boundary is larger, and is larger. When the state points in the stable region, is zero.
According to the vehicle instability degree, the instability region can be further divided into the moderately unstable and the severely unstable regions exhibited in Figure 8.
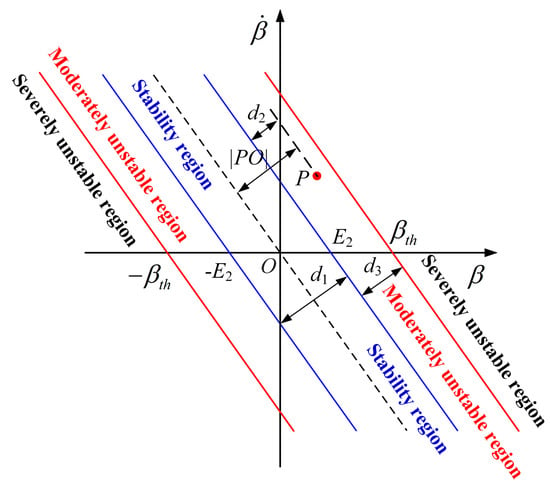
Figure 8.
Region division of phase plane.
βth is the threshold value, commonly set as 10 deg [37]. The vehicle is severely unstable when β > βth, and the boundary of the severely unstable region is formulated as follows:
The boundary of the moderately unstable region can be formulated as follows:
The width of the moderately unstable region is given as follows:
In the moderately unstable region, the distance between point P with the stability boundary is described as follows:
Inside the moderately unstable region, the main objective is to restore the vehicle from unstable to stable, while meanwhile taking into account the vehicle handling. Thus, the side slip angle and yaw rate are both managed with the corresponding weight. The distance between the state point and the stability boundary is larger, is higher and the control weight of the side slip angle should be increased. is lower, the control weight of the yaw rate should be increased. Inside the severely unstable region, the side slip angle exceeds the threshold value, and the driver cannot change the front wheel angle by manipulating the steering wheel; in this case, the major control objective is vehicle stability. According to the above analysis, the weight coefficient of the side slip angle is defined as follows:
where Cβ is the weight coefficient, and 1 ≤ Cβ ≤ 0.
Inside the moderately unstable region, the control weight of the yaw rate is 1 − Cβ, and inside the severely unstable region, the control weight is 0. Finally, the extra yaw moment is deduced as follows:
5. Torque Allocation Controller
5.1. Allocation Objective
The torque distribution can be regarded as an optimization allocation issue with multi-objective and multi-constraints. The allocated longitudinal tire forces of four wheels must satisfy the total longitudinal force requirement of the driver. Meanwhile, the yaw moment derived from longitudinal tire force should equal the one determined in the decision controller, which is described as follows:
Equation (88) can be rewritten in matrix form as follows:
where
- ,
- ,
- .
The first objective function J1 is constructed to minimize the torque allocation error:
where , WF and WM are the weight matrix of longitudinal and lateral force, and, here, [38].
The tire utilization ratio is expressed in Equation (91), and it represents the vehicle stability margin:
where ηij is the tire utilization ratio, and 0 ≤ ηij ≤ 1. The higher tire utilization ratio means that more road adhesion force is consumed, and less road adhesion force is used to keep stable; at the same time, the tire forces tend to saturate, and the vehicle stability margin is reduced.
Therefore, to maximize the vehicle stability margin, the second objective function J2 is constructed. The longitudinal tire force can be adjusted by the motor controller, but the lateral tire force is difficult to control directly. With the assumption that the road adhesion coefficient is fixed, J2 can be expressed as follows:
where
- .
5.2. Constraints
The tire force ellipse describes the connection between the longitudinal and lateral tire forces. The resultant of these two forces is restricted by maximum road adhesion force, which can be formulated as follows:
The longitudinal tire force should be less or equal to the maximum output torque of the motor:
where Tdmax is the maximum driving torque, and Tbmax is the maximum braking torque.
Above all, the constraints of this optimization problem are summarized as follows:
5.3. Solution of the Optimization Problem
According to Equations (90) and (92), the torque distribution can be treated as a quadratic programming (QP) problem [39] as follows:
By introducing the weight coefficient ρ, Equation (96) can be rewritten as follows:
where , .
The active set method [40] is utilized to tackle this quadratic programming issue and produce the optimal allocated longitudinal tire force of four wheels.
6. Simulation and Analyses
To confirm that the presented DYC method is feasible, the simulation test is conducted on the co-simulation platform of Simulink and Carsim. The main geometric and inertial parameter settings of the DDEV model are given in Table 3. The relevant parameters of the control strategy are given in Table 4. The closed-loop simulation of double lane change and serpentine maneuvers and the open-loop simulation of sine steering angle input maneuvers are conducted, respectively. Furthermore, the simulation results of uncontrol and traditional SMC [16] strategies are compared with the proposed controller.

Table 3.
Parameters of DDEV.

Table 4.
Parameters of DYC strategy.
6.1. Double Lane Change Maneuver
The double lane change test is carried out (vx = 80 km/h, μ = 0.3). The scheme of double lane change is shown in Figure 9. The total length of the test road is 200 m, and the length and width of each road section are indicated.
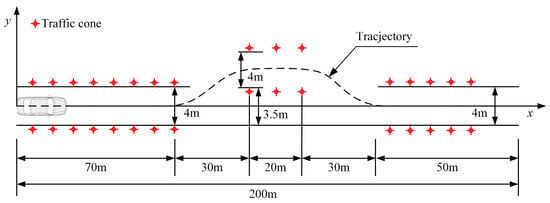
Figure 9.
The path of double lane change.
Figure 10a shows the driving trajectories with uncontrolled, SMC, and ANFTSMC strategies, and it is evident that the uncontrolled vehicle is significantly deviating from the target trajectory. However, the vehicle with SMC and ANFTSMC strategies both can drive along the target trajectory, and the discrepancy in lateral displacement with the ANFTSMC strategy is less than with SMC.
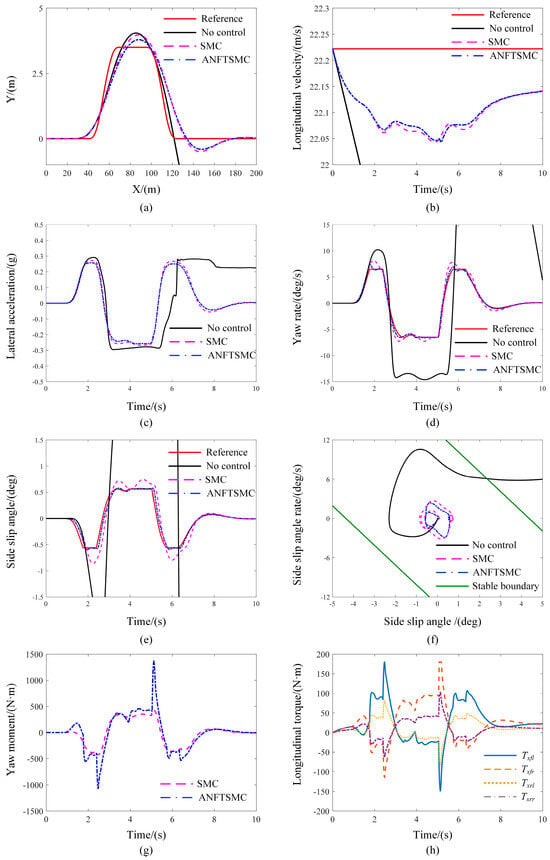
Figure 10.
The simulation results of double lane change. (a) Trajectory; (b) longitudinal velocity; (c) lateral acceleration; (d) yaw rate; (e) side slip angle; (f) phase plane; (g) yaw moment; (h) longitudinal torque of ANFSMC.
According to Figure 10b, the longitudinal velocity of uncontrolled vehicles declined dramatically. Meanwhile, there is some fluctuation in the velocity with the SMC and ANFTSMC strategies because of the sudden steering operation.
The state tracking performance is demonstrated in Figure 10d,e. For the uncontrolled vehicle, at 2 s, there is a sharp fluctuation of the yaw rate and side slip angle, and the lateral acceleration is close to 0.4 g according to Figure 10c, which shows that the vehicle has the risk of instability. After 2 s, the state response curve diverges seriously, and the vehicle loses control completely. For the SMC and ANFTSMC strategies, the lateral acceleration is less than 0.4 g. However, the tracking accuracy of ANFTSMC is better than SMC, especially in the moment of steering operation, so the tracking error of SMC is increased. The root mean square error (RMSE) is listed in Table 5, and, compared with SMC, the RMSE of yaw rate and side slip angle with the ANFTSMC strategy decreased by 53.9% and 60.7%, respectively. It is indicated that the state tracking error is decreased, and both the handling and stability of the vehicle are improved with the presented control method.

Table 5.
The RMSE of yaw rate and side slip angle under double lane change maneuver.
Figure 10f is the phase trajectory; for the uncontrolled vehicle, the phase trajectory is obviously beyond the stability boundary and unable to converge to the equilibrium point, which means that the vehicle loses control. For the SMC and ANFTSMC strategies, the phase trajectory can converge to the equilibrium point. However, the convergence speed of ANFTSMC is faster, and the side slip angle can be maintained within a smaller range.
6.2. Serpentine Maneuver
The serpentine maneuver is employed on slippery roads (μ = 0.3) to test the emergency obstacle avoidance ability of DDEV. The scheme of the serpentine road is shown in Figure 11. The traffic cone is placed every 30 m, the length of each road section is marked, and the total length of the test road is 300 m. The longitudinal speed is 80 km/h. The test results are demonstrated in Figure 12.
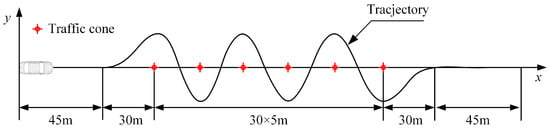
Figure 11.
The path of serpentine.
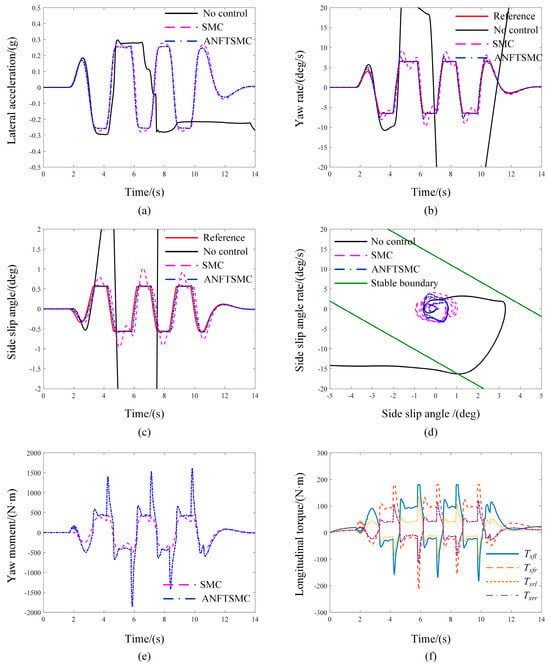
Figure 12.
The simulation results of the serpentine. (a) Lateral acceleration; (b) yaw rate; (c) side slip angle; (d) β−phase plane; (e) yaw moment; (f) longitudinal torque of ANFSMC.
The state tracking performance of different control strategies is compared in Figure 12b,c. Under the condition without stability control, the yaw rate and side slip angle increase sharply; combined with the phase plane in Figure 12d, the phase trajectory cannot converge to the equilibrium point and beyond the stability boundary, which means that the vehicle is out of control completely. Compared with the SMC strategy, the ANFTSMC strategy presents a better tracking performance. In particular, in the moment of abrupt steering wheel angle changes, the actual state value can accurately track the desired value with the ANFTSMC strategy, whereas the obvious fluctuation of the state response curve exists with the SMC strategy. As displayed in Table 6 and Figure 12d, for the side slip angle, the RMSE is 0.0943 deg and the change range is −0.6017 deg~0.6013 deg with the ANFTSMC strategy, which is smaller than those of the SMC strategy (0.2805 deg, −0.9590 deg~1.0175 deg). As for the yaw rate, it can keep up with the change in the steering wheel angle, and its RMSE of 0.4939 deg/s is lower than that of SMC. It is indicated that the vehicle has a greater stability margin and better handling performance with ANFTSMC. This is because the ANFTSMC strategy can accurately compute the additional yaw moment as shown in Figure 12e, and realize the real-time distribution of four-wheel torque as shown in Figure 12f.

Table 6.
The RMSE of yaw rate and side slip angle under serpentine maneuver.
6.3. Sine Steering Angle Input Maneuver
This test is conducted to further verify the stability under drastic steering conditions; the initial velocity is 90 km/h and the road adhesion coefficient is 0.4. The simulation results as shown in Figure 13. Figure 13a displays the steering wheel input, with an amplitude of 50 deg.
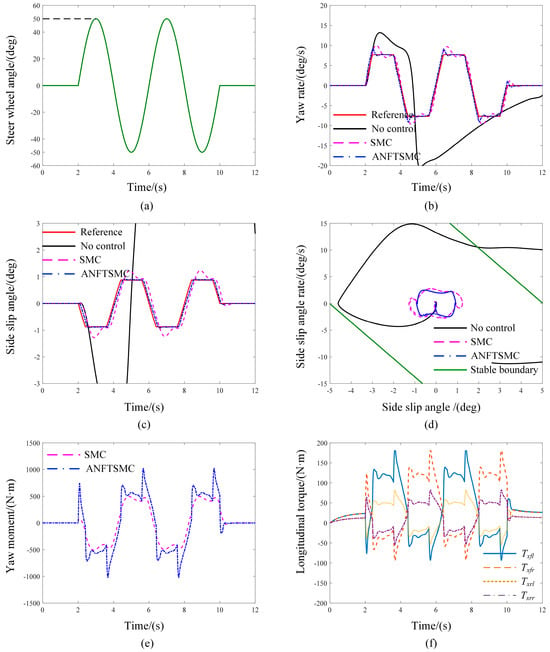
Figure 13.
The simulation results of the sine steering angle input. (a) Steering wheel angle; (b) yaw rate; (c) side slip angle; (d) β−phase plane; (e) yaw moment; (f) longitudinal torque of ANFSMC.
As depicted in Figure 13b–d, for the uncontrolled vehicle, the actual state response curve significantly deviates from the desired one, and the phase trajectory extends outside the stable domain. The maximum absolute value of the yaw rate and side slip angle with the ANFTSMC approach is 9.2095 deg/s and 0.9137 deg, respectively, which are both less than that of SMC (10.0363 deg/s, 1.2809 deg). It is suggested that the lateral stability can be improved with the ANFTSMC approach. Meanwhile, as illustrated in Table 7, the RMSE of the yaw rate and side slip angle reduce to 0.5699 deg/s and 0.0943 deg, respectively. The additional yaw moment is shown in Figure 13e, and it is evident that more required yaw moment is produced to keep the vehicle stable at the maximum steering wheel angle. The state tracking performance is improved because the ANFTSMC strategy can accurately determine the extra yaw moment and dynamically distribute the longitudinal tire force.

Table 7.
The RMSE of yaw rate and side slip angle under sine steering angle input maneuver.
In addition, different from the control law of the SMC strategy, the presented control law of the ANFTSMC strategy contains the upper bounds of uncertain parameters and external disturbances, and the inappropriate upper bounds will lead to the chattering of the system. However, the simulation results of Figure 10, Figure 12 and Figure 13 show that the vehicle state response curves are smooth and there is no jitter back and forth, and it further confirms the effectiveness of introducing adaptive law to adjust the upper boundary of uncertain parameters and external disturbances for the control system.
7. Conclusions
A novel direct yaw moment control approach with a three-level structure is presented to enhance the handling and stability of DDEV in emergency maneuvers. At the supervisory level, the β− phase trajectory is drawn under different road adhesion coefficients, and the stability boundary function is obtained. Meanwhile, the vehicle instability degree is introduced based on the distance between the state point and the stability boundary, and the β− phase plane is partitioned into stable, moderately unstable, and severely unstable regions. At the decision level, two state tracking controllers are designed to produce the corresponding extra yaw moments using the ANFTSMC algorithm. For the coordination control of stability and handling, an adaptive control weight coefficient between side slip angle and yaw rate is designed based on the vehicle instability degree. In addition, finite-time convergence and system stability are proven. At the executive level, the QP method is employed to distribute the optimization four-wheel torque. The objectives of torque distribution are minimum tire utilization ratio and allocation error, which also satisfy the constraints of motor peak torque and friction ellipse. The co-simulation test is conducted to confirm the efficacy of the proposed ANFTSMC strategy. Among these tests, under the double lane change maneuver with the ANFTSMC strategy, the RMSE of yaw rate and side slip angle decreased by 53.9% and 60.7%, respectively. Under the sine steering angle input maneuver, the maximum absolute values of these two parameters are 9.2095 deg/s and 0.9137 deg, which are both less than that of SMC (10.0363 deg/s, 1.2809 deg). The simulation results indicated that the ANFTSMC strategy has superior tracking accuracy of the intended state compared to SMC, and this benefits from the fast convergence speed and adaptive weight between the handling and stability.
In future work, the experimental research on a real-world DDEV will be focused on to assess the performance of the DYC method. Additionally, the impact of various tire operating conditions on the control strategy performance will be investigated.
Author Contributions
Conceptualization, Y.Z. (Yixi Zhang) and J.M.; methodology, Y.Z. (Yixi Zhang); software, Y.Z. (Yixi Zhang); validation, Y.Z. (Yixi Zhang), J.M. and Y.Z. (Yang Zhou); formal analysis, Y.Z. (Yixi Zhang) and J.M.; investigation, Y.Z. (Yixi Zhang); resources, Y.Z. (Yixi Zhang), and Y.Z. (Yang Zhou); data curation, Y.Z. (Yixi Zhang); writing—original draft preparation, Y.Z. (Yixi Zhang); writing—review and editing, Y.Z. (Yixi Zhang), J.M. and Y.Z. (Yang Zhou); visualization, Y.Z. (Yixi Zhang); supervision, Y.Z. (Yixi Zhang), J.M. and Y.Z. (Yang Zhou); project administration, Y.Z. (Yixi Zhang); funding acquisition, Y.Z. (Yixi Zhang). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Scientific Research Program Funded by the Shaanxi Provincial Education Department, grant number 23JK0493; the Key Laboratory of Transportation Industry of Automotive Transportation Safety Enhancement Technology (Chang’an University), grant number 300102223507; and the Scientific Foundation of Xi’an Aeronautical University, grant number 2021KY0207.
Data Availability Statement
Data are contained within the article.
Acknowledgments
Thanks to the Key Laboratory of Transportation Industry of Automotive Transportation Safety Enhancement Technology (Chang’an University) for providing financial and equipment support.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Wang, L.; Ma, J.; Zhao, X.; Li, X.; Zhang, K.; Jiao, Z. Adaptive robust unscented Kalman filter-based state-of-charge estimation for lithium-ion batteries with multi-parameter updating. Electrochim. Acta 2022, 426, 140760. [Google Scholar] [CrossRef]
- Sun, X.; Wang, Y.; Quan, Z.; Cai, Y.; Chen, L.; Bei, S. DYC Design for Autonomous Distributed Drive Electric Vehicle Considering Tire Nonlinear Mechanical Characteristics in the PWA Form. IEEE Trans. Intell. Transp. Syst. 2023, 24, 11030–11046. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhao, X.; Wang, S.; Yu, Q.; Zhang, H.; Li, Z.; Chai, H.; Han, Q. Extension coordinated control of distributed-driven electric vehicles based on evolutionary game theory. Control Eng. Pract. 2023, 137, 105583. [Google Scholar] [CrossRef]
- Liu, H.; Liu, C.; Han, L.J.; Xiang, C.L. Handling and Stability Integrated Control of AFS and DYC for Distributed Drive Electric Vehicles Based on Risk Assessment and Prediction. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23148–23163. [Google Scholar] [CrossRef]
- Chen, W.W.; Liang, X.T.; Wang, Q.D.; Zhao, L.F.; Wang, X. Extension coordinated control of four wheel independent drive electric vehicles by AFS and DYC. Control Eng. Pract. 2020, 101, 104504. [Google Scholar] [CrossRef]
- Zhang, R.; Zhao, W.; Wang, C. A phase plane H∞ controller for distributed drive electric vehicles with stability enhancement based on tire road friction coefficient estimation. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023. [Google Scholar] [CrossRef]
- Zhao, Y.; Deng, H.; Li, Y.; Xu, H. Coordinated control of stability and economy based on torque distribution of distributed drive electric vehicle. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 1792–1806. [Google Scholar] [CrossRef]
- Wang, H.; Sun, Y.; Tan, H.; Lu, Y. Stability control of in-wheel motor driven vehicle based on extension pattern recognition. Sci. Prog. 2020, 103, 36850420958531. [Google Scholar] [CrossRef]
- Shen, T.; Wang, F.; Yan, Y.; Zhao, M.; Ren, Y.; Liang, J.; Yin, G. Stability Analysis and Control Validation of DDEV in Handling Limit via SOSP: A Strategy Based on Stability Region. IEEE Trans. Autom. Sci. Eng. 2023, 1–13. [Google Scholar] [CrossRef]
- Liang, J.; Feng, J.; Fang, Z.; Lu, Y.; Yin, G.; Mao, X.; Wu, J.; Wang, F. An Energy-Oriented Torque-Vector Control Framework for Distributed Drive Electric Vehicles. IEEE Trans. Transp. Electrif. 2023, 9, 4014–4031. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Z.; Zhang, L.; Dorrell, D.G. Braking/steering coordination control for in-wheel motor drive electric vehicles based on nonlinear model predictive control. Mech. Mach. Theory 2019, 142, 103586. [Google Scholar] [CrossRef]
- Mok, Y.M.; Zhai, L.; Wang, C.P.; Zhang, X.Y.; Hou, Y.H. A Post Impact Stability Control for Four Hub-Motor Independent-Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2022, 71, 1384–1396. [Google Scholar] [CrossRef]
- Park, G.; Han, K.; Nam, K.; Kim, H.; Choi, S.B. Torque Vectoring Algorithm of Electronic-Four-Wheel Drive Vehicles for Enhancement of Cornering Performance. IEEE Trans. Veh. Technol. 2020, 69, 3668–3679. [Google Scholar] [CrossRef]
- Chae, M.; Hyun, Y.; Yi, K.; Nam, K. Dynamic Handling Characteristics Control of an in-Wheel-Motor Driven Electric Vehicle Based on Multiple Sliding Mode Control Approach. IEEE Access 2019, 7, 132448–132458. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.; Zhang, X.; Hou, R.; Mok, Y.M.; Hou, Y. Handling stability control strategy for four-wheel hub motor-driven vehicle based on adaptive control for road adhesion. IET Intell. Transp. Syst. 2022, 16, 586–601. [Google Scholar] [CrossRef]
- Ding, S.; Liu, L.; Zheng, W.X. Sliding Mode Direct Yaw-Moment Control Design for In-Wheel Electric Vehicles. IEEE Trans. Ind. Electron. 2017, 64, 6752–6762. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability Research of Distributed Drive Electric Vehicle by Adaptive Direct Yaw Moment Control. IEEE Access 2019, 7, 106225–106237. [Google Scholar] [CrossRef]
- Asiabar, A.N.; Kazemi, R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z.; Zhang, L.; Liu, M.; Zhu, J. Lateral stability enhancement based on a novel sliding mode prediction control for a four-wheel-independently actuated electric vehicle. IET Intell. Transp. Syst. 2018, 13, 124–133. [Google Scholar] [CrossRef]
- Zhai, L.; Wang, C.; Hou, Y.; Liu, C. MPC-Based Integrated Control of Trajectory Tracking and Handling Stability for Intelligent Driving Vehicle Driven by Four Hub Motor. IEEE Trans. Veh. Technol. 2022, 71, 2668–2680. [Google Scholar] [CrossRef]
- Peng, H.; Wang, W.; Xiang, C.; Li, L.; Wang, X. Torque Coordinated Control of Four In-Wheel Motor Independent-Drive Vehicles With Consideration of the Safety and Economy. IEEE Trans. Veh. Technol. 2019, 68, 9604–9618. [Google Scholar] [CrossRef]
- Hu, X.; Chen, H.; Li, Z.; Wang, P. An Energy-Saving Torque Vectoring Control Strategy for Electric Vehicles Considering Handling Stability Under Extreme Conditions. IEEE Trans. Veh. Technol. 2020, 69, 10787–10796. [Google Scholar] [CrossRef]
- Guo, N.; Lenzo, B.; Zhang, X.; Zou, Y.; Zhai, R.; Zhang, T. A Real-Time Nonlinear Model Predictive Controller for Yaw Motion Optimization of Distributed Drive Electric Vehicles. IEEE Trans. Veh. Technol. 2020, 69, 4935–4946. [Google Scholar] [CrossRef]
- Berntorp, K.; Di Cairano, S. Tire-Stiffness and Vehicle-State Estimation Based on Noise-Adaptive Particle Filtering. IEEE Trans. Control Syst. Technol. 2019, 27, 1100–1114. [Google Scholar] [CrossRef]
- Li, Z.; Chen, H.; Liu, H.; Wang, P.; Gong, X. Integrated Longitudinal and Lateral Vehicle Stability Control for Extreme Conditions With Safety Dynamic Requirements Analysis. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19285–19298. [Google Scholar] [CrossRef]
- Arricale, V.M.; Genovese, A.; Tomar, A.S.; Kural, K.; Sakhnevych, A. Non-Linear Model of Predictive Control-Based Slip Control ABS Including Tyre Tread Thermal Dynamics. Appl. Mech. 2022, 3, 855–888. [Google Scholar] [CrossRef]
- Mosconi, L.; Farroni, F.; Sakhnevych, A.; Timpone, F.; Gerbino, F.S. Adaptive vehicle dynamics state estimator for onboard automotive applications and performance analysis. Veh. Syst. Dyn. 2023, 61, 3244–3268. [Google Scholar] [CrossRef]
- Lin, J.; Zou, T.; Zhang, F.; Zhang, Y. Yaw Stability Research of the Distributed Drive Electric Bus by Adaptive Fuzzy Sliding Mode Control. Energies 2022, 15, 1280. [Google Scholar] [CrossRef]
- Zhu, Z.; Tang, X.; Qin, Y.; Huang, Y.; Hashemi, E. A Survey of Lateral Stability Criterion and Control Application for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10382–10399. [Google Scholar] [CrossRef]
- Chen, J.; Shuai, Z.; Zhang, H.; Zhao, W. Path Following Control of Autonomous Four-Wheel-Independent-Drive Electric Vehicles via Second-Order Sliding Mode and Nonlinear Disturbance Observer Techniques. IEEE Trans. Ind. Electron. 2021, 68, 2460–2469. [Google Scholar] [CrossRef]
- Dong, H.; Yang, X.; Gao, H.; Yu, X. Practical Terminal Sliding-Mode Control and Its Applications in Servo Systems. IEEE Trans. Ind. Electron. 2023, 70, 752–761. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Wang, D.; Ju, F.; Chen, B.; Wu, H. Adaptive Time-Delay Control for Cable-Driven Manipulators With Enhanced Nonsingular Fast Terminal Sliding Mode. IEEE Trans. Ind. Electron. 2021, 68, 2356–2367. [Google Scholar] [CrossRef]
- Rangel, M.A.G.; Manzanilla, A.; Suarez, A.E.Z.; Muñoz, F.; Salazar, S.; Lozano, R. Adaptive Non-singular Terminal Sliding Mode Control for an Unmanned Underwater Vehicle: Real-time Experiments. Int. J. Control Autom. Syst. 2020, 18, 615–628. [Google Scholar] [CrossRef]
- Si, Y.; Song, S. Adaptive reaching law based three-dimensional finite-time guidance law against maneuvering targets with input saturation. Aerosp. Sci. Technol. 2017, 70, 198–210. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite Time Fault Tolerant Control for Robot Manipulators Using Time Delay Estimation and Continuous Nonsingular Fast Terminal Sliding Mode Control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.H.; Li, W.C.; Wang, J.Y.; Luo, Y.G.; Li, K.Q. Safe and Energy-Efficient Car-Following Control Strategy for Intelligent Electric Vehicles Considering Regenerative Braking. IEEE Trans. Intell. Transp. Syst. 2022, 23, 7070–7081. [Google Scholar] [CrossRef]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2012. [Google Scholar]
- Ono, E.; Hattori, Y.; Muragishi, Y.; Koibuchi, K. Vehicle dynamics integrated control for four-wheel-distributed steering and four-wheel-distributed traction/braking systems. Veh. Syst. Dyn. 2006, 44, 139–151. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Quadratic Programming. In Numerical Optimization; Nocedal, J., Wright, S.J., Eds.; Springer: New York, NY, USA, 2006; pp. 448–492. [Google Scholar]
- Stellato, B.; Banjac, G.; Goulart, P.; Bemporad, A.; Boyd, S. OSQP: An operator splitting solver for quadratic programs. Math. Program. Comput. 2020, 12, 637–672. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).