A Novel Extended Unscented Kalman Filter Is Designed Using the Higher-Order Statistical Property of the Approximate Error of the System Model
Abstract
1. Introduction
2. Unscented Kalman Filtering Algorithm
3. Unscented Kalman Filtering Algorithm Considering High-Order Approximate Error
- Forecasting Phase:
4. Comparative Analysis of HUKF and UKF Performance
4.1. Performance Analysis of the Prediction Phase
4.2. Performance Analysis of the Update Phase
5. Simulation
5.1. Simulation 1
5.2. Simulation 2
5.3. Summary of Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.; Zhang, Z.; Zhao, S.; Li, Q.; Hong, Z.; Li, F.; Huang, S. Robust adaptive Unscented Kalman Filter with gross error detection and identification for power system forecasting-aided state estimation. J. Frankl. Inst. 2023, 360, 10297–10336. [Google Scholar] [CrossRef]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Wen, C.; Cheng, X.; Xu, D.; Wen, C. Filter design based on characteristic functions for one class of multi-dimensional nonlinear non-Gaussian systems. Automatica 2017, 82, 171–180. [Google Scholar] [CrossRef]
- Wen, T.; Liu, J.; Cai, B.; Roberts, C. High-Precision State Estimator Design for the State of Gaussian Linear Systems Based on Deep Neural Network Kalman Filter. IEEE Sens. J. 2023, 23, 31337–31344. [Google Scholar] [CrossRef]
- Liu, X.; Wen, C.; Sun, X. Design Method of High-Order Kalman Filter for Strong Nonlinear System Based on Kronecker Product Transform. Sensors 2022, 22, 653. [Google Scholar] [CrossRef]
- Smith, G.L.; Schmidt, S.F.; McGee, L.A. Application of Statistical Filter Theory to the Optimal Estimation of Position and Velocity on Board a Circumlunar Vehicle; NASA Tech. Rep. TR R-135; National Aeronautics and Space Administration: Washington, DC, USA, 1962. [Google Scholar]
- Yue, M.; Zhe, G. Estimation for state of charge of lithium-ion batteries by adaptive fractional-order unscented Kalman filters. J. Energy Storage 2022, 51, 104396. [Google Scholar] [CrossRef]
- Cui, T.; Sun, X.; Wen, C. A Novel Data Sampling Driven Kalman Filter Is Designed by Combining the Characteristic Sampling of UKF and the Random Sampling of EnKF. Sensors 2022, 22, 1343. [Google Scholar] [CrossRef] [PubMed]
- Lee, A.S.; Hilal, W.; Gadsden, S.A.; Al-Shabi, M. Combined Kalman and sliding innovation filtering: An adaptive estimation strategy. Measurement 2023, 218, 113228. [Google Scholar] [CrossRef]
- Gustafsson, F.; Hendeby, G. Some Relations Between Extended and Unscented Kalman Filters. IEEE Trans. Signal Process. 2012, 60, 545–555. [Google Scholar] [CrossRef]
- Stepanov, O.A.; Litvinenko, Y.A.; Vasiliev, V.A.; Toropov, A.B.; Basin, M.V. Polynomial Filtering Algorithm Applied to Navigation Data Processing under Quadratic Nonlinearities in System and Measurement Equations. Part 1. Description and Comparison with Kalman Type Algorithms. Gyroscopy Navig. 2021, 12, 205–223. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the 1995 American Control Conference—ACC’95, Seattle, WA, USA, 21–23 June 1995. [Google Scholar]
- Juryca, K.; Pidanic, J.; Mishra, A.K.; Moric, Z.; Sedivy, P. Wind Turbine Micro-Doppler Prediction Using Unscented Kalman Filter. IEEE Access 2022, 10, 109240–109252. [Google Scholar] [CrossRef]
- Yang, F.; Zheng, L.; Wang, J.Q.; Pan, Q. Double Layer Unscented Kalman Filter. Acta Autom. Sin. 2019, 45, 1386–1391. [Google Scholar]
- Lei, Z.; Zidong, W.; Donghua, Z. Moving horizon estimation with non-uniform sampling under component-based dynamic event-triggered transmission. Automatica 2020, 120, 109154. [Google Scholar] [CrossRef]
- Juntao, W.; Jifeng, S.; Yuanlong, L.; Tao, R.; Zhengye, Y. State of charge estimation for lithium-ion battery based on improved online parameters identification and adaptive square root unscented Kalman filter. J. Energy Storage 2024, 77, 109977. [Google Scholar] [CrossRef]
- Cheng, C.; Wang, W.; Meng, X.; Shao, H.; Chen, H. Sigma-Mixed Unscented Kalman Filter-Based Fault Detection for Traction Systems in High-Speed Trains. Chin. J. Electron. 2023, 32, 982–991. [Google Scholar] [CrossRef]
- Mengli, X.; Yongbo, Z.; Huimin, F. Three-stage unscented Kalman filter for state and fault estimation of nonlinear system with unknown input. J. Frankl. Inst. 2017, 354, 8421–8443. [Google Scholar] [CrossRef]
- Stojanovski, Z.; Savransky, D. Higher-Order Unscented Estimator. J. Guid. Control Dyn. 2021, 44, 2186–2198. [Google Scholar] [CrossRef]
- Stepanov, O.A.; Isaev, A.M. A Procedure of Comparative Analysis of Recursive Nonlinear Filtering Algorithms in Navigation Data Processing Based on Predictive Simulation. Gyroscopy Navig. 2023, 14, 213–224. [Google Scholar] [CrossRef]

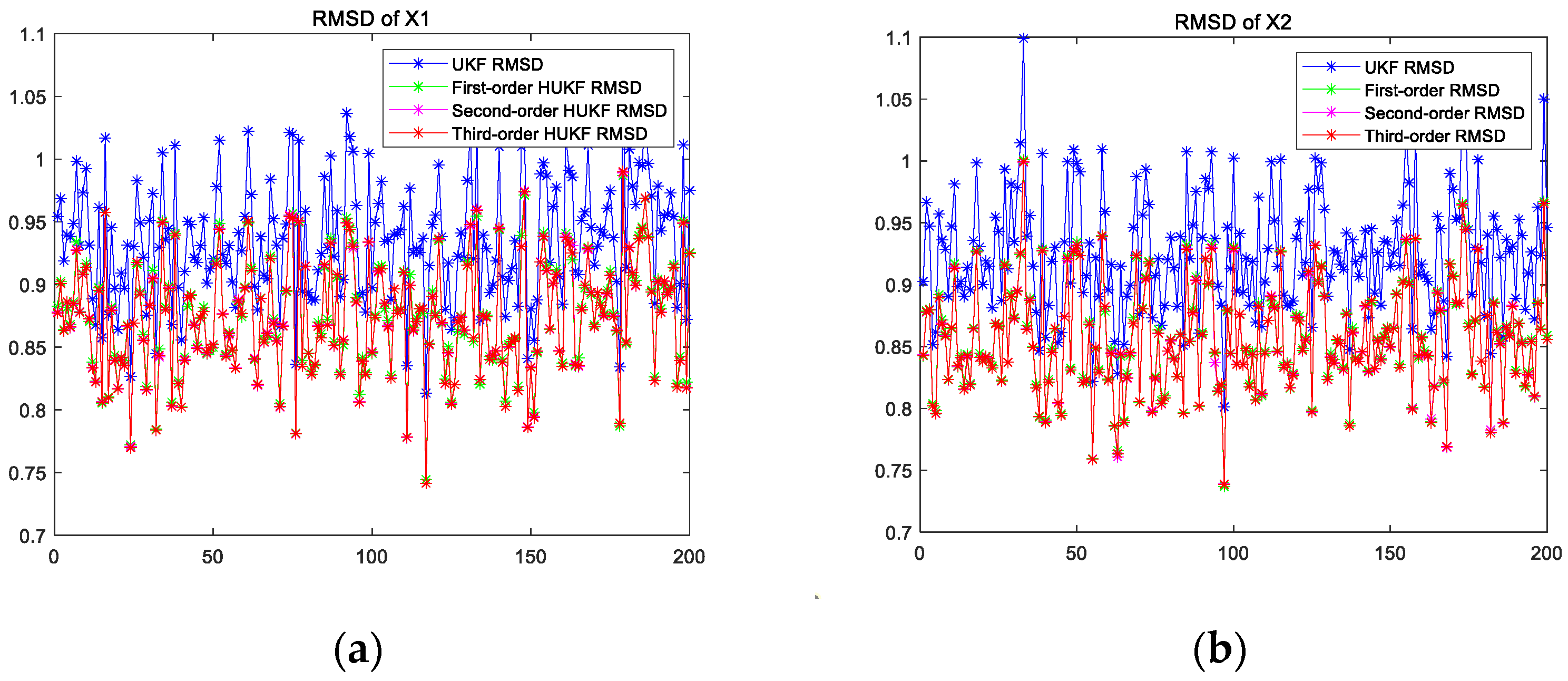
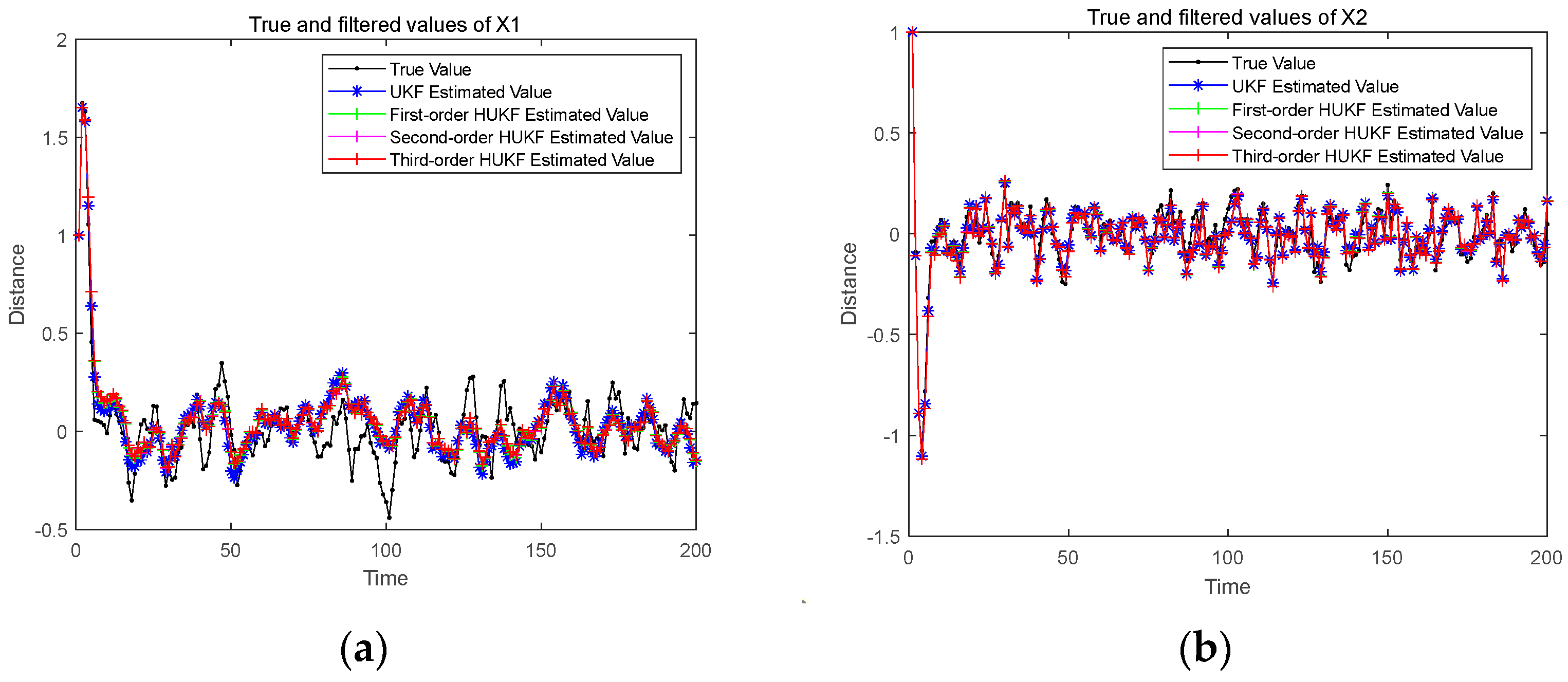
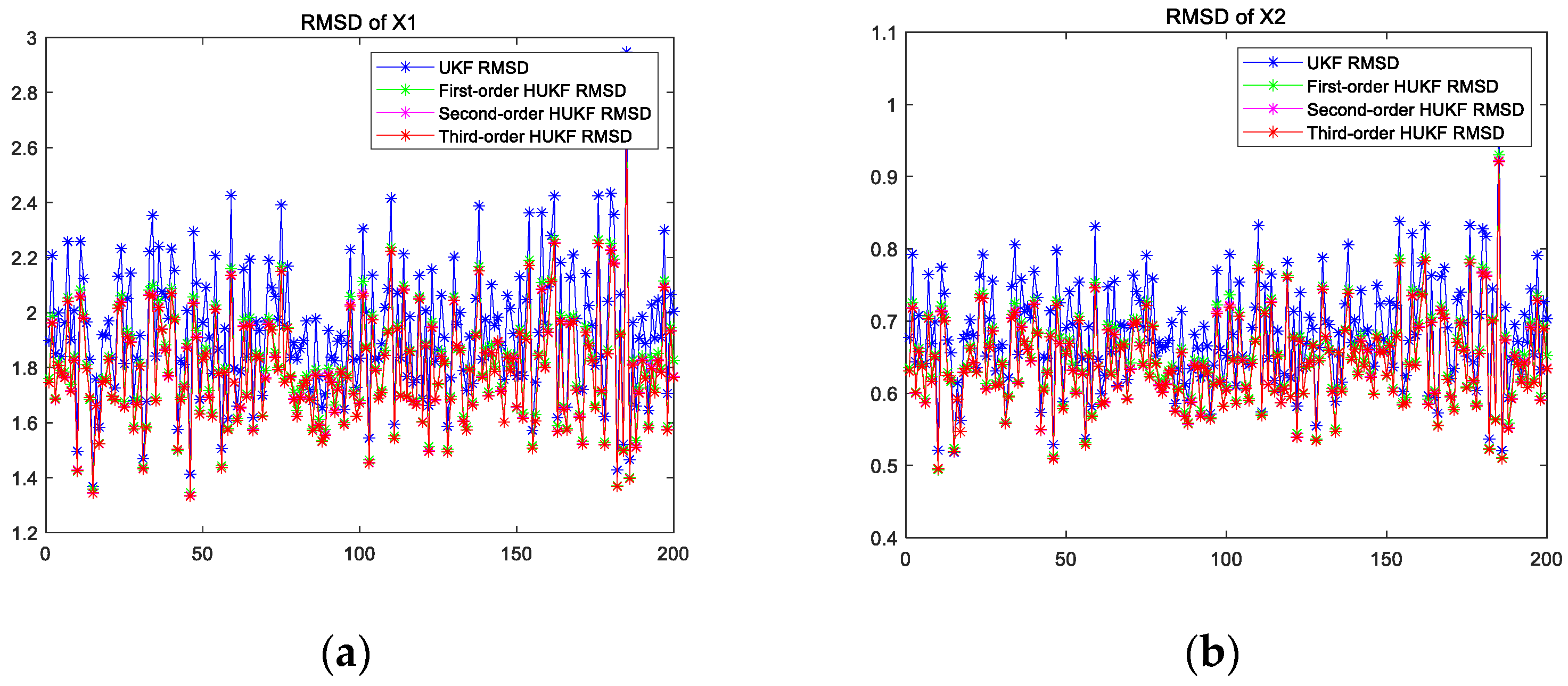
| State | RMSD of X1 | RMSD of X2 | |
|---|---|---|---|
| Methods | |||
| UKF | 0.936764 | 0.926681 | |
| First-order estimate | 0.875919 | 0.857522 | |
| Improvement | 6.50% | 7.46% | |
| Second-order estimate | 0.874897 | 0.856663 | |
| Improvement | 6.60% | 7.56% | |
| Third-order estimate | 0.874817 | 0.856622 | |
| Improvement | 6.61% | 7.56% | |
| State | RMSD of X1 | RMSD of X2 | |
|---|---|---|---|
| Methods | |||
| UKF | 1.93416 | 0.683426 | |
| First-order estimate | 1.79871 | 0.646101 | |
| Improvement | 7.00% | 5.46% | |
| Second-order estimate | 1.78669 | 0.642469 | |
| Improvement | 7.62% | 5.99% | |
| Third-order estimate | 1.78524 | 0.642038 | |
| Improvement | 7.70% | 6.06% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Wen, C. A Novel Extended Unscented Kalman Filter Is Designed Using the Higher-Order Statistical Property of the Approximate Error of the System Model. Actuators 2024, 13, 169. https://doi.org/10.3390/act13050169
Li C, Wen C. A Novel Extended Unscented Kalman Filter Is Designed Using the Higher-Order Statistical Property of the Approximate Error of the System Model. Actuators. 2024; 13(5):169. https://doi.org/10.3390/act13050169
Chicago/Turabian StyleLi, Chengyi, and Chenglin Wen. 2024. "A Novel Extended Unscented Kalman Filter Is Designed Using the Higher-Order Statistical Property of the Approximate Error of the System Model" Actuators 13, no. 5: 169. https://doi.org/10.3390/act13050169
APA StyleLi, C., & Wen, C. (2024). A Novel Extended Unscented Kalman Filter Is Designed Using the Higher-Order Statistical Property of the Approximate Error of the System Model. Actuators, 13(5), 169. https://doi.org/10.3390/act13050169






