Abstract
This paper presents the experimental results of separation and reattachment transient flow processes over a NACA0015 airfoil wing when using a plasma actuator for flow control. In addition, it addresses the flow behavior in the transient processes when the flow control device is activated or deactivated, providing insights for future feedback-based active flow control. This approach offers the benefit of enhanced aerodynamic capabilities. The experiments were conducted at a Reynolds number of 66,000 and an angle of attack of 13 degrees for leading-edge separation without control. The plasma actuator was installed on the leading edge of the wing, with a voltage of 8 kV, base frequency of 30 kHz, and burst frequencies ranging from 100 Hz to 600 Hz. Particle image velocimetry was employed for the flow field velocity measurements, and surface pressure data were obtained using eight piezoelectric pressure sensors. The first proper orthogonal decomposition mode of the transient flow velocity field is the focus of this paper and the flow behavior is quantitatively discussed. The results reveal details about the flow separation and reattachment transient processes such as their flow structures and their evolution over time. It is concluded that the time asymmetry between the separation and reattachment transient processes could be leveraged for further improvements to the efficiency of actuators.
1. Introduction
In recent years, interest in active flow control devices for separation suppression has increased significantly. One such device is the dielectric barrier discharge plasma actuator (hereafter, the plasma actuator), the control performance of which has been extensively researched in its multiple variations. The application of a high voltage between two electrodes separated by a dielectric material has several uses that depend on the configuration and the input electrical signal. These uses include inducing linear momentum [1,2] and creating spanwise vortices [3,4], streamwise vortices [5,6], three-dimensional vortices [7,8], synthetic jets [9,10], or thermal perturbations [11,12]. Another aspect that attracts great interest in the research of plasma actuators is their diverse range of practical applications, such as drag reduction [13], lift and rolling-moment control [14], and noise control [15,16]. In this work, a spanwise vortex generator plasma actuator will be used as a reference. Figure 1 shows an illustration of the device layout. This type of plasma actuator typically consists of two electrodes that are separated by a layer of dielectric material and are connected to a high-voltage power supply [17]. The power supply is usually an alternating current (AC) with a voltage in the order of kilovolts. In its simplest configuration, one electrode is exposed to the air while the other is fully covered by a thin layer of dielectric material. The thickness of the dielectric layer should be chosen carefully so that dielectric breakdown is prevented. When the device is powered on, an electric field is created between the two electrodes. When a voltage that exceeds the breakdown voltage of the air is applied to the plasma actuator, the electric field will weakly ionize the air surrounding the exposed electrode. This ionized air, also called cold plasma, simultaneously interacts with the electric field, leading to the induction of momentum in the surrounding air. As a result, the surrounding air moves from the exposed electrode toward the covered electrode.
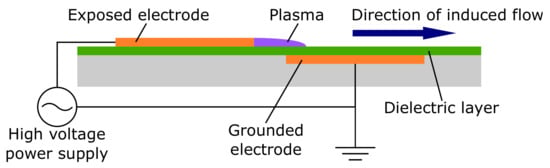
Figure 1.
Schematic diagram of a plasma actuator.
Multiple studies have indicated that the performance of a plasma actuator is affected by the flow [18,19,20,21,22,23,24,25,26] or environmental [27,28,29] conditions, which change the optimal settings for the plasma actuator. Furthermore, recent efforts have been made toward the implementation of feedback control of flow separation by plasma actuators [30,31,32,33,34,35,36,37]. However, one area that is still not well known is the transient flow processes between flow separation and reattachment caused by the activation and deactivation of a plasma actuator. The flow typically becomes pseudo-stationary, with small vortices shedding at the burst frequency under continuous burst actuation; however, the flow is likely to start reattachment and separation transient processes when feedback control is turned on and off, respectively. Because of this, it is necessary to describe these transient processes and identify the flow field state from pressure sensors. Previous works [38,39] have indicated that the reattachment process is fast, with a brief period of lifting force loss caused by vortex shedding, and that the separation process is slow, with a brief period of lifting force increase caused by large vortices. However, the separation process has not been studied in detail. This asymmetry in the transient processes could be leveraged to lower the power consumption of the plasma actuator.
The objective of this study is to investigate the reattachment and separation transient processes to identify their flow structures and understand their time evolution. It is expected that this knowledge could be used in the future to improve the efficiency of plasma actuators. The methodology used to investigate the transient processes includes obtaining simultaneous time-resolved PIV data and unsteady pressure measurements of multiple runs using predetermined input signals for the plasma actuator. These input signals with a finite time window contain both an initial and a final time span where the plasma actuator is inactive and a middle time span during which the actuator is active, with varying actuation settings (more precisely, the burst frequency) across different sets of runs. This process enables us to obtain a statistically significant amount of information on how flow separation and reattachment transient processes occur. The PIV data are then processed using proper orthogonal decomposition (POD), which enables us to express the complex measured velocity field using a simpler representation based on the superposition of spatial modes, accounting for as much kinetic energy as possible using a limited number of modes [40,41,42,43]. The reattachment and separation transient processes are quantitatively discussed. In addition to the mode analyses, the ensemble-averaged flow fields and flow features are discussed. These processes can simplify the flow field, extract key flow field phenomena, and allow us to analytically study the velocity fields and compare the transient processes.
2. Experimental Setup
The Tohoku University Basic Aerodynamic Research Wind Tunnel (T-BART) was employed for the experiments. It is an open-circuit, closed test section suction-type wind tunnel, featuring a test section with dimensions of 0.3 × 0.3 m. The test model, shown in Figure 2, was a NACA0015 airfoil wing, with a chord length of 100 mm and a span width of 300 mm, which was manufactured using stereolithography. The freestream velocity was set at 10 m/s for a Reynolds number of 66,000, and the angle of attack was set at 13 deg. Under these conditions, the flow was completely separated from the leading edge of the wing without control. Additionally, the wing model had nine piezoelectric pressure sensors (Model 8507C-1, MEGGITT), eight of which were usable with the plasma actuator installed. Static pressure sensors were also available, but their sampling rate is low, and since many of the pressure taps near the leading edge were covered by the plasma actuator, a lift coefficient estimation would be mediocre and have no use beyond comparisons within this work. The wing had a plasma actuator installed on the leading edge, with the exposed electrode on the pressure side and the covered electrode on the suction side. The dotted line in Figure 2 shows the geometric leading edge of the wing, and it also coincides with the location of the gap between the electrodes. This configuration is often used and has been shown to be nearly as effective in separation control as the coflow-blowing configuration [44].

Figure 2.
Wing model with leading-edge PA installed in the wind tunnel.
The electrodes were made from 0.07 mm thick copper tape, with the exposed electrode being 6 mm wide and the covered electrode 14 mm wide, with a gap of 1 mm between them. The spanwise length of the electrodes was approximately 200 mm, and their corners were curved to limit the concentration of the electric charge. The dielectric material was polyimide tape with a width of 20 mm, length of 220 mm, and thickness of 0.05 mm. The electrodes were connected to a high-voltage power supply (PSI-PA1050, PSI) with an 8 kV peak-to-peak output. The signal for the power supply was generated by a function generator (WF1948, NF). The plasma actuator was turned on and off during the experiment and burst actuation was considered when turning the plasma actuator on. Figure 3 (left) shows an enlarged view of the signal for burst mode actuation, where the superscript “+” denotes the quantities related to the modulation of the signal. The signal had a base frequency of ( 30 kHz), a burst ratio () of 0.1, and a nondimensional burst frequency of 1, 2, 3, or 6, depending on the ensemble, with the and defined as
where is the burst frequency in Hz, c is the wing chord length, and is the freestream velocity. The same characteristic quantities were also used for the normalization of time, and the normalized time is simply expressed as . Figure 3 (left) illustrates an overall view of the input signal of the plasma actuator. The predefined signal lasted ( 0.55 s) and included periods of time of ( 0.1 s) at the beginning and ( 0.25 s) at the end of the run where the plasma actuator was turned off. The flow behavior under the signal considered here shows the full transient processes between the flow separation and reattachment. Additionally, when studying the transient processes, it is necessary to shift the time origin using the relevant time points s and s, which correspond to the instances when the plasma actuator is turned on and off, respectively, as follows:
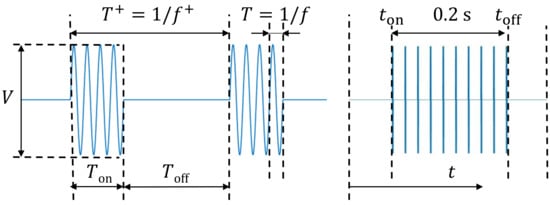
Figure 3.
Measurements of periods of bursting signal (left) and temporal structure of test runs (right).
The velocity field measurement was performed using the particle image velocimetry (PIV) technique. A Nd:YLF (LDY-303PIV, Litron) laser was utilized to illuminate the dioctyl sebacate seeding particles. The particle images were captured at 5000 fps in double-frame mode using a Phantom v2640 high-speed camera equipped with a 35 mm lens and a 527 ± 10 nm band-pass filter. The PIV data were then processed using Dynamic Studio 6.11 by Dantec Dynamics. The processing steps included the elimination of the background by the minimum value of each run, use of the adaptive PIV algorithm with an 8 px × 8 px interrogation window for the estimation of the velocity vectors in the flow field, and application of the included moving-average validation algorithm with the surrounding 3 × 3 arrays of vectors to smooth out the velocity vector fields. Then, all of the data for each ensemble were stacked together, POD was applied to the stacked data of the same condition, and the ensemble average (the average of all 30 runs of the ensemble) was obtained before performing a series of analytical studies of the flow field. In other words, the spatial POD mode was fixed for the different runs of the same flow-control parameters. It should be noted that the first six modes contained most of the valuable information for a reconstruction of the flow, whereas the seventh and higher modes contained fine turbulent and noise information.
During the experiments, there were undetected irregularities in the laser-camera synchronization, which caused issues with background elimination. Each frame used for PIV was composed of two images, where one pulse from the laser was captured for each image. Reflections other than particles were eliminated by subtracting the background image, which was estimated by the minimum illumination intensity at each pixel position throughout the entire run. However, the second image of a few frames turned out to be extremely dark and the minimum intensity of the entire run became almost zero in some cases. In such cases, the construction of the background image for the second image of nearly every other frame failed. This created error vectors over significant regions of the flow field. We found that the synchronization issues did not happen during the first 500 frames of any run, and it was proposed to obtain the minimum intensity from those initial 500 frames as a solution to the problem. This resolved the background subtraction problem, with minimum impact from the remaining background reflections on the image. Figure 4a,b show that the results obtained using this method proved to be consistent with the typical use of minimum intensity on runs with no synchronization problems. Additional processing was carried out and the frames at which synchronization issues occurred were systematically ignored. The velocity components were calculated at discrete sensing points across each frame. This array of velocities was rearranged into a single-column vector that contained a velocity component for all of the sensing points of each frame, and a new array for the entire run was created, with each column vector representing a frame. The standard deviation of each column vector was found to smoothly change from frame to frame when the number of error vectors was similar; however, a frame with a significantly increased number of error vectors (camera-laser synchronization problem) will vary greatly from the surrounding frames. These column vectors were identified and made equal to the previous column, and the influence of the synchronization problem was minimized. Figure 4c shows the curve of of U over time after processing the frames with large numbers of error vectors.
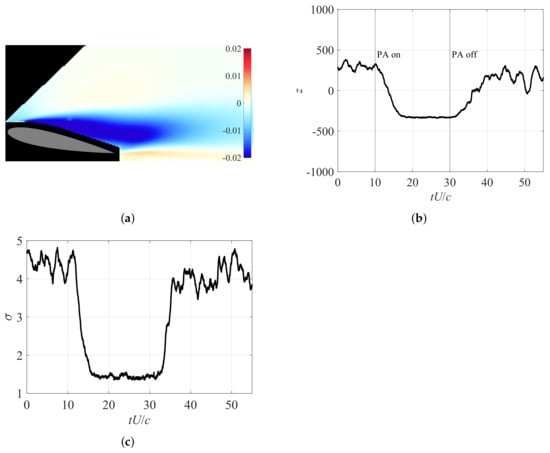
Figure 4.
Analysis of a singular case with synchronization issues. (a) Spatial distribution of first POD mode of U for 30 runs. (b) Temporal evolution of first POD mode of U of a single run without ensemble average. (c) Standard deviation of U values after complete processing.
A basic diagram of the entire setup is shown in Figure 5. The surface pressure was sensed by eight unsteady pressure sensors, which were distributed over the wing chord at locations between 0.1 c and 1.0 c. The sensors were connected to signal amplifiers (Endevco model 126, MEGGITT), and the amplifiers were connected to low-pass analog filters (3625, NF). The cut-off frequency of the filters was set at 2 kHz in an attempt to eliminate the high-frequency noise from the plasma actuator because due to the internal design of the wing, proper shielding from the electric field was not practical. The data were acquired using a DAQ (terminal block BNC-2120, multifunction I/O USB 6366, National Instruments) with a sampling rate of 25,000 Hz and were immediately converted to digital data.
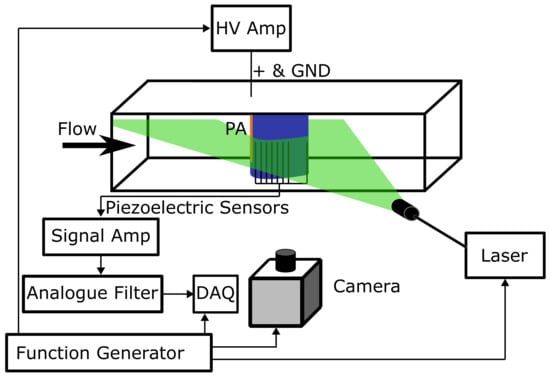
Figure 5.
Schematic diagram of experimental setup.
3. Results
The baseline flow characteristics of the typically separated and typically attached flows were first studied, and the reference points for the stationary states were clarified. Attention then shifted to the transient processes of flow reattachment and separation. The first POD mode was the primary focus of this study because it consistently represented the same flow features across different ensembles and accounted for a significant portion (>60%) of the total energy of the POD decomposition, which was nearly ten times more than the second mode. This justified the use of only the first POD mode for the analysis. The spatial distribution of the first POD mode seemed to correspond to the change in the recirculation region after separation. Therefore, the discussion of the first POD mode is considered to be directly related to the change in the recirculation region. Note that the higher POD modes tended to represent various complicated flow features across different cases, and therefore, the use of those POD modes makes their comparison difficult. Several processes in the transient response for pressure signals were selected for a more simplified discussion. First, the average pressure during complete separation was subtracted from the measurement of each pressure tap. Additionally, the data before were ignored so that the time period affected by noise caused by each burst of the plasma actuator was excluded. This particular noise vastly dominated the pressure sensor output, making it unusable during actuation time. A Butterworth low-pass filter with a cut-off frequency of 100 Hz implemented in Matlab was applied to the data, and the impact of other noise sources on the data was minimized. A constant high-frequency noise that affected the data was removed using this filter while preserving the basic behavior of the data. These measures made the visualization of the data easier for analysis. We measured only two runs from the case in which the plasma actuator was unable to reliably reattach the boundary layer, based on results from previously unpublished experiments at Tohoku University. These cases were not considered in the main analysis; however, their baseline flow field results are presented in Appendix B.
3.1. Baseline Flow Characteristics
3.1.1. Separated Flow
Figure 6 shows the ensemble-averaged time history of the POD coefficients and their standard deviations when the flow was fully separated. Figure 6 demonstrates that the POD representations of the separated flow for ranging from 2 to 6 were highly consistent, with the time average of the first POD coefficient z within 15% and the standard deviation of z within 20% of each other. The data for these values can be found in Table A1 in Appendix A. The reconstruction from the first POD mode shown in Figure 7 also proved to be an accurate representation of the averaged flow field.
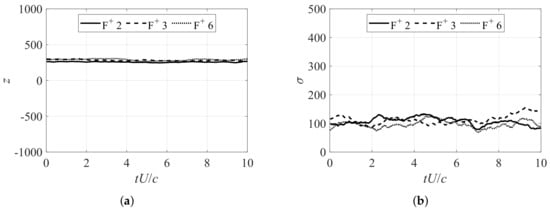
Figure 6.
Analysis of first POD mode during normally separated flow conditions. (a) First POD coefficient z of 30-run ensemble average for , 3, 6. (b) Standard deviation of first POD coefficient z of 30-run ensemble for , 3, 6.
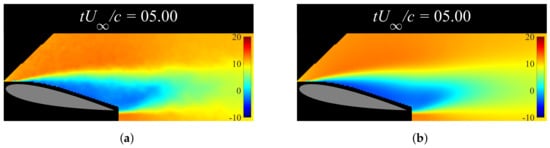
Figure 7.
Flow visualization and reconstruction from first POD coefficient of ensemble average during normally separated flow conditions for . (a) Ensemble-averaged flow field at (ensemble for ). (b) Reconstructed flow field from the first POD mode at (ensemble for ).
3.1.2. Attached Flow
Figure 8 shows the ensemble-averaged time history of the POD coefficients and their standard deviations when the flow was fully attached. Figure 8 also demonstrates that the POD representations of the attached flow for ranging from 2 to 6 were highly consistent, with the time average of the first POD coefficient z within 10% of each other. The standard deviations of z for and 6 were within 15% of each other, but the cases had an outlier with significantly higher freestream velocity (possibly due to atmospheric factors during the particular run). A strong outlier, coupled with relatively low values of , significantly increased the deviation and the relative error. The values were almost constant compared with those under fully separated conditions, and the time-averaged value of was less than half of that of the fully separated conditions in the case of and 6. The data for these values can also be found in Table A1 in Appendix A. These results illustrate that the first POD mode was comparable among the different conditions, and the following analysis should provide reasonable estimations of the phenomena that occurred during the transient processes. The reconstruction from the first POD mode in Figure 9 also proved to be an accurate representation of the averaged flow field, as it was under fully separated conditions.
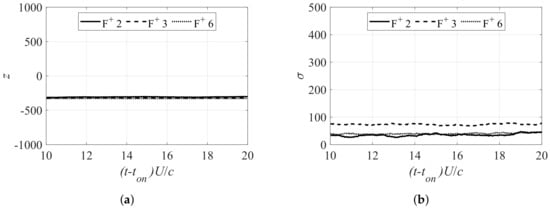
Figure 8.
Analysis of first POD mode during PA actuation and pseudo-stationary flow conditions. (a) First POD coefficient z of 30-run ensemble average for actuation with , 3, 6. (b) Standard deviation of first POD coefficient z of 30-run ensemble for actuation with , 3, 6.
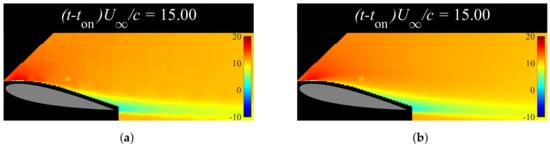
Figure 9.
Flow visualization and reconstruction from first POD coefficient of ensemble average during PA actuation and pseudo-stationary flow conditions for . (a) Averaged flow field at (ensemble for ). (b) Reconstructed flow field from first POD mode at (ensemble for ).
3.2. Reattachment Transient Process
Here, the reattachment transient process is discussed. Figure 10 shows the ensemble-averaged time history of the POD coefficients and their standard deviations when the flow was in the reattachment transient process. Figure 10 illustrates that a nearly pseudo-stationary state was achieved by under all actuation frequencies, and there was a brief period of sustained z and increased . The latter observation indicates the large vortex shed at the start of the actuation. The reattachment transient process was found to be consistent with previous studies by Amitay and Glezer [38] and Asada et al. [39].
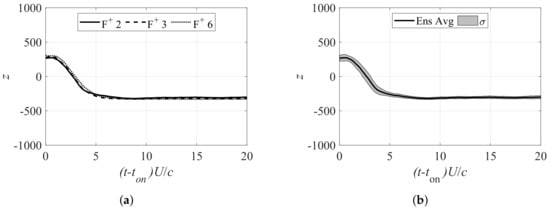
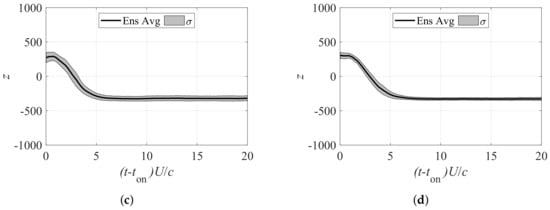
Figure 10.
z value of first POD mode during reattachment transient process. (a) First POD coefficient z of 30-run ensemble average for , 3, 6. (b) First POD coefficient z of 30-run ensemble average for and its standard deviation range. (c) First POD coefficient z of 30-run ensemble average for the actuation with and its standard deviation range. (d) First POD coefficient z of 30-run ensemble average for the actuation with and its standard deviation range.
Then, the ensemble-averaged flow fields are discussed, together with the time history of the first POD mode. Figure 11 shows the ensemble-averaged flow fields. Figure 11a,b, respectively, illustrate that the vortex first grew over the wing surface and was then shed. Figure 11c shows that there was a smaller one that followed immediately after this vortex, but this second one was not very clear owing to its smaller size, making it more sensitive to small differences in vortex-shedding behavior across runs. The shaded area of amplitude was also observed to be larger at lower burst frequencies, mainly before , which may be due to the interaction between the plasma actuator and the type of boundary layer separation, as discussed by Sato et al. [45]. However, the transient response time was found to be largely independent of the actuation frequency, as long as the conditions were suitable for suppressing separation. Finally, maintained the minimum value of any point in time during the experiments after , as only small periodic vortices from the PA were shed and the flow reached the pseudo-stationary state (Figure 11d).
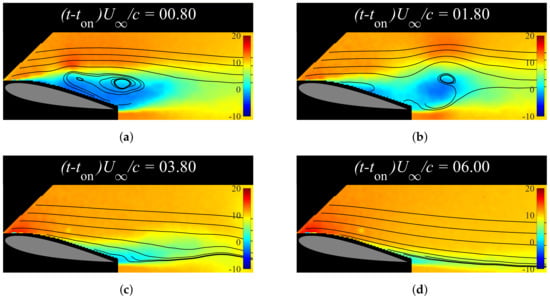
Figure 11.
Flow visualization during reattachment transient process. (a) Flow visualization of 30-run ensemble average of the actuation with at . (b) Flow visualization of 30-run ensemble average of the actuation with at . (c) Flow visualization of 30-run ensemble average of the actuation with at . (d) Flow visualization of 30-run ensemble average of the actuation with at .
3.3. Separation Transient Process
3.3.1. Flow Field Analysis
Next, the flow field in the separation transient process is discussed. Figure 12 shows the ensemble-averaged time history of the POD coefficients and their standard deviations when the flow was in the separation transient process. There were three stages in the separation transient process: vortex growth, vortex shedding, and recirculation region recovery. The vortex growth started when the plasma actuator was turned off. Initially, the vortices were small (similar in size to those generated by the plasma actuator) and dissipated quickly until they reached a critical size to combine and form a recirculation region. This point happened at approximately 3 to 5 , as shown in Figure 12.
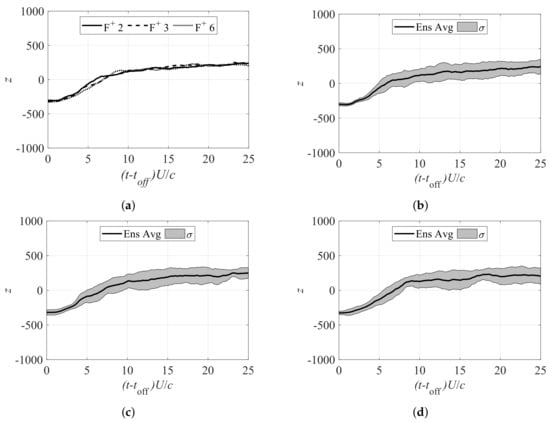
Figure 12.
z value of first POD mode during separation transient process. (a) First POD coefficient z of 30-run ensemble average for the actuation with , 3, 6. (b) First POD coefficient z of 30-run ensemble average for the actuation with and its standard deviation range. (c) First POD coefficient z of 30-run ensemble average for the actuation with and its standard deviation range. (d) First POD coefficient z of 30-run ensemble average for the actuation with and its standard deviation range.
Next, the ensemble-averaged flow fields in the separation transient process are discussed, along with the time history of the first POD mode and the instantaneous flow fields, because the ensemble-averaged flow fields did not show the smaller key vortices in the initial stage of the process in this case. Figure 13 shows the instantaneous and ensemble-averaged flow fields in the separation transient process. The growth in the coefficient of the first POD mode was consistent across all runs, with slowly increasing z and very low , although the ensemble average could be misleading. The small vortices generated randomly make this stage look like a separation bubble in the ensemble average shown in Figure 13a, which differs from what actually happened in each individual run shown in Figure 13b. Here, z and its standard deviation increased rapidly on , as shown in Figure 13b–d, indicating the beginning of the vortex-shedding stage. This stage was characterized by the shedding of large vortices. However, many of these vortices were not observed to be strong and they did not lead to a recovery of suction. Large vortex shedding was not observed at all in some cases. Figure 13e,f show that strong vortices were randomly generated after but their distribution made them invisible in the ensemble average. Here, was the largest in the entire run due to the mentioned variations during this stage. The occurrence of large vortex shedding was not completely eliminated but it decreased notably after approximately , which indicated the beginning of the recirculation region recovery process. This last stage was characterized by a slow increase in z and a slow decrease in , which showed that the flow approached normally separated conditions. However, the recirculation area recovery was very slow. The value of at was still nearly twice as high as that in Figure 6b, which indicates lingering effects from the controlled flow conditions. Although the measurement time might be insufficient for capturing the full recovery of the recirculation region (i.e., 99% or 99.9% of recovery of some statistic indices used in the following sections), capturing this entire transient process (likely up to ) using time-resolved PIV would be experimentally too expensive to address only a small change in the flow fields.
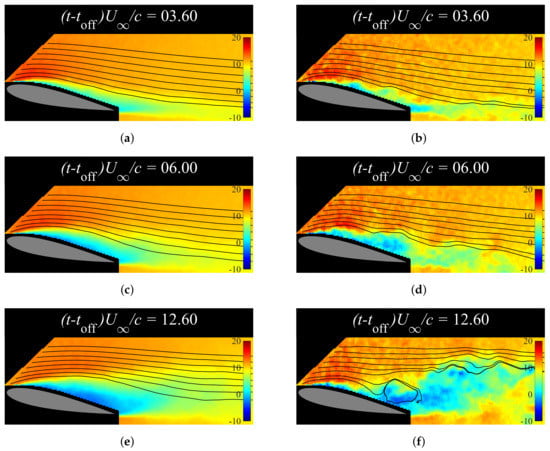
Figure 13.
Flow visualization during separation transient process. (a) Flow visualization of 30-run ensemble average of the actuation with at . (b) Flow visualization of single run of the actuation with ensemble at . (c) Flow visualization of 30-run ensemble average of the actuation with at . (d) Flow visualization of single run of the actuation with ensemble at . (e) Flow visualization of 30-run ensemble average of the actuation with at . (f) Flow visualization of single run of the actuation with ensemble at .
3.3.2. Surface Pressure Analysis
Finally, the pressure history in the separation transient process is discussed. Figure 14 shows the ensemble-averaged pressure measurements and their standard deviations at the position 0.1 c for . Figure 14 shows the decent consistency of the pressure at 0.1 c, with the POD analysis of the velocity field shown in Figure 12 regarding the vortex-shedding and recirculation region recovery stages. However, it was not possible to draw conclusions on the initial vortex growth, as the period of time was severely affected by noise. This also potentially made it more difficult to analyze the of the pressure signals, as the expected period with low deviation was out of range (). This , however, was significantly higher than that under the normally separated conditions and exhibited similar behavior to that of the first POD modes of the PIV measurements. Lastly, the actuation with showed stronger suction than the actuation with lower frequencies, which may explain the differences in the separation transient response time.
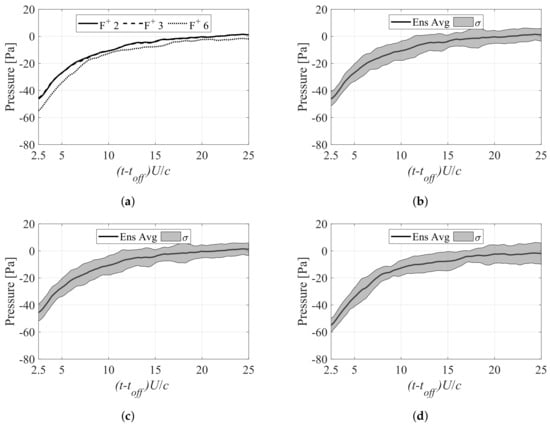
Figure 14.
Pressure measurements at 0.1 c of 30-run ensemble average for , 3, 6 during separation transient process. (a) Pressure at 0.1 c of 30-run ensemble average for , 3, 6. (b) Pressure and its standard deviation at 0.1 c of 30-run ensemble average for . (c) Pressure and its standard deviation at 0.1 c of 30-run ensemble average for . (d) Pressure and its standard deviation at 0.1 c of 30-run ensemble average for .
One more relevant point is the ability to identify the flow field state from pressure measurements, as it is one of the most practical and reliable means of obtaining information about the surrounding flow in the field. Figure 14a exhibits a similar pattern to that shown in Figure 12a after , although the piezoelectric sensors were strongly affected by the plasma actuator before , as mentioned before. The time history of the pressure signal followed a similar trend to that of the first POD mode coefficient. This suggests that it may be possible to use unsteady pressure measurements to estimate the flow state and determine the need for flow control, especially during the transient process when the plasma actuator is inactive.
4. Quantitative Evaluation
In Section 3, the initial results revealed a noticeable asymmetry between the transient processes of reattachment and separation. To determine the completion ratio of the transient process over time, the difference between the ensemble average of z in the pseudo-stationary state with and without flow control activated was quantitatively evaluated as a range from fully attached to fully separated flow conditions. The completion ratio of the reattachment transient process and the separation transient process are, respectively, defined by
where and are, respectively, the time averages of z on when the flow is fully separated and z on when the flow is attached. Subsequently, three comparison points within each transient process were selected, and arbitrary times of , , and were chosen for this purpose. Additionally, the nondimensional times it took each transient process to reach completion ratios of 0.3, 0.6, and 0.9 were also calculated. The completion ratios at designated points in time, and the time taken to reach the designated completion ratios are graphically represented in Figure 15.
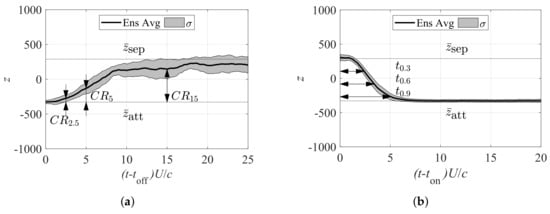
Figure 15.
Analysis of first POD mode during PA actuation with pseudo-stationary flow conditions. (a) Graphical representation of completion ratios , , and at times 2.5, 5, and 15, respectively. (b) Graphical representation of times , , and , which reach completion ratios of 0.3, 0.6, and 0.9, respectively.
Figure 16 presents the estimated completion ratios of the transient processes (both reattachment and separation) for the actuation with , 3, 6. In Figure 16a–c, the completion ratios for the different burst frequencies at times are compared, and in Figure 16d,e, the time each burst frequency took to reach completion ratios of 0.3, 0.6, and 0.9 is shown. Figure 16 demonstrates that the separation and reattachment processes behaved differently. The reattachment process exhibited nearly four times the progression compared to the separation process when , whereas the reattachment process exhibited almost full completion, with completion ratios ranging from 0.89 to 0.95 and very low deviations for all values based on a 30-run ensemble average at a time of . Figure 10 illustrates that the reattachment was complete for all conditions by . Early in the transient process, the actuation with was capable of reaching the highest completion ratio, whereas the actuation with was the slowest. However, the quality and reliability of the reattachment for the actuation with were arguably the best out of the three, which, in turn, had an effect on the separation transient process. The times to reach completion ratios of 0.3, 0.6, and 0.9 showed very similar curves that were almost linear for all the conditions in the reattachment transient process. This suggests that the reattachment transient process is not strongly dependent on the burst frequency.
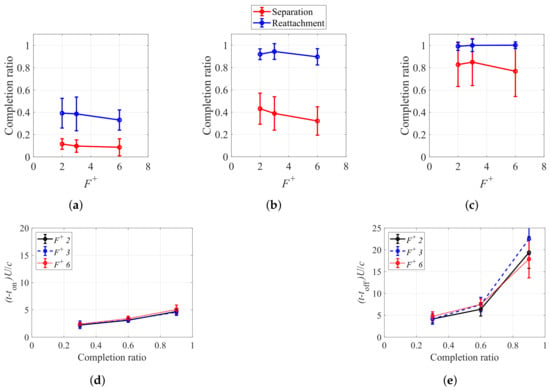
Figure 16.
Analysis of transient process completion ratio. (a) Completion ratio at (red) and (blue). (b) Completion ratio at (red) and (blue). (c) Completion ratio at (red) and (blue). (d) Times after PA state switch (off → on) to achieve completion ratios of 0.3, 0.6, and 0.9. (e) Times after PA state switch (on → off) to achieve completion ratios of 0.3, 0.6, and 0.9.
The separation transient process exhibited significantly less progress during the same time windows, with an average completion ratio of 0.10 and 0.42 for the actuation with at and , respectively. As increased, the completion ratio further decreased, achieving values as low as 0.07 and 0.30 for the actuation with at and , respectively. Moreover, the dispersion was large at and , as the separation vortices had already reached a critical size and large vortices were being shed. The reason for the difference in the completion ratio between the various conditions could be attributed to the fact that, despite the flow being practically fully attached and pseudo-stationary, it was not actually attached until the trailing edge under any of the tested actuation frequencies. The actuation with , however, was capable of sustaining flow attachment until slightly further downstream than the lower frequencies, which slowed down the transient response. In the separation transient process, the times to reach completion ratios of 0.3, 0.6, and 0.9 showed an almost exponential behavior, and the actuation with was the slowest process overall.
The discussion above demonstrates that under the given experimental conditions, was the most effective actuation frequency out of the tested frequencies. Additionally, it exhibited the smallest overall deviation (fewer random events) and delayed the separation transient process the longest. The asymmetric behavior of the reattachment and separation processes can be leveraged by turning off the plasma actuator when the flow is attached and by turning it on before the separation transient process progresses to a significant extent and the wing performance is significantly worsened. By efficiently turning on and off the plasma actuator, its power consumption can be reduced without significantly degrading performance. The findings in this work illustrate that intervals longer than should be avoided, as the benefit of extending the reattachment transient process beyond is minimal, and the disadvantage of allowing the separation transient process to take longer than becomes significant.
The results regarding the reattachment transient process align with those reported in the previous studies conducted by Amitay and Glezer [38] and Asada et al. [39]. This study confirms the flow structures and, more importantly, the quantitative completion time of the transient process by using the first POD mode of the velocity field. Additionally, this work identifies new characteristics of the separation transient process. Understanding the various stages of the separation transient process, such as the vortex growth and vortex-shedding stages, is crucial in the field of active flow control. Knowing that the separation transient response is much slower than that of the reattachment is an important consideration when designing feedback control systems for flow separation control, as the efficiency of a plasma actuator can be enhanced by turning it on and off at appropriate times during the transient processes. Furthermore, the flow state can be inferred from the pressure measurements, which is key to the application of feedback-based flow control. However, it would be preferable to use a different high-frequency pressure-sensing method that is not sensitive to a strong electric field generated by plasma actuators.
5. Conclusions
In this study, we investigated the transient processes for flow reattachment and separation under the effect of a leading-edge plasma actuator. The wind tunnel experiments were conducted for a NACA0015 wing with a leading-edge plasma actuator and piezoelectric sensors. This was coupled with a high-speed PIV setting, providing simultaneous time-resolved PIV and pressure data. The angle of attack was set at 13 and the Reynolds number was 66,000 of which the flow field had boundary layer separation at the leading edge. An ensemble of 30 runs was obtained for each of the burst frequencies of the plasma actuator, with the exception of , which could not reliably control the separation. The results from the ensemble-averaged data were presented and discussed. The behavior of the separation transient process was observed using both PIV and pressure measurements. However, the reattachment process was primarily studied using PIV measurements, supplemented partially by piezoelectric pressure sensors. The signals contaminated by strong noise from the plasma actuator were excluded. The reattachment transient process was found to be consistent with previous studies, with a quick completion soon after an initial large vortex shedding. The separation transient process was found to be not only significantly slower than the reattachment process but also had considerable variations. Once the recirculation region reappeared, there was a possibility that no, one, or multiple large vortices would be shed for a long period of time after turning off the plasma actuator, leading to a flow condition with greater deviation than before actuation. Finally, alternating between reattachment and separation transient processes at appropriate times, as carried out in the ‘burst in burst’ actuation in the previous study, is recommended to significantly improve the efficiency of the plasma actuator due to the slow progress of the separation, as shown in this study.
Author Contributions
Conceptualization, R.V. and T.N.; methodology, R.V. and T.N.; software, R.V. and Y.A.; validation, R.V. and T.N.; formal analysis, R.V. and T.N.; investigation, R.V. and T.N.; resources, R.V. and T.N.; data curation, R.V. and Y.A.; writing—original draft preparation, R.V., Y.S. and T.N.; writing—review and editing, R.V., Y.S. and T.N.; visualization, R.V., Y.S. and T.N.; supervision, Y.S. and T.N.; project administration, T.N.; funding acquisition, T.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Japan Science and Technology Agency, FOREST Grant Number, JPMJFR202C.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| z | First POD coefficient |
| Standard deviation | |
| Time average of z during pseudo-stationary controlled conditions | |
| Time average of z during fully separated conditions | |
| AC | Alternating current |
| c | Wing chord |
| f | Frequency of sinusoidal wave |
| Burst frequency | |
| Nondimensional burst frequency | |
| PA | Plasma actuator |
| t | Time |
| Instant at which the plasma actuator is turned off | |
| Instant at which the plasma actuator is turned on | |
| Instant at which the plasma actuator is either turned on or off | |
| T | Period of sinusoidal wave |
| Period of burst | |
| Inactive period during burst | |
| Active period during burst | |
| U | Horizontal component of wind velocity |
| Freestream velocity | |
| V | Voltage |
Appendix A. Experimental Results
Table A1 shows the quantitative values of the POD mode coefficients.

Table A1.
Properties of test cases and their subdivisions.
Table A1.
Properties of test cases and their subdivisions.
| Case 1 | Case 2 | |||||
|---|---|---|---|---|---|---|
| mean(z) | 179.2 | 219.6 | 257.6 | 281.8 | 289.0 | |
| mean((z)) | 107.3 | 113.3 | 97.1 | |||
| mean(z) | −116.4 | −334.2 | −306.3 | −320.6 | −328.7 | |
| mean((z)) | 35.2 | 73.6 | 40.0 | |||
Appendix B. Analysis of F+ = 1
Here, the flow control capability of the condition is discussed with the time history of the first POD mode, as well as the instantaneous flow fields. Figure A1 shows the time history of the POD coefficients for both cases before applying flow control and during actuation. Figure A1 shows that the cases with burst frequency had a significantly lower average z value than the cases shown in Figure 6, likely due to a different feature representation by their first POD mode. In the first case, the actuation with could not achieve reattachment. Conversely, the second case of could achieve partial reattachment, and the coefficient of the first POD mode coefficient became closer to the ensemble-averaged values of the higher cases.
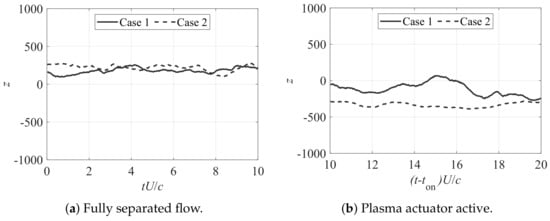
Figure A1.
z of first POD mode during complete separation (left) and steady plasma actuator activation for (right).
Figure A2 shows the instantaneous flow fields of both cases at . In the case of , there were significant variations, which indicates that it was unreliable for flow control under the given test conditions. Figure A2a displays a recirculation region of significant size, whereas Figure A2b displays relatively large vortices. Therefore, actuation with higher burst frequencies is capable of completely suppressing the separation, along with the near trailing-edge region, and achieving a pseudo-stationary state, as indicated by the almost constant values of z and low shown in Figure 8. The inability to successfully control the flow field led to the decision to exclude the cases from further analyses.
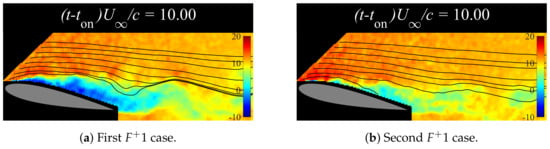
Figure A2.
U velocity fields of both cases at .
References
- Post, M.L.; Corke, T.C. Separation control on high angle of attack airfoil using plasma actuators. AIAA J. 2004, 42, 2177–2184. [Google Scholar] [CrossRef]
- Roth, J.R. Aerodynamic flow acceleration using paraelectric and peristaltic electrohydrodynamic effects of a one atmosphere uniform glow discharge plasma. Phys. Plasmas 2003, 10, 2117–2126. [Google Scholar] [CrossRef]
- Aono, H.; Kawai, S.; Nonomura, T.; Sato, M.; Fujii, K.; Okada, K. Plasma-actuator burst-mode frequency effects on leading-edge flow-separation control at Reynolds number 2.6 × 105. AIAA J. 2017, 55, 3789–3806. [Google Scholar] [CrossRef]
- Greenblatt, D.; Schneider, T.; Schüle, C.Y. Mechanism of flow separation control using plasma actuation. Phys. Fluids 2012, 24, 077102. [Google Scholar] [CrossRef]
- Vernet, J.A.; Örlü, R.; Alfredsson, P.H. Flow separation control behind a cylindrical bump using dielectric-barrier-discharge vortex generator plasma actuators. J. Fluid Mech. 2018, 835, 852–879. [Google Scholar] [CrossRef]
- Wicks, M.; Thomas, F.; Schatzman, D.; Bowles, P.; Corke, T.; Patel, M.; Cain, A. A parametric investigation of plasma streamwise vortex generator performance. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; p. 824. [Google Scholar]
- Riherd, M.; Roy, S. Serpentine geometry plasma actuators for flow control. J. Appl. Phys. 2013, 114, 083303. [Google Scholar] [CrossRef]
- Mohammadpour, P.; Mani, M.; Saeedi, M. Experimental investigation of induced velocity by dielectric barrier discharge plasma actuator in different configurations. AIP Adv. 2021, 11, 105007. [Google Scholar] [CrossRef]
- Caruana, D.; Rogier, F.; Dufour, G.; Gleyzes, C. The Plasma Synthetic Jet Actuator, Physics, Modeling and Flow Control Application on Separation. Aerosp. Lab 2013, 1–13. [Google Scholar]
- Zong, H.; Chiatto, M.; Kotsonis, M.; De Luca, L. Plasma synthetic jet actuators for active flow control. Actuators 2018, 7, 77. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E.; Zouzou, N.; Rabat, H.; Pons, J.; Hong, D.; Leroy, A.; Peschke, P.; Hollenstein, C. Nanosecond Pulsed Plasma Actuators. ERCOFTAC Bull. 2013, 94, 11–16. [Google Scholar]
- Lehmann, R.; Akins, D.; Little, J. Effects of Nanosecond Pulse Driven Plasma Actuators on Turbulent Shear Layers. AIAA J. 2016, 54, 637–651. [Google Scholar] [CrossRef]
- Subrata, R.; Pengfei, Z.; Arnob, D.; Jignesh, S. Dielectric barrier discharge actuator for vehicle drag reduction at highway speeds. AIP Adv. 2016, 6, 025322. [Google Scholar] [CrossRef]
- Iranshahi, K.; Mani, M. Dielectric Barrier Discharge Actuators Employed as Alternative to Conventional High-Lift Devices. J. Aircr. 2018, 55, 2104–2113. [Google Scholar] [CrossRef]
- Al-Sadawi, L.; Chong, T.P.; Kim, J.H. Aerodynamic noise reduction by plasma actuators for a flat plate with blunt trailing edge. J. Sound Vib. 2019, 439, 173–193. [Google Scholar] [CrossRef]
- Patel, T.K.; Lilley, A.J.; Shen, W.; Porrello, C.; Schindler-Tyka, A.; Roy, S.; Lear, W.E.; Miller, S.A. Fundamental investigation using active plasma control to reduce blade–vortex interaction noise. Int. J. Aeroacoust. 2021, 20, 870–900. [Google Scholar] [CrossRef]
- Corke, T.C.; Post, M.L.; Orlov, D.M. Single dielectric barrier discharge plasma enhanced aerodynamics: Physics, modeling and applications. Exp. Fluids 2009, 46, 1–26. [Google Scholar] [CrossRef]
- Abdollahzadeh, M.; Pascoa, J.; Oliveira, P. Comparison of DBD plasma actuators flow control authority in different modes of actuation. Aerosp. Sci. Technol. 2018, 78, 183–196. [Google Scholar] [CrossRef]
- Asada, K.; Ninomiya, Y.; Fujii, K.; Oyama, A. Airfoil Flow Experiment on the Duty Cycle of DBD Plasma Actuator. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- Fujii, K. Three Flow Features behind the Flow Control Authority of DBD Plasma Actuator: Result of High-Fidelity Simulations and the Related Experiments. Appl. Sci. 2018, 8, 546. [Google Scholar] [CrossRef]
- Moreau, E.; Debien, A.; Breux, J.M.; Benard, N. Control of a turbulent flow separated at mid-chord along an airfoil with DBD plasma actuators. J. Electrost. 2016, 83, 78–87. [Google Scholar] [CrossRef]
- Sato, M.; Nonomura, T.; Okada, K.; Asada, K.; Aono, H.; Yakeno, A.; Abe, Y.; Fujii, K. Mechanisms for laminar separated-flow control using dielectric-barrier-discharge plasma actuator at low Reynolds number. Phys. Fluids 2015, 27, 1–29. [Google Scholar] [CrossRef]
- Sato, M.; Aono, H.; Yakeno, A.; Nonomura, T.; Fujii, K.; Okada, K.; Asada, K. Multifactorial effects of operating conditions of dielectric-barrier-discharge plasma actuator on laminar-separated-flow control. AIAA J. 2015, 53, 2544–2559. [Google Scholar] [CrossRef]
- Sekimoto, S.; Nonomura, T.; Fujii, K. Burst-mode frequency effects of dielectric barrier discharge plasma actuator for separation control. AIAA J. 2017, 55, 1385–1392. [Google Scholar] [CrossRef]
- Sekimoto, S.; Fujii, K.; Anyoji, M.; Miyakawa, Y.; Ito, S.; Shimomura, S.; Nishida, H.; Nonomura, T.; Matsuno, T. Flow Control around NACA0015 Airfoil Using a Dielectric Barrier Discharge Plasma Actuator over a Wide Range of the Reynolds Number. Actuators 2023, 12, 43. [Google Scholar] [CrossRef]
- Visbal, M.; Gaitonde, D.; Roy, S. Control of Transitional and Turbulent Flows Using Plasma-Based Actuators. In Proceedings of the 36th AIAA Fluid Dynamics Conference and Exhibit, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar] [CrossRef]
- Benard, N.; Balcon, N.; Moreau, E. Electric Wind Produced by a Surface Dielectric Barrier Discharge Operating Over a Wide Range of Relative Humidity. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- Lilley, A.J.; Roy, S.; Michels, L.; Roy, S. Performance recovery of plasma actuators in wet conditions. J. Phys. D Appl. Phys. 2022, 55, 155201. [Google Scholar] [CrossRef]
- Wicks, M.; Thomas, F.O. Effect of Relative Humidity on Dielectric Barrier Discharge Plasma Actuator Body Force. AIAA J. 2015, 53, 2801–2805. [Google Scholar] [CrossRef]
- Benard, N.; Moreau, E.; Griffin, J.; Cattafesta, L.N.I. Slope seeking for autonomous lift improvement by plasma surface discharge. Exp. Fluids 2009, 48, 791–808. [Google Scholar] [CrossRef]
- Benard, N.; Cattafesta, L.N.; Moreau, E.; Griffin, J.; Bonnet, J.P. On the benefits of hysteresis effects for closed-loop separation control using plasma actuation. Phys. Fluids 2011, 23, 083601. [Google Scholar] [CrossRef]
- Broglia, R.; Choi, K.S.; Houston, P.; Pasquale, L.; Zanchetta, P. Output feedback control of flow separation over an aerofoil using plasma actuators. Int. J. Numer. Anal. Model. 2018, 15. [Google Scholar]
- Pasquale, L.; Durante, D.; Broglia, R. Flow separation prevention around a NACA0012 profile through multivariable feedback controlled plasma actuators. Comput. Fluids 2019, 182, 85–107. [Google Scholar] [CrossRef]
- Patel, M.P.; Sowle, Z.H.; Corke, T.C.; He, C. Autonomous Sensing and Control of Wing Stall Using a Smart Plasma Slat. J. Aircr. 2007, 44, 516–527. [Google Scholar] [CrossRef]
- Ogawa, T.; Asada, K.; Sekimoto, S.; Tatsukawa, T.; Fujii, K. Dynamic Burst Actuation to Enhance the Flow Control Authority of Plasma Actuators. Aerospace 2021, 8, 396. [Google Scholar] [CrossRef]
- Segawa, T.; Suzuki, D.; Fujino, T.; Jukes, T.; Matsunuma, T. Feedback control of flow separation using plasma actuator and FBG sensor. Int. J. Aerosp. Eng. 2016, 2016, 8648919. [Google Scholar] [CrossRef]
- Shimomura, S.; Sekimoto, S.; Oyama, A.; Fujii, K.; Nishida, H. Closed-Loop Flow Separation Control Using the Deep Q Network over Airfoil. AIAA J. 2020, 58, 1–11. [Google Scholar] [CrossRef]
- Amitay, M.; Glezer, A. Controlled transients of flow reattachment over stalled airfoils. Int. J. Heat Fluid Flow 2002, 23, 690–699. [Google Scholar] [CrossRef]
- Asada, K.; Nonomura, T.; Aono, H.; Sato, M.; Okada, K.; Fujii, K. LES of transient flows controlled by DBD plasma actuator over a stalled airfoil. Int. J. Comput. Fluid Dyn. 2015, 29, 215–229. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef]
- Nankai, K.; Ozawa, Y.; Nonomura, T.; Asai, K. Linear Reduced-order Model Based on PIV Data of Flow Field around Airfoil. Trans. Jpn. Soc. Aeronaut. Space Sci. 2019, 62, 227–235. [Google Scholar] [CrossRef]
- Nonomura, T.; Nankai, K.; Iwasaki, Y.; Komuro, A.; Asai, K. Quantitative evaluation of predictability of linear reduced-order model based on particle-image-velocimetry data of separated flow field around airfoil. Exp. Fluids 2021, 62, 112. [Google Scholar] [CrossRef]
- Sekimoto, S.; Asada, K.; Anyoji, M.; Nonomura, T.; Fujii, K. Comparative Study of Co-flow and Counter Blowing DBD Plasma Actuators for Separated Flow over an Airfoil. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. [Google Scholar] [CrossRef]
- Sato, M.; Okada, K.; Asada, K.; Aono, H.; Nonomura, T.; Fujii, K. Unified mechanisms for separation control around airfoil using plasma actuator with burst actuation over Reynolds number range of 103–106. Phys. Fluids 2020, 32, 025102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).