Model-Based Design Optimization of Soft Polymeric Domes Used as Nonlinear Biasing Systems for Dielectric Elastomer Actuators
Abstract
:1. Introduction
2. DEA Operating Principle
2.1. DEA Operating Principle
- ϵ0 is the vacuum permittivity;
- ϵr is the DE relative permittivity;
- V is the applied voltage;
- t is the thickness of the dielectric film.
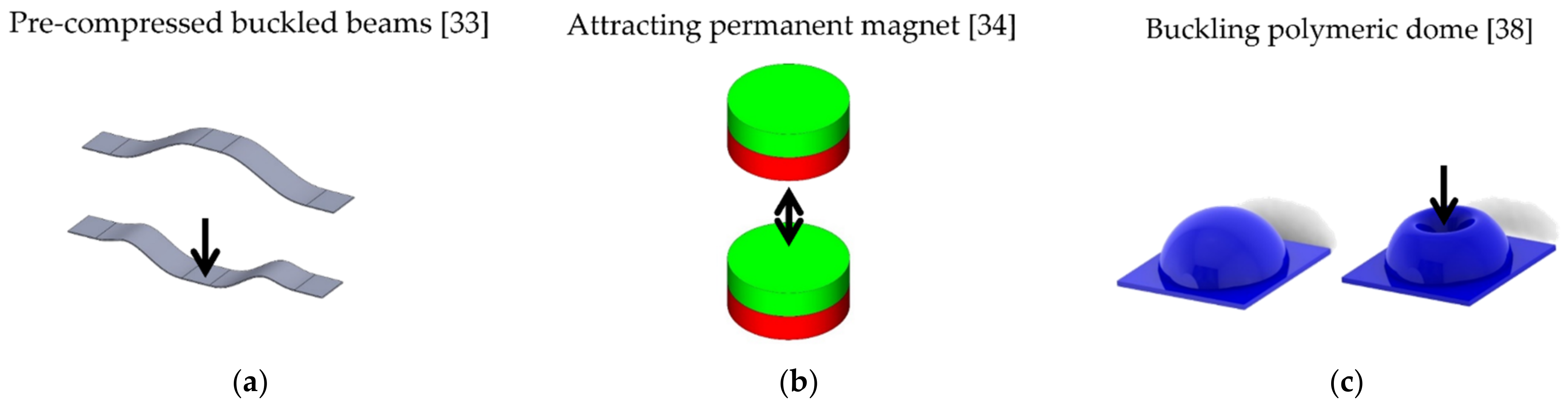
2.2. Bias Elements for DEAs
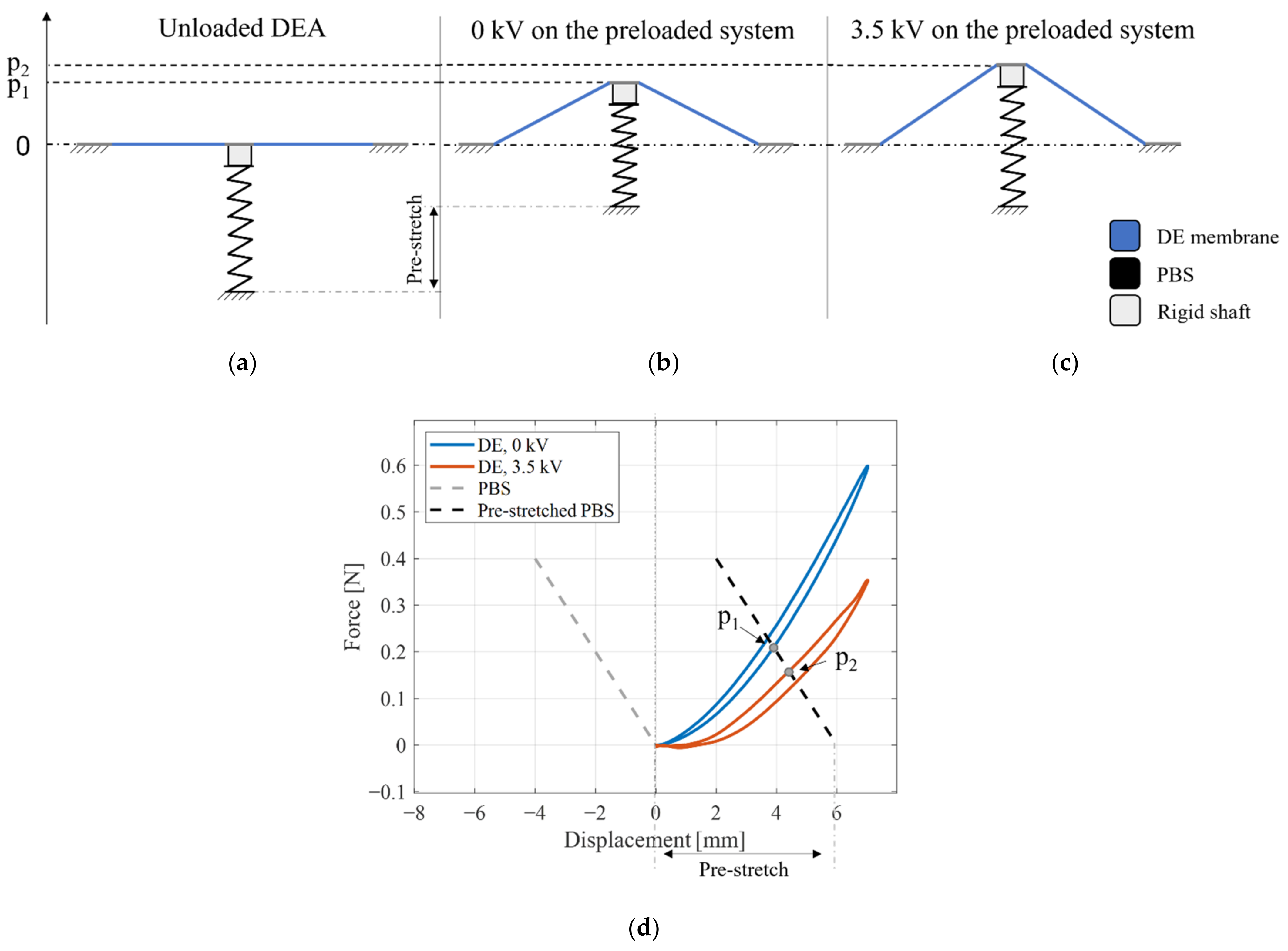
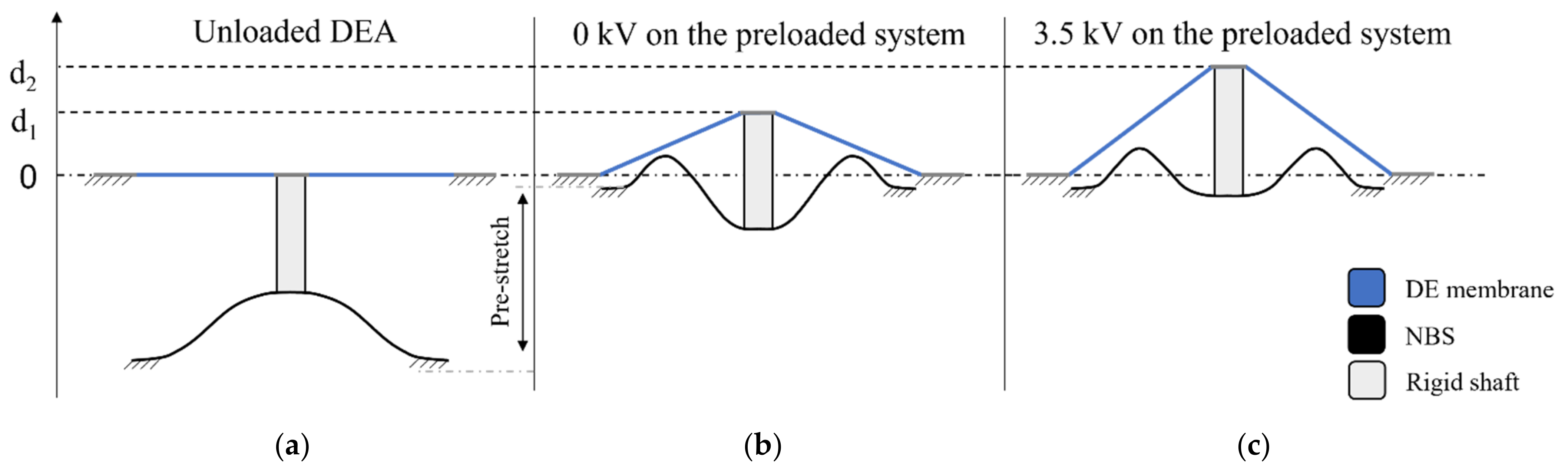
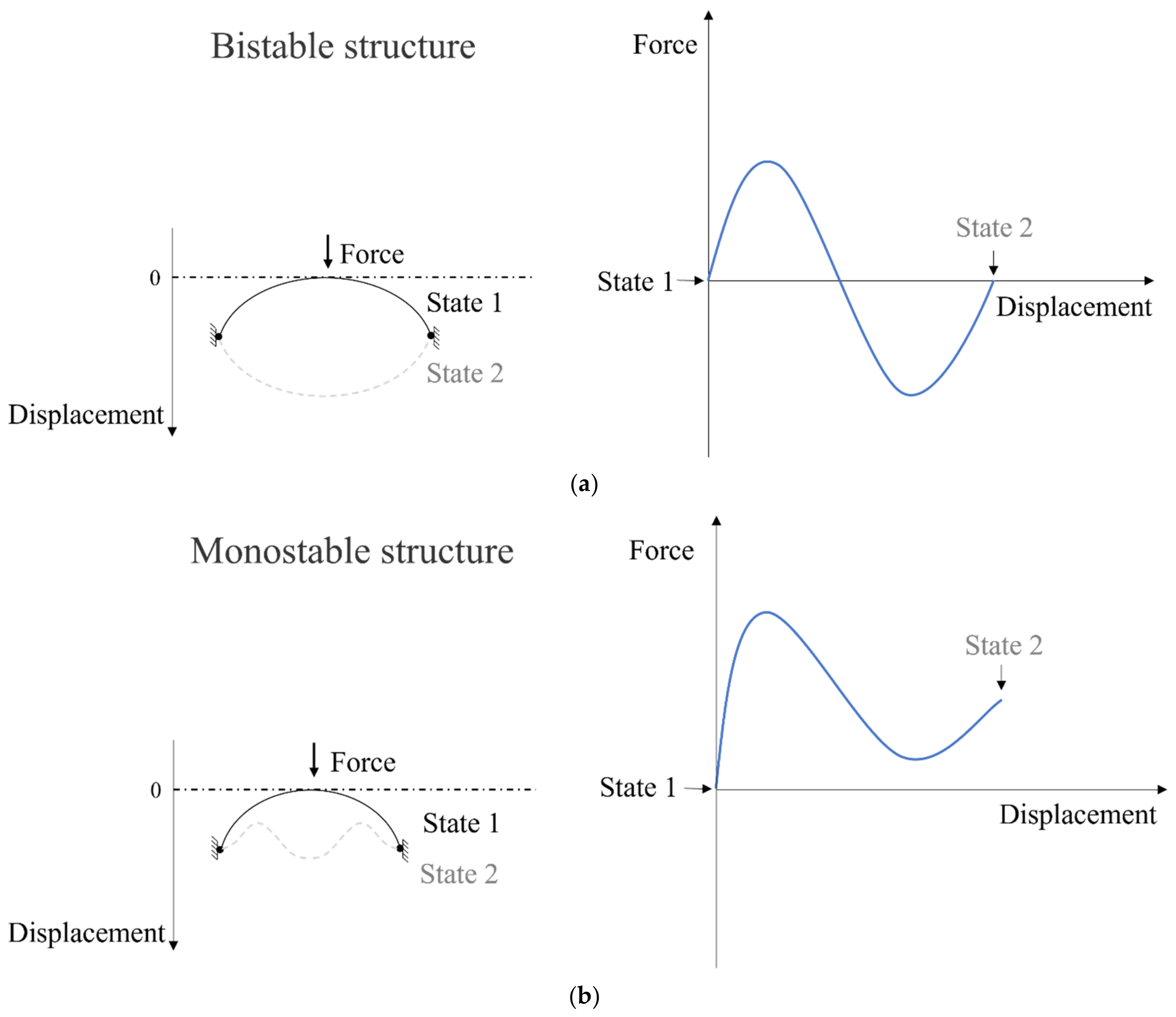
2.3. Bistable and Monostable NBS Elements
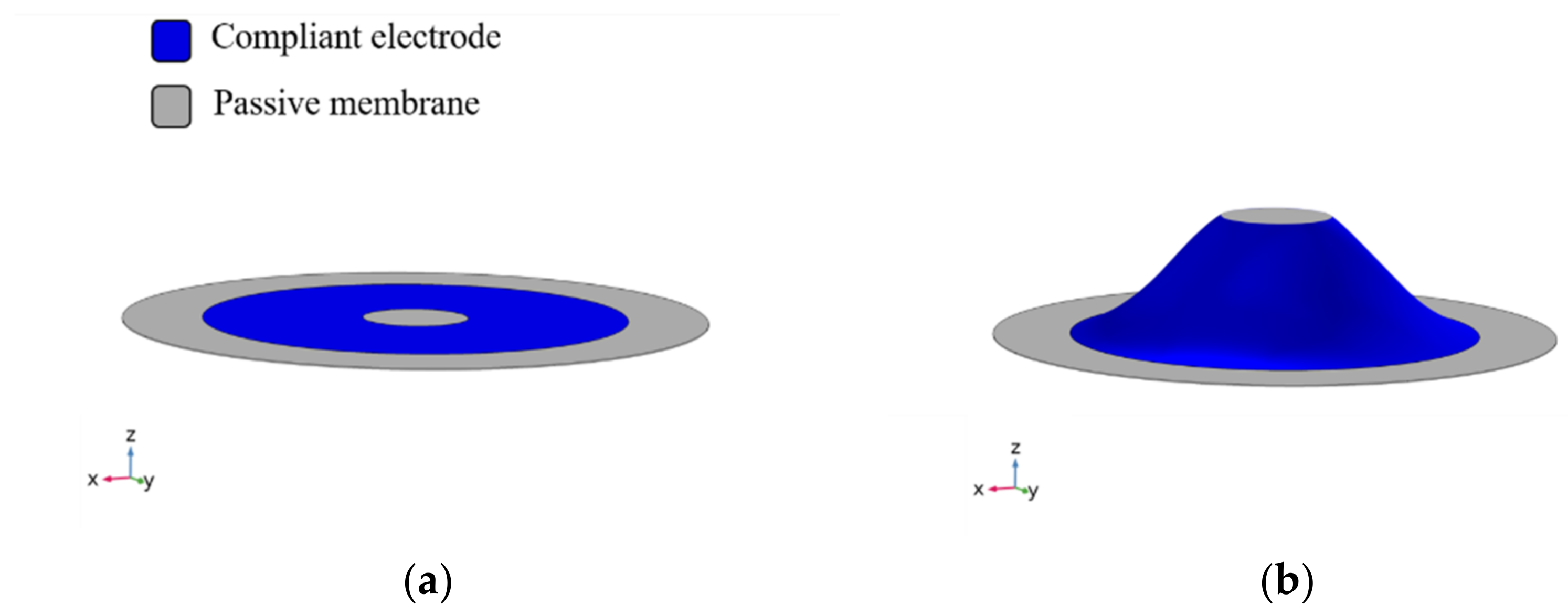
3. Nonlinear Biasing Dome
3.1. Dome FE Model
3.2. Post-Buckling Analysis and Numerical Implementation Aspects
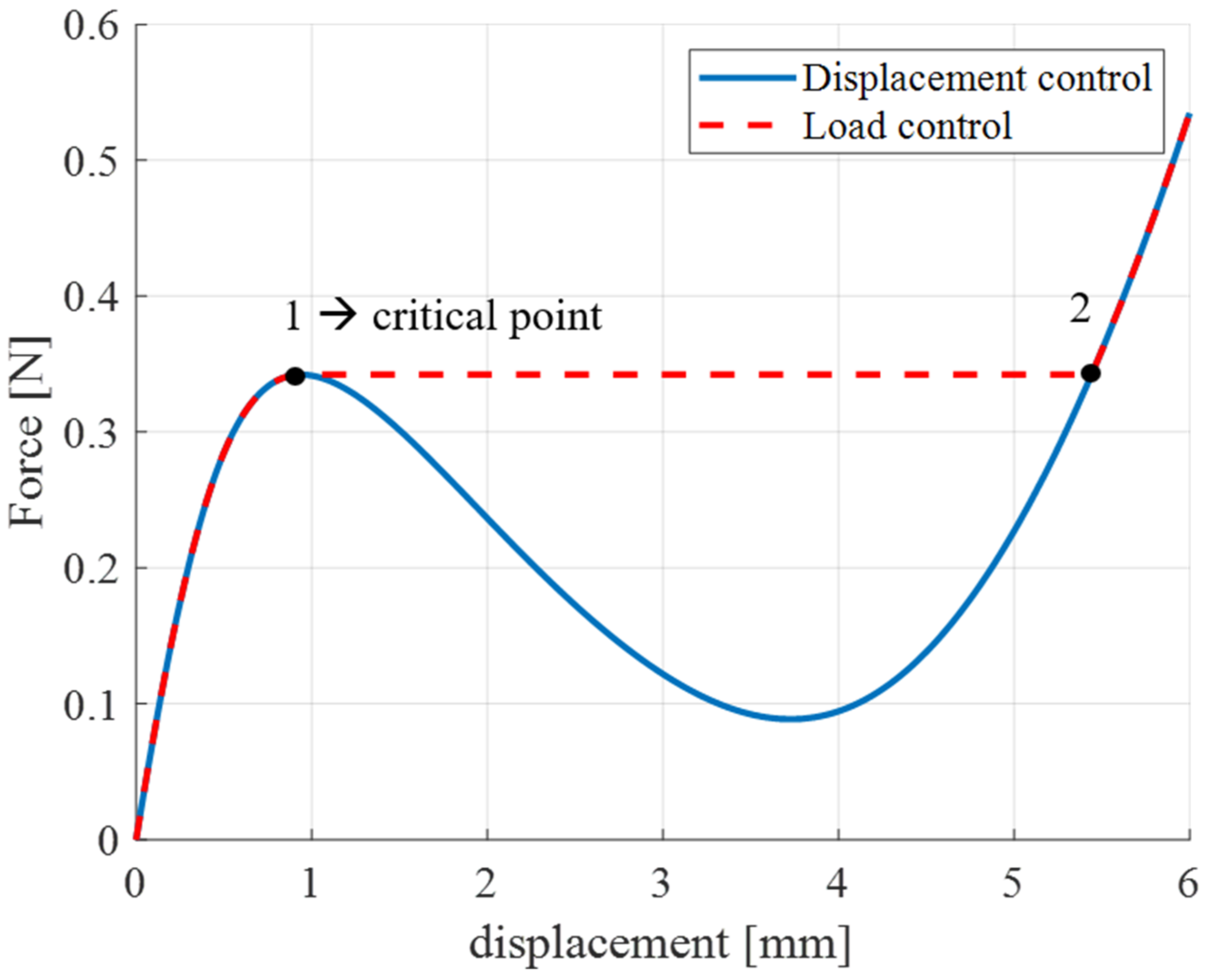
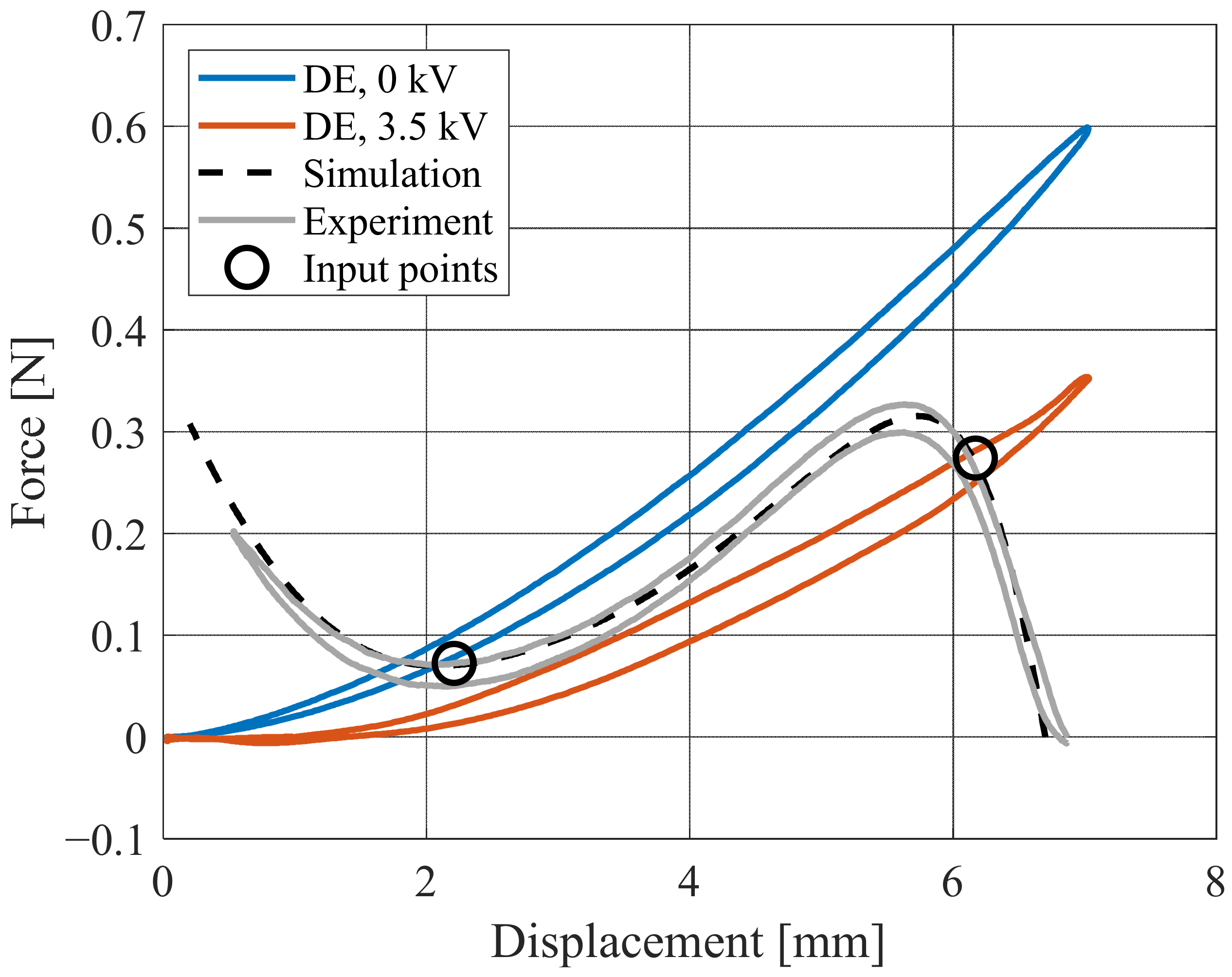
- Load control mode: the load force must necessarily be prescribed via nonlinear dynamic solver to solve the singularity of the problem, thus performing a time-dependent study. If a time-based analysis is conducted, there is a balance between the applied external load and elastic forces (note that all dynamic forces are neglected in this study). After that, the axial displacement represents the quantity calculated as the output. The final result is equivalent to the dashed red curve depicted in Figure 11, in which the dynamic jump from state 1 to state 2 is clearly visible.
- Displacement control mode: as the deformation represents the quantity increasing monotonically, it can be used as an input control parameter. In this way, the description of the load softening effect (occurring after the critical point) is derived unambiguously based on the simulation output.
- Principal stretches λ1, λ2, λ3;
- Material constitutive parameters ci0, i = 1, 2, 3;
- Bulk modulus κ, which allows practical accounting of the material incompressibility in a numerically efficient way;
- Volume ratio J, equal to the determinant of the deformation gradient.
4. Dome Calibration Based on the Experimental Characterization Process
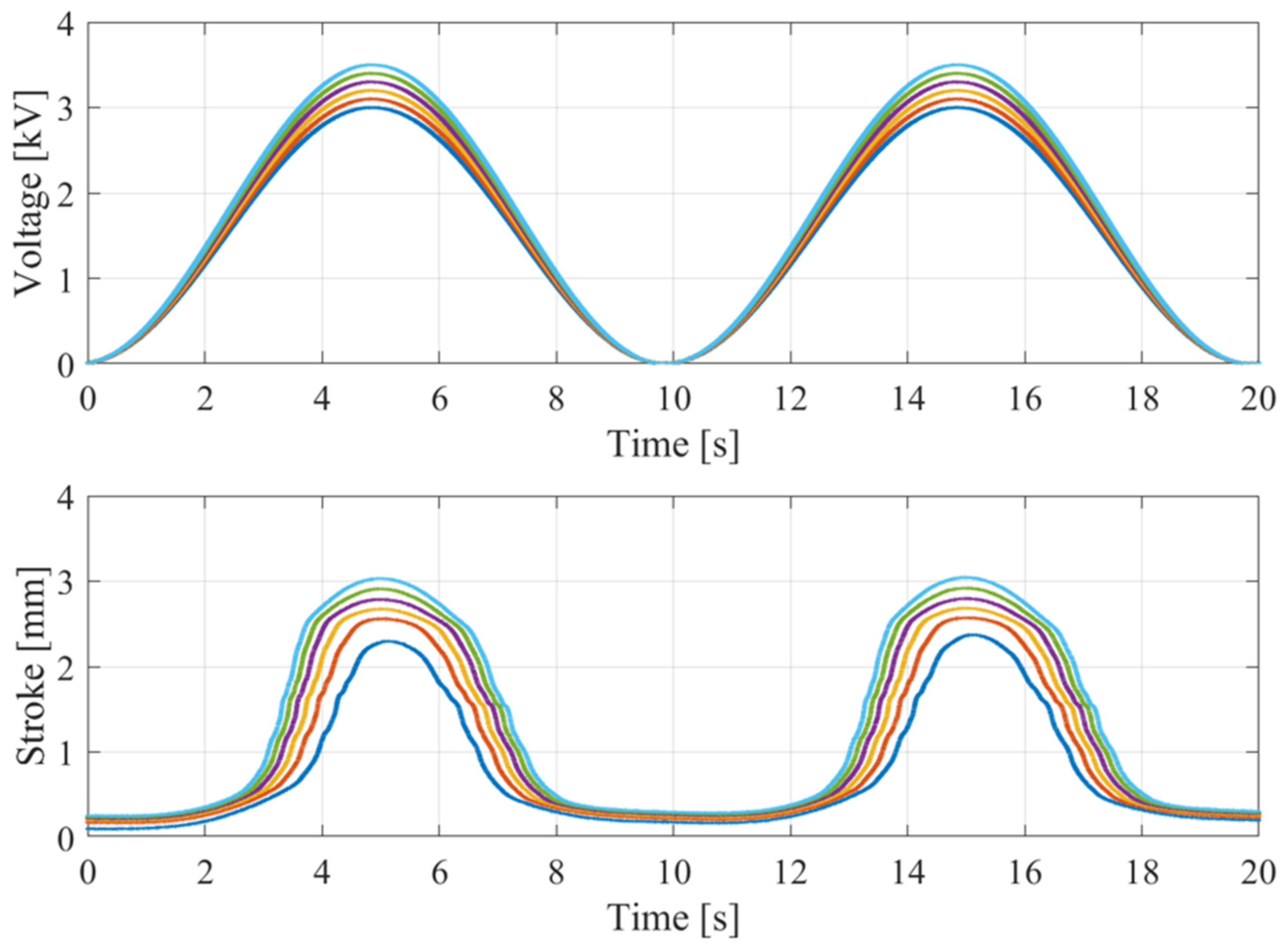
4.1. Dome Experimental Characterization Process
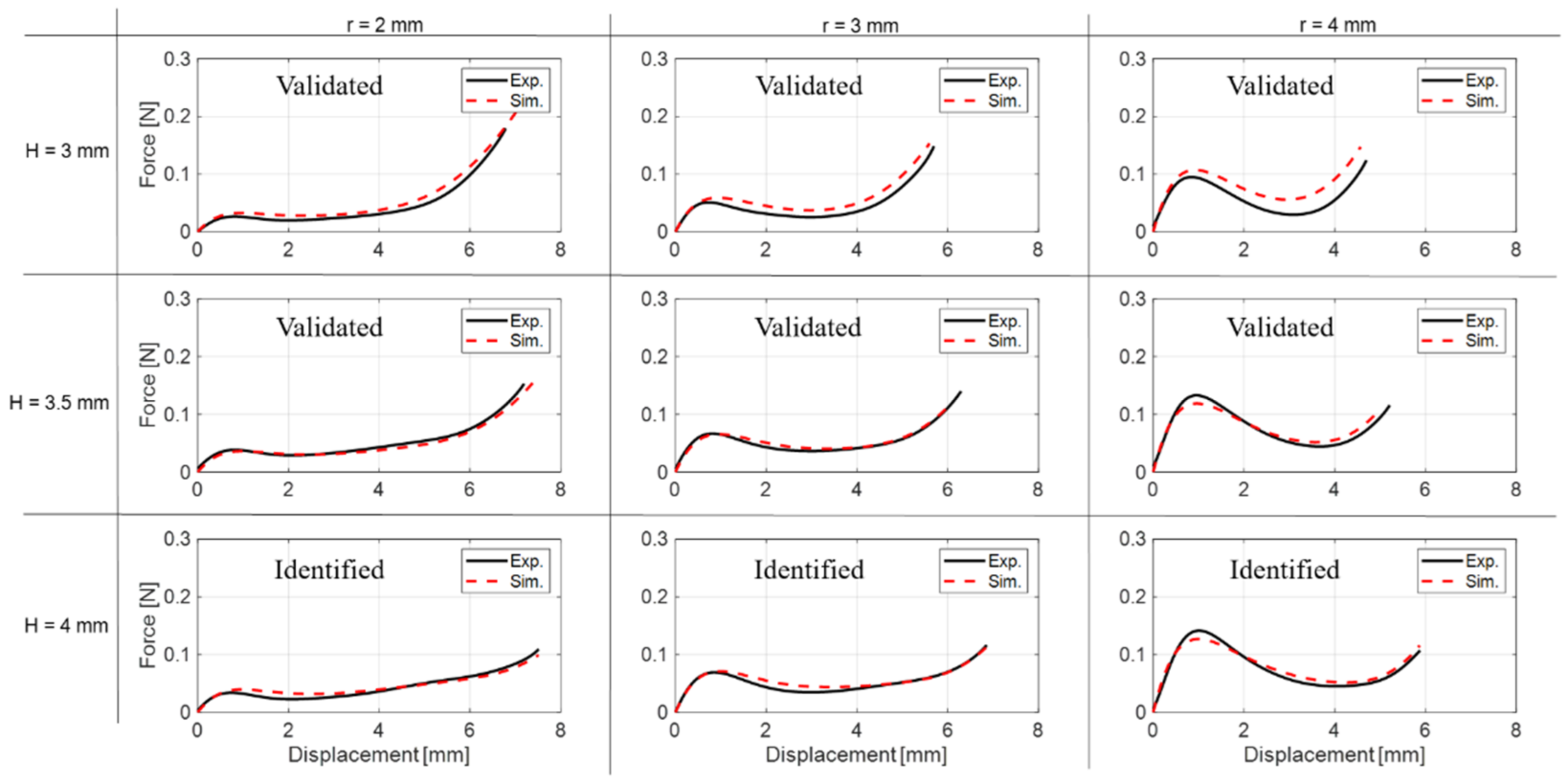
4.2. Dome Identification and Validation
5. Dome Design Optimization and Experimental Validation
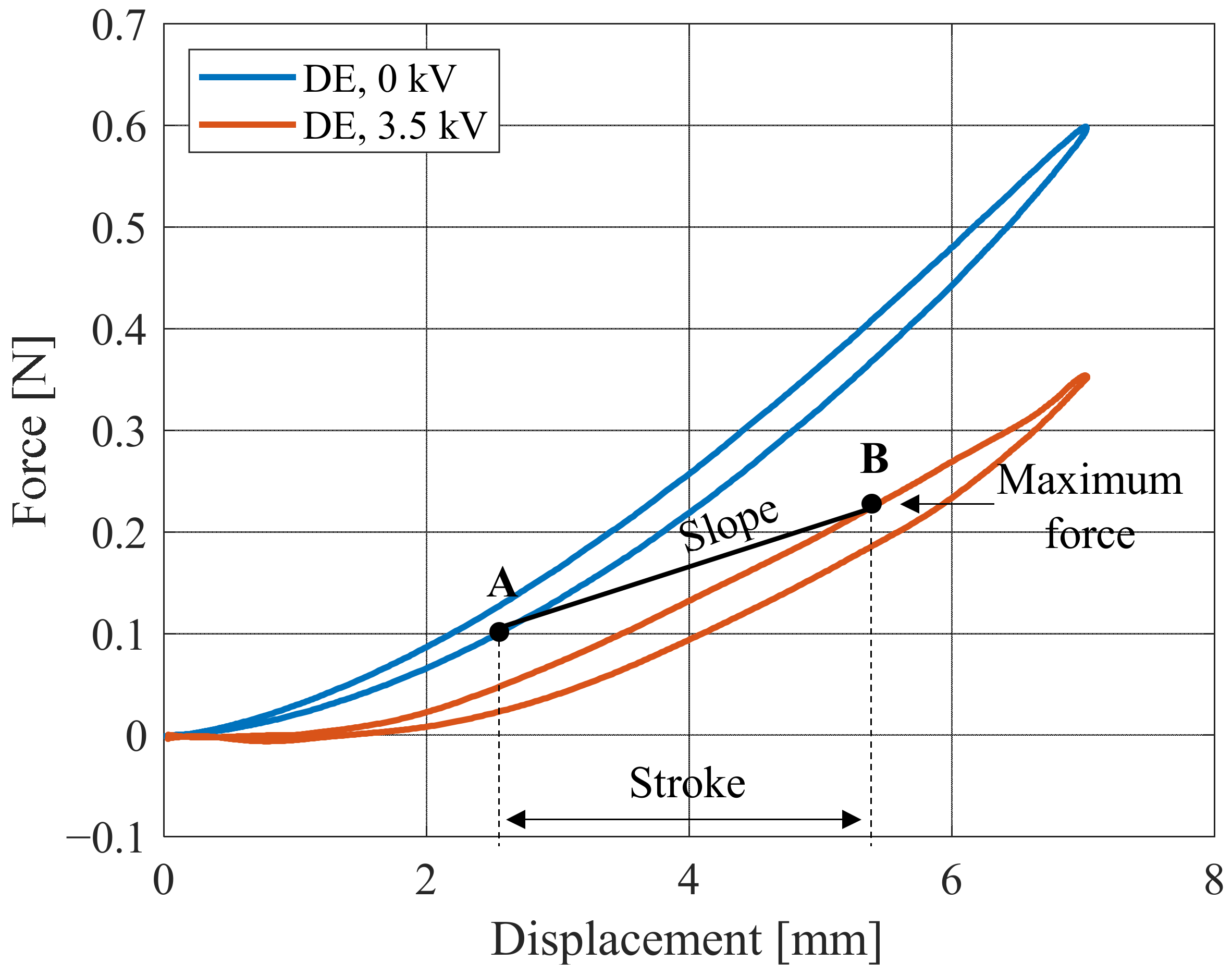
- Stroke, computed as the distance between states A and B along the x-axis, i.e., Bx − Ax;
- Slope, defined as the angular coefficient of the line connecting equilibrium points A and B, i.e., (By − Ay)/(Bx − Ax);
- Maximum force, defined as By;
- Horizontal shift, defined as a constant offset applied to both Ax and Bx.
5.1. Optimal Parameter Selection
- The calibrated FE model (described in the Section 4) is used to realize a dataset of simulated force-strain curves for different dome geometries. For the considered case study, the ranges of H and r are chosen in a physically meaningful way as follows: H ∈ [3, 5], r ∈ [2, 4];
- The entire design algorithm is implemented in MATLAB®, based on the obtained simulation dataset. For each simulated force-strain curve, the minimum and maximum force points defining the unstable branch of the dome characteristic are calculated and collected, in order to determine corresponding slope, stroke, and maximum force. Those minimum and maximum points are therefore considered as representatives of A and B, where the intersection with the DE characteristic curves occurs;
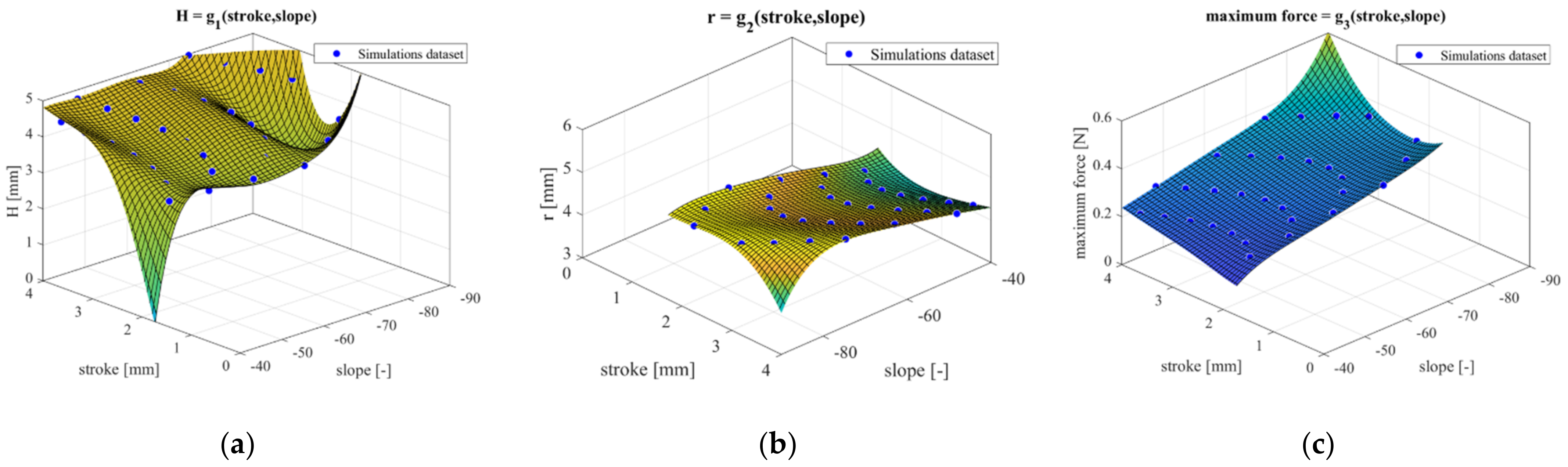
- Surface fitting functions are generated to express H, r, and maximum force as a function of the stroke and slope, based on the computations performed in the previous step. Resulting functions H = g1(stoke, slope), r = g2(stoke, slope), and maximum force = g3(stoke, slope) are shown in Figure 15. As it can be seen, such surfaces allow unique determination of H, r, and the maximum force, once the target stroke and slope are known.
5.2. Design Optimization Algorithm
- Select a target DE membrane, and characterize it experimentally under quasi-static conditions in order to obtain the characteristic curves for minimum and maximum applied voltage;
- Based on the obtained DE curves, estimate an ideal biasing behavior, and compute the coordinates of the corresponding intersection points A and B (cf. Figure 14);
- Based on the coordinates of A and B, determine the desired stroke, the slope, and the maximum force values, i.e., the features that must be satisfied by the dome force–displacement curve in order to ensure the desired performance;
- If the maximum force is not satisfactory, one can eventually start again rom point 2 and try different combinations of stroke and slope values, until an overall desirable behavior is obtained.
5.3. Design Procedure Validation
6. Discussion and Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Carpi, F.; de Rossi, D. Dielectric Elastomers as Electromechanical Transducers; Elsevier: Amsterdam, The Netherlands, 2008. [Google Scholar]
- Lau, G.K.; La, T.G.; Foong, E.S.W.; Shrestha, M. Stronger multilayer acrylic dielectric elastomer actuators with silicone gel coatings. Smart Mater. Struct. 2016, 25, 125006. [Google Scholar] [CrossRef]
- Rosset, S.; Ararom, O.A.; Schlatter, S.R.H. Shea Fabrication process of silicone-based dielectric elastomer actuators. J. Vis. Exp. 2016, 2016, 53423. [Google Scholar] [CrossRef] [Green Version]
- York, A.; Dunn, J.; Seelecke, S. Experimental characterization of the hysteretic and rate-dependent electromechanical behavior of dielectric electro-active polymer actuators. Smart Mater. Struct. 2010, 19, 094014. [Google Scholar] [CrossRef]
- Pelrine, R.E.; Kornbluh, R.D.; Joseph, J.P. Electrostriction of polymer dielectrics with compliant electrodes as a means of actuation. Sens. Actuators Phys. 1998, 64, 77–85. [Google Scholar] [CrossRef]
- Sahu, R.K.; Saini, A.; Ahmad, D.; Patra, K.; Szpunar, J. Estimation and validation of maxwell stress of planar dielectric elastomer actuators. J. Mech. Sci. Technol. 2016, 30, 429–436. [Google Scholar] [CrossRef]
- Hoffstadt, T.; Maas, J. Self-Sensing Control for Soft-Material Actuators Based on Dielectric Elastomers. Front. Robot. AI 2019, 6, 133. [Google Scholar] [CrossRef] [Green Version]
- Rizzello, G.; Naso, D.; York, A.; Seelecke, S. A Self-Sensing Approach for Dielectric Elastomer Actuators Based on Online Estimation Algorithms. IEEE/ASME Trans. Mechatron. 2017, 22, 728–738. [Google Scholar] [CrossRef]
- Kornbluh, R.D.; Pelrine, R.; Prahlad, H.; Wong-Foy, A.; McCoy, B.; Kim, S.; Eckerle, J.; Low, T. Dielectric elastomers: Stretching the capabilities of energy harvesting. MRS Bull. 2012, 37, 246–253. [Google Scholar] [CrossRef]
- Hill, M.; Rizzello, G.; Seelecke, S. Development and experimental characterization of a pneumatic valve actuated by a dielectric elastomer membrane. Smart Mater. Struct. 2017, 26, 085023. [Google Scholar] [CrossRef]
- Linnebach, P.; Rizzello, G.; Seelecke, S.; Seelecke, S. Design and validation of a dielectric elastomer membrane actuator driven pneumatic pump. Smart Mater. Struct. 2020, 29, 075021. [Google Scholar] [CrossRef]
- Ghazali, F.A.M.; Mah, C.K.; AbuZaiter, A.; Chee, P.S.; Ali, M.S.M. Soft dielectric elastomer actuator micropump. Sens. Actuators A Phys. 2017, 263, 276–284. [Google Scholar] [CrossRef]
- Hosoya, N.; Masuda, H.; Maeda, S. Balloon dielectric elastomer actuator speaker. Appl. Acoust. 2019, 148, 238–245. [Google Scholar] [CrossRef]
- Moretti, G.; Rizzello, G.; Fontana, M.; Seelecke, S. A multi-domain dynamical model for cone-shaped dielectric elastomer loudspeakers. In Proceedings of the Electroactive Polymer Actuators and Devices (EAPAD) XXIII Meeting, Online, 22–26 March 2021; Volume 53. [Google Scholar] [CrossRef]
- Qu, X.; Ma, X.; Shi, B.; Li, H.; Zheng, L.; Wang, C.; Liu, Z.; Fan, Y.; Chen, X.; Li, Z.; et al. Refreshable Braille Display System Based on Triboelectric Nanogenerator and Dielectric Elastomer. Adv. Funct. Mater. 2021, 31, 2006612. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhang, E.; Plamthottam, R.; Pei, Q. Dielectric Elastomer Artificial Muscle: Materials Innovations and Device Explorations. Acc. Chem. Res. 2019, 52, 316–325. [Google Scholar] [CrossRef] [PubMed]
- Sîrbu, D.; Moretti, G.; Bortolotti, G.; Bolignari, M.; Diré, S.; Fambri, L.; Vertechy, R.; Fontana, M. Electrostatic bellow muscle actuators and energy harvesters that stack up. Sci. Robot. 2021, 6, eaaz5796. [Google Scholar] [CrossRef] [PubMed]
- Carpi, F.; Frediani, G.; Gerboni, C.; Gemignani, J.; de Rossi, D. Enabling variable-stiffness hand rehabilitation orthoses with dielectric elastomer transducers. Med. Eng. Phys. 2014, 36, 205–211. [Google Scholar] [CrossRef] [PubMed]
- Almanza, M.; Clavica, F.; Chavanne, J.; Moser, D.; Obrist, D.; Carrel, T.; Civet, Y.; Perriard, Y. Feasibility of a Dielectric Elastomer Augmented Aorta. Adv. Sci. 2021, 8, 2001974. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Hussain, A.M.; Israr, A.; Vogt, D.M.; Duduta, D.M.; Clarke, D.R.; Wood, D.R. A Wearable Soft Haptic Communicator Based on Dielectric Elastomer Actuators. Soft Robot. 2020, 7, 451–461. [Google Scholar] [CrossRef]
- Gratz-Kelly, S.; Meyer, A.; Motzki, P.; Nalbach, S.; Rizzello, G.; Seelecke, S.S. Force measurement based on dielectric elastomers for an intelligent glove providing worker assessment in the digital production. In Proceedings of the SPIE Smart Structures + Nondestructive Evaluation, Online, 27 April–9 May 2020. [Google Scholar] [CrossRef]
- Gu, G.-Y.; Zhu, J.; Zhu, L.-M.; Zhu, X. A survey on dielectric elastomer actuators for soft robots. Bioinspir. Biomim. 2017, 12, 011003. [Google Scholar] [CrossRef]
- Wang, L.; Hayakawa, T.; Ishikawa, M. Dielectric-elastomer-based fabrication method for varifocal microlens array. Opt. Express 2017, 25, 31708. [Google Scholar] [CrossRef]
- Schmitt, S.; Haeufle, D. Mechanics and Thermodynamics of Biological Muscle—A Simple Model Approach; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Ghazali, F.A.M.; Jie, W.Y.; Fuaad, M.R.A.; Ali, M.S.M. Soft dielectric elastomer microactuator for robot locomotion. Bull. Electr. Eng. Inform. 2020, 9, 2286–2293. [Google Scholar] [CrossRef]
- Berlinger, F.; Duduta, M.; Gloria, H.; Clarke, D.; Nagpal, R.; Wood, R. A Modular Dielectric Elastomer Actuator to Drive Miniature Autonomous Underwater Vehicles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA) 2018, Brisbane, QLD, Australia, 21–25 May 2018; pp. 3429–3435. [Google Scholar] [CrossRef]
- Prechtl, J.; Kunze, J.; Nalbach, S.; Seelecke, S.S.; Rizzello, G. Soft robotic module actuated by silicone-based rolled dielectric elastomer actuators: Modeling and simulation. In Proceedings of the ACTUATOR; International Conference and Exhibition on New Actuator Systems and Applications 2021, Online, 17–19 February 2021. [Google Scholar] [CrossRef]
- Christianson, N.N.; Goldberg, D.D.; Deheyn, S.; Cai, M.; Tolley, T. Translucent soft robots driven by frameless fluid electrode dielectric elastomer actuators. Sci. Robot. 2018, 3, eaat1893. [Google Scholar] [CrossRef] [Green Version]
- Hodgins, M.; York, A.; Seelecke, S. Experimental comparison of bias elements for out-of-plane DEAP actuator system. Smart Mater. Struct. 2013, 22, 094016. [Google Scholar] [CrossRef]
- Hodgins, M.; York, A.; Seelecke, S. Modeling and experimental validation of a bi-stable out-of-plane DEAP actuator system. Smart Mater. Struct. 2011, 20, 094012. [Google Scholar] [CrossRef]
- Hau, S.; Bruch, D.; Rizzello, G.; Motzki, P.; Seelecke, S. Silicone based dielectric elastomer strip actuators coupled with nonlinear biasing elements for large actuation strains. Smart Mater. Struct. 2018, 27, 074003. [Google Scholar] [CrossRef]
- Follador, M.; Cianchetti, M.; Mazzolai, B. Design of a compact bistable mechanism based on dielectric elastomer actuators. Meccanica 2015, 50, 2741–2749. [Google Scholar] [CrossRef]
- Bruch, P.; Loew, S.; Hau, G.; Rizzello, S.S. Fast model-based design of large stroke dielectric elastomer membrane actuators biased with pre-stressed buckled beams. In Proceedings of the SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, CO, USA, 4–8 March 2018. [Google Scholar] [CrossRef]
- Loew, P.; Rizzello, G.; Seelecke, S. Permanent magnets as biasing mechanism for improving the performance of circular dielectric elastomer out-of-plane actuators. In Proceedings of the Electroactive Polymer Actuators Devices 2017, Portland, OR, USA, 25–29 March 2017; p. 10163. [Google Scholar] [CrossRef]
- Berselli, G.; Vertechy, R.; Vassura, G.; Parenti-Castelli, V. Optimal synthesis of conically shaped dielectric elastomer linear actuators: Design methodology and experimental validation. IEEE/ASME Trans. Mechatron. 2011, 16, 67–79. [Google Scholar] [CrossRef]
- Madhukar, D.; Perlitz, M.; Grigola, D.; Gai, K.J. Hsia Bistable characteristics of thick-walled axisymmetric domes. Int. J. Solids Struct. 2014, 51, 2590–2597. [Google Scholar] [CrossRef] [Green Version]
- Alturki, M.; Burgueño, R. Multistable cosine-curved dome system for elastic energy dissipation. J. Appl. Mech. Trans. ASME 2019, 86, 091002. [Google Scholar] [CrossRef]
- Neu, J.; Hubertus, J.; Croce, S.; Schultes, G.; Seelecke, S.; Rizzello, G. Fully Polymeric Domes as High-Stroke Biasing System for Soft Dielectric Elastomer Actuators. Front. Robot. AI 2021, 8, 695918. [Google Scholar] [CrossRef]
- Jia, K.; Wang, M.; Lu, T.; Wang, T. Linear control of multi-electrode dielectric elastomer actuator with a finite element model. Int. J. Mech. Sci. 2019, 159, 441–449. [Google Scholar] [CrossRef]
- Simone, F.; Linnebach, P.; Rizzello, G.; Seelecke, S. A finite element model of rigid body structures actuated by dielectric elastomer actuators. Smart Mater. Struct. 2018, 27, 065001. [Google Scholar] [CrossRef]
- Croce, S.; Neu, J.; Hubertus, J.; Rizzello, G.; Seelecke, S.; Schultes, G. Modeling and simulation of compliant biasing systems for dielectric elastomer membranes based on polymeric domes. In Proceedings of the ACTUATOR; International Conference and Exhibition on New Actuator Systems and Applications 2021, Online, 17–19 February 2021; pp. 3–6. [Google Scholar]
- Hubertus, J.; Croce, S.; Neu, J.; Rizzello, G.; Seelecke, S.; Schultes, G. Electromechanical characterization and laser structuring of Ni-based sputtered metallic compliant electrodes for DE applications. In Proceedings of the ACTUATOR; International Conference and Exhibition on New Actuator Systems and Applications 2021, Online, 17–19 February 2021; pp. 1–4. [Google Scholar]
- Fasolt, B.; Hodgins, M.; Rizzello, G.; Seelecke, S. Effect of screen printing parameters on sensor and actuator performance of dielectric elastomer (DE) membranes. Sens. Actuators A Phys. 2017, 265, 10–19. [Google Scholar] [CrossRef]
- Rosset, S.; Shea, H.R. Flexible and stretchable electrodes for dielectric elastomer actuators. Appl. Phys. A Mater. Sci. Process. 2013, 110, 281–307. [Google Scholar] [CrossRef] [Green Version]
- Schlatter, S.; Rosset, S.; Shea, H. Inkjet printing of carbon black electrodes for dielectric elastomer actuators. Electroact. Polym. Actuators Devices 2017, 1016311. [Google Scholar] [CrossRef] [Green Version]
- Wacker Chemie AG ELASTOSIL Film 2030. 2013, pp. 1–4. Available online: https://www.wacker.com/h/en-us/silicone-rubber/silicone-films/elastosil-film-2030/p/000038005 (accessed on 1 July 2021).
- Qiu, J.; Lang, J.H.; Slocum, A.H. A curved-beam bistable mechanism. J. Microelectromech. Syst. 2004, 13, 137–146. [Google Scholar] [CrossRef]
- COMSOL. Multiphysics Optimization Module. User’s Guide; COMSOL: Burlington, MA, USA, 2015. [Google Scholar]
- Martins, P.A.L.S.; Jorge, R.M.N.; Ferreira, A.J.M. A comparative study of several material models for prediction of hyperelastic properties: Application to silicone-rubber and soft tissues. Strain 2006, 42, 135–147. [Google Scholar] [CrossRef]
- Wacker Chemie AG WACKER SilGel 612 EH A/B. 2021, pp. 2–4. Available online: https://www.wacker.com/h/de-de/siliconkautschuk/silicongele/wacker-silgel-612-ab/p/000007546 (accessed on 2 December 2020).










| r = 2 mm | r = 3 mm | r = 4 mm | |
|---|---|---|---|
| H = 3 mm | Validated | Validated | Validated |
| H = 3.5 mm | Validated | Validated | Validated |
| H = 4 mm | Identified | Identified | Identified |
| c10 | c20 | c30 | κ | A1 | A2 | A3 |
|---|---|---|---|---|---|---|
| 0.11 MPa | 3.29 kPa | 5.73 kPa | 0.25 × 106 | 0.44 mm | 0.78 mm | 2.2 mm |
| PBS | PM | NBS + PBS | Silicone Dome |
|---|---|---|---|
| 0.1 [-] | 0.31 [-] | 0.4 [-] | 0.62 [-] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Croce, S.; Neu, J.; Hubertus, J.; Seelecke, S.; Schultes, G.; Rizzello, G. Model-Based Design Optimization of Soft Polymeric Domes Used as Nonlinear Biasing Systems for Dielectric Elastomer Actuators. Actuators 2021, 10, 209. https://doi.org/10.3390/act10090209
Croce S, Neu J, Hubertus J, Seelecke S, Schultes G, Rizzello G. Model-Based Design Optimization of Soft Polymeric Domes Used as Nonlinear Biasing Systems for Dielectric Elastomer Actuators. Actuators. 2021; 10(9):209. https://doi.org/10.3390/act10090209
Chicago/Turabian StyleCroce, Sipontina, Julian Neu, Jonas Hubertus, Stefan Seelecke, Guenter Schultes, and Gianluca Rizzello. 2021. "Model-Based Design Optimization of Soft Polymeric Domes Used as Nonlinear Biasing Systems for Dielectric Elastomer Actuators" Actuators 10, no. 9: 209. https://doi.org/10.3390/act10090209
APA StyleCroce, S., Neu, J., Hubertus, J., Seelecke, S., Schultes, G., & Rizzello, G. (2021). Model-Based Design Optimization of Soft Polymeric Domes Used as Nonlinear Biasing Systems for Dielectric Elastomer Actuators. Actuators, 10(9), 209. https://doi.org/10.3390/act10090209








