Prediction of the Seismic Response of Multi-Storey Multi-Bay Masonry Infilled Frames Using Artificial Neural Networks and a Bilinear Approximation

Abstract

In order to test the reliability of neural networks for the prediction of the behaviour of multi-storey multi-bay infilled frames, neural network processing was done on an experimental database of one-storey one-bay reinforced-concrete (RC) frames with masonry infills. From the obtained results it is demonstrated that they are acceptable for the prediction of base shear (BS) and inter-storey drift ratios (IDR) in characteristic points of the primary curve of infilled frame behaviour under seismic loads. The results obtained on one-storey one-bay infilled frames was extended to multi-bay infilled frames by evaluating and comparing numerical finite element modelling(FEM) modelling and neural network results with suggested approximating equations for the definition of bilinear capacity by defined BS and IDRs. The main goal of this paper is to offer an interpretation of the behaviour of multi-storey multi-bay masonry infilled frames according to a bilinear capacity curve, and to present the infilled frame’s response according to the contributions of frame and infill. The presented methodology is validated by experimental results from multi-storey multi-bay masonry infilled frames.

1. Introduction

The use of masonry infilled frames is very common for most types of building, accordingly state of the art of masonry infilled frame behaviour [1,2,3] in general is known but there is still no suggestion of regulations on how to model or use it properly in structural analysis.

The use of neural networks in the civil engineering field is already approved [4,5] however the application of neural networks for the prediction of infilled frame behaviour is rare. There are only a few studies [6,7,8] that have explored this topic. With a lack of available data from experiments of masonry infilled frames and with the uncertainty of numerical modelling, this research area needs to be further investigated. In order to connect most of the previously published data with new valuable conclusions, an experimental database of masonry infilled frames was collected. It was limited to only one-storey, one-bay infilled frames according to the availability and uniformity of the structural type.

Previous assumptions based on the monolithic behaviour of confined masonry [9] will be evaluated and validated for the possible monolithic behaviour of masonry infilled frames in this study. The methodology is based on the processing of the collected database with neural networks, accurate FEM modelling of infilled frames, a bilinear approximation of observed results and the capacity curve range definition with validation by multi-storey multi-bay infilled frame experimental results.

The experimental database of infilled frames is expressed with general geometric and material input and output data based on inter-storey drift ratios (IDR) and base shear (BS) in two stages of behaviour. First, damage indication introduced by the first major crack in the infill, which is presented by a decline of the initial stiffness of infilled frames. The second stage is related to the maximum strength of the infilled frame where the infill and RC frames still act together as monolithic elements. Inputs and outputs are then used for the prediction of behaviour by neural network processing. The number of hidden neurons is defined according to suggested equations by the amount of input and output data. The Levenberg-Marquardt learning algorithm is used for neural network processing to obtain output data.

Numerical FEM models of infilled frames are defined in order to connect predicted results from neural networks based on one-storey one-bay infilled frame with results from calibrated numerical multi-bay models.

A comparison and definition of the relation of IDRs and BSs between one- and multi-bay infilled frames is based on the contribution of infill in infilled frames in regard to bare frames. According to the results, new equations are defined, and their accuracy confirmed for both regular and irregular bay lengths.

The applicability of presented equations for capacity curve definition is verified on multi-storey multi-bay experimental models.

These relations present the connection between behaviour measures expressed by IDRs and BSs from one-storey one-bay to multi-storey multi-bay real buildings. They present the first proposed relations which are limited to RC frames with fully infilled frames and behaviour based on capacity.

2. Experimental Database of Infilled Frames, EDIF

The results of experimental tests conducted on one-story one-bay infilled reinforced-concrete frames with masonry infill are collected, systematized and processed in the Experimental Database of Infilled Frames called EDIF [7]. The tests that were observed had no shear connection, outside adhesion between the frame and infill, and no openings in the infill.

The database was obtained from a previous work by the authors [7] in which a large number of in-plane lateral tests reported in the literature were considered. Although many tests have been performed since then, the database is still representative of the typical lateral behaviour of masonry infilled frames.

The collected experimental database contains 113 published tests (Table 1) based on all available data including material and geometric properties from RC frame and masonry infill, type and size of load, failure mode, and capacity values obtained from the capacity curves. Although the initial goal was to create a database that has identical parameters for a large number of samples, some parameters were omitted as they were incomplete or unavailable (transverse reinforcement of columns and beams, material properties of mortar and masonry units, masonry shear strength, the maximum drift).

Table 1. Experimental database: authors and samples list.

Author	Year	Laboratory	Scale	Load	No of Samples
Combescure [10]	2000.	LNEC, Lisbon	1:1.5	C	1
Colangelo [11]	1999.	L’aquila, Italy	1:2	C	11
Cavaleri [12]	2004.	-	1:2	C	1
Lafuente [13]	1998.	U.C.V. Caracas, Venezuela	1:2	C	10
Kakaletsis [14]	2007.	-	1:3	C	2
Dukuze [15]	2000.	-	1:3	M	23
Žarnić [16,17]	1985.	Institute for Testing and Research in Materials and Structures (ZRMK), Ljubljana	1:2	C	1
	1992.		1:3		3
Al-Charr [18]	1998.	USACERL, Illinois	1:2	M	2
Angel [19]	1994.	University of Illinois, Champaign	1:1	C	7
Mehrabi [20]	1994.	University of Colorado, Boulder	1:2	C	8
				M	3
Crisafulli [21]	1997.	-	1:1.33	M	2
Fiorato [22]	1970.	University of Illinois, Urbana	1:8	C	3
Yorulmaz [23]	1968.	University of Illinois, Urbana	1:8	M	7
Benjamin [24]	1958.	Stanford University, California	1:2.94	M	5
			1:1.33		2
			1:1		1
			1:4		5
			1:2.38		7
Zovkić [25]	2012.	Faculty of Civil Engineering, Osijek, Croatia	1:2.5	C	9

According to the analysis of the most influenced parameters [7], the input data (Table 2) that were used for this study are:

Table 2. The range of input and output data in the EDIF Database.

Statistical Function	Input Data							Output Data
	a	b	g	rc	fy (MPa)	λh	V (kN)	IDRc	IDRc	BSc (kN)	BSc (kN)
min	0.33	0.60	1	0.01	203.37	1.78	0	0.01	0.03	55.9	76.95
max	2.28	8.00	6.1	0.04	607	8.56	2343.75	0.55	2.91	2278.4	2563.2
average	0.74	2.04	2.01	0.02	406.94	3.68	599.06	0.13	0.72	594.64	878.22

• a—height to length ratio,
• b—ratio of moments of inertia of beam to column,
• g—ratio of column width to the thickness of masonry infill,
• r_c—reinforcement ratio of column,
• f_y—yield strength of the reinforcing steel,
• λ_h—stiffness ratio (Equation (1)),
• V—axial load on columns.

The parameter λ_h is a measure of the relative stiffness between the frame and masonry infill; a greater λ_h corresponds to a more flexible frame. It can be determined using the following equation:

$${\mathsf{\lambda }}_{{}_{\mathrm{h}}}{}_{}=\mathrm{h}\sqrt[4]{\frac{{\mathrm{E}}_{\mathrm{i}}·\mathrm{t}·\sin \left(2\mathsf{\theta }\right)}{4{\mathrm{E}}_{\mathrm{c}}·\mathrm{I}·{\mathrm{h}}_{\mathrm{w}}}}$$

(1)

where:

• h—height of frame between the beam axis,
• h_w—height of masonry infill,
• E_c—modulus of elasticity of column,
• E_i—modulus of elasticity of masonry infill,
• I—moment of inertia of the column,
• θ—whose tangent is equal to the relation between height and length of infill.

For evaluation of the performance of infilled frame structures the measured resistance envelope curve from experiments is presented by bilinear curve using the equal energy rule. Therefore, two points are obtained on the idealized bilinear curve defined by IDR and BS in the first cracking point (IDR_c and BS_c) and maximum point (IDR_m and BS_m) of the capacity curve. The first cracking point is characterized by a sudden decline in stiffness and the maximum point is associated with the maximum lateral capacity of the system. Post-ultimate behaviour could not be determined from the available data since that region was not observed in most of the tests. In Table 2 are given output data including both IDR_c and BS_c, and IDR_m and BS_m from neural network processing and they are expressed as dimensionless because of the simplicity in neural network modelling.

3. Neural Network Modelling

Neural networks have demonstrated their capability in dealing with highly nonlinear relationships between the applied load and the measured displacement values [26]. In this paper, neural networks are designed to examine their capability in estimating the values of output data from EDIF database for the performance of infilled frames.

The employed neural network is a multi-layer neural network with a fully connected configuration. Totally, 113 data sets were obtained from experimental tests. The early stopping method is used for training neural networks. According to this method, data are divided into three groups of training, testing and validation. Herein, 70% of data was randomly allocated to training and the rest are equally divided between validation and testing data. The testing data set presents the unseen data set that was not included in the training of neural networks.

The Levenberg–Marquardt (LM) backpropagation algorithm was employed for training the neural networks by using the Matlab ANN toolbox. Moreover, the gradient descent weight/bias learning function was used with a hyperbolic tangent function as the activation function for neural network processing. To avoid the saturation of neural networks, the input and output data were scaled to [0, 1]. The training of data was stopped when the MSE in the validation set started to increase signifying that the ANN generalization stopped increasing. General neural network parameters of used NN model are presented in Table 3.

Table 3. The values of neural network parameters used in NN model.

Parameters	ANN
Number of input layer units	7
Number of hidden layers	1
Number of hidden layer units	3, 5, 8
Number of output layer units	1
Learning rate	0.01
Performance goal	0
Maximum number of epochs	10,000

It has been shown in many damage identification studies that the application of one hidden layer is adequate for accurate prediction [27,28]. The number of hidden layers was determined by the analysis of empirical criteria (Table 4) according to the suggestions from different authors [29,30] based on the number of input data N_i and number of outputs (in this study No = 1, neural networks processing was done always with only one output). As is visible in Figure 1, the most frequent values are three, five and eight neurons. Accordingly, further analysis was done with those three suggestions in order to obtain the best results with neural network processing.

Table 4. Empirical criteria for the number of hidden neurons N_h.

No	Method and Reference	Nh	Number of Nh
1.	Hecht-Nielsen (1987) [30]	≤2·Ni	14
2.	Hush (1989) [30]	3·Ni	21
3.	Popovics (1990) [31]	(Ni + No)/2	4
4.	Gallant (1993) [31]	2·Ni	11
5.	Wang (1994) [30]	2·Ni/3	5
6.	Masters (1994) [30]	(Ni + No)1/2	3
7.	Li (1995) [29]	((1 + 8 Ni)1/2 − 1)/2	3
8.	Tamura (1997) [29]	Ni + 1	8
9.	Lai (1997) [31]	Ni	7
10.	Nagendra (1998) [31]	Ni + No	8
11.	Zhang (2003) [29]	2Ni/n + 1	19
12.	Shibata (2009) [29]	(Ni·No)1/2	3
13.	Sheela (2013) [29]	(4 Ni2 + 3)/(Ni2 − 8)	5

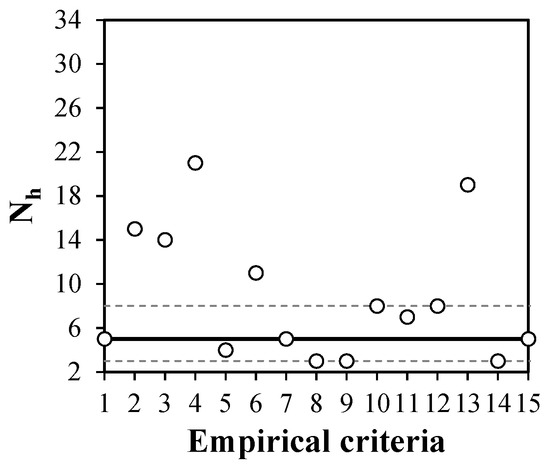
Figure 1. Range of number of hidden neurons according to Ni = 7, No = 1.

As it can be seen from Table 5, the best performance was achieved when the hidden layer had five neurons. For the evaluation of accuracy, performance measures used are: mean absolute error (MAE), root mean squared error (RMSE), mean absolute percentage error (MAPE) and coefficient of correlation (R). These performance measures are based on average values from four output data observed.

Table 5. Statistical performance of ANN models.

ANN Model
Neural Network Label	Learning Algorithm	No. of Hidden Nodes	MAE 1	RMSE 2	MAPE 3 (%)	R 4
LM_3	Levenberg-Marquardt	3	13.709	0.926	13.157	0.829
LM_5		5	10.0265	0.481	11.633	0.919
LM_8		8	12.189	0.558	17.844	0.886

¹ Mean absolute error (MAE), ² root mean squared error (RMSE), ³ mean absolute percentage error (MAPE) and ⁴ coefficient of correlation (R).

The obtained results from the processed neural networks are presented in Figure 2. All output data (BS and IDR) results for training, validation and the testing set are presented. As it can be seen from the correlation coefficients (R), all four output data are successfully predicted. It is evident that the trained neural networks demonstrate capability for the generalization of processed neural networks. It can be concluded that NNs can be used for accurate estimation of capacity curve of masonry infilled frames.

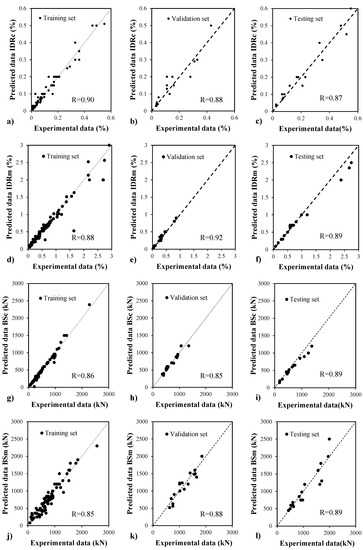
Figure 2. Results of neural network processing for 5 hidden neurons.(a) for IDRc training set; (b) for IDRc validation set; (c) for IDRc testing set; (d) for IDRm training set; (e) for IDRm validation set; (f) for IDRm testing set; (g) for BSc training set; (h) for BSc validation set; (i) for BSc testing set; (j) for BSm training set; (k) for BSm validation set; (l) for BSm testing set.

4. Definition of Models for Numerical Nonlinear FEM Analysis and Neural Network Processing

The accepted numerical FEM model for masonry infill is implemented in Seismostruct 2018 [32] and calibrated according to multi-storey multi-bay infilled frame experimental results [33]. Infilled framed models (Figure 3) applied for analysis with neural networks and nonlinear numerical analysis are based on different length to height ratios of frames with a medium type of masonry infill (according to value of compressive strength). The accuracy and relation between numerical models and prediction was carried out for equivalent and various frames with two and three bays.

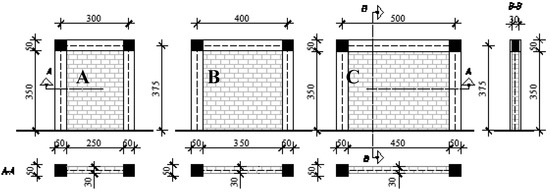
Figure 3. Infilled frame models.

Reinforced concrete frames with height of 375 m has different bay length (A frame–3 m, B frame –4 m, C frame–5 m). Cross-section dimensions are kept constant for all three bay lengths, columns with 50 × 50 cm, and beams with 30 × 50 cm. The RC frames are designed according to seismic regulations [34]. Therefore, material properties for concrete members are based on concrete class C30/37 with reinforcement B500, with reinforcement ratio of 2% of the cross sections. Pushover analysis was carried out in order to evaluate the capacity of infilled frames.

The masonry infill type is defined according to compressive strength values. In order to define the basic material properties of the masonry infill (compressive strength of the masonry and the stress-strain relation in compression), verified recommendations are used for determining the compressive strength of masonry infill based on the masonry and mortar strength according to Hendry and Malek [35] presented in Equation (2):

$${\mathrm{f}}_{\mathrm{k}}=0.334{\mathrm{f}}_{\mathrm{b}}{}^{0.778}{\mathrm{f}}_{\mathrm{m}}{}^{0.234}$$

(2)

For the analysis, as is stated earlier and according to Table 6, the medium type of masonry infill was used, which is the most commonly used masonry unit—a clay block with vertical hollow perforations, with dimensions of 29 × 19 × 19 cm and 10 MPa masonry unit compressive strength.

Table 6. Definition of masonry infill type based on the compressive strength.

Masonry Infill Type	Compressive Strength
	Masonry Unit fb (MPa)	Mortar fm (MPa)	Masonry Infill fk (MPa)–Equation (2)
Weak—ytong block	3	10	1.35
Medium—hollow clay block	10	5	2.92
Strong—solid brick	20	5	5.01

A definition of the behaviour in compression is determined according to the recommendations of Kaushik [36] as is presented in Figure 4.

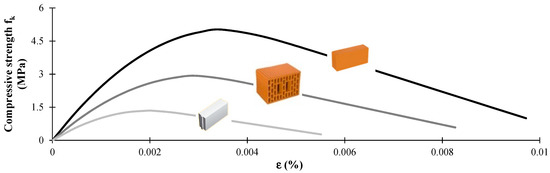
Figure 4. Stress-strain relation for three masonry infill types according to Kaushik [36].

For nonlinear FEM analysis, Mander’s model [37] for concrete and Menegotto-Pinto’s model [38] for reinforcement are used to define the force-based plastic hinge (FBPH) fiber elements, while masonry infill model is based on inelastic infill panel element (Table 7) defined by strut/shear curve properties [32]. The masonry infill wall was modelled as the infill panel model with calibrated parameters of hysteretic behavior. The initial diagonal width w₁ was determined according to proposal of Stafford et al. [39]. It is based on the parameter λ_h which presents a measure of the relative stiffness of the frame to infill. The reduced area A_ms2 of the compressed diagonal depends on the stiffness coefficient λ_h, according to the recommendations of Decanini [40]. Corresponding deformations were determined according to the limit states: the start of reduction of the initial area A_ms1 corresponds to the deformation at the end of linear elastic behaviour (ε_m/3) while the A_ms2 secondary area is reached at 70% of the maximum compressive stress and the associated strain corresponds to the 1.5 × ε_m (Figure 5).

Table 7. Material and geometric properties for nonlinear FEM model of masonry infill.

Masonry Infill	fk (MPa)	Ei (MPa)	εm	εu	ε1	ε2	λh	fmθ∗ (MPa)	Ams1 (m2)	Ams2 (%Ams1)
A	2.92	1610	0.0030	0.0083	0.001	0.0045	2.47	0.273	0.494	76.37
B							2.51		0.563	76.17
C							2.48		0.637	76.28

f_k—compressive strength of masonry; E_i—modulus of elasticity of masonry; ε_m—strain at maximum axial stress; ε_u—ultimate strain; ε₁—strut area reduction strain; ε₂—residual strut area strain; λ_h—relative panel-to-frame stiffness parameter; f_mθ∗—compressive strength; A_ms1—initial area of strut; A_ms2—final area of equivalent diagonal strut.

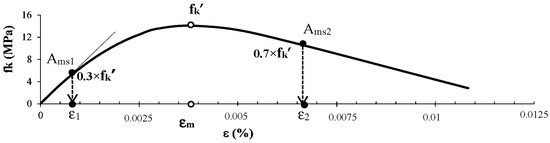
Figure 5. Stress-strain relation for masonry axial compression and the definition of limit states corresponded to the variability of areas and related axial strain.

Unfortunately, the damage pattern type cannot be evaluated with this numerical model. This model can only give the information of RC members damage, but if we have only masonry infill damage it cannot be directly defined. Therefore, the structural performance levels for masonry infilled frames defined by values of IDRs [41] can be used for evaluation of possible damage in a composite system but not separately for every component individually.

4.1. Results of Analysis and Prediction of Neural Networks

The results of the predicted characteristic points of the capacity curve and the numerical calculation are verified on the basis of a relative error between values obtained from neural networks and numerical modelling values.

In Figure 6 the force-displacement curves for reinforced concrete frames without infills (bare frame—BF) and with infills are shown in order to detect the contribution of bearing capacity and the stiffness of infill and frame separately. An infilled frame has eight-fold greater stiffness and 1.5-fold larger ultimate capacity than the bare frame. Verification of the use of neural networks for the one-storey, one-bay frame is shown in Table 8, where relative errors are shown for each of the models. By comparing the results of neural networks and modelling, it can be concluded that yield strengths are very close, while, secondary stiffness is somewhat smaller (25%), unlike initial stiffness. The average relative error values are satisfactorily small (<10%), so it can be concluded that numerically obtained results, and prognosis results using neural networks are equivalent.

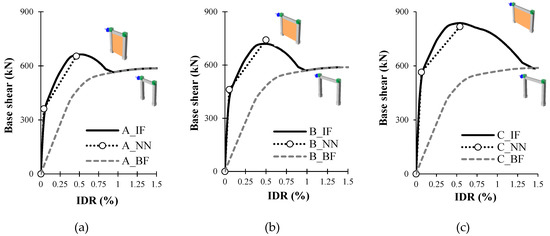
Figure 6. Capacity curves of RC infilled frames A (a), B (b) and C (c) with and without masonry infill in comparison with NN results.

Table 8. Evaluation of compatibility of neural networks processing for infilled frames A, B and C.

Capacity Curve Data	A_IF	B_IF	C_IF	A_NN	B_NN	C_NN
IDRc (%)	0.04	0.054	0.067	0.038{5}	0.053{2}	0.066{1}
IDRm (%)	0.49	0.50	0.51	0.46{8}	0.5{2}	0.54{6}
BSc (kN)	357.92	447.04	545.96	363{2}	462{3}	565{3}
BSm (kN)	663.83	719.69	815.47	658{1}	742{3}	818{1}

¹—values in braces { } presents relative error from data obtained by neural networks in regard to results from numerical analysis.

From the comparison of the bare frame with an infilled frame by observing the two areas (yield and ultimate) can be concluded that:

• in the cracking area the infill wall retains 80% load capacity, while the RC frame assumes 20% load capacity (10% per column);
• in the area of the maximum strength, the infill takes on average 40%, while the frame or each of the columns assume 30% of the load capacity.

According to these values it can be concluded that by adding an additional frame to the initial one, the bearing capacity in the yield area will be increased by 90%, while in the range of the maximum load for each new additional frame bearing capacity will be increased by 70%.

4.2. Application of Neural Networks on Multi-bay Frames with Same Bay Length

Previous considerations and conclusions will be extended to multi-bay frames with the same bay length for two or three bays (Figure 7). Multi-bay frames cannot be directly applied and processed by neural networks in this paper, however they are expressed and included in approximation formulas with factors depending on the number of bays.

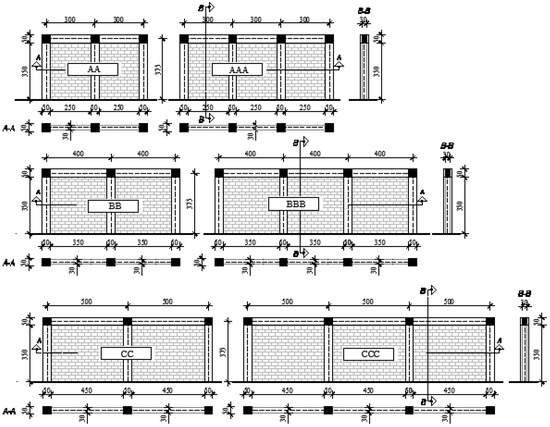
Figure 7. Infilled frame models—multi-bay models with same bay length.

Bilinear approximation (BA) equations:

$$\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{c},\mathrm{i}}=\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{c}}(\mathrm{N}\mathrm{N})·\left(1+0.3·\left(\mathrm{i}-1\right)\right)$$

(3)

$$\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{m},\mathrm{i}}=\mathrm{I}\mathrm{D}\mathrm{R}\mathrm{m}(\mathrm{N}\mathrm{N})$$

(4)

$$\mathrm{B}{\mathrm{S}}_{\mathrm{c},\mathrm{i}}=\mathrm{B}{\mathrm{S}}_{\mathrm{c}}(\mathrm{N}\mathrm{N})·\left(1+0.9·\left(\mathrm{i}-1\right)\right)$$

(5)

$$\mathrm{B}{\mathrm{S}}_{\mathrm{m},\mathrm{i}}=\mathrm{B}{\mathrm{S}}_{\mathrm{m}}(\mathrm{N}\mathrm{N})·\left(1+0.7·\left(\mathrm{i}-1\right)\right)$$

(6)

where:

• IDR_c,i—inter-storey drift Ratio at cracking point of multi-bay infilled frame,
• IDR_m,i—inter-storey drift Ratio at maximum capacity point of multi-bay infilled frame,
• BS_c,I—base shear at first cracking point of multi-bay infilled frame,
• BS_m,i—base shear at maximum capacity point of multi-bay infilled frame,
• IDRc_y (NN)—inter-storey drift ratio at cracking point of one story one bay infilled frame obtained by NN
• IDR_m (NN)—inter-storey Drift Ratio at maximum point of one story one bay infilled frame obtained by NN
• BS_c (NN)—base shear at cracking point of one story one bay infilled frame obtained by NN
• BS_m (NN)—base shear at maximum point of one story one bay infilled frame obtained by NN
• i = 2 ..., n—number of bays of multi-bay frame.

Multi-bay frames with equal bays (Figure 6) are obtained by adding one (AA, BB, CC) or two (AAA, BBB, CCC) additional equal ranges to the initial frame (A, B, C). For each of the models, results from nonlinear analysis are obtained by pushover method in Seismostruct 2018 [32] and are shown in the following pictures and tables.

Bilinear approximation equations are then used for the calculation of the same responses by the use of neural network results (Table 8) from one-story one-bay infilled frames.

An acceptability of the Equations (3)–(6) is shown in Figure 8 and Table 9, for multi-bay frames with two and three bays. The curves show the results of the nonlinear analysis for three observed frames, while the bilinear curves show solutions observed by a bilinear approximate equations (BA).

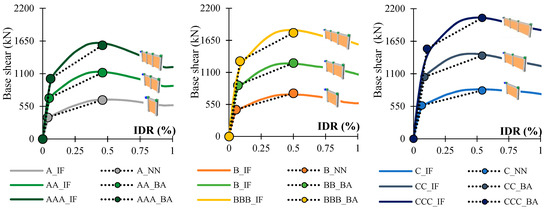
Figure 8. Capacity curves for multi-bay frames with same bay length.

Table 9. Evaluation of accuracy of proposed bilinear approximation equations for equal bay length.

Frame Type	Frame Combination	IDRc (%)	IDRm (%)	BSc (kN)	BSm (kN)
A	AA_IF	0.053	0.47	656.83	1129.91
	AAA_IF	0.067	0.47	996.97	1617.87
	AA_BA (3)-(6)	0.049{5}	0.46{1}	689.7{9}	1118.6 {2}
	AAA_BA (3)-(6)	0.061{10}	0.46{2}	1016.4 {2}	1579.2 {2}
B	BB_IF	0.08	0.48	846.43	1253.28
	BBB_IF	0.093	0.47	1219.77	1827.99
	BB_BA (3)-(6)	0.069{14}	0.5{4}	877.8{4}	1261.4{1}
	BBB_BA (3)-(6)	0.085{9}	0.5{6}	1293.6{6}	1780.8{3}
C	CC	0.08	0.55	1005.25	1386.18
	CCC	0.107	0.55	1405.98	2046.39
	CC_BA (3)-(6)	0.086{7}	0.54{2}	1045.25{4}	1406.96{2}
	CCC_BA (3)-(6)	0.1056{1}	0.54{2}	1525.5{9}	2045{1}

¹—values in brackets { } represent relative error from data obtained by BA with respect to results from numerical analysis.

Relative errors for the multi-bay frames with equal bays are small. The average value of error for two and three bays for A frame is 4%, for B frame is 6% and for C frame is 4%. According to the observed results it can be concluded that the capacity curve for multi-bay frame with same bay length can be accurately calculated (94%) by the proposed bilinear approximation equations.

4.3. Application of Neural Networks on Multi-Bay Frames with Different Bay Length

The same idea from the previous section was applied to multi-bay frames with different bay lengths (Figure 9). The following equations are suggested:

$$\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{c}\mathrm{r},\mathrm{i}}=\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{c}1}(\mathrm{N}\mathrm{N})+0.3{\displaystyle \sum _{\mathrm{j}=2}^{\mathrm{n}}\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{c}\mathrm{j}}(\mathrm{N}\mathrm{N})}$$

(7)

$$\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{m}\mathrm{r},\mathrm{i}}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{n}}\mathrm{I}\mathrm{D}{\mathrm{R}}_{\mathrm{m}\mathrm{j}}(\mathrm{N}\mathrm{N})}$$

(8)

$$\mathrm{B}{\mathrm{S}}_{\mathrm{c}\mathrm{r},\mathrm{i}}=\mathrm{B}{\mathrm{S}}_{\mathrm{c}1}(\mathrm{N}\mathrm{N})+0.9{\displaystyle \sum _{\mathrm{j}=2}^{\mathrm{n}}\mathrm{B}{\mathrm{S}}_{\mathrm{c}\mathrm{j}}(\mathrm{N}\mathrm{N})}$$

(9)

$$\mathrm{B}{\mathrm{S}}_{\mathrm{m}\mathrm{r},\mathrm{i}}=\mathrm{B}{\mathrm{S}}_{\mathrm{m}1}(\mathrm{N}\mathrm{N})+0.7{\displaystyle \sum _{\mathrm{j}=2}^{\mathrm{n}}\mathrm{B}{\mathrm{S}}_{\mathrm{m}\mathrm{j}}(\mathrm{N}\mathrm{N})}$$

(10)

where:

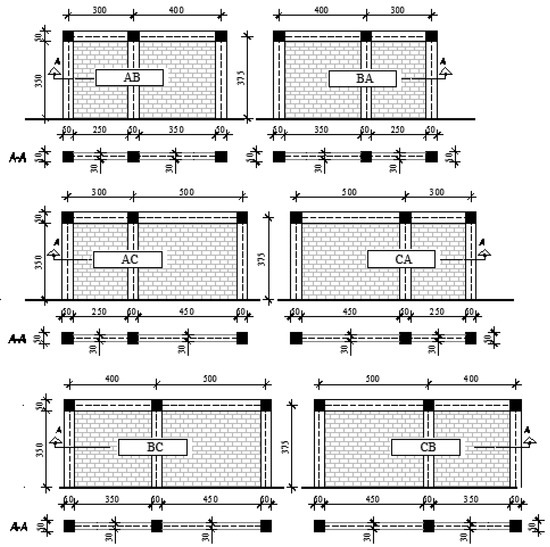
Figure 9. Infilled frame models—multi-bay models with different bay length.

• IDR_cr,i—inter-storey drift ratio at cracking point of multi-bay infilled frame with different bay length,
• IDR_mr,i—inter-storey drift ratio at maximum capacity point of multi-bay infilled frame with different bay length,
• BS_cr,I—base shear at first cracking point of multi-bay infilled frame with different bay length,
• BS_mr,i—base shear at maximum point of multi-bay infilled frame with different bay length,
• IDR_cj (NN)—inter-storey drift ratio at cracking point of one story one bay infilled frame obtained by NN
• IDR_mj (NN)—inter-storey drift ratio at maximum capacity point of one story one bay infilled frame obtained by NN
• BS_cj (NN)—base shear at cracking point of one story one bay infilled frame obtained by NN
• BS_mj (NN)—base shear at maximum point of one story one bay infilled frame obtained by NN
• i = 2, ..., n—number of bays of multi-bay frame
• j = 1, ..., n—ordinal number of bay in multi-bay frame

In Figure 10, the results for two-bay frames with combinations of A, B and C frames of different bays are shown. The curve shows the results from nonlinear FEM modelling of the two bay frames, while the bilinear curves show the initial results obtained by neural networks (ANN, BNN), and bilinear curves of approximating Equations (7)–(10), which are compared with the results of the nonlinear analysis (Table 10).

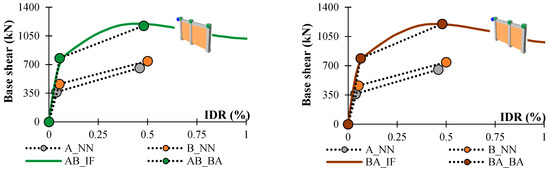
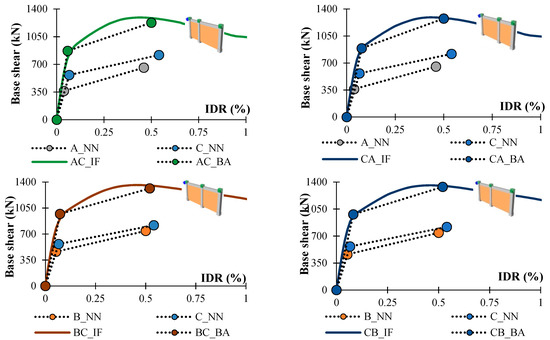
Figure 10. Capacity curves for multi-bay frames with different bay length.

Table 10. Evaluation of accuracy of proposed bilinear approximation equations for different bay length for frames with two bays.

Frame Type	Frame Combination	IDRc (%)	IDRm (%)	BSc (kN)	BSm (kN)
A/B	AB_IF	0.06	0.44	764.33	1198.25
	BA_IF	0.06	0.44	765.62	1198.61
	AB_BA (7)-(10)	0.054{10}	0.48{9}	777.8{2}	1173.4{2}
	BA_BA (7)-(10)	0.064{7}	0.48{9}	787.8{3}	1199.8{0}
A/C	AC_IF	0.067	0.48	829.41	1292.75
	CA_IF	0.08	0.48	898.88	1291.81
	AC_BA (7)-(10)	0.058{13}	0.5{4}	870.5{5}	1226.6{5}
	CA_BA (7)-(10)	0.077{3}	0.5{4}	890.8{1}	1275.8{1}
B/C	BC_IF	0.08	0.49	934.02	1359.93
	CB_IF	0.08	0.49	986.58	1357.18
	BC_BA (7)-(10)	0.073{9}	0.52{6}	970.5{4}	1314.6{3}
	CB_BA (7)-(10)	0.082{2}	0.52{6}	980.8{1}	1337.4{1}

¹—values in braces { } presents relative error from data obtained by BA in regard to results from numerical analysis.

For the AB and BA models, the greatest deviations are for IDRs with an average relative error of 9%. The average relative error for all four observed output values for the combination of AB and BA frames is 6% and 5%, respectively. As the results for frames with the same combination, but different frame distributions are not the same, it has been proved that the first frame is the one that contributes most to the behaviour of the multi-bay frame, with 100% value for both the yield area and the maximum capacity range, as it is assumed in bilinear approximation equations.

For the combination of frames A and C, the MRE is 7%, while for combination of the AC and CA frames MRE is 2%.

After the results showed the applicability of the approximate Equations (7)–(10) for the different bay length ranges in two-bay frames, further analysis was performed for frames having a different length in three bay frames (Figure 11).

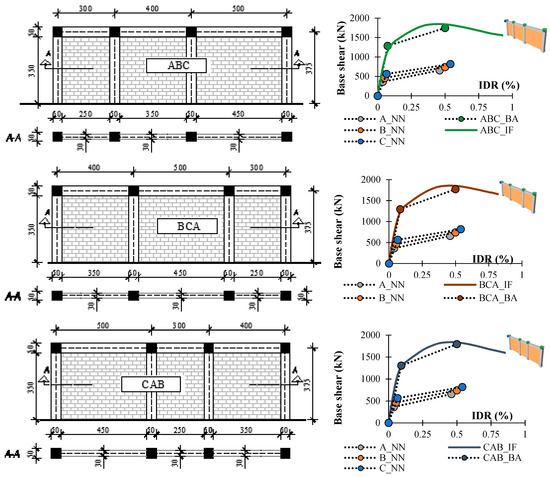
Figure 11. Multi-bay frame models and capacity curves for multi-bay frames with different bay length.

With the use of Equations (7)–(10), the prediction of the behaviour of multi-bay frames with different bay lengths resulted in very small deviations (maximum error was 11%) in relation to values obtained by nonlinear modelling (Table 11). Accordingly, the acceptability of approximation and applicability for multi-bay frames has been demonstrated, regardless of the type (equal or different length of bay), number of bays and their distribution.

Table 11. Evaluation of accuracy of proposed bilinear approximation equations for different bay length for frames with three bays.

Frame Type	Frame Combination	IDRc (%)	IDRm (%)	BSc (kN)	BSm (kN)
A/B/C	ABC_IF	0.08	0.45	1197.65	1848.31
	ABC_BA (7)-(10)	0.073{8}	0.5{11}	1286.3{7}	1746{6}
	BCA_IF	0.085	0.47	1275.44	1857.63
	BCA_BA (7)-(10)	0.084{1}	0.5{6}	1296.3{2}	1772.4{5}
	CAB_IF	0.09	0.48	1285.47	1840.39
	CAB_BA (7)-(10)	0.093{4}	0.5{4}	1306.6{2}	1795.2{3}

¹—values in braces { } presents relative error from data obtained by BA in regard to results from numerical analysis.

The primary curves of reinforced-concrete multi-bay frames with masonry infills are compared with the results of neural networks for one-bay frames and using the approximation Equations (3)–(10). From the comparison it is concluded that the behaviour of multi-bay frames can be predicted with an accuracy of at least 92%. The results of neural networks have shown that the prediction of behaviour with respect to the BS of reinforced frames with masonry infills is very realistically with a small average error of 5% for cracking capacity, and 4% for maximum capacity.

Equation suggestions used to determine the primary curves of the multi-bay frames include the rules that the first frame fully participates in the multi-bay frame capacity. The following frames in the sequence involve 90% for the cracking area, or 70% for the maximum range. For the determination of IDRs at the ultimate capacity, the mean value of all individual frames in a series of multi-bay frames is relevant.

5. Validation of Proposed Equations on Mult-Storey Multi-Bay Infilled Frames

In order to determine the applicability of the neural networks trained on the experimental database of masonry infilled frames, the evaluation of the expressions for multi-bay frames of different and the same lengths on multi-bay structures was performed. As neural networks emerged as a result of single-storey and single-bay frames, approximation models were developed. It is based on the assumption that masses and loads from all floors can be transferred to the columns of the ground floor. In multi-bay models, each of the bays is taken as a one-bay frame (Figure 12, Figure 13 and Figure 14). Definition of the vertical forces that act on columns for input data in neural networks processing are determined according to the boundary conditions and the assumption that both forces are mutually equivalent.

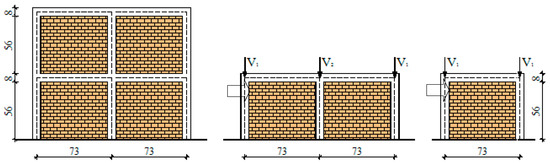
Figure 12. Approximation model for multi-storey multi-bay infilled frame IFS.

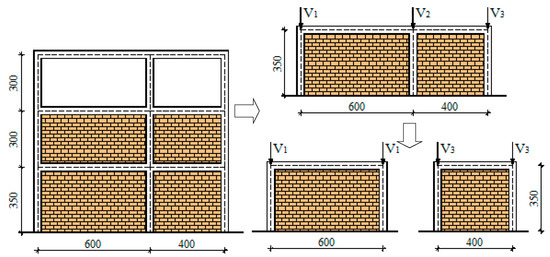
Figure 13. Approximation model for multi-storey multi-bay infilled frame Patras.

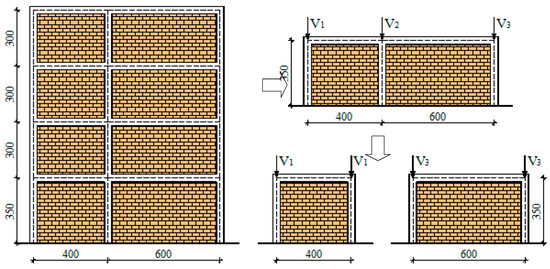
Figure 14. Approximation model for multi-storey multi-bay infilled frame EC8.

Validation was performed on experimental samples: two-storey IFS building [42], three-storey Patras building [43] and four-storey building designed according to EC2 and EC8 [44]. Since all of the frames that were used for validation are multi-storey structure, the gravitational load from the floors is modelled as a nodal force, acting on the columns of the ground floor. It represents its own weight of columns, beams, slabs and masonry, together with load of 2 kN/m². The Patras multi-storey muti-bay frame (Figure 13) consists of the three floors, of which only the ground floor and the first floor are filled with masonry infills (uneven distribution of masonry infill by height of the structure) with two bays. Since the bays have different bay length, for the application of approximation formulas it was necessary to use expressions (7–10). Although the second floor was a bare frame example, the same procedure was applied as in the IFS frame; floor masses are represented by a vertical load on the one-bay columns. The EC8 four-storey two-bay frame (Figure 14) was simplified by the use of approximate terms on a two one-storey one-bay frames of 4 and 6 m.

Neural network processing is done on previously trained neural networks with new input data from Table 12, calculated according to the loads from Table 13.

Table 12. Input data for neural network processing.

Buildings		a	b	g	rc	fy	λh	N
IFS		0.87	1	2.66	1.76	240	2.65	21.2
Patras	4m	0.875	0.76	3.57	2.00	555.0	2.22	194.9
	6m	0.583	0.76	3.57	2.00	555.0	2.12	146.7
EC8	4m	0.875	0.76	3.57	2.35	553.5	2.47	233.3
	6m	0.583	0.76	3.57	2.35	553.5	2.38	309.5

Table 13. Load on columns on one-story one bay approximated frames.

Buildings	V1 (kN)	V2 (kN)	V3 (kN)
IFS	21.2	21.2	-
Patras	194.85	292.49	146.66
EC8	233.26	464.02	309.52

An approximation of IFS infilled frame consisted of a one-storey one-bay frame with the corresponding load, the vertical concentric forces representing the mass of the floor. As for the symmetrical system, equations for the equal length bays (3)–(6) were applied for the approximation. By comparing the results obtained from numerical modelling on the IFS frame and the application of approximate expressions of capacity curve, it can be concluded that the obtained values have sufficient acceptability that approves their application for multi-storey and multi-bay frames. The largest relative error in the IFS frame was 8%, while the mean relative error was 4.5% (Table 14, Figure 14).

Table 14. Evaluation of accuracy of proposed bilinear approximation equations for multi-storey multi-bay frames.

Buildings	Approximation	IDRc (%)	IDRm (%)	BSc (kN)	BSm (kN)
IFS	IFS_NN	0.08	0.65	7.8	10.3
	IFS_IF	0.104	0.65	14.82	17.51
	IFS_BA (7)-(10)	0.104{0}	0.67{3}	13.7{8}	17.13{2}
Patras	Patras 6m_NN	0.09	0.7	290	420
	Patras 4m_NN	0.05	0.54	250	380
	Patras_IF	0.11	0.69	446.24	711.25
	Patras_BA (7)-(10)	0.105{5}	0.62{9}	515{14}	686{4}
EC8	EC8 4m_NN	0.05	0.54	250	380
	EC8 6m_NN	0.07	0.73	290	450
	EC8_IF	0.071	0.635	511	695
	EC8_BA (7)-(10)	0.08{11}	0.615{3}	451.15{13}	701.65{1}

¹—values in braces { } presents relative error from data obtained by BA in regard to results from numerical analysis.

The same principle was used for Patras and EC8 buildings. Obtained results are presented in Figure 15 and Table 14. It can be concluded that proposed bilinear Equations (7)–(10) can be used for both uniformly and non-uniformly distributed infilled frames. For the Patras frame, MRE was 8% and for EC8 frame error was 7%.

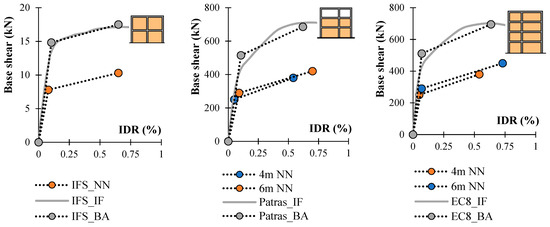
Figure 15. Multi-storey multi-bay frame models capacity curves.

6. Conclusions

The main idea of study was definition of the contribution of infill in masonry infilled frame response. According to the conducted experimental database and successfully processed neural networks results, further application in term of behaviour prediction was indispensable. The limit of direct use of neural network results was based on the fact that structural system which is used was a one-storey one-bay infilled frame. Therefore, the equations for definition of capacity curves for real buildings of infilled frame were proposed.

The attempt to simplify multi-bay infilled frames and the connection with obtained neural network results are presented by bilinear approximation equations for IDRs and BS for two behaviour ranges: cracking and maximum load. Equations were suggested for equal and different bay length.

In order to validate proposed method, multi-storey multi-bay frames with experimental results are used for evaluation. As it is presented the method was fully approved with the prediction of the characteristic values of the primary curve, displacement and forces, regardless of the number of floors, the difference of the bays and the unequal distribution of the masonry infills by the height of the structure with a mean accuracy of 92%.

It can be concluded and confirmed that approximate bilinear equations can be reliably applied for masonry infilled frame behaviour prediction. The contribution of masonry infill can be quantitatively summed for the prediction of the infilled frames capacity curve.

Direct contribution is based on the conclusion that the known response of a one-storey one-bay infilled frame can be used for the prediction of a multi-storey multi-bay infilled frame response. The initial response of one-storey one-bay frame can be defined by neural networks or by nonlinear FEM model, as it is approved that used FEM model is accurate and correct. According to this method the monolithic behaviour of masonry infilled frames is approved.

A performance based assessment can be implemented by using the proposed procedure in correspondence with the known performance levels for masonry infills based on IDR values.